Franc J-P. Fundamentals of Cavitation

Подождите немного. Документ загружается.

6 - SUPERCAVITATION 103

h=70m

0.4

0.1

0.080.06 0.2

h [mm]

70 0.36 1.20

140 0.31 1.41

210 0.36 1.51

2γ

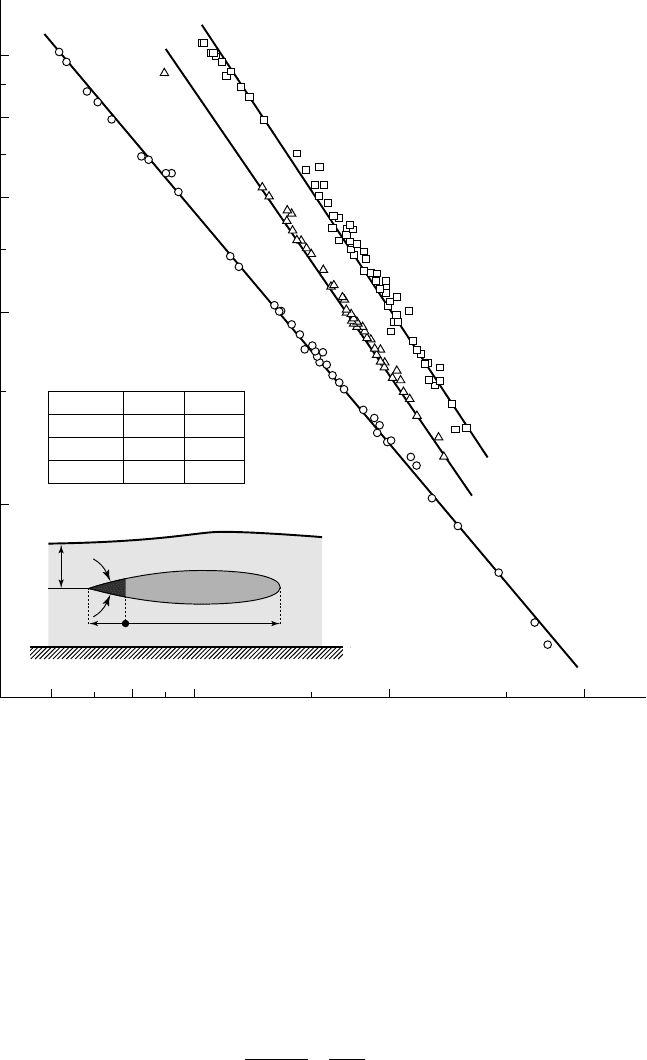
6.7 - Evolution of the relative cavity length with the cavitation number

for three values of the submersion depth (vapor cavities)

Case of a symmetrical wedge of chord

cmm= 60

, base height 17 mm and vertex

angle

216

= deg.

, in a free surface channel of height 280 mm. The three values of

the submersion depth h are shown [from M

ICHEL, 1973].

The smaller the submersion depth h, the smaller is the exponent n. For small values

of the submersion depth h, the exponent n approaches unity. In that case, the liquid

flow above the cavity can be considered as a circular jet submitted to pressures p

and p

on its two faces, where p

is the pressure on the free surface and p

the cavity

pressure. The normal E

ULER equation gives:

(6.4)

FUNDAMENTALS OF CAVITATION104

where R is the mean radius of curvature of the circular jet. Assuming that the cavity

free streamline originates from the body at an angle g equal to half the wedge vertex

angle (fig. 6.7), we obtain, from purely geometrical considerations:

ªg

(6.5)

By combining equations (6.4) and (6.5), we get:

(6.6)

Equation (6.6) shows that the cavity length varies as

-1

for small submersion depths.

By using a linearized theory with the T

ULIN wake model, ROWE and MICHEL (1975)

obtained variations of the cavity length which follow a law of the type

l /c A

with n-values close to experimental results but with A-values about 2.4 times too

small. Meanwhile, the calculated cavity was too thick, for the same value of s, with

respect to the experimental shape. By modifying the wake velocity distribution, a

better agreement was found between theory and experiment for both the length

and the shape of the cavity [M

ICHEL 1977].

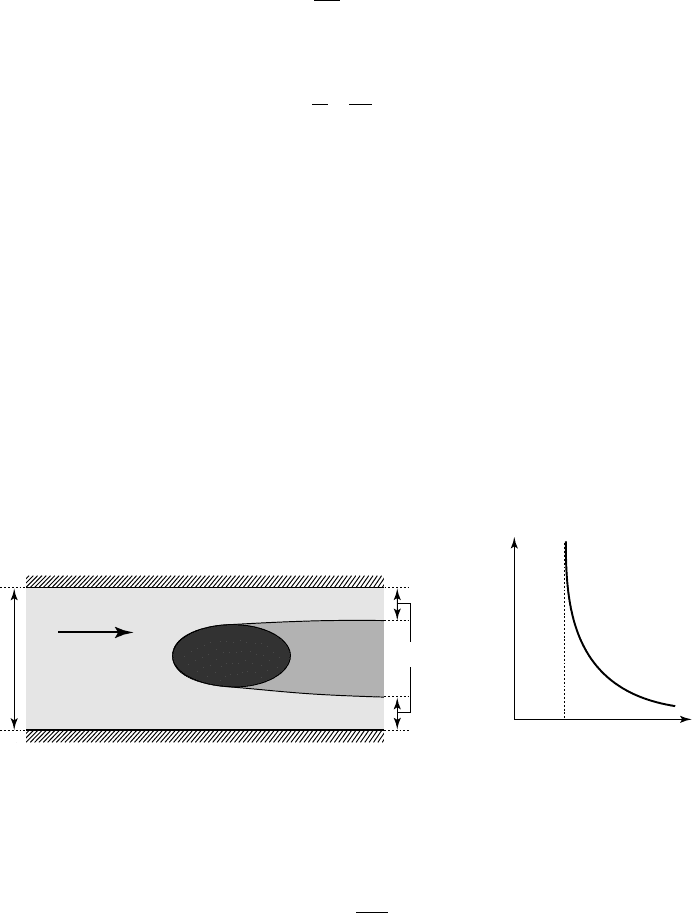
Blockage

Contrary to the previous cases, in a flow confined by solid walls, the cavity

becomes infinite for a value of the cavity pressure p

smaller than the pressure at

infinity p

•

i.e. for a non-zero value of the cavitation parameter (fig. 6.8-b). This

phenomenon corresponds to blockage of the flow.

blockage

–

∞

, p

∞

6.8 - Illustration of blockage in supercavitating flows

From the mass conservation and the B

ERNOULLI equations, the critical value of the

cavitation parameter corresponding to blockage can be estimated by:

blockage

(6.7)

where S

and S

stand respectively for the cross-sectional areas of the upstream and

downstream regions of the liquid flow (fig. 6.8-a).

6 - SUPERCAVITATION 105

For a symmetrical wedge of chord c and small vertex angle 2g, in the center of a

channel of height H, the linearized theory [C

OHEN et al. 1958] gives:

blockage

ch e

(6.8)

This equation agrees fairly well with experiments. For example, for

cH/.= 02

and

216g= deg.

, the theoretical value of the blockage cavitation number s

blockage

is 0.250

whereas the experimental value is 0.254 [M

ICHEL 1973].

From an experimental viewpoint, the closeness of blockage conditions results in a

critical behavior of the flow, since small pressure variations induce large variations

in cavity length.

6.2. SUPERCAVITY FLOW MODELING

USING STEADY POTENTIAL FLOW THEORY

In this section, attention is particularly focused on the hydrodynamics of cavity

flows disregarding viscous and surface tension effects. Viscous effects can easily be

taken into account in a second step by conducting a classical boundary layer

calculation on the wetted walls, on the basis of the pressure distribution obtained

from potential flow modeling. Such a procedure is necessary if the cavity

detachment point is unknown and if the laminar separation criterion is used for

its determination. This requires an iterative process which will be discussed in

chapter 8. In the present section, the position of the detachment point is supposed

to be known, a priori, for simplicity.

6.2.1. THE MAIN PARAMETERS

As an example, consider the case of a supercavitating steady horizontal flow around

a two-dimensional hydrofoil (fig. 6.9).

Body

Cavity, p

∞

6.9 - Case of a horizontal supercavitating flow with an external free surface

FUNDAMENTALS OF CAVITATION106

In addition to the geometrical parameters defining the shape of the foil, its

chordlength c, its angle of attack and the position of the external boundaries, the

main parameters which influence the cavity flow are:

— the relative cavity underpressure:

•

(6.9)

— and, if gravity effects are included, the F

ROUDE number based either on the chord

length c:

•

(6.10)

or on the cavity length l:

•

(6.11)

In the previous relations, V

•

is the free-stream velocity, g the acceleration due to

gravity, r the liquid density, p

the absolute pressure inside the cavity and p

•

reference pressure at upstream infinity conventionally chosen at the ordinate

y = 0

(fig. 6.9).

The modeling of the potential flow allows us to calculate the shape y

of the cavity

and particularly its length l as well as the velocity and pressure fields and more

especially the drag and lift coefficients:

pdy

••

body

(6.12)

pdx

••

body

(6.13)

where D and L stand respectively for the drag and the lift forces per unit span

length. The integrals are taken clockwise around the body.

6.2.2. EQUATIONS AND BOUNDARY CONDITIONS

For an inviscid fluid in irrotational flow, the velocity

is the gradient of a velocity

potential j which satisfies the L

APLACE equation

Dj = 0

. The boundary conditions

on the velocity potential are the following.

On the solid walls, the usual slip condition

V.n=0

∂j ∂n = 0

has to be satisfied

where

is a unit vector normal to the wall.

6 - SUPERCAVITATION 107

On the cavity interface, the shear stress and the mass transfer due to phase change

are neglected. The pressure is assumed constant, uniform and equal to the cavity

pressure p

and the velocity is tangential (see § 1.3.2). Using the BERNOULLI equation

between upstream infinity and a point of ordinate y

on the cavity interface where

the velocity is assumed to be V

, we get:

pgy

•

+=++rrr

(6.14)

so that the tangential velocity on the cavity

=∂j ∂t

is given by (t is the curvi-

linear distance along the free streamline):

•

=+-1

(6.15)

In the case of large supercavities, i.e. for small s-values, the maximum value of y

is of the order of

ls/2

(see eq. 6.29). Thus, we have approximately:

•

@+ -

(6.16)

According to this equation, gravity terms can be neglected if the F

ROUDE number

based on cavity length Fr

is much larger than one. If so, the condition of constant

pressure on the cavity interface reduces to a condition of constant tangential velocity:

•

=+1 s

(6.17)

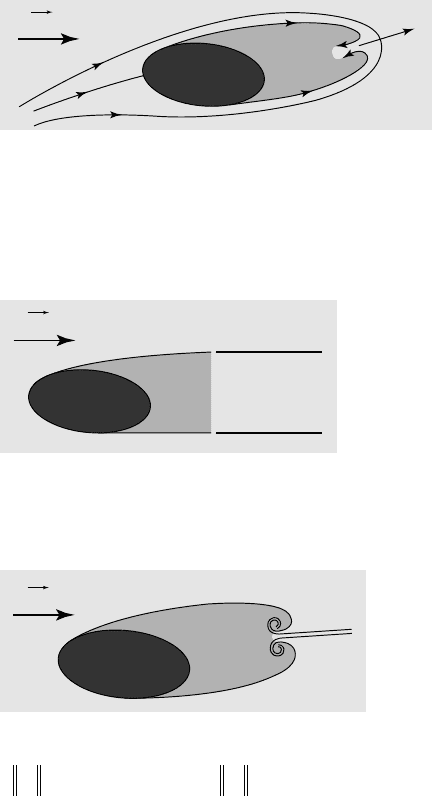
6.2.3. CAVITY CLOSURE MODELS

6.10

Firstly, it should be noted that the stagnation point cannot be the

junction of two free streamlines as schematically shown in figure 6.10

since the overpressure at this point would not be consistent with the

constant pressure condition in the cavity. Therefore, several cavity closure models

have been proposed in the past to close the cavity more or less artificially.

6.11

RIABOUCHINSKY model

In the R

IABOUCHINSKY model (1920), the cavity is

closed by a solid body, which is supposed to be

held in the flow from outside. According to d'A

LEMBERT's paradox, the cavitator, the

cavity and the closure body form a closed body on which the drag is zero.

FUNDAMENTALS OF CAVITATION108

6.12

Re-entrant jet model

The re-entrant jet model

ILBARG & SERRIN 1950]

assumes that a re-entrant jet develops at cavity closure. It is supposed steady and

to evolve on a R

IEMANN sheet, which allows the flowrate coming from the re-

entrant jet to be continuously withdrawn from the cavity. Indeed, the stagnation

point formed in the fluid is highly unstable as already mentioned in section 6.1.3.

6.13

WU model

In the W

U model (1956), the upper and

lower free streamlines of the cavity are

supposed continued by two solid plates, parallel to the velocity at infinity and

starting at the rear part of the cavity.

6.14

TULIN spiral vortices model

Finally, the TULIN model (1964)

assumes that the cavity is closed by

two

spiral vortices which result from conditions superimposed on the cavity

()

and its wake

VV=

()

•

Such models are necessary to close the cavity within the framework of a steady

potential approach. If the steady restriction is released and if an unsteady

computation is conducted, it is no longer necessary to use such closure models and

the cavity naturally exhibits an unsteady behavior with a more or less cyclic

development of the re-entrant jet.

6.2.4. OVERVIEW OF CALCULATION TECHNIQUES

Different techniques can be used to calculate steady supercavity flows. In the past,

non-linear, analytic techniques have been used, principally for bodies limited by a

few straight lines, such as the flat plate considered in section 6.3.1. Theoretical

∞

6 - SUPERCAVITATION 109

results concerning the conditions of existence and uniqueness of solutions were also

obtained that way. Further information on these techniques can be found in the book

of J

ACOB (1959) referenced in chapter 1 and also in BIRKHOFF & ZARANTONELLO (1957),

ILNE-THOMSON (1960) and LOGVINOVICH (1969).

For bodies with continuous curvature, the technique leads to integrals which have to

be evaluated numerically and requires an iterative procedure, whose convergence

is not guaranteed. The solution is made even more complicated if a criterion for the

cavity detachment has to be used. Thus, at the present time, the non-linear, analytic

technique remains a reference rather than an operative method to solve practical

problems.

Linearized, analytic methods

were developed to model supercavitating flows around

slender lifting bodies. Such methods assume that the perturbed velocity components

remain small compared to the free-stream velocity. This condition cannot be met in

the vicinity of the leading edge and the cavity closure, so that singularities of the

solution appear at those points.

Two classical problems can be solved easily on the basis of the linearized theory:

® The inverse problem which consists in computing the shape of the foil and the

cavity, given the pressure coefficient on the cavity interface and on the external

boundaries (D

IRICHLET problem).

® The direct problem which consists in computing the pressure coefficient any-

where in the flow field and the cavity shape and length (alternatively the

s-value) given the foil shape and the relative underpressure s (or alternatively

the cavity length l) (mixed N

EUMANN problem).

A detailed example of the use of the linearized method can be found in R

OWE

and MICHEL (1975). In this work, the singularity at the leading edge is removed,

using the method of matched asymptotic expansions, which allows us to obtain a

uniformly valid solution near the rounded nose of a truncated foil. It turns out

that the numerical results agree pretty well with the experimental ones. This is

particularly the case for the range of attack angles for which cavitation does not

occur near the leading edge.

Finally there are the purely numerical techniques such as the boundary element

method which is particularly suitable to the modeling of supercavity flows (see

e.g. L

EMONNIER & ROWE 1988). More recently, other techniques of direct interface

tracking have been developed on the basis of the resolution of the E

ULER or

AVIER-STOKES equations, such as marker techniques or volume of fluid (VOF)

techniques (see e.g. S

CARDOVELLI & ZALESKI 1999). These methods are inherently

unsteady and allow the time evolution of the cavity interface to be followed.

FUNDAMENTALS OF CAVITATION110

6.3. TYPICAL RESULTS

In this section, some results taken from analytic models are given. They allow us

to point out the main trends of supercavity flows. The following assumptions are

common to all models:

— flows are irrotational, steady and two-dimensional while the liquid is

incompressible and inviscid;

— gravity and surface tension are neglected;

— the stress at the liquid-vapor interface has a unique normal component equal to

the cavity pressure p

, supposed uniform throughout the cavity.

In most cases, the relative cavity underpressure s is assumed much smaller than 1,

so that the cavity is considered long.

6.3.1. INFINITE CAVITY BEHIND A FLAT PLATE

IN AN INFINITE FLOW FIELD

(

␴

= 0

)

Let c the chord AB of the plate. The cavity underpressure s is assumed to be zero,

so that the pressure p

in the cavity is equal to the reference pressure p

•

far

upstream the foil (fig. 6.15).

6.15

Flat plate

an infinite medium (

␴ = 0

)

The force F applied by the

flow on the plate, per unit

span length, is given by:

Ucr

•

sin

(6.18)

The distance between its application point R and the middle M of the plate is:

cos

sin

(6.19)

The lift and drag coefficients are respectively:

•

cos

sin cos

sin

paa

(6.20)

= p

∞

6 - SUPERCAVITATION 111

The asymptotic shape of the free streamlines is parabolic:

sin

(6.21)

If the plate is held perpendicular to the incident velocity (

ap= /2

), the drag

coefficient is equal to

088

@ .

, whereas the experimental value in the very

different case of a fully wetted flow is about 1.95.

At small angles of attack a, we have:

(6.22)

The slope of the curve C

(a) is p/2.

The distance between the stagnation point O and the leading edge A is about

c a

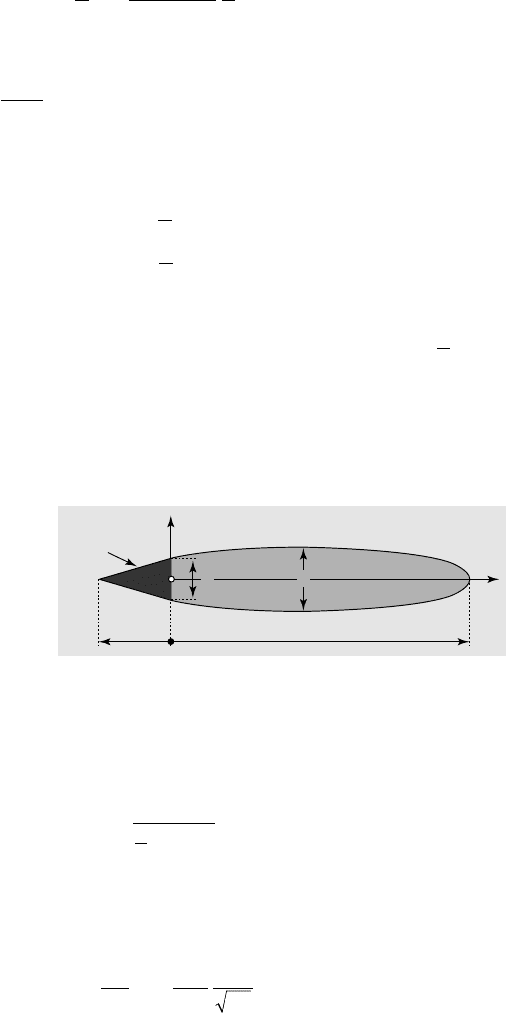
6.3.2. FINITE CAVITY BEHIND A SYMMETRICAL BODY

IN AN INFINITE FLOW FIELD

6.16

Symmetrical body

with finite cavity

in infinite medium

This model was developed

by T

ULIN (1953) on the basis of a linearized theory in which the cavity was

considered closed downstream at first order. Let b the wedge base and c its chord

(fig. 6.16). The linearization procedure requires the condition

bc<<

to be fulfilled.

For small s-values, the drag coefficient defined by:

•

(6.23)

can be approximated by:

() ()[ ]ss@+01

(6.24)

with

()0

(6.25)

(x)

FUNDAMENTALS OF CAVITATION112

The cavity length is given by:

(6.26)

and is approximated, when s is small, by:

()

(6.27)

Hence, the cavity length varies as

-2

for small s-values. As for the cavity thickness e,

it is given by:

40()

(6.28)

The cavity is approximately elliptic, except in the vicinity of the body, and its relative

thickness is:

(6.29)

Finally, for

s=0

, the asymptotic shape of the cavity is given by:

()

(6.30)

6.3.3. FINITE CAVITY BEHIND A CIRCULAR ARC IN AN INFINITE FLOW FIELD

This non-linear, two-dimensional, solution was developed by WU (1956). The far

wake is represented by two rigid plates parallel to the incident velocity. The near

wake is made up of the cavity limited by two free streamlines which link the

leading and the trailing edges of the circular arc to the two plates (fig. 6.17).



2

∞

6.17 - Circular arc with finite cavity in infinite medium