Franc J-P. Fundamentals of Cavitation

FUNDAMENTALS OF CAVITATION72

HABERMAN W.L. & MORTON R.K. –1953– An experimental investigation of the drag

and shape of air bubbles rising in various liquids. DTMB, Rpt 802.

I

SSELIN J.C., ALLONCLE A.P., DUFRESNE D. & AUTRIC M. –1996– Comportement

d'une bulle de cavitation à proximité d'une paroi solide: contribution à

l'étude du mécanisme d'érosion. Proc. 3

e

Journées Cavitation SHF,

Grenoble (France), 175-182.

J

OHNSON V.E. & HSIEH T. –1966– The influence of the trajectories of gas nuclei

on cavitation inception. Trans. 6

th

ONR Symp. Washington DC .

L

AUTERBORN W. & BOLLE H. –1975– Experimental investigations of cavitation-

bubble collapse in the neighbourhood of solid boundary. J. Fluid Mech. 72,

391-399.

N

AUDÉ C.F. & ELLIS A.T. –1961– On the mechanism of cavitation damage

by non-hemispherical cavities collapsing in contact with a solid boundary.

Trans. ASME D, 633-648.

P

LESSET M.S. & CHAPMAN R.B. –1971– Collapse of an initially spherical cavity in

the neighbourhood of a solid boundary. J. Fluid Mech. 47-2, 283-290.

S

HRIDAR G. & KATZ J. –1995– Drag and lift forces on microscopic bubbles

entrained by a vortex. Phys. Fluids 7(2), 389-399.

TOMITA Y. & SHIMA A. –1986– Mechanisms of impulsive pressure generation

and damage pit formation by bubble collapse. J. Fluid Mech. 169, 535-564.

V

ILLAT H. –1943– Leçons sur les fluides visqueux. Gauthier-Villars Ed.

V

OINOV –1973– On the force acting on a sphere in a non-uniform stream

of perfect incompressible fluid. J. Appl. Mech. Techn. Phys. 14, 592-594.

YAN K. & MICHEL J.M. –1998– Numerical simulation of bubble dynamics

in vortex core by the BUBMAC Method. Proc. 3

rd

Int. Symp. on Cavitation,

vol. 1, Grenoble (France), 75-80.

APPENDIX TO SECTION 4.3.3

In order to evaluate the equation:

dM

dt

pdS

d

dt

dS

S

e

SS

e

SS

r

rr

=- -

{}

++

ÚÚ ÚÚ

nrfn

01 01

(4.47)

and particularly the second term derivation of (4.47), let us consider the general

integral:

r

rr

JdSxdS

ekk

= qn qn

SS

ÚÚ ÚÚ

=

4 - BUBBLES IN A NON-SYMMETRICAL ENVIRONMENT 73

where

r

x

k

stands for the unit vectors in cartesian coordinates and q for any function.

For an incompressible fluid, the derivative is (see B

ATCHELOR, p. 133):

dJ

dt

d

dt

xdS

u

x

dS x

kk

k

i

ik

r

rr

=

Û

ı

Ù

Û

ı

Ù

-

Û

ı

Ù

Û

ı

Ù

q

nq

∂

n

S

which gives here, with

qrf∫

:

d

dt

dS

d

dt

dS grad dS

e

SS

e

SS

rfn r

f

nrf

∂

∂n

f

rr r

01

+

ÚÚ

{}

=

Û

ı

Ù

Û

ı

Ù

-

()

Û

ı

Ù

Û

ı

Ù

(4.48)

In (4.48), the last term is obtained from:

∂

n

∂f

∂n

∂f

∂n

u

x

grad x

x

grad

k

i

ik

k

r

rr

r

=

()

=

()

.

Introducing the BERNOULLI equation for unsteady flow in (4.47):

pp

t

V

=- -

•

r

∂f

∂

r

2

and combining with (4.48) leads to the equation:

dM

dt t

V

dS

d

dt

dS grad dS

S

e

SS

e

SS

r

rr r

=+

Ê

Ë

Á

ˆ

¯

˜

Û

ı

Ù

Û

ı

Ù

-

Û

ı

Ù

Û

ı

Ù

+

()

Û

ı

Ù

Û

ı

Ù

+

r

∂f

∂

nr

f

nf

∂

∂n

f

2

01

Taking the following expression for the Lagrangian derivative of f:

d

dt t

Vgrad

t

V

f∂f

∂

f

∂f

∂

=+ =+

r

.

2

one finally obtains:

dM

dt

grad

V

dS

S

e

SS

r

=

()

-

È

Î

Í

˘

˚

˙

Û

ı

Ù

Û

ı

Ù

+

rf

∂f

∂n

n

2

01

(4.49)

At great distances from the bubble, f behaves as a source term. Thus,

f

∂f

∂n

ª

()

ª

Ï

Ì

Ô

Ó

Ô

1

2

3

/

r

Vr

grad

r

FUNDAMENTALS OF CAVITATION74

and the function in the integral of equation (4.49) behaves as

1

2

/r

. Two cases can be

considered:

® If S

0

and S

1

are far from the bubble (case of an infinite medium), the integral in

(4.49) is zero and we have:

dM

dt

S

r

= 0

(4.50)

® If S

0

only goes to infinity, the integral on S

0

is zero and we have:

rr

MFdt

Sp

t

=

Ú

0

(4.51)

with

r

F

grad

V

dS

pe

S

=

()

-

È

Î

Í

˘

˚

˙

Û

ı

Ù

Û

ı

Ù

rf

∂f

∂n

n

2

1

(4.52)

Taking into account the fact that the Laplacian of f is zero, we have (see the note

below):

r

rr

F

V

grad dS

pe

S

=-

È

Î

Í

˘

˚

˙

Û

ı

Ù

Û

ı

Ù

rn

∂f

∂n

f

2

1

(4.53)

Note on the passage from (4.52) to (4.53)

Let us write:

r

rr

A

grad

V

dS A A

e

SS

=

()

-

È

Î

Í

˘

˚

˙

Û

ı

Ù

Û

ı

Ù

=+

+

f

∂f

∂n

n

2

12

2

01

with

r

rr

rrrr

rr

A

u

x

xdS

u

x

xdS ux dS

grad

x

dS x grad dS

AA

k

i

ik

k

i

ik kk

k

ek

1

11

=

Û

ı

Ù

Û

ı

Ù

=

Û

ı

Ù

Û

ı

Ù

-

Û

ı

Ù

Û

ı

Ù

=

Ê

Ë

Á

ˆ

¯

˜

Û

ı

Ù

Û

ı

Ù

-

Û

ı

Ù

Û

ı

Ù

=+

f

∂

n

∂f

∂

n

∂f

∂n

f

∂f

∂

nf

∂f

∂n

()

'''

The GREEN-OSTROGRADSKI transformation allows us to write:

r

A

x

dv x

k

'

1

=

Ê

Ë

Á

ˆ

¯

˜

Û

ı

Ù

Û

ı

Ù

Û

ı

Ù

Df

∂f

∂



4 - BUBBLES IN A NON-SYMMETRICAL ENVIRONMENT 75

with

DD Df

∂f

∂

f

∂f

∂

f

∂f

∂

f

∂f

∂

f

∂f

∂xx

grad grad

xx

grad grad

x

kk kk k

Ê

Ë

Á

ˆ

¯

˜

=+ +

Ê

Ë

Á

ˆ

¯

˜

=22

rr rr

..

Actually,

Df=0

, and

D

∂f

∂

∂f

∂xx

kk

Ê

Ë

Á

ˆ

¯

˜

==

()

0

.

Thus we have:

Df

∂f

∂

∂f

∂

∂f

∂

∂x

Vgrad

x

V

grad

x

V

x

V

x

kkkkk

Ê

Ë

Á

ˆ

¯

˜

==

()

==22 2

2

r

.. .

and

r

rr r

A

V

x

x dS gradV dS V dS

k

ke

'

1

2

22

=

Û

ı

Ù

Û

ı

Ù

Û

ı

Ù

=

ÚÚÚ

=

ÚÚ

∂

n

The last relation results from the GAUSS formula. Therefore:

rr

r

AA

V

dS

e

'.

12

2

+=

Û

ı

Ù

Û

ı

Ù

n

and the final result is:

r

rr

A

V

grad dS

e

SS

=-

È

Î

Í

˘

˚

˙

Û

ı

Ù

Û

ı

Ù

+

2

01

n

∂f

∂n

f

It allows us to write relation (4.53) for

r

F

p

, taking into account that the contribution

from S

0

is zero.

5. FURTHER INSIGHTS INTO BUBBLE PHYSICS

The dynamics of cavitation bubbles is controlled mainly by inertia and pressure

forces, as analysed in chapters 3 and 4. However, other physical phenomena may

also have a non-negligible influence on their growth and collapse. These include:

® Liquid compressibility which affects the final stages of bubble collapse and causes

the emission of shock waves and/or acoustic waves, essential in cavitation noise

and erosion.

® Heat transfer between the entrapped gas and the surrounding liquid, which is

decisive with regard to the phenomenon of sonoluminescence, i.e. light emission

by collapsing bubbles, as it controls the temperature reached inside the bubble

at the end of the collapse.

® Vaporization, which requires heat transfer and consequently temperature

gradients between the liquid and the bubble and which is the cause of thermal

delay in cavitation. This phenomenon is currently referred to as the thermo-

dynamic effect.

The present chapter is devoted to the presentation of the fundamental ideas and

classical results concerning these problems. More detailed analyses can be found in

books dedicated to specialized aspects, for example L

AUTERBORN (1979), TREVENA

(1987), LEIGHTON (1994).

5.1. THE EFFECT OF COMPRESSIBILITY

5.1.1. TAIT'S EQUATION OF STATE

In order to account for compressibility effects, it is necessary to have an equation

of state for the liquid which takes into account the variation of density with the

pressure.

An appropriate law is the barotropic one proposed by T

AIT, which is given by:

pB

n

+

=

Ê

Ë

Á

ˆ

¯

˜

00

r

(5.1)

where 1/nB is the compressibility coefficient defined by

1

r

rd

dp

and the subscript 0

refers to normal conditions.

FUNDAMENTALS OF CAVITATION78

In the case of water,

B MPa= 304 9.

and

n =715.

, so that the compressibility

coefficient is relatively small and of the order of

46 10

1

0

1

. ¥

--

Pa

.

It is useful to define the following classical quantities:

— enthalpy h:

h

dp

p

=

Û

ı

Ù

r

0

(5.2)

— velocity of sound c:

c

dp

d

dh

dp

==

r

(5.3)

Combined with T

AIT's law, these take the following form:

h

c

n

=

-

Ê

Ë

Á

ˆ

¯

˜

-

È

Î

Í

˘

˚

˙

-

0

2

0

1

r

(5.4)

cc

n

=

È

Î

Í

˘

˚

˙

-

0

12

r

()/

(5.5)

where the velocity of sound c

0

in normal conditions is given by:

c

np B

0

=

+()

r

(5.6)

5.1.2. BASIC EQUATIONS

Consider a spherical bubble in an infinite medium. The radial velocity

urt(,)

,

pressure

prt(,)

and density

r (,)rt

are governed by the mass conservation and

E

ULER equations:

∂

+

∂

=-

∂

rr

r

t

u

r

ru

r

1

2

()

(5.7)

∂

+

∂

=-

∂

u

t

u

r

p

r

1

r

(5.8)

The law of state of the liquid must be added in order to close the previous system

of partial differential equations.

Using the enthalpy defined by equation (5.2), the mass conservation equation and

the EULER equation become respectively:

∂

+

∂

=-

∂

h

t

u

h

r

c

r

ru

r

2

1

()

(5.9)

5 - FURTHER INSIGHTS INTO BUBBLE PHYSICS 79

∂

+

∂

=-

∂

u

t

u

r

h

r

(5.10)

The velocity potential

j (,)rt

is defined by:

u

r

=

∂

j

(5.11)

and the E

ULER equation has the following first integral, which is a generalized

B

ERNOULLI equation:

∂j

∂t

u

hCt++=

2

()

(5.12)

where C(t) is a time dependant function. We consider here the collapse of a bubble

under a constant pressure at infinity equal to p

0

, so that C is then a constant which

can be set equal to zero by a correct choice of the velocity potential j.

The elimination of the enthalpy h between equations (5.9) and (5.12) leads to the

following hyperbolic equation for the velocity potential j:

()cu

r

u

rt

t

c

rr

22

2

22

2

---=-

∂

∂j

∂

∂j

∂∂

∂j

∂

j

(5.13)

This equation allows us to compute the solution numerically from the initial

conditions.

The characteristic lines are given by:

()c u dt u dr dt dr

222 2

20-- -=

(5.14)

i.e.

dr

dt

uc=±

(5.15)

Hence, the velocity of the characteristic lines can be very different from the velocity

of sound since the radial velocity u can reach very high values.

5.1.3.THE QUASI ACOUSTIC SOLUTION [HERRING 1941& TRILLING 1952]

In this approach, the sound velocity is assumed constant and equal to c

0

and the

terms in u

2

and u are neglected on the left-hand side of equation (5.13). This

equation then reduces to the classical equation for an acoustic wave:

∂

=

∂

Ê

Ë

Á

ˆ

¯

˜

2

0

2

1

j

t

c

r

(5.16)

FUNDAMENTALS OF CAVITATION80

whose solution is a spherical wave propagating outwards from the bubble wall:

j= -

Ê

Ë

Á

ˆ

¯

˜

1

0

r

Ft

r

c

(5.17)

In this equation, F is an unknown function which characterizes the shape of the wave.

Moreover, the quasi acoustic solution assumes that the density is constant and

equal to r

0

, so that the relation between pressure and enthalpy is simply:

h

pp

=

-

0

r

(5.18)

On the bubble interface, the generalized B

ERNOULLI equation (5.12) gives:

11

2

0

2

0

R

Ft

Rt

c

R

Pt p

˙

()

˙

()

-

Ê

Ë

Á

ˆ

¯

˜

++

-

=

r

(5.19)

where

˙

R

is the interface velocity and P(t) the liquid pressure on the interface which

is known from the boundary conditions. As an example, the pressure P reduces to

the sum of the vapor pressure and the partial pressure of any incondensable gases,

if viscosity and surface tension are neglected.

The computation of the first term in equation (5.19) needs some further development

which are given in the appendix at the end of the chapter. When only the first order

terms in

˙

/Rc

are considered, the following differential equation for the evolution

of the bubble radius is obtained:

RR

R

c

RR

c

R

c

dP

dt

Pp

˙˙

˙˙ ˙

1

23

2

1

4

3

0

2

000

0

-

Ê

Ë

Á

ˆ

¯

˜

+-

Ê

Ë

Á

ˆ

¯

˜

=+

-

rr

(5.20)

This equation is a generalization of the R

AYLEIGH-PLESSET equation which takes

into account liquid compressibility.

5.1.4. THE GILMORE APPROACH (1952)

GILMORE used the KIRKWOOD-BETHE hypothesis, which was introduced for sub-

marine explosions, according to which the quantity rj propagates with a velocity

equal to the sum of the sound velocity and the fluid velocity. The G

ILMORE approach

leads to the following equation of evolution for the bubble radius:

RR

R

C

RR

C

H

R

C

R

C

R

C

dH

dt

˙˙

˙˙ ˙ ˙ ˙

1

3

2

1

3

11

2

-

Ê

Ë

Á

ˆ

¯

˜

+-

Ê

Ë

Á

ˆ

¯

˜

=+

Ê

Ë

Á

ˆ

¯

˜

+-

Ê

Ë

Á

ˆ

¯

˜

(5.21)

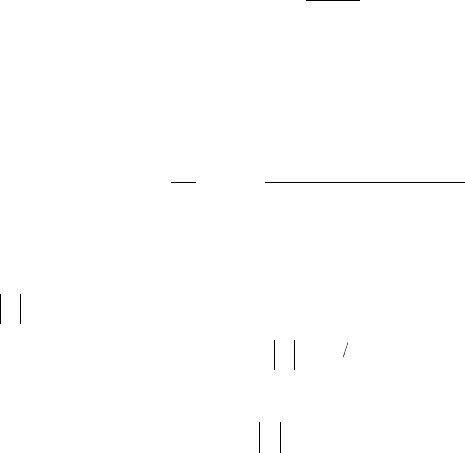
5 - FURTHER INSIGHTS INTO BUBBLE PHYSICS 81

In this equation, H and C stand respectively for the liquid enthalpy and the sound

velocity on the bubble interface and correspond to the pressure on the bubble wall

PpR= ()

. When density is assumed constant, we simply have:

H

Pp

=

-

0

r

(5.22)

In the case of the collapse of a pure vapor bubble submitted to an external pressure

greater than the vapor pressure, the pressure inside the bubble P is constant and

equal to the vapor pressure. Equation (5.21) then has the following first integral:

Log

R

RR C

RCRHRC

dR

R

0

32

0

2

32

=-

-

()

-++

()

Û

ı

Ù

˙˙

˙˙ ˙

˙

(5.23)

At the end of the collapse, the interface velocity

˙

R

is negative and tends to infinity.

Hence, the terms in

˙

R

in equation (5.23) are dominant and the integral behaves as

Log R

˙

. This leads to the following asymptotic behavior:

˙

RR@

-12

(5.24)

Therefore, in the compressible case, the G

ILMORE approach leads to an exponent

m =12/

for the asymptotic law

˙

RR

m

@

-

instead of the value 3/2 which was

obtained in the incompressible case (see § 3.2.2). The collapse velocity appears to

be significantly slowed down by compressibility.

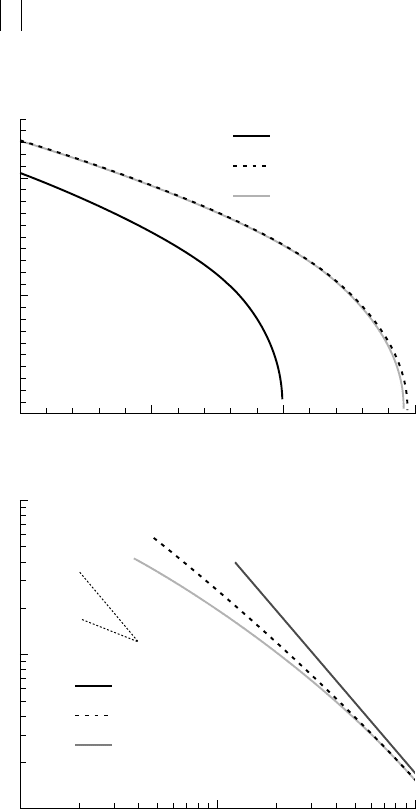
On figure 5.1, we present the results of the G

ILMORE model compared to the

R

AYLEIGH and HERRING models. Only the very last stages of the collapse are

influenced by the liquid compressibility. The lifetime of the bubble is slightly

increased as a result. Both the G

ILMORE and the HERRING and TRILLING models, are

similar. The main difference lies in the exponent of the asymptotic law for the

interface velocity, the G

ILMORE model leading to a somewhat less violent collapse.

However, let us note that the last stages of the collapse which lead to very high

values of the M

ACH number calculated with the interface velocity are beyond the

assumptions of such models.

The first numerical solution which describes the bubble collapse and rebound by

taking into account the liquid compressibility was given by H

ICKLING and PLESSET

(1963). The calculation was made on the basis of the GILMORE model for MACH

numbers

˙

/RC

smaller than 0.1. For higher values, a Lagrangian form of the EULER

equation was used.

The computational results of H

ICKLING and PLESSET clearly show the emission of

a pressure wave from the instant of rebound. The pressure wave propagates

outwards and its amplitude decreases approximately as 1/r. Such steep-fronted

waves, which can become shock waves, have been found by many authors. As an

FUNDAMENTALS OF CAVITATION82

example, we present in section 5.4 the pressure distributions in the liquid obtained

by F

UJIKAWA and AKAMATSU (1980) on the basis of a more complicated model, but

which show the same general behavior.

With velocity of the bubble wall in the final stages of collapse approximated

by a power law

˙

RR

m

@

-

, HICKLING and PLESSET found the value 0.785 for the

exponent m, whereas H

UNTER (1963) found 0.801 from a direct study of the

asymptotic behavior of the bubble.

m

=3/

2

m

=1/

2

0.2

0.1

0

0.99 0.995 1 1.005

10

1

0.1

0.001 0.01 0.1

Non-dimensionalized time t/τ

Non-dimensionalized radius R/R

0

Non-dimensionalized radius R/R

0

Mach number (dR/dt)/c

R

AYLEIGH

H

ERRING

& T

RILLING

G

ILMORE

R

AYLEIGH

H

ERRING

& T

RILLING

G

ILMORE

5.1 - Collapse of a 1 cm radius vapor bubble

under a constant pressure difference

pp

v0

-

equal to 10

5

Pa

Comparison of the solutions of R

AYLEIGH, HERRING & TRILLING and GILMORE.

Franc J-P. Fundamentals of Cavitation

Подождите немного. Документ загружается.