Fowler A. Mathematical Geoscience
Подождите немного. Документ загружается.

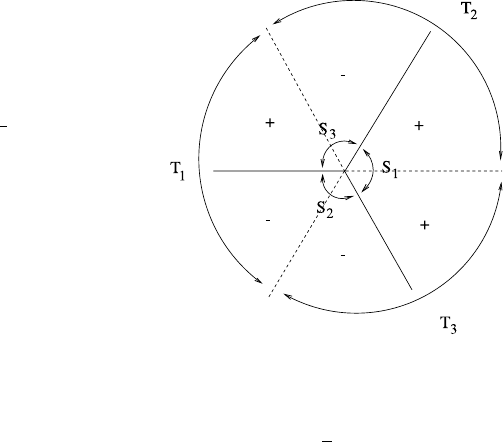
810 C Asymptotic Solution of the Orr–Sommerfeld Equation
Fig. C.2 The Stokes sectors
T
i
(bounded by the Stokes
lines) and the anti-Stokes
sectors S
i
(bounded by the
anti-Stokes lines) for (C.15).
The signs in the sectors
indicate the sign of arg
2
3
z
3/2
as z →∞
where B
p
is a polynomial in ζ for integral p, in particular B
p
=0forp ≤0, and
B
1
(ζ ) =1,B
2
(ζ ) =ζ, B
3
(ζ ) =
1
2
ζ
2
. (C.18)
The functions A
p
satisfy the equations
LD
2
A
p+1
=−(p −1)A
p
,
DA
p
= A
p−1
, (C.19)
ζA
p
= pA
p+1
+A
p−2
,
the last of these following from the first two together with (C.16). In particular,
LA
0
= 0 and A
(k)
0
are the Airy functions; for example, A
(1)
0
(ζ ) = Ai (ζ ).Wealso
have the rotation formulae
A
(2)
p
(ζ ) =e
−2(p−1)π i/3
A
(1)
p
ζe
2πi/3
,
A
(3)
p
(ζ ) =e
2(p−1)π i/3
A
(1)
p
ζe
−2πi/3
.
(C.20)
It is clear from (C.19) that the solution for χ
0
in (C.13)isoftheform
χ
0
=χ
00
+χ
01
ζ +α
0
A
(1)
2
(ζ ) +β
0
A
(3)
2
(ζ ). (C.21)
(Although A
(2)
2
is another possible solution, it is not independent because of (C.17),
and because B
2
(ζ ) =ζ .)
Drazin and Reid (1981) give the asymptotic behaviour as ζ →∞of the functions
A
(k)
p
, based on the method of steepest descents and the rotation formulae (C.20). The
Stokes sectors T
i
are delimited by Stokes lines at arg ζ =0, 2π/3, 4π/3, and within
these, the anti-Stokes lines are argζ = π/3, π,5π/3(seeFig.C.2). Note that we
seek the behaviour of A
(k)
2
as ζ →∞along argζ =π/6 (since ζ = (ikRU
0
)
1/3
z),

C Asymptotic Solution of the Orr–Sommerfeld Equation 811
which lies in the sector S
1
:−
π
3
< argζ<
π
3
, in which the functions A
+
and A
−
defined by Drazin and Reid (p. 463, Eq. (A12)) respectively grow and decay expo-
nentially. From their Eq. (A14), we then see that A
(1)
p
→ 0asζ →∞e
iπ/6
, while
A
(3)
p
grows exponentially. Therefore β
0
=0in(C.21).
Next we turn to the solution for χ
1
.From(C.13), we have, using D
2
A
2
=A
0
,
LD
2
χ
1
=
U
0
U
0
1
2
α
0
ζ
2
A
(1)
0
−χ
00
−χ
01
ζ −αA
(1)
2
. (C.22)
The solution to this equation is (using (C.18))
χ
1
= χ
10
+χ
11
ζ +α
1
A
(1)
2
(ζ ) +
U
0
U
0
α
0
−
1
2
A
(1)
0
+
1
10
A
(1)
−3
+A
(1)
3
+
1
2
χ
01
ζ
2
−χ
00
φ
, (C.23)
whereweuseLD
2
B
3
=−B
2
and again suppress A
(3)
2
(ζ ), and φ is a particular
solution to
LD
2
φ =B
1
. (C.24)
For matching purposes, φ must not grow exponentially at ∞e
πi/6
.
The use of the relation LD
2
B
p+1
=−(p −1)B
p
does not help here, because if
p =1, then LD
2
B
2
= 0. To find a solution, we now define the further generalised
Airy functions
A
(k)
pq
(ζ ) =
1
2πi
L
k
t
−p
(lnt)
q
e
ζt−
1
3
t
3
dt, (C.25)
where arg t ∈(0, 2π). (Drazin and Reid write A
(k)
pq
(ζ ) as A
k
(ζ,p,q).) We also de-
fine the loop integrals
B
(k)
pq
(ζ ) =
1
2πi
(0+)
∞e
2(k−1)iπ/3
t
−p
(lnt)
q
e
ζt−
1
3
t
3
dt, (C.26)
where the loop contours in (C.26) are defined by Erdélyi et al. (1953, p. 13), and
used by Olver (1974) and Reid (1972). The notation
(0+)
a
denotes an integral over
a contour which is a loop beginning and ending at the point a, and which encloses
the origin (and encircles it counterclockwise). For the integrands with branch points
as in (C.26), these are thus the keyhole contours
ˆ
L
k
as indicated in Fig. C.3.
It is straightforward to derive analogues of (C.19) (which apply to any of the
contours L
k
or
ˆ
L
k
), and these are (for A
pq
or B
pq
)
DA
pq
= A
p−1,q
,
(LD +p −1)A
pq
= qA
p,q−1
, (C.27)
LD
2
A
p+1,q
=−(p −1)A
pq
+qA
p,q−1
,

812 C Asymptotic Solution of the Orr–Sommerfeld Equation
Fig. C.3 Two of the three
loop contours for (C.26),
ˆ
L
1
and
ˆ
L
2
and in particular we see that
LD
2
A
21
=A
1
, (C.28)
since it is clear that A
p0
= A
p
for any p. Incidentally, note that when q = 0, the
integrands of (C.26) do not have a branch point, and therefore the loop contours
ˆ
L
k
are all equivalent to L
0
, so that B
(k)
p0
=B
p
, and in particular
LD
2
B
(k)
21
=B
1
(C.29)
for each contour
ˆ
L
k
. Consulting (C.24), we see that any of B
(k)
21
is a particular so-
lution for φ in (C.23), but we require one which does not grow exponentially. It is
clear, since LD
2
A
(k)
2
=0, that the difference between the various B
(k)
21
for different
k will be a sum of multiples of A
(k)
2
, and this is explicitly provided by the connection
formulae of Drazin and Reid (p. 475, Eq. (A43)):
B
(2)
21
−B
(3)
21
=2πiA
(1)
2
,
B
(1)
21
−B
(2)
21
=2πiA
(3)
2
.
(C.30)
The object now is to find an appropriate solution of (C.29) which does not grow
exponentially as ζ →∞e
πi/6
, and for this we need to know the asymptotic be-
haviour of one of the B
(k)
21
. At this point we diverge from the discussion by Drazin
and Reid (pages 178, 474). We consider explicitly the contour integral over
ˆ
L
2
:
B
(2)
p
1
=
1
2πi
(0+)
∞e
2πi/3
t
−p
lnte
ζt−
1
3
t
3
dt. (C.31)
In choosing the contour, we anticipate that we will require Re(ζ t) < 0, and to be
specific, we define argt ∈(−
4π
3
,
2π
3
) in (C.31). We have, successively,
B
(2)
p1
=−
∂
∂p
1
2πi
(0+)
∞e
2πi/3
t
−p
e
ζt−
1
3
t
3
dt
(C.32)
C Asymptotic Solution of the Orr–Sommerfeld Equation 813
and thus (put t
3
=3u)
B
(2)
p1
=−
∂
∂p
1
2πi
(0+)
∞e
2πi/3
∞
n=0
−
1
3
n
n!
t
3n−p
e
ζt
dt
; (C.33)
the method of proof of Watson’s lemma then implies
B
(2)
p1
∼−
∂
∂p
∞
n=0
−
1
3
n
n!
1
2πi
(0+)
∞e
2πi/3
t
3n−p
e
ζt
dt
, (C.34)
provided Re(ζ t) < 0.
Equation (6), page 14, of Erdélyi et al. (1953)gives
1
2πi
(0+)
∞e
iδ
t
−3
e
−tX
dt =
(Xe
−iπ
)
s−1
(s)
(C.35)
for any value of s, where, if argt ∈(δ, 2π +δ), then −(
1
2
π +δ) < arg X<
1
2
π −δ.
In the present case, argζ =
π
6
, so that if we define δ =−
4π
3
, (and note that
∞e
−4πi/3
=∞e
2πi/3
), X =ζe
iπ
, then argX =
7π
6
and lies between −
π
2
−δ =
5π
6
and
π
2
−δ =
11π
6
. We thus have, for argζ =
π
6
,
1
2πi
(0+)
∞e
2πi/3
t
−s
e
tζ
dt =
ζ
s−1
(s)
, (C.36)
and hence (C.34) gives, with s =p −3n,
B
(2)
p1
(ζ ) ∼−
∂
∂p
∞
n=0
−
1
3
n
n!
ζ
p−3n−1
(p −3n)
. (C.37)
Carrying out the differentiation,
B
(2)
p1
(ζ ) ∼
∞
n=0
−
1
3
n
n!
−
ζ
p−3n−1
lnζ
(p −3n)
+ζ
p−3n−1
(p −3n)
2
(p −3n)
. (C.38)
Finally we put p = 2. Noting that
/
2
is finite and 1/(r)= 0 for non-positive
integers r,wehave
B
(2)
21
(ζ ) ∼−ζ ln ζ +ψ(2)ζ +O
ζ
−2
, (C.39)
for ζ →∞with −
π
6
< arg ζ<
5π
6
, and in particular when argζ =
π
6
; ψ =
/ is
the digamma function.
We may now finally define a particular solution for φ in (C.24)tobe(cf.(C.29))
φ =B
(2)
21
(ζ ). (C.40)

814 C Asymptotic Solution of the Orr–Sommerfeld Equation
Before we complete the solution by matching to the outer solution, we compare
(C.40) with results of Drazin and Reid (page 178). They choose (Eq. (27.49)) φ
DR
=
B
(3)
21
, and match in the sector −π<argζ<
1
3
π, where their Eq. (27.50) implies
φ
DR
∼−ζ [ln ζ −2πi]+ψ(2)ζ. (C.41)
The connection formula (C.30)
1
implies that φ
DR
and φ have the same asymptotic
behaviour, since A
(1)
2
is exponentially small for −
π
3
< arg ζ<
π
3
(Drazin and Reid,
Eq. (A36), page 473). The only distinction between (C.39) and (C.41) is thus in the
phase of lnζ . (Note that the error term in Eq. (27.50) of Drazin and Reid should
read O(ξ
−2
).)
In fact, neither Drazin and Reid (nor Reid 1972) are specific about the phase
either of t or of ζ in the definition of the loop integrals B
(k)
pq
, although earlier (page
468) they suppose −
4
3
π<argζ<
2
3
π. If we define the modified loop integral
ˆ
B
(2)
21
(ζ ) =
1
2πi
(0+)
[∞e
2πi/3
,∞e
8πi/3
]
t
−2
ln te
ζt−
1
3
t
3
dt, (C.42)
just as in (C.31), but with arg t ∈ (
2π
3
,
8π
3
), then we see immediately that (since
B
(k)
20
(ζ ) =B
2
(ζ ) =ζ)
ˆ
B
(2)
21
(ζ ) =B
(2)
21
(ζ ) +2πiζ, (C.43)
which allows consistency between (C.39) and (C.41)ifφ
DR
=
ˆ
B
(2)
21
or, equivalently,
ˆ
B
(3)
21
. We thus consider the discrepancy between the two accounts to be due to the
choice by Reid (1972) of a different phase of ζ in applying Erdélyi et al.’s formula.
C.1 Matching
To summarize thus far, we have an outer solution (C.8):
Ψ ∼Λ
P
21
Ψ
1
(z) −P
11
ψ
2
(z) +O
ε
3
, (C.44)
where, as z =εζ →0,
Ψ ∼Λ
−P
11
+εζ
P
21
−P
11
U
0
U
0
ln ε
−εP
11
U
0
U
0
ζ ln ζ +···
. (C.45)
The inner solution is, from (C.12), (C.21) with β
0
=0, (C.23) and (C.40),
Ψ ∼ Λ
χ
00
+χ
01
ζ +α
0
A
(1)
2
(ζ )
+ε
χ
10
+χ
11
ζ +α
1
A
(1)
2
(ζ ) +
U
0
U
0
α
0
−
1
2
A
(1)
0
+
1
10
A
(1)
−3
+A
(1)
3
+
1
2
χ
01
ζ
2
−χ
00
B
(2)
21
(ζ )
+···
, (C.46)

C.1 Matching 815
which must satisfy the boundary conditions (from (C.2)) Ψ = 0, dΨ/dζ = ε on
ζ =0. To accommodate these, we choose
Λ =εΛ
1
+ε
2
Λ
2
+···, (C.47)
and thus specify (using the fact that DA
p
=A
p−1
, DB
pq
=B
p−1,q
)
χ
00
+α
0
A
(1)
2
(0) =0,
χ
01
+α
0
A
(1)
1
(0) =1/Λ
1
,
χ
10
+α
1
A
(1)
2
(0) +
U
0
U
0
α
0
−
1
2
A
(1)
0
(0) +
1
10
A
(1)
−3
(0) +A
(1)
3
(0)
−χ
00
B
(2)
21
(0)
=0,
χ
11
+α
1
A
(1)
1
(0) +
U
0
U
0
α
0
−
1
2
A
(1)
−1
(0) +
1
10
A
(1)
−4
(0) +A
(1)
2
(0)
−χ
00
B
(2)
11
(0)
=−Λ
2
/Λ
2
1
.
(C.48)
It remains to choose α
0
,α
1
,Λ
1
,Λ
2
, and these must follow from matching (C.45)
and (C.46). For large ζ ,(C.46)is
Ψ ∼ Λ
χ
00
+χ
01
ζ +ε
χ
10
+χ
11
ζ
+
U
0
U
0
1
2
χ
01
ζ
2
−χ
00
−ζ lnζ +ψ(2)ζ
+···
. (C.49)
Matching thus requires (we telescope the terms in lnε)
χ
00
=−P
11
,
χ
01
=0,
χ
10
=0,
χ
11
=P
21
−
P
11
U
0
U
0
ln ε −χ
00
ψ(2)
U
0
U
0
.
(C.50)
The eight equations in (C.48) and (C.50) determine the unknowns α
0
, α
1
, Λ
1
, Λ
2
,
χ
00
, χ
01
, χ
10
and χ
11
. In particular, we want to calculate
d
2
Ψ
dz
2
|
z=0
. At leading order,
this is (with ε =(ikRU
0
)
−1/3
)
d
2
Ψ
dz
2
z=0
∼(ikRU
0
)
1/3
Λ
1
α
0
A
(1)
0
(0), (C.51)
816 C Asymptotic Solution of the Orr–Sommerfeld Equation
so it suffices to determine Λ
1
and α
0
.Wehaveχ
00
=−P
11
which is known by
solving the Rayleigh equation, and χ
01
=0. Therefore
α
0
=
P
11
A
(1)
2
(0)
,Λ
1
=
A
(1)
2
(0)
P
11
A
(1)
1
(0)
. (C.52)
Notice that calculation of other coefficients requires the knowledge of B
(2)
21
(0) and
B
(2)
11
(0). In view of our circumspection concerning B
(2)
pq
, we would need to be suspi-
cious of the definitions given by Drazin and Reid (Eq. (A39), page 474). The values
of A
(1)
p
(0) are given by Drazin and Reid (page 468, Eq. (A11)), in particular,
A
(1)
1
(0) =−
1
3
,A
(1)
2
(0) =
1
3
4/3
4
3
. (C.53)
Note that α
0
Λ
1
=1/A
(1)
1
(0) =−3, and A
(1)
0
(0) =Ai(0) =
1
3
2/3
(
2
3
)
≈0.355, thus
d
2
Ψ
dz
2
0
∼−3(ikRU
0
)
1/3
Ai(0) ≈−1.06(ikRU
0
)
1/3
. (C.54)
Note that this result (see comment after (C.11)) applies for k>0 (and U
0
> 0). For
k<0, we use the fact that Ψ is the Fourier transform of a real function, and hence
Ψ(z,−k) =
Ψ(z,k). (C.55)

Appendix D
Melting, Dissolution, and Phase Changes
The study of phase change and chemical reactions involves from the outset the mag-
ical art of thermodynamics. I have yet to meet an applied mathematician who claims
to understand thermodynamics, and the interface of the subject with fluid dynamics
raises serious fundamental issues. These we skirt, providing instead a cookbook of
recipes. The initial material can be found in Batchelor (1967), while its extension to
phase change and reaction involves (geo)chemical thermodynamics, as expounded
by Kern and Weisbrod (1967) and Nordstrom and Munoz (1994), for example.
D.1 Thermodynamics of Pure substances
The state of a pure material is described by two independent quantities, such as
temperature and pressure. Any other property of the material is then in principle a
function of these two. Among such properties we have the volume, V ; the internal
energy, E; and a number of thermodynamic variables: the entropy S, the enthalpy
H , the Helmholtz free energy F , and the Gibbs free energy G.
We distinguish between intensive and extensive variables. Intensive variables are
those which describe properties of the material; they are local. Pressure and tem-
perature are examples of intensive variables. Extensive variables are those which
depend on the amount of material; volume is one such variable. Typically, exten-
sive variables are simply intensive variables multiplied by the amount of substance,
measured in moles.
1
If n moles of a substance have extensive variables V , H , S, E,
F and G (all capitals), then the corresponding intensive variables are the specific
volume v =V/n, and the specific enthalpy, entropy, internal energy, Gibbs free en-
1
A mole of a substance is a fixed number (Avogadro’s number, ≈6×10
23
) of molecules (or atoms,
as appropriate) of it. The weight of one mole in grams is called the (gram) molecular weight. The
molecular weight of compound substances is easily found. For example, carbon (C) has a molecular
weight of 12, while oxygen (O
2
) has a molecular weight of 32; thus the molecular weight of CO
2
is 44, and we can write M
CO
2
=44 ×10
−3
kg mole
−1
.
A. Fowler, Mathematical Geoscience, Interdisciplinary Applied Mathematics 36,
DOI 10.1007/978-0-85729-721-1, © Springer-Verlag London Limited 2011
817
818 D Melting, Dissolution, and Phase Changes
ergy and Helmholtz free energy are defined similarly (and may be denoted as lower
case variables). In addition, the material density ρ is equal to 1/v.
Definitions of H , F and G are
H =E +pV,
F =E −TS, (D.1)
G = H −TS.
Two further relations are then necessary to determine E and S. An equation of
conservation of energy (discussed in Sect. D.2) determines E, and the entropy S is
determined via the differential relation
TdS=dE +pdV. (D.2)
It will be convenient sometimes to work with the intensive forms of the variables,
thus division of (D.2) yields
Tds=de +pdv. (D.3)
From this latter relation we have the expressions
∂e
∂v
s
=−p,
∂e
∂s
v
=T, (D.4)
and if we now form the mixed second derivative
∂
2
e
∂s∂v
in two ways, we derive the
relation
∂p
∂s
v
=−
∂T
∂v
s
, (D.5)
which is one of the four Maxwell relations. The others are derived in a similar way
by considering mixed partial derivatives of h, f and g, yielding
∂v
∂s
p
=
∂T
∂p
s
,
∂v
∂T
p
=−
∂s
∂p
T
, (D.6)
∂p
∂T
v
=
∂s
∂v
T
.
Four partial derivatives are associated with specifically named quantities, which
can be measured. These are the coefficient of thermal expansion
β =
1
v
∂v
∂T
p
, (D.7)
D.2 The Energy Equation 819
the coefficient of isothermal compressibility
ξ =−
1
v
∂v
∂p
T
, (D.8)
the specific heat at constant pressure,
c
p
=T
∂s
∂T
p
, (D.9)
and the specific heat at constant volume,
c
v
=T
∂s
∂T
v
. (D.10)
With these definitions, we can write
Tds=de +pdv=c
p
dT −βvT dp, (D.11)
which is useful in writing the energy equation, as we will now see.
D.2 The Energy Equation
The basic equations of conservation of mass, momentum and energy for a fluid with
density ρ, velocity u and internal energy e are
∂ρ
∂t
+∇.(ρu) =0,
∂ρu
i
∂t
+∇.(ρu
i
u) =∇.σ
i
+ρf
i
,
∂
∂t
1
2
ρu
2
+ρe +ρχ
+∇.
1
2
ρu
2
+ρe +ρχ
u
=∇.(σ
i
u
i
) −∇.q,
(D.12)
where σ
i
=σ
ij
e
j
, q is the heat flux, and the conservative body force f is defined by
f =−∇χ, (D.13)
where χ is the potential. Algebraic manipulation of the energy equation using the
other two leads to the energy equation in the form
ρ
de
dt
=σ
ij
˙ε
ij
−∇.q, (D.14)
where
˙ε
ij
=
1
2
∂u
i
∂x
j
+
∂u
j
∂x
i
(D.15)
