Fowler A. Mathematical Geoscience

Подождите немного. Документ загружается.

800 B Turbulent Flow

two-dimensional equilibria no longer exist there, two-dimensional disturbances will

still decay on the slow viscous time scale, thus allowing the rapid three-dimensional

growth. Essentially the same story occurs in pipe ﬂow, although there it seems that

=∞. Numerical experiments have also found unstable travelling wave struc-

tures, now in the form of arrays of longitudinal vortices, and transition is associated

with their existence (Eckhardt et al. 2007).

Since in fact, turbulence is an irregular, chaotic motion, it seems most likely

that its occurrence is associated with the occurrence of a homoclinic bifurcation

(Sparrow 1982), which not only produces the strange turbulent motion, but also the

various travelling wave structures that can be found.

B.1 The Reynolds Equation

The actual calculation of turbulent ﬂows is usually done following Reynolds’s

(1895) formulation of averaged equations. We write the Navier–Stokes equations

for an incompressible ﬂow in the form

∂u

∂x

=0,

∂u

∂t

+ρ

∂

∂x

) =−

∂p

∂x

+μ∇

(B.2)

where sufﬁxes i represent the components, and the summation convention is used

(i.e., summation over repeated sufﬁxes is implied). If we denote time averages by

an overbar, and ﬂuctuations by a prime, thus

=¯u



, (B.3)

then averaging of (B.2) yields

∂ ¯u

∂x

=0,

∂

∂x

( ¯u

¯u

) +

∂

∂x

(ρu



) =−

∂ ¯p

∂x

+μ∇

¯u

(B.4)

The second of these can be written in the form

(

u.∇)

u =−∇p +∇.



τ +τ



, (B.5)

where

=2μ

¯ε



∂ ¯u

∂x

∂ ¯u

∂x



(B.6)

is the ordinary molecular mean stress, and

=−ρu



(B.7)

B.2 Eddy Viscosity 801

is called the Reynolds stress. The essential problem in describing fully turbulent

ﬂows is to close the averaged model by prescribing the Reynolds stress.

B.2 Eddy Viscosity

The simplest way to close the Reynolds equation is to suppose that

=2μ

¯ε

, (B.8)

by analogy to (B.6). The coefﬁcient μ

is called the eddy viscosity. This itself can

be prescribed in various ways, but the simplest is to take it as constant. For example,

in a channel ﬂow we might take

=ρε

¯ud, (B.9)

where d is the depth and ¯u the mean velocity. More generally, one allows μ

to vary

with distance from bounding walls, as described below.

Measurements in turbulent wall-bounded ﬂows lead to the deﬁnition of a friction

factor f through the wall stress

=fρ ¯u

. (B.10)

Here, ¯u is the mean velocity, and the friction factor f =

λ in Schlichting’s (1979)

notation. For an open channel ﬂow, (B.9) is consistent with (B.10)ifε

f .

Typical values for f are small, for example Blasius’s law in smooth-walled pipe

ﬂows has

f ≈

0.04

1/4

(B.11)

for Reynolds numbers in the range 10

–10

, and thus f ∼ 0.004 and ε

∼ 0.001.

Roughness of the wall gives correspondingly larger values of f and ε

. Notice that

−1

is the Reynolds number based on the eddy viscosity, and is relatively large,

reﬂecting the well-known fact that the turbulent eddies disturbing the mean ﬂow

are of relatively small amplitude. A more realistic form for the eddy viscosity uses

Prandtl’s mixing length theory, which is motivated by observations that the mean

velocity proﬁle is approximately logarithmic. The following discussion is based on

that of Schlichting (1979).

The friction velocity is deﬁned as

∗



(B.12)

(note that u

∗

¯u since generally f 1), thus

f =



∗

¯u



. (B.13)

802 B Turbulent Flow

For a one-dimensional shear ﬂow, with coordinate z normal to the wall (at z =0),

Prandtl’s mixing length hypothesis is

τ =ρl



∂u

∂z



∂u

∂z

, (B.14)

where τ is the shear stress, l is the mixing length, and u the velocity; Prandtl further

suggests

l =κz, (B.15)

with κ a constant. If we suppose τ =τ

= constant, then

∗

=κz

∂u

∂z

, (B.16)

thus

∗

=C +



∗



, (B.17)

which is the famous universal logarithmic velocity proﬁle. See also Question 5.11

and the discussion on turbulent ﬂow and eddy viscosity in the notes in Sect. 5.9 for

Chap. 5.

B.3 Pipe Flow

We now consider the case of ﬂow in a pipe of radius a, and suppose that (B.17)

applies, where z is radial distance inwards from the wall. If u

is the maximum

velocity at z =a, then (B.17) implies

−u =

∗





, (B.18)

and the mean velocity ¯u =



(a −z)u dz satisﬁes

−¯u =

∗

2κ

. (B.19)

In addition, comparison of (B.17) and (B.18) implies

∗



∗



∗

C. (B.20)

Using (B.19) and (B.13), and deﬁning the Reynolds number

Re =

¯ud

, (B.21)

B.4 Extension to Rivers 803

where the pipe diameter d =2a, we ﬁnd

√







+C −

2κ

−

ln2. (B.22)

Extensive measurements indicate that this formula is very successful in predicting

f(Re) assuming κ = 0.4, C =5.5. The principal assumption involved is that of an

eddy viscosity

=κ



∂u

∂z



. (B.23)

B.4 Extension to Rivers

The above results are easily extended to a river of depth d. Suppose now that

τ =τ



1 −



=ρκ

2

, (B.24)

where u



=∂u/∂z. Integrating, we ﬁnd, with u =u

at z =d,

−u =

∗



z/d

(1 −ξ)

1/2

dξ

∗



lncot

α −cos α



, (B.25)

where α =sin

−1



. With the mean ﬂow ¯u =



udz, we ﬁnd

−¯u =

∗

3κ

, (B.26)

while comparison of (B.25)asz →0 with (B.17) yields

∗

=C −



∗



, (B.27)

and elimination of u

between (B.26) and (B.27) gives, with Re =¯ud/ν,

√







+C −

3κ

ln2, (B.28)

essentially the same result as (B.22).

B.5 Manning’s Law

It is of interest to compare the laboratory born ﬂow law (B.28) with a ﬂow law such

as that of Manning. Manning’s law is

¯u =

2/3

1/2

, (B.29)

804 B Turbulent Flow

where R is the hydraulic radius and S is the downstream slope. For a wide river, we

take R =d and τ

=ρgdS. We thus have

¯uR =νRe,f¯u

=gRS, (B.30)

from which we ﬁnd

¯u =



gSνRe



1/3

,R=





1/3

, (B.31)

and Manning’s law (B.29) can be written in the form

f =



1/10

9/5

1/5



−1/5

, (B.32)

broadly comparable to (B.28). (As mentioned above, the often used Blasius relation

(B.11) approximating (B.28) has f ∝Re

−1/4

B.6 Entry Length

It is well-known that the development of laminar pipe Poiseuille ﬂow from a plug

entry ﬂow occurs over an extended distance (the entry length) which scales as dRe.

The entry length scale is determined by the diffusion of vorticity through laminar

boundary layers into the core potential ﬂow. If we scale up this process to rivers, with

d = 1m,Re =10

, it would suggest entry lengths of 1000 km! In reality, however,

such boundary layers would be turbulent, and a better notion of entry length would

be d/ε

, perhaps 100 m; and in fact sinuous channels and bed roughness will ensure

that river ﬂow will always be fully turbulent.

However, the entry length concept provides a framework within which one can

pose Kennedy’s (1963) potential ﬂow model for dune formation (see Chap. 5), even

if in practice it is not realistic. Further, if one adopts a constant eddy viscosity model

of turbulent ﬂow, then the small value of ε

is consistent with an inviscid outer

solution away from the boundary, even if the assumption of a shear free velocity is

not. On the other hand, it is conceivable that in laboratory experiments, the outer

inviscid ﬂow might indeed be a plug ﬂow if the entry conditions are smooth.

B.7 Sediment Deposition

Suppose now that a suspended sediment concentration c(z) is maintained in a turbu-

lent ﬂow by the action of an eddy viscosity. The units of c are taken to be mass per

unit volume of the stream. In equilibrium, we have a balance between the upward

turbulent ﬂux and the downward velocity, which we take as v

−ν

∂c

∂z

c. (B.33)

B.7 Sediment Deposition 805

We suppose Reynolds’ analogy that the eddy momentum diffusivity is equal to the

eddy sediment diffusivity, and between (B.23) and (B.24), we have

=κu

∗



1 −



1/2

. (B.34)

Solving this gives

c =c





exp



−Z



z/d

dξ



(1 −ξ)

1/2

−1



, (B.35)

where Z is the Rouse number,

Z =

κu

∗

. (B.36)

Unfortunately, this gives c =0atz =0 and thus zero deposition there! This is due

to the artiﬁcial singularity in u as z →0, and an artiﬁcial escape from this quandary

is to evaluate c at a small distance above the bed. As a simple alternative we suppose

is constant, given by (B.9) for example. Then

c =c

exp



−



, (B.37)

and the mean concentration is

¯c =



1 −e

−R



, (B.38)

where

R =

. (B.39)

If we use (B.9) and (B.13), then

R =

¯u

√

Z. (B.40)

The sediment deposition rate is, from (B.33) and cf. (5.10),

=¯cv

D, (B.41)

where (B.38) implies

D(R) =

1 −e

−R

. (B.42)

Other expressions involving ν

(z) give similar expressions which increase with R

(or Z) (Einstein 1950).

Appendix C

Asymptotic Solution of the Orr–Sommerfeld

Equation

In this appendix we provide an asymptotic solution of the Orr–Sommerfeld equa-

tion describing rapid shear ﬂow over a slightly wavy boundary. The description is

based on the asymptotic theory described by Drazin and Reid (1981), which itself

describes a body of research stemming from original investigations by Heisenberg

and Tollmien. The theory is, however, rather difﬁcult to follow, and is gone through

in detail here for that reason.

The Orr–Sommerfeld equation is







−k



−U







−2k





, (C.1)

and describes the z-dependent amplitude of a horizontal Fourier mode (of zero wave

speed) of wave number k. U(z) is the basic horizontal velocity proﬁle. The boundary

conditions we impose are those corresponding to no slip at the perturbed boundary

and free slip at the top surface:

Ψ =0,Ψ



=1atz =0,

Ψ =0,Ψ



=0atz =1.

(C.2)

We seek asymptotic solutions for R 1. Accordingly, there is an outer solution

Ψ ∼Λ



+···



, (C.3)

where Λ is a scaling parameter to be chosen so that Ψ

= O(1). The equation for

is the inviscid (Rayleigh) equation





−k



−U



=0, (C.4)

and we might expect to satisfy the boundary conditions on the free surface z =1. In

fact, we see that speciﬁcation of Ψ

=0onz =1 automatically implies that Ψ



there. The outer solution is written in terms of two independent Frobenius series of

A. Fowler, Mathematical Geoscience, Interdisciplinary Applied Mathematics 36,

807

808 C Asymptotic Solution of the Orr–Sommerfeld Equation

(C.4), expanded about z = 0. Assuming U(0) =0, U



(0) =U



=0, we have these

two solutions given by

=zP

(z),

(z) +





ln z,

(C.5)

where

=1 +





z +







+···,

=1 +







−

2

2



+···,

(C.6)

and the functions P

and P

are easily found numerically (Drazin and Reid 1981,

pp. 137–138).

We denote

(1) =P

; (C.7)

then the outer solution at leading order is

Ψ ∼Λ



−P



−1



. (C.8)

Evidently, this does not satisfy the boundary conditions at z = 0, and we antic-

ipate a boundary layer of thickness ε  1 (to be chosen), in which the neglected

terms become important. We deﬁne

z =εζ, (C.9)

and expand (C.8) in terms of ζ . The result is that

Ψ ∼Λ



−P

+εζ



−P





ln(εζ )



+···



, (C.10)

and Van Dyke’s (1975) matching principle indicates that we may need two terms of

the inner expansion to match to this.

In the boundary layer, it is appropriate to choose

ε =

(ikRU



)

1/3

, (C.11)

with the phase of ε (ph ε) deﬁned as −π/6 (we suppose U



> 0 and k>0). In this

case R

−1

∼ε

, and the second term in the outer solution is of relative order ε

.We

then write

Ψ ∼Λ[χ

+εχ

+···], (C.12)

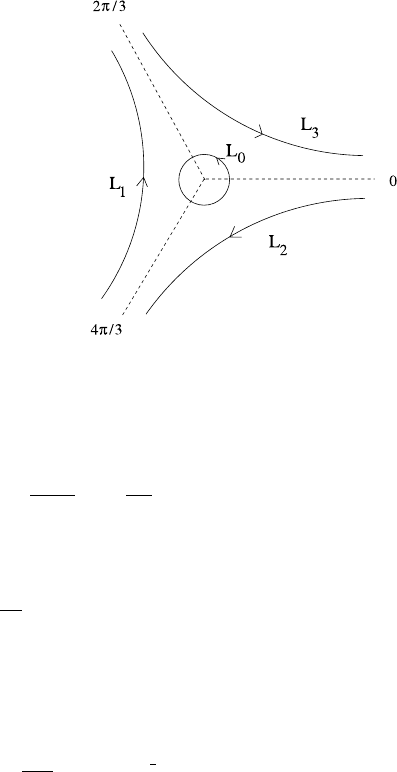
C Asymptotic Solution of the Orr–Sommerfeld Equation 809

Fig. C.1 Contours for the

Airy integral (C.15)

and the equations for χ

and χ

are

=0,







−





(C.13)

where the operators L and D are deﬁned by

D =

dζ

,L=D

−ζ. (C.14)

Reid (1972), see also Drazin and Reid (1981, pp. 465 ff.) shows how to solve these

equations in terms of a class of generalised Airy functions.

We begin by deﬁning the functions

(L)

(ζ ) =

2πi



−p

ζt−

dt, (C.15)

where L is one of the contours shown in Fig. C.1, and p is an integer. We denote the

function deﬁned via the contour L

as A

(k)

. (Drazin and Reid’s notation is different;

they write A

(k)

(ζ ) as A

(ζ, p).) These functions are analytic, and satisfy the third

order differential equation

(LD +p −1)A

=0. (C.16)

The functions A

(1)

(2)

(3)

are independent, and by contraction of L

∪L

we see that

(1)

(2)

(3)

(0)

=−B

(ζ ), (C.17)