Flechtner F.M., Gruber Th., G?ntner A., Mandea M., Rothacher M., Sch?ne T., Wickert J. (Eds.) System Earth via Geodetic-Geophysical Space Techniques

Подождите немного. Документ загружается.

240 R. Shako et al.

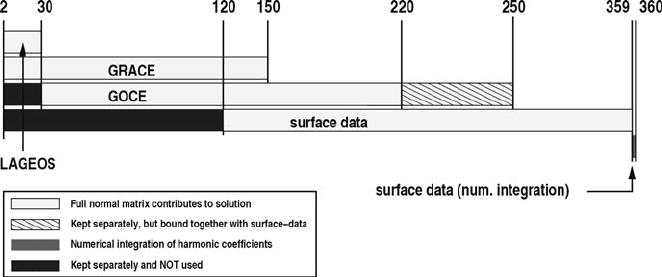
Fig. 6 Details of the planned GOCE-combination-model

coefﬁcients separately during the solution of the normal equation system. In the

transition zone from d/o 220 up to d/o 250, the coefﬁcients solved by GOCE are

bound to together with the surface data coefﬁcients by introducing degree-weighted

pseudo-observations as discussed in Sect. 3.2. After ﬁnding the optimum weighting

for the surface normal equations, the resulting combined normal equation system

is solved by Cholesky decomposition. For the optimum weighting a variance com-

ponent estimation will be established. Finally, the degree 360 coefﬁcients (obtained

through numerical integration) are added for completeness.

Once the ﬁrst real GOCE observations are available, it may be necessary to adapt

the strategy to the real characteristics of GOCE gradiometry measurements. For

instance, the reality may show that introducing a transition zone for the highest

GRACE degrees is necessary, or that the transition zone for GOCE should start

earlier or later, or that the contribution of the surface data should not begin at 120,

but at 90. Once the real GOCE observations are accessible, the details will be ﬁxed

both by thoroughly computation and validation of the results.

When surface data of global coverage with higher resolution than 30



×30



become publicly available (for instance the 5



×5



data-set used for the NGA

EGM2008 model; Pavlis et al., 2008), the goal will be to solve for a higher res-

olution model as well; for instance, a 15



×15



global surface data set would allow

for a model up to d/o 720. The strategy will be then a composition of the two previ-

ously discussed approaches. For degrees higher than d/o 360, the surface data will

contribute to the solution as block-diagonals.

4 Conclusions

With the GOCE gradiometry measurements, the door to a new age in geopotential

modelling will be opened, not only for satellite-only models, but for combination

solutions as well. GFZ is waiting for the ﬁrst GOCE observations with an improved

strategy, based on longterm experiences in gravity ﬁeld determination. A gravity

GOCE and Its Use for a High-Resolution Global Gravity Combination Model 241

ﬁeld model, complete up to at least 360 (in terms of spherical harmonics) with an

improved accuracy and quality will result. Surface data will contribute to d/o 359

as complete normal equations. The use of block-diagonal-techniques is planned if

future surface data sets allow for a higher resolution.

References

Abrikosov O, Jarecki F, Müller J, Petrovic S, Schwintzer P (2004) GOCE-GRAND: Gradiometer

data reduction, combination and processing. GEOTECHNOLOGIEN Statusseminar, GFZ

Potsdam, 5 July 2004 (Poster).

Abrikosov O, Schwintzer P (2004) Recovery of the Earth’s gravity ﬁeld from GOCE satellite grav-

ity gradiometry: A case study. Proceedings of the Second International GOCE User Workshop

“GOCE, the Geoid and Oceanography”, 8–10 March 2004, ESA-ESRIN, Frascati, Italy, ESA

SP-569.

Catastini G, Cesare S, de Sanctis S, Dumontel M, Parisch M, Sechi G (2007) Predictions of

the GOCE in-ﬂight performances with the end-to-end system simulator. Proceedings of the

3rd International GOCE User Workshop, 6–8 November 2006, Frascati, Italy, ESA SP-627,

pp. 9–16.

CIGAR IV (1996) Study of Advanced Reduction Methods for Spaceborne Gravimetry Data, and

of Data Combination with Geophysical Parameters, Final Report. ESA contract No. 152163 –

ASA study ESTEC/JP/95-4-137/MS/nr.

Biancale R, Balmino G, Lemoine J-M, Marty J-C, Moynot B, Barlier F, Exertier P, Laurain O,

Gegout P, Schwintzer P, et al. (2000) A new global Earth’s gravity ﬁeld model from satellite

orbit perturbations: GRIM5-S1. Geophys. Res. Lett. 27, 3611–3614.

Förste C, Flechtner F, Schmid R, Stubenvoll R, Rothacher M, Kusche J, Neumayer H, Biancale

R, Lemoine J-M, Barthelmes F, et al. (2008a) EIGEN-GL05C – A new global combined

high-resolution GRACE-based gravity ﬁeld model of the GFZ-GRGS cooperation, General

Assembly European Geosciences Union (Vienna, Austria, 2008), Geophysical Research

Abstracts, Vol. 10, Abstract No. EGU2008-A-06944/2008.

Förste C, Schmidt R, Stubenvoll R, Flechtner F, Meyer U, König R, Neumayer H, Biancale R,

Lemoine JM, Bruinsma S, et al. (2008b) The GeoForschungsZentrum Potsdam/Groupe de

Recherche de Gèodésie: Spatiale satellite-only and combined gravity ﬁeld models: EIGEN-

GL04S1 and EIGEN-GL04C. J. Geod. 82, 331–346, doi: 10.1007/s00190-007-0183-8.

Gruber T (2000) Hochauﬂösende Schwerefeldbestimmung aus Kombination von terrestrischen

Messungen und Satellitendaten über Kugelfunktionen. Scientiﬁc Technical Report STR00/16,

GeoForschungsZentrum, Potsdam.

Lemoine FG, Kenyon SC, Factor JK, Trimmer RG, Pavlis NK, Chinn DS, Cox CM, Klosko SM,

Luthcke SB, Torrence MH, et al. (1998) The Development of the Joint NASA GFSC and

NIMA Geopotential Model EGM96. NASA/TP-1998-206861, Goddard Space Flight Center,

Greenbelt, MD.

Migliaccio F, Reguzzoni M, Sanso F (2004) Space-wise approach to satellite gravity ﬁeld

determination in the presence of coloured noise. J. Geod. 78, 304–313, doi: 10.1007/s00190-

004-0396-z.

Pail R. Schuh W-D, Wermuth M (2005) GOCE gravity ﬁeld processing. In: Jekeli C, Bastos L,

Fernandez J (eds.), Gravity, Geoid and Space Missions, Springer, Berlin, ISDN 978-3-540-

26930-4, pp. 36–41.

Pavlis NK, Holmes SA, Kenyon SC, Factor JK (2008) An Earth Gravitational Model to Degree

2160: EGM2008. EGU General Assembly 2008. Vienna, Austria, 2008. Geophysical Research

Abstracts, Vol. 10, Abstract No. EGU2008-A-01891/2008.

Petrovic S, Reigber C, Schmidt R, Flechtner F, Wünsch J, Güntner A (2004) Comparing temporal

gravity variations derived from GRACE satellite observations and existing physical models.

Geophysical Research Abstracts, Vol. 6, EGU04-A-06903.

242 R. Shako et al.

Reigber C, Schmidt R, Flechtner F, König R, Meyer U, Neumayer K-H, Schwintzer P, Zhu SY

(2005) An Earth gravity ﬁeld model complete to degree and order 150 from GRACE: EIGEN-

GRACE02S. J. Geodyn. 39, 1–10, doi: 10.1016/j.jog.2004.07.001.

Rummel R, Gruber T, Koop R (2004) High level processing facility for GOCE: Products and

processing strategy. Proceedings of the 2nd International GOCE User Workshop, 8–10 March

2004, Frascati, Rome, Italy, ES SP-569.

Schmidt R, Petrovic S, Güntner A, Barthelmes F, Wünsch J, Kusche J (2008) Periodic components

of water storage changes from GRACE and global hydrological models. J. Geophys. Res. 113,

B08419.

Stubenvoll R (2006) GOCE and Terrestrial Data: A High Resolution Earth Gravity Combination

Model, GEOTECHNOLOGIEN Statusseminar “Beobachtung des Systems Erde aus dem

Weltraum”, Bonn, 18.-19.09.2006 (Poster).

Tapley B, Ries J, Bettadpur S, Chambers D, Cheng M, Condi F, Gunter B, Kang Z, Nagel P, Pastor

R, et al. (2005) GGM02: An improved Earth gravity ﬁeld model from GRACE. J. Geod. 79,

467–478, doi: 10.1007/s00190-005-0480-z.

Spectral Approaches to Solving the Polar

Gap Problem

Oliver Baur, Jianqing Cai, and Nico Sneeuw

1 Introduction

Launched on March 17, 2009, the GOCE (Gravity ﬁeld recovery and steady-state

Ocean Circulation Explorer) satellite mission will upgrade our present knowledge

about the Earth’s gravitational structure considerably. The mission’s major concern

is recovering the short-scale features of the terrestrial gravity ﬁeld, the gravitational

potential or geopotential respectively, with an anticipated geoid accuracy of about

2 cm, and a spatial resolution around 100 km (ESA, 1999).

In order to continuously supply the spacecraft with energy, the surface of the

satellite is equipped with solar panels, hence has to be oriented towards the sun

during the whole mission lifetime as good as possible. Due to the low satellite

altitude of around 250 km, the sun-synchronous orbit constraint causes the orbit

inclination to be around I ≈ 96.6

◦

. Consequently, in terms of data coverage, the

satellite ground track leaves out two circular-shaped polar areas completely. The

lack of observations in these regions is referred to as the polar gap problem (PGP).

In case of GOCE, the polar caps enclose 0.66% of the total Earth surface, adversely

affecting gravity ﬁeld determination from the satellite’s observations.

Conventionally, the geopotential is parameterized in spherical harmonics. This

representation can be interpreted as a two-dimensional Fourier expansion on the

sphere. Two base function indices characterize the individual spectral constituents,

referred to as degree l and order m. Based on spherical harmonics, the GOCE obser-

vation equations assembly is straightforward (e.g., Rummel et al., 1993; Ditmar

et al., 2003; Baur et al., 2008). Inversion, e.g. by means of least-squares (LS)

adjustment, of the resulting normal equations system yields the unknown series

coefﬁcients.

As a matter of fact, the lack of observations in the polar caps leads to a reduced

numerical stability of the normal equations, i.e., the system becomes ill-posed

(Metzler and Pail, 2005). Consequently, spatial data gaps map into non-resolvable

O. Baur (B)

Institute of Geodesy, University of Stuttgart, 70174 Stuttgart, Germany

e-mail: oliver.baur@gis.uni-stuttgart.de

243

F. Flechtner et al. (eds.), System Earth via Geodetic-Geophysical Space Techniques,

Advanced Technologies in Earth Sciences, DOI 10.1007/978-3-642-10228-8_19,



Springer-Verlag Berlin Heidelberg 2010

244 O. Baur et al.

spectral constituents. Particularly the low-order constituents can not be recovered

at all. In turn, r educed spectral domain resolvability for low orders implicates poor

spatial results in the polar caps. Moreover, the limited observation geometry distorts

gravity ﬁeld modelling in regions nearby the polar areas as well, although there

is high data coverage (Sneeuw and van Gelderen, 1997; M etzler and Pail, 2005).

According to van Gelderen and Koop (1997) the maximum non-resolvable order

max

depends on both the orbital inclination I and the spectral degree l subject to

the rule of thumb m

max

≈|0.5π – I | l, with I in radian. Hence, the number of

non-resolvable spherical harmonic coefﬁcients per degree increases with increasing

spectral resolution.

Solving the PGP means minimizing its impact on data analysis. In order to deter-

mine the terrestrial gravity ﬁeld as good as possible, various methods have been

proposed for and applied to the GOCE observation geometry. From the data point

of view they can be separated in approaches either using GOCE observations only,

or considering additional external data such as provided by space-borne gravimetry.

Alternatively, one can distinguish spectral and spatial domain approaches. As we

point out later, from the computational point of view, spectral domain approaches

are more convenient to overcome the PGP in the context of GOCE.

In this contribution we investigate two approaches to solving the PGP. Both

strategies are spectral domain methods. The ﬁrst one incorporates external data

in terms of spectral a priori information. The combination of both the GOCE

data and the additional spectral information is performed by tailored regulariza-

tion. The second approach belongs to the class of GOCE-only solutions. It is based

on the parameterization of the geopotential in band-limited base functions that are

optimally concentrated on the area of GOCE data coverage.

The next section gives a brief, referenced overview on selected strategies to solve

the PGP. In Sects. 3 and 4 we address the two spectral domain approaches mentioned

before in more detail. Finally, Sect. 5 summarizes the major conclusions of this

contribution.

2 Selected Strategies – A Review

2.1 Stabilization with External Data

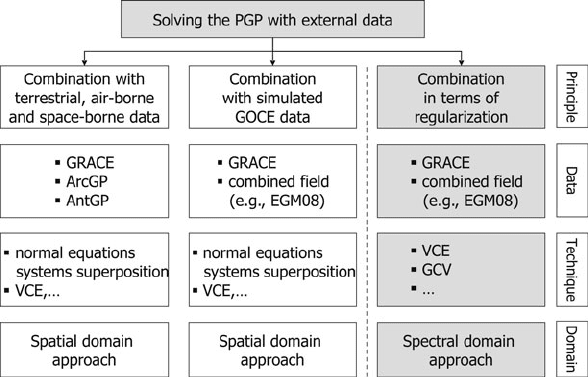
As outlined in Fig. 1, stabilization approaches including external data combine

GOCE observations with measurements provided by terrestrial, airborne or space-

borne gravimetry. GRACE (Gravity Recovery And Climate Experiment) observa-

tions, for example, have global coverage, as the GRACE spacecraft orbit the Earth

on an almost polar orbit (Tapley et al., 2004). Incorporating GRACE data in terms of

a combined analysis results in an additional (linear) model between observed grav-

ity ﬁeld functionals on the one hand and the unknown parameters of the geopotential

on the other hand. Opposed to the combination on the observation level, the GRACE

gravity ﬁeld information may be introduced by means of simulated GOCE measure-

ments. The method would require the conversion of GRACE spherical harmonic

Spectral Approaches to Solving the Polar Gap Problem 245

Fig. 1 Selected strategies to solving the polar gap problem with external data

coefﬁcients to simulated gravitational gradients in the spatial domain. The perfor-

mance of this combination approach depends on a variety of yet unsolved issues

such as the preferable spatial density of the simulated gradients and their weigthing

against the GOCE observations.

As a matter of fact, GRACE only resolves long- and medium-scale gravity ﬁeld

features. Terrestrial gravity observations such as provided by the Arctic gravity

project (ArcGP) and the Antarctic geoid project (AntGP) essentially augment the

satellite data (Forsberg and Kenyon, 2004; Scheinert, 2005). The individual obser-

vation models, normal equations systems respectively, are superposed in terms of

a joint LS adjustment procedure. Variance component estimation (VCE) may be

applied for the proper weighting of each kind of observation (e.g., Kusche, 2003).

Alternatively to the combination approach in the spatial domain, external grav-

ity ﬁeld information can also be introduced in the spectral domain. In this case, the

combination is performed in terms of regularization. The consideration of additional

spatial data exclusively in the polar areas has its spectral analogue in the regulariza-

tion of non-resolvable orders only. The r egularization of the whole spectrum, on

the other hand, corresponds to globally available external data. In the framework

of spectral domain stabilization techniques, we prefer the adoption of a combined

terrestrial gravity ﬁeld model, such as EGM08, as it contains terrestrial, airborne as

well as spaceborne measurements. Combined models are best ﬁtting the presently

available data sets.

The selected strategies in Fig. 1 outline a broad variety to solve the PGP with

external data. Within GOCE-GRAND II we focused on combination in terms of

regularization. We prefer spectral over spatial domain approaches for practical rea-

sons. Spectral approaches entail lower computational costs opposed to their spatial

counterparts. Predominantly the assembly of various additional normal equations

246 O. Baur et al.

systems is a challenging task. Incorporating external (spectral) information in “post-

processing” avoids any superposition effort. The GOCE normal equations system

is simply extended by some additional terms. From the computational point of

view, this extension is largely independent of the spectral a priori information used.

Consequently, the impact of different a priori information can be evaluated without

signiﬁcant additional implementation effort. In Sect. 3, we address the combination

in terms of regularization in more detail.

2.2 Stabilization without External Data

As a matter of fact, gravity ﬁeld solutions solely based on GOCE data do not consti-

tute the best state-of-the-art global description of t he terrestrial gravitational features

as they do not include all presently available gravity ﬁeld information. However,

GOCE-only solutions are characterized by the outstanding property to be internally

consistent, hence not prone to systematic errors of additional data sets. This is the

reason for the ESA (European Space Agency) requirement for the determination of

the Earth’s gravity ﬁeld from GOCE data only (ESA, 1999).

Without introducing any additional external data, a solution of the PGP leads to

the minimization of numerical instabilities and distortions within the data analysis

process, i.e., avoiding the normal equations to be ill-conditioned. Making no claim

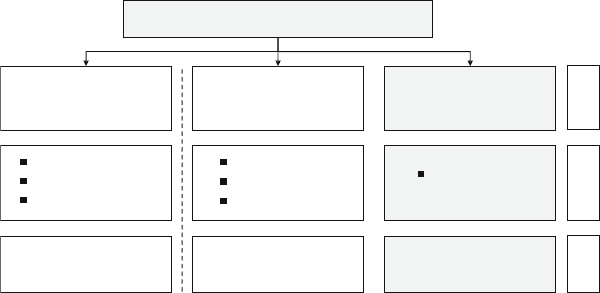
to be complete, Fig. 2 gives an overview on possible strategies.

Most stabilization methods applied in practice are related to tailored regu-

larization. Tikhonov-Phillips regularization (Phillips, 1962; Tikhonov, 1963), in

particular, is a commonly applied tool in satellite geodesy to treat ill-posed prob-

lems. The method stabilizes spectral constituents subject to a so-called penalty

term, which is added to the LS optimization functional. Its impact on the normal

equations matrix depends on the choice of the regularization matrix and the regular-

ization parameter. To ﬁx both, numerous proposals exist in literature (e.g., Kusche

Spectral domain

regularization

Slepian

parameterization

Spatial domain

regularization

Solving the PGP without external data

band-limited

base functions

artificial signal

gravity signal

SCRA

Kaula

order-dependent

VCE,GCV,…

Spectral domain

approach

Spectral domain

approach

Principle

Technique

Domain

Spatial domain

approach

Fig. 2 Selected strategies to solving the polar gap problem without external data

Spectral Approaches to Solving the Polar Gap Problem 247

and Klees, 2002). With regard to the PGP, the regularization of low orders only may

be the appropriate approach.

Alternatively, spatial domain regularization techniques force the geopoten-

tial towards a pre-deﬁned artiﬁcial or gravity signal at discrete locations. The

spherical cap regularization approach (SCRA), for example, implies a contin-

uous function, which is exclusively deﬁned in the polar regions (Metzler and

Pail, 2005).

Both the combination principles in Sect. 2.1 and the regularization approaches

mentioned before try to adapt the GOCE measurements to the gravity ﬁeld model

parameterized in spherical harmonics. A completely different approach starts from

the other point of view, i.e., not to adapt the observation geometry to the modeling

but instead, to adapt the parameterization of the geopotential to GOCE observations.

This results in band-limited base functions, also called Slepian functions that are

optimally concentrated on the spherical belt of GOCE data coverage. The Slepian

parameterization of the geopotential will be discussed in Sect. 4.

3 Regularization and Combination

In order to solve the PGP by spectral domain stabilization, we use a priori informa-

tion in terms of spherical harmonic coefﬁcients. Augmenting the minimization of

squared residuals r = Ax – y by a parameter component x – x

min

{||Ax −y||



−1

+ α||x − x

} (1)

yields the normal equations system

x = (A



−1

A +α R)

−1



−1

y +α Rx

). (2)

In Eqs. (1) and (2), 

is the variance-covariance matrix of the observations y,

and R indicates the regularization matrix, which is typically symmetric and positive

deﬁnite. The parameter α denotes the (a priori unknown) regularization parameter. It

balances the residual norm ||Ax – y||against the (reduced) parameter norm ||x – x

||.

Amongst alternative (predominantly heuristic) approaches, Cai (2004) developed a

method to compute the optimal regularization parameter analytically.

Equation (2) accounts for both regularization and combination. When x

= 0,

i.e. the a priori information consisting of null pseudo-observables, the penalty term

in Eq. (1) only impacts the normal equations matrix. This is the case of regu-

larization. In its simplest form, the regularization matrix may be set to identity,

R =I, often referred to as ordinary ridge regression. Commonly, however, the Kaula

matrix is used for regularization (Reigber, 1989). Its entries follow a simple power

law, approximating the signal content per spherical harmonic degree.

Data combination in the spectral domain is achieved by incorporating non-trivial

a priori information x

= 0, yielding the mixed estimator with additional informa-

tion as stochastic linear restrictions (Rao and Toutenburg, 1999). The regularization

248 O. Baur et al.

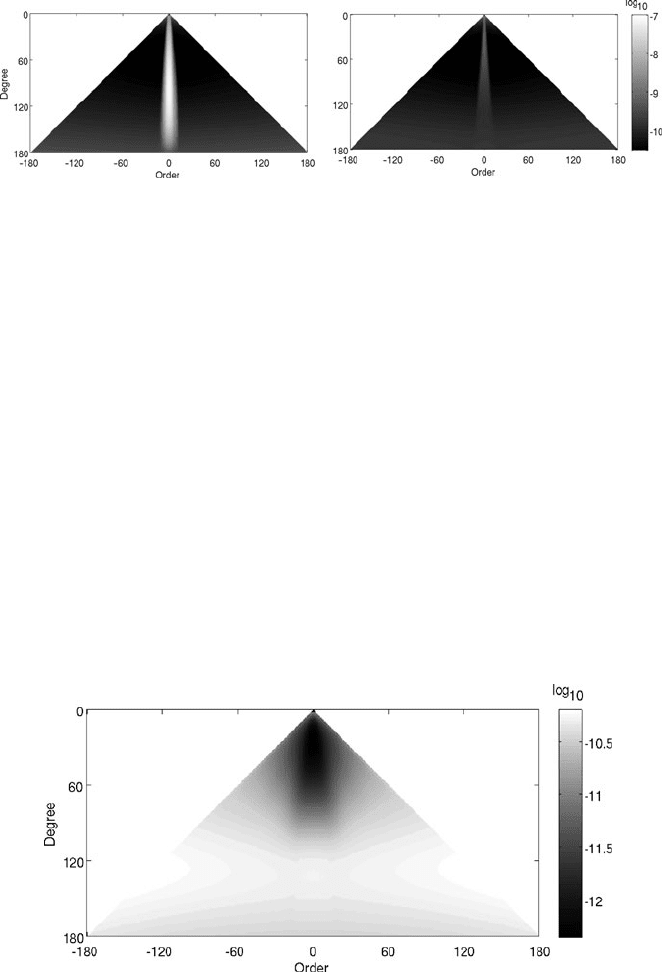
Fig. 3 Formal errors of GOCE spherical harmonic coefﬁcients (negative orders indicate sine, pos-

itive orders cosine coefﬁcients). Left panel: non-stabilized solution; right panel: Kaula-regularized

solution

matrix becomes the inverse error variance-covariance matrix of the parameter vector

.Bothx

and its error variance-covariance information are derived by the analy-

sis of observations either collected in the polar areas or over the whole globe. Here

we incorporate the gravity ﬁeld model EGM08 as spectral a priori information, as it

includes a multitude of currently available data sets. In order to deal with a diagonal

structure of the regularization matrix, we restrict ourselves on the error variances.

The left panel in Fig. 3 presents the a posteriori error standard deviations of

GOCE spherical harmonic coefﬁcients if neither regularization nor combination is

performed, i.e. R = 0 and x

= 0 holds true. The PGP causes a wedge-shaped

band around the zonal coefﬁcients to be poorly resolved. Kaula regularization,

cf. the right panel in Fig. 3, improves the overall quality of the parameter esti-

mate. The formal errors of the zonal and near-zonal coefﬁcients decrease by

roughly two orders of magnitude. However, the estimator turns out to be not

complete due to the non-proper introduction of a priori information in terms of zero

observations.

Fig. 4 Formal errors of spherical harmonic coefﬁcients for the mixed estimator solution, incor-

porating EGM08 spherical harmonic coefﬁcients and their variances as a priori information

(negative orders indicate sine, positive orders cosine coefﬁcients); different scale opposed to Fig. 3

applied

Spectral Approaches to Solving the Polar Gap Problem 249

Figure 4 displays the formal errors of spherical harmonic coefﬁcients incor-

porating the mixed estimator with a priori parameters x

= 0 and appropriate

variance information. For the combined solution, the quality of the parameter esti-

mate improves considerably. The different options for stabilization in the spectral

domain, cf. Eq. (2) and Figs. 3 and 4, outline the range of the regularization and

combination performance. The more accurate the a priori information the better the

accuracy of the coefﬁcient estimate.

4 Slepian Parameterization

Any strategy to solving the PGP using spherical harmonics faces the problem that

globally deﬁned base functions are forced to model spatially limited signals. The

orthogonality of Legendre functions, though, does not hold within a spatially limited

area. The misﬁt causes the normal equations to be ill-conditioned, and hence the

need to overcome the resulting numerical instabilities, cf. Sect. 3. With regard to

GOCE data analysis, opposed to Legendre functions, band-limited base functions

that are optimally concentrated on the spherical belt of data coverage are much

more convenient to ensure the consistency between the observations and the gravity

ﬁeld modelling.

The methodology of deriving band-limited base functions traces back to Slepian

(1978). Originally developed in communication theory to optimally transmit

band-limited signals in limited time he referred them to as prolate spheroidal wave

functions. Later, the simple term “Slepian functions” became more popular. Slepian

himself solved the concentration problem on the line only. However, the approach

can be easily transferred to the sphere as shown in Albertella et al. (1999), Pail

et al. (2001) and Simons et al. (2006). Concerning GOCE, the basic idea of the

Slepian parameterization approach is to ﬁnd a set of base functions that are opti-

mally concentrated within the data-covered spherical belt B = {0 ≤ λ <2π;

≤θ ≤ π – θ

}, with θ

denoting the co-latitude of the (double) spherical data gap.

Back in 1999, Albertella et al. (1999) investigated the method for space geodetic

applications. But they only succeeded in the calculation of non-structured band-

limited functions, leading to unsatisfactory results. Based on recent developments

(e.g., Miranian, 2004; Simons et al., 2006) we make use of an analytical expression

for the unique transformation to the Slepian base, deﬁnitively solving the concentra-

tion problem on the sphere. Simons et al. (2006), in particular, address special focus

on the axisymmetric double polar cap conﬁguration, hence the GOCE observation

geometry.

Slepian functions are derived by means of a maximum concentration problem, or

its equivalent algebraic eigenvalue problem (EVP):

 =

max ⇔ Dg = g .(4)