Flechtner F.M., Gruber Th., G?ntner A., Mandea M., Rothacher M., Sch?ne T., Wickert J. (Eds.) System Earth via Geodetic-Geophysical Space Techniques

Подождите немного. Документ загружается.

GOCE Data Analysis: From Calibrated Measurements to the Global Earth Gravity Field 219

2.2.1 Functional Model for In-Situ SGG Data Processing

As mentioned earlier, the in-situ approach to SGG data processing avoids trans-

formations of the data. Instead, to obtain the observation equations, the functional

model has to be expressed in t he GRF. To begin with, the equation describing

the gravitational potential of the Earth at a position with spherical coordinates

(r, ϑ, λ) in the EFRF, in terms of a spherical harmonic series up to d/o l

max

reads

V(r,ϑ ,λ) =

max



l=0





l+1



m=0



cos mλ + s

sin mλ





cos ϑ



,(5)

where l and m denote the spherical harmonic degree and order, c

and s

the

unknown coefﬁcients of spherical harmonic expansion, a the equatorial radius of

the Earth reference ellipsoid, P

(cos ϑ) the fully normalized associated Legendre

functions, and GM the geocentric gravitational constant.

The ﬁrst and second derivatives of Eq. (5) with respect to r, ϑ, λ in the EFRF can

be found e.g. in Hausleitner (1995). These derivatives are t ransformed into a local

north-oriented frame (LNOF), that is, an ˆx,ˆy,ˆz frame, where ˆx is pointing positive

to the north, ˆy positive east and ˆz positive along the radius; the resulting second

derivativesV

ˆxˆx

ˆyˆy

ˆzˆz

ˆxˆy

ˆxˆz

and V

ˆyˆz

are found to be certain combinations of the

ﬁrst and second-order derivatives in the EFRF (Hausleitner, 1995), and are thus also

linear functions of the spherical harmonic coefﬁcients. The corresponding design

matrix A

LNOF,i

is composed of 6 rows (one for each of the non-redundant tensor

components) and m columns (one for each spherical harmonic coefﬁcient) for each

position r

:= r(t

) (with i∈{1,...,n}).

Finally, the transformation of the design matrix A

LNOF,i

into the GRF has to be

found. For this purpose, we use the rotation between the LNOF and the GRF via

the inertial reference system (IRF) by means of the rotation matrices R

LNOF-GRF

and R

IRF-GRF

. The former is derived from GPS tracks and Earth rotation models,

the latter from star tracker data (reﬂecting the orientation of t he satellite in space),

and can be combined to R

LNOF-GRF

= R

IRF-GRF

LNOF-IRF

. This combined rotation

is applied to the tensor T

LNOF,i

by pre- and post-multiplication with R

LNOF-GRF

that is, T

GRF,i

= R

LNOF-GRF

LNOF,i

LNOF-GRF

. This yields six equations in the

non-redundant elements of T

GRF,i

, each of which is a linear function of the ele-

ments of T

LNOF,i

. These can therefore be written as t

GRF,i

= M

LNOF-GRF

LNOF,i

(where M

LNOF-GRF

is a 6×6 matrix, and t

GRF,i

, t

LNOF,i

denote the vectorized six

non-redundant tensor elements of T

GRF,i

and T

LNOF,i

, respectively). Substituting

the parametric model for the tensor components t

LNOF,i

it is seen that the design

matrix in the GRF results from A

LNOF,i

by premultiplication of M

LNOF-GRF

, that is,

GRF,i

= M

LNOF-GRF

LNOF,i

As we do not use the mixed tensor components V

, V

, the dimension of

GRF,i

is reduced to 3×m per position by deleting the rows of the unused tensor

components. Then we can write the in-situ observation equations with respect to the

given data l

(the observed gravity gradients V

, V

), unknown residuals v

and

220 J.M. Brockmann et al.

point-wise given design matrix A

GRF,i

(with i∈{1,...,n}), as

⎡

⎢

⎣

⎤

⎥

⎦

⎡

⎢

⎣

⎤

⎥

⎦

⎡

⎢

⎣

GRF,1

GRF,n

⎤

⎥

⎦

or in short l

SGG

+ v

SGG

= A

SGG

x to express the fact that Eq. (6) represents the full

SGG observation equation system.

Since the measurement frequency of GOCE is 1 Hz throughout the two measure-

ment phases, each of which is of approximately 6 months duration, the number of

positions is then n > 30,000,000. With three processed tensor components per posi-

tion and the number of parameters m given by m =(l

max

+1)

– 4 (as the coefﬁcients

with respect to degrees zero and one are not estimable) the resulting design matrix

SGG

will have approximately 100,000,000 rows and 73,437 columns (assuming

a resolution of l

max

= 270), requiring more than 50,000 GB of memory. Thus it

becomes evident that a numerically highly efﬁcient adjustment algorithm must be

applied which is capable of processing such a huge amount of data.

2.2.2 Stochastic Model of SGG Data

GOCE SGG data are auto-correlated in their three components V

, V

and V

because the gradiometer produces a ﬂat error spectrum only within a certain mea-

surement bandwidth in which the gradiometer measures most accurately (ESA,

1999). The three components are assumed to have negligible cross-correlations in

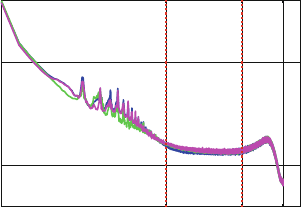
these simulations, which must still be validated for the real data. From simulations

we know the typical features and the approximate shape of the normalized spec-

tral density function (i.e. the Fourier transform of the autocorrelation function) of

the SGG data (see Fig. 2). Besides its aforementioned ﬂat behaviour within the

measurement bandwidth between 0.005 and 0.1 Hz, the error spectrum is mainly

characterized by an inverse proportional dependence (approx. f

–2

) and a large

number of sharp peaks on frequencies ranging from 0 to 0.005 Hz.

0.005 0.1 0.5

Frequency [Hz]

Error [mE/sqrt(Hz)]

Fig. 2 Simulated error

spectra of the three main

diagonal tensor components

GOCE Data Analysis: From Calibrated Measurements to the Global Earth Gravity Field 221

When estimating the gravity ﬁeld parameters via a rigorous least-squares adjust-

ment, this correlation pattern would normally have to be taken into account by

including the known data covariance matrix into the normal equations. However,

due to the huge number of SGG data, this covariance matrix cannot be stored

considering a memory requirement of more than 20 PetaByte. An effective solu-

tion to this problem consists in a full decorrelation of the SGG data before the

evaluation of the normal equations. Such a decorrelation can be performed effec-

tively through an application of digital ﬁlters to the SGG observation equations. To

achieve a full decorrelation, the autocorrelation pattern must be completely reversed

in the frequency domain. For this purpose, we used a sequential cascade of high-

pass ﬁlters (levelling the strongly correlated and inaccurate low-frequency part of

the error spectrum; see Schuh, 2002), notch ﬁlters (eliminating the narrow peaks;

see e.g. Siemes, 2008; Schuh, 2003), and ARMA ﬁlters (ﬂattening the entire resid-

ual spectrum; see Schuh, 1996 and e.g. Klees et al., 2003). Although these three

ﬁlter steps are recursive by design, the combined ﬁlter operation acting on the

SGG observation equations can be expressed via the linear transformation relations

F(l

SGG

+ v

SGG

) = FA

SGG

x (cf. Siemes, 2008) resulting in the decorrelated

observation equations

SGG

x with 

SGG

= I.(7)

In principle, the true autocorrelations are unknown as ground simulations cannot

replace GOCE in its operational mode in space. The above mentioned spectral den-

sity function is therefore considered as an approximate model to be adapted to the

real data in the course of the overall GOCE real data analysis (see Sect. 3).

2.3 Introduction of Regularizing Prior Information

Due to power supply requirements, the GOCE satellite has to take a sun synchronous

orbit, with an orbit of an inclination of about 96.5

◦

. This results in data gaps, because

the satellite will never cross the polar regions (cf. Fig. 3).

Fig. 3 GOCE orbit on the earth surface after 1 day, 1 week and 1 month mission duration

222 J.M. Brockmann et al.

The combined normal equation system, resulting from Sects. 2.1 to 2.2 with

respect to the SST and SGG data (see also Sect. 2.4) is ill-conditioned as a con-

sequence of both the absence of measurements above the polar regions (see Sneeuw

and van Gelderen, 1997; Kusche and Ilk, 2000, for this so-called polar gap problem)

and the attenuation of the gravity ﬁeld signal at the satellite’s altitude. To stabilize

the gravity ﬁeld solution, some kind of regularization is necessary, usually by adding

a third group of normal equations to the SGG and SST normal equations (see e.g.

Ditmar et al., 2003; Metzler and Pail, 2005).

The information contained in this additional group can be interpreted as pseudo-

observations (i.e. stochastic prior information in a Bayesian sense)

= s

= 0, for l ∈

{

min

...l

max

}

, m ∈

{

0 ...l

}

,(8)

reﬂecting the fact that the coefﬁcients tend to zero with higher degrees (accounted

for by smoothness conditions in Hilbert space). The assumed standard deviations

= σ

= 10

−5

,forl ∈

{

min

...l

max

}

, m ∈

{

0 ...l

}

(9)

of the coefﬁcients (8) are speciﬁed according to Kaula’s rule of thumb (cf. Kaula,

1966) and realistically rescaled by variance component estimation (cf. Sect. 3.2).

In summary, this group of (pseudo-)observation equations serves the purpose of

smoothing the parameter estimates and regularizing the effect of the polar gap and

the downward continuation; they take the form

REG

+ v

REG

= A

REG

x, 

REG

= diag





(10)

which results in the normal equations

REG



−1

REG

x = A

REG



−1

REG

⇔ 

−1

REG

x = 0 (11)

due to the fact that, ﬁrstly, the design matrix A

REG

is the identity-matrix and

secondly, the pseudo-observations are zero. Coefﬁcients for which the pseudo-

observations are not introduced (i.e. which are not regularized) are omitted by

setting the corresponding weights in



−1

REG

equal to zero.

2.4 Combination of All Observation Groups

Assuming the three observation types SST, SGG and REG to be uncorrelated, the

joint normal equation system is found by adding up the normal equations of each

observation group,



SST

+ ω

SGG

+ ω

REG



−1

REG



x = ω

SST

+ ω

SGG

(12)

GOCE Data Analysis: From Calibrated Measurements to the Global Earth Gravity Field 223

where ω

, k∈{SST,SGG,REG} denote factors by which the individual normal equa-

tions are weighted optimally. Besides the solution of this combined normal equation

system for the unknown parameters x, also the unknown weight factors ω

must be

estimated. From a numerical point of view, it is recognized from the normal equation

matrices in Eq. (12) that the memory requirements are to a great extent due to the

SGG group, whereas they are negligible for the preprocessed SST data (which cover

only a small subset of the parameter space and is zero outside) and the (diagonally

structured) regularizing prior information (see Table 2).

Table 2 Matrix sizes of the data types for different resolutions (with 1 year of GOCE data)

d/o m N

SST

[MB] 

REG

[MB] A

SGG

[TB] 

SGG

[PB] Remark

90 8,277 523.19 0.06 5.62 20.62 Speciﬁed Resolution

GOCE (SST only)

180 32,757 0.25 22.24 Resolution of current

GRACE models

200 40,397 0.31 27.43 Speciﬁed resolution of

GOCE (SST+SGG)

270 73,437 0.56 49.86 Expected maximum

resolution of GOCE

Thus the computation of the normal equation matrix N

SGG

is seen to be particularly expensive and is therefore avoided in our algorithm.

Consequently, this consideration applies also to the joint normal equation matrix

N = ω

SST

+ ω

SGG

+ ω

REG



−1

REG

. Instead, Eq. (12) is solved by

applying a tailored algorithm based on the method of conjugate gradients, which

allows data combination based upon both normal and observation equations as

described in the following Sect. 3.

3 Solving the Combined Normal Equation System

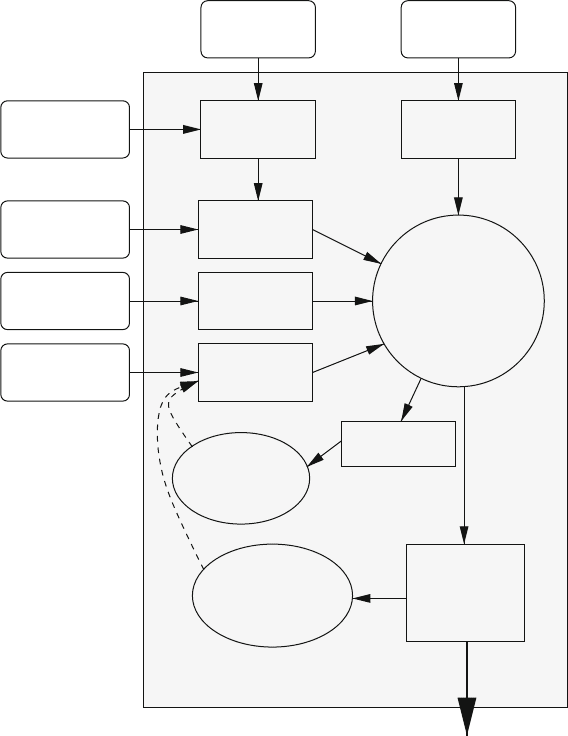
We will now give an outline of the iterative PCGMA algorithm (see Fig. 4), which

avoids the solution of the joint normal equation system in Eq. (12) via computation

of the combined normal equation matrix N. The core of PCGMA (Schuh, 1995,

1996) is an advanced version of the conjugate gradient (CG) method (Hestenes and

Stiefel, 1952; Schwarz, 1970), which allows for the combination of both normal

equations (in our case given by the SST group) and additional observation equa-

tions (such as given by the SGG and REG groups). PCGMA has been extended

recently by features such as data-adaptive preconditioning (Boxhammer and Schuh,

2006), efﬁcient decorrelation ﬁlters (cf. Sect. 2.2.2 and Siemes, 2008), Monte-Carlo-

based variance/covariance estimation (Alkhatib and Schuh, 2007; Alkhatib, 2007),

and implementation on a massive parallel computer cluster based on a client/master

concept (Boxhammer, 2006).

224 J.M. Brockmann et al.

deterministic

model

measurements

SGG

model

stochastic

coefficients

with

(co)variances

estimated

potential

SST normal

equations

information

SST a priori

information

precise orbit

information

gravity field

model

evaluation

data

inspection

parameters

a priori

spectral density

disturbances

a priori known

functionals

SGG

correlated

SGG+SST Gravity Field Processing

pcgma

residuals

Fig. 4 Processing chain for the in-situ adjustment of GOCE data

3.1 Preconditioned Conjugate Gradients Multiple Adjustment

The basic idea of PCGMA is to combine the CG method based on normal equations

(Hestenes and Stiefel, 1952) with the CG method based on observation equations

(Schwarz, 1970). Thus, any number of uncorrelated heterogeneous data types can

be adjusted jointly. If we tentatively assume that the weight factors ω

, an initial

solution x

(0)

and the fully decorrelated SGG observation equations are known, then

Eq. (12) can be solved directly by PCGMA. Within each iteration step, the standard

CG algorithm for normal equations requires knowledge of the residual-dependent

search direction and step length (resulting in a parameter update x). The residuals

GOCE Data Analysis: From Calibrated Measurements to the Global Earth Gravity Field 225

r = Nx–n of the combined normal equation system is found after rearranging terms

in Eq. (12)

r =



SST

+ ω

SGG

+ ω

REG



−1

REG



x −



SST

+ ω

SGG



(

SST

x −ω

SST

)



SGG

x −ω

SGG





REG



−1

REG



(

SST

)



SGG



SGG

x −

SGG





REG



−1

REG



Introducing the observation residuals

SGG

x −

SGG

, we obtain

r =

(

SST

)



SGG





REG



−1

REG



. (13)

Note that the residuals r can be computed very efﬁciently since the expensive com-

putation of

SGG

is thereby reduced to two matrix-vector products

SGG

x and

SGG

. In the following iteration steps both types of residuals (r and v) can be

updated by recursion formulas (see e.g. Schuh, 1996).

The convergence and stability of the CG algorithm just described can be acceler-

ated considerably by preconditioning the combined normal equation system, i.e. by

premultiplying Eq. (12)

−1

⊕

Nx = N

−1

⊕

n, (14)

where N

⊕

is chosen to be a sparse preconditioning matrix, approximating the domi-

nant structure of N. It constitutes the weighted sum of the non-zero entries of N

SST

the diagonal matrix



−1

REG

, and a subset of

SGG

. The latter is computed

within the so-called Kite structure (Boxhammer, 2006; Boxhammer and Schuh,

2006), i.e. only the block-diagonal correlations and the near-zonal correlations are

modeled. To achieve a most simple sparse structure within N

⊕

it is useful to rear-

range the elements of the parameter vector x according to the Free Kite Numbering

(FKN) scheme (Boxhammer, 2006), which allows one in particular (i) to keep the

SST parameters within a single coherent block, (ii) to maintain the block-diagonal

structure, and (iii) to model additional zonal correlations.

The residuals ρ of the preconditioned problem Eq. (14) are given by

ρ = N

−1

⊕

Nx −N

−1

⊕

n = N

−1

⊕

(

Nx −n

)

= N

−1

⊕

r (15)

i.e. the new residuals ρ result from preconditioning the original residuals r which

are computed in an efﬁcient way by Cholesky reduction of the sparse preconditioner.

With these tools at hand the standard CG algorithm can be applied (see e.g. Schuh,

1996). This procedure is easily modiﬁed to enable the solution of Eq. (12) for mul-

tiple right-hand sides, which allows for efﬁciently estimating the unknown weight

226 J.M. Brockmann et al.

factors or the variance/covariance matrix of the spherical harmonic coefﬁcients by

Monte-Carlo methods (Alkhatib, 2007).

3.2 Integration of VCE into PCGMA

In Sect. 3.1 the optimal weights of the observation groups k∈{SST,SGG,REG} in

the combination were treated as known quantities, which is however not a realistic

assumption. Interpreting these weights as variance factors ω

= 1/σ

0 k

, they can be

estimated via variance component estimation (VCE). These variance components

may be determined for uncorrelated groups by (see e.g. Koch and Kusche, 2002)

− m



− m

(16)

where n

denotes the (known) number of observations within observation group

k. The unknown weighted squared sum of residuals 

as well as the number of

parameters m

, determined by the corresponding observation group k, can be com-

puted from the normal equations as well as directly from the observation equations

by evaluating the trace of N

–1

or A

–1

using a stochastic trace estimator

(see e.g. Alkhatib, 2007; Brockmann and Schuh, 2008 for the convergence behav-

ior). As the residuals on the one hand change within each CG step but also depend on

the weights used for parameter estimation, the two iterative methods CG and VCE

are nested loops. Starting with initial guesses ω

(0)

, the CG steps are repeated until

convergence. The residuals of the ﬁnal CG step ν

max

are used to compute updated

weight factors, which in turn are used to solve Eq. (12) again for new parameter

estimates:

for τ = 1...τ

max

//VCE − iterations

for ν = 1...ν

max

//CG −iterations

x

(ν)

= estimateParameterUpdate(ω

(τ )

);

(ν+1)

= x

(ν)

+ x

(ν)

;

end

(τ +1)

= estimateWeights();

end

3.3 Integration of the Decorrelation Filters into PCGMA

Variance component estimation as described in the previous section requires that

the SGG observation equations have been decorrelated according to Eq. (7). As

we do not know the true PSD of the SGG data, but only an approximation thereof

GOCE Data Analysis: From Calibrated Measurements to the Global Earth Gravity Field 227

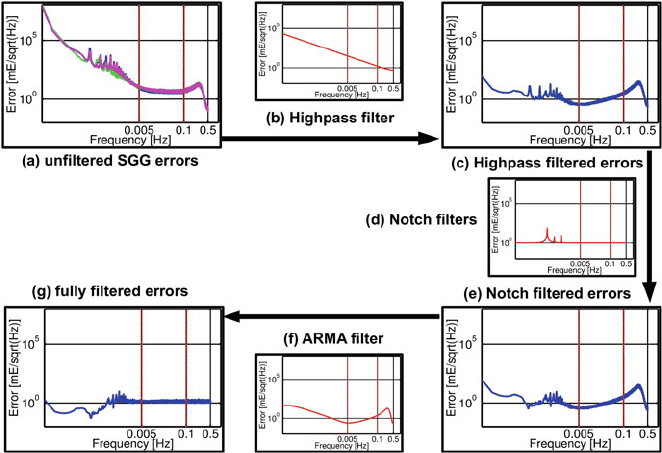
Fig. 5 Visualization of the power spectral densities (PSD) of the decorrelation process

from ground simulations, the PSD is estimated from the real data itself. As the

presence of the spherical harmonic trend function distorts the PSD estimate, it must

be ﬁrst eliminated from the data. Evidently, the trend at this stage is still unknown so

that some start values for the spherical harmonic coefﬁcients (or for the PSD) may

be used instead; eliminating the trend thus approximately results in start residuals,

whose PSD takes a form such as in Fig. 5a.

The goal is to ﬁlter the residuals (and thus the given observation equations) such

that their initial PSD (a) is transformed into a ﬂat spectrum, reﬂecting uncorrelat-

edness of the observations (g). This is achieved by applying three consecutive ﬁlter

steps: Firstly, a high-pass ﬁlter in the form of a difference or Butterworth ﬁlter (b) is

used to reduce the amplitudes below the measurement bandwidth (<0.005 Hz). The

thus ﬁltered residuals then still exhibit multiple sharp peaks below the measurement

bandwidth (c). These can, secondly, be reduced by using notch ﬁlters, wherein each

of these corresponds to one peak (d). The resulting ﬁltered residuals with PSD as in

(e) is in turn, thirdly, ﬁltered by means of an ARMA ﬁlter (f) which is speciﬁcally

designed to ﬂatten primarily the spectrum within the high-priority measurement

bandwidth. The ﬁnal PSD (g) of the ﬁltered residuals should be practically ﬂat,

which is statistically veriﬁed via white-noise tests (cf. Schuh and Kargoll, 2004).

Once these ﬁlters have been adjusted to the start residuals, they may be applied

to the given SGG observation equations via linear transformations. After a subse-

quent CG step (including VCE), improved trend coefﬁcients and residuals will be

available, which in turn enable a more realistic adjustment of the decorrelation ﬁlter

components along the same steps as just explained (Fig. 5).

228 J.M. Brockmann et al.

4 Conclusion and Outlook

The presented methods were applied to closed-loop simulations using synthetic

GOCE observations based on the EGM96 (Lemoine et al., 1998), and the latest error

models. Details of the simulation results concerning the modeling and processing of

SST data, implementation and convergence behaviour of PCGMA, variance com-

ponent estimation and ﬁlter design can be found in Wermuth (2008), Boxhammer

(2006), Alkhatib (2007), Brockmann and Schuh (2008), and Siemes (2008), respec-

tively. With these developments PCGMA is ready for the processing of the real data,

expected as of mid-2009.

Acknowledgments Parts of this work were ﬁnancially supported by the BMBF Geotechnologien

program GOCE-GRAND II and the ESA contract No. 18308/04/NL/MM. The computations were

performed on the JUMP supercomputer in Jülich. The computing time was granted by the John

von Neumann Computing Institute (project 1827).

References

Alkhatib H (2007) On Monte Carlo methods with applications to the current satellite gravity mis-

sions. Schriftenreihe des Instituts für Geodäsie und Geoinformation der Universität Bonn No.

7. PhD thesis. http://hss.ulb.uni-bonn.de/diss_online/landw_fak/2007/alkhatib_hamza/

Alkhatib H, Schuh WD (2007) Integration of the Monte Carlo covariance estimation strategy into

tailored solution procedures for large-scaled least squares problems. J. Geod. 70, 53–66.

Boxhammer C (2006) Efﬁziente numerische Verfahren zur sphärischen harmonischen Analyse

von Satellitendaten. Mitteilungen aus den Geodätischen Instituten der Rheinischen Friedrich-

Wilhelms-Universität Bonn, No. 94. PhD thesis. http://hss.ulb.uni-bonn.de/diss_online/

landw_fak/2006/boxhammer_christian/

Boxhammer C, Schuh WD (2006) GOCE gravity ﬁeld modeling: Computational aspects – Free

kite numbering scheme. In: Rummel R, Reigber C, Rothacher M, Boedecker G, Schreiber U,

Flury J (eds.), Observation of the Earth System from Space, Springer, Berlin/Heidelberg.

Bouman J, Rispens S, Gruber T, Koop R, Schrama E, Visser P, Tscherning CC, Veicherts M (2008)

Preprocessing of gravity gradients at the GOCE high-level processing facility. J. Geod., doi:

10.1007/s00190-008-0279-9.

Brockmann JM, Schuh WD (2008) Fast variance component estimation in GOCE data process-

ing. In: Mertikas S (ed.), Gravity, Geoid and Earth Observation, IAG Symposia 135, Springer,

Berlin.

Ditmar P, Kusche J, Klees R (2003) Computation of spherical harmonic coefﬁcients from grav-

ity gradiometry data to be acquired by the GOCE satellite: regularization issues. J. Geod. 77,

465–477.

Drinkwater MR, Haagmans R, Muzi D, Popescu A, Floberghagen R, Kern M, Fehringer M

(2007) The GOCE gravity mission: ESA’s ﬁrst core Earth explorer. Proceedings of the 3rd

International GOCE User Workshop in Frascati, Italy.

ESA (1999) Gravity ﬁeld and steady-state ocean circulation mission. Report for Mission Selection

of the Four Candidate Earth Explorer Missions. ESA-Document SP-1233(1).

ESA (2006) GOCE Level 2 Product Data Handbook. ESA-Document GO-TN-HPF-GS-0111.

Gerlach C, Földváry L, Svehla D, Gruber T, Wermuth M, Sneeuw N, Frommknecht B, Oberndorfer

H, Peters T, Rothacher M, et al. (2003) A CHAMP-only gravity ﬁeld model from kinematic

orbits using the energy integral. Geophys. Res. Lett. 30(20), 2037.

Hausleitner W (1995) Orbit and SGG Data Simulations. CIGAR III/Phase 2, Final Report, Part 1.

Hestenes M, Stiefel E (1952) Methods of conjugate gradients for solving linear systems. J. Res.

Natl. Bur. Stand. 49(6), 2379.