Fishwick P.A. (editor) Handbook of Dynamic System Modeling

Подождите немного. Документ загружается.

3-16 Handbook of Dynamic System Modeling

DeModel

has-TimeSet

Instance*

Instance

Instance*

TimeSet

has-Mechanism

has-Mechanism*

has-Component

time-Specified-by

time-Specified-by*

ModelMechanism

ModelComponent

TimingSpecification

StateOrientedModel

transitions-Triggered-by

TransitionTriggering

has-ClockFunction

has-TransitionFunction

TransitionFunction

TransitionEnabling

transitions-Enabled-by

events-Scheduled-by

EventScheduling

ClockFunction

TimingSpecification TransitionEnabling

EventScheduling

Initialization

ClockSetting TransitionTriggering

_Event_Enabling

_State_Machine_Scheduling

_Multiple_Event_Triggering _Single_Event_Tr

iggering

isa

state-initialized-by

clocks-Set-by

—

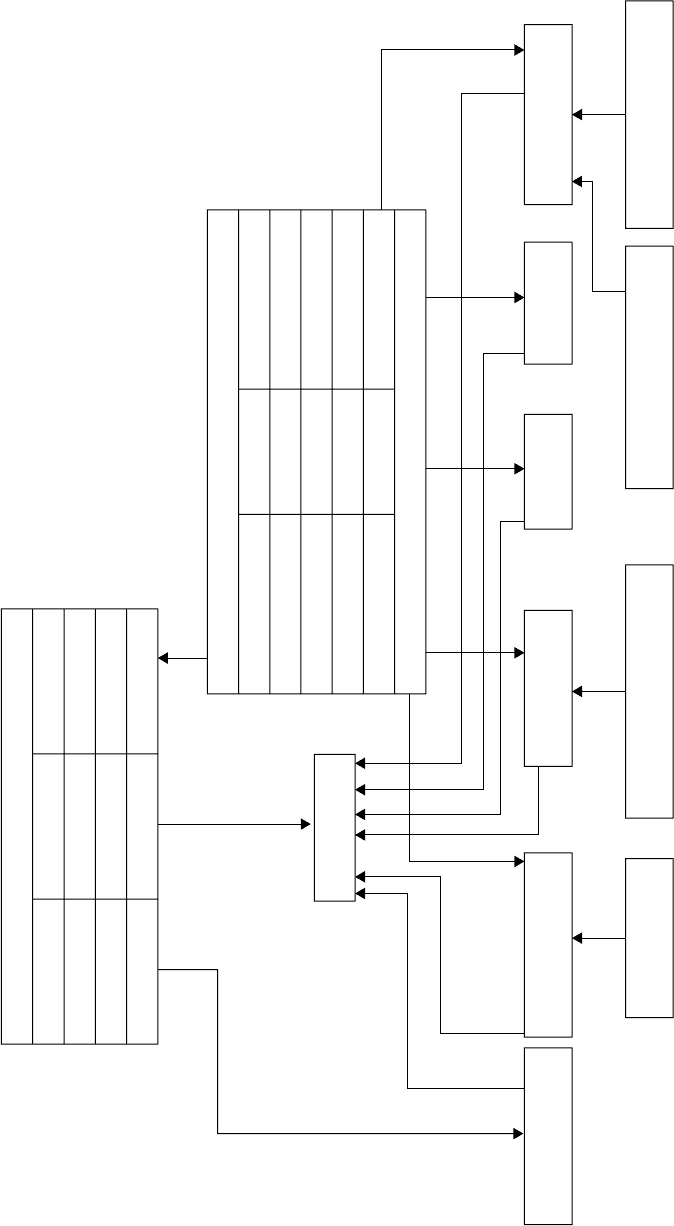
FIGURE 3.3

DeMO model component class hierarchy.

Impact of the Semantic Web on Modeling and Simulation 3-17

isa

ModelComponent

isa

InitialState

PlaceSet

TransitionFunction IncidenceFunction

StateSpace TimeSet

ClockFunction EventSet ActivitySet

ProbabilisticInitialState FinitePlaceSet

ProbabilisticTransitionFunction DiscreteStateSpace

ContinuousTimeSet DiscreteTimeSet

StochasticClockFunction NoClockFunction

FiniteEventSet

DeterministicClockFunction

FiniteStateSpace

DeterministicTransitionFunction

DeterministicInitialState

FIGURE 3.4

DeMO model mechanism.

3-18 Handbook of Dynamic System Modeling

DeModel

StateOrientedModel ActivityOrientedModel EventOrientedModel

GeneralizedSemiMarkovProcess

ExpandedStochasticPetriNet

EventGraph

StochasticTimedAutomata GSMP-SE QueuingNetwork GeneralizedStochasticPetriNet

TimedPetriNet

PetriNet

SimpleNet FreeChoiceNet

DiscreteTimeMarkovChain

ContinuousTimeMarkovChain

SemiMarkovProcessTimedAutomata

StateAutomata

FiniteStateAutomata

isaisaisa

isa

isa isa isa isa

isaisaisa

isa isa isa isa

isaisaisa

isa isa

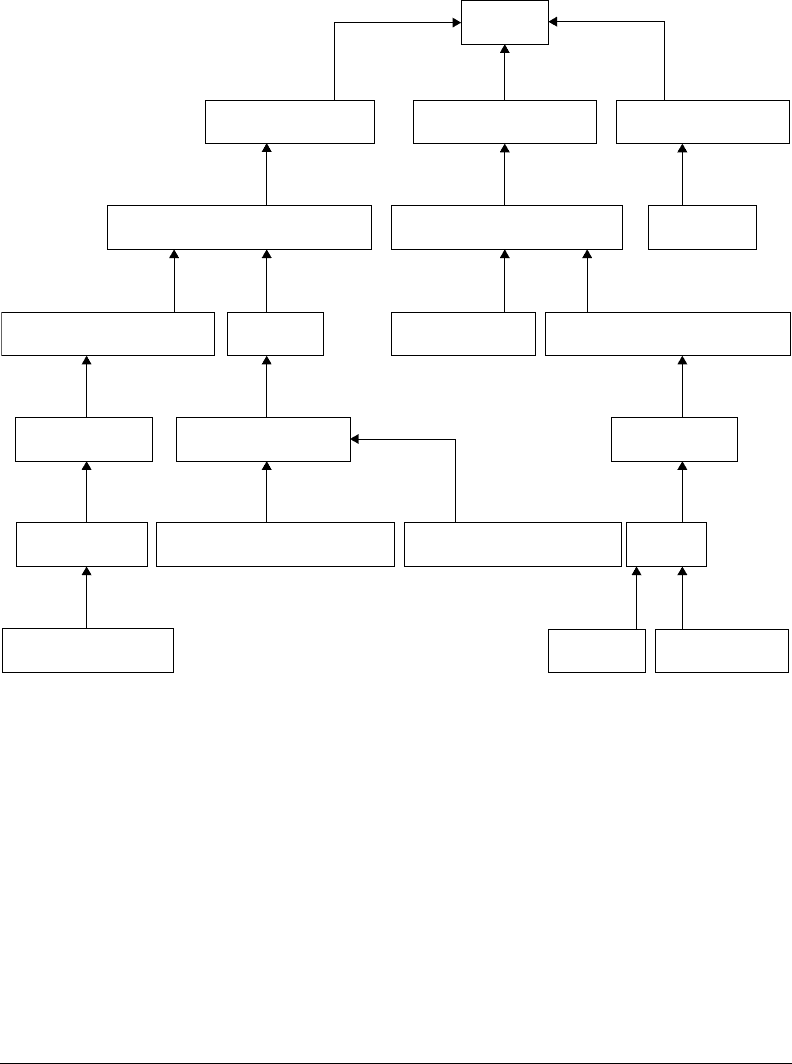
FIGURE 3.5 DeMO DeModel class hierarchy.

(for example, the following properties, has-ActivitySet, has-ArcSet, has-Component, has-Mechanism,

has-PlaceSet, has-TimeSet, time-Speciﬁed-by, deﬁne the structure and mechanics of a PetriNet). Since

Petri nets formalism is very popular, there are several simulators that run Petri nets. For the purposes

of standardization and interoperability, the Petri net markup language (PNML; Jngel et al., 2000) has

been created. Several of the simulators accept input in this format. One existing application of DeMO

is the automatic generation of PNML speciﬁcations from instances stored in DeMO. Note that DeMO

maintains topological information on the PetriNet, while PNML requires geometrical coordinates. Rules

could be developed to select layout algorithms that will take the topological information and convert it

into geometrical coordinates. This could lead to visually appealing animations of Petri net executions.

3.8 Summary

New developments in the semantic Web, especially in the ontology layer, present many opportunities for

the M&S community. This chapter has highlighted several of them. We have developed a general conceptual

framework for M&S as represented by DeSO and DeMO shown in Figures 3.1–3.5. The potential impact

of semantic Web research on the M&S communities has been discussed. In particular, the use of OWL and

SWRL have been demonstrated in the development of DeSO. Several issues in the construction and use of

ontology for M&S have also been addressed in this chapter.

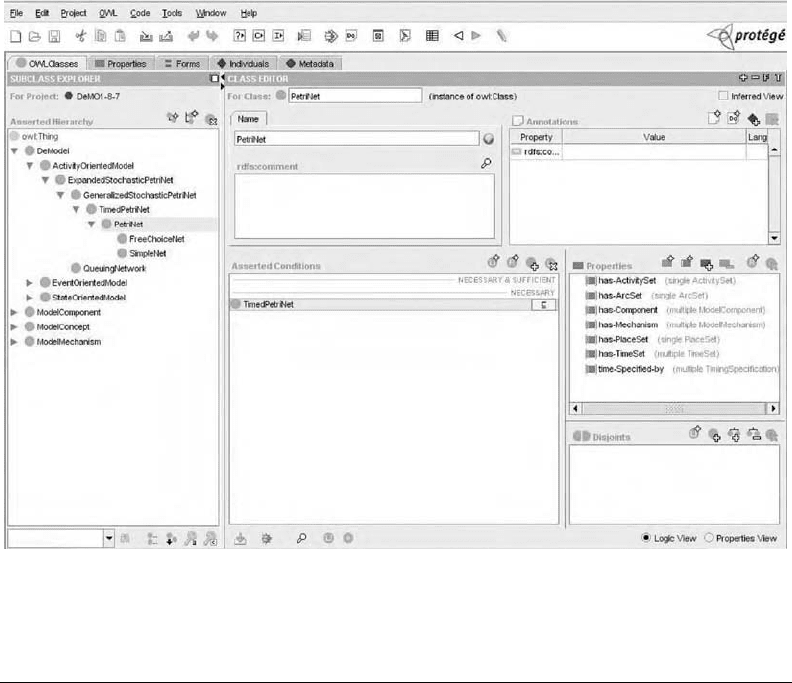
Impact of the Semantic Web on Modeling and Simulation 3-19

FIGURE 3.6 Protégé screenshot of DeMO.

Appendix: Semantics—Some Perspectives

Semantics has been a major topic of inquiry for a long time. As a traditional branch of linguistics, it refers

to the study of the meaning of language. Deeply rooted in philosophy, semantics was ﬁrst formalized in

logic in the nineteenth century and was later expanded to deal with programming-language semantics.

Now, the semantic Web initiative is bringing new life to this research and is attempting to make it practical

and scalable at the Web level. In this appendix, we look at semantics from the standpoint of philosophy,

linguistics, logic, programming languages, and the semantic Web.

Linguistics divides the world distinctly into “language” and “meaning.” Words, go in a lexicon, axioms

encoding meaning go in an ontology, and semantic lexicographers create bidirectional mappings between

the two. A lexicon of words or symbols is mapped to concepts, listing multiple concept types for words

that have more than one meaning. With many variations of notation and terminology, the basis for most

systems in computational linguistics consists of the following (Sowa, 2000): (i) lexicon—a set of symbols,

(ii) grammar—rules governing the ordering of symbols, and (iii) ontology—a topology of concepts.

A mapping that involves all three serves as a foundation for establishing meaning.

Given a description in a formal language, a difﬁcult question is“what does it mean.” Such a description,

as with natural language, will contain objects/nouns and actions/verbs. The meaning of the nouns and

verbs may be reﬁned using adjectives and adverbs, respectively. The elements of the description can

therefore be naturally decomposed into the two parts: objects and actions.

The study of the nature of objects has long been pursued in the ﬁeld of ontology. First, deﬁned by

Aristotle as “the science of being qua being,” ontology studies the existence of things. It concerns the nature

and meaning of existence as well as the basic categories of entities. Ontology is considered fundamental

because it tells people what words refer to entities, and it provides the classiﬁcation (including classes and

subclasses) of entities as well as their properties and relationship to other entities. Languages for modeling

3-20 Handbook of Dynamic System Modeling

ontology (or the related notion of schema) include the entity-relationship model (Chen, 1976), UML

(Rumbaugh et al., 1998), knowledge interchange format (Genesereth and Fikes, 1992), RDF (Klyne and

Carroll, 2004), OWL (McGuinness and Van Harmelen, 2004), and SWRL (Horrocks et al., 2003). The last

four of these languages are based on logic, primarily, description logic, and ﬁrst-order predicate logic.

Now that we have a way of describing entities, statically, we need to describe their dynamics. Issues

of behavior and interaction come to the forefront. One might look for an analog to ontology used to

describe nouns, objects, or entities that would work for verbs or actions. Unfortunately, dynamics is

much more challenging that statics. The ﬁrst phase of science is to describe the entities (e.g., genes and

proteins), while the second phase is to describe (better yet predict) how they will behave or interact (e.g.,

biochemical pathway models). Dynamic models involve entities that change (appear, disappear, move,

change properties, and affect others) over time.

Verbs are most naturally captured in ontology as relationships such as “student A enrolls in course B.”

However, this begs the question, what does enrolls in mean. The verb is not so much modeled as it is used

in the model of student. Still, one could in OWL deﬁne the enrolls in property to be a subproperty of takes

to claim some semantics is provided. A few comprehensive attempts at verb classiﬁcation have been done,

e.g., see VerbNet (Palmer, 2004).

A more complete treatment of dynamics calls for space-time models, which have a collection of inter-

acting entities that change over time. (Note, for generality, space is often represented abstractly as a state

which may include coordinates as well as other types of information.)

In formal logic, semantics provides a way to show that a statement (logical expression) is true. The most

prevalent approach is model-theoretic semantics (Tarski, 1983). A logical expression consists of constants,

variables, logical connectives, functions, and predicates. In ﬁrst-order logic, variables can be quantiﬁed,

while in second-order logic, functions and predicates may also be quantiﬁed. Unless, the expression is

a tautology, a “model” is required to determine its truth value. The “model” (not to be confused with a

simulation model) will indicate the domain that variables can range over, as well as, how to evaluate the

functions and predicates. If the “model” relates to something meaningful (e.g., a part of the real world)

then the expression can be meaningfully interpreted. There are also other alternative approaches such as

proof-theoretic semantics (Gentzen, 1969).

The semantics of programming languages formally or mathematically deals with the meaning of pro-

gramming languages. The symbols and the allowable orderings of these symbols are deﬁned using the

language’s lexicon (what symbols) and grammar (what order). The lexicon is often described using a reg-

ular language, while the grammar is often deﬁned using a context-free language. Together these constitute

the syntax of the language. Capturing what a sequence of symbols means is not so easy. For example, what

does x +y mean? Does the addition operator mean integer addition, ﬂoating point addition, or string

concatenation? There are three approaches to deﬁning the meaning of programs: denotational semantics,

operational semantics, and axiomatic semantics (Hoare, 1969; Scott-Strachey, 1971; Plotkin, 1981).

There is an ongoing debate about whether the semantic Web is really semantic (i.e., will it explicate

the meaning of resources on the Web). This debate involves open issues in philosophy and science, which

are not likely to be resolved any time soon. Hence, we simply claim that the approach makes things

“more” meaningful, in the sense of being easier to ﬁnd, use, and understand. Whether the machine truly

understands it, is an issue for others to tackle.

References

Akkiraju, R., J. Farrell, J. Miller, M. Nagarajan, M. Schmidt, A. Sheth, and K. Verma (2005). Web service

semantics—wsdl-s. http://www.w3.org/Submission/WSDL-S/.

Berners-Lee, T. (1998). Why rdf model is different from the xml model. http://www.w3.org/DesignIssues/

RDF-XML.html.

Berners-Lee, T., J. Hendler, and O. Lassila (2001). The semantic web. Scientiﬁc American 284(5), 34–43.

Impact of the Semantic Web on Modeling and Simulation 3-21

Brutzman, D. (2004). Extensible modeling and simulation framework (xmsf). http://www.movesinstitute.

org/xmsf.

Caprotti, O., M. Dewar, and D. Turi (2004). Mathematical service matching using description logic and

owl. http://monet.nag.co.uk/cocoon/monet/publicdocs/monet_onts.pdf.

Cellier, F. E. (1991). Continuous System Modeling. New York: Springer.

Chen, P. P. (1976). The entity-relationship model—Toward a uniﬁed view of data. ACM Transactions on

Database Systems 1(1), 9–36.

DEVS (2005). Devs. http://www.sce.carleton.ca/faculty/wainer/standard/.

Farrell, J. and H. Lausen (2006). Semantic annotations for wsdl. http://www.w3.org/2002/ws/sawsdl/spec/

SAWSDL.html.

Fishwick, P. A. and J. A. Miller (2004). Ontologies for modeling and simulation: Issues and approaches. In

Proceedings of the 2004 Winter Simulation Conference (WSC’04), Washington, DC, pp. 259–264.

Genesereth, M. and R. Fikes (1992). Knowledge Interchange Format, Version 3.0 Reference Manual. Stanford,

CA: Computer Science Department, Stanford University.

Gentzen, G. (1969). Investigations into Logical Deduction. Amsterdam: North-Holland.

Horrocks, I., P. F. Patel-Schneider, H. Boley, S. Tabet, B. Grosof, and M. Dean (2003). Swrl: A semantic

web rule language combining owl and ruleml. http://www.daml.org/2003/11/swrl/.

Hoare, C. (1969). An axiomatic basis for computer programming. Communications of the ACM 12(10),

576–585.

Jngel, M., E. Kindler, and M. Weber (2000). The Petri net markup language. The Workshop AWPN,

Koblenz, Germany.

Johnston, P. (2005). Xml, rdf, and dcaps. http://www.ukoln.ac.uk/metadata/dcmi/dc-elem-prop/.

Klyne, G. and J. J. Carroll (2004). Resource description framework (rdf): Concepts and abstract syntax.

http://www.w3.org/TR/2004/REC-rdf-concepts-20040210/.

McGuinness, D. L. and F.Van Harmelen (2004). Xml, rdf, and dcaps. http://www.w3.org/TR/owl-features/.

Miller, G., R. Beckwith, C. Fellbaum, D. Gross, and K. Miller (1990). Introduction to WordNet: An on-line

lexical database. International Journal of Lexicography 3(4), 235–244.

Miller, J. A. and G. Baramidze (2005). Simulation and the semantic web. In Proceedings of the 2005 Winter

Simulation Conference (WSC’05), Orlando, FL, pp. 2371–2377.

Miller, J. A., G. Baramidze, P. A. Fishwick, and A. P. Sheth (2004). Simulation and the semantic web. In

Proceedings of the 37th Annual Simulation Symposium (ANSS’04), Arlington, Virginia, pp. 55–71.

Minsky, M. (1974). A framework for representing knowledge. MIT-AI Laboratory Memo 306. Cambridge,

MA: MIT.

Mitkov, R. (2003). The Oxford Handbook of Computational Linguistics. Oxford: Oxford University Press.

Niles, I. and A. Pease (2001). Towards a standard upper ontology. In C. Welty and B. Smith (Eds.),

Proceedings of the 2nd International Conference on Formal Ontology in Information Systems (FOIS-

2001), Ogunquit, Maine.

Noronha, N. and M. J. Silva (2004). Using the semantic web for web searches. http://xldb.di.fc.ul.pt/data/

Publications_attach/NormanPaperInteraccao2004.pdf.

OpenMath (2006). Openmath. http://www.openmath.org/cocoon/openmath/index.html.

Palmer, M. (2004). Verbnet. http://www.cis.upenn.edu/ mpalmer/project_pages/VerbNet.htm.

Plotkin, G. D. (1981). A structural approach to operational semantics. Tech. Rep. DAIMI FN-19.

Pritsker, A. A. (1986). Introduction to Simulation and SLAM II (3rd ed.). New York, NY: Wiley.

Reichenthal, S. (2002). Srml: A foundation for representing boms and supporting reuse. In Proceedings of

the 2002 Fall Simulation Interoperability Workship, Orlando, Florida.

Rumbaugh, J., I. Jacobson, and G. Booch (1998). The Uniﬁed Modeling Language Reference Manual

(Addison-Wesley Object Technology Series). Essex, UK: Addison-Wesley Longman Ltd.

Scott, D. and C. Strachey (1971). Toward a mathematical semantics for computer languages. In Proceedings

of the Symposium on Computers and Automata, New York, pp. 19–46.

Shaya, E., B. Thomas, P. Huang, and P. Teuben (2006). Astroonto. http://archive.astro.umd.edu/.

3-22 Handbook of Dynamic System Modeling

Sheth, A., C. Ramakrishnan, and C. Thomas (2005). Semantics for the semantic web: The implicit, the

formal and the powerful. International Journal on Semantic Web and Information Systems 1(1), 1–18.

Silver, G., L. Lacy, and J. A. Miller (2006). Ontology based representations of simulation models follow-

ing the process interaction world view. In Proceedings of the 2006 Winter Simulation Conference.

Monterey, CA, pp. 1168–1176.

Sivashanmugam, K., K. Verma, A. P. Sheth, and J. A. Miller (2003). Adding semantics to web services

standards. In Proceedings of the 1st International Conference on Web Services (ICWS’03), Las Vegas,

Nevada, pp. 395–401.

Sowa,J. F. (2000). Knowledge Representation: Logical, Philosophical, and Computational Foundations. Paciﬁc

Grove, CA: Brooks/Cole Publishing Co.

Tarski, A. (1983). Logic, Semantics, Metamathematics (2nd ed.). Indianapolis, IN: Hackett.

Wikipedia (2006a). Wikipedia. http://www.wikipedia.org/.

Wikipedia (2006b). Wikipedia. http://en.wikipedia.org/wiki/Model_%28abstract%29.

Zalta, E. N. (2006). Stanford encyclopedia of philosophy. http://plato.stanford.edu/contents.html.

Systems Engineering

Andrew P. Sage

George Mason University

4.1 Introduction ...................................................................... 4-1

4.2 Systems Engineering ......................................................... 4-2

4.3 The Importance of Technical Direction and

Systems Management ........................................................ 4-4

4.4 Other Parts of the Story .................................................... 4-8

4.5 Summary ........................................................................... 4-9

4.1 Introduction

There are many ways in which we can deﬁne and describe systems engineering. It can be described

according to structure, function, and purpose. It may also be described in terms of efforts needed at the

levels of systems management, systems methodology, and systems engineering methods and tools. We can

speak of systems engineering organizations in terms of their organizational management facets, in terms

of their business processes or product lines, or in terms of their products or services. We can speak of

systemsengineering in terms of the knowledge principles,knowledgepractices, and knowledge perspectives

necessary for present and future success in systems engineering. This chapter takes a multifaceted and

transdisciplinary view of systems engineering. It attempts to describe systems engineering in terms of this

relatively large number of trilogies. the process view of systems engineering is expanded on in some detail.

Within this, a large number of necessary roles for systems engineering are described. A brief discussion

of systems engineering from the perspective of each of these necessary roles concludes the chapter. We

provide brief discussions on the theme of this handbook: dynamic system modeling.

The main objective of this chapter is to provide a multifaceted perspective on systems engineering and,

within that, systems management. This is a major challenge for a single chapter, one that is particularly

focused on the role of systems engineering in dynamic system modeling. Hopefully, this objective will be

realized. We believe that some appreciation for the overall process of systems engineering will lead naturally

to a discussion of the important role for systems management, and the applications of this to important

areas such as how best to use dynamic system modeling in the engineering of systems of all types.

We are concerned with the engineering of large-scale systems, or systems engineering (Sage, 1992a),

especially strategic-level systems engineering, or systems management (Sage, 1992b). We begin by ﬁrst

discussing the need for systems engineering, and then providing several deﬁnitions of systems engineering.

We next present a structure describing the systems engineering process. The result of this is a life-cycle

model for systems engineering processes. This is used to motivate discussion of the functional levels, or

considerations, involved in systems engineering efforts: systems engineering methods and tools, systems

methodology, and systems management. There is a natural hierarchical relationship among these levels and

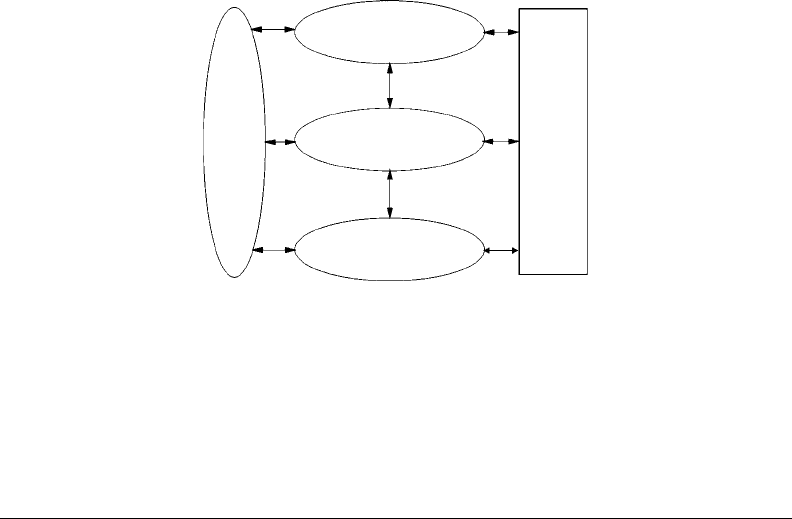
this is shown in Figure 4.1. There will be some discussions throughout this chapter on systems engineering

methods. Simulation and modeling is one of the major methods of systems engineering and, of course,

the theme of this work. Our primary focus here, however, is on systems engineering processes and systems

management for the technical direction of efforts that are intended to ultimately result in appropriate

systems, products or services. These result from an appropriate set of systems engineering methods and

4-1

4-2 Handbook of Dynamic System Modeling

Systems management

Systems engineering

processes

Systems engineering

methods and tools

Systems engineering

development team

System under

development

FIGURE 4.1 Conceptual illustration of the three levelsfor systems engineering. (FromSage, A.P., Systems Management

for Information Technology & Software Engineering, Wiley, Hoboken, NJ, 1995.)

tools, the resulting product line or process effort, and are guided by efforts at systems management, as

suggested in Figure 4.1. Considerably more details are presented in Sage (1992a, 1992b), which are the

sources from which much of this chapter is derived.

4.2 Systems Engineering

Systems engineering is a transdisciplinary management technology. Technology is organization, appli-

cation, and delivery of scientiﬁc knowledge for the betterment of a client group. This is a functional

deﬁnition of technology as a fundamentally human activity. A technology inherently involves a purposeful

human extension of one or more natural processes. For example, the stored program digital computer is

a technology in that it enhances the ability of a human to perform computations and, in more advanced

forms, to process information.

Management involves the interaction of the organization with the environment. The purpose of man-

agement is to enable organizations to cope better with their environments such as to achieve purposeful

goals and objectives. Consequently, a management technology involves the interaction of technology,

organizations concerned with both the evolvement and use of technologies, and the environment.

Information and associated knowledge are the catalysts that enable these necessary interactions and

allows them to be satisfactory. Information and knowledge are very important quantities that are assumed

to be present in the management technology that is systems engineering. This strongly couples notions of

systems engineering with those of technical direction or systems management of technological develop-

ment, rather than exclusively with one or more of the methods of systems engineering, important as they

may be for the ultimate success of a systems engineering effort. It suggests that systems engineering is the

management technology that controls a total system life-cycle process, which involves and results in the

deﬁnition, development, and deployment of a system that is of high quality, trustworthy, and cost-effective

in meeting user needs. This process-oriented notion of systems engineering and systems management will

be emphasized here.

As suggested in Sage (1992a, 1992b) systems engineering knowledge comprises three types of knowledge

(Sage, 1987a). Knowledge principles generally represent formal problem-solving approaches to knowledge,

and are employed in new situations and unstructured environments. Knowledge practices represent the

accumulated wisdom and experiences that have led to the development of standard operating policies

for well-structured problems. Knowledge perspectives represent the view that is held relative to future

directions and realities in the technological area under consideration. Clearly, one form of knowledge

leads to another. Knowledge perspectives may create the incentive for research that leads to the discovery

of new knowledge principles. As knowledge principles emerge and are reﬁned, they generally become

embedded in the form of knowledge practices. Knowledge practices are generally the major inﬂuences of

Systems Engineering 4-3

System

definition

Marketing

and

product

planning

life cycle

Research

development,

test and

evaluation

life cycle

System

deployment

System

development

System acquisition life cycle

FIGURE 4.2 Three primary systems engineering life cycles. (From Sage, A.P., Systems Management for Information

Technology & Software Engineering, Wiley, Hoboken, NJ, 1995.)

the systems that can be acquired or ﬁelded. These knowledge types interact with each other and support

one another. In a non-exclusive way, they each support one of the principal life cycles associated with

systems engineering. There are a number of feedback loops that are associated with learning to enable

continual improvement in performance over time. This supports our view that it is a serious mistake to

consider these life cycles in isolation from one another.

It is on the basis of the appropriate use of these knowledge types that we are able to accomplish the

technological system planning and development and the management system planning and development

that lead to a new innovative system, product or service. All three types of knowledge are needed. We

envision three different life cycles for technology evolution: system planning and marketing; research,

development, test and evaluation (RDT&E); and system acquisition, production, or procurement. Each of

these are generally needed, and each primarily involves the use of one of the three types of knowledge. We

will discuss these brieﬂy here, and will illustrate how and why these make major but non-exclusive use of

knowledge principles, practices, and perspectives. Figure 4.2 illustrates interactions across these life cycles

for one particular three-phase realization of a system acquisition life cycle.

It is important to deﬁne an area of intellectual inquiry for a better understanding. We have provided

one deﬁnition of systems engineering thus far. It is primarily a structural and process-oriented deﬁnition.

A related deﬁnition, in terms of purpose, is that systems engineering is a management technology to

assist and support policy making, planning, decision making, and associated resource allocation or action

deployment. Systems engineers accomplish this by quantitative and qualitative formulation, analysis,

and interpretation of the impacts of action alternatives upon the needs perspectives, the institutional

perspectives, and the value perspectives of their clients or customers. Each of these three steps is generally

needed in solving systems engineering problems, and models are especially useful supports in achieving

these ends. Issue formulation is an effort to identify the needs to be fulﬁlled and the requirements associated

with these in terms of objectives to be satisﬁed, constraints and alterables that affect issue resolution, and

generation of potential alternate courses of action. Issue analysis and assessment enables us to determine the

impacts of the identiﬁed alternative courses of action, including possible reﬁnement of these alternatives.

It is in this step that model development and use are of particular value. Issue interpretation enables

us to rank order the alternatives in terms of need satisfaction and to select one for implementation or

additional study. This particular listing of three systems engineering steps and their descriptions is rather

formal. The steps of formulation, analysis, and interpretation may also be accomplished in an “as if” basis

by application of a variety of often useful heuristic approaches. These may well be quite appropriate in

situations where the problem solver is experientially familiar with the task at hand, and the environment

into which the task is embedded.