Fishwick P.A. (editor) Handbook of Dynamic System Modeling

Подождите немного. Документ загружается.

5-14 Handbook of Dynamic System Modeling

Recall that functions such as the exponentials of Eq. (5.28) and Eq. (5.29), as well as sinusoids and

logarithms, are transcendental functions that can always be represented as power series. For example, the

power series for the exponential function is

x/λ

= 1 +









+ +





+ (5.30)

It is clear that the argument of the exponential must be dimensionless because without this property

Eq. (5.30) would not itself be a rational equation. Furthermore, one could not calculate numerical values

for the exponential—or any other transcendental—function, if its argument was not dimensionless. The

presence of a scale factor in Eq. (5.30) renders the exponential’s argument dimensionless, and so numerical

calculations can be performed.

Now, a charged capacitor draining through a resistor produces a voltage drop V (t)atarateproportional

to the value of the voltage at any given instant. The mathematical model is

dV(t)

=−λV(t) (5.31)

which can be rewritten as

dV(t)

V(t)

=−λ dt (5.32)

For this rate equation to be a rational equation, the net dimensions of each side of Eq. (5.32) must be

the same, which means that each side must be dimensionless. The left-hand side is clearly dimensionless

because it is the ratio of a voltage change to the voltage itself. The right hand will be dimensionless only if

the scale factor, λ, has physical dimensions such that [λ] =1/T. Furthermore, the dimensionless product

λt can be used to derive a measure of the time that it takes to discharge the capacitor being modeled. Thus,

deﬁne a decay or characteristic time as the time it takes for the voltage to decrease to a speciﬁed fraction of

its initial value, say 1/10. The characteristic or decay time of the charged capacitor would then be

V(t

decay

) ≡

(5.33)

The value of the characteristic time t

decay

can be calculated from the solution to Eq. (5.32) as

∼

2.303

decay

(5.34)

Equation (5.34) says that the scale factor λ for the discharging capacitor is inversely proportional to the

characteristic (decay) time, and so the voltage in the capacitor can then be written as

V(t)

∼

−2.303(t/t

decay

)

(5.35)

5.3.4 Consequences of Choosing a Scale

Since all actions have consequences, it should come as no surprise that the acquisition of experimental

data, its interpretation, and its perceived meaning(s) generally can be very much affected by the choice of

scales for presenting and organizing data. To illustrate how scaling affects data acquisition, consider the

diagnosis of a malfunctioning electronic device such as an audio ampliﬁer. Such ampliﬁers are designed to

reproduce their electrical input signals without any distortion. The outputs are distorted when the input

signal has frequency components beyond the ampliﬁer’s range, or when the ampliﬁer’s power resources

are exceeded. Distortion also occurs when an ampliﬁer component fails, in which case the failure must be

diagnosed to identify the particular failed component(s).

A common approach to doing such diagnoses is to display (on an oscilloscope) the device’s output to

a known input signal. If the device is working properly, a clear, smooth replication of the input would

Basic Elements of Mathematical Modeling 5-15

Square wave input

Square wave output on

timescale of 0.5 s/division

Square wave output on

timescale of 0.5 ms/division

Square wave output on

timescale of 0.5 ␮s/division

(a)

(b)

(c)

(d)

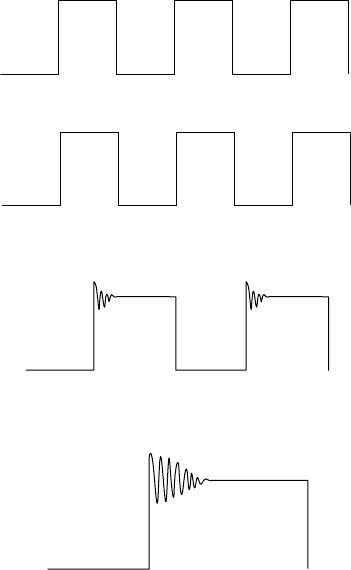
FIGURE 5.5 A square wave (a) is the input signal to a (hypothetical) malfunctioning electronic device. Traces

of the output signals are shown at three different timescales (i.e., long, short, and shorter): (b) 0.5 s/division; (c)

0.5 ms/division; and (d) of 0.5 µs/division.

be expected. One standard test input is the square wave shown in Figure 5.5(a). A nice replication of

that square wave is shown in Figure 5.5(b), and it seems just ﬁne until it is noticed that the horizontal

timescale is set at a fairly high value, that is, 0.5 s/division. To ensure that something that might not show

up on this scale is not overlooked, the same signal we spread out on shorter timescales of 0.5 ms/division

(Figure 5.5[c]) and 0.5 µs/division (Figure 5.5[d]), neither of which is a nice square wave. This suggests that

the device is malfunctioning. Had the oscilloscope not been set to shorter, more appropriate timescales,

an erroneous conclusion might have been reached. Thus, it is important to understand that scaling issues

are central not only to displaying experimental data, but also to its measurement and interpretation.

5.3.5 Scaling and Perceptions of Data Presentations

The scales used to present modeling “results” also signiﬁcantly inﬂuence how such data are perceived, no

matter whether those models are analytical or experimental in nature. Indeed, individuals and institutions

have been known to choose scales and portrayals to disguise or even deny the realities they purport to

present. Thus, whether by accident or by intent, scales can be chosen to persuade. While this is more of

a problem in politics and the media than it is in the normal practice of engineering and science, it seems

useful to touch on it brieﬂy here since the underlying issue is a consequence of scale.

Figure 5.6 and Figure 5.7 illustrate the consequences of scale in contexts somewhat beyond the normal

professional concerns of engineers and scientists. Both examples are shown because they use the same

5-16 Handbook of Dynamic System Modeling

1955 1956

325

300

275

Before stricter

enforcement

After stricter

enforcement

Connecticut traffic deaths,

before (1955) and after (1956)

stricter enforcement by the police

against cars exceeding speed limit

(a)

1951 1953 1955 1957 1959

225

250

275

300

325

Connecticut traffic deaths,

1951–1959

(b)

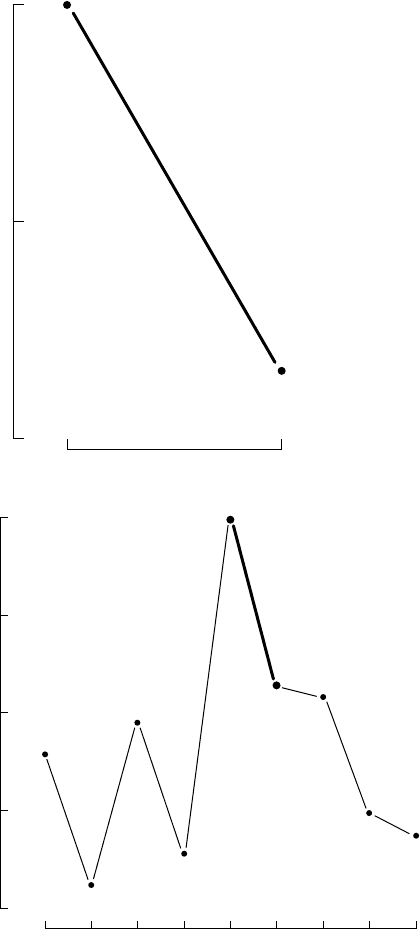
FIGURE 5.6 Plots of trafﬁc fatalities in the state of Connecticut, showing the dangers of truncating scales and deleting

comparative data: (a) Connecticut data for 1955–1956; (b) Connecticut data for 1951–1959; and (c) normalized data

for Connecticut and three neighboring states for 1951–1959. (From Tufte, E. R., The Visual Display of Quantitative

Information, Graphics Press, Cheshire, Connecticut, 1983.)

technique of carefully choosing a scale in a ﬁgure to present data out of context. Figure 5.6(a) shows a

rather dated picture of trafﬁc deaths in the state of Connecticut during the time interval 1956–1957, and a

sharp drop in trafﬁc deaths can be seen to have occurred then. But, was that drop real? And, in comparison

to what? It turns out that if more data are added, as in Figure 5.6(b), the drop is seen to follow a rather

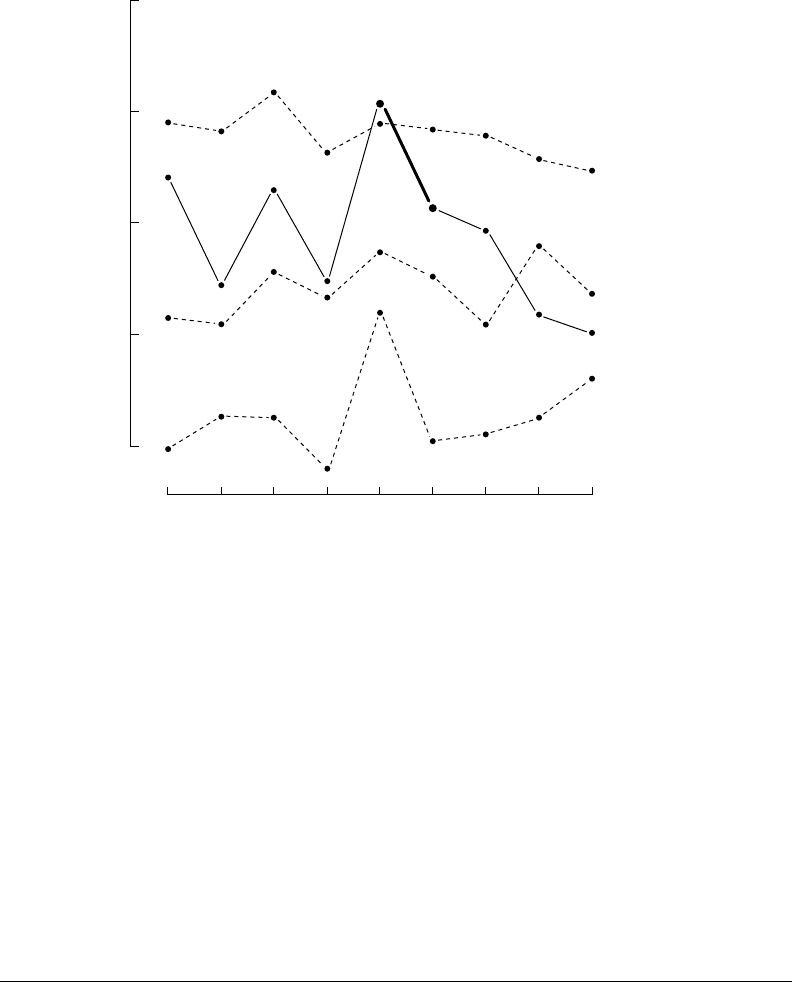
Basic Elements of Mathematical Modeling 5-17

1951 1953 1955 1957 1959

New York

Connecticut

Massachusetts

Rhode Island

Traffic deaths per 100,000

persons in Connecticut,

Massachusetts, Rhode Island,

and New York, 1951–1959

(c)

FIGURE 5.6 (Continued)

precipitous increase in the number of trafﬁc fatalities. Further, data from adjacent states were added and

the number of deaths was normalized against a common base, as shown in Figure 5.6(c), it would then be

seen that the numbers of Connecticut’s trafﬁc fatalities was similar to those of its neighbors, although the

impact of the stricter enforcement is still visible after 1955.

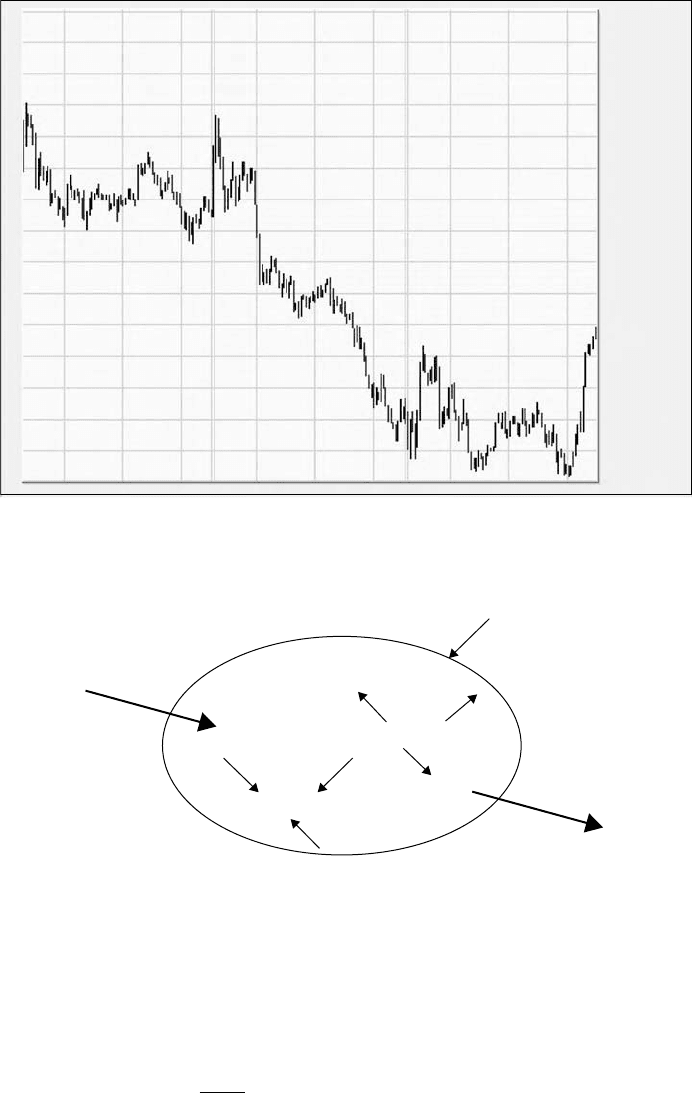
Similarly, one of the most often shown graphics in the ﬁnancial pages of newspapers, or in their televised

equivalents, are graphics such as that shown in Figure 5.7. Here, the immediate sense conveyed is that the

bottom has dropped out of the market because the scale used on the ordinate (or y- or vertical axis) has

been so foreshortened that it includes only one week’s trading activities. Thus, a decline of a few percent

in a stock market barometer such as the Dow Jones Industrial Average (DJIA) appears initially like a much

more precipitous decline—especially if the curve itself is drawn in red ink!

5.4 Conservation and Balance Principles

The development of mathematical models often starts with statements that indicate that some property of

an object or system is being conserved. For example, the motion of a body moving on an ideal, frictionless

path could be analyzed by noting that its energy is conserved. Sometimes, as when modeling the population

of an animal colony or the volume of a river ﬂow, quantities that cross a deﬁned boundary (whether

individual animals or water volumes) must be balanced. Such balance or conservation principles are applied

to assess the effect of maintaining or conserving levels of important physical properties. Conservation and

balance equations are related—in fact, conservation laws are special cases of balance laws.

The mathematics of balance and conservation laws are straightforward at this level of abstraction.

Denoting the physical property being monitored as Q(t) and the independent variable time as t, a balance

5-18 Handbook of Dynamic System Modeling

10,360

10,340

10,320

10,300

10,280

10,260

10,240

10,220

10,200

10,180

10,160

10,140

10,120

10,100

10,080

10,060

FIGURE 5.7 A plot of the performance of the New York Stock Exchange during 13–15 May 2002, as exempliﬁed by

that universally-cited barometer, the Dow Jones Industrial Average (DJIA). (From www.bigcharts.com, 2002)

Efflux, q

out

System boundary

Q (t )

Influx, q

Consumption, c

Generation, g

FIGURE 5.8 A system boundary surrounding the object or system being modeled. The inﬂux q

in(t)

, efﬂux q

out(t)

generation g(t), and consumption c(t) affect the rate at which the property of interest, Q(t), accumulates within the

boundary. (After Cha, P. D., Rosenberg, J. J., and Dym, C. L., Fundamentals of Modeling and Analyzing Engineering

Systems, Cambridge University Press, New York, 2000.)

law for the temporal or time rate of change of that property within the system boundary depicted in

Figure 5.8 can be written as

dQ(t)

= q

(t) +g(t) −q

out

(t) −c(t) (5.36)

where q

and q

out

represent the ﬂow rates of Q(t) into (the inﬂux) and out of (the efﬂux) the system

boundary, g(t) is the rate at which Q is generated within the boundary, and c(t) the rate at which Q is

consumed within that boundary. Note that Eq. (5.36) is also called a rate equation because each term has

both the meaning and dimensions of the rate of change with time of the quantity Q(t).

Basic Elements of Mathematical Modeling 5-19

In those cases where there is no generation and no consumption within the system boundary (i.e., when

g =c =0), the balance law in Eq. (5.36) becomes a conservation law:

dQ(t)

= q

(t) −q

out

(t) (5.37)

Here, then, the rate at which Q(t) accumulates within the boundary is equal to the difference between the

inﬂux, q

(t), and the efﬂux, q

out

(t).

5.5 The Role of Linearity

Linearity is one of the most important concepts in mathematical modeling. Models of devices or systems

are said to be linear when their basic equations—whether algebraic, differential, or integral—are such

that the magnitude of their behavior or response produced is directly proportional to the excitation or

input that drives them. Even when devices like the classic pendulum are more fully described by nonlinear

models, their behavior can often be approximated by linearized or perturbed models, in which cases the

mathematics of linear systems can be successfully applied.

Linearity is applied during the modeling of the behavior of a device or system that is forced or pushed

by a complex set of inputs or excitations. The response of that device or system to the sum of the individual

inputs is obtained by adding or superposing the separate responses of the system to each individual input.

This important result is called the principle of superposition. Engineers use this principle to predict the

response of a system to a complicated input by decomposing or breaking down that input into a set of

simpler inputs that produce known system responses or behaviors. However, some typicalbehaviors cannot

be captured by linear models, in which case it is important to be careful not to oversimplify inappropriately.

5.5.1 Linearity and Geometric Scaling

The geometric scaling arguments discussed earlier can also be used to demonstrate some ideas about

linearity in the context of geometrically similar objects, that is, objects whose basic geometry is essentially

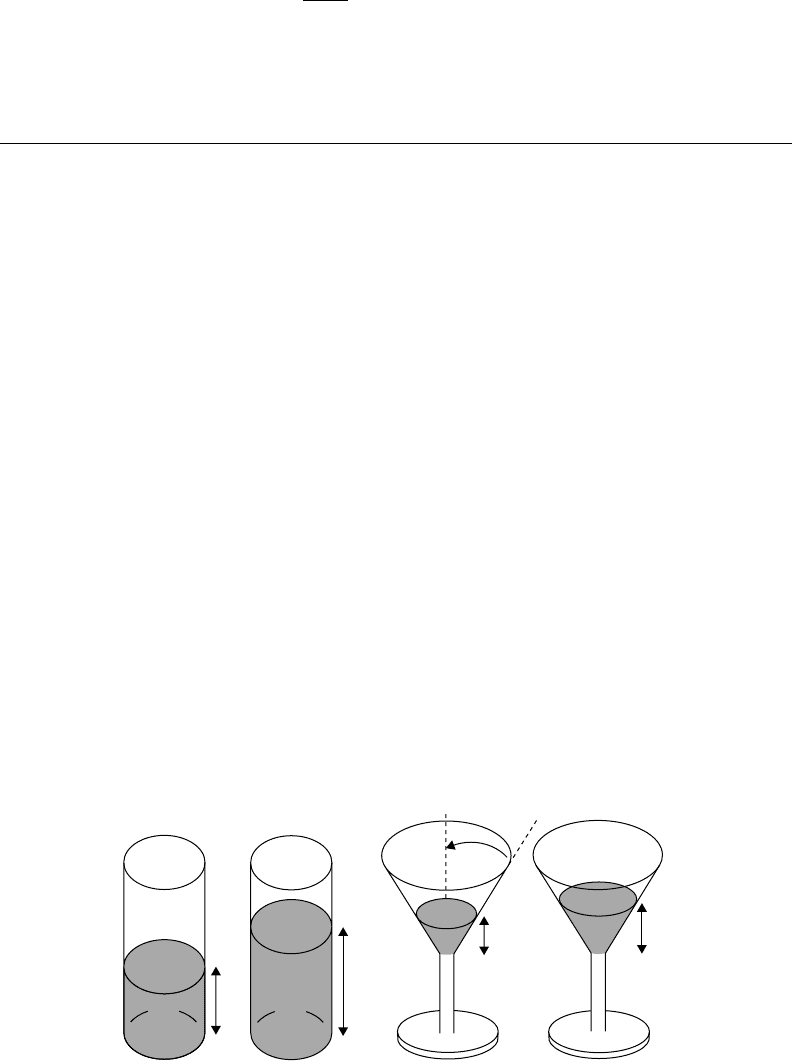
the same. Figure 5.9 shows two pairs of drinking glasses: one pair are right circular cylinders of radius r

and the second pair are right circular inverted cones having a common semi-vertex angle α. If the ﬁrst pair

is ﬁlled to heights h

and h

respectively, the total ﬂuid volume in the two glasses is

= πr

+πr

= πr

) (5.38)

Eq. (38) demonstrates that the volume is linearly proportional to the height of the ﬂuid in the two

cylindrical glasses. Further, since the total volume can be obtained by adding or superposing the two

heights, the volume V

is a linear function of the height h. Note, however, that the volume is not a linear

function of radius r.

h⬘

FIGURE 5.9 Two pairs of drinking glasses: one pair are cylinders of radius r, the second pair are inverted cones

(sometimes referred to as martini glasses) having a common semivertex angle α.

5-20 Handbook of Dynamic System Modeling

In the two conical glasses, the radii vary with height. In fact, the volume, V

, of a cone with semivertex

angle, α, ﬁlled to height, h,is

tan

(5.39)

Hence, the total volume of ﬂuid in the two conical glasses of Figure 5.9 is

3

tan

3

tan

=



)

tan

(5.40)

That is, the relationship between volume and height is nonlinear for the conical glasses, the total volume

cannot be calculated just by superposing the two ﬂuid heights, h



and h



. Note that this result, while to

a simple, even obvious case, is emblematic of what happens to superposition when a linearized model is

replaced by its (originating) nonlinear version.

5.6 Conclusions

This chapter has provided a very brief summary of the most basic foundations of mathematical modeling.

In this context, the discussion began with a statement of principles under which the activity of mathe-

matical modeling could be properly performed. This was followed by a discussion of basic foundational

matters, including dimensional homogeneity and dimensional analysis, abstraction and scaling, balance

and conservation laws, and an introduction to the role of linearity. It is important to note that this overview

emphasized brevity, dictated by chapter length limitations, and so it will hopefully serve as a stimulant to

the reader’s appetite for further reading and application of these basic ideas and methods.

Acknowledgment

The author is very grateful to Elsevier Academic Press for permission to summarize (or scale down!) the

ﬁrst three chapters of Dym, C. L., Principles of Mathematical Modeling, 2nd Edition, Elsevier Academic

Press, Orlando, Florida, 2004, and to reprint Figures 5.1–5.9 (as numbered here) from that book.

References

Alexander, R. M., Size and Shape, Edward Arnold, London, 1971.

Carson, E. and Cobelli, C. (Eds.), Modelling Methodology for Physiology and Medicine, Academic Press, San

Diego, 2001.

Cha, P. D., Rosenberg, J. J., and Dym, C. L., Fundamentals of Modeling and Analyzing Engineering Systems,

Cambridge University Press, New York, 2000.

Dym, C. L., Principles of Mathematical Modeling, 2nd Edition, Elsevier Academic Press, Orlando, Florida,

2004.

Tufte, E. R., The Visual Display of Quantitative Information, Graphics Press, Cheshire, Connecticut, 1983.

Tufte, E. R., Envisioning Information, Graphics Press, Cheshire, Connecticut, 1990.

DEVS Formalism for

Modeling of

Discrete-Event Systems

Ta g G on K im

KAIST

6.1 Introduction .................................................................... 6-1

6.2 System-Theoretic DES Modeling ................................... 6-3

6.3 DEVS Formalism for DES Modeling ............................. 6-3

Atomic DEVS Model

•

Coupled DEVS Model

•

Example of DEVS Modeling: Ping-Pong Protocol

•

State Equation Form of Atomic DEVS

6.4 DES Analysis with DEVS Model ..................................... 6-7

Composition of Atomic DEVS Models

•

System Analysis by Composed DEVS Model

6.5 Simulation of DEVS Model ............................................ 6-10

DEVS Modeling Simulation Methodology and

Environment

•

Simulation Speedup and

Simulators Interoperation

6.6 Conclusion ...................................................................... 6-12

This chapter introduces the discrete-event systems speciﬁcation (DEVS) formalism for modeling of

discrete-event systems (DESs). Based on set theory, the formalism speciﬁes DESs in a hierarchical, modular

manner. Models speciﬁed by the formalism can be used for analysis as well as performance simulation of

DESs.

6.1 Introduction

A DES consists of a collection of components that interact with each other via events exchange to perform

a given function. A component of such a system is represented by a discrete states set and operations

deﬁned on the set. The operations are mainly a set of rules for states transition, which is performed only

with an occurrence of instantaneous events over time. An event in DES may occur either by an external

stimulus to the component (external event) or an internal condition within the component (internal

event). A message arrival and a timeout in a communication system are examples of an external and an

internal event, respectively. Consider a DES of a ping-pong protocol system whose state transition diagram

is shown in Figure 6.1.

The protocol system consists of two components, SENDER and RECEIVER, each of which has its

own states and associated transition rules. Note that components, SENDER and RECEIVER, are cou-

pled together via two events: msg and ack. Let us ﬁrst give an informal description of each component

and then the interaction between the two. SENDER has two states, “Send” and “Receive,” the input

event ?ack and the output event !msg. Initially, SENDER stays at the “Send” state at which an output

event !msg is generated with a state transition to the “Receive” state. It then waits for an input event

6-1

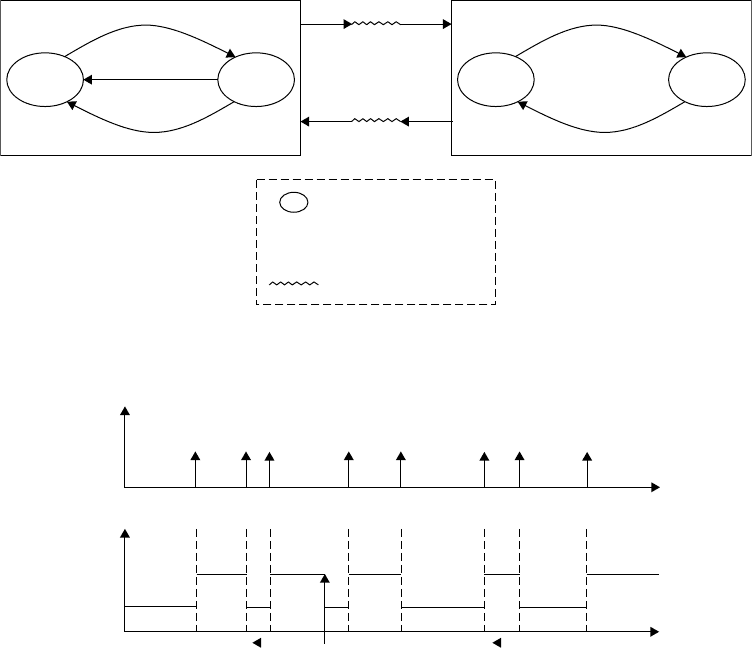
6-2 Handbook of Dynamic System Modeling

!msg ?msg

!ack?ack

Receiver

Send

Receive

!msg

?ack

*timeout

Sender

Receive

?msg

!ack

: state “q”

: input event “a”

: output event “b”

: internal event “c”

: components coupling

FIGURE 6.1 State transition diagram for ping-pong protocol.

Time

Event (external view)

msg

?ack

msg

?ack

msg

!msg

Time

State (internal view)

Send

Receive

*timeout

FIGURE 6.2 External and internal views for SENDER.

?ack to be arrived from RECEIVER. When SENDER receives the ?ack event at the “Receive” state it returns

to the “Send” state again. However, if the ?ack event is not arrived before a speciﬁed period SENDER

changes its state to the “Send” state. The state change is based on an assumption that !msg or ?ack is lost

during transmission through components coupling. Once SENDER comes back to the“Send”state it sends

!msg again, which may be a new one or the one previously sent. Note that SENDER changes its state from

“Receive”to“Send” either by an external input event ?ack or an internal event *timeout of the timeout

condition. The operation of RECEIVER can be described similarly.

The informal description of SENDER allows one to identify an external and an internal view of a

DES. The external view is a sequence of two events !msg and ?ack. The order of the two depends on

a rate of lost events and/or a value of the timeout. Thus, a legal events sequence may be one such as

!msg →?ack →!msg →!msg →!msg … →!ack. However, an events sequence !msg →?ack →?ack is not

a legal one. In contrast, the internal view of SENDER is a sequence of states which is a piecewise constant

function over time. For example,“Send”→“Receive”→“Send”→“Receive”… →“Send” is one such states

sequence. Figure 6.2 shows an external as well as an internal view of SENDER. Note that a state transition

from “Receive”to“Send” has been made by an internal event

∗

timeout.

A DES can be viewed as a system whose abstraction level in modeling is at the discrete-event one. In

the level, a modeler is interested only in what happens if an event occurs while ignoring details of system

behavior between events occurrences. In this sense most systems can be modeled at the discrete-event level

which we call a DES. Examples of DES include a communication protocol viewed at or above the data

DEVS Formalism for Modeling of Discrete-Event Systems 6-3

link layer, a computer system viewed at or above the operating system level, a military war game at the

operation level, and others.

Rest of this chapter is organized as follows. Section 6.2 presents DES modeling in the system-theoretic

view and Section 6.3 introduces the DEVS formalism. Analysis and simulation of DES with DEVS models

are given in Sections 6.4 and 6.5, respectively. Section 6.6 concludes this chapter.

6.2 System-Theoretic DES Modeling

The system-theoretic approach for systems modeling views a system as an object in which its representation

and associated operations are explicitly deﬁned. In the view a system is represented by three sets: inputs

set, outputs set, and states set; operations on the sets are deﬁned as a collection of rules, or functions, for

state transition and output generation.

In DES, both inputs and outputs are ﬁnite event sets. However, a states set is not ﬁnite. To be precise

recall the deﬁnition of state at t in system theory: information required at t which uniquely determines

output at t



> t. In fact, an output in DES is generated at a speciﬁed time when a certain condition is

satisﬁed. Thus, a state at t is represented by a discrete state, s, and an associated elapsed time, e, which is

a real number. Of course, the maximum elapsed time for each discrete state is predeﬁned, which we call

the maximum sojourn time, r, from now on. Then, a state (s,e) means that the discrete state s has been

kept for the e time unit without any external input. If no input is arrived at the state before the maximum

sojourn time r an output would be generated. Of course, an input event can be arrived anytime before

the r time unit. In such a case, the discrete state s is changed to a new one s



that has its own maximum

sojourn time r



. To be clear we call s a discrete state and q =(s,e) a total state or just a state of DES. Since e

is a real number q is not ﬁnite.

We are now ready to explain how system theory deﬁnes state transition functions of a dynamic system.

In the theory, two state transitions are considered: one with an input and the other without an input. For

example, a well-known vector differential equation for state transition of a linear continuous system is

dQ/dt =AQ + BX,whereQ is a state set, X an inputs vector, and A and B are the coefﬁcient matrices.

Note that dQ/dt =AQ speciﬁes state transition without inputs and dQ/dt =BX speciﬁes that with inputs

X. As will be shown later, the same view would be applied in DES modeling. More speciﬁcally DES has a

state transition either with an external input event or with a condition internal to a system, which causes

an internal event. Such a condition at a state q =(s,e) includes e =r, meaning that an elapsed time e is

reached to the maximum sojourn time r at s. From now on we call state transition with an input as external

state transition and that without an input as internal state transition. Similarly, an output is a function of

both an input and a state. However, an output function can be represented only by state information, for

the information memorizes history of inputs information.

As shown in Figure 6.1, a DES consists of components that are connected together for interaction with

events exchange. Thus, speciﬁcation of DES should have a means to specify the connection. In sum,

modeling of DES in the system-theoretic approach requires the following expression:

•

each component needs inputs set, outputs set, states set, state transition functions, both external

and internal transitions, and output function;

•

connection of components needs a means for coupling between events associated with components.

The DEVS formalism to be introduced in the following chapter supports such an expression in a formal

manner for modeling of DES.

6.3 DEVS Formalism for DES Modeling

The DEVS formalism, developed by Zeigler, speciﬁes a DES with the following three major features

(Zeigler, 1984; Zeigler et al., 2000):

•

set theory-based formalism