Fishwick P.A. (editor) Handbook of Dynamic System Modeling
Подождите немного. Документ загружается.

6-4 Handbook of Dynamic System Modeling
•
system-theoretic representation
•
hierarchical, modular specification.
The DEVS formalism is constructed based on set theory in which a static structure, such as states, is
represented by a set and dynamic behavior, such as state transition, is specified by operations on sets.
Set-theoretic modeling is known to be very intuitive in a modeling process. Moreover, with the set theory
the formalism represents a DES in a system-theoretic view. With the view the formalism specifies a system
as a static representation of inputs, outputs, and states sets and dynamic operations defined on sets.
Finally, the formalism specifies a system in a hierarchical, modular manner. This feature allows a modeler
to decompose a discrete-event model into a collection of modular submodels, each of which in turn is
decomposed into modular submodels, and so on. To do so develops a discrete-event model with a powerful
combination of top-down model design and bottom-up model implementation.
6.3.1 Atomic DEVS Model
The DEVS formalism defines a DES into two classes of models: atomic model and coupled model. An
atomic model is a nondecomposable model in hierarchical decomposition; a coupled one is a collection
of either atomic or coupled model. An atomic model specifies state transition and output generation over
time. In contrast, a coupled model specifies a list of components and their coupling information. Formally,
an atomic DEVS model (AM) is defined as follows:
AM = <X, S, Y, δ
ext
, δ
int
, λ,ta>
where
X: a set of input events;
S : a set of sequential states;
Y : a set of output events;
with the following constraints:
ta: S →R (nonnegative real number), time advance function;
δ
int
: Q →Q, an external transition function;
where Q =S ×R ={(s, e) |s ∈S and 0 ≤e ≤ ta(s)}, states set of M;
λ: Q →Y , an output function;
δ
ext
: Q ×X →Q, an external transition function.
As shown in the above definition, AM has three sets and four functions which we call characteristic
functions. Note that AM has two transitions, δ
ext
and δ
int
. δ
ext
is state transition with an input event and
δ
int
is that without an input event but with an internal condition. The internal transition, δ
int
: Q →Q,
changes states from q ∈Q to q
∈Q, which is different from that of δ
int
: S →S in the original DEVS
formalism (Zeigler, 2000). Note that q =(s,e) ∈Q represents a discrete state and an associated elapsed
time at the state. Thus, the use of Q in the definition of internal transition here allows us to explicitly
specify a condition for when an internal transition would have occurred. For similar reasons, external
transition and output functions are defined with Q, which is slightly different from that in Zeigler (2000).
As will be shown later, the transitions with Q allow us to formulate state/output equations for DEVS that
would be analogous to the ones for continuous dynamic systems. Note also that S is defined as a set of
discrete states although it can represent a continuous set.
Let us briefly explain the four functions. Time advance function defines the maximum sojourn time
for which each discrete state can stay unless an external input is arrived before the time. Note that the
sojourn time at a discrete state s, defined by ta(s), should be updated whenever a discrete state is changed.
The sojourn time can model such information as delay time for information transmission, work time for
processing tasks, and interdeparture time for generation of events. The internal transition specifies state
transition without an input but with an internal condition. The condition is whether an elapsed time
at a discrete state s is reached to the maximum sojourn time ta(s)ats. More specifically, assume that a
discrete state of an atomic model is s and that no input is arrived until the ta(s) time unit. Then, a state
DEVS Formalism for Modeling of Discrete-Event Systems 6-5
q = (s, ta(s)) of the model is changed into another state q
=(s
, 0). Recall that the internal transition of
Q →Q, instead of S →S, explicitly specifies when the transition occurs. That is, no internal transition
occurs at a state q
=(s, e), where e < ta(s), although discrete states for both q =(s, ta(s)) and q
=(s,
e) are identical. Note that the elapsed times at the discrete state in q and that in q
at which an internal
transition occurs are always ta(s) and 0, respectively.
Definition of the external transition can be similarly explained in which an elapsed time for a new state
immediately after the transition is also 0. The output function, Q =S ×R →Y , specifies which discrete
state in S generates what output in Y at what time in R. Recall that the output function, S →Y , only
specifies which discrete state in S generates what output in Y with no information about what time.
6.3.2 Coupled DEVS Model
A coupled DEVS model is a composition of DEVS models, each of which can be either atomic or coupled,
thus supporting hierarchical construction of a complex model. A well-known DEVS property of closed
undercoupling is a theoretical basis for such hierarchical models construction, similar to a process of
assembling a complex hardware from pieces of components. A formal definition of a coupled DEVS
model (CM) is as follows:
CM = <X, Y, D, {M
i
|i ∈D},EIC,EOC,IC,Select>
where
X, Y: same as in AM;
D: a set of component names;
M
i
: a component DEVS model, atomic or coupled;
with the following constraints:
EIC ⊆X ×∪
i∈D
X
i
, external input coupling relation;
EOC ⊆∪
i∈D
Y
i
×Y, external output coupling relation;
IC ⊆∪
i∈D
Y
i
×∪
j∈D
X
j
, internal coupling relation;
Select: 2
D
−Ø →D, tie-breaking selector.
A coupled DEVS model has three sets and four functions. A set of components M
i
is coupled to form
a coupled model. The coupling specification is defined by three mathematical relations: external input,
external output, and internal coupling relations. Each relation is a set of ordered pairs of events, each of
which is represented by (e1, e2), indicating that an event e1 is coupled to an event e2. With the coupling
in DEVS theory, all information in e1 is transmitted to e2 without any time delay. Let us look into the
three relations. The external input coupling relation, EIC, specifies how an input event of CM is routed to
input events of component models. The external output coupling relation, EOC, specifies how an output
event of a component is connected to an output event of CM. Lastly, the internal coupling relation, IC,
specifies how an output event of a component of CM is coupled to input events of other components
of CM. Note that the selection function, select, designates a component to be selected out of many if the
selection is required. The function is activated when more than one component is ready to generate their
output events while events can be handled one by one.
6.3.3 Example of DEVS Modeling: Ping-Pong Protocol
Let us illustrate DEVS modeling of ping-pong protocol. We first specify atomic DEVS models for SENDER
and RECEIVER, and then the overall coupled DEVS model for the protocol. We call two atomic DEVSs
AMsender and AMreceiver for SENDER and RECEIVER,respectively, and the overall DEVSmodel CMppp.
The atomic DEVS model of AMsender is defined as follows:
AMsender = <X, S, Y , δ
ext
, δ
int
, λ, ta>
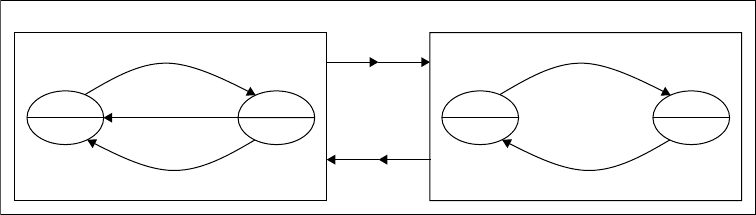
6-6 Handbook of Dynamic System Modeling
!msg ?msg
!ack?ack
AMreceiverAMsender
CMppp
?msg
!ack
Send
ST(!m)
!msg
?ack
Timeout
Receive
Accept
ST(!a)
⬁
Receive
FIGURE 6.3 DEVS model for ping-pong protocol.
where
X ={?ack}; Y ={!msg}; S ={Send, Receive};
ta(Send) =ST(!m) // Sending time of !msg;
ta(Receive) =Timeout // Maximum waiting time for input ?ack;
δ
int
(Send, ST(!m)) =(Receive, 0);
δ
int
(Receive, Timeout) =(Send, 0);
λ (Send, ST(!m)) =!msg;
δ
ext
((Receive, e < Timeout), ?ack) =(Send, 0).
AMreceiver can be similarly specified. Figure 6.3 shows AMsender and AMreceiver. Note that each discrete
state in Figure 6.3 has an associated sojourn time defined by the time advance function of ta, such as ST(!m),
Timeout, ST(!a), and ∞. Interpretation of the time is as follows. ST(!m) associated with the discrete state
“Send” is a time to be spent for transmission of !msg from SENDER to RECEIVER. It may be modeled
as a fixed real number including zero or a random number depending on a modeling objective. Timeout
associated with the discrete state “Receive” is the maximum waiting time for the input ?ack to arrive. Thus,
as shown in Figure 6.3 SENDER can change its discrete state either by the condition of Timeout or by the
input event ?ack, depending on which one occurs first between the condition and the input. Meaning of
ST(!a) associated with the discrete state “Accept” is similar to that of ST(!m). The sojourn time of ∞ at
the discrete state “Receive” in RECEIVER means that RECEIVER does not know how long it should wait
for the input ?msg to arrive from SENDER.
The internal transition of AMsender, δ
int
(Send, ST(!m)) =(Receive, 0), means that if an elapsed time
at the discrete state “Send” is reached to the maximum sojourn time ST(!m) then AMsender changes
its state to the beginning of the discrete state “Receive.” The output function, λ(Send, ST(!m)) =!msg,
means that if an elapsed time at “Send” is reached to the maximum sojourn time ST(!m) then the output
!msg is generated. Note that the output generation at a given state occurs at the same time as an internal
transition at the state. The external transition function of δ
ext
((Receive, e < Timeout), ?ack) =(Send, 0)
specifies what to do when the input ?ack has arrived at an elapsed time e before the maximum sojourn
time of Timeout. In this case AMsender changes its state to (Send, 0). Note that both internal and external
transition functions are piecewise constant functions over time.
Let us specify the coupled model CMppp. As shown in Figure 6.3, CMppp consists of two atomic models
AMsender and AMreceiver. Thus, CMppp is defined as
CMppp = <X, Y, {M
i
}, EIC, EOC, IC, Select>
where
X =Y ={ } (no input and output to environment);
{M
i
} ={AMsender, AMreceiver};
EIC =EOC ={ } (no interaction with external world);

DEVS Formalism for Modeling of Discrete-Event Systems 6-7
IC ={(AMsender.!msg, AMreceiver.?msg),
(AMreceiver.!ack, AMsender.?ack)};
Select({AMsender, AMreceiver}) =AMsender.
Note that CMppp has no interaction with an external environment, thus X =Y =EIC =EOC ={}.
However, if the coupled model has any such interaction specification of the sets it should reflect it.
Specification of {M
i
} is self-evident. Specification of IC employs a list of ordered pairs each of which
represents coupling information between two models. An ordered pair of (M1.m1, M2.m2) means that
an output event m1 of a model M1 is coupled to an input event m2 of a model M2. By the coupling, all
information associated with m1 is transferred to m2 with no delay. Thus, by the coupling (AMsender.!msg,
AMreceiver.?msg), two models change their states simultaneously, “Send”to“Receiver” for AMsender and
“Receiver”to“Accept” for AMreceiver. If a model is coupled to more than one model all such couplings
should be listed in ordered pairs by following the definition of mathematical relation on two sets. Finally,
the select function Select specifies that if AMsender and AMreceiver are ready to change its state at the
same time then AMsender executes the change first, then AMreceiver. Such selection priority should be
carefully specified with the deep domain knowledge of a target system to be modeled. The priority does
not matter in system analysis for some cases, but it does matter for most cases.
6.3.4 State Equation Form of Atomic DEVS
As described earlier, the DEVS formalism specifies a DES in the system-theoretic viewpoint. Recall that
the viewpoint considers system’s dynamics both with and without inputs. Following the viewpoint the
DEVS formalism has two transition functions: internal and external. Thus, a state transition in an atomic
DEVS model can occur either by an internal event (i.e., timeout condition) or by an external event. No
specification is given for a state transition to be performed by the two events that have occurred at the same
time. A priority rule for selection of such conflict events is specified at a coupled DEVS model to which
the atomic DEVS belongs as a component. Thus, a state equation of an atomic DEVS is represented as
q
= δ
int
(q) ⊕δ
ext
(q, x)or(s
, r
) = δ
int
(s, r) ⊕δ
ext
((s, e ≤ ta(s)), x) (6.1)
y = λ(q) = λ(s, r) (6.2)
where the binary operator, ⊕, is used to represent that a state transition can occur by either δ
int
or δ
ext
,
but not by both at any time. Note that Eq. (6.1) is similar to the state equation dQ/dt =AQ +BX for a
continuous dynamic system, where Q is a states set, X an inputs vector, and A and B are the coefficient
matrices. The state equation indicates that a state change (dQ/dt) is composed of a state change without
input (dQ/dt =AQ) and a state change with input (dQ/dt =BX). Comparison of the two state equations
show that δ
int
(q) and δ
ext
(q, x)inDEVScorrespondtodQ/dt =AQ and dQ/dt =BX in a continuous
system, respectively.
6.4 DES Analysis with DEVS Model
Generally, the purpose of systems modeling is twofold: verification of desired behavior and performance
evaluation. A DEVS model for a DES can be used for such purposes. Verification of behavior for a DES
includes properties of the system such as liveness and safeness, desired states/events sequences, and others.
Safeness is a property which claims that a bad thing will never happen; liveness is another property which
claims that a good thing will eventually happen. An example of safeness is deadlock-free and that of
liveness is an arrival of a message ?ack at SENDER in the ping-pong protocol introduced in Section 6.1.
A desired events sequence is one that satisfies functionality of the system to be modeled. An example of
a desired events sequence in the ping-pong protocol is !msg →?msg →!ack →?ack, meaning of which is
self-explained.
6-8 Handbook of Dynamic System Modeling
6.4.1 Composition of Atomic DEVS Models
Verification of DES usually relies on a state space exploration approach. The approach generates a global
state space of an overall system model by composition of component models. Composition of atomic
DEVS models considers all atomic models on a whole as a timed state transition model. Although the
composition deals with more than two components, we restrict our definition of composition on two
atomic models without loss of generality. A composed model of two atomic DEVS models of AM
i
and
AM
j
, noted by (AM
i
||AM
j
), is defined as follows:
AM
i
||AM
j
= <E, S, T, ta, {AM
i
,AM
j
}>
where
E : events set;
S : composed discrete states set;
T : transition relation of composed discrete states;
ta: time advance function;
with the following constraints:
E =(X
i
∪Y
i
∪{φ}) ×(X
j
∪Y
j
∪ {φ}), where φ is a null event;
S ⊆S
i
×S
j
;
T ⊆S ×E ×S;
ta: S →R.
To complete the definition, we define transition relation and time advance function with the following
three rules:
•
Rule 1: Transit AM
i
only
— Transition relation
If (s
i
, s
i
) ∈δ
int
i
and (s
i
, !a) ∈λi and (s
j
, ?a, s
j
) /∈δ
ext
j
then ((s
i
, s
j
), (!a, φ), (s
i
, s
j
)) ∈T for all s
j
∈S
j
— Time advance
ta((s
i
, s
j
)) = min{ta
i
(s
i
), ta
j
(s
j
) −ta
i
(s
i
)}
•
Rule 2: Transit AM
j
only
— Transition relation
If (s
j
, s
j
) ∈δ
int
j
and (s
j
, !b) ∈λ
j
and (s
i
, ?b,s
i
) /∈δ
ext
i
then ((s
i
, s
j
), (φ, !b), (s
i
, s
j
)) ∈T for all s
i
∈S
i
— Time advance
ta((s
i
, s
j
)) = min{ta
i
(s
i
) −ta
j
(s
j
), ta
j
(s
j
)}
•
Rule 3: Transit both AM
i
and AM
j
— Transition relation
If (s
i
, s
i
) ∈δ
int
i
and (s
i
, !c) ∈λ
i
and (s
j
, ?c, s
j
) ∈δ
ext
j
(or [(s
j
, s
j
) ∈δ
int
j
and (s
j
, !c) ∈λ
j
and (s
i
, ?c, s
i
) ∈δ
ext
i
])
then ((s
i
, s
j
), (!c, ?c), (s
i
, s
j
)) ∈T
(or [(s
i
, s
j
), (?c, !c), (s
i
, s
j
) ∈T]) for all s
i
∈S
i
and s
j
∈S
j
— Time advance
ta((s
i
, s
j
)) = min{ta
i
(s
i
), ta
j
(s
j
)}
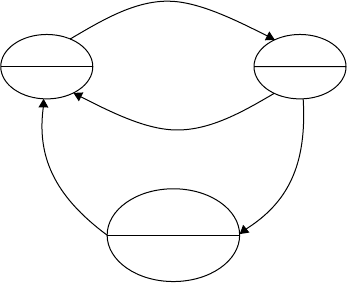
DEVS Formalism for Modeling of Discrete-Event Systems 6-9
Note that each rule separates specifications of transition for a composed state from time advance for the
state. The separation allows us to specify a composed DEVS model as a timed state automation which is
closed from an external world. Althoughthe composed model does not havean explicit state representation,
a composed state should be represented by q =((s
i
, s
j
), e) ∈Q,wheree is an elapsed time at the composed
discrete state (s
i
, s
j
).
An event e ∈E is an ordered pair of two events of component models. An event (!m, ?m) ∈E in transition
relation means that an output event !m of AM
i
is successfully transmitted to AM
j
as an input event ?m.
Likewise, an event (?m, !m) in transition relation means that an output event !m of AM
j
is successfully
transmitted to AM
i
as an input event ?m. In the above cases, both AM
i
and AM
j
concurrently perform
state transitions of their own. However, (φ, !m)or(!m, φ) represents a failure of such concurrent state
transitions; instead, it represents that either one of the two performs its own state transition.
Figure 6.4 shows a composed model of AMsender ||AMreceiver by application of the above composition
rules. For the composition, we assume that !msg is never lost and that !ack may be lost during transmis-
sion. Also assume that Timeout > ST(!a). In the figure a state of AMsender ||AMreceiver is represented by
q =((s1, s2), r), where s1 and s2 are discrete states of AMsender andAMreceiver, respectively, and r =ta((s1,
s2)). Initially, the states of AMsender and AMreceiver are at SD(“Send”) and RV(“Receive”), respectively,
thus being represented by (SD, RV). Time advance of (SD,RV) is the minimum of ta(SD) of AMsender and
ta(RV) of AMreceiver which is ST(!m). Combining the event and an associate sojourn time, a state ((SD,
RV), ST(!m)) is represented in an oval with two partitions in Figure 6.4: the top, (SD, RV), representing
the composed discrete state and the bottom, ST(!m), representing the sojourn time of (SD, RV). With the
event (!msg, ?msg), (SD, RV) changes to (RV, AP) after ST(!m) is completely elapsed. The discrete state (RV,
AP) stays for ST(!a) time. At the end of ST(!a), (RV,AP) is changed either to (SD, RV) with (?ack, !ack)orto
(RV, RV) with (φ, !ack). Now note that the maximum sojourn time at (RV, RV) is min{Timeout −ST(!a),
∞} =Timeout −ST(!a) according to Rule 2. In fact, Timeout −ST(!a) is a remaining time for which the
discrete state (RV, RV) is changed to the discrete state (SD, RV) without any event.
6.4.2 System Analysis by Composed DEVS Model
We now are ready to analyze a DES whose analysis model is represented by a composed DEVS model. We
first exemplify an intuitive analysis of the ping-pong protocol in Figure 6.3 using the composed DEVS
model of Figure 6.4. We then briefly introduce a method for automatic verification of DESs using composed
DEVS models.
As explained in Section 6.4.1, Figure 6.4 represents a global state transition with a sojourn time between
each transition. Thus, an intuitive investigation of Figure 6.4 can answer questions on states sequence as
(RV, RV)
Timeout–ST(!a)
(!msg, ?msg)
(?ack, !ack)
(SD, RV)
(, !ack)
ST(!m)
(RV, AP)
ST(!a)
FIGURE 6.4 Composed DEVS model of ping-pong protocol (SD, send; RV, receive; AP, accept).

6-10 Handbook of Dynamic System Modeling
well as timing property of the protocol to be analyzed. The following questions–answers for ping-pong
protocol can be performed using Figure 6.4:
•
Question 1 on safeness: Is the protocol deadlock-free?
Answer 1: Yes, because each state in the Figure 6.4 has a next state to move.
•
Question 2 on liveness: Can 10 !msg be eventually transmitted to RECEIVER?
Answer 2: Yes, because SENDER will eventually receive 10 ?ack if the probability of loss of !ack is
less than 1.0.
•
Question 3 on a discrete state sequence: Is (SD, RV) → (RV, AP) →(SD, AP) a legal state sequence?
Answer 3: No, because no such sequence can be constructed in Figure 6.4.
•
Question 4 on the minimum and maximum round trip times from (SD, RV) to (SD, RV)?
Answer 4: ST(!m) +ST(!a) is minimum; ST(!m) +Timeout is maximum.
Although the above example shows the concepts of DES analysis using composed DEVS models, comput-
erized automatic verification needs a systematic method for construction of a complete global state space
from a composed DEVS model. Generally, the global state space is represented by an infinite number of
timed events/states sequences. The sequences can be constructed by a combination of basic sequences each
of which is a loop in the composed model. Once all possible events/states sequences are constructed, a
complete verification of a system’s property and behavior is possible.
Consider Figure 6.4, the composed DEVS model of Figure 6.3, and assume that states sequences are of
interest in analysis. Intuitively, Figure 6.4 has the following two basic states sequences:
•
((SD, RV), ST(!m)) → ((RV, AP), ST(!a)) →((SD, RV), ST(!m));
•
((SD, RV), ST(!m)) →((RV, AP), ST(!a)) →((RV, RV), Timeout −ST(!a)) →((SD, RV), ST(!m)).
The first sequence is a sequence for a successful message transmission, and the second for a failure one. Let
us call the successful one and the failure one ss and fs, respectively. Combinations of the two sequences can
construct all possible states sequences of the composed DEVS model, which include ss →ss →ss… →ss,
ss →fs →fs →ss… →fs, fs →fs →ss →ss →… →ss, and so on. Note that each sequence may be infinite
in general, but it can be finite if conditions, such as a total number of messages to be transmitted and a
failure rate of each transmission are given. A method for the systematic generation of the minimum set of
basic loops of states/events sequences is a research issue and one such method can be found in Hong and
Kim (2005).
Once all possible sequences of a composed DEVS model are given, questions on the system can be
answered. To get an answer required is an efficient search method that finds properties translated from
questions in the state space. Recall that the size of a global state space of DES is infinite. Thus, a construction
of the state space causes a well-known state explosion problem, a general solution of which has not been
proposed so far. To solve the problem, subclasses of DEVS, such as schedule-preserved DEVS (SP-DEVS)
(Hwang and Cho, 2004) and schedule-controllable DEVS (SC-DEVS) (Hwang, 2005), have been proposed
in which some restrictions are applied to bound an infinite state space to a finite one.
6.5 Simulation of DEVS Model
DEVS models can be used for performance simulation of a DES. Since DEVS modeling is based on
the concept of the object-oriented (OO) worldview so does simulation of such models. Recall that DEVS
defines two model classes, atomic and coupled models, with which a hierarchical construction of a complex
model is specified.
6.5.1 DEVS Modeling Simulation Methodology and Environment
Figure 6.5 shows a generic architecture for a DEVS-based modeling and simulation environment using
a programming language L, where L can be any OO language such as C++and Java.
Note that the DEVS modeling environment and the simulation engine are explicitly separated. Within
the environment, modelers can develop DEVS models using modelers’interface which is a set of application
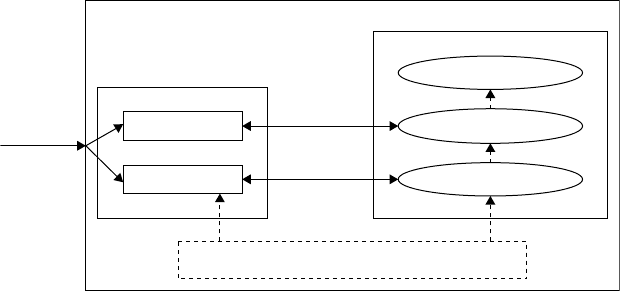
DEVS Formalism for Modeling of Discrete-Event Systems 6-11
Utility class library of language L
Request
ack
DEVS modeling
Coupled DEVS
Atomic DEVS
Request
ack
DEVSim-L
Modeler’s
interface
Hierarchical simulation engine
Coordinators
Simulators
Root coordinator
FIGURE 6.5 DEVS modeling/simulation environment.
programming interfaces (APIs) tospecify DEVSmodels in DEVSsemantics. Thus,APIs for the specification
of DEVS models are defined such that there is a one-to-one correspondence between APIs in the formalism.
For example, APIs for specification of atomic DEVS models in a C++modeling/simulation environment
include TimeAdvanceFn(), ExtTransFn(Message &, e), IntTransFn(), and OutputFn(Message &). APIs for
the specification of coupled DEVS models are similarly defined.
The hierarchical simulation engine realizes the concepts of abstract simulators (or simulation algo-
rithms) developed in Zeigler (1984). The abstract simulators are a set of distributed simulation algorithms
which can be implemented in a sequential as well as a distributedcomputing environment. Also, it is natural
to implement the abstract simulators algorithm in an OO language such as C++. The first implementation
is DEVSim++ (Kim and Park, 1992), which is a C++ environment for DEVS modeling and simula-
tion. Different implementations are available in public domains and efforts for standardization of DEVS
modeling/simulation environmentsis ongoing byDEVSStandardizationOrganization (DEVS-STD,2005).
The main purpose of OO implementations of DEVS modeling/simulation is to exploit the reusability
of DEVS models in models development. In fact, a carefully designed environment would support two-
dimensional (2D) reusability of DEVS models: one from the OO paradigm and the other from the DEVS
methodology (Kim and Ahn, 1996). The former exploits inheritance mechanism in the paradigm; the
latter does modular, hierarchical model construction in the methodology (Kim, 1991). Reuse metrics for
DEVS models developed in the DEVSim++ environment are proposed and measure of such reusability
was reported in Choi and Kim (1997).
Simulation-based performance analysis requires careful design of experimental frame, the concepts of
which has been proposed in Zeigler (1984). The experimental frame is a coupled DEVSmodel, independent
of the DEVS model of a target system to be simulated. The frame usually includes at least two models: one
for the generation of events which is input scenarios to the simulated DEVS model and the other for the
collection of simulation data which is output from the simulated DEVS model. Design of experimental
frame is objective-driven, meaning that different design objectives require different experimental frames.
More specifically, a set of simulation objectives is transformed into a set of performance indices. Then, an
experimental frame is designed such that the desired performance indices are measured by simulation.
For example, assume that the ping-pong protocol described in Section 6.1 is simulated and that the
simulation objective is to know how fast messages are to be transmitted with the protocol. Then, we employ
the DEVS model, CMppp, in Figure 6.3 and identify that the throughput of message transmission is a
performance index to be measured. The throughput is measured as a ratio of the total messages success-
fully transmitted to the total time spent for the transmission. To measure the ratio, an experimental frame
consists of at least one atomic DEVS model which is connected to CMppp via appropriate coupling rela-
tions. Of course, ST(!m) for AMsender and ST(!a) for AMreceiver should be identified before simulation

6-12 Handbook of Dynamic System Modeling
starts. The values may be fixed ones or random ones depending on a simulation objective. However, the
values should be identical or statistically equivalent to those in a real ping-pong protocol. Data modeling
of the values in terms of a distribution function with statistical parameter(s) is an important activity in a
modeling process.
6.5.2 Simulation Speedup and Simulators Interoperation
Simulation for performance evaluation of practical scale DESs may spend a large amount of time. To
reduce such simulation time in DEVS simulation, some attempts have been made. Among others three
approaches are introduced here. The first one is distributed simulation of DEVS models in which an
overall simulation is partitioned into a set of distributed computing resources (Kim et al., 1996; Seong
et al., 1995). Speedup for the approach depends not only on a balance between partitioned workloads but
also on a communication overhead between distributed computing resources. The second one is a hybrid
simulation method in which simulation models are a combination of DEVS models and analytic models
(Ahn and Kim, 1994). Speedup would be made without sacrificing accuracy if analytic models satisfy
certain assumptions in the system behavior. The third one is a model composition approach in which an
overall DEVS model is first composed into an atomic DEVS model and then simulate the atomic DEVS
model (Lee and Kim, 2003). A tool for automatic composition of an overall DEVS model into an atomic
model is developed and experimental results show about five times faster simulation than of the original
DEVS model.
Recently, simulation interoperation between heterogeneous simulators is of interest first in the military
domain and then in the civilian one. Accordingly, a standard for such interoperation has been proposed.
High-level architecture (HLA) is a standard specification for simulators interoperation; run-time infra-
structure (RTI) is implementation of HLA. HLA was first adapted as a defense modeling and simulation
office (DMSO) standard in 1966 and then as an institute of electrical and electronics engineers (IEEE) stan-
dard in 2000. In conjunction with the simulators interoperation, the DEVSim++ environment has been
extended such that simulators developed in DEVSim++is HLA-compliant, meaning that the simulators
can interoperate with other simulators via RTI interface. The extended environment, called DEVSimHLA
(Kim, 1999; Kim and Kim, 2005) has been developed based on the concepts of a simulation bus of
DEVS-BUS (Kim and Kim, 2003). The DEVSimHLA environment has been successfully employed for
the development of HLA-compliant military war game simulators in Korea, which have been certified by
DMSO.
6.6 Conclusion
Analysis and performance simulation of DESs should be based on a mathematical model for the systems.
The DEVS formalism is one such modeling means, which supports specification of DESs in a hierarchical,
modular manner. An advantage of the DEVS formalism is that it provides us with a unified model which
can not only be used in analysis but also to study the performance simulation of a system. Analysis of
DES with composed DEVS models requires a computerized tool for a state space construction and an
associate search method for a state space exploration. Composition of more than two DEVS models can
be done in an incremental manner for which only two models are composed at a time. Performance
simulation of DEVS models needs a modeling/simulation environment which is usually implemented in
OO programming languages such as C++ or Java.
References
M. S. Ahn and T. G. Kim, “A Framework for Hybrid Modeling/Simulation of Discrete Event Systems,”
Proceedings of AIS’94, pp. 199–205, December 1994, Gainesville, FL.
Y. Choi and T. G. Kim, “Reusability Measure of DEVS Simulation Models in DEVSim++ Environment,”
Proceedings of SPIE-97, pp. 244–255, 1997, Orlando, FL.
DEVS Formalism for Modeling of Discrete-Event Systems 6-13
DEVS-STD, 2005, http://www.devs-world.org.
K. J. Hong and T. G. Kim, “Timed I/O Sequences for Discrete Event Model Verification,” LNAI 3397:
Artificial Intelligence and Simulation, pp. 275–284, Springer, Berlin, 2005.
M. H. Hwang, “Generating Finite-State Global Behavior of Reconfigurable Automation Systems: DEVS
Approach,” Proceedings of 2005 IEEE-CASE, August 1–2, 2005, Edmonton, Canada.
M. H. Hwang and S. K. Cho,“Timed Behavior Analysis of Schedule Preserved DEVS,” Proceedings of 2004
Summer Computer Simulation Conference, pp. 173–178, July 2004, San Jose, USA.
J. H. Kim and T. G. Kim, “DEVS Framework and Toolkits for Simulators Interoperation Using HLA/RTI,”
Proceedings of Asia Simulation Conference, pp. 16–21, 2005, China.
K. H. Kim, Y. R. Seong and T. G. Kim,“Distributed Simulation of Hierarchical DEVS Models: Hierarchical
Scheduling Locally and Time Warp Globally,” Transactions for SCS, vol. 13, no. 3, pp. 135–154, 1996.
T. G. Kim, “Hierarchical Development of Model Classes in DEVS-Scheme Simulation Environment,”
Expert Systems with Applications, vol. 3, no. 3, pp. 343–351, 1991.
T. G. Kim, DEVSimHLA User’s Manual, SMSLab, Department of EECS, KAIST, 1999,
http://smslab.kaist.ac.kr.
T. G. Kim and M. S. Ahn, “Reusable Simulation Models in an Object-Oriented Framework,” Chapter 4,
Object-Oriented Simulation, IEEE Press, Piscataway, NJ, 1996.
T. G. Kim and S. B. Park, “The DEVS Formalism: Hierarchical Modular Systems Specification in C++,”
Proceedings of European Simulation Multiconference, pp. 152–156, June 1992, York, England.
Y. J. Kim and T. G. Kim,“Heterogeneous Simulation Framework Using DEVS Bus,” SIMULATION, vol. 79,
no. 1, pp. 3–18, 2003.
W. B. Lee and T. G. Kim,“Performance Evaluation of Concurrent System Using Formal Method: Simula-
tion Speedup,” IEICE Transactions on Fundamentals of Electronics, Communications and Computer
Sciences, vol. E86-A, pp. 2755–2766, 2003.
Y. R. Seong, T. G. Kim, and K. H. Park, “Mapping Modular, Hierarchical Discrete Event Models in a
Hypercube Multicomputer,” Simulation Practice and Theory, vol. 2, no. 6, pp. 257–275, 1995.
B. P. Zeigler, Multifacetted Modelling and Discrete-Event Simulation, Academic Press, London, 1984.
B. P. Zeigler, H. Praehofer, and T. G. Kim, Theory of Modelling and Simulation (2nd ed.), Academic Press,
New York, 2000.
