Fishwick P.A. (editor) Handbook of Dynamic System Modeling

Подождите немного. Документ загружается.

28-12 Handbook of Dynamic System Modeling

TABLE 28.1

Continued

No. Rate (or Auxiliary) Equation

Units

Meaning

Used in Eq. No.

(017) J0FCS

K0FCS

J/y

Nonmarsh food assimilation by ﬁshes, crabs, and shrimps

(016)

(018) J0LM

=1.42009e+017

J/y

Light inﬂux

(027) and (031)

(019) JFCS0

KFCS0

∗

QFCS

J/y

Metabolic heat losses by ﬁshes, crabs, and shrimps

(016)

(020) Jrain

=Rain

kg-H

O/y Rain on marsh

(002)

(021) JW2M2

=Tide

∗

KW2M2

∗

(WQ2

−KW2M2n

∗

kg-H

O/y Water exchange with estuary

(002)

MQ2)

(022) JW3M3

=KW3M3

∗

(WQ3 −

KW3M3n

∗

MQ3) kg-salt/y Salt exchange with estuary

(003)

(023) JW4M4

=KW4M4

∗

(WQ4 −

KW4M4n

∗

MQ4) kg-N/y

Inorganic nutrient exchange with estuary

(004)

(024) JW5M1

=KW5M1

∗

(WQ5 −

KW5M1n

∗

MQ1) J/y

Organic detritus exchange with estuary

(001)

(025) JW6M5

=KW6M5

∗

(WQ6 −

KW6M5n

∗

MQ5) kg-sediment/y Sediment exchange with estuary

(005)

(026) Jyield

=Yield

J/y

Catch of ﬁshes, crabs, and shrimps in estuary and creeks

(016)

(027) MA07a

=J0LM /(1

+(MK07

∗

MA07b

∗

MQ7)+

J/y

Light inﬂux available to low marsh plants

(029) and (033)

(MK20E

∗

MK20

∗

MQ2))

(028) MA07b

=(MQ2

∗

MQ4

∗

MQ6)/MQ3

Complex Environmental conditions for low marsh plant

photosynthesis

(027), (031), and (033)

(029) MA09a

=MA07a /(1

+(MK09

∗

MA09b

∗

MQ9)) J/y

Light inﬂux available to benthic microalgae

(034)

(030) MA09b

=(MQ2

∗

MQ4

∗

MQ6)/MQ3

Complex Environmental conditions for benthic microalgal

photosynthesis (034) and (029)

(031) MA20

=J0LM /(1

+(MK07

∗

MA07b

∗

MQ7)

J/y

Light inﬂux available to evaporate water from marsh

(040)

(MK20E

∗

MK20

∗

MQ2))

(032) MJ06

=Tide

J/y

Inﬂux of tidal energy to marsh

(006)

(033) MJ07

MK07

∗

MA07b

∗

MQ7

∗

MA07a

J/y

Gross primary production by low marsh plants

(007), (041), (042), and (047)

(034) MJ09

=MK09

∗

MA09b

∗

MQ9

∗

MA09a

J/y

Gross primary production by benthic microalgae

(008) and (043)

(035) MJ15

=MK15

∗

MQ1

J/y

Burial of detritus in sediment (in energy units)

(001)

(036) MJ15D

=MK15D

∗

MQ1

kg-sediment/y Burial of detritus in sediment (in sediment units)

(005)

(037) MJ1a

=MK1a

∗

MQ1

∗

Mqa

J/y

Assimilation of detritus by microbes

(001) and (009)

(038) MJ1b

=MK1b

∗

MQ1

∗

Mqb

J/y

Assimilation of detritus by meiofauna

(001) and (010)

(039) MJ1c

=MK1c

∗

MQ1

∗

Mqc

J/y

Assimilation of detritus by macrofauna

(001) and (011)

(040) MJ20

=MK20

∗

MQ2

∗

MA20

kg-H

O/y Evaporation of water in marsh

(002)

(041) MJ207

=MK207

∗

MJ07

kg-H

O/y Transpiration of water by low marsh plants

(002)

(042) MJ47

=MK47

∗

MJ07

kg-N/y

Uptake of inorganic nutrients by low marsh plants

(004)

(043) MJ49

=MK49

∗

MJ09

kg-N/y

Uptake of inorganic nutrients by benthic microalgae

(004)

(044) MJ60

=MK60

∗

MQ6

J/y

Baseline dissipation of water circulation energy in marsh

(006)

(045) MJ607

=MK607

∗

MQ6

∗

MQ7

J/y

Dissipation of circulation energy by low marsh plants

(006)

(046) MJ70

=MK70

∗

MQ7

J/y

Baseline metabolic heat losses by low marsh plants

(007)

(047) MJ706

=MK706

∗

MJ07

J/y

Metabolic heat losses by low marsh plants due to production

processes (007)

Dynamic Simulation with Energy Systems Language 28-13

(048) MJ71

=MK71

∗

MQ7

J/y

Death of low marsh plant tissue and ﬂow to detritus

(001) and (007)

(049) MJ7e

=MK7e

∗

MQ7

∗

MQe

J/y

Assimilation of low marsh plants by insects

(007) and (013)

(050) MJ90

=MK90

∗

MQ9

J/y

Metabolic heat losses by benthic microalgae

(008)

(051) MJ9b

=MK9b

∗

MQ9

∗

MQb

J/y

Assimilation of benthic microalgae by meiofauna

(008) and (010)

(052) MJ9c

=MK9c

∗

MQ9

∗

MQc

J/y

Assimilation of benthic microalgae by macrofauna

(008) and (011)

(053) MJ9e

=MK9e

∗

MQ9

∗

MQe

J/y

Assimilation of benthic microalgae by macrofauna

(008) and (013)

(054) MJa0

=MKa0

∗

MQa

J/y

Metabolic heat losses by detritus microbes

(009) and (055)

(055) MJa4

=MKa4

∗

MJa0

kg-N/y

Nutrient regeneration by detritus microbes

(004)

(056) MJab

=MKab

∗

MQa

∗

MQb

J/y

Assimilation of microbes by meiofauna

(009) and (010)

(057) MJac

=MKac

∗

MQa

∗

MQc

J/y

Assimilation of microbes by macrofauna

(009) and (011)

(058) MJb0

=MKb0

∗

MQb

J/y

Metabolic heat losses by meiofauna

(010) and (059)

(059) MJb4

=MKb4

∗

MJb0

kg-N/y

Nutrient regeneration by meiofauna

(004)

(060) MJbc

=MKbc

∗

MQb

∗

MQc

J/y

Assimilation of meiofauna by macrofauna

(010) and (011)

(061) MJbFCS

=MKbFCS

∗

MQb

∗

QFCS

J/y

Assimilation of meiofauna by ﬁshes, crabs, and shrimps

(010) and (016)

(062) MJc0

=MKc0

∗

MQc

J/y

Metabolic heat losses by macrofauna

(011) and (063)

(063) MJc4

=MKc4

∗

MJc0

kg-N/y

Nutrient regeneration by macrofauna

(004)

(064) MJcd

=MKcd

∗

MQc

∗

MQd

J/y

Assimilation of macrofauna by raccoons and rats

(011) and (012)

(065) MJcFCS

=MKcFCS

∗

MQc

∗

QFCS

J/y

Assimilation of macrofauna by ﬁshes, crabs, and shrimps

(011) and (016)

(066) MJcg

=MKcg

∗

MQc

∗

MQg

J/y

Assimilation of macrofauna by birds

(011) and (015)

(067) MJd0

=MKd0

∗

MQd

J/y

Metabolic heat losses by raccoons and rats

(012)

(068) MJe0

=MKe0

∗

MQe

J/y

Metabolic heat losses by insects

(013)

(069) MJef

=MKef

∗

MQe

∗

MQf

J/y

Assimilation of insects by spiders

(013) and (014)

(070) MJeg

=MKeg

∗

MQe

∗

MQg

J/y

Assimilation of insects by birds

(013) and (015)

(071) MJf0

=MKf0

∗

MQf

J/y

Metabolic heat losses by spiders

(014)

(072) MJfg

=MKfg

∗

MQf

∗

MQg

J/y

Assimilation of spiders by birds

(014) and (015)

(073) MJg0

=MKg0

∗

MQg

J/y

Metabolic heat losses by birds

(015)

(074) MJgd

=MKgd

∗

MQd

∗

MQg

J/y

Assimilation of birds eggs by raccoons and rats

(012) and (015)

No.

Inputs

Units

Meaning

Used in Eq. No.

(075)

Rain

=4.5e+010

kg-H

O/y

Annual rainfall on marsh

(020)

(076)

Tide =

1.03752e+014

J/y

Tidal energy inﬂux to marsh

(021) and (032)

(077)

WQ2

=1e+011

kg-H

Water in estuary and tidal creeks

(021)

(078)

WQ3

=2.5641e+009

kg-salt

Salt in estuary and tidal creeks

(022)

(Continued)

28-14 Handbook of Dynamic System Modeling

TABLE 28.1

Continued

(079)

WQ4

=5600

kg-N

Nutrients in estuary and tidal creeks

(023)

(080)

WQ5

=5.1e+013

Organic detritus in estuary and tidal creeks

(024)

(081)

WQ6

=7e+006

kg-sediment

Sediment in estuary and tidal creeks

(025)

No. Model constants

Units

Meaning

Used in Eq. No.

(082) K0FCS

=2.898e+012

J/y

Nonmarsh food assimilation by ﬁshes, crabs, and shrimps

(017)

(083) KFCS0

=0.38375

1/y

Fraction of biomass energy used per year in metabolic proc

esses by ﬁshes, crabs, and shrimps (019)

(084) KW2M2

=5.86735e−014 1/y

Rate constant for water exchange with estuary

(021)

(085) KW2M2n

=18934.6

dmls

Equilibration constant for water exchange with estuary

(021)

(086) KW3M3

=3.04375

1/y

Rate constant for salt exchange with estuary

(022)

(087) KW3M3n

=10007.5

dmls

Equilibration constant for salt exchange with estuary

(022)

(088) KW4M4

=8.11667

1/y

Rate constant for inorganic nutrient exchange with estuar

(023)

(089) KW4M4n

=−1.09205 dmls

Equilibration constant for inorganic nutrient exchange with

estuary

(023)

(090) KW5M1

1/y

Rate constant for organic detritus exchange with estuary

(024)

(091) KW5M1n

=0.0555556 dmls

Equilibration constant for organic detritus exchange with

estuary

(024)

(092) KW6M5

=1.33333

1/y

Rate constant for sediment exchange with estuary

(025)

(093) KW6M5n

=0.000492821 dmls

Equilibration constant for sediment exchange with estuary

(025)

(094) MK07

=1.1316e−033

complex Rate constant for primary production by low

marsh plants

(027), (031), and (033)

(095) MK09

=1.03014e−031 complex Rate constant for pr

imary production by benthic algae

(029) and (034)

(096) MK15

=0.0206749

1/y

Rate constant for detritus burial in sediment (detritus outﬂo

(035)

(097) MK15D

=1.21617e−009 1/y

Rate constant for detritus burial in sediment (sediment inﬂo

(036)

(098) MK1a

=2.37925e−012 1/(J-y) Rate constant for assimilation

of detritus by microbes

(037)

(099) MK1b

=2.18782e−014 1/(J-y) Rate constant for assimilation

of detritus by meiofauna

(038)

(100) MK1c

=5.46954e−015 1/(J-y) Rate constant for assimilation

of detritus by macrofauna

(039)

(101) MK20

=9.51857e−014 1/J

Fraction of water evaporated per unit of available light energ

(027), (031), and (040)

(102) MK207

=1.26752e−005 kg-H

O/J Water transpired per unit of energy assimilated

by low marsh plants

(041)

(103) MK20E

1.36889e+007 J/kg-H

O Energy required to evaporate water

(027) and (031)

(104) MK47

=2.25e−008

kg-N/J Inorganic nutrients assimilated per

unit energy assimilated by low marsh plants

(042)

(105) MK49

=2.5e−008

kg-N/J Inorganic nutrients assimilated per

unit energy assimilated by benthic microalgae

(043)

(106) MK60

=635.217

1/y

Fraction of water circulation energy dissipated per unit time

(044)

(107) MK607

7.68842e−014 1/(J-y) Fraction of circulation

energy dissipated year per unit of low marsh plants

(045)

(108) MK70

=0.773471

1/y

Fraction of biomass energy used in metabolic processes by low

marsh plants

(046)

(109) MK706

0.005

dmls

Fraction of low marsh plant production lost as heat

(047)

(110) MK71

=0.689162

1/y

Fraction of low marsh plant biomass that dies per year

(048)

(111) MK7e

=3.03863e−014 1/(J-y) Fraction of

low marsh plants consumed per year per unit insect

(049)

Dynamic Simulation with Energy Systems Language 28-15

(112) MK90

=69.0035

1/y

Fraction of biomass energy used per y

ear in metabolic processes by benthic microalgae

(050)

(113) MK9b

=1.36912e−011 1/(J-y) Fraction of benthic

microalgae consumed per year per unit meiofauna

(051)

(114) MK9c

=1.09529e−011 1/(J-y) Fraction of benthic

microalgae consumed per year per unit microfauna

(052)

(115) MK9e

=2.73823e−012 1/(J-y) Fraction of benthic

microalgae consumed per year per unit insect

(053)

(116) MKa0

=1747.32

1/y

Fraction of biomass energy used per year in metabolic proc

esses by detritus microbes

(054)

(117) MKa4

=5e−008

kg-N/J Regenerated nutrients per unit energy metaboliz

ed by detritus microbes

(055)

(118) MKab

=1.04007e−010 1/(J-y) Fraction of microbes

consumed per year per unit meiofauna

(056)

(119) MKac

=6.93382e−011 1/(J-y) Fraction of detritus

microbes consumed per year per unit macrofauna

(057)

(120) MKb0

=72.7162

1/y

Fraction of biomass energy used per year in metabolic proc

esses by meiofauna

(058)

(121) MKb4

=6e−008

kg-N/J Regenerated nutrients per unit energy metaboliz

ed by meiofauna

(059)

(122) MKbc

=1.60309e−012 1/(J-y) Fraction of meiofauna

consumed per year per unit macrofauna

(060)

(123) MKbFCS

=8.36395e−014 1/(J-y) Fraction of meiofauna

consumed per year per unit ﬁshes, crabs, and shrimps

(061)

(124) MKc0

=48.7219

1/y

Fraction of biomass energy used per year in metabolic proc

esses by macrofauna

(062)

(125) MKc4

=6e−008

kg-N/J Regenerated nutrients per unit energy metaboliz

ed by macrofauna

(063)

(126) MKcd

=1.71895e−012 1/(J-y) Fraction of macrofauna

consumed per year per unit raccoons and rats

(064)

(127) MKcFCS

=4.48327e−014 1/(J-y) Fraction of macrofauna

consumed per year per unit ﬁshes, crabs, and shrimps

(065)

(128) MKcg

=4.29646e−013 1/(J-y) Fraction of macrofauna

consumed per year per unit birds

(066)

(129) MKd0

=4.93012

1/y

Fraction of biomass energy used per year in metabolic proc

esses by raccoons and rats

(067)

(130) MKe0

=31.3155

1/y

Fraction of biomass energy used per year in metabolic proc

esses by insects

(068)

(131) MKef

=6.90377e−012 1/(J-y) Fraction of insects

consumed per year per unit spiders

(069)

(132) MKeg

=6.90377e−013 1/(J-y) Fraction of insects

consumed per year per unit birds

(070)

(133) MKf0

=15.6578

1/y

Fraction of biomass energy used per year in metabolic proc

esses by spiders

(071)

(134) MKfg

=6.90377e−

013 1/(J-y) Fraction of spiders consumed

per year per unit birds

(072)

(135) MKg0

2.69679

1/y

Fraction of biomass energy used per year in metabolic processes

by birds

(073)

(136) MKgd

2.37812e−013 1/(J-y) Fraction of birds eggs

consumed per year per unit raccoons and rats

(074)

(137) Yield

J/y

Capture of ﬁshes, crabs, and shrimps in estuary and creeks

(026)

No.

Simulation time parameters

Units

Meaning

(138)

FINAL TIME

The ﬁnal time for the simulation

(139)

INITIAL TIME

The initial time for the simulation

(140)

TIME STEP

=2e−007

The time step for the simulation

(141)

SAVEPER

=0.001

The frequency with which output is stored

INTEG(inﬂows

−outﬂows) refers to the integration of the net ﬂow rate

to determine the storage value. The initial values given for each stor

age are the assumed steady-

state values used for

model calibration. These values yield a ﬂat-line output. To obtain

dynamic output, halve the initial value for MQd.

Vensim simulation software was used with the fourth-order

Runge–Kutta routine se

lected. The model was run with identical results both

on a MacIntosh

PowerBook G4 (1 Ghz PowerPC

G4 (3.3) processor, OS: Apple Classic 9.2.2 under OS10.4.6) and

on an Abit KT7-RAID PC motherboard with an AMD Duron 700

processor (OS: Windows 2000 Pro

fessional).

28-16 Handbook of Dynamic System Modeling

28.3.2 Basic Equation Forms Indicated in Energy Systems

Language Diagrams

Each storage in an EnergySystems Language diagram has lines indicating one or more inﬂows and outﬂows.

The equation for each storage is simply the integral of its net ﬂow rate over time, that is to say, the integral

of the sum of all inﬂows into it minus the sum of outﬂows from it from all time past to the present

moment. Because the concept of “all time past” is indeﬁnite, an initial starting time is speciﬁed (Time

Zero), at which point each storage is represented by an initial value. Eq. (001)–(016) in Table 28.1 show

the rates contained in an integration function and the initial value supplied for each of the model storages.

The form of each rate equation, however, is tied to speciﬁc details in the diagram. Each rate arises from a

symbol combination. The translation rules can be illustrated best with simpler diagrams of processes that

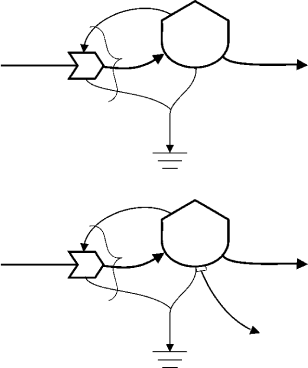
repeat many times in Figure 28.3. By applying a few simple rules, the entire equation list can be constructed.

The composite symbols for primary producers (bullet shapes) and consumers (hexagons) have the

same standard symbol combination to represent a reproduction process called “autocatalytic growth.”

This standard structure is given in Figure 28.4. The only difference between primary producers and

consumers is the type of energy assimilated: usually sunlight for primary producers and some form of

organic matter for consumers.

In either case, the designated energy source R passes at rate J

through a multiplicative interaction to be

assimilated and stored in biomass Q

. As shown in Figure 28.4, energy from the recipient storage (Q

) feeds

back and intersects the top of the interaction symbol, and then dissipates as heat to the heat sink symbol.

TherateJ

is a net assimilation rate. Assimilation measurements for most living organisms are usually of

net assimilation. As the curly bracket in Figure 28.4 indicates the energy of Q

fed back and used speciﬁcally

in the production process is rarely separated explicitly from the amount assimilated. In ecological literature,

the rate J

is known simply as “assimilation” for consumers. For primary producers, it is the gross primary

production. The net production rate is J

−J

, which is net primary production in the case of plants and

net secondary production for consumers. Old age death, or other passive loss of biomass is indicated by

rate J

The equations for the relevant energy ﬂows and their combined effect on the storage are indicated in

the top panel of Figure 28.4. Consider ﬁrst the net assimilation rate J

, the form of which arises from the

multiplicative interaction symbol involved. According to the translation rules of Energy Systems Language,

allﬂows(J

) into and out of an interaction term have the same equation form. Equations differ only by

the numerical value of an associated constant (k

). In the case of multiplicative interaction, the resource

(R) and the biomass (Q

) multiply together to produce the indicated equation for net assimilation rate

. In other words, the rate of production is proportional to the multiple of the amount of energy

availablefor transformation in resource R and the amount already available in the autocatalyticbiomass Q

The biomass acquires resources to form additional biomass. That is to say, in the presence of its resources,

growth is autocatalytic. The rate constant k

is analogous to the second-order rate constant in chemical

reaction kinetics. The dimensional units for k

are fractions of R assimilated per unit Q

per unit time.

The outﬂows J

and J

in Figure 28.4 do not pass through an interaction symbol as drawn. If they did,

the form of the equation would follow interaction rules like those for J

. When the rate of outﬂow is simply

a constant proportion of the donor storage, the outﬂow line does not pass through an explicit interaction

symbol downstream. Hence, the equations for J

and J

in Figure 28.4 are constant proportions of Q

.The

dimensional units of the rate constants involved are simply the fraction of Q

that is degraded per unit

time for k

, or in the case of k

, the fraction of upgraded material (Q

) that dies from old age, leaks out,

or is otherwise passively lost (per unit time).

In the complete marsh sector diagram (Figure28.3), all of the metabolic heat losses from living organisms

are constant proportions of the energy in biomass. These ﬂows are identiﬁed in the equation list (Table 28.1)

as MJx0, where x is the subscript associated with the standing stock Q of a living component x. Donor

proportional outﬂows are used elsewhere in Figure 28.3 as well. The ﬂow from plants to detritus (MJ

Eq. [048]) is proportional to plant biomass (MQ

) and the burial of detritus in sediments as peat (MJ

Eq. [035]) is proportional to the detritus accumulation (MQ

Dynamic Simulation with Energy Systems Language 28-17

(a)

(b)

 k

/dt  J

J

 k

FIGURE 28.4 Basic symbolic representation and equations for the autocatalytic process usually used in the com-

posite symbols for primary producers and consumers: (a) without nutrient regeneration indicated; (b) with nutrient

regeneration indicated (J

). The curly bracket pointing to J

indicates combined ﬂows (see text). R is a variable that

represents the energy resource to be transformed, J’s are for the various ﬂows, k’s are rate constants, Q

represents the

storage of biomass, and dQ

/dt is the rate of change of biomass with time.

Although not illustrated in Figure 28.4, some of the biomass of one living component may be captured

and consumed by predators or other consumers. The amount is called the yield of biomass, and it becomes

the resource for the autocatalytic growth of the recipient consumers. The equation for such an outﬂow

from Q

to a downstream consumer would have the same multiplicative form as used for J

. If, for example,

was the food of consumer Q

, the ﬂow between them—call it J

—would be J

. The constant

would represent the fraction of Q

assimilated per unit time by each unit of consumer Q

A food Web can be represented by linking primary producer symbols to a network of consumer symbols.

Consumers may represent trophic levels, feeding guilds, or other functionally similar combinations of

species. Figure 28.3 includes a food Web based on marsh plant detritus, live marsh plants, and benthic

microalgae that after passing through a number of intermediate consumers, culminates in the birds,

raccoons,and rats of the salt marsh and the ﬁshes, crabs, and shrimps of the tidal creeks and adjacent estuary

FCS

). Each equation for an energy transfer from resource to consumer uses the two-way multiplicative

interaction described above.

The composite symbol for consumers sometimes has a ﬂow of regenerated nutrients indicated in

conjunction with the metabolic energy loss. One way to handle this is illustrated by the ﬂow labeled J

in the bottom panel of Figure 28.4. The ﬂow line emanates from a small rectangle attached close to the

bottom of the storage tank. The small rectangle, called a “sensor,” denotes that no loss of the storage of

energy occurs, in this case because the ﬂow is in units of something else besides the energy that is stored in

biomass (nutrients). Nutrient regeneration is a product of metabolism. Nutrients accompany the energy

losses denoted by the ﬂow to the sink, but they must be tracked in a separate ﬂow stream. Regenerated

nutrients ﬂow from the consumer to a nutrient storage elsewhere. The lower panel of Figure 28.4 shows

the equation for nutrient regeneration (J

). It has the same form as the metabolic energy loss equation

), but the dimensional units for the constant (k

) are nutrient units released per unit time per unit of

energy stored, rather than fraction of energy per time.

The marsh sector diagram (Figure 28.3) shows nutrient regeneration by microbes (MQ

), meiofauna

(MQ

), and macrofauna (MQ

). The nutrient regeneration ﬂow lines arise from the vicinity of the

28-18 Handbook of Dynamic System Modeling

metabolic heat losses for these three consumers and cycle up and to the left terminating in the nutrients

storage (MQ

). The tiny sensor symbols are left out of the diagram in Figure 28.3, and in the equation list

(Table 28.1) an alternate equation form is used for MJ

,MJ

, and MJ

(Eq. [055], Eq. [059], and Eq.

[063], respectively). In this form, nutrient regeneration is a constant proportion of the respective metabolic

heat losses rather than to the amount of energy stored in each consumer’s biomass. The constants therefore

deﬁne the amount of nutrients regenerated per unit of energy metabolized, which may be conceptually

more familiar to some. Either way is consistent with the diagram.

In either case, the ﬂow of regenerated nutrients is not subtracted from the accumulations of energy

(MQ

,MQ

, and MQ

) because the associated energy subtraction takes place with the respective ﬂows

to the heat sink (see Eqs. [009]–[011]). The nutrient ﬂows are, however, added to the accumulation of

nutrients (Eq. [004]).

28.3.2.1 The Flow-Limited Source

A curved line entering the system boundary from a source and then passing back out, while being tapped

along the way inside the boundary, means that the equation for a “ﬂow-limited source”is to be used. In the

coastal system and marsh sector diagrams (Figure 28.1 and Figure 28.3), sunlight is tapped by evaporation

of water and by the various primary producers in the system. Unused light is reﬂected by the system (the

system’s albedo), as represented by the line that curves back out of the system boundary.

Some resources, such as fossil fuels, are limited by the amount available in storage. For these resources,

use rate exceeds the regeneration rate. Once the storage is depleted, further use is limited by the rate of

regeneration. The resource then becomes ﬂow-limited. Water ﬂowing in a hillside stream is limited by the

ﬂow from upstream. From its ﬁrst diversion for irrigation or drinking water, a stream is recognized as

ﬂow-limited. After diversion only the remaining ﬂow is available for additional withdrawals. Likewise, the

ﬂow of sunlight ultimately limits photosynthesis. Sunlight used in evaporating water is not available for

photosynthesis, and only the sunlight remaining in the shade and sunﬂecks beneath the tallest plants can

be used by the shorter ones.

When storage is the resource transformed for the production of an autocatalytic component, the

associated ﬂow rate equationsarebased on the multiple of the donor and recipient storages. The production

rates of all consumers of the food Web illustrated in the marsh sector diagram (Figure 28.3) are of this type.

For primary producers, however, the main energy resource is ﬂow-limited. Hence, the equation for gross

primary production is based on the remaining unused ﬂow of the resource, rather than a donor storage.

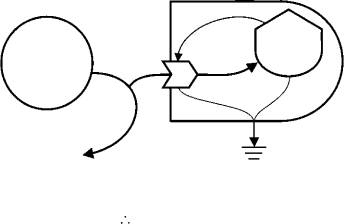
The remaining ﬂow is known generally as J

. A simple diagram of this process is shown in Figure 28.5.

In this case, the only tap is for gross primary production (J

), so the remaining light (J

) is simply the

solar input (J

) less that already incorporated into production. Substituting and rearranging this set of

implicit equations yields the explicit relationship suitable for models. The equation for J

is hyperbolic

and declines to zero as the storage grows. The ﬁrst equation for J

is simply the multiple of J

and Q

The dimensional units of the constant k

are the inverse of the storage units. The constant represents the

fraction of the remaining light assimilated by each unit of biomass.

The equation derived for J

from the deﬁnitions of J

and J

(shown in Figure 28.5) is the Monod

function (or the Michaelis–Menten equation), often used in ecological models to represent ﬂow saturation

at high levels of a resource and limitation at low levels. In the case illustrated, the maximum gross primary

production rate is equal to J

and the level of biomass energy (Q

) at which the rate is half the maximum

is the inverse of k

. The practical maximum is actually considerably less than J

for two reasons: (a) other

factors also limit photosynthesis; and (b) other processes compete for sunlight, such as water evaporation,

conversion to heat on dark surfaces, and reﬂection.

In the marsh sector diagram (Figure 28.3), the taps of sunlight for evaporation and for marsh plant

production originate from the same point, and the tap for benthic microalgae occurs afterwards. Usually,

tapping from the same point means the processes are all competing for the same remaining light, however,

this is not the case when the point refers to different areas. The vertically overlapping primary producer

symbols for low and high marsh plants indicate this distinction. The various grasses, rushes, and sedges that

comprise each of the two elevation regions exist literally side by side in the marsh, so they receive the same

Dynamic Simulation with Energy Systems Language 28-19

 k

 J

J

 J

/(1  k

)

 J

/[(1/k

)  Q

)

]

Sun

Plants

FIGURE 28.5 Flow-limited source coupled with an autocatalytic primary production process. Equations for J

and

are given two ways.

amount of light from overhead. A complete model of the marsh sector would have two subsectors: one for

the low elevation marsh and the other for the high marsh. The equations of Table 28.1 show only the low

marsh subsector. The high marsh would be represented by an identical set of equations calibrated for high

marsh conditions. The total marsh sector would consist of the sum of each component in each subsector.

The independent process of water evaporation shown at the same tap point as plant production,

however, is a competing process, separately competing in both the low marsh and the higher elevation

marsh. Processes competing for the same ﬂow-limited resource use the same calculation of remaining light

for its functions. Water evaporates through an interaction with sunlight, as illustrated in the diagram. The

equation for the evaporation rate (MJ

, Eq. [040]) is based on the multiple of the storage of water (MQ

and an auxiliary that provides the remaining light available (MA

, Eq. [031]). The right-hand side of the

corresponding auxiliary equation for plants is identical (MA

07a

, Eq. [027]). The form of each equation

for light remaining at the combined tap is similar to that given for a single tap in the simple diagram of

Figure 28.5, except that the denominator is based on the sum of the competing uses: evaporation of water

and production by low marsh plants. Note also the conversion of evaporation from water to energy using

the constant MK

20E

(speciﬁed in Eq. [103]) for dimensional consistency.

Benthic microalgae exist in water-saturated soil often covered by water, and they grow in the shade of the

emergent vascular plants of the marsh. Accordingly, the diagram shows the sunlight for benthic microalgae

drawn downstream of the simultaneous tap for the marsh plant production and water evaporation. The

source light available to benthic microalgae (analogous to J

in Figure 28.5) is the light remaining after

evaporation of water and assimilation by the plants that shade them. This was already determined by

07a

in Eq. (027) (or equivalently by MA

in Eq. [031]). Otherwise the calculation of J

for benthic

microalgae (MA

09a

) follows the form given in Figure 28.5, as shown in Eq. (029).

28.3.2.2 Multiple Simultaneous Interactions in Energy Systems Language

According to Figure 28.1 ﬁve other factors inﬂuence the transformation of sunlight by plants. These are

illustrated more precisely in the marsh sector diagram (Figure 28.3). Water, nutrients, sediment, and

circulation energy (caused by winds and tide) all positively inﬂuence gross primary production. In Energy

Systems Language, these combine in a series of multiplicative interactions to determine the rate of gross

primary production. Salt negatively inﬂuences gross production, however, so it is represented by a divisor.

The resulting autocatalytic production equation for plants consists of a constant multiplied by the four

positive inﬂuence variables, divided by salt, and all multiplied as before by the remaining light and the

energy stored in plant biomass. A total of seven state variables are combined with one constant creating a

seventh-degree equation for gross photosynthesis.

The multiplication of all these values to achieve a given rate of gross photosynthesis means that the

single constant involved will have very complex dimensional units. Because production units and light

28-20 Handbook of Dynamic System Modeling

ﬂux units are both in energy units per time, a production function based only on the multiple of remaining

light and biomass involves a constant with dimensions of inverse biomass units (as shown in Figure 28.5).

If, however, two additional variables (say A and B) multiply and one divides (C), then for dimensional

consistency, the implied units for the constant are C units per A unit per B unit per biomass unit. In the case

given by the marsh sector diagram in Figure 28.3, the constant must cancel units from a total of six variables.

An additional practical detail concerning the constant is the small numerical value that must be assigned

to it. The multiple of all the variables involved in a complex interaction produces a very large number that

is proportional to the much smaller number that represents the resulting production rate. A very small

constant does the conversion. In fact, it can be too small to represent on a computer!

The need for a tiny constant became a signiﬁcant practical issue in the marsh sector simulation, so the

multiplier auxiliaries for the gross photosynthesis equations, MA

07b

and MA

09b

(Eq. [028] and Eq. [030]),

do not include the inﬂuence of sediment (MQ

). To include the sediment inﬂuence, the constant needed

was on the order of 10

−44

. The number was too small to be represented precisely enough to run a required

model check on the available computer. Sediment was potentially the least dynamic inﬂuence on gross

production. The timescale of sediment dynamics in the model was on the order of 10,000 y, whereas the

next longest time scale (that of salt) was around 3 y. Sediment was unlikely to inﬂuence model output

spanning less than a few decades. By leaving out the sediment inﬂuence on production, the order of

magnitude for the gross production constant was increased to 10

−33

, large enough to allow the simulation

check (the check involved reproducing the steady-state condition used to calibrate the model).

28.3.2.3 Feedback Effect of Production Processes on the Environmental

Variables Involved

Some of the environmental inﬂuences on production are signiﬁcantly consumed in the process. Nutrients,

for example, are used at a rate proportional to gross production of low marsh plants (MJ

, Eq. [042]) and

benthic microalgae (MJ

, Eq. [043]). Likewise, water is transpired by low marsh plants (MJ

207

, Eq. [041]),

and circulation energy is dissipated by marsh plant biomass (MJ

607

, Eq. [045]). The accumulations of salt

and sediment, however, are not changed directly by gross primary production. This lack of effect is denoted

in Figure 28.3 by the use of the sensor symbol (small rectangle attached to the storage symbol where the

line of inﬂuence originates).

Because gross production by benthic microalgae is not explicitly drawn on the marsh sector diagram,

the inﬂuencing variables and any inﬂuences on them are unspeciﬁed. The same variables involved in

low marsh plant production are involved with benthic microalgae. An examination of the equation list

(Table 28.1) shows that with the exception of nutrient uptake (MJ

, Eq. [043]), gross primary production

by benthic microalgae does not consume any of the variables that inﬂuence it, at least for this model.

28.3.2.4 Two-way Interactions

In coastal systems, water circulating with the tides creates an exchange of materials between marshes

and adjacent estuarine waters. Five exchanges are illustrated at the top left of the marsh sector diagram

using two-way interaction symbols acted upon as a group by the tides. These are water, salt, nutrients,

detritus, and sediment. All of these exchanges are driven by tidal energy. A two-way interaction indicates

a balance of forces arising from storages of the same material on the two sides of the interaction. In the

case of Figure 28.3, the storages are in the marsh and in the adjacent waters. A tendency toward dynamic

equilibrium of materials is expected. The rate equation involves the difference between the two storages.

Its general form is

J = k

−k

)

where Q

is the quantity stored in the designated source location, and Q

is that stored in the receiving

location. A positive difference in parentheses sends the ﬂow toward the recipient, and a negative difference

establishes ﬂow in the opposite direction. For the marsh sector model, a positive ﬂow represents an import

into the marsh from the estuary. The constant k

is the dimensionless equilibrium ratio of Q

expected

once a dynamic equilibrium is established. The other constant k

is a rate constant: the fraction of the

Dynamic Simulation with Energy Systems Language 28-21

difference within the parentheses that can be closed per unit time. It is inversely proportional to the half-life

of the difference (half-life =ln 2/k

The above rate equation was applied to the two-way ﬂow for water, salt, inorganic nutrients, organic

detritus, and sediment in Eqs. (021)–(025) in Table 28.1. Note that Eq. (021) for exchange of water (J

W2M2

)

includes the multiplication by tide. This is not the case for the other four variables. In those cases, the

effect of tide is implicit in the selection of a value for the rate constant. As long as tidal inﬂux is constant,

this distinction is unimportant to the model output; however, before tidal energy inﬂux can be tested as

a variable, all the two-way exchanges must be converted to the form of Eq. (021). The conversion can be

done simply by dividing each rate constant by the constant tidal inﬂux used now (Eq. [086]). The values

in question are given in Eq. (086), Eq. (088), Eq. (090), and Eq. (092), respectively.

28.3.2.5 Passive Inputs and Environmental Conditions

A basic input from the environment passively received by storage within the system is perhaps the simplest

concept used to create a rate equation. Unlike with ﬂow- and storage-limited sources from outside the

system boundary, nothing within the system feeds back to limit the availability of such inputs. Examples

in the marsh sector model are the input of rain to marsh water (Rain, Eq. [075]) and the input of tidal

power to circulation (Tide, Eq. [076]).

When modeling a sector of a larger system, inputs from other sectors become basic environmental

conditions similar to passive inputs. For example, inputs to the marsh sector include the storages of water,

salt, nutrients, organic detritus, and sediment in the adjacent estuarine water (Eqs. [077]–[081]). These

storages would become dynamic model variables of the water sector in a complete model of the coastal

system diagrammed in Figure 28.1. Instead, they are set as passive inputs that do not change in response

to the ﬂows in and out of the marsh.

A passive input may be an average represented as a constant, a test pattern (such as a sine wave), a statis-

tical distribution, or a complex time variable based on real data. In the early stages of model analysis, such

variables are often set to average conditions represented by constants so as to not confound dynamics gener-

ated by the model’s own feedback structure with those that are simply responding to variable driving forces.

Holding the environmental inputs constant allows the internally created dynamics to be revealed ﬁrst.

28.3.2.6 An Unspeciﬁed Process (Rectangle)

The interaction of tide with the exchange of water circulation is represented by a small rectangle, indicating

a general process that must be made explicit in the documentation. In Figure 28.3, the rectangle merely

signiﬁes that water circulation energy is affected by the tide and by other forces provided through the water

sector. Wind effects, for example, are shown in the coastal system diagram of Figure 28.1. The two kinds

of forces are additive, but the marsh sector model only uses tidal power to drive circulation.

28.4 Calibration of Model Constants

All of the types of rate equation indicated or implied in the marsh sector diagram and given in the equation

list have now been deﬁned. The next step is to provide numerical values for all constants. In Energy

Systems Language, this is nearly always accomplished by back calculation from quantitative estimates of

all storages, rates, and system inputs. To do this, the rate equations are algebraically rearranged to solve for

the constants in terms of the rates, storages, and inputs involved. The process of back-calculating constants

in this manner is called model calibration.

To illustrate, consider the detailed diagram for a living composite symbol given in Figure 28.4(a). With

estimates of the amount storage (Q

), the amount of resources (R), and ﬂow J

, an estimate for the constant

can be calculated. Likewise, with estimates of the storage Q

and each of the other ﬂows (J

, and J

the constants k

and k

can be made.

Obtaining a complete set of applicable estimates for model calibration can be a time-consuming task;

however, it is easier than obtaining independent estimates for the constants themselves. Many of the