Fishwick P.A. (editor) Handbook of Dynamic System Modeling

Подождите немного. Документ загружается.

26-26 Handbook of Dynamic System Modeling

SGY 0 TF

C : L

C : 1/K

⫺nBl

⫺nBlv

dLi/dt

dl/dt

FIGURE 26.25 Addition of elastic cone suspension resulting in the decomposition of a two-port storage element.

which can be written dλ/dt =dLi/dt +nBlv =dLi/dt +nBldx/dt, after integration: λ =Li +nBlx. If this

constitutive relation is put in preferred integral causality i =1/Lλ −(nBl)/(L)x and combined with the

relation of the mechanical port F =−nBli =(−nBl/L)λ +((nBl)

/L)x into a relation of a two-port C in

matrix form:





⎡

⎢

⎣

−

nBl

−

nBl

(nBl)

⎤

⎥

⎦





(26.27)

it can be concluded that this two-port satisﬁes Maxwell symmetry, but that it is singular

(1/L((nBl)

/L) −(−nBl/L)

=0), such that a positive mechanical spring constant K representing the

connection to the frame of the moving voice coil, has to be added to make it intrinsically stable:

1/L(((nBl)

/L) +K) −(−nBl/L)

> 0 (Figure 26.25).

The junction structure with the transformer and the two Cs coincides with the so-called congruent

canonical decomposition of a linear two-port C of which the energy can be used as a generating function

of the constitutive relations (Breedveld, 1984b). When starting again without a mechanical spring, the

energy of this two-port should be written in terms of λ and x:

dE(λ, x) = idλ +Fdx =



−

(nBl)x



dλ +



−

(nBl)λ

(nBl)



dx = d

(λ −(nBl)x)

such that E(λ, x) =(λ −(nBl)x)

/2L, but is commonly mistaken by what is actually the coenergy in terms

of i and x: E

∗

(i, x) =Li

/2 +nBlix.

If this is the case and the force is incorrectly derived by taking the partial derivative of this coenergy as

if it were an energy F

incorrect!

= ∂E

∗

(i, x)/∂x =(i

/2)dL/dx +nBli, a sign error is obtained, as it should be

F =

∂E(λ, x)

∂x

∂

∂x

(λ −(nBl)x)

=−(nBl)



−

(nBl)x



−



−

(nBl)x



=−(nBl)i −

Note that the mere difference in the form of a minus sign between these results only occurs for the

particular case in which the current i depends linearly on the ﬂux linkage λ. In case of a nonlinear relation,

the error is larger than “just” a sign error that is commonly not noticed as it is compensated by an implicit

change in orientation: in contrast with the global convention, the mechanical port is then taken positively

outbound.

If a spring is added to satisfy intrinsic stability the energy increases with the potential energy

E(x) =Kx

/2 and similar constitutive relations are found from the energy function:





⎡

⎢

⎣

∂i

∂λ

∂i

∂x

∂F

∂λ

∂F

∂x

⎤

⎥

⎦





⎡

⎢

⎣

∂

∂λ

∂

∂x∂λ

∂

∂λ∂x

∂

∂x

⎤

⎥

⎦





⎡

⎢

⎣

−

nBl

−

nBl

(nBl)

⎤

⎥

⎦





(26.28)

Port-Based Modeling of Engineering Systems in Terms of Bond Graphs 26-27

⫺0.08⫺0.06 0.06

⫺0.2

⫺0.1

0.1

0.2

⫺0.04⫺0.02 0.02 0.04 0.080

Mech_state

Mech_effort

Model

(a)

⫺0.15

⫺0.2

⫺0.1

0.1

0.2

⫺0.1 ⫺0.05 0.05 0.1 0.150

Magn_state

Magn_effort

Model

(b)

FIGURE 26.26 Simulation of the mechanical and magnetic cycle with frequency sweep input.

which is intrinsically stable as long as (nBl)

+K/L −(nBl)

=K/L > 0. Figure 26.26 shows the

simulation results of a loudspeaker model containing this two-port, with a sinusoidal frequency sweep

input at the electric port. Both ports indeed perform a cycle process in which the magnetic port cycles

clockwise and the mechanical port counterclockwise (large loops, i.e., more energy transferred per cycle,

represent a simulation at the resonance frequency of the speaker), which demonstrates that indeed per

cycle a net amount of magnetic (electric) energy is transduced into mechanical energy. The areas of the

loops are equal in the conservative case.

Obviously, if the coenergy is explicitly identiﬁed as being different from the energy, the derivations lead

to the correct results too

∗

(i, x) =−(E(λ, x) −iλ) = iλ − E(λ, x) =

+nBlix −

(26.29)

∗

(i, x) = λdi − Fdx = Lidi +nBlidx −Kxdx (26.30)

Hence

∗

(i, x) =

+nBlix −

λ =

∂E

∗

(i, x)

∂i

= Li +nBlx (26.31)

so u =dλ/dt =d/dt(∂E

∗

(i, x)/∂i) =L(di/dt) +nBlv =u

self ind

Lorentz

and F =−∂E

∗

(i, x)/∂x =

−nBli +Kx, in matrix form:





⎡

⎢

⎣

∂λ

∂i

∂λ

∂x

∂F

∂i

∂F

∂x

⎤

⎥

⎦

⎡

⎢

⎣

∂

∗

∂i

∂

∗

∂i∂x

−∂

∗

∂x∂i

−∂

∗

∂x

⎤

⎥

⎦



L nBl

−nBl K





(26.32)

i.e., no symmetry of the Jacobian if energy and coenergy are confused.

This example demonstrates that the concept of multiport storage, in particular two-port storage, may

not only lead to conceptual models of transduction phenomena, but also that reversible transduction

requires a cycle process in principle. This means that a transducer cannot continuously transduce a DC

input. By changing its conﬁguration into that of an electric motor, the conﬁguration takes care of the cycle

of the conductors in the magnetic ﬁeld.

26-28 Handbook of Dynamic System Modeling

Hence, pure “DC”-type transduction can only be achieved by some form of “carrier” that performs a

cycle: gears carrying teeth (with elastic deformation!) during contact, a cooling ﬂuid, and a rolling wheel

that cycles its interaction point, which is a useful insight during conceptual design of transducers.

26.5 Conclusion

In this chapter, the basics of the port-based approach were introduced as well as their natural notation,

viz. bond graphs. The main advantages of the use are

(1) the domain-independence of the elementary behaviors and their graphical notation that allow quick

analysis of dynamic interaction across domain boundaries;

(2) that not all ports have an a-priori ﬁxed causality, thus allowing ﬂexible reuse of submodels;

(3) the combination of physical and computational structure in one notation, thus allowing

a. direct physical interpretation of required changes in model structure, e.g., for controller design,

b. direct feedback on modeling decisions,

c. direct graphical input for simulation software.

All these features contribute to rapid insight and the ability of efﬁcient iteration during the modeling

process.

It was also demonstrated that various domains of physics that use some form of energy-based model

formulation technique are all strongly related, even though terminologyand a loss of conceptual distinction

between conserved energy and its nonconserved Legendre transforms commonly obstructs this insight.

References

Ascher, U. M. and Petzold, L. R. 1998. Computer Methods for Ordinary Differential Equations and

Differential-Algebraic Equations. Philadelphia: SIAM.

Bos, A. M. 1986. Modelling Multibody Systems in Terms of Multibond Graphs. Ph.D. Thesis, Electrical

Engineering, University of Twente, Enschede, Netherlands.

Bos, A. M. and Tiernego, M. J. L. 1985. Formula manipulation in the multibond graph modelling and

simulation of large mechanical systems. J. Franklin Inst., Vol. 319, No. 1/2, pp. 51–65.

Breedveld, P. C. 1982. Thermodynamic bond graphs and the problem of thermal inertance. J. Franklin

Inst., Vol. 314, No. 1, pp. 15–40.

Breedveld, P. C. 1984a. Physical Systems Theory in Terms of Bond Graphs. ISBN 90-9000599-4. University

of Twente, Enschede, The Netherlands. Distributed via the author.

Breedveld, P. C. 1984b. Decomposition of multiport elements in a revised multibond graph notation.

J. Franklin Inst., Vol. 318, No. 4, pp. 253–273.

Breedveld, P. C. 1985. Multibond graph elements in physical systems theory. J. Franklin Inst., Vol. 319, No.

1/2, pp. 1–36.

Breedveld, P. C. 1999. Insight in rigid body motion stability via an alternative for the Eurlerian junc-

tion structure. Proceedings 1999 International Conference on Bond Graph Modeling and Simulation

(ICBGM’99), San Francisco, USA, Western Multi Conference Simulation Series, Vol. 31, No. 1, pp.

269–274.

Callen, H. B. 1960. Thermodynamics. New York: Wiley.

Golo, G. 2002. Interconnection Structures in Port-Based Modelling: Tools for Analysis and Simulation. Ph.D.

Thesis, University of Twente, Twente University Press.

Golo, G., Breedveld, P. C., Maschke, B. M. and van der Schaft, A. J. 2000. Input–output representations of

Dirac structures and junction structures in bond graphs. Proceedings 14th International Symposium

on Mathematical Theory of Networks and Systems, MTNS 2000, Perpignan, France, June 19–23.

Hayt, W. H., Jr., Kemmerly, J. E. and Durbin, S. M. 2002. Engineering Circuit Analysis, 6th edition. New

York: McGraw-Hill.

Port-Based Modeling of Engineering Systems in Terms of Bond Graphs 26-29

Hogan,N. J. and Fasse, E. D. 1988. Conservation principles and bond graphjunctionstructures. Proceedings

of the ASME 1988 WAM, DSC-Vol. 8, pp. 9–14.

Karnopp, D. C. and Rosenberg, R. C. 1968. Analysis and Simulation of Multiport Systems: The Bond Graph

Approach to Physical System Dynamics. Cambridge, MA: MIT Press.

Ligterink, N. E., Breedveld, P. C. and van der Schaft, A. J. 2006. Physical model reduction of interacting,

continuous systems. Proceedings 17th International Symposium on Mathematical Theory of Networks

and Systems, Kyoto, Japan, July 24–28.

Maschke, B. M. and van der Schaft, A. J. 2001. Canonical interdomain coupling in distributed param-

eter systems: An extension of the symplectic gyrator. Proceedings of the International Mechanical

Engineering Congress and Exposition, New York, USA, November 11–16.

Maschke, B. M., van der Schaft, A. J. and Breedveld, P. C. 1995. An intrinsic Hamiltonian formulation

of the dynamics of LC-circuits. Trans. IEEE on Circuits and Systems, I: Fundamental Theory and

Applications, Vol. 42, no. 2, pp. 73–82.

Paynter, H. M. 1961. Analysis and Design of Engineering Systems. Cambridge, MA: MIT Press.

Paynter, H. M. and Busch-Vishniac, I. J. 1988. Wave-scattering approaches to conservation and causality.

J. Franklin Inst., Vol. 325, No. 3, pp. 295–313.

Stramigioli, S. 1998. From Differentiable Manifolds to Interactive Robot Control. Ph.D. Thesis, Delft

University of Technology, Netherlands.

Tiernego, M. J. L. and van. Dixhoorn, J. J. 1979. Three-axis platform simulation: Bond graph and

Lagrangian approach. J. Franklin Inst., Vol. 308, No. 3, pp. 185–204.

Van Johannes, Dijk and Breedveld, P. C. 1991. Simulation of system models containing zero-order causal

paths—part I: Classiﬁcation of zero-order causal paths and part II: Numerical implications of

class-1 zero-order causal paths. J. Franklin Inst., Vol. 328, No. 5/6, pp. 959–979, 981–1004.

Wheeler, H. A. and Dettinger, D. 1949. Wheeler Monograph 9.

System Dynamics

Modeling of

Environmental Systems

Andrew Ford

Washington State University

27.1 Introductory Examples...................................................27-1

27.2 Comparison of the Flowers and Sales Models...............27-4

27.3 Background on Daisy World .........................................27-6

27.4 The Daisy World Model..................................................27-6

27.5 The Daisy World Management Flight Simulator .........27-9

This chapter provides a short tutorial on the system dynamics approach to computer simulation modeling.

The modeling usually begins when managers face a dynamic pattern that is causing a problem. The

modeling is based on the premise that we can improve our understanding of the dynamic behavior by the

construction and testing of models that focus on the information feedback. The approach was pioneered

by Forrester (1961) and is explained in recent texts by Ford (1999) and Sterman (2000). The models are

normally implemented with visual software such as

Stella (http://www.iseesystems.com),

Vensim (http://www.vensim.com/), and

Powersim (http://www.powersim.com/).

These programs use “stock and ﬂow” icons to help us see the accumulation in the system. The programs

also help one to see the information feedback in the simulated system. The programs use numerical

methods to show the dynamic behavior of the simulated system.

This chapter begins with simple models to demonstrate that different systems can exhibit the identical

pattern of growth over time. One model shows the growth in ﬂowered area; the second shows the growth

in a sales company. These systems show the same dynamic behavior because their growth is governed by

the same feedback loop structure. The ﬂower model is then extended to simulate the imaginary Daisy

World created by Watson and Lovelock (1983). Daisy World provides an additional example of feedback

loop structure. It also provides a convenient way to illustrate interactive “ﬂight simulators,” one of the

several methods to promote communication and learning from system dynamics models. The chapter

concludes with a list of readings for those who wish to learn more about system dynamics modeling of

environmental systems.

27.1 Introductory Examples

Figure 27.1 shows a ﬂow diagram of a model to simulate the growth in the area covered by ﬂowers. (This

diagram is in Stella.) In this example, we start with 10 acres of ﬂowers located within a suitable area of

1000 acres. The area of ﬂowers is called a stock variable; the growth and decay variables are called ﬂows.

27-1

27-2 Handbook of Dynamic System Modeling

Area of flowers

Growth

Decay

Decay rate

Intrinsic growth rate

Actual growth rate

Growth rate multiplier

Fraction occupied

Suitable area

FIGURE 27.1 Stella diagram of a model to simulate growth in the area of ﬂowers (from Island Press, 1999).

Growth

Area of

flowers

Decay

Intrinsic

growth rate

Actual growth rate

Growth rate

multiplier

Fraction occupied

Suitable area

Decay rate

Lookup for growth

rate multiplier

FIGURE 27.2 Vensim diagram of the ﬂowers model.

The growth ﬂow increases the area of ﬂowers over time. The decay ﬂow reduces the ﬂowered area over

time. The remaining variables in the Stella diagram are called converters. The converters are used to help

explain the ﬂows. Stella depicts the action of the ﬂows by the double lines leading into or out of the stocks.

Stella represents the information connections by single lines. For example, the single lines connecting to

the decay ﬂow indicate that the decay is inﬂuenced by the area of ﬂowers and the decay rate. The variables

in system dynamics models are normally assigned long names to make their meaning clear. When this is

done, the reader can usually guess the equation for each variable. For example, you can probably guess

that the equation for the decay is the product of the area of ﬂowers and the decay rate.

Figure 27.2 shows the Vensim version of the ﬂow diagram for the ﬂowers model. The two programs

use somewhat different icons, but the stock and ﬂows are clear to see. Figure 27.2 shows that the area of

ﬂowers is a stock which is increased by growth and reduced by decay. Additional variables (such as the

decay rate) appear in Figure 27.2 by their names. Vensim allows the user to assign a variety of symbols to

the variables, but the convention is to avoid extra symbols to minimize clutter in the diagram.

System dynamics models may be viewed as a coupled set of differential equations. In the ﬂowermodel, we

have only one stock variable, so the model may be represented by a single differential equation, as shown

in Table 27.1. This format will be familiar to many handbook readers who have studied calculus and

differential equations. These readers will appreciate that an analytic solution to the differential equation is

difﬁcult because of the nonlinear relationship for the growth rate multiplier.

System dynamics models are ﬁlled with nonlinear relationships, so the software programs are designed

to make it easy to ﬁnd a numerical solution to the equations. Most simulations are performed with Euler’s

method. The model user is responsible for setting a sufﬁciently short step size to ensure accurate results.

Accuracy is usually checked by simply repeating the simulation with the step size cut in half. If we see the

same results, we know the results are numerically accurate.

System Dynamics Modeling of Environmental Systems 27-3

TABLE 27.1 Flower Model in the Form of a Differential

Equation

Let dA(t)/dt =G(t) −D(t)

A =area of ﬂowers A(0) =10

G =growth

D =decay D(t) =A(t)*d

G(t) =A(t)*g

d =decay rate g(t) =ig*gm(t)

g =actual growth rate gm =f (FO)

ig =intrinsic growth rate FO(t) =A(t)/SA

SA =suitable area SA =1000

gm =growth rate multiplier ig =1.0

FO =fraction occupied d =0.2

1000

400

500

200

02468101214161820

Time (year)

Area of flowers: CRC 1st example

Growth: CRC 1st example

Decay: CRC 1st example

FIGURE 27.3 Vensim graph of ﬂower simulation results. (The area is scaled to 1000 acres. The growth and decay are

scaled to 400 acres/year.)

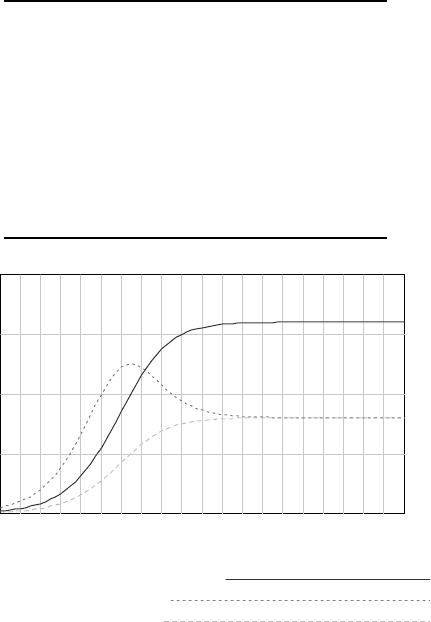
Figure 27.3 shows a Vensim time graph of a 20-year simulation. The graph shows rapid growth in the

space occupied by ﬂowers during the ﬁrst 5 years as the growth far exceeds the decay. As the ﬂowers ﬁll

up the suitable area, their growth rate falls below the intrinsic growth rate that applied at the start of the

simulation. The growth gradually declines until it matches the decay. At this point, the system has reached

a dynamic equilibrium with 800 acres of ﬂowers. The ﬂowered area is maintained by a growth and decay

of 160 acres/year.

Figure 27.4 shows a somewhat more complicated model. This is a Vensim ﬂow diagram of a model to

simulate the growth in a sales company. A stock variable represents the size of the sales force. The stock

is increased by the new hires, and it is reduced by the departures. Departures are controlled by the exit

rate, which is set to 20% per year. The new hires are controlled by the budgeted size of the sales force.

To illustrate, consider a numerical example with the sales force initially at 50 people. With a small sales

force, we assume that each person can sell 2 widgets per day. If the widget price is $100, the 50 people

could generate $3.65 million in annual revenues. If the company assigns half of the revenues to the sales

department budget, the company could budget for 73 sales persons paid an annual salary of $25,000. In

this situation, the new hires would be calculated to build the stock toward the goal of 73 persons. The pace

at which the new hires builds the stock is controlled by the hiring fraction, which is measured as a fraction

per year. When new hires exceed departures, the sales force will grow toward saturation. With so many

sales persons working the market, their effectiveness will fall below the initial value of 2 widgets per day.

27-4 Handbook of Dynamic System Modeling

Size of

sales force

New hires

Departures

Exit rate

Budgeted size of

sales force

Hiring fraction

Sales department

budget

Average salary

Fraction of revenue

to sales

Annual revenue in

millions

Widget price

Widget sales

Saturation size

Sales force ratio

Sales person effectiveness

in widgets sold per day

Nonlinear lookup for

the effectiveness

FIGURE 27.4 Vensim diagram of a model to simulate the growth of a sales company.

1000

400

500

200

0 2 4 6 8 10 12 14 16 18 20

Time (year)

Size of sales force: CRC 2nd example

New hires: CRC 2nd example

Departures: CRC 2nd example

FIGURE 27.5 Vensim time graph for the sales model. (The sales force is scaled to 1000 persons. The new hires and

departures are scaled to 400 persons per year.)

Figure 27.5 shows the simulated growth in the sales force when the model is simulated over a 20-year

period. The graph shows rapid growth in the size of the sales force during the ﬁrst 9 years as the new

hires far exceed the departures. However, as the sales force climbs past 500 persons, the new hires begins

to decline. New hires gradually decline until the company achieves dynamic equilibrium with around

150 new hires and departures per year. The equilibrium size of the company is around 750 persons.

27.2 Comparison of the Flowers and Sales Models

Figure 27.3 and Figure 27.5 show that the sales company exhibits essentially the same pattern of behavior

as the ﬂowers system. Both simulations begin with rapid growth. The growth is powered by a high growth

rate of ﬂowers and by the high effectiveness of the sales persons. But both systems face limits, so they

cannot grow forever. As the systems encounter these limits, their growth declines in a gradual manner.

System Dynamics Modeling of Environmental Systems 27-5

Suitable area

(⫺)

(⫹)

Fraction occupied

Growth rate

Decay rate

Decay

Growth

Area of flowers

⫺

⫹

⫺

⫹

FIGURE 27.6 Feedback loop structure of the ﬂowers model (from Island Press, 1999).

(⫺)

(⫹)

Effectiveness of

each sales person in

widgets sold per day

Widget price

Fraction to sales

Average salary

Budgeted

number of sales

persons

Sales department

budget

Annual revenues

Widget sales

New hires

Exit rate

Departures

Number of

sales persons

⫺

⫹

⫺

⫹

⫺

⫹

⫺

⫹

FIGURE 27.7 Feedback loop structure of the sales model (from Island Press, 1999).

Eventually, they reach a state of dynamic equilibrium, an equilibrium which could be maintained year after

year. The similarity in these patterns is no coincidence. It arises from the similarity in their underlying

structure. You can see some similarity by comparing the model diagrams. But the similarity will be even

more apparent when we draw causal loop diagrams to focus our attention on the feedback in the systems.

We expect to see positive feedback when a system is able to grow on its own; we expect to see negative loops

that limit or shape the growth of the system. These loops come into clearer view when we show variables

and their interconnections as in Figure 27.6 and Figure 27.7.

Figure 27.6 shows the three feedback loops in the ﬂowers model. The rapid growth is powered by the

positive feedback loop in the upper left corner of the diagram: more ﬂowered area leads to more growth,

which leads to more ﬂowered area. The convention is to label the positive feedback loops with a (+).

These loops will be found whenever a system has the power to exhibit exponential growth on its own.

Figure 27.6 shows two negative loops, both of which are marked with a (−). One negative loop involves

the decay of ﬂowered area over time. The strength of this loop is controlled by the decay rate, which is

assumed to remain constant in this example. The other negative loop involves the reduction in the growth

rate as the ﬂowers occupy a larger and larger fraction of the suitable area. This is a negative loop that

becomes stronger and stronger over time. (Such feedback is sometimes called density-dependent feedback

in environmental systems.) The negative feedback on ﬂower growth eventually reaches the point where

growth and decay are in dynamic equilibrium.

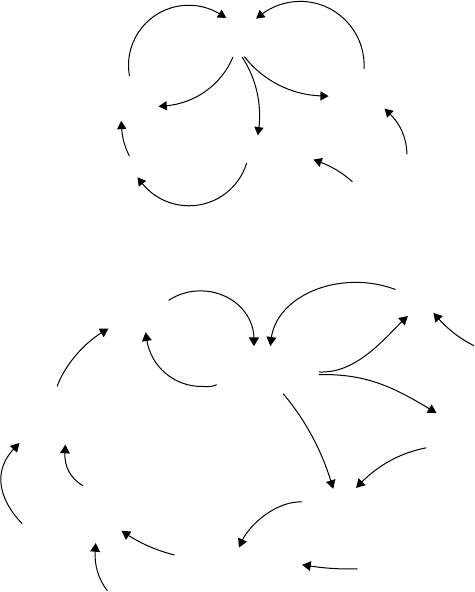
Figure 27.7 shows a somewhat similar set of loops in the sales model. Since the sales force grows rapidly

on its own, we know that there should be positive feedback in the system. This loop involves the size

of the sales force and the annual revenues: a larger sales force leads to greater sales, increased revenues,

a larger budget for the sales department, a larger budgeted number of sales persons, more new hires, and