Fishwick P.A. (editor) Handbook of Dynamic System Modeling

Подождите немного. Документ загружается.

28-2 Handbook of Dynamic System Modeling

A process of natural selection is at work that replaces components that become less competitive for the

energy sources with more productive ones that accomplish a similar function. As long as a constant source

of energy is available, and changes are not too great and sudden, the self-organization of a natural system,

once begun, is self-perpetuating.

Odum’s systems philosophy and methodology therefore focused on energy. The theoretical basis com-

bines the principles of natural selection and the laws of thermodynamics to account for the development

and structure of natural systems and so their response to environmental change. Out of the theory and

some massive ﬁeld studies of energy ﬂow through entire ecosystems, came complex ideas that were difﬁcult

to communicate to other ecologists at a time when few incorporated energy concepts in their research

(mid-1950s).

Energy Systems Language was then developed to address the need for precise communication of (a) the

likely structure of naturally organized energy systems; and (b) the consequences of a given arrangement of

energetic components and connections on the response of a natural system to environmental change. The

language consists of symbols that can be arranged in a diagram for precise communication of the energy

and resource network that deﬁnes a given model. The methodology is accomplished through a process of

diagramming a network of ﬂows and storages, followed by numerical simulations and analyses derived

directly from the diagram, given limited empirical estimates with which to calibrate the model.

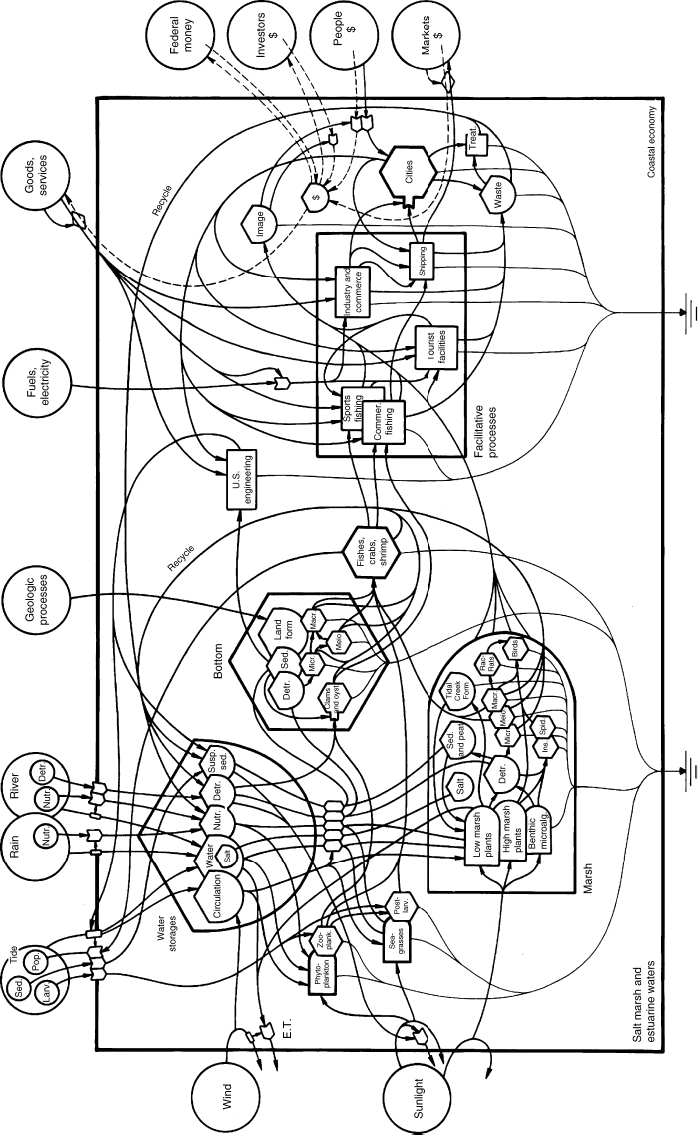
An example diagram, Figure 28.1, is used in this chapter to illustrate the process. The diagram was

developed originally to help describe salient features of the ecological and economic system associated

with marsh estuaries of the Gulf of Mexico coast (Montague and Odum, 1997). At ﬁrst glance, the diagram

may seem overwhelming and cluttered, but the rules for diagram layout are strict and the symbols have

precise meaning. The diagram is not primarily a visual aid. Rather, it communicates speciﬁc ideas in a

systematic way. Both the choice of symbols and their layout in the diagram have speciﬁc meanings. This is

the reason for calling the method a language. The symbols are simply words and sentences. The sense of the

document is contained in the arrangement of these on the page. Increasing familiarity with the rules and

uses of Energy Systems Language will demystify such diagrams. The process can begin with this chapter.

As can be seen in Figure 28.1, an Energy Systems Language diagram connects energy resources, plants,

animals, ecological processes, people, mineral resources, economic products, and socioeconomic processes

in a complex network of ﬂow and control based on careful thought about the nature of each individual ﬂow,

storage, and interaction in the set thought to deﬁne a given system. The diagram then is an expression

of a complex hypothesis of system structure that will produce speciﬁc dynamic responses to change.

Compared with a verbally stated or mental model, it is a very rigorous representation of the hypothesis. The

computer is required because the brain cannot fathom the consequences of the many inﬂuences thought

to be operating simultaneously in the real system. Like many scientiﬁc hypotheses, complex models of

poorly known self-organized systems cannot be proven correct, but they are capable of disproof. Often

the disproof comes with the output from the ﬁrst simulation model!

An important aspect of Energy Systems Language is the ﬁxed relationship between a sufﬁciently detailed

diagram and a set of differential and algebraic equations that describe dynamic change in all storages

and ﬂows. The unique feature of the approach is the use of relatively few types of control and storage

processes to represent a complex system by arranging them in a highly speciﬁc, information rich diagram.

Accordingly, a few basic types of equation are sufﬁcient to represent most of the individual ﬂows, storages,

and interactions in an Energy Systems Language diagram. The diagram consists of a complex arrangement

of relatively simple symbols that corresponds to a complex system of relatively simple equations.

In this chapter, a portion of Figure 28.1 (the Marsh sector) will be translated into equations and

simulated to illustrate this process and the highly dynamic output that can result even in a constant

environment. A caveat: The experienced user of Energy Systems Language has intimate knowledge of

the equations implied by the diagram, and chooses to draw subtle details in a certain way so that the

proper process occurs. Because a sufﬁciently detailed diagram can be translated nearly by rote, beginners

are often encouraged to draw a diagram and see what simulation model it produces. This speeds up the

process of getting interesting model output to discuss; however, it postpones the need to recognize how to

represent known processes adequately by combining model components appropriately. Experimentation

Dynamic Simulation with Energy Systems Language 28-3

FIGURE 28.1

Energy Systems Language diagram of a marsh estuary system

of the Gulf of Mexico coast of the United States (Reproduced with

permission from Montague, C

.L.

and H.T. Odum, 1997. Introduction: The intertidal marshes

of Florida’s Gulf coast. In Coultas, C.L. and Y.-P. Hsieh (eds.),

Ecology and Management of Tidal Marshes: A Model from

the Gulf of Mexico

. St Lucie Press, Delray Beach, Florida, pp. 1–7, 355pp.)

28-4 Handbook of Dynamic System Modeling

with various model structures is helpful, along with advanced reading on the subject. A good introduction

to the approach along with many simple model examples can be found in Odum and Odum (2000). The

most complete description of the behavior of combinations of components is in Odum (1983, revised and

retitled as Odum, 1994).

28.2 Reading an Energy Systems Language Diagram

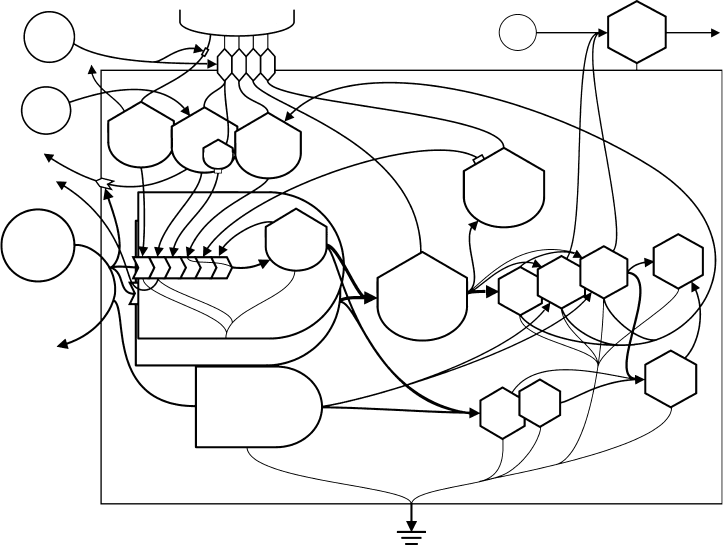
The diagram in Figure 28.1 includes the nine most commonly used symbols of Energy Systems Language.

For reference, these symbols are listed in Figure 28.2. Lines throughout the diagram connect various

symbols to one another. Flows of energy and materials are represented by solid lines. Dashed lines represent

ﬂows of money. Money always ﬂows in the opposite direction of the products and sources it purchases.

Reading the diagram involves the symbols, their combination in connected pairs, and the overall layout

scheme that together provide a wealth of information about the system under study. Complex Energy

Systems Language diagrams, such as Figure 28.1, communicate several levels of detail about system

organization. Translating the diagram involves the ﬁnest level of detail. At the highest level, a sense of

system self-organization is imparted. Reading Energy Systems Language diagrams is easier once major

features of diagram layout are recognized. With experience, the richness of the diagram becomes more

apparent, while at the same time, the complexity of it seems less daunting.

28.2.1 Layout of a Diagram and its Connection to Energy Theory

The layout process imparts distinctive left–right, up–down, clockwise, and counterclockwise facets of

meaning to the diagram. Lines of energy and material ﬂow generally from left to right and from up to

Source

Sink

Interaction

Two-way flow

General process

Price-controled flow

Storage

Producer

Consumer

Transformations

Living subsystems

FIGURE 28.2 The nine most common symbols used in Energy Systems Language diagrams.

Dynamic Simulation with Energy Systems Language 28-5

down. Toward the center and further right, however, some lines bend upward and back to the left creating a

counterclockwise impression of ﬂow. Conversely, dashed lines representing money ﬂows enter the system

generally from the right and bend upward and back to the right in a clockwise manner.

In the theory behind Energy Systems Language, the primary function of a persistent self-organizing

system is to combine and upgrade energy and material sources into products that reproduce and maintain

its lasting components. The products include the living components and concentrated stores of nonliving

resources. The processes of upgrading and maintaining the system components use large amounts of

energy. Most of the energy that enters the system is consumed and degraded into relatively dilute heat no

longer able to do useful work. Relatively little of the energy is left behind in the form of upgraded products.

Some of the upgraded products leave the system, either by leakage, migration, or by export in trade for

high-quality inputs.

Diagram layout incorporates the distinction between energy sources, upgraded energy, and downgraded

energy. The diagram is drawn so that sources enter each symbol from the left or top,and upgraded products

exit to the right. Upgraded products also cross the right side of the system boundary. Lines representing

heat losses, however, leave the bottom of each energy-using component and terminate in a heat sink symbol

outside the lower boundary. In general, the lines in the diagram that curve continuously downward are

heat losses. In Figure 28.1, these lines converge at one of two heat sinks at the bottom of the diagram.

Diagram layout itself is not critical to equation translation, but knowing the scheme helps to organize

the process. Understanding the overall principle behind the layout allows the diagram to be read and

studied at telescoping levels of detail. For those ﬂuent in Energy Systems Language and indoctrinated into

its theory, a diagram can begin to impart a sense of system self-organization and of the response to be

expected with a given change.

28.2.1.1 Transformity Principle of Diagram Layout

The concept of transformity—central to Odum’s energy systems theory of self-organization—provides the

principle for layout of Energy Systems Language diagrams. Essentially, transformity is the amount of basic

source energy (usually sunlight) used in the necessary network of ﬂows and transformations to place a

single unit of source energy into a given upgraded product. Each component of the network depicted in

Figure 28.1, for example, has its own transformity, which can be calculated from amounts of the various

sources that ultimately lead to it. To do this, each source must be weighted by its own transformity.

Each source represented by a circle is itself a product of energetic processes that occur in a network. This

network must be identiﬁed to determine the transformity of the source. The progression then extends to

the sources for the source until ultimately each can be traced back to primary sources for all processes on

Earth (sunlight, the Earth’s internal heat, and the planetary motions that create tides, seasons, etc.).

Transformity analysis is beyond the scope of this chapter, but it is a second major use of Energy Systems

Language diagrams. The procedures are described in detail in Odum (1996).

28.2.1.2 Arrangement of Sources in Order of Transformity

In Energy SystemsLanguage diagrams,circlesare arrangedoutside the sides and topof the system boundary

in order of the transformity of the indicated source. The arrangement is clockwise beginning with sunlight

at the lower left, which, as the basis for the approach, has a transformity of 1. All other sources have higher

transformities. In Figure 28.1, the next one is wind energy, a joule of which, according to transformity

analysis, requires on the order of 1500 J of sunlight.

Third is tide, which is a primary energy source. Part of transformity analysis requires establishing a

sunlight energy equivalence for the work of tide. Extrapolation from the solar tide would not yield the

required equivalence to light energy; however, sunlight energy can lift water through evaporation, which

is the usual basis for establishing a sunlight equivalence for tide.

In any case, the layout of sources continues clockwise. Those above the middle of Figure 28.1 change

from natural energy sources of high transformity (geological processes that form land) to sources that

have been transformed into commodities in part through human work. In Figure 28.1 these sources

include electricity, fuels, goods and services, and others arranged around the diagram. In Figure 28.1,

28-6 Handbook of Dynamic System Modeling

the last source is labeled markets. It has such a high transformity because markets are based largely on

information. According to transformity analysis, useful information is the highest transformity product

of society (Odum, 1996).

28.2.1.3 Overall Effect of Transformity on Diagram Organization

Inside the diagram, the various symbols are arranged according to their proximity to the resources needed

for their production. Given the layout of sources and the rules of connecting ﬂows to symbols, a progression

occurs from left to right across the diagram that reﬂects a general increase in transformity of the various

components as the number of preceding transformations increases, and higher transformity sources are

used. The layout procedure results in nonhuman processes and the products of nature generally appearing

to the left side of a diagram, while those involving greater amounts of human labor and education are

further to the right.

High transformity components of systems are often involved with the production of lower transfor-

mity products, thereby forming positive feedback loops. Animals, for example, regenerate nutrients that

inﬂuence rates of plant production, which ultimately provides more food for more animal production.

Likewise, people farm foods and direct natural resources for their own use. Feedback from higher transfor-

mity components to lower ones is distinguished by the counterclockwise return ﬂows that sweep upward

and back to the left in the diagram.

28.2.2 Symbols within the System Boundary

Two categories of symbol are used in Energy Systems Language: basic symbols and composite symbols.

Composite symbols represent commonly occurring sets of basic symbols. The two most common compos-

ite symbols are for living components: the bullet-shaped symbol for primary producers and the hexagon

for consumers.

The basic symbols include the circles that denote sources and the heat sinks that are generally shown

outside the system boundaries. Five other basic symbols occur within the system boundary and within

various composite symbols. These include the storage symbol (reminiscent of a water storage tank), and

the ﬁve transformation symbols listed in Figure 28.2.

In Figure 28.1 storages include water, salt, nutrients, detritus, circulation of water, land formations,

coastal image, money, and waste. A storage is part of the two composite symbols as well. A total of 43

separate storages are shown in Figure 28.1. The amount of material or energy within each storage changes

according to the net effect of all inﬂows and outﬂows connected to them.

A variety of symbols represent speciﬁc energy transformation processes that have standard mathematical

representations. The most common one is the interaction symbol shown in Figure 28.2. Figure 28.1 also

includes several two-way ﬂows, a price-controlled interaction, and several rectangular general process

symbols. The general process remains unspeciﬁed in the diagram. It may be a simple transformation, or a

composite. In any case, the rectangle is the only transformation symbol that requires further speciﬁcation

than appears in the diagram before it can be used in an equation.

When the interaction symbol is used, the primary source of energy to be used in the transformation

process enters from the left and the product exits from the right and usually enters a storage symbol.

Smaller amounts of upgraded energy from elsewhere in the system enter the symbol from the top. These

assist or subsidize the transformation. In this way, the main energy source appears to pass through the

interaction, while the interacting subsidy appears to control or assist the rate of transformation.

By far the most frequently used function associated with the interaction symbol is multiplication.

Multiplication is so common that an unspeciﬁed interaction is assumed to be multiplicative. Otherwise, a

mathematical character, such as a division sign, will appear within the interaction symbol to indicate its

function. The rationale for this frequent use stems from its similarity to the second-order reaction kinetics

in physical chemistry. A rate of reaction of two chemicals is often adequately represented by the multiple

of the concentrations of the two reactants times a rate constant. The rate declines as the reactants are

converted to products. As in chemical kinetics, multiplication is thought to adequately represent many

kinds of energy transformation that combine several necessary forms of energy and materials.

Dynamic Simulation with Energy Systems Language 28-7

All of the ﬂows entering and leaving the interaction symbol have the same equation form. This applies

to the formation rate of the product, the loss of raw materials from the main source and the assisting

variables, and heat loss associated with the transformation. The equation form consists of the indicated

combination of source and assisting variable multiplied by a constant. Only the value of the constant will

differ for the associated ﬂows.

When two or more variables assist a transformation, adjacent interaction symbols will occur in series,

and the terms of the equation are built accordingly. One multiplicative interaction gives a rate equation with

a second-degree term. Likewise, a series of three multiplicative interactions will produce a fourth-degree

term. Again all the reactant and product ﬂows will have the same equation form.

A two-way interaction symbol denotes a ﬂow of energy and materials back and forth created by an

interacting source of energy. The tide is such an energy source in Figure 28.1. The tide moves water and

the materials it contains between the marsh and the estuary. The rate of movement depends also on the

relative amounts of material stored on each side of the interaction relative to an equilibrium ratio, and on

various ﬁxed conditions that along with the tide determine the rate at which equilibrium can be restored.

The speciﬁc equation structure is given in the section on equation writing.

The price-controlled ﬂow is a symbol that converts a ﬂow of purchased products to a ﬂow of money. The

ﬂow of product may be caused by a variety of events. The price controls the ﬂow of money in return. The

supply of money and products may also feed back and inﬂuence the price. When the price is so inﬂuenced,

lines will enter the price-controlled ﬂow from the top and the details of the equation must be speciﬁed.

Often the effect on price is simply proportional to the supply of product or to the ratio of product and

available money. Figure 28.1 shows a situation where the markets outside the system inﬂuence the price.

If no explicit price controls are speciﬁed, a ﬁxed price is implied that will be represented in the model by

a constant.

The rectangle is reserved for unspeciﬁed processes. This symbol can represent a single transformation

equation, or a combination of symbols. Rectangles are used to reduce clutter when the process involved is

complex. In any case, the detail must be provided before a simulation model can be built. In Figure 28.1,

the rectangle is used for many of the processes associated with the economic system on the right side of

the diagram.

Rectangles and price controls are the only symbols for which no direct translation to equations is

possible. Before simulation can be done, the process within each rectangle must be represented either

in a special diagram of its own, or by a suitable input–output relationship already in equation form (a

regression equation, for example).

A variety of other symbols were introduced by Odum over the years to represent speciﬁc recurring

processes found in open energy systems; however, these are not as often used as those listed in Figure 28.2.

Among others, they include ratio interactions, switches, backﬂow interactions, and saturation limits; all

are described in Odum (1983, 1994).

28.2.3 Stylistic Diagramming Features not Directly Involved in

Equation Formulation

Certain features of Energy Systems Language diagrams are primarily stylistic, but help organize like

components, indicate relative importance, and reduce clutter. These include the use of different sizes for

symbols and line thickness, grouping related symbols within sector boundaries, and stacking or clustering

related symbols. Symbol size and line thickness indicate the relative sizes of various storages and ﬂows

of upgraded materials. Lines of degraded energy are often thinner than other lines even though most of

the energy travels through them. This is to reduce clutter and provide an additional way to distinguish an

upgrade from a downgrade in a transformation process.

28.2.3.1 Sector Boundaries

Sector boundaries are lines that encompass a group of related symbols within the system boundary. Sector

boundaries can be rectangles or, when the overall effect of the sector on the larger system is similar to that

of a given symbol, sector boundaries may take the shape of the relevant symbol.

28-8 Handbook of Dynamic System Modeling

Several sectors are identiﬁed by boundaries in Figure 28.1. On the right side of Figure 28.1, a grouping

labeled “Facilitative processes” is outlined with a rectangle. The sector contains some of the infrastructure

of the coastal economic system. Near the top of the left side of Figure 28.1 is a group of “Water storages”

enclosed in a sector boundary resembling a storage tank. Below that is a sector called “Marsh.” Because in

general more organic matter is produced in coastal marshes than is consumed there, the sector boundary

is bullet shaped like the primary producer symbol. Finally in Figure 28.1 is a hexagonal sector boundary

labeled “Bottom” because the living organisms and biochemical reactions within the estuarine bottom

consume more organic matter than they produce.

28.2.3.2 Nested Symbols

Sometimes basic symbols contain smaller and differently labeled symbols of the same type inside them.

Nested within the tide source in Figure 28.1, for example, are source symbols for larvae, adult animal

populations, and sediments that move into the coastal system from nearshore waters with the tide. The

rain and river symbols contain source symbols for nutrients and detritus that are delivered in signiﬁcant

amounts along with the freshwater that enters the system.

In the water storage sector, the symbol for the water storage itself includes a storage of salt. The sector

boundary already points out the collection of important constituents that it contains. Salt is treated

differently to highlight an important difference in its effect from the other constituents. The saltiness of

coastal water is represented by its salinity. Production in estuaries is often higher at lower salinity. The

nesting of salt within the water represents salinity.

28.2.3.3 Vertical and Horizontal Stacks of Symbols

Throughout Figure 28.1 are symbols that touch or partially overlap one another. The proximity suggests

tight coupling of the symbols. In the marsh sector, for example, is a vertical stack of three primary producer

symbols. The stack shows that all the three are inﬂuenced by the set of ﬁve variables entering the top of

the stack. The order in the stack is also important. Low and high refer to elevation relative to sea level. By

being closer to the estuarine water, the low marsh plants receive the effects of the water constituents ﬁrst

and then the high marsh plants.

At the bottom of the stack, the smaller size of the symbol for benthic microalgae indicates their lower

biomass and the inset of the symbol under the other two indicates their existence in the shade of the other

plants. This latter issue does affect the primary production equation for benthic microalgae. The part of

the diagram that dictates this for the equation is found on the line that represents the ﬂow of sunlight

energy to primary producers. The benthic microalgae receive light last. This will be clariﬁed below when

the marsh sector is redrawn for equation writing.

Also in the marsh sector is an illustration of a horizontal stacking of the community of detritivores.

In this case, the stack means that all three consume detritus, meiofauna also consume microbes, and

macrofauna, which are the last consumers in the stack, consume all three. To write equations from a

diagram requires that such details be explicitly shown. The ﬂow lines were left out to reduce clutter.

28.2.3.4 Converging and Diverging Flow Lines

Figure 28.1 includes a variety of convergent and divergent ﬂow lines to reduce clutter. The line labeled

recycle, for example, originates from the three components of the detritivore community in the marsh

sector. Three separate lines converge into one at the marsh sector boundary. Divergent lines are also used

in Figure 28.1. A single line from the source labeled “Goods, Services” splits into several as it crosses the

right side of the upper system boundary.

28.3 Translating a Diagram to Dynamic Equations

From a sufﬁciently detailed diagram, a mathematical system of ﬁrst-order, nonlinear differential equations

can be derived. The set of differential equations represents the net rate of change over time for each material

and energy storage in the model system. The rates are based on cause and effect inﬂuences from the storages

Dynamic Simulation with Energy Systems Language 28-9

themselves and various environmental inputs to the system. The equations are solved on a computer to

reveal the dynamic patterns produced in each model variable.

The set of equations that can be developed from an Energy Systems Language diagram will at a minimum

consist of one equation for each ﬂow and one integrating equation for each storage that combines the

ﬂows into and out of it. In total, Figure 28.1 contains 43 storages and nearly 120 explicitly represented

ﬂows, plus a number of ﬂows implied in the stacking of symbols. A complete translation of Figure 28.1

for simulation would have close to 200 equations for dynamic variables, and another 200 that specify

inputs, constants, and initial conditions. Figure 28.1, however, is incompletely speciﬁed and the resulting

model would provide an unwieldy demonstration at best! So to illustrate the process, a portion of the

diagram (the marsh sector) is redrawn, the corresponding equations derived, and the resulting model

simulated.

Equation writing is easier than it may appear from a complex diagram, especially one that includes all

necessary details. However, only a few types of equation are actually needed. Like the repeated use of the

same symbols in the diagram, the same equation form is repeated many times.

Equations are based upon symbol connections in Energy Systems Language diagrams. The individual

symbols provide only a part of the equation. In general, a combination of two components connected by

a line are necessary to determine the form of each equation used.

The necessary details for deriving model equations for the Marsh sector are given in the diagram

shown in Figure 28.3. A close examination of the marsh sector in Figure 28.1 will reveal a few important

differences. First, the effect of Tidal Creek Form is excluded because the intended effect is not clearly

understood. Second, the line from high marsh plants to birds is misplaced in Figure 28.1. In the revised

Tide

Rain

Sun

Water sector

Water

circulation

in marsh

Water

Salt

Nutrients

Sed. and

peat

Detritus

Micr.

Spid.

Birds

Marsh sector

Ins.

Meio.

Macr.

Rac-

Rats

Other

sources

Fsh, crb,

and shr.

LM plants

Benthic

microalgae



XXX

HM plants

FIGURE 28.3 Detailed Energy Systems Language diagram of the marsh sector of the coastal system diagram. The

diagram is sufﬁciently detailed for the derivation of model equations.

28-10 Handbook of Dynamic System Modeling

marsh sector diagram of Figure 28.3, a line from high marsh plants goes to detritus and another line from

insects to birds is added. The line from rats and raccoons to birds is also reversed (rats and raccoons eat

birds eggs but few rats and raccoons are eaten by birds in the marsh). Finally, a missing line is added from

salt to the primary producers.

Only the low-elevation portion of the marsh sector has been translated into equations and simulated

in this chapter. The equation list for this simulation is given in Table 28.1. Equations for the high marsh

portion would differ little other than in the calibration of constants to reﬂect high marsh conditions.

The correspondence between equations in Table 28.1 and the symbols on the diagram (Figure 28.3)

will become apparent by cross-referencing the diagram labels with the column of Table 28.1 labeled

“Meaning.”

The 16 storages involved in the low marsh subsector are listed ﬁrst in Table 28.1 (Eqs. [001]–[016]).

These are followed by the rate equations, then model inputs, model constants, and the time parameters

used in the simulation. A total of 141 entries are made in Table 28.1.

28.3.1 Equation Naming Convention Used in this Chapter

The equation list uses a naming convention for variables that helps to track the relationship among model

variables. In general, storage i is indicated by Q

and rates of ﬂow from storage j to storage

by J

. Marsh

variables are preceded by an M and estuarine water variables by a W. For example, MQ

represents the

marsh plants (Eq. [007]), and WQ

the nutrients in estuarine water (Eq. [077]). MJ

represents the ﬂow

from plants to detritus (MQ

) in the marsh (Eq. [048]). J

W4M4

represents the two-way interaction (upper

left of the diagram in Figure 28.3) that deﬁnes exchange of nutrients between the water and the marsh.

By listing W

as the ﬁrst subscript, the positive direction is toward the marsh for this two-way nutrient

exchange. Equally, a negative ﬂow represents export of nutrients from the marsh.

Constants in rate equations are indicated by a K. An A denotes an auxiliary variable that must ﬁrst

be calculated to assign a value to a ﬂow rate. Constants and auxiliaries are preﬁxed and subscripted like

the rate to which they apply. MA

, for example, denotes the light available for evaporation of water

(Eq. [031]), which is used to compute evaporation (MJ

, Eq. [040]). The latter equation also uses the

proportionality constant denoted as MK

A subscript of 0 indicates a location outside the system boundary. A ﬂow from a source outside the

boundary to a given storage i is labeled J

. Sunlight from outside the system is assimilated by benthic

microalgae (MQ

), for example, so their rate of gross primary production is labeled MJ

(Eq. [034]).

Conversely, ﬂows that leave the system from storage i are denoted by J

. The ﬂow MJ

, for example,

identiﬁes the metabolic heat loss from microbes (MQ

). The equation number for MJ

is 054 in Table 28.1.

Note that the constant in the equation, MK

, has the same subscript. If more than one ﬂow from a given

source connects to the same sink, the ﬂows are distinguished by a third character appended to the name.

Evaporation and transpiration, which are two ways in which water leaves the marsh system boundary, are

represented by MJ

(Eq. [040]) and MJ

207

(Eq. [041]), respectively. The added 7, in this case, indicates

plants (MQ

) that are involved in the rate. Additional characters are also used to distinguish the same ﬂow

converted to different units. Burial of detritus in sediment requires energy units when subtracted from

the detritus storage as MJ

(Eq. [035]), but requires mass units when added to the sediment as MJ

15D

(Eq. [036]).

Likewise, if more than one auxiliary variable is calculated for the same ﬂow rate, a third subscript is

used. To calculate gross primary production of low marsh plants (MJ

, Eq. [033]), for example, requires

calculation of available light (MA

07a

, Eq. [027]), and a multiplier based on other environmental conditions

(MA

07b

, Eq. [028]).

Model constants associated with a ﬂow have the same subscript as the ﬂow. For example, the equation

for assimilation of meiofauna by macrofauna, MJ

, has a constant MK

(Eq. [060]). As before, where

a given equation has more than one constant, a third character is appended to distinguish the two. The

equation for the two-way exchange of sediment between estuary and marsh (J

W6M5

, Eq. [025]) has a rate

constant K

W6M5

for restoring equilibrium, and an equilibrium constant K

W6M5n

Dynamic Simulation with Energy Systems Language 28-11

TABLE 28.1

Equations Corresponding to the Energy Systems Language D

iagram of the Marsh Sec

tor (Low Marsh Portion). The Table is Organized into Fiv

e Sections: St

orage

Equations, Rates, Inputs, Model Constants, and Simulation

Time Parameters

No. Storage Equation

Units

Meaning

Used in Eq. No.

(001) MQ1

INTEG(JW5M1+MJ71−MJ15−MJ1a−MJ1b−MJ1c,

Organic detritus in marsh

(024), (035), (036),

Initial value: 9.18000e

+014)

(037), (038), and (039)

(002) MQ2

INTEG(JRain+JW2M2−MJ20−MJ207,

kg-H

O Water in marsh

(021), (027), (028), (030),

Initial value: 5.43750e

+006)

(031), and (040)

(003) MQ3

=INTEG(JW3M3,

kg-salt

Salt in marsh

(022), (028), and (030)

Initial value: 2.56217e

+005)

(004) MQ4

=INTEG(JW4M4+MJa4+MJb4+MJc4−MJ47−MJ49,

kg-N

Inorganic nutrients in marsh

(023), (028), and (030)

Initial value: 2.52000e

+004)

(005) MQ5

=INTEG(JW6M5+MJ15D,

kg-sediment Sediment and peat in marsh

(025)

Initial value: 1.59030e

+010)

(006) MQ6

=INTEG(MJ06−MJ60−MJ607,

Water circulation energy in marsh (028), (030), (044),

and (045)

Initial value: 1.47000e

+011)

(007) MQ7

=INTEG(MJ07−MJ70−MJ706−MJ71−MJ7e,

Low marsh plants

(027), (031), (033), (045),

Initial value: 9.18000e

+014)

(046), (048), and (049)

(008) MQ9

=INTEG(MJ09−MJ90−MJ9b−MJ9c−MJ9e,

Benthic microalgae

(029), (034), (050), (051),

Initial value: 2.52000e

+012)

(052), and (053)

(009) MQa

=INTEG(MJ1a−MJa0−MJab−MJac,

Microbes on detritus

(037), (054), (056), and (057)

Initial value: 2.52000e

+011)

(010) MQb

=INTEG(MJ1b+MJ9b+MJab−MJb0−MJbc

−MJbFCS,

Meiofauna in marsh

(038), (051), (056), (058),

Initial value: 2.52000e

+012)

(060), and (061)

(011) MQc

=INTEG(MJ1c+MJ9c+MJac

+MJbc−MJc0−MJcd−MJcFCS−MJcg, J

Macrofauna in marsh

(039), (052), (057), (060),

Initial value: 2.52000e

+012)

(062), (064), (065), and (066)

(012) MQd

=INTEG(MJcd+MJgd

−MJd0,

Raccoons and rats in marsh

(064), (067), and (074)

Initial value: 1.26000e

+012)

(013) MQe

=INTEG(MJ7e+MJ9e−MJe0−MJef

−MJeg,

Insects in marsh

(049), (053), (068), (069), and

Initial value: 2.52000e

+012)

(070)

(014) MQf

INTEG(MJef

−MJf0−MJfg,

Spiders in marsh

(069), (071), and (072)

Initial value: 2.52000e

+011)

(015) MQg

=INTEG(MJcg+MJeg

+MJfg

−MJg0−MJgd,

Birds in marsh

(066), (070), (072), (073), and

Initial value: 2.52000e

+012)

(074)

(016) QFCS

=INTEG(J0FCS+MJbFCS+MJcFCS−JFCS0−JYield,

Fishes, crabs, and shrimps in marsh (019), (061), and

(065)

Initial value: 4.83000e

+013)

creeks and estuary

(Continued)