Fishwick P.A. (editor) Handbook of Dynamic System Modeling

Подождите немного. Документ загружается.

28-32 Handbook of Dynamic System Modeling

represents. An Energy Systems Language model can become a record of the evolving state-of-the-art

understanding about a given system that can transcend generations of environmental managers. Each

generation can improve the model as the interplay between measured phenomena and model prediction

proceeds.

Flaws in understanding and difﬁculty in detecting dynamic phenomena each interfere with success-

ful environmental systems management. Environmental data in the absence of an explanation may add

description, but does little for understanding. Simulation models, in the absence of dynamic phenomena

from the real system, are untested hypotheses that produce a prediction of dynamics waiting to be tested.

With continued cycling between model formulation and measurement of phenomena, the high level of

understanding of self-organized environmental systems required to manage such systems will be forth-

coming. It is the interplay between models and measurement of dynamics that can guide understanding

toward management principles that work.

A system model can be built that shows impossible dynamics, sometimes intriguing ones, and perhaps

less often accurate ones. Nevertheless, Energy Systems Language opens the door to a rigorous energy

theory of nature that, perhaps unlike the models themselves, continues to have an enormous practical

impact on the observation, analysis, and management of ecosystems today.

Acknowledgments

This chapter is dedicated to the memory of Professor H.T. Odum with whom the author was privileged to

work and learn as a colleague and friend for over 20 years. This chapter reﬂects the author’s understanding

of Professor Odum’s methods. Thanks to Dr. Mark T. Brown, also a longtime colleague of Dr. Odum, and

to Elizabeth C. Odum, Dr. Odum’s spouse and frequent coauthor, for reviewing the ﬁrst draft manuscript

of this chapter. A third in-house reviewer, Mr. Mike Lemmons, provided in-depth review from a novice’s

point of view. Considerable revision resulted from these reviews, the comments of three anonymous

reviewers, and the editor, Paul Fishwick. The author owes a debt of gratitude to each of these reviewers for

a greatly improved, clariﬁed, and more substantive presentation of Energy Systems Language.

References

Coultas, C.L. and Y.-P. Hsieh (eds.), Ecology and Management of Tidal Marshes: A Model from the Gulf of

Mexico. St Lucie Press, Delray Beach, FL, 355pp.

Forrester, J. 1961. Industrial Dynamics. MIT Press, Cambridge, MA.

Forrester, J. 1968. Principles of Systems. Wright-Allen Press, Cambridge, MA.

Montague, C.L. and H.T. Odum. 1997. Introduction: The intertidal marshes of Florida’s Gulf coast. In

Coultas, C.L. and Y.-P. Hsieh (eds.), Ecology and Management of Tidal Marshes: A Model from the

Gulf of Mexico. St Lucie Press, Delray Beach, FL, pp. 1–7, 355pp.

Odum, H.T. 1983. Systems Ecology: An Introduction. Wiley, New York, 644pp.

Odum, H.T. 1994. Ecological and General Systems: An Introduction to Systems Ecology. University Press of

Colorado, Boulder, CO, 644pp. (revised edition of Odum, 1983).

Odum, H.T. 1996. Environmental Accounting: Energy and EnvironmentalDecision Making. Wiley, NewYork,

370pp.

Odum, H.T. and E.C. Odum. 2000. Modeling for All Scales: An Introduction to System Simulation. Academic

Press, London, 458pp.

Odum, H.T. and E.C. Odum. 2001. A Prosperous Way Down. University Press of Colorado, Boulder, CO,

326pp.

Ecological Modeling and

Simulation: From

Historical Development

to Individual-Based

Modeling

David R.C. Hill

Blaise Pascal University

P. Coquillard

Université de Nice-Sophia Antipolis

29.1 Introduction ...............................................................29-1

29.2 An Old Story? .............................................................29-2

29.3 Determinism or Probability?......................................29-5

29.4 Modeling Techniques .................................................29-5

29.5 The Use of Models in Ecology ...................................29-6

29.6 Models are Scientiﬁc Instruments ............................29-7

29.7 Levels of Organization and Methodological

Choices .......................................................................29-8

29.8 Individual-Based Models ...........................................29-9

29.9 Applications ...............................................................29-12

29.10 Conclusion .................................................................29-15

29.1 Introduction

Ecology studies the relationships between living organisms (individuals)—vegetal or animal—and the

environment in which they live. The biosphere in which we live is made up of the whole set of terrestrial,

marine, and aerial ecosystems. A scientist who endeavors to explain the relationships and the interactions

within an ecosystem must often be in contact with colleagues more specialized in other ﬁelds like chemistry,

genetics, oceanography, geography, hydrology, ethology, and climatic sciences. Considering the complexity

of this multidisciplinary study, modeling is a fundamental tool to understand ecosystems. A good modeling

practice is to design a model with a precise goal in mind; a modeler expects that his model outputs (results)

will help understanding the real system under study. The model ﬁnal objective also helps selecting the

model simplifying assumptions and the level of realism, taking into account the limits of our knowledge

and the limits of our modeling techniques. Even if we had precise descriptions and observations, estimating

future trends will always be considered very risky. Considering the lack of biological data, we see in Begon

et al. (1990) that many ecologists focus on the following levels of organization: individuals, populations

of individuals, and ecosystems.

In this chapter, we will ﬁrst focus on the history of ecological modeling, starting in the twelfth century. A

discussion will present the controversy opposing deterministic and probabilistic approaches in ecological

29-1

29-2 Handbook of Dynamic System Modeling

modeling. We follow this discussion by an overview of the model types employed by ecological modelers.

The main focus is then given to individual-based models (IBMs). They appeared in the seventies (Kaiser,

1976, 1979; Lomnicki, 1978) and have been more intensively used since the remarkable paper from

Huston et al. (1988). Individual-based modeling is a bottom-up approach focusing on the individuals

(i.e., the parts) of an ecological population (i.e., the system). Then, the modeler tries to understand how

the properties of the population can emerge from the interaction among individuals. The strengths and

weakness of IBMs will be presented. Despite their advantages, bottom-up approaches are not sufﬁcient

to build theories at the population level (Grimm, 1999). Indeed, more traditional mathematical models,

with state variables, described “top-down” and used like black boxes, provide integrated views replying to

relevant questions at the population level.

29.2 An Old Story?

The great adventure of modeling ecological processes began at the end of the twelfth century with regard

to a story about rabbits, in Pisa, Italy. In this thriving commercial town, young Leonardo of Pisa (1175–

1240) is very rapidly confronted with practical problems of arithmetic. Leornardo, son of Guilielmo and

a member of the Bonacci family, is trying to solve what appears at ﬁrst sight to be quite a simple problem:

a couple of young rabbits will become adult and then will produce at each mating season, a new couple of

young rabbits. After a new season, the new couple has grown up and is in turn able to produce another

couple of rabbits. The question is how many rabbits will there be after “n” seasons?

In Table 29.1, it can be seen that the number of adult couples at season n is equal to the total number of

couples at season n −1, and that the number of young couples at season n is equal to the total number of

couples at season n −2. A little reﬂection convinces us very quickly that the total number of rabbit couples

at season n can be computed with the following sequence:

= T

n−1

n−2

(29.1)

This formula generates a series of numbers whose characteristic is that each number is equal to the sum

of the two previous numbers. Generally, this sequence is known as Fibonacci numbers: 1, 1, 2, 3, 5, 8,

13, 21, 34, 55, 89, 144, 233, 377, 610... The Fibonacci name was given in the nineteenth century by

Guillaume Libri, a mathematics historian (Leonardo of Pisa, was son of Bonacci: Filius Bonacci—which

gave the Fibonacci nickname). Naturally, the Fibonacci sequence is not very realistic for this problem, since

for instance it takes no account of mortality and running out of food resources. However, this sequence

has numerous other interesting applications for basic ecological models. Indeed, Fibonacci numbers

are interesting in understanding honeybees family trees, petals on ﬂowers, seed heads, pinecones, leaf

arrangements, and even shell spirals. All the previously cited natural elements use what mathematicians

call the golden ratio. Curiously, we can perceive that the ratio T

n−1

is converging to a particular value,

21/13 1.615; 34/21 1.619; 144/89 1.617; 610/377 1.618. This value is called the golden ratio or the

TABLE 29.1 Number of Couples at Season n

Season Total Number of Couples Number of Adult Couples Number of Young Couples

n (= T

)(= T

n−1

)(= T

n−2

)

11 0 1

21 1 0

32 1 1

43 2 1

55 3 2

68 5 3

713 8 5

8 ... ... ...

Ecological Modeling and Simulation 29-3

golden number (∼1.618034 and often represented by a Greek letter Phi [φ]) and it has also been used by

humans in many artistic creations, including architecture.

Thereafter, several centuries go by before mathematicians take an interest in biological and ecological

problems: Bernouilli in the eighteenth century proposes a mathematical theory of smallpox epidemic;

then, in the nineteenth, Malthus and Quetelet take an interest in the dynamics of human populations. But

it is Pierre François Verhulst (Verhulst, 1845), a Belgian mathematician, who invents in 1844 the famous

S curve known as the logistic curve:

= ry



K − y



(29.2)

This is the foundation of mathematical modeling applied to biological sciences, strongly inﬂuencing the

modeling of system dynamics throughout the twentieth century. This equation has been studied in depth,

notably in its discrete form. It will also be integrated in the famous double equation system, attributed

independently to Lokta (1925) and Volterra (1926), where they propose a mathematical formalism for the

relationship between consumers and resources.

Finally, mathematical modeling of sciences, apart from the strict circle of Physics, does not take off

until the twentieth century. In the nineteenth century, biological sciences were not particularly favorable

to using mathematical formalism. According to Giorgio Israel this can be explained by“The old ambition,

still alive and kicking, to achieve a uniﬁed mechanical and reductionistic description of the world, an

ambition resisting all difﬁculties and all failures.”Again, according to the same author: “The fundamental

method of modeling in the 20th, is mathematical analogy (where the fragment of mathematics uniﬁes all

the phenomena it is supposed to represent), and no longer mechanical analogy, which has been for a very

long time, the principal mathematical method.”

With a mathematical analogy, Leslie (1945) presentedto an adaptation of MarkovChainsto the dynamics

of populations. This technique is interesting for modeling the changes in age-structured populations

(Figure 29.1).

In 1965, Lefkovitch introduced an alternative approach. A similar matrix model considers population

growth in organisms grouped by stages instead of age (Lefkovitch, 1965) (stage-speciﬁc survival rates).

Kent Holsinger gives the following reasons to explain why Lefkovitch models are often preferred to Leslie

matrix:

•

It’s often difﬁcult or impossible to age animals and plants accurately.

•

In some organisms, especially perennial plants, survivorship and fecundity are more related to size

(or some other variable by which a population might be stage-classiﬁed) than to age.

•

In some organisms, especially herbaceous perennial plants, individuals may actually revisit stages

they already left, e.g., they may get smaller from one season to the next.

•

Focusing on life-cycle stages helps to focus attention on identifying the critical transitions that may

provide opportunities for management. (Holsinger, 2005)

At the end of the eighties, Caswell (1989) also adapted Leslie’s matrix to model the development of a species

of a vegetal species (Dipsacus sylvestris) in six development stages (from seed to ﬂowering plant). Finally,

P ⫽

...

n⫺1

...

......

...

FIGURE 29.1 A Leslie matrix. The ﬁrst row contains the fertilities (F

)ofeachthen class of age. p

represents the

transition probability (i.e., the survival probability) from one class of age to the next.

29-4 Handbook of Dynamic System Modeling

(p) ⫽

FFFF

...00

(a)

...............

00...0

...

Where the submatrices F (fertilities) and T (transition) are for instance:

and

000

F ⫽

T ⫽

(b)

FIGURE 29.2 (a) A stage-by-age model or multistate model. (b) Fertilities and transition matrix.

Folding of the

dimensions

To obtain a torus:

pseudo-infinite 2D grid

Finite 2D grid

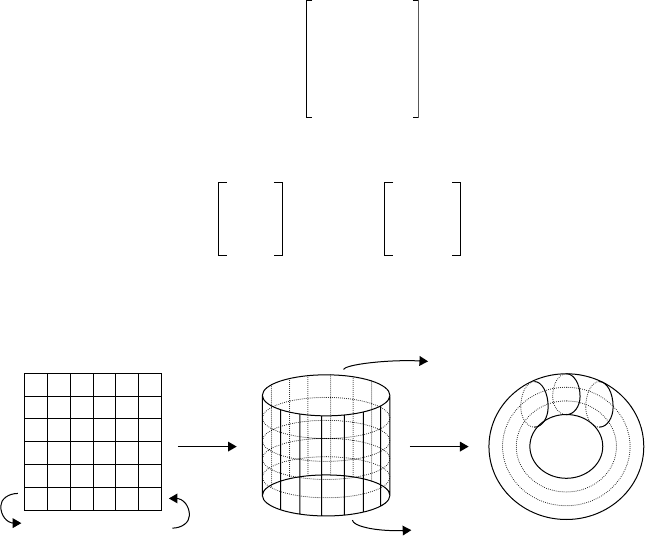
FIGURE 29.3 Folding of a ﬁnite 2D grid to obtain a pseudo-inﬁnite grid.

Lebreton (2005) proposed a stage-by-age models (or a multistate model) uniting the two characteristics

state and time (Figure 29.2[a] and Figure 29.2[b]).

After the Second World War, the original thoughts on self-reproducing cellular automata were intro-

duced. “This introduction can be traced back to 1948 when John von Neumann gave a talk entitled “The

General and Logical Theory of Automata” (Von Neumann, 1951). More than a decade later, Von Neu-

man, Ulam, and John Conway introduced self-reproducing cellular automata (Von Neumann, 1966; Burks,

1970) and the Game of Life (Gardner, 1970). Von Neumann and Ulam were modeling a minimal biological

self-reproduction and the Conway mathematical game was introduced to a wide public thanks to columns

written by Martin Gardner in Scientiﬁc American. The result was a famous synchronous spatial model,

centered on cells, and with a time-based evolution. The future of a cell depends on rules relying on the

other cells in its neighborhood. Each cell on a pseudo-inﬁnite 2D grid (obtained by folding, Figure 29.3)

has two potential states: dead or alive. The generated cells are clones, exactly the same as the parent. From

these basic elements, more complex models can take into account heredity, variability, ﬁtness and other

characteristics, which can be useful to model for instance the evolution by means of natural selection. Here

are the basic transition rules applied at each time step in the ﬁrst issue of the Game of Life:

•

If two or three neighbors of a cell are alive and the cell itself is currently alive, its next state is alive.

•

If three neighbors of a cell are alive and the cell itself is currently not alive, its next state is alive.

•

Otherwise the next cell state is dead.

Those simple rules weresufﬁcient to give risetoorder from an apparent“chaos.”Scientists rapidly identiﬁed

patterns like blinkers, gliders, guns, which grow and evolve for very long periods. Some other patterns

lead to dying or stagnating conﬁgurations. Since the theory of cellular automata was introduced, many

enhancements were proposed and the theory was simpliﬁed in the 1980s by Langton and Byl (Wolfram,

Ecological Modeling and Simulation 29-5

1986). Cellular automata have also been recently embedded in the powerful Cell-DEVS environment,

which has been successfully applied to different ecological models (Wainer and Giambiasi, 2001). We

would not stay too long on cellular automata since they are detailed in a speciﬁc chapter of this book,

proposed by Peter Sloot.

29.3 Determinism or Probability?

Evidently, from what has just been said, the mathematical approach, i.e., deterministic, represents the base

on which modeling and simulation in environmental sciences has been developed. The introduction of

randomness with Monte Carlo simulation and the question of using models with probabilistic components

provoke ﬁerce scientiﬁc controversy. For example, Papoulis explains: “The controversy of determinism

and causality versus randomness and probability has been the topic of extensive discussions […] the

phenomenon is thus inherently deterministic, and probabilistic considerations are necessary only because

of our ignorance” (Papoulis, 1965). Up to the early seventies, the majority of models concerning ecology

are deterministic. The position of Norman E. Kowal (1971, pp. 123–171) sums up the aversion of scientists

at that time to use probabilistic processes. Concerning ecological processes, which present: “Changes in

Space, or in Space and Time,” he writes:“Since there is more than one independent variable (two or three for

space, and, perhaps, one for time), the required mathematical theory becomes very complex and difﬁcult

to work analytically. The most useful mathematical structures to use as models of such systems are partial

differential equations […] these models will probably always be solved by numerical approximation on

digital computers.” In the last sentence of his paragraph he also states that: “Probability density functions

may also be used.” In the Coda Volume I of System Analysis and Simulation in Ecology, Bernard C. Patten

writes: “Simulation models do not have to reproduce dynamic behavior realistically to be useful […] the

thought that goes into them may be their greatest value” (Patten, 1971). Patten preferred to reduce the

realism of the model rather than include stochastic aspects. From our point of view, the ﬁnal modeling

goal has to be borne in mind when deciding whether or not a modeler can abandon the reproduction of

realistic behavior.

Thanks to the steady increase in memory capacity and calculation speed, to the emergence of procedural

and object-oriented programming languages, the limits of ecosystem modeling have rapidly extended.

Dealing with spatial systems and processes dependant on time, scientists found themselves confronted

with such a complexity that deterministic mathematics alone could not resolve (Jorgensen, 1994).

29.4 Modeling Techniques

Whether deterministic or not, there is a plethora of modeling techniques. Using the “Science direct”

database from Elsevier, we have built a classiﬁcation of the most employed techniques found in papers

published in the Ecological Modeling journal since 1975 (Table 29.2). Most of them are not speciﬁc to

ecological modeling and they are detailed in other chapters of this book.

Two expressions in Table 29.2 do not belong to usual simulation vocabulary: Individual Based Model

and Gap Model. It is an example of vocabulary introduced by ecologists to qualify some kinds of simulation

models. IBMs have already been introduced, so we will present the Gap models. They are dedicated to the

simulation of vast forest spaces, discretized into small units (a few m

) on which the number of trees of

different categories and species, the transition probabilities and the reproduction success probabilities are

known. The term Gap model comes from the fact that these models were developed originally to simulate

the behavior of a forest area in which, over the course of time, a natural process of clearings healed up

more or less rapidly depending on characteristics of their immediate environment.

If we analyze more deeply the published databases in ecological modeling, we can see that ecological

specialists have now been using discrete simulation and IBMs more intensively particularly over the last

two decades (Grimm et al., 1999). Multiagent models can be considered as a special case of IBMs where

29-6 Handbook of Dynamic System Modeling

TABLE 29.2 Results Extracted using the Science Direct Database on the Ecological

Modeling Journal (between 1975 and 2005). Expressions were Researched in the Titles,

Keywords, and Abstracts. In Brackets the Results Obtained by Extending the Search to

Journals Filed in Environmental Sciences

Expression Number of Articles

Model OR Modeling 3576 (36308)

Simulation 1361 (8146)

Mathematical model 298 (9396)

Individual-based model 106

Neural network 104 (1801)

Markov OR Leslie 91 (2273)

Cellular automata 46 (441)

Bayesian statistics 42 (120)

Mixed model 25 (561)

Gap model 26

Multiagent 6 (28)

Multimodel(ing) 4 (96)

individuals have shown a social behavior. This modeling technique is not speciﬁc to ecological modeling,

it has been introduced in Artiﬁcial Intelligence and more precisely in Distributed Artiﬁcial Intelligence.

AdelindeUhrmacher is devoting a chapter of this book to agent-oriented modeling. In ecological modeling,

this approach is particularly interesting for of ethological systems. We have for instance studied herbivorous

animals, and also the memory of ewes at pasture using this approach (Dumont and Hill, 2001, 2004).

This development of individual-based modeling and its derivative can be explained ﬁrst by the avail-

ability of powerful desktop computers, of user friendly software development environments, and of

prototyping design methods. With such tools and techniques, ecological modelers can study the complex-

ity of many systems they are interested in, in terms of number of animals, plants (or trees), strips of land,

volumes of air, ﬂow of energy, interacting in time and in three dimensions.

This quick review of techniques in ecological models shows that a long road is ahead to use multiagents,

coupled models, mixed models and multimodels with different formalisms. The formalization of models,

using DEVS (Zeigler et al., 2000) or other more formal speciﬁcation techniques, is still extremely rare

in ecological modeling. In our opinion, their use can be very promising, the introduction of Cell-DEVS

mentioned above, and other recent applications demonstrate the interest of the simulation community in

applying such advances to ecological and environmental models (Muzy et al., 2005).

29.5 The Use of Models in Ecology

In ecological modeling, the knowledge acquired these last decades experienced a spectacular growth

correlatively with the mastering of new sampling techniques (satellite and space imagery; radiogoniometric

follow-up of animals; automation of the physicochemical data acquisition of air and water), of numerical

analysis techniques (statistical analysis of multidimensional data and analysis of time series), and of data-

processing tool (hardware and software). At the same time, this amount of data made decision makers

aware of a wiser management of human activities. Table 29.3 presents several ecological topics discussed

in the Ecological Modeling Journal (still between 1975 and 2005).

In Table 29.3, we notice that the predominant subject of interest is incontestably the problem of

biodiversity, followed, but at a considerable distance, by global change, forestry problems, and population

dynamics. We therefore ﬁnd here subjects covered by the media in the news, even though fundamental

research subjects are not neglected, as is proved by the 334 articles on population dynamics or the prey–

predator relationship. The greenhouse effect is almost not covered by the Ecological Modeling journal.

This can also be noticed in the “Environmental Sciences” section where only 197 references are found on

this subject, which, in reality, is dealt with by climatology specialists in collaboration with ecologists.

Ecological Modeling and Simulation 29-7

TABLE 29.3 Number of Articles found in the Ecological Modeling

Review (1975–2005) Related to Several Ecological Topics

Expression Number of Articles

Organic matter 100

Nitrogen OR nitrogen cycle 295

Carbon OR carbon cycle 290

Global change 344

Greenhouse effect 2

Fish model 122

Fishing model 83

Trees OR forest 636

Populations dynamics 344

Predator–Prey 97

Productivity 187

Behavioral model 192

Biodiversity 2947

Plant architecture 34

TABLE 29.4 Number of Articles found in the Ecological

Modeling Review (1975–2005) Related to Ecosystems

Expression Number of Articles

Taïga 44

Tundra 145

Temperate forest 130

Tropical forest 198

Meadows 206

Arid ecosystem 18

Lake 141

River 227

Desert 275

Marine ecosystem 187

Estuarine ecosystem 29

Coral reef 10

Alga(e) 39

From Table 29.4, we observe that the ecosystems mostly studied by ecologists are mainly terrestrial

ecosystems, notably forest, tropical or not, where an attempt is made to predict their evolution in terms of

production, population structure, and biodiversity for future decades with a supposed changing climate.

Lakes and rivers are also the subject of numerous studies. One could advance the hypothesis that the

management of fresh and drinkable water resources arises today as one of the major challenges over the

next decades. Again from Table 29.4 we note that marine ecosystems are less studied, in spite of their

extremely dominant situation on the globe, and their capital importance in regulating climate. We have

developed models in oceanography and we could explain this small number of studies by the fact that

oceanographic model parameters are difﬁcult to measure, involving costly and occasionally dangerous

operations (Hill et al, 1998; Coquillard et al., 2000).

29.6 Models are Scientiﬁc Instruments

From our simulation experience in various application ﬁelds, Ecological models basically do not differ—

not even by their complexity—frommodels developed in other disciplines such as meteorology and nuclear

physics, or from the models developed for manufacturing systems.

29-8 Handbook of Dynamic System Modeling

The incredible complexity of the operation of an ecosystem cannot be seized by the simple acquisition

of the whole set of parameters that characterizes it, as this has been the case for a long time when ecology

was conﬁned within a descriptive approach. The latter was a necessary stage, but the multiple interactions

and feedbacks within ecosystems reveal behaviors which one could not seize by the interpretation of data

collected (were they exhaustive). Even if we do not know all the ecosystem parts, studies in complexity

showed that the behavior of a complex system is not equivalent to the sum of the behaviors of the parts

(this is known as the “system effect”). Only a software, modeling the interaction of the various parts of a

system, can reveal the emerging behaviors. Even if models could also show impossible behaviors that only

ﬁeld experts will be able to detect, they are more and more used for a better comprehension of ecosystems.

In his state-of-the-art textbook, Jorgensen (1994) summarizes in four points the advantages of modeling:

1. Models have their utility in the monitoring of complex systems.

2. Models can be used to reveal the properties of ecological systems.

3. Models can show deﬁciencies in our knowledge and can be used to deﬁne priorities in research.

4. Models are useful to test scientiﬁc assumptions, insofar as the model can simulate the reactions of

the ecosystem, which can be compared with the observations.

29.7 Levels of Organization and Methodological Choices

In practice, the development of a model is based on the two following constraints:

1. The objectives to be reached (which types of results are we expecting?).

2. The state of our knowledge concerning the studied system and the data at our disposal (or at least what

it is reasonable to hope to acquire in an assigned time).

These two constraints will deﬁne the level of organization (or the scale of the study). The choice of this

scale is in direct relationship with the complexity of the model. Will we be interested in the individuals,

in parts of individuals, in sets of individuals, in whole populations even in sets of populations? It is also

necessary to have in mind that the level of organization will also inﬂuence the choice of the modeling

technique that will be implemented. For instance, if we organize our model around the population level,

an individual-based modeling is completely unnecessary. In addition, there must be a close consistency

between the objectives (ﬁrst point) and the available data (second point). If we only have data at the

molecular level, will it be really consistent to expect results at the population level? The identiﬁcation of

the level of organization imposes a thorough examination of the data: the objectives being ﬁxed and thus

the working scale determined, it is still necessary to have available data relating to this level of organization.

It is a frequent case that for a given level it is advisable to obtain data concerning a lower scale. Even if the

level of a population is retained, it could be necessary to collect data relating to the individuals. Indeed, the

behavior of the population results from the individual interactions. Biological individuals themselves are

not free from inﬂuences coming from the higher levels of the organization hierarchy: other populations,

environmental factors. How many factors do we have to take into account? Which one among them can

be regarded as negligible? There is no absolute rule in this ﬁeld; a wise approach would be to bear in mind

the main goal of the modeling (i.e., the principal expected results). This will help to simplify the making

of choices.

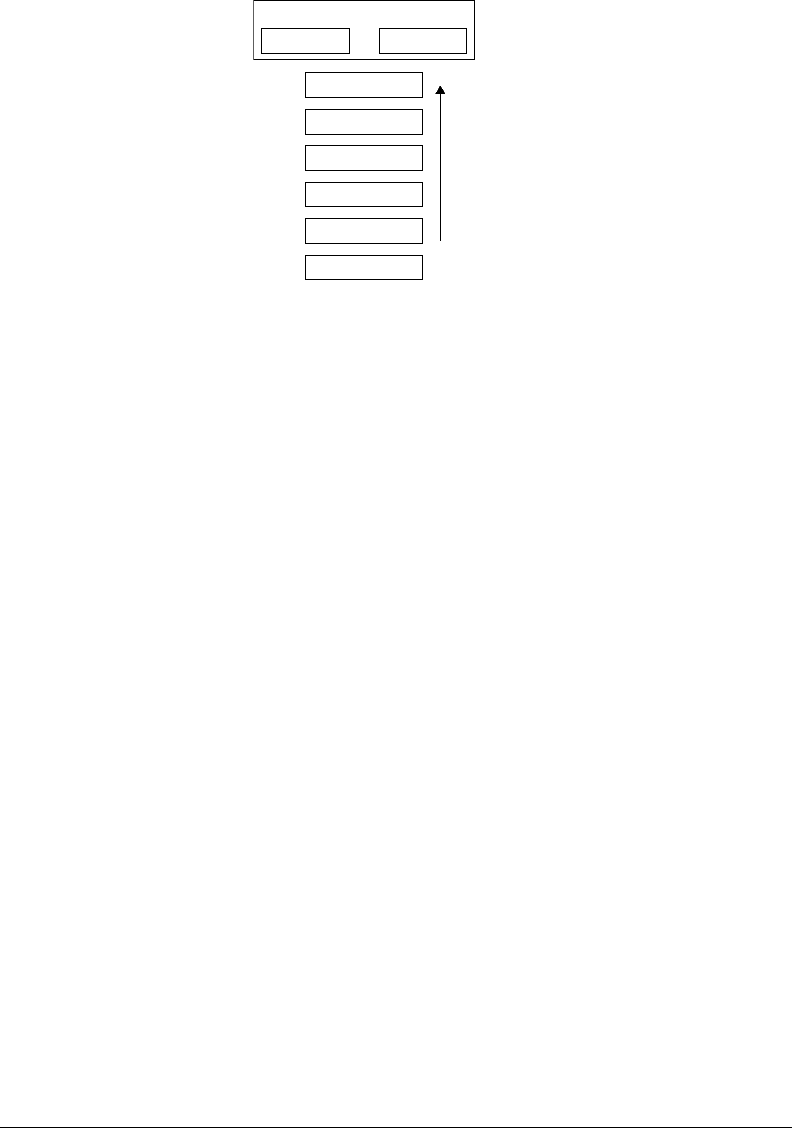
The level of organization being selected according to the objectives (Figure 29.4), it is appropriate

to specify what is the level of detail. Thus, for a model of forest growth (with a level of organization

corresponding to a population), will we have to take into account, or not, the following nonexhaustive set

of parameters?

•

Seasonal variation of the light intensity.

•

partial pressure of the atmosphere.

•

Competition for water resources and ground nutrients.

•

Competition for space.

Ecological Modeling and Simulation 29-9

Biocenosis

Biotope

ECOSYSTEM

Organization

level (scale)

Cell

Organ

Individual

Group

Population

Molecular level

FIGURE 29.4 Organization levels.

•

Density of the settlement.

•

Competition for light.

•

Competition with the shrubby and herbaceous species.

One quickly sees that objectives and data will interact; the choices will be in accordance with the exper-

imental framework. Thus, if we want to model the growth of a local forest over the next 5 years, it is

certainly not necessary to take into account the possible inﬁnitesimal variations of the CO

on this interval

of time. In the same way, the seasonal variation of the light intensity received by the settlement does

not appear crucial in the modeling, the whole settlement being subjected to the same light conditions.

Lastly, the competition for resources with the shrubby/herbaceous species will have to be neglected if we

consider that trees escape from this competition. We can also suppose that the forest ecosystem is relatively

homogeneous from this point of view.

A systematic increase in the model complexity by addition of variables will often not make a substantial

improvement in terms of model validation. Beyond a certain point, the addition of new variables does

nothing but increase the complexity of the model and accumulate uncertainties. It even occurs that

these increases in uncertainty make the model radically diverge from the real system under study. It is

often advisable to prefer holistic variables to several elementary variables whose uncertainties can only

obliterate the quality of the model. It goes without saying that an increase in model complexity will add

to the implementation difﬁculties, the ability to check the internal consistency of the software is reduced,

and computing speed problems can also occur even with our fastest computers. Unless we have speciﬁc

goals requiring the implementation of many details, simpliﬁcation is a virtue in modeling.

Now that we have presented some methodological elements, we will give our main focus to IBMs.

We have seen in the previous sections that many modeling techniques used in ecological modeling are

common to other research ﬁelds, most of them are presented in this textbook and our preference goes to

individual-based modeling. This choice is not a way to champion this technique among others and we will

also discuss its drawbacks. However, this technique has met with an interesting development linked to the

evolution of computer technologies. In the next sections we will not distinguish IBMs from individually

oriented models (IOM), though the latter can be more powerful, see Fishwick et al. (1998).

29.8 Individual-Based Models

The IBM approach completes the set of mathematical methods that are still interesting for many appli-

cations (Grimm, 1994; Sultangazin, 2004). For instance, differential equations or partial differential

equations are very efﬁcient to give a rough estimation of the spatial evolution of large areas. However,