Fishwick P.A. (editor) Handbook of Dynamic System Modeling

Подождите немного. Документ загружается.

1-6 Handbook of Dynamic System Modeling

<math>

<apply>

<eq/>

<apply>

<diff/>

<bvar>

</bvar>

</apply>

<apply>

<apply>

</apply>

</math>

FIGURE 1.3 Content MathML for

=1 −ax.

0 1 2 3

STATE D 0 1 2

STATE C 0 1 2

STATE B 0 1 2

STATE A 0 1 2

0 0

State: left Input: 2

aab

(a) (b)

FIGURE 1.4 Four interpretations of the same state machine. (a) Christina Sirois. (b) TimWinfree. (c) BrettBaskovich.

(d) Emily Welles.

for most model types one generally ﬁnds researchers on the Web who are pioneering their own XML

applications.

Figure 1.1 shows example presentations of dynamic models; however, we are not limited to two dimen-

sions, the use of a single color, or a digital medium (i.e., as long as the interaction can be communicated

digitally) (Fishwick, 2006). For example, Figure 1.4 demonstrates the creative application of students in a

computer simulation class being given a canonical iconographic representation of a ﬁnite state machine

The Languages of Dynamic System Modeling 1-7

(FSM) and then being allowed to create different representations for both the model itself (left-hand side)

and the behavior of the model (right-hand side). This concept mirrors Minsky’s (1988) adage of knowing

something “in more than one way.” It also captures the importance of multiple representations discussed

in mathematics education (Kaput, 1989).

In viewing these models, we are ultimately led to think about which presentations would be used under

which circumstances. This modeling aspect is covered in Section 1.7. Besides capturing the syntax of signs

such as

, the other key area of syntax is in specifying rules for which icons can appear next to each other,

and in what order, or using which types of connectors. For example, given the Petri net in Figure 1.1(a),

where is the rule which states that Petri net transitions (i.e., the “t”identiﬁers) must be connected to places

(i.e., the “p” identiﬁers)? For this, as in natural language, we need a grammar. In semiotics, the difference

between the raw syntactic connections and grammar is captured, respectively, by the terms syntagmatic

and paradigmatic (Chandler, 2002). For English, we have paradigms such as “noun” and “verb,” and for

Petri nets, we have “place” and “transition.” Grammars can be expressed in XML, but simpler notations

based on the Backus-Naur Form (BNF) capture the grammar. For example,

<num> ::= 0|1|...|9

<var> ::= x|y|z

<diff> ::= D( <var> )

represents a grammar that can parse the equation in Figure 1.1(c) along with many other equations. This is

not a particularly robust grammar since it is limited to restricted equational forms; there are no functions

aside from“D,”and only single digit numbers. However, it serves the purpose of exemplifying the BNF. The

tokens in angle brackets are nonterminals and the other tokens are terminals. Only nonterminals appear

on the left-hand side of a rule. “|” is logical disjunction. The most powerful aspect of this grammar is its

use of recursion in deﬁning expressions. “D” is the differential operator, presumed to be deﬁned relative

to “t” so that D(x) ≡

The study of grammars obtains signiﬁcant headway in computing as a result of Chomsky’s (1956)

hierarchy, which deﬁnes different types of grammars according to their relative power (regular, context-

free, context-sensitive, and unrestricted). The unrestricted grammars generate recursive languages. In

practice, the context-free type of language is the most common and easily implemented.

Nontext models in Figure 1.1 can be formalized with graph grammars that follow the same approach

as the expression grammar. However, instead of terminal separators such as whitespace and newline, one

uses spatial relations such as “connected to.” It is not particularly common for newly introduced system

model structures to come with formally speciﬁed grammars. This may seem odd, although this condi-

tion may be partially due to the different historical paths taken by systems modeling and programming

languages.

1.6 Semantics

If syntax is form and structure, not only of content and the presentation of the content, then semantics is

about function and meaning. Semantics and syntax are intertwined in that functional semantic mappings

involve taking one form of syntax and manifesting another. In this sense, semantics is syntax that is

presumed to be more uniformly understood. To understand what X means, deﬁne X in terms of Y where Y

is better understood by a given population. The essence of this translation lies with the mapping processes

inherent within sign formation. Thus, the mapping of XML content to presentation is a semantic act

in itself even though the source and target structures have their own syntax. The topic of behavior in

1-8 Handbook of Dynamic System Modeling

language can be considered to be part of semantics. The argument for this view begins with the core

notion of computability: input to a machine, system, or model that undergoes state and event changes

resulting in output. From the standpoint of a program, it makes no difference whether the input and

output are different models or signals since this is a matter of encoding and decoding. In the semiotic

sense, the “box” separating input and output is the sign vehicle and so one may view the output from the

box, whether structural or signal in nature, as being part of semantics.

Meaning is often associated, at least in informal languages, with two concepts: denotation and con-

notation. Denotation is what a sign formally represents: the relation of signiﬁer to signiﬁed. However,

connotation is a kind of secondary meaning attributed to signs. When one looks at a Petri net (Peterson,

1981), there may be the thought of biological cells splitting and joining. This “meaning” is secondary to

the formal semantics, and yet through metaphor allows the modeler to better understand the modeling

mechanism. Finer threads of meaning could result from someone seeing a blue-colored square icon and

thinking of a blue sky or a familiar road intersection reminiscent of a square shape. In semiotics, these

kinds of associations are discussed at length by Barthes (1977). Perhaps, a more uniform way of viewing

semantics is that a model may have multiple threads or connections to other concepts, as well as models,

and that some of these connections are more pronounced depending on the human interpreter. Thus, the

denotation is the primary, or the most used, reference.

The way that meaning is deﬁned varies substantially based on community and discipline. Possibilities

for deﬁning meaning include

1. Natural language: while informal and sometimes ambiguous, natural languages such as English are

widely used in textbooks and journals where computational models are being deﬁned.

2. Pseudocode: a more constrained form of natural language frequently used to deﬁne semantics.

3. Computer language: a language such as assembly language, Java, C++, or FORTRAN may serve

well to deﬁne what an artifact means.

4. Mathematics: this is a textual language that, while undergoing change, tends to have standard

notations (Cajori, 1993), which reduce the risk of ambiguity.

Frequently, natural language is interspersed with diagrams and textual mathematics to clarify what a

modeling component “means” and how the coupled components can be legally connected together. For

example, a Petri net model can be deﬁned as a four-tuple NET =<P, T, I, O>, but then natural language

is necessary to deﬁne how these symbols are supposed to be understood. Without the natural language,

the symbols and their corresponding functions would literally make no sense. It is possible to have a purely

mathematical explanation, and yet very little is learned unless the explanation is described or related to

an example. Even though the Petri net might be seen as a purely algebraic construct without any further

attributed meaning, the visual presentation of Petri nets has come to be associated with what the Petri net

actually means, and as a guide to its operational characteristics. The Petri net is composed of places and

tokens. The tokens move around the network. So far, this is a fairly straightforward metaphor that relies

on a mathematical map involving the functions I and O. I and O are visually associated with object (i.e.,

token) motion. There is another biologically inspired metaphor of joining or splitting that is required to

complete the modeler’s understanding of what it means to execute the net. In the case of the Petri net,

these metaphors are naturally associated with generating meaning.

In the ﬁelds of programming languages and software engineering, semantics are associated with formal

methods (Winskel, 1993), where one uses languages that are based on either lambda calculus or ﬁrst-order

logic, with set theory underlying both. For system dynamics models, we can use systems theory which

similarly relies on set theory but is more tuned to deﬁning temporal change. System models are viewed

semantically in terms of changes in states, events, and ﬂow among interconnected functions, possibly

involving feedback. Consider the formal semantics for Figure 1.1(d):

x(t) =





(t)dt



(t) = 1 −ax(t)

The Languages of Dynamic System Modeling 1-9

It represents the original model using another syntactical form that has a more standardized, and more

widely accepted, meaning and so we term it the semantics of Figure 1.1(d).

For dynamic models involving discrete events, one may use a variety of semantic speciﬁcations.

For example, the discrete-event system speciﬁcation (DEVS) (Zeigler et al., 2000) is deﬁned as a

tuple <I, S, O, δ

int

, δ

ext

, λ, ta>,where

•

I and O represent the set of input and output values, respectively.

•

S is the set of system states

•

int

: S →S is the internal transition function

•

ext

: Q ×I →S is the external transition function, where Q ={(s, e) |s ∈S,0≤e ≤ta(s)}is the total

state set, and e the time elapsed since the last transition.

•

λ : S →O is the output function

•

ta : S →R

0,∞

deﬁnes the time advance function.

DEVS extends traditional systems theory with the semantics of event transition, with key differences being

the addition of an internal transition function δ

int

and events associated with elapsed time dictated by the

ta function. Another event-based semantic language is based on the event graph model (Schruben, 1983;

Buss and Sanchez, 2002) where the time advance function of DEVS, for example, is constructed at a layer

beneath the deﬁnition of event causality (i.e., speciﬁc events and their times are behavioral artifacts of

event causality).

A concern for formal methods is how they are actually implemented. The degree of meaning ascribed to

a formalism is based on shared consensus for its notation, and even shared consensus is problematic since

there are layers of machine implementation that form the “real meaning.” One approach to address this

is to deﬁne semantics at a lower machine level where the semantics of the formalism are one step closer to

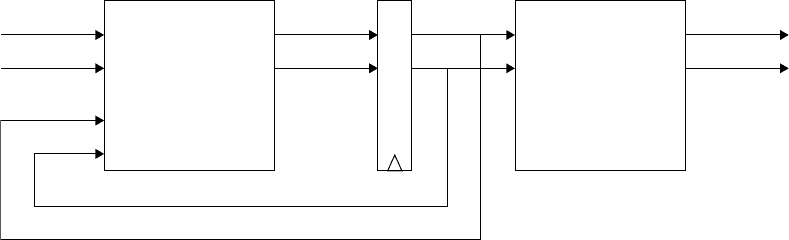
hardware implementation. For example, consider the necessary circuit for an FSM of the Moore variety

depicted in Figure 1.5. This “next state” logic for this machine is termed “FSM synthesis” in digital design,

and can be manually accomplished through a Karnaugh map, which leads to an expression in Boolean

algebra suitable for translation to a combinational circuit. The clocked register stores the state, which is

then fed back into the combinational box. Other types of dynamic system models have direct correlations

at the hardware design level, facilitating a rigorous and formal understanding of their behavior. If there is

a shared understanding of the nature of digital circuits, this can lead to a clearer understanding of system

semantics.

The realization that model meaning and sign chains are accomplished through transformation leads

us to the study of the nature of the transformations themselves, which can be seen as either intra-

or intermodel. As discussed, the set-theoretic concepts of relation and function lie at the heart of the

transformation process. We have the following possibilities, among others: (1) linear chains forming a

graph and (2) encapsulation forming a hierarchy. Making models work at both levels is challenging (Zeigler,

Input Output

Current state

CLK

Sequential logic

(state register)

Combinational

logic

(next state)

Combinational

logic

(output)

FIGURE 1.5 FSM Moore machine semantics.

1-10 Handbook of Dynamic System Modeling

1990; Mosterman and Vangheluwe, 2004; Fishwick and Zeigler, 1992) and there are several higher-level

approaches to mapping. It is possible to create a mathematical morphism linking structures or use a

method such as graph transformation, or a production system containing rules. The mapping itself may

preserve structure, behavior, or neither. While it may be convenient to consider complete preservation

when dealing with semantic mappings, each representation may have slightly different connotations,

complicating the notion of identical levels of meaning. A classic example of this is in models that have a

diagrammatic presentation. These models are laden with spatial metaphors that may be missing from a

text-based model from which a transformation is occurring.

The semantic Web plays a key role in the deﬁnition of semantics and how semantics may be practically

encoded. In particular, the construction of an ontology (Maedche, 2002; Fishwick and Miller, 2004; Lacy

and Gerber, 2004) can span everything from a simple index or taxonomy to a semantic network that also

deﬁnes a series of simple and complex logical constraints. The application of ontologies to modeling will

gradually result in model taxonomies that are capable of being queried or processed. Models can then be

more easily related to one another, possibly through morphism and transformation. With regard to the

latter, XSLT offers one approach to generating one model from another using a pattern-based language.

1.7 Pragmatics

Pragmatics introduces the human into the mixture of model structure, transformation, and execution.

Broadly speaking, pragmatics makes itself apparent in any computer-based task through topics found in

areas such as HCI, pervasive computing, tangible computing, and virtual environments. By reviewing the

methods in these areas of study and asking how these methods can be used in the practice of modeling,

we ﬁnd an abundance of approaches to how humans can interact with models.

When seeking answers as to how pragmatics affects modeling, we need to address the following:

•

Purpose: What is the goal of creating the model? In what larger context is the model being

designed, tested, and evaluated? Is the model to be used for science, engineering, education, or

for entertainment? Are there multiple goals to be achieved?

•

Context: Is the model part of a larger model that includes the human? This kind of situation is

associated with experiments where the experimental apparatus can be simultaneously viewed as

being yet another higher-level model or a form of pragmatics.

•

Decision making: How does one build a model to facilitate human planning and decision mak-

ing (Sage, 1977)? What support tools are available to assist the human in choosing the right model

for the goals of a project?

•

Analysis: To what extent is there an adequate set of tools and methodologies to support

analyzing the model either via the process of veriﬁcation or validation (Overstreet and Nance,

1985; Balci et al., 1990)?

•

Interaction: What modalities are employed to allow the human to interact with the model? Is the

model to be purely digital, or rather a hybrid analog/digital artifact? How will the human experience

the model: can they touch it, move it around, or hear it (Singhal and Zyda, 1999; Burdea and Coiffet,

2003)? Is the model interacted with over the Web (Page et al., 2000) or using other more exotic

interfaces? Is the model construction process collaborative or accomplished in phases?

•

Culture: Are there modeling modes that encourage customization or personalization of a model

structure depending on the individual or group that needs to model? Is a balance between form and

function evident in the modeling practice?

1.8 Summary

We have presented the concept of dynamic system models as languages. As seen through this particular lens,

models have structure (syntax), meaning and behavior (semantics), and a relationship with the human

The Languages of Dynamic System Modeling 1-11

(pragmatics). As with any taxonomy, we are promoting a different way or world-view for viewing the

modeling practice. As such, using language we are naturally led to linkages that other taxonomies might

not stress. For example, the language focus suggests a concrete connection to media, communication, and

human interaction. With language, there is a requirement to formalize not only the model semantics but

also the textual or graphical syntax that deﬁnes legal model structures of a particular sort. One might also

view the language orientation as a return of sorts to an understanding of system models that is closer to

computer science or possibly to cybernetics, where the language and communication emphasis tends to

be pronounced.

References

Ashby, W. R. (1963). An Introduction to Cybernetics. New York: Wiley.

Balci, O., R. E. Nance, E. J. Derrick, E. Page and J. L. Bishop (December 1990). Model generation issues in a

simulation support environment. In Winter Simulation Conference, New Orleans, LA, pp. 257–263.

Barthes, R. (1977). Image, Music, Text. New York: Hill and Wang.

Berners Lee, T., J. Hendler and O. Lassila (May 2001). The Semantic Web. Scientiﬁc American.

Bertalanffy, L. V. (1968). General System Theory. New York: George Braziller.

Burdea, G. C. and P. Coiffet (2003). Virtual Reality Technology (2nd ed.). New York: Wiley.

Buss, A. H. and P. J. Sanchez (2002). Modeling very large scale systems: Building complex models with

LEGOs (listener event graph objects). In Proceedings of the Winter Simulation Conference,SanDiego,

CA, pp. 732–737.

Cajori, F. (1993). A History of Mathematical Notations.NewYork:Dover.

Chandler, D. (2002). Semiotics: The Basics. London: Routledge.

Chomsky, N. (1956). Three models for the description of language. IRE Transactions on Information

Theory, 2, 113–124.

de Saussure, F. (1959). Course in General Linguistics. New York: Philosophical Library.

Fishwick, P. (1995). Simulation Model Design and Execution: Building Digital Worlds. Upper Saddle River,

NJ: Prentice-Hall.

Fishwick, P. (1996). A taxonomy for simulation modeling based on programming language principles. IIE

Transactions, 30, 811–820.

Fishwick, P. (Ed.) (2006). Aesthetic Computing. Cambridge, MA; MIT Press.

Fishwick, P. and J. A. Miller (December 2004). Ontologies for modeling and simulation: Issues and

approaches. In Proceedings of the Winter Simulation Conference, Washington, DC, pp. 259–264.

Fishwick, P. A. and B. P. Zeigler (1992). A multimodel methodology for qualitative model engineering.

ACM Transactions on Modeling and Computer Simulation, 2(1), 52–81.

Hartshorne, C. and A. W. Cambridge (Eds.) (1997). Collected Papers of Charles Pierce: Vols 1–6: 1931–58.

Cambridge, MA: Harvard University Press.

Hodges, W. (2005). Model theory (entry). http://plato.stanford.edu.

Kalman, R. E., P. L. Falb and M. A. Arbib (1962). Topics in Mathematical Systems Theory.NewYork:

McGraw-Hill.

Kaput, J. J. (1989). Linking representations in the symbolic systems of algebra. In S. Wagner and C. Kiernan

(Eds.), Research Agenda for Mathematics Education: Research Issues in the Learning and Teaching of

Algebra, National Council of Teachers, pp. 167–194.

Kim, T., J. Lee and P. Fishwick (July 2002). A two-stage modeling and simulation process for web-based

modeling and simulation. ACM Transactions on Modeling and Computer Simulation, 12(3), 230–248.

Klir, G. J. (1985). Architecture of Systems Problem Solving. New York: Plenum Press.

Lacy, L. and W. J. Gerber (2004). Potential modeling and simulation applications of the web ontology

language-OWL. In Proceedings of the Winter Simulation Conference, pp. 265–270.

Lakoff, G. and M. Johnson (2003). Metaphors We Live By (2nd ed.). Chicago: University of Chicago Press.

Lakoff, G. and R. Nunez (2000). Where Mathematics Comes From: How the Embodied Mind Brings

Mathematics into Being. New York: Basic Books.

1-12 Handbook of Dynamic System Modeling

Maedche, A. (2002). Ontology Learning for the Semantic Web. Nocwell, MA: Kluwer Academic Publishers.

Minsky, M. (1988). Society of Mind. New York: Simon & Schuster.

Morgan, M. S. and M. Morrison (1999). Models as Mediators. Cambridge: Cambridge University Press.

Perspective on Natural and Social Science.

Morris, C. W. (1993). Symbolism and Reality: A Study in the Nature of Mind, Philadelphia, PA: Benjamin

Pub. Co.

Mosterman, P. J. and H. Vangheluwe (2004). Computer Automated Multi-Paradigm Modeling: An

Introduction, 80(9), 433–450. Special Issue: Grand Challenges for Modeling and Simulation.

Nance, R. E. (December 1995). Simulation programming languages: An abridged history. In Winter

Simulation Conference, Washington, DC, pp. 1307–1313.

Noth, W. (1990). Handbook of Semiotics. Bloomington, IN: Indiana University Press.

Ören, T. I. (1984). Model-based activities: A paradigm shift. In T. I. Oren, B. P. Zeigler, and M. S. Elzas

(Eds.), Simulation and Model-Based Methodologies: An Integrative View, pp. 3–40, Berlin: Springer.

Ören, T. I. (1987). Simulation: Taxonomy. In M. G. Singh (Ed.), Systems and Control Encyclopedia,pp.

4411–4414. New York: Pergamon Press.

Overstreet, C. M. and R. E. Nance (February 1985). A speciﬁcation language to assist in analysis of discrete

event simulation models. Communications of the ACM, 28(2), 190–201.

Padulo, L. and M. A. Arbib (1974). Systems Theory: A Uniﬁed State Space Approach to Continuous and

Discrete Systems. Philadelphia, PA: W. B. Saunders.

Page, E., A. Buss, P. Fishwick, K. Healy, N. Richard and R. Paul (2000). Web-based simulation: Revolution

or evolution? ACM Transactions on Modeling and Computer Simulation,10(1), 3–17.

Peterson, J. L. (1981). Petri Net Theory and the Modeling of Systems. Englewood Cliffs, NJ: Prentice-Hall.

Pinker, S. (1994). The Language Instinct: How the Mind Creates Language. New York: Harper Collins

Publishers.

Sage, A. P. (1977). Methodology for Large-Scale Systems. New York: McGraw-Hill.

Schruben, L. W. (1983). Simulation modeling with event graphs. Communications of the ACM, 26(11),

957–963.

Singhal, S. and M. Zyda (1999). Networked Virtual Environments: Design and Implementation.NewYork:

Addison-Wesley.

Wiener, N. (1948). Cybernetics: Or the Control of Communication in the Animal and the Machine.

Cambridge, MA: MIT Press.

Winskel, G. (1993). The Formal Semantics of Programming Languages: An Introduction. Cambridge,

MA: MIT Press.

Zeigler, B. P. (1990). Object-Oriented Simulation with Hierarchical, Modular Models: Intelligent Agents and

Endomorphic Systems. San Diego, CA: Academic Press.

Zeigler, B. P., T. G. Kim and H. Praehofer (2000). Theory of Modeling and Simulation (2nd ed.). New York:

Academic Press. First edition published in 1976.

The Dynamics of the

Computational Modeling

of Analogy-Making

Robert M. French

University of Burgundy

2.1 Introduction .................................................................. 2-1

2.2 Analogy-Making as Sameness ....................................... 2-2

2.3 Analogy-Making as a Means of

“Bootstrapping” Cognition ........................................... 2-3

2.4 The Necessity of Malleable Representations ................ 2-3

2.5 The Dynamics of Representation-

Building in Analogy-Making ........................................ 2-5

2.6 Context-Dependent Computational Temperature ...... 2-6

2.7 Interaction between Top-Down and

Bottom-Up Processes: An Example .............................. 2-6

2.8 Computational Models Implementing

this Bottom-Up/Top-Down Interaction ...................... 2-8

2.9 Architectural Principles ................................................ 2-8

The “Slipnet,” a Semantic Network

•

The Workspace

•

The Worldview

•

Codelets

•

The Coderack

•

Dynamic

Codelet Selection via Computational Temperature

•

Local, Stochastic Processing

•

Integration of

Representation-Building and Correspondence-Finding

2.10 How this Type of Program Works: The Details ........... 2-12

Copycat

•

Ta bl e to p

2.11 How Tabletop Finds a Reasonable Solution ................ 2-13

2.12 The Issue of Scaling Up ................................................. 2-16

2.13 The Potential Long-Term Impact of

the Mechanisms Presented ........................................... 2-16

2.14 Conclusions ................................................................... 2-16

2.1 Introduction

In this chapter we begin by introducing a notion of analogy-making that is considerably broader than

the normal construal of this term. We argue that analogy-making, thus deﬁned, is one of the most

fundamental and powerful capacities in our cognitive arsenal. We claim that the standard separation of

the representation-building and mapping phases cannot ultimately succeed as a strategy for modeling

analogy-making. In short, the context-speciﬁc representations that we use in short-term memory—and

2-1

2-2 Handbook of Dynamic System Modeling

that computers will someday use in their short-term memories—must arise from a continual, dynamic

interaction between high-level knowledge-based processes and low-level, largely unconscious associative

memory processes. We further suggest that this interactive process must be mediated by context-dependent

computational temperature, a means by which the system dynamically monitors its own activity, ultimately

allowing it to settle on the appropriate representations for a given context.

Itis importantto be clear about the goals of this chapter. It is not intended to be a review of computational

models of analogy-making. For such a review, see, for example, Hall (1989), Gentner et al. (2001), French

(2002), or Kokinov and French (2003). Rather, I will present a particular class of models developed,

in the main, by Hofstadter and colleagues from the mid-1980s, in which dynamic, stochastic control

mechanisms play a deﬁning role. This, of course, is not to say that no other computer models of analogy-

making incorporate dynamic control mechanisms. Certainly, for example, the settling mechanisms of

Holyoak and Thagard’s (1989) ACME, a constraint-satisfaction connectionist model, or the mechanisms

of dynamic binding over distributed representations of Hummel and Holyoak’s (1997) LISA model, are

dynamic. The models by Gentner and colleagues (e.g., Gentner, 1983; Falkenhainer et al., 1989; Forbus

et al., 1995) clearly have dynamic mechanisms built into them. Why, then, do I choose to discuss the

Hofstadter family of models?

Several points set these models apart from all others (with the exception of a model, independently

developed by Kokinov (1994) that adopted a similar design philosophy). One key principle is the eschewal

of hand-coded representations. Instead, these programs rely on a dynamic feedback loop between

the program’s workspace and its long-term semantic memory that allows it to gradually converge on

context-appropriate representations. This architecture was explicitly designed to allow scaling up with-

out combinatorial explosion. The second key feature was the use of a context-dependent computational

temperature function that mediated the degree to which the activity of the program was deterministic:

the higher the temperature, the more random the program’s choices became. Temperature is a measure of

the overall quality of the structures perceived and as that structure becomes more and more coherent, the

temperature gradually falls and the program settles into a set of coherent, stable representations. When

the temperature is low enough, the program will stop.

2.2 Analogy-Making as Sameness

Before entering into a discussion of the dynamics of computational modeling of analogy-making, we must

ﬁrst make clear what we mean analogy-making. Frequently, what is understood by analogy-making is the

classic, but more restricted, Aristotelian notion of proportional analogies. These take the form “A is to B as

C is to D.” For example,“Left is to right as up is to down” is an example of this kind of analogy. While this

is certainly part of the story, I will take a broader view of analogy-making, one originally adopted, among

others, by Hofstadter (1984), Mitchell and Hofstadter (1990), Chalmers et al. (1992), Mitchell (1993),

French (1995), Hofstadter et al. (1995), and Kokinov (1994). In this view, analogy-making involves our

ability to view a novel object, experience, or situation that belongs to one category as being the same as

some other object, experience, or situation, generally belonging to another category. This view is summed

up by French (1995, p. xv) as follows:

If only by deﬁnition, it is impossible for two things, any two things, to be exactly the same. And yet,

there is nothing puzzling or inappropriate about our everyday use of the word“same.”We see nothing

odd or wrong about ordinary utterances such as: “That’s the same man I saw yesterday at lunch,” or

“We both wore the same outﬁt,” or, “I felt the same way when Julie and I broke up,” or, ﬁnally,“That’s

the same problem the Americans had in Vietnam.”What makes all these uses of “the same” (and this

one, too) the same?

The answer is: analogy-making. ....Since no two things are ever identical, what we really mean

when we say “X is the same as Y,” is that, within the particular context under discussion, X is the

counterpart of Y. In other words, X is analogous to Y.

The Dynamics of the Computational Modeling of Analogy-Making 2-3

This way of looking at analogy-making, unlike the classic view of proportional analogy, allows us to

speak of a continuum of analogy-making. This continuum runs from simple recognition—an apple we

have never seen before is recognized as being a member of the category Apple because it is “the same

as” other apples we have seen before—to deep “structural” analogies where elements in one situation

are mapped to completely dissimilar elements in another situation—a fellow baseball player once said of

homerun king, Hank Aaron, “Trying to sneak a fastball by Hank Aaron is like trying to sneak the sun

past a rooster.” In this analogy, Hank Aaron is mapped, completely naturally, to a rooster, and fastballs

are mapped to the sun, even though, under normal circumstances, roosters have precious little to do with

Hank Aaron and fastballs have even less to do with the sun.

2.3 Analogy-Making as a Means of “Bootstrapping’’ Cognition

The ability to see new things as being already familiar things with a twist is, unquestionably, one of the

most powerful tools in the human cognitive arsenal from early infancy to adulthood. This ability to use

analogies to understand novel situations allows infants (and adults in unfamiliar settings) to “bootstrap”

new knowledge based on previously learned knowledge. In short,analogy-making allows us to comprehend

new situations by seeing them as being“the same”as familiar situations that we already know how to handle,

even if they require a bit of behavioral ﬁne tuning.

In its simplest form, analogy-making involves ﬁnding a set of correspondences between a “base” object

(or situation, experience, etc.) and a corresponding “target.” For example, you understand the statement

“A credit card is like a check book,” because, even though credit cards do not physically resemble check

books in the least, you effortlessly extract the appropriate parts of the representations of both—in this

case, attributes related to their monetary function—and bring them into correspondence.

Young children, as we have said, constantly engage in analogy-making of the most complex kind.

A perfectly run-of-the-mill example was provided one day by my not-yet-3-year-old son. He lightly touched

the front bumpers of twoof his little toycars together and told me,“The cars aregiving each other a little kiss,

Dada.”What most people fail to realize, because it happens so often and seems so completely natural—“Of

course little kids say things like that! It’s so cute!” remarked one of my friends, thoroughly unimpressed—is

that his remark constitutes an amazing cognitive leap fora2yearold. Think of the machinery put into play

for him to have made that remark: people must be mapped to cars, a car’s front bumpers to lips, touching

them together lightly (as opposed to slamming them together) constitutes “a little kiss,” etc.

2.4 The Necessity of Malleable Representations

Well over a century ago, William James (1890) recognized just how malleable our representations of the

world had to be:

There is no property ABSOLUTELY essential to one thing. The same property which ﬁgures as the

essence of a thing on one occasion becomes a very inessential feature upon another. Now that I

am writing, it is essential that I conceive my paper as a surface for inscription .... But if I wished

to light a ﬁre, and no other materials were by, the essential way of conceiving the paper would

be as a combustible material .... The essence of a thing is that one of its properties which is so

important for my interests that in comparison with it I may neglect the rest ....The properties which

are important vary from man to man and from hour to hour .... many objects of daily use—as

paper, ink, butter, overcoat—have properties of such constant unwavering importance, and have

such stereotyped names, that we end by believing that to conceive them in those ways is to conceive