Fishwick P.A. (editor) Handbook of Dynamic System Modeling

Подождите немного. Документ загружается.

Contributors

Rohit Badal

Agricultural and Biological

Engineering Department

University of Florida

Gainesville, Florida

J.C.M. Baeten

Department of Mathematics

and Computer Science

Eindhoven University of Technology

Eindhoven, The Netherlands

Howard Beck

Agricultural and Biological

Engineering Department

University of Florida

Gainesville, Florida

Peter Breedveld

Faculty of Electrical

Engineering, Mathematics

and Computer Science

University of Twente

Enschede, The Netherlands

Christos G. Cassandras

Department of Manufacturing

Engineering and Center for

Information and Systems

Engineering

Boston University

Brookline, Massachusetts

Gilbert Gang Chen

Department of Computer Science

Rensselaer Polytechnic Institute

Troy, New Yor k

Wolfgang Christian

Davidson College

Charlotte, North Carolina

Gary Consolazio

Department of Civil and

Coastal Engineering

University of Florida

Gainesville, Florida

P. Coquillard

Gestion de la biodiversité

Université de Nice-Sophia Antipolis

Nice, France

Julia I. Couto

Computer Science Department

University of Georgia

Athens, Georgia

Clive L. Dym

Department of Engineering

Harvey Mudd College

Claremont, California

Hilding Elmqvist

Dynasim AB

Lund, Sweden

Francisco Esquembre

Universidad de Murcia

Spain

Paul A. Fishwick

Department of Computer

and Information Sciences

and Engineering

University of Florida

Gainesville, Florida

Andrew Ford

School of Earth and

Environmental Sciences

Washington State University

Pullman, Washington

Benjamin FrantzDale

Scientiﬁc Computation

Research Center

Troy, New Yor k

Robert M. French

LEAD-CNRS UMR 5022

University of Burgundy

Dijon, France

Antony Galton

University of Exeter

Exeter, United Kingdom

Aniruddha Gokhale

Institute for Software Integrated

Systems

Vanderbilt University

Nashville, Tennessee

Jeff Gray

Computer and Information Sciences

University of Alabama

at Birmingham, Alabama

Congzhou He

Computer Science Department

University of Georgia

Athens, Georgia

David R.C. Hill

ISIMA/LIMOS – UMR CNRS 6158

Blaise Pascal University

Aubiere, France

Alfons G. Hoekstra

Section Computational Science

University of Amsterdam

Amsterdam, The Netherlands

Marc Hoit

Department of Civil and Coastal

Engineering

University of Florida

Gainesville, Florida

Yunchul Jung

Agricultural and Biological

Engineering Department

University of Florida

Gainesville, Florida

Steven Kelly

MetaCase

Jyväskylä, Finland

xxi

xxii Contributors

Tag Gon Kim

Department of Electrical

Engineering and

Computer Science

KAIST

Daejeon, Korea

Stefan C. Kremer

Department of Computing

and Information Science

University of Guelph

Guelph, Ontario, Canada

Jinho Lee

Samsung Electronics

Suwon, Korea

E. Lefeber

Department of Mechanical

Engineering

Eindhoven University of

Technology

Eindhoven, The Netherlands

Sven Erik Mattsson

Dynasim AB

Lund, Sweden

Brian McKay

The MathWorks, Inc.

Natick, Massachusetts

John A. Miller

Computer Science Department

University of Georgia

Athens, Georgia

Clay L. Montague

University of Florida

Gainesville, Florida

Pieter J. Mosterman

The MathWorks, Inc.

Natick, Massachusetts

Sandeep Neema

Institute for Software

Integrated Systems

Vanderbilt University

Nashville, Tennessee

James Nutaro

Oak Ridge National Laboratory

Oak Ridge, Tennessee

Martin Otter

DLR Institute of Robotics

and Mechatronics

Germany

Ernest H. Page

The MITRE Corporation

McLean, Virginia

Minho Park

Department of Computer Science

Stephen F. Austin State University

Nacogdoches, Texas

Kalyan S. Perumalla

Oak Ridge National Laboratory

Oak Ridge, Tennessee

Michael Pidd

Department of Management

Science

Lancaster University

Management School

Lancaster, United Kingdom

Stewart Robinson

Warwick Business School

University of Warwick

Coventry, United Kingdom

Mathias Röhl

University of Rostock

Rostock, Germany

J.E. Rooda

Department of Mechanical

Engineering

Eindhoven University of Technology

Eindhoven, The Netherlands

Andrew P. Sage

Department of Systems Engineering

and Operations Research

George Mason University

Fairfax, Virginia

Lee Schruben

University of California

Berkeley, California

Hassan Sedaghat

Department of Mathematics

Virginia Commonwealth University

Richmond, Virginia

E. Seegyoung Seol

Scientiﬁc Computation

Research Center

Troy, New Yor k

Jonathan Sprinkle

Electrical Engineering and

Computer Science

University of Arizona

Tucson, Arizona

Rohit Shenoy

The MathWorks, Inc.

Natick, Massachusetts

Mark S. Shephard

Scientiﬁc Computation Research

Center

Troy, New Yor k

Peter M.A. Sloot

Section Computational Science

University of Amsterdam

Amsterdam, The Netherlands

Roger Smith

Modelbenders LLC

Orlando, Florida

Boleslaw K. Szymanski

Department of Computer Science

Rensselaer Polytechnic Institute

Troy, New Yor k

Simon J.E. Taylor

School of Information Systems,

Computing and Mathematics

Brunel University

Uxbridge, United Kingdom

Juha-Pekka Tolvanen

MetaCase

Jyväskylä, Finland

Adelinde M. Uhrmacher

University of Rostock

Rostock, Germany

D.A. van Beek

Department of Mechanical

Engineering

Eindhoven University of Technology

Eindhoven, The Netherlands

Jiacun Wang

Department of Software Engineering

Monmouth University

West Long Branch, New Jersey

Introduction

I-1

The Languages of

Dynamic System

Modeling

Paul A. Fishwick

University of Florida

1.1 Introduction .................................................................... 1-1

1.2 Dynamic System Modeling Examples ............................ 1-2

1.3 Taxonomic Approaches ................................................... 1-3

1.4 Language .......................................................................... 1-3

1.5 Syntax ............................................................................... 1-5

1.6 Semantics ......................................................................... 1-7

1.7 Pragmatics ....................................................................... 1-10

1.8 Summary ......................................................................... 1-10

1.1 Introduction

Just as we use natural language to communicate verbally or in writing, we use models as a form of scientiﬁc

language to communicate about the world. Models are more compact than natural languages, and tend

to be more structured using mathematical expressions, diagrams, or analog machinery. Morgan and

Morrison (1999) underscore the relevance of models in theory construction as being vital to science:

models mediate between humans and phenomena. We begin the study of dynamic models with a brief

historical review of the word “model” and then we continue with an overview of “dynamic model” as a

subtype. Hodges (2005) provides a concise description of how the word originated as well as different uses

for the word:

In late Latin a modellus was a measuring device, for example to measure water or milk. By the vagaries

of language, the word generated three different words in English: mould, module, model. Often a

device that measures out a quantity of a substance also imposes a form on the substance. We see this

with a cheese mould, and also with the metal letters (called moduli in the early 17th century) that

carry ink to paper in printing. So model comes to mean an object in hand that expresses the design

of some other objects in the world: the artist’s model carries the form that the artist depicts, and

Christopher Wren’s module of St Paul’s Cathedral serves to guide the builders.

Later on, models began to include mathematical forms, in addition to the relatively recent computa-

tional forms (i.e., computer-based text and graphics). All models serve as a convenient substitute for a

phenomenon, but the type of substitution differs slightly depending on the context. For example, a model

house captures the mould legacy since one can imagine a machine that stamps out real houses based on the

model house “mould.”This is an example of using model as an archetype or prototype: the model precedes

the phenomenon. Contrast this use of“model”withthe artifactthat interests us: the dynamic system model.

This kind of model captures only the behavioral, or dynamic, aspects of the phenomenon, which precedes

1-1

1-2 Handbook of Dynamic System Modeling

the model. It is possible to see this difference in precedence as the duality of synthesis (i.e., model as proto-

type) and analysis (i.e., model as theory). The idea of dynamic system models as theories might be debated,

but they act in this way, as hypotheses that remain to be proven within the contextof real-world phenomena.

This process is known as veriﬁcation and validation, with veriﬁcation being assumed to test truth against

requirements and validation to test system behavior against empirical observation. The mathematical

topic of model theory adds to the literature on models, by introducing models of logical formulae.

We will introduce three distinct ways of categorizing models:

•

Synthesis:ModelX is a model for Y, with X being the prototype and Y being the instance model. The

model house X is a model for a speciﬁc house Y.Themapping between X and Y is achieved through

property inheritance, much as derived classes from base classes in object-oriented languages.

•

Analysis:ModelX is a model of Y, with X and Y being instance objects. For example, the wave tank

is a model of the ocean, or the Petri net is a model of an asynchronous communication network.

The mapping involves a transformation of objects in X to those in Y.

•

Theory:Themapping isamodelofX, with Y generated as a logical consequence. For example,

for X being the formula ∀x, y(P(x, y) ∧ Q(x) ∧ R(y)), the mapping (P ≡ bigger, Q ≡ whale,

R ≡human)isamodelforX since whales are bigger than humans. Model theory captures this

approach since a model is the mapping itself, rather than an object speciﬁed as a model. The model

is the interpretation that makes speciﬁc logical formulae true.

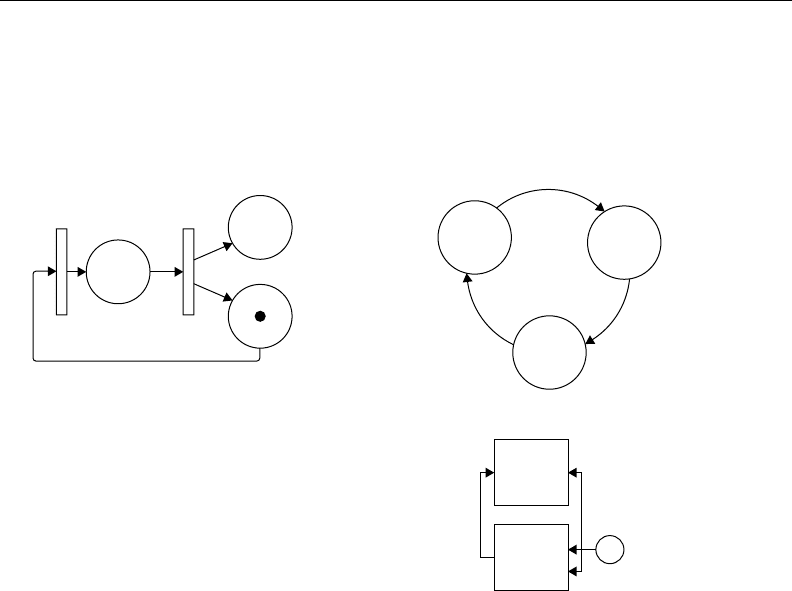
1.2 Dynamic System Modeling Examples

Within the prior discussion of model types, dynamic models fall under analysis; however, other model types

(i.e., synthesis and theory) may play subsidiary roles. We may have a set of equations that dynamically

models the population dynamics within an ecosystem, or a diagram that is translated into this set. Our

dynamic models are also “digital” since they are executed on a digital computer. Models can take many

forms as indicated in the examples shown in Figure 1.1.

t1 t2

set_time

Mode_pressed1

Mode_pressed1 Mode_pressed1

set_timer

set_stop

watch

x  1  ax

x x

兰

兺

a

(a) (b)

FIGURE 1.1 Four types of dynamic system models. (a) Petri net. (b) Finite state machine. (c) Ordinary differential

equation. (d) Functional block model.

The Languages of Dynamic System Modeling 1-3

We observe the following from this illustration:

•

Except for Figure 1.1(c), all the models are graphical, which suggests that models can take

many forms. Not only can models look different but they might be made of different media,

in different styles according to metaphor, and using different forms of human–computer

interaction (HCI).

•

Figure 1.1(c) and Figure 1.1(d) have almost equivalent semantics, although their syntax is different.

This difference is surfaced through the use of different metaphors that form the structural bases.

•

Some models are static in appearance, whereas others have natural dynamics duringmodel execution

as in Figure 1.1(a). This is not apparent from a static ﬁgure, but the solid circle moves through the

network.

•

Models operate in different scales over spacetime. So, models in Figure 1.1(a) and Figure 1.1(b) have

discrete events and those in Figure 1.1(c) and Figure 1.1(d) operate over a temporal continuum

offering no recognizable events separate from the initial and ﬁnal conditions necessary for unique

solution.

1.3 Taxonomic Approaches

The ﬁeld of dynamic system modeling is vast and there has been research in creating theories and

approaches for studying and classifying systems. The initial work in cybernetics (Wiener, 1948; Ashby,

1963) and, subsequently, systems theory (Kalman et al., 1962; Padulo and Arbib, 1974; Bertalanffy, 1968)

provided the context for viewing dynamic systems as control systems with feedback. More recent work has

identiﬁed a systems theoretical approach to speciﬁc types of systems, such as discrete event (Zeigler et al.,

2000). Other taxonomic approaches are based on a systems philosophy (Klir, 1985; Ören, 1984, 1987) or

a language-based approach (Fishwick, 1995, 1996; Nance, 1995). The latter approach is one that we stress

in this chapter as a way to understand the nature of dynamic models as language components. By treating

the models in Figure 1.1 as “statements” within a language (i.e., the type or category of the model), we are

able to surface a comprehensive approach to the study of dynamic system modeling.

Taxonomies have always played a key role in the way a group perceives what they do. By thinking of a

task in terms of the metaphor of “agent,” one cannot but help envision agents acting in a way similar to

human agents. The metaphor (Lakoff and Johnson, 2003; Lakoff and Nunez, 2000) provides an important

mechanism for reasoning how the model is presented to the user as well as how it operates when executed.

Here are three different ways of viewing models:

•

Models as mathematical constructs: Models are mathematical structures, encoded in traditional

textually based mathematical notation.

•

Models as physical constructs: Models are physical objects made of organic or engineered materials.

•

Models are language constructs: Models are formal languages with syntax, semantics, and pragmatics.

These views are not complete and views may easily be combined; however, the key observation is that

the view taken by someone determines their philosophy about modeling. The adopted views also provide

different emphases: a view of modeling as mathematical construct de-emphasizes human presentation

and interaction, whereas a language view emphasizes presentation and semantics equally, along with how

the human interacts with the symbols. Fortunately, a combination of views fosters a more pluralistic view

of modeling, and allows for mathematical rigor to be combined with human interaction.

1.4 Language

Pinker (1994) begins his manuscript with “As you are reading these words, you are taking part in one

of the wonders of the natural world.” It is amazing that language exists and works as well as it does.

Language provides us with the ability to communicate, and it is pervasive within human societies. The

1-4 Handbook of Dynamic System Modeling

interesting thing is that language operates over many levels and layers. The oldest and most prominent

type of language is natural language. However, there are regional dialects, colloquialisms, codes, signs, and

formal languages that grew from mathematics. It is somewhat ironic that while we think of mathematics

as rigorously deﬁned, the semantics of mathematics are fundamentally based on natural language, which

includes the gesticulations of numerous parents and teachers. For example, to know the meaning of

integral, one must know the meaning of summation, and that is ultimately gleaned through examples,

gesture, analogy, and metaphor, all of which are delivered with the assistance of natural language. Still,

natural language is notoriously ambiguous and so if science is to progress, we need other more rule-based

approaches to model building. The consensual agreement in a scientiﬁc community of signs and rules is

termed formalism. Formalisms, such as logic-based systems with axioms and rules, tend to minimize the

number of components in an attempt to reduce potential semantic ambiguity.

Semiotics (Noth, 1990) is the theory of language (i.e., or more atomistically of signs) ﬁrst discussed

in depth by de Saussure (1916). Along with de Saussure, Pierce (Hartshorne and Cambridge, 1997) is

considered to be the theory’s cofounder. de Saussure’s deﬁnition of a“sign” is a dyadic structure containing

a signiﬁer and a signiﬁed. The signiﬁer, for de Saussure, was primarily phonetic, although one can easily

broaden this perspective to more materialistic interpretations. Pierce invented a triadic view of the sign

with these components: the representamen (i.e., the sign), the object, and the interpretant. He proceeded

to create a somewhat complex taxonomy, but we will focus on what Morris (1925) deﬁned, since his

taxonomy of language has since permeated computing: syntax, semantics, and pragmatics. We will deﬁne

these, and place them into the context of dynamic system models:

•

Syntax: relation of signiﬁers to each other—structure of models.

•

Semantics: relation of the signiﬁer to the signiﬁed—meaning of models.

•

Pragmatics: relation of the signiﬁer and signiﬁedtothe human—interaction of humans withmodels.

In computing, one normally uses these three terms within the context of computational linguistics for

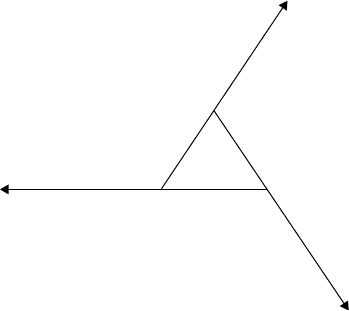
natural-language processing, or programming languages for formal languages. Figure 1.2 is based on

Morris’ taxonomy with slight simpliﬁcations.

The “sign vehicle” represents the complete process where syntax, semantics, and pragmatics can take

place. Let us consider dynamic system models from this perspective.

Semantics

Pragmatics

Syntax

Sign

vehicle

Object

(signified)

Human

interaction

(interpreter)

Sign

(signifier)

FIGURE 1.2 Triangular relationship in sign formation (After Morris, C.W. Symbolism and Reality: A Study in the

Nature of Mind, Benjamin Pub. Co., Philadelphia, PA, 1993.)

The Languages of Dynamic System Modeling 1-5

Syntax, semantics, and pragmatics interact in several ways, and looking at these topics from a math-

ematical perspective is enlightening. Since the language of set theory underpins most formalisms, let us

consider syntax as the mathematical structure deﬁned by elements such as variables, tuples, graphs, and

trees. Semantics captures the concept of the relation, or its restriction in the form of function. Pragmatics is

difﬁcult to deﬁne mathematically except to note that it involves the human context of doing mathematical

modeling. The syntax/semantics duality exists elsewhere as in architecture: syntax is form and semantics

is function. Syntax, therefore, is concerned not only with structure, but also what the structure looks

and sounds like–its presentation. The essence of semantics is in the act of representation. In the chain of

meaning, we translate from one form to another, and still yet, to another in a seemingly endless set of

transformations. Meaning is generated or induced through these transformations, where an increasing

knowledge level provides the human with understanding. This is true of dynamic system models as well

since we translate from one model to another model, and eventually to behavior. Whether a speciﬁc model

is viewed as syntax or semantics is relative to the goal of the modeling exercise. A mathematical equation

may be viewed as the semantic speciﬁcation for a diagrammatic model, or it may be viewed as the syntax

where the semantics are deﬁned in a programming language such as C++ or Java.

The leading edge for language development in computing has evolved fromprogramming languages, and

currently manifests itself in the area of the semantic Web (Berners Lee et al., 2001), which is an extension

and evolution of the World Wide Web (WWW). The Web provides a comprehensive infrastructure for

discussing the three categories of language for both natural and formal languages. The originalWeb focused

on markup for human consumption with regard to the underlying semantic content. The semantic Web,

by contrast, is concerned with the development of ontologies (Maedche, 2002), which can be deﬁned

as an evolutionary structure beginning with the concept of a glossary, proceeding to a taxonomy, and

gradually maturing into a semantic network complete with logical axioms and formulae that can be used

for reasoning. The semantic Web begins with the extensible markup language (XML) and contains a slew

of additional languages for transformation using extensible stylesheet transformation (XSLT). XML is

described as being used for communication among machines, whereas one may present XML using a

variety of methods to humans using XSLT, for example. It may seem odd that XML is humanly readable

for a language meant for consumption by machines; however, humans must still cooperate with each other

ﬁrst in standardizing the structure. Also, while the Web maintains its early vestiges of “document markup,”

the documents have become full-ﬂedged objects in their own right and the metaphor of “documentation”

seems outdated. For ontology speciﬁcation, there is the resource description language (RDF) and the

ontology Web language (OWL). The semantic Web represents a new way of thinking about system models

using the three categories.

1.5 Syntax

Syntax is concerned with notation: the way a system model looks; however, we might expand this to the

other senses. For example, parts of the model may be associated with a sound or a tactile sense. For

the graph-based models in Figure 1.1, we realize that the icons are positioned in certain ways, and with

regularly speciﬁed connections. This is part of the syntax of the model: how we sense and organize the

signs that comprise the model structure. The semantic Web has dramatic consequences for the way in

which we think about dynamic system models. In the original Web, as in most traditional media, the

artifact in Figure 1.1(c) would have been considered to represent the raw mathematical expression. Within

the parlance of the semantic Web (i.e., hereafter referred to as the “Web”), however, this ﬁgure is one

presentation of the underlying content. There are multiple presentations for the same content. The content

of Figure 1.1(c) is expressed in the mathematics markup language (MathML) deﬁned in Figure 1.3.

From the Web’s perspective, this represents the “real” mathematics, and model artifacts such as

Figures 1.1(c) and Figure 1.1(d) are viewed as alternate presentations of this machine-readable content.

There are equally as expressive XML languages for other dynamic system models (Kim et al., 2002), and