Филатов О.А. Шпаргалки по алгебре и геометрии
Подождите немного. Документ загружается.

г----~-----T-----------I
ББК
22.1
k
1.
Линейная
функция,
I 2.
Функция
у
=
х
'
ф51
ее
график
и
свойства
ее
график
и
свойства
Зависимость
между
величинами
х
и
у,
Зависимость
между
величинами
х и
у.
которая
выражается
формулой
у
=
kx
при
k
"#-
О,
называется
прямо
nроnорциональ
которая
выражается
формулой
у
=
l!-,
х
ной
зависимостью.
где
х"#-
О,
называется
обратно
nроnор
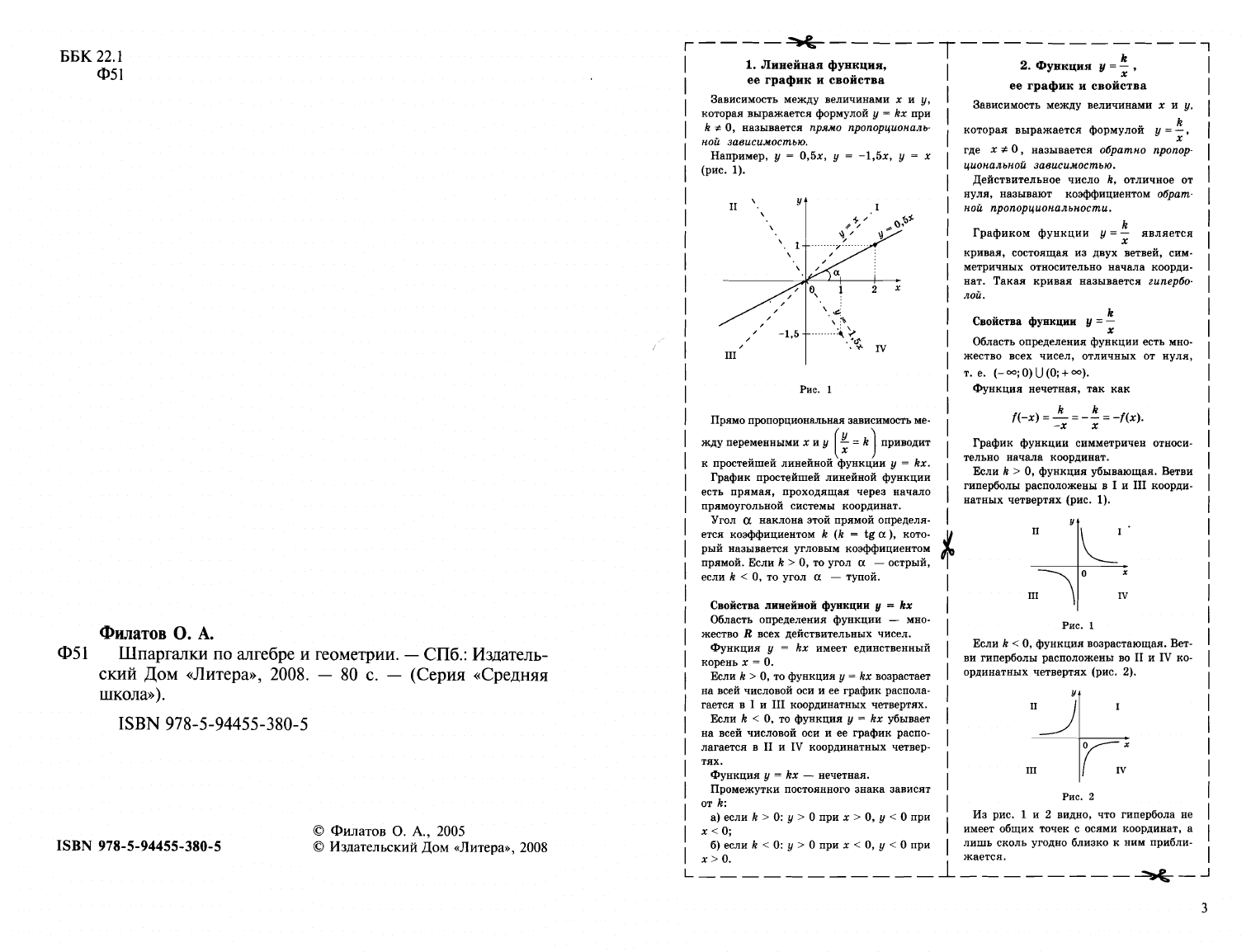
Например,
у
=
0,5х,
У
=
-1,5х,
у
=
х
циональной
зависимостью.
(рис.
1).
Действительное
число
k,
отличное
от
нуля,
называют
коэффициентом
обрат·
у
II
ной
nроnорциональности.
Графиком
функции
у
=
l!-
является
х
кривая,
состоящая
из
двух
ветвей,
сим
метричных
относительно
начала
коорди
нат.
Такая
кривая
называется
гипербо
"
"
"
"
"
~
2
х
лой.
u
\
~
С
воиства
функции
у
= -
k
,,"
"
-1,5
........
\~
х
.:~
IV
Область
определения
функции
есть
мно
III
"
жество
всех
чисел,
отличных
от
нуля,
т.
е.
(-00;0)
U
(О;
+00).
Рис.
1
Функция
нечетная,
так
как
Прямо
пропорциональная
зависимость
ме
f(-x)
=!!...-
=
_l!-
=
-f(x).
-х
х
График
функции
жду
переменными
х
и
у
(~=
k )
при
водит
симметричен
относи
тельно
начала
координат.
К
простейшей
линейной
функции
у
=
kx.
Если
k >
О,
функция
убывающая.
Ветви
График
простейшей
линейной
функции
гиперболы
расположены
в
1
и
111
коорди
есть
прямая,
проходящая
через
начало
натных
четвертях
(рис.
1).
прямоугольной
системы
координат.
Угол
а
наклона
этой
прямой
определя
ется
коэффициентом
k (k =
tg
а),
кото
11
рый
называется
угловым
коэффициентом
~I
~
прямой.
Если
k >
О,
то
угол
а
-
острый,
если
k <
О,
то
угол
а
-
тупой.
~IO
х
IV
III
\
Свойства
линейиой
функции
у
=
kx
Область
определения
функции
-
мно
Рис.
1
Филатов
о.
А.
жество
R
всех
действительных
чисел.
Если
k <
О,
функция
возрастающая.
Вет
Функция
у
=
kx
имеет
единственный
ф51
Шпаргалки
по
алгебре
и
геометрии.
-
СПб.:
Издатель-
ви
гиперболы
расположены
во
11
и
IV
ко
корень
х
=
О.
ординатных
четвертях
(рис.
2).
ский
Дом
«Литерю>,
2008. -
80
с.
-
(Серия
«Средняя
Если
k >
О,
то
функция
у
=
kx
возрастает
на
всей
числовой
оси
и
ее
график
распола
школа»).
гается
в
1
и
111
координатных
четвертях.
II~
y~
1
Если
k <
О,
то
функция
у
=
kx
убывает
ISBN 978-5-94455-380-5
на
всей
числовой
оси
и
ее
график
распо
лагается
в
11
и
IV
координатных
четвер
тях.
III
~:
Функция
У
=
kx
-
нечетная.
Промежутки
постоянного
знака
зависят
Рис.
2
от
k:
а)
если
k >
О:
у
>
о
при
х
>
О,
У
<
О
при
Из
рис.
1
и
2
видно,
что
гипербола
не
11
©
Филатов
О.
А,
2005
I
х
<
О;
имеет
общих
точек
с
осями
координат,
а
б)
если
k <
О:
у
>
О
при
х
<
О,
У
<
О
при
I
лишь
сколь
угодно
близко
к
ним
прибли
ISBN 978-5-94455-380-5
©
Издательский
Дом
«Литера»,
2008
I
х>
О.
жается.
L
~
~-~
3
г-----------T-----~----I
г----~-----------------I
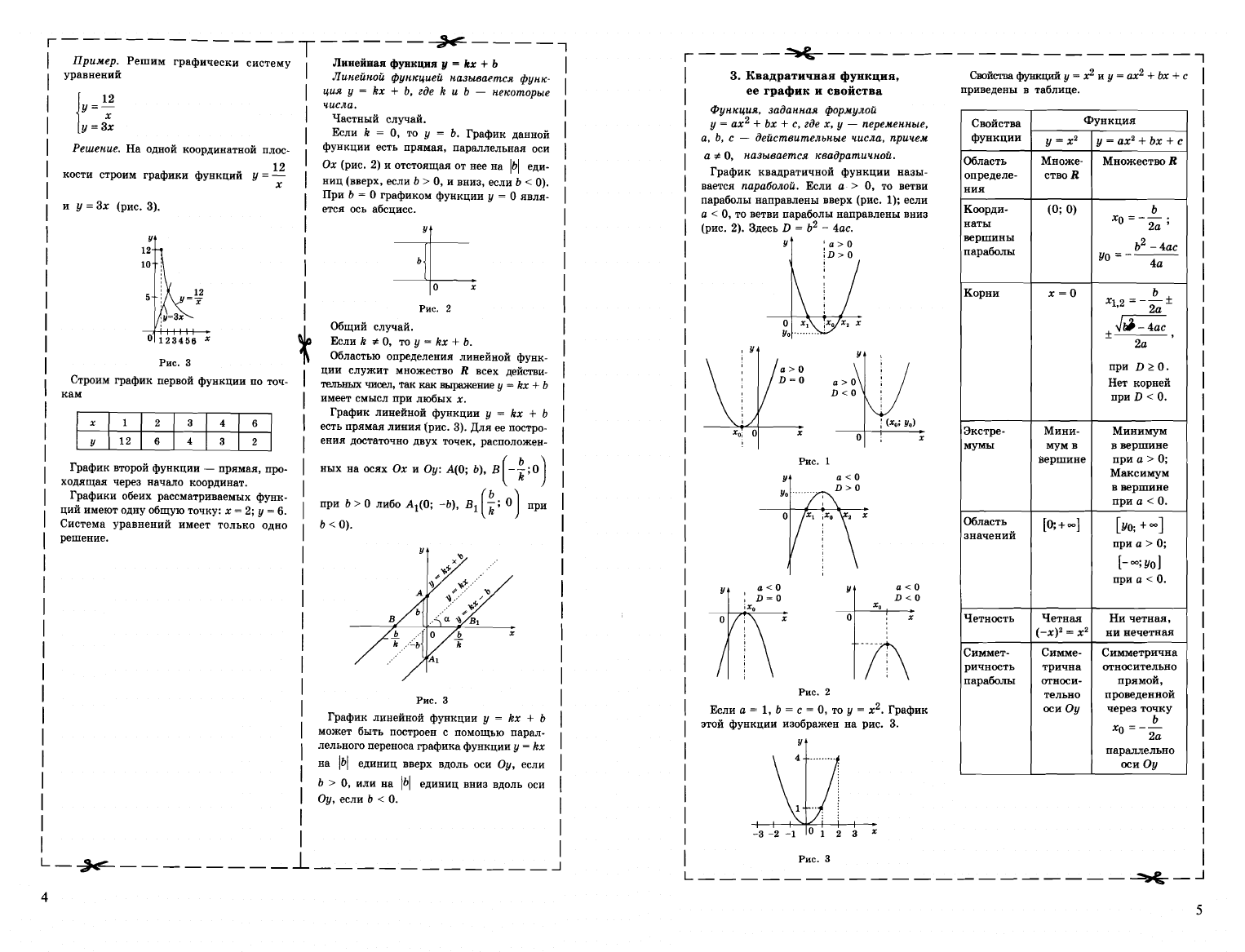
Пример.
Решим
графически
систему
Линейная
функция
у
=
kx
+
Ь
I
уравнений
Линейной
фУНI(;цией
называется
фУНI(;·
I
3.
Квадратичиая
функция,
Свойства
функций
у
=
х2
и
у
=
ах
2
+
Ьх
+
с
Свойства
Функция
функции
У
=
х
2
У
=
ах
2
+
Ьх
+
с
Область
Множе'
МножествоR
определе
ствоН
ния
Коорди
(О;
О)
Ь
наты
хо
= -
2а
;
вершины
параболы
ь
2
-
4ас
Уо
=----
4а
Х12
=-~±
,
2а
+
~1irJ-4ас
,
Корни
х=О
2а
при
D
~
О.
Нет
корней
при
D <
О.
Экстре
Мини
Минимум
мумы
мумв
В
вершине
вершине
при
а
>
О;
Максимум
в
вершине
при
а
<
О.
Область
[0;+00]
[УО;
+
00]
значений
при
а
>
О;
[-00;
УО]
при
а
<
О.
Четность
Четная
Ни
четная,
(-х)2
=
х
2
ни
нечетная
Симмет
Симме
Симметрична
ричность
трична
относительно
параболы
относи
прямой,
тельно
проведенной
осиОу
через
точку
Ь
ХО
=--
2а
параллельно
оси
Оу
у
=-
12
х
!
у
=
3х
Решение.
На
одной
координатной
плос
12
кости
строим
графики
функций
у
=
-;-
•
у
=
эх
(р
••
о
:>0
~~
5
=~
х
123456
х
Рис.
3
Строим
график
первой
функции
по
точ
кам
х
1 2 3 4 6
ffitEEВ±Бj
У
12
6 4 3 2
График
второй
функции
-
прямая,
про
ходящая
через
начало
координат.
ГрафИКИ
обеих
рассматриваемых
функ
ции
имеют
одну
общую
точку:
х
=
2;
у
= 6.
Система
уравнений
имеет
только
одно
решение.
ция
у
=
kx
+
Ь,
где
k
и
Ь
-
Hel(;omopble
I
числа.
Частный
случай.
Если
k =
О,
то
у
=
Ь.
График
данной
I
функции
есть
прямая,
параллельная
оси
I
Ох
(рис.
2)
и
отстоящая
от
нее
на
Ibl
еди-
I
ниц
(вверх,
если
Ь
>
О,
и
вниз,
если
Ь
<
О).
При
Ь
=
О
графиком
функции
у
=
О явля-
I
""".
о'"
'боЦ~."О
:
у
ь
I
О х
I
I
Рис.
2
Общий
случай.
I
Еслиk
*0,
Toy=kx+b.
Областью
определения
линейной
функ-
I
ции
служит
множество
R
всех
действи-
I
*
I
тельных
чисел,
так
как
выражение
у
=
kx
+
Ь
I
I
имеет
смысл
при
любых
х.
График
линейной
функции
у
=
kx
+
Ь
I
I
есть
прямая
линия
(рис.
3).
Для
ее
постро
I
ения
достаточно
двух
точек,
расположен-
I
I
ных
на
осях
Ох
и
Оу:
А(О;
Ь),
в(-*;о)
I
I
при
Ь>
О
либо
А
(О;
-Ь),
В
(~;
о)
при
1 1 k
I
Ь
<
О).
I
у
'о
х
Рис.
3
График
линейной
функции
у
=
kx
+
Ь
может
быть
построен
с
помощью
парал
лельного
переноса
графика
функции
у
=
kx
на
Ibl
единиц
вверх
вдоль
оси
Оу,
если
Ь
>
О,
или
на
jbl
единиц
вниз
вдоль
оси
Оу,
если
Ь
<
О.
ее
график
и
свойства
фУНI(;ция,
заданная
формулой
у
=
ах
2
+
Ьх
+
с,
где
х,
у
-
nеременные,
а,
Ь,
с
-
действительные
числа,
причем
а
*
О,
называется
I(;вадратичноЙ.
График
квадратичной
функции
назы
вается
параболой.
Если
а
>
О,
то
ветви
параболы
направлены
вверх
(рис.
1);
если
а
<
О,
то
ветви
параболы
направлены
вниз
(рис.
2).
Здесь
D =
ь
2
-
4ас.
yt
'а>
О
iD>O
у
у
х
о
;
а>О
а>О
D=O
D<O
:
(х
о
;
Уо)
х
01
х
Рис.
у
! D =
О
D <О
'Хо
х
О
О
.
О
,х
а<О
Yg<O
_
~
..
'
:
х
i
i
ОП
i
j
Рис.
2
Если
а
= 1,
Ь
=
с
=
О,
то
у
=
х
2
•
График
этой
функции
изображен
на
рис.
3.
у
4
-3 -2
-1
10
1 2 3
х
приведены
в
таблице.
Рис.
3
L_~--------~-----------~
L
~-~
4
5

г-----------------~----I
г----~-----T-----
Пример
1.
Построить
график
функции
у
=
х
2
-
2х
- 3,
указать
промежутки,
в
которых
функция
возрастает
и
убывает.
Указать
значения
х,
при
которых
у
>
О.
Указать
минимум
функции.
Решение.
Поскольку
а
>
О,
то
графиком
функции
является
парабола, ветви
кото
рой
направлены
вверх
(см.
рис.
1).
1.
Находим
координаты
хо
и
уо
верши
ны
параболы:
Ь
(-2)
хо
==
-
2а
==
- 2
==
1;
ь
2
-4ас
(_2)2
-4(-3)
уо
=----=
4а
4
==
_ 4 + 12
==
-4.
4
2.
Находим
точку
на
оси
Оу
при х
=
О:
у(О)
=
02
- 2 .
О
- 3 = -
3.
Точка
на
оси
Оу
(О;
-3).
3.
Находим
корни
функции:
b~
хl
=--+
2а 2а
-2
~4-4(-3)
=--+
=1+2=3;
2 2
X2=-~
~
==1-2=-1.
2а 2а
4.
Дополнительную
точку
рассчитаем
при
х
= 4:
у(4)
= 16 - 2 .4 - 3 = 5,
получим
точку
(4; 5).
5.
Осью
симметрии
параболы
служит
прямая
хо
==
-
~
==
1.
Строим
график
функ
2а
ции
у
=
х
2
-
2х
- 3
(рис.
4).
Рис.
4
Из
рис.
4
видно:
функция
убывает
при
-
00
<
х
< 1 ,
функция
возрастает
при
1 <
х
< +
00;
у
>
о
при
-
00
<
х
<
-1
и
3 <
х
< +
00
,
так
как
график
функции
при
этих
зна
чениях
лежит
выше
оси Ох.
Минимум
функции
уо
=
-4.
L_~
График
функции
у
=
ах
2
+
Ьх
+
с
можно
получить
из
графика
функции
у
=
х
2
с
помощью
следующих
преобразований:
•
параллельного
переноса
(-
:а
;
О
);
•
сжатия
(или
растяжения)
в
а
раз;
•
параллельного
переноса
ь
2
О;
_ -
4ас
]
4а
.
[
Пример
2.
Построить
график
функции
2х
2
+
2х+
2.
Осуществив
все
указанные
выше
преоб
разования,
получим
график,
приведенный
на
рис.
5.
у
" 2
у=2х
2
+2х+2
3
2
1
О х
-2
Рис.
5
4.
Квадратное
уравнение
Определения
Уравнение
вида
ах
2
+
Ьх
+
с
=
О,
где
х
-
переменная,
а,
Ь,
с
-
действительные
чис
ла,
причем
а"*
О,
называется
квадрат
ным
уравнением.
В
квадратном
уравнении
число
а
назы
вают
первым
коэффициентом,
Ь
-
вто
рым
коэффициентом,
с
-
свободным
чле
ном.
Если
хотя
бы
один
из
коэффициентов
Ь
или
с
равен
нулю,
то
квадратное
уравне
ние
называется
неnолным.
Неполные
квадратные
уравнения
быва
ют
трех
видов:
а)
если
Ь
==
О,
с
==
О,
то
ах
2
==
О;
б)
если
Ь
==
О,
с
"*
О,
то
ах
2
+
с
==
О;
в)
если
Ь"*
О,
с
==
О,
то
ах
2
+
Ьх
==
О.
Пример
1.
Решим
уравнение
зх
2
- 48 =
О.
Решение:
зх
2
= 48,
х
2
= 16,
хl
==
+М
==
4,
Х2
==
-М
==
-4.
Ответ:
хl
= 4,
Х2
= - 4.
Пример
2.
Решим
уравнение:
2х
2
+ 8 =
О.
Решение: 2х
2
=
-8,
х
2
=
-4.
Ответ:
В
области
действительных
чисел
уравнение
не
имеет
решения.
Полное
квадратное
уравнение
Уравнение
вида
ах
2
+
Ьх
+
с
=
О,
где
а,
Ь,
с
-
действительные
числа,
не
равные
нулю,
причем
а"*
1,
называется
полным
квад
ратным
уравнением.
Корни
полного
квадратного
уравнения
вычисляют
по
формуле
-b±~
х1,2
2а
' (1)
где
выражение
ь
2
-
4ас
называется
дискри
минантом
квадратного
уравнения
и
обо
значается
буквой
D.
•
Если
D =
О,
то
существует
только
одно
значение
переменной,
удовлетворяющее
уравнению
ах
2
+
Ьх
+
с
=
О.
Однако
усло
вились
говорить,
что
в
этом
случае
квад
ратное
уравнение
имеет
два
равных
дей
Ь
ствительных
корня,
а
само
число
- 2
называют
корнем
кратности
два.
а
•
Если
D >
О,
то
квадратное
уравнение
имеет
два
различных
действительных
кор
ня,
вычисляемых
по
формуле
(1).
•
Если
D
~
О,
то
квадратное
ууавнение
не
имеет
деиствительных
корнеи.
L
I 5.
Теорема
Виета
Сумма
корней
приведенного
квадратно
I
го
уравнения
х
2
+
рх
+ q =
О
равна
коЭФ
I
фициенту
при
неизвестном
х,
взятому
с
противоположным
знаком,
а
произведе
I
ние
корней
равно
свободному
члену:
хl
+
Х2
=
-р,
хl
.
Х2
=
q.
Пример
1.
Уравнение
х
2
+
2х
- 80 =
О
имеет
корни
хl
= 8,
Х2
=
-10,
так
как
выполняются
равенства
теоремы
Виета:
хl
+
Х2
= 8 - 10 =
-2,
хl
.
Х2
= 8
(-10)
=
-80.
Пример
2.
Уравнение
х
2
+
9х
+ 14 =
О
имеет
корни
хl
и
Х2'
дЛЯ
которых,
согласно
теореме
Виета,
выполняются
следующие
равенства:
хl
+
Х2
=
-9,
хl
.
Х2
= 14.
Решив
эту
систему
двух
уравнений
с
двумя
неизвестными,
получим
Х1
=
-7,
Х2
=
-2.
I-----~-----I
6.
Разложение
квадратного
I
I
I
трехчлена
на
множители
I 1.
Квадратный
трехчлен
х
2
+
рх
+q
мож-
I
JI
но
разложить
на
множители
следующим
/{о
образом:
I
х
2
+
рх
+q =
(х
-
хl)
(х
-
Х2)'
I
где
хl
и
Х2
-
корни
уравнения
х
2
+
рх
+q =
О.
Пример.
Разложим
на
множители
трехчлен
х
2
-
14х
+ 48.
Решение.
Находим
корни
уравнения
х
2
-
14х
+ 48 =
О
по
теореме
Виета:
хl
= 6,
Х2
= 8.
Следовательно,
х
2
- 14 + 48 =
(х
- 6)
(х
- 8).
I 2
2.
Квадратный
трехчлен
ах
+
Ьх
+
с
I
можно
разложить
на
множители
следую
I
щим
образом:
I
ах
2
+
Ьх
+
с
=
а
(х
-
хl)
(х
-
Х2)'
где
х
их
-
корни
уравнения
I 1
~
_
ах
+
Ьх
+
с-О.
~
~-~
~
6
7

г----~-----T-----------I
г-----------T-----~----I
7.
Неравенства,
их
основные
свойства
I
8.
Арифметическая
прогрессия
В
том
случае,
если
приведенное
квад-
I
При,мер
1.
Определения
Определения
ратное
уравнение
имеет
действительные
Решим
уравнение
2х
2
-
3х
+ 1 =
О.
При
сравнении
двух
действительных
I
Числовая
последовательность.
каждый
корни,
теорема
Виета
позволяет
судить
I
Решение:
чисел
х и
у
возможны
три
случая:
I
член
которой.
начиная
со
второго.
равен
как
о
знаках,
так
и
о
значениях
корней:
I 3 ±
../з2
- 4 . 2 .1 3 ±
Ji
1)
х
=
у
(х
равно
у);
I
nредшествующе,му
члену.
сложенно,му
С
если
q >
О,
Р
>
О,
то
оба
корня
отрица-
Хl,2
=
2.2
4
2)
х
>
у
(х
больше
у);
oдHUМ
и
те,м
же
число,м.
называется
ариф
тельны;
I D
если
q >
О,
Р
<
О,
то
оба
корня
поло-
Так
как
= 1,
т.
е.
D >
О,
то
уравнение
3)
х
<
у
(х
меньше
у).
I
,метической
nрогрессиеЙ.
жительны;
I
имеет
два
корня:
Число
х
равно
числу
у,
если
разность
Обозначают
арифметическую
прогрес
х
-
у
равна
нулю.
Число
х
больше
числа
у,
I
сию,
употребляя
знак
+,
т.
е.
пишут
если
q <
О,
Р
>
О,
то
корни
имеют
раз-
I
хl
=3 +1 =
1,
3-1
1
Х2
=-4-="2'
если
разность
х
-
у
больше
нуля.
ные
знаки,
причем
4
+аl,а2,
...
,а
n
,·
...
Число
х
меньше
числа
у,
если
разность
отрицательный
ко
1
Общий
член
арифметической
прогрессии
х
- у
меньше
нуля.
рень
по
модулю
боль
Ответ:
Хl
= 1,
Х2
=
2"
рассчитывается
по
формуле
Например,
6 > 4,
т.
к.
6 - 4 = 2 >
О,
ше
положительного;
При,мер
2.
а
n
=
аl
+ d
(n
- 1),
(1)
3 < 5,
т.
к.
3 - 5 =
-2
<
О.
если
q <
О,
Р
<
О,
то
корни
имеют
раз
Решим
уравнение
2х
2
-
3х
+ 4 =
О.
где
аl
и
d -
любые
заданные
числа.
Запись
х
~ у
или
у:5:
х
читается
так:
ные
знаки,
причем
Число
а
называется
nервы,м
члено,м
отрицательный
ко
.х
больше
или
равно
у.
или
.у
меньше
Решение:
арифметической
прогрессии,
число
d -
или
равно
х
•.
рень
по
модулю
мень
разностью
арифметической
прогрессии.
ше
положительного.
3 ±";9 - 4 .2 .4
Запись.
в
которой
два
числа
или
два
Разность
между
любым
членом
арифме
Хl,2
выражения.
содержащие
nере,менные.
со
2·2
тической
прогрессии
и
ему
предшествую
единены
знако,м
>. <.
~
или
~.
называ
Так
как
D =
-23,
т. е.
D <
О,
то
уравне-
щим
членом
равна
одному
и тому
же
чис
*
ется
неравенство,м.
лу:
ние
не
имеет
действительных
корней.
I
Неравенства,
составленные
с
помощью
При,мер
3.
знаков
>
или
<,
называют
строги,ми;
а2
-
аl
=
аз
-
а2
=
...
=
ak
-
ak-l
=
d.
Решим
уравнение
9х
2
+
6х
+ 1 =
О.
Для
того
чтобы
задать
арифметическую
неравенства,
составленные
с
помощью
I
Решение:
знаков
:5:
или
~,
называют
нестроги,ми.
прогрессию,
достаточно
знать
ее
первый
I
-6
±";36 - 4 . 9 .1
-6
Два
неравенства
вида
а>
Ь
и
С
> d
назы
член
аl
и
разность
d.
Хl,2
= 2 .9 = 18 = -
3'
.
ваются
неравенствами
одинакового
смыс
Если
разность
арифметической
прогрес
ла,
а
вида
а
>
Ь,
С
< d -
неравенствами
сии
-
положительное
число,
то
такая
Так
как
D =
О,
то
уравнение
имеет
два
прогрессия
является
возрастающей;
если
I
противоположного
смысла.
Например,
-----X------
равных
корня
-
'3
1
.
разность
-
отрицательное
число,
то
та
5 > 2
и
-4
>
-6
-
неравенства
одинаково
При,мер.
го
смысла,
анеравенства
6 > 4
и
5 < 10
кая
прогрессия
является
убывающей.
Разложим
на
множители
трехчлен
Приведенное
квадратное
уравнение
являются
неравенствами
При,мер
1.
Назвать
первые
пять
членов
противополож
2х
2
-
3х
+ 1.
'Уравнение
вида
х
2
+
рх
+q =
О,
где
р
и
прогрессии:
Решение.
q -
действительные
числа,
называется
Неравенства,
содержащие
только
чис-
J
а)
аl
= 2, d = 3: +2,
5,
8, 11, 14;
Находим
корни
уравнения
nриведенны,м
квадратны,м
уравнение,м.
ла,
называются
числовы,ми
HepaвeHcmвa,ми.
б)
аl
= 12, d = - 3: +12, 9, 6, 3,
О.
ного
смысла.
't
2х
2
-
3х
+ 1 =
О:
Число
р
называют
коэффициентом
при
Если
неравенство
представляет
собой
1
неизвестном
х,
а
q -
свободным
членом.
истинное
высказывание,
то
оно
называ-
I
Свойства
арнфметнческой
прогрессии
хl
= 1;
хl
=
2'
.
Корни
приведенного
квадратного
урав
ется
верны,м.
I 1.
Каждый
член
арифметической
про
нения
вычисляют
по
формуле
Следовательно,
Вместо
двух
неравенств
х
<
а,
а
<
у
упот-
грессии,
начиная
со
второго,
равен
пре
ребляется
запись
х
<
а
<
у;
такое
неравен-
I
дыдущему,
сложенному
с
разностью
d,
2х
2
-
3х
+ 1 = 2
(х
- 1)
(х
-
2'
).
Хl,2
=_l!..+
Р-ру
ство
называется
двоЙны,м.
I
т. е.
2 -
1
vl2)
-q.
Если
неравенство
содержит
буквенные
_ +d = k = 1 2
ak+l
-
ak
,аl
а,
"
....
Приведенное
квадратное
уравнение
име-
выражения,
то
оно
является
верным
лишь
2
К
~
Ф
~
п
и
оп
еделенных
значениях
входящих
в
I
.
аждыи
член
ари
метическои
про
ет
два
равных
корня,
если
(f
r=
q.
р
р
I
грессии
есть
среднее
арифметическое
двух
него
переменных.
равноудаленных
от
него
членов
этой
про
При,мер.
Например,
неравенство
(а
+
ь)2
~
О
вер-
I
грессии,
т. е.
Решим
уравнение
х
2
-
12х
- 28 =
О.
но
при
любых
значениях
а
и
Ь,
так
как
ak+m
+
ak-m
Решение:
квадрат
любого
числа
есть
число
поло-
ak
= 2 '
жительное;
неравенство
х
2
>
О
верно
при
I
где
k
и
т
-
любые
натуральные
числа
и
12
P-=
I
12J
2
любых
значениях
х,
кроме
нуля.
I k >
т.
Х1,2
=
'2
±
Vl'2
J +
28
=
Решить
неравенство
-
значит
указать
3.
Любой
член
арифметической
прогрес
= 6 ±.)36 +
28
= 6 ±
J64
= 6 ±8;
границы,
в
которых
должны
заключать-
I
сии,
начиная
со
второго,
является
сред
хl
= 14,
Х2
=
-2.
ся
действительные
значения
неизвестных
I
ним
арифметическим
предшествующего
и
Ответ:
хl
= 14,
Х2
=
-2.
величин,
чтобы
неравенство
было
верным.
последующего
членов,
т. е.
Решить
приведенное
квадратное
урав
При,мер.
Решим
неравенство
-2х
> 4. I
а
+
а
n n+2
нение,
т. е.
найти
его
корни,
можно
по
2
L~=:HepaBeHcT~ePHo~~~~~_~n+l~~_~~~_~
теореме
Виета.
L_~
~
~
2
Шпаргалки
по
алгебре
и
геометрии
9
8

1
г-----------T-----~----I
г----~-----T-----------I
4.
Для
любой
конечной
арифметической
I
Свойства
неравенств
прогрессии
сумма
двух
членов,
равноот-
1.
Если
а
>
Ь,
то
Ь
<
а.
стоящих
от
ее
концов,
есть
величина
по-
I 2.
Если
а
>
Ь
и
Ь
>
С,
то а
>
с.
стоянная
для данной
прогрессии,
равная
П
ри,мер.
сумме
крайних
членов:
I
Если
х
>
3у,
а
3у
> 12,
то
х
> 12.
ak
+
а
m
=
аl
+
а
n
,
I 3.
Если
к
обеим
частям
верного
неравен
где
k
и
т -
номера
членов,удовлетворяю-
I
ства
прибавить
одно и
то
же
число,
то
щие
условию
k + т = 1 + n.
получится
верное
неравенство,
т.
е.
если
При,мечание.
I
а
>
Ь,
то
а
+
с
>
Ь
+
с
или
а
-
с
>
Ь
-
с.
Свойство
1,
так
же
как
и
свойство
2,
При,мер.
является
условием,
достаточным
для
того,
I
Если
к
обеим
частям
неравенства
9 > 5
чтобы
соответствующая
последователь-
I
прибавить
7,
то
получим
16 > 12,
а
если
ность
аl' а2'
...,
а
n
,
...
была
арифметичес-
вычтем
7,
то
получим
2 >
-2.
кой
прогрессиеЙ.
I 4.
Любой
член
неравенства
можно
пере
нести
из
одной
части
в
другую,
переменив
Сумма
членов
его
знак
на
противоположный,
т. е.
из
арнфметической
прогрессии
а
+
Ь
>
с
следует,
что
а
>
с
-
Ь,
а
+
Ь
-
с
>
О.
Обозначим
Sn
сумму
n
последователь
Например, х
+ 9 > 4,
х
> 4 - 9,
х
>
-5.
ных
членов
арифметической
прогрессии:
5.
Если
обе
части
верного
неравенства
Sn =
аl
+
а2
+
аз
+ ... +
а
n
-l
+
а
n
.
(2)
умножить
на
одно
и
то
же
положительное
Эта
сумма
вычисляется
по
формуле
число, то
получится
верное
неравенство.
Например,
если
а
>
Ь,
то
5а
>
5Ь.
8 =
(аl
+
а
n
)
6.
Если
обе
части
верного
неравенства
n
2 . n
(3)
умножить
на одно и
то
же
отрицатель
*
Су,м,ма
n
последовательных
членов
ариф
ное
число
и
из,менить
зна/С
неравенства
,метичес/Сой
nрогрессии
равна
nолусу,м,ме
на
противоположный,
то
получится
вер
ее
/Срайних
членов,
у,множенной
на
число
ное
неравенство.
членов.
Например,
если
а>
Ь,
то
а
(-1)
<
Ь
(-1),
Иначе
Sn
можно
вычислить
по
формуле
т.
е.
-а
<
-Ь.
7.
Так
как
деление
можно
заменить
ум
Sn =
2аl
+d
(n
- 1)
ножением
на
число,
обратное
делителю,
2
·n.
(4)
то
аналогичные
правила
можно
применить
и к
делению.
При,мер.
В
арифметической
прогрессии
(сп)
известно,
что
С2
=
-2,
d = 3.
Найдем
Действия
снеравенствами
сl
и
сумму
первых
пяти
членов
прогрес
1.
Неравенства
одинакового
смысла
сии.
можно
почленно
складывать.
Решение:
Например,
при
(а
>
Ь)
+
(с
> d)
С2
=
сl
+ d,
откуда
сl
=
С2
- d =
-2
- 3 =
-5.
а
+
с
>
Ь
+
d.
По
формуле
(1)
найдем
С5:
2.
Неравенства
противоположного
смыс
С5
=
сl
+ d (5 - 1) =
-5
+ 3 . 4 =
7.
ла
можно
почленно
вычитать,
оставляя
По
формуле
(3)
найдем
сумму
первых
пяти
знак
того
неравенства,
из
которого
про
членов
данной
арифметической
прогрес
изводится
вычитание.
сии:
Например,
при
(а
>
Ь)
-
(с
<
d)
а
-
с
>
Ь
-
d.
85 =
(сl
+
С5)
.5=
-5
+7
.5
= 5.
2 2
3.
Неравенства
одинакового
смысла
с
Можно
вычислить
эту
же
сумму
и по
положительными
членами
можно
почлен
формуле
(4):
но
умножать.
Например,
при
а
>
Ь
>
О
и
с
> d >
О
2 (
-5)
+ 3 (5 - 1)
85=
2
·5=
ас>
bd.
4.
Обе
части
неравенства
с
положитель
=
-10
+
12'5
= 5.
ными
членами
можно
возводить
в
одну
и
2
ту
же
натуральную
степень.
Например, при
а>Ь
a
k
> b
k
L_~
-l
гдеа>О,ь>о',
kEN.
___________
...J
9.
Геометрическая
прогрессия
I 10.
Степенная
функция
Определения
Степенной
фун/Сцией
называется
фун/С
Числовая
последовательность,
первый
I
ция
вида
у
=
х
n
,
где
n -
любое
действ
и
член
/Соторой
отличен
от
нуля,
а
/Саж-
I
тельное
число
(показатель
степени).
дый
член,
начиная
со
второго,
равен
nред
шествующе,му
члену,
у,множенно,му
на
I
Функции
у
=
Х,
у
=
х
2
,
У
=
-.;
-
част
од
по и
то же
число,
nе
р.авnое
пулю,
,nа-
I
ные
виды
степенной
функции
(n
= 1, n =
2,
зывается
гео,метричес/Сои
nрогрессиеи:
I n =
-1).
Ь
1
,
Ь
2
,
Ь
З
'
... ,
Ь
N
'
...
x
2k
Свойства
функции
у
=
(с
четным
Число
q,
не
равное
нулю,
называетсязnа
положительным
показателем
степени),
,меnателе,м
геометрической
прогрессии.
где
k -
число
натуральное
Согласно
определению,
члены
геометри
Например,
у
=
х
2
,
У
=
х
4
(рис.
1)
и
т.
д.
ческой
прогрессии
формируются
по
пра
вилу:
у
Ь
2
= b
1
q;
Ь
з
= b
2
q = b
1q
2;
Ь
4
=
Ьзq
=
ь
1q
з
и
т.
д.
Следовательно,
~:Ьt=Ьз:~=
..
·=
=
Ь
n
:
ь
n
-l
=
ь
n
+l
:
Ь
n
=
q.
Формула
общего
члена
(n-го
члена)
гео
-1
10
х
метрической
прогрессии
имеет
вид
Ь
n
=
ьt
.
qn-l,
(1)
Рис.
1
где
nЕ
N.
1.
Область
определения
-
множество
R
Из
условия
ьt
*-
О,
q
*-
О
следует,
что
действительных
чисел.
ни
один
из
членов
геометрической
про
2.
Область
значений
-
множество
поло
грессии
не
может
быть
равен
нулю.
жительных
действительных
чисел,
т.
е.
Для
того
чтобы
задать
геометрическую
[0;00).
прогрессию
(Ь
n
)'
достаточно
знать
ее
пер
2k
3.
Функция
четная,
так
как
(-x)2k
...
x ,
вый
член
Ь
1
и
знаменатель
q.
Если
Ь
1
>
О
и
поэтому
ее
достаточно
исследовать
лишь
на
q>
1,
то
геометрическая
прогрессия
будет
возрастающей;
если
Ь
1
>
О
и О
< q < 1 -
полуинтервале
[О;
+00).
График
функции
убывающей.
симметричен
относительно
оси
Оу.
~
Если
q <
О,
то
знаки
членов
прогрессии
4.
На
интервале
(_00;
О]
функция
убы
будут
чередоваться
и она
не будет
моно
вает,
а
на
интервале
[О;
+00) -
возрастает.
тонной.
5.
Минимум
функции
равен
нулю.
При,меры.
Определим
первые
пять
чле
6.
Промежутки
знакопостоянства:
функ
нов
геометрической
прогрессии:
2k
а)
Ь
1
= 1, q = 2
ция
у
= x
принимает
положительные
значения
при
всех
х
*-
О.
в
точке
Х
=
О
1,2,4,8,
16 -
возрастающая
прогрессия;
она
равна
нулю.
Графиком
функции
явля
1
ется
парабола,
ветви
которой
направле
б)
Ь
1
= 24, q =
'2
ны
вверх.
24, 12, 6, 3,
'2
3
-
убывающая
прогрес-
Свойства
функции
у
= x
2k
+ 1
(с
нечет
ным
положительным
показателем
степе
сия;
в)
Ь
1
= 2, q =
-3
ни),
где
k -
число
натуральное
2,
-6,
18,
-52,
156 -
прогрессия
не
яв
Например,
у
=
х
з
,
у
=
х
5
(рис.
2)
и
т.
д.
ляется
монотонной.
1.
Область
определения:
Х
Е
R
2.
Область
значений:
у
Е
R .
Свойства
геометрической
прогрессии
3.
Функция
нечетная,
так
как
1.
Каждый
член
геометрической
прогрес
сии,
начиная
со
второго,
равен
предыду
(-х)
2k+l
=
_x
2k
+
1
.
щему,
умноженному
на
знаменатель
про
грессии,
т. е.
I
График
функции
симметричен
относи
bk+l
=
bk
. q,
где
k = 1, 2,
...
(2)
тельно
начала
координат.
L
~
~-...J
11
10

г-----------T-----~----I
4.
Функция
возрастает
на
всей число-
I 2.
Квадрат
каждого
члена
геометричес
вой
оси.
В
самом
деле,
если
О
<
Хl
<
Х2'
кой
прогрессии
равен
произведению
двух
то
x
2k
+
1
< x
2k
+1 I
равноудаленных
от
него
членов
этой
про
1 2
грессии,
т.
е.
Если
Хl
<
Х2
<
О,
то
вновь
I
ь
2
-
Ь Ь
(3)
k -
k-m
k+m'
k
xr
+
1
<
x~k+l
<
О.
I
где
k
и
т
-
любые
натуральные
числа,
причем
k >
т.
у
Из
формулы
(2)
следует,
что
если
все
чле
ны
геометрической
прогрессии
положи
тельны,
то
можно
записать
Х
-1
Рис.
2
*
Графики
функций
у
=
х
n
для
n =
2k
и
n =
2k
+ 1
называются
параболами.
При
n = 2 -
это
просто
парабола,
при
n = 3 -
кубическая
парабола.
Свойства
функции
у
=
..Б
Рассмотрим
функцию
у
=
J;,
обратную
функции
у
=
х
2
(рис.
3).
у
1,.,/
,
/f'
,
........
~~
Сумма
члеиов
геометрической
А"
прогрессии
"
~~'
Сумма
n
членов
конечной
геометричес
О
Х
кой
прогрессии
ВN
=
~
+
~
+ ... +
ь
n
вы
числяется
по
формуле
Рис.
3
S _
~(1-qn)
1.
Область
определения
-
множество
n -
1-q
,
(4)
положительных
действительных
чисел,
Пример.
Определим
сумму
первых
деся
т. е.
[О;
+ 00).
ти
членов
геометрической
прогрессии,
у
2.
Область
значений
-
множество
поло
которой
Ь
1
= 5, q = 2.
жительных
действительных
чисел,
т. е.
Решение.
Используя
формулу
(4),
полу
[О;
+00).
чим
3.
Функция
монотонно
возрастает
от
О
5
(1-
210) =
5.1023
=
5115.
+00.
8:1.0
до
1-2
График
функции
у
=
J;
может
быть
получен
путем
зеркального
отображения
относительно
биссектрисы
координатно
го
угла
графика
у
=
х
2
,
соответствующего
участку
Х;:::
О.
L_~
~
~
12
г----~-----T-----
I 11.
Показательная
функция
12.
ЛогарИфмическая
I
u
функция,
Показательной
функцией называется
ее
график
и
своиства
функцuя
вида
у
=
аХ,
где
а
-
некоторое
I
Построение
графика
логарифмической
положительное
число,
не
равное
единице
I
функции
(основание
степени).
I
Рассмотрим
показательную
функцию
у
=
аХ
(где
а
>
О,
а"#
1 ).
Функция
у
=
аХ
Свойства
функции
у
=
аХ
при
а
> 1
является
монотонной
(возрастающей
при
1.
Область
определения
-
множество
R
а>
1
и
убывающей
при
О
<
а
<
1).
Моно
действительных
чисел.
тонная
функция
имеет
обратную
функ
2.
Область
значений
-
множество
поло
цию.
жительных
действительных
чисел,
т.
е.
Чтобы
найти
обратную
функцию,
нуж
(0;00).
но
из
формулы
у
=
аХ
выразить
Х
через
у:
3.
Функция
-
возрастающая.
Х
= 10ga
Y
'
а
затем
поменять
обозначения
Х
4.
При
х
=
О
значение
функции
равно
1.
на
У
и
У
на
Х,
тогда
получим
У
= logax,
5.
Если
х
>
О,
то
аХ
> 1;
Функция
У
= logax,
где
а
-
заданное
если
х
<
О,
то
О
<
аХ
< 1.
число,
а
>
1,
а"#
1,
называется
логарифми
ческой
функцией.
асимптоту
-
ось
абсцисс
(рис.
1).
Таким
образом,
показательная
и
лога
рифмическая
функции
при
одном
и
том
6.
График
функции
имеет
единственную
же
основании
являются
взаимно
обрат
ными
функциями.
График
логарифмической
функции
мож
но
построить,
используя
график
обрат
ной
ей
функции
У
=
аХ.
График
функции
У
= logax
будет
сим
О
х
метричен
графику
У
=
аХ
относительно
прямой
У
=
Х
при
условии,
что
основание
Рис.
логарифма
и
основание
степени
одинако
Свойства
функции
у
=
аХ
при
О
<
а
< 1
и
равны
вы
а.
1.
Область
определения
-
множество
В.
На
рис.
1
изображен
график
функции
2.
Область
значений
(О;
00)
.
у
= logax
при
а
> 1,
а
на
рис.
2 -
график
3.
Функция
-
убывающая.
функции
У
= logax
при
О
<
а
< 1.
4.
При
х
=
О
значение
функции
равно
1.
5.
Если
х
>
О,
то
О
<
У
< 1;
если
х
<
О,
то
У
> 1.
у+:;
а>
1
t
6.
График
функции
имеет
единственную
~/~
..
>'
асимптоту
-
ось
абсцисс
(рис.
2).
Ц~,/
\1
'"
\O~.,;
у
Х
,/10
у
=
а'
О<а<1
""
Рис.
1
Х
О
Рис.
О<а<1
Построение
графиков
Построим
графики
следующих
показа
тельных
функций:
/,//10
I~X
а)
У
=
2
Х
;
б)
У
=
-3'
2
Х
;
в)
у
=
21
x
l.
Oк.~
а)
У
=
2
Х
•
Так
как
а
> 1,
то
функция
-
возрастающая.
Рассчитав
значения
функ-
I
Рис.
2
ции
при
четырех
значениях
аргумента:
I
График
логарифмической
функции
рас
-1;
О;
1; 2,
получим
четыре
значения
функ-
положен
правее оси
Оу
и
проходит
через
ции
'
!.
l'
2'
4 I
точку
(1;
О).
.
2'
, , .
..1
L___________
_
~-~
13
г-----------T-----~----I
Свойства
логарифмической
функции
1.
Область
определения
-
множество
положительных
действительных
чисел,
т. е.
(О;
00)
.
2.
Область
значений
-
множество
R
всех
действительных
чисел.
3.
Монотонность:
Если
а>
1,
функция
является
возраста
ющей.
Если
О
<
а
< 1,
функция
является убы
вающей.
4.
Промежутки
знакопостоянства:
•
Если
а
> 1
(рис.
1),
то
при
О
<
х
< 1
функция
принимает
отри
цательные
значения:
у
<
О;
при
х
= 1
функция
равна
нулю;
при
х
> 1
функция
принимает
положи
тельные
значения:
у
>
О.
•
Если
О
<
а
< 1
(рис.
2),
то
при
О
<
х
< 1
функция
принимает
поло
жительные
значения:
у>
О;
при
х
= 1
функция
равна
нулю;
при
х
> 1
функция
принимает
отрица
тельные
значения:
у
<
О.
5.
Функция
непериодическая,
ни
чет
ная,
ни
нечетная.
6.
Единственной
асимптотой
графика
логарифмической
функции
является
ось
ординат.
I
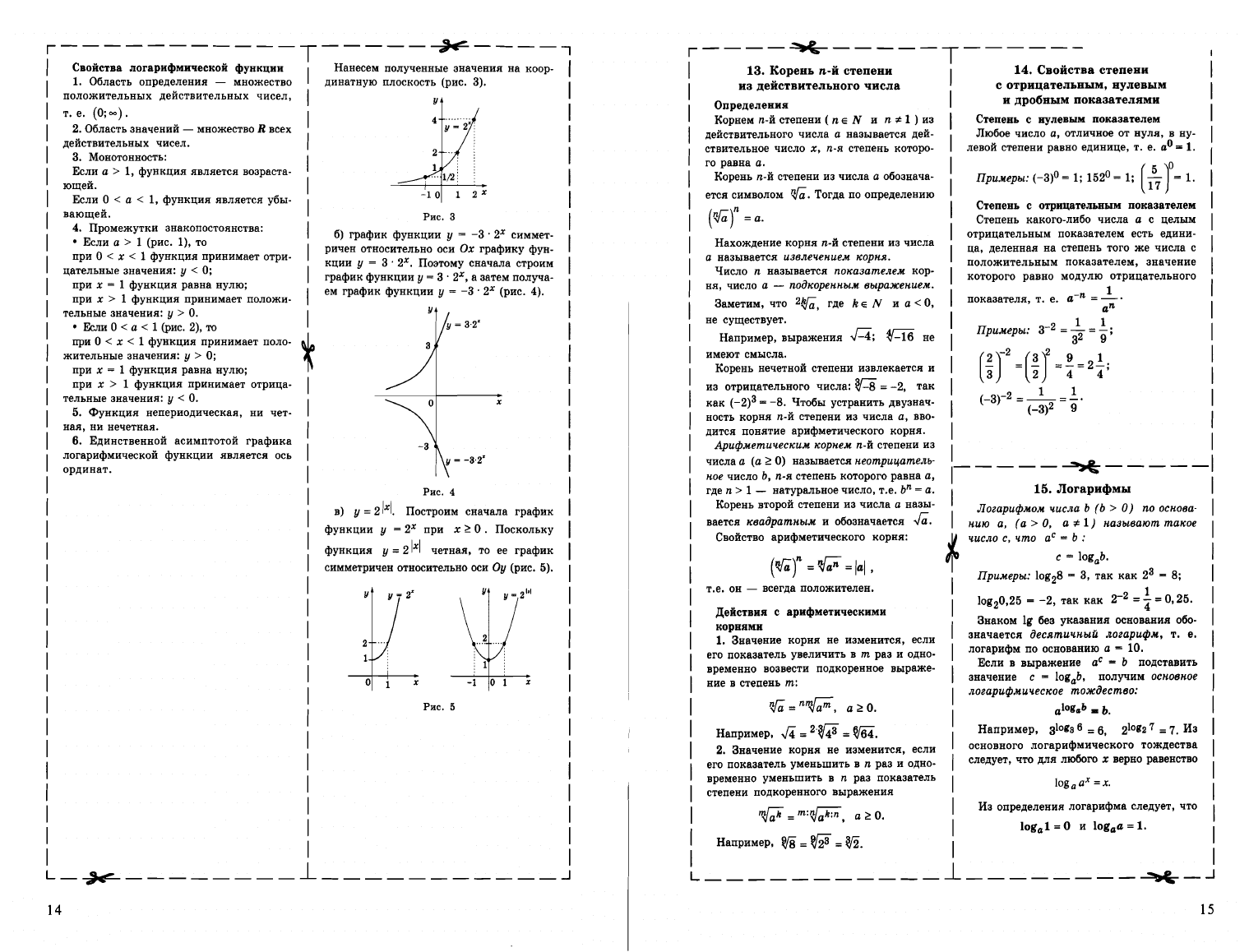
Нанесем
полученные
значения
на
коор
динатную
плоскость
(рис.
3).
I
у
-1
О
4,
у
=
2У:
2
х
Рис.
3
б)
график
функции
у
=
-3
.
2
Х
симмет
ричен
относительно
оси
Ох
графику
фун
кции
у
= 3 .
2
Х
•
Поэтому
сначала
строим
график
функции
у
= 3 .
2
Х
,
а
затем
получа
ем
график
функции
у
=
-3'
2
Х
(рис.
4).
*
у
х
Рис.
4
в)
У
=
21
x
l.
Построим
сначала
график
функции
у
=
2
Х
при
х
~
О.
Поскольку
функция
у
=
21
x
l
четная,
то
ее
график
симметричен
относительно
оси
Оу
(рис.
5).
о
х
-1
Рис.
5
L_~
~
~
г----~-----T-----
13.
Корень
n-й
степени
I 14.
Свойства
степени
из
действительного
числа
с
отрицательным,
нулевым
и
дробным
показателями
Определения
Корнем
n-й
степени
( n
Е
N
и
n *1 )
из
Степеиь
с
нулевым
показателем
действительного
числа
а
называется
дей
Любое
число
а,
отличное
от
нуля,
в
ну
а
О
ствительное
число
х,
n-я
степень
которо
левой
степени
равно
единице,
т.
е.
= 1.
го
равна
а.
Корень
n-й
степени
из
числа
а
обознача
Примеры:
(-з)0
= 1; 1520 = 1;
(157
J= 1.
ется
символом
'{jQ,.
Тогда
по
определению
Степень
с
отрицательным
показателем
('{jQ,)n
=
а.
Степень
какого-либо
числа
а
с
целым
отрицательным
показателем
есть
едини
Нахождение
корня
n-й
степени
из
числа
ца,
деленная
на
степень
того
же
числа
с
а
называется
извлечением
lCорня.
положительным
показателем,
значение
Число
n
называется
nОlCазателем
кор
которого
равно
модулю
отрицательного
ня,
число
а
-
nодlCоренным
выражением.
показателя,
т. е.
а-
n
=
-.!.....
Заметим,
что
2~,
где
k
Е
N
и
а
<
О,
а
n
не
существует.
Примеры:
з-2
=
J:...
=
!;
Например,
выражения
Н;
~
не
з2
9
имеют
смысла.
(
!)-2
=
(~J2
=
~
=
2!'
Корень
нечетной
степени
извлекается
и
3 2 4
4'
из
отрицательного
числа:
W::S
=
-2,
так
(_з)-2
=
_1_
=!.
как
(-2)3
=
-8.
Чтобы
устранить
двузнач
(-з)2
9
ность
корня
n-й
степени
из
числа
а,
вво
дится
понятие
арифметического
корня.
АрифметичеСlCим
lCорнем
n-й
степени
из
числа
а
(а
~
О)
называется
неотрицатель
I-----~----
ное
число
Ь,
n-я
степень
которого
равна
а,
где
n > 1 -
натуральное
число,
Т.е.
ь
n
=
а.
I 15.
Логарифмы
Корень
второй
степени
из
числа
а
назы
Логарифмом
числа
Ь
(Ь
>
О)
по
основа
вается
lCвадратным
и
обозначается
.Jii.
I
нию
а,
(а
>
О,
а
*
1)
называют
таlCое
Свойство
арифметического
корня:
(~)n
=~
=Ial,
Т.е.
он
-
всегда
положителен.
I
Действия
с
арифметическими
кориями
1.
Значение
корня
не
изменится,
если
I
I
его
показатель
увеличить
в
т
раз
и
одно
временно
возвести
подкоренное
выраже
I
ние
в
степень
т:
'{jQ,=n~,
а;::О.
I
I
Например,
J4
=
2·f43
=~.
2.
Значение
корня
не
изменится,
если
I
I
его
показатель
уменьшить
в
n
раз
и
одно
временно
уменыIитьъ
в
n
раз
показатель
I
степени
подкоренного
выражения
rr(;;k
=
m:~,
а;::
О.
I
I
Например,
~
=
~
=~.
I
L
~
число
с,
что
аС
=
_Ь
:
/{о с
- loga
b
.
Примеры:
log28 = 3,
так
как
23 = 8;
!og2
0
,25
=
-2,
так
как
2-2 =
~
=
0,25.
Знаком
19
без
указания
основания
обо
значается
десятичный
логарифм.,
т. е.
логарифм
по
основанию
а
= 10.
Если
в
выражение
аС
=
Ь
подставить
значение
с
= 10iab,
получим
основное
логарифм.ичеСlCое
тождество:
aloiab
•
Ь.
Например,
= 6, = 7.
Из
з
lоg
з
6 2
1og
2 7
основного
логарифмического
тождества
следует,
что
для
любого
х
верно
равенство
!oga
аХ
=х.
Из
определения
логарифма
следует,
что
loga1
=
о
и
logaa = 1.
I
~
~
~
14
15

г-----------T-----~----I
I
Степень
с
дробным
показателем
I 3.
Корень
из
произведения
нескольких
I
Степень
какого-либо
числа
а
с
дробным
сомножителей
равен
произведению
кор
J!..
DГ"::q
I
ней
той
же
степени
этих
сомножителей:
I
показателем
q
есть
корень
'Vа
Ч
,
где
чис
литель
р
является
показателем
корня,
а
I
~=~'!fbrry;;,
a~O;
b~O;
C~O.
I
знаменатель
q -
показателем
степени
под
р
Например,
I
коренного
выражения. Число
q -
раци
j;;4b3
= J:l
Jb3
= a
2
Jb2b
= a
2
bJb;
I
ональная
дробь.
Е~ли
РЕ
Z, q
Е
N,
то
J75
=
J25
.3 =
J25
.
J3
=
5JЗ.
I
по
определению
а
q =
if;;P.
Можно
выполнять
обратные
преобразо
вания
по
этому
свойству:
I
Примеры:
2 2
~'!fbrry;;=~.
I 273
1=
~
=
(т)
=
з2
=
9;
Например,
v;;2щ;'(;5
=~a2bc5;
I
(-8)3
=~
=-2.
I 1 3
м,J;;bЗ
=
Ja
4
b
4
=а
2
ь
2
.
Выражения
(-8)2
и
(-8)4
смысла
не
4.
Корень
из
частного
равен
частному
от
I
имеют.
деления
корня
из
делимого
на
корень
из
I
Степень
с
рациональным
показателем
делителя,
показатели
будут
одинаковые:
Степень
с
рациона~ьным
показателем
'"
I
обладает
теми
же
своиствами,
что
и
сте-
~
~=~:".!:/b,
a~O,
b~O.
I
пень
с
натуральным
показателем,
а
имен-
I
М
об
преоб
но:
если
а
>
О
и
n
Е
Q,
т
Е
Q,
то
ожно
выполня:ъ
ратные
разова
пия
по
этому
своиству:
I
а)
а
m
.
а
n
=
а
m
+
n
;
б)
а
m
:
а
n
=
а
m
-
n
;
I
I
в)
(amh
n
=
а
mn
;
г)
(аЬс)n
=
аnЬnс
n
;
I
~
J~
".!:/Ь
='~b'
I
д)
(~)
=
::
. I
-----х-----
~{27
_m =
~
=1,5.
Например,
VB
-
w8
2
При
меры
вычисления
логарифмов
Вычислить:
5.
Чтобы
возвести
корень
в
какую-либо
1
степень,
достаточно
возвести
в
эту
сте·
а)
lоgз
81;
б)
logO,5
32;
пень
подкоренное
выражение:
1
Y+21og!.
6
в)
3")
(
3
(~(
=~,
a~O.
Решение.
а)
Логарифм
-
это
показатель
Справедливо
и
обратное
преобразова
1
степени,
в
которую
нужно
возвести
осно
ние:
вание
3,
чтобы
получилось
число
81'
Обозначив
показатель
степени
через
х,
по-
~
=(~)n,
a~O.
лучим
3
Х
=
8\'
3
Х
=
з-4,
т. е.
х
=
-4.
Например,
1
Ответ:
lоgз
81 =
-4.
(~)2
=~c4d2
=~c3cd2
=cW;
б)
logO,5
32 =
х,
0,5
Х
= 32;
(~T
=
(~
Т5;
х
=
-5.
J27
=.J33
=
(J3)З
.
Ответ:
logO,5
32 =
-5.
[~Г2106i
6=
Ш[
~lo6i
6]'
в)
=.!..
62 =
36
= 4
9
9'
Ответ:
4.
L
__
~--
l..
...J
16
г----~-----T-----------I
16.
Решение
I
17.
Основные
свойства
квадратных
неравенств
логарифмов.
Формула
перехода
к
новому
основанию
пределения
О
I
Квадратным
неравенством
называет-
I
Свойства
логарифмов
ся
неравенство
вида
ах
2
+
Ьх
+
с
>
О,
где
1.
Логарифмы
существуют
только
для
а,
Ь,
с
-
действительные
числа,
а
*
О.
I
положительных
чисел,
т.
е.
loga
N
(где
(Вместо
знака
>
может
стоять
любой
I
а
>
О
и а
*1)
существует,
если
N >
О.
из
знаков
~;
::;;
<.)
I 2.
При
основании
а
> 1
логарифмы
чи
Решить
неравенство,
содержащее
неиз- сел
N > 1
положительны,
а
логарифмы
вестную
переменную,
-
значит
найти
мно-
I
чисел о
< N < 1
отрицательны.
Например,
жество значений
переменной,
при
кото-
1
рых
это
неравенство
является
верным.
Эле-
I
lоgз
7 >
О,
lоgЗ"2
<
О.
менты
этого
множества
называются
I 3.
При
основании
О
<
а
< 1
логарифмы
решениями
неравенства.
чисел
N > 1
отрицательны,
а
логарифмы
чисел
О
< N < 1
положительны.
Неполные
квадратные
неравенства
1.
Если
с
=
О,
а
>
О,
то
неравенство
име
Например,
log!
6 <
о,
log!
4'
1
>
О.
ет
вид
ах
2
+
Ьх
>
О,
ах
(
х
+
~
) >
О.
3 2
4.
Равным
положительным
числам
со
Ь
Неравенство
имеет
два корня:
О;
-
~.
ответствуют
и
равные
логарифмы,
т.
е.
Таким
образом,
неравенство
решаем
ме
если
N
1
= N
2
,
то
loga N
1
=
loga
N2'
тодом
интервалов,
раскладывая
левую
5.
Если
а
> 1,
то
большему
числу
со
часть
неравенства
на
сомножители.
ответствует
и
больший
логарифм,
т.
е.
Ответом
будут
два
промежутка:
если
N
1
> N
2
,
то
loga
Nl
>
loga
N2'
(_oo;_~)
И
(0;+00).
Например,
log29
> log2 5.
6.
Если
О
<
а
< 1,
то
большему
числу
2.
Если
Ь
=
с
=
О,
а
>
О,
то
неравенство
соответствует
меньший
логарифм,
т. е.
ах
2
>
О
имеет
множество
решений:
все
действительные
числа,
кроме
нуля.
если
N
1
> N
2
,
то
loga
N
1
< loga N
2
•
Решение
неравенства
ах
2
+
Ьх
+
с
>
О
Например,
10g1 9 < 10g1 5.
В
зависимости
от
знака
дискриминанта
3 3
D =
ь
2
-
4ас
могут
иметь
место
три
случая:
7.
Логарифм
единицы
по
любому
осно
1.
Если
D <
О,
то
график
квадратного
t
ванию
(а
>
О,
а
*1 )
равен
нулю,
т.
е.
уравнения
у
=
ах
2
+
Ьх
+
с
не
пересекает
loga
1 =
О.
оси
Ох
и
лежит
выше
этой оси
при
а
>
О
и
8.
Логарифм
самого
основания
равен
1,
ниже
ее
при
а
<
О.
т. е.
logaa=l.
В
первом
случае
множество
решений
неравенства
есть
вся
числовая
прямая
Формула
перехода
от
одного
основания
(рис.
1),
а
во
втором
оно
является
пустым
логарифмов
к
новому
основанию
(рис.
2).
Пусть
существует
logab,
т.
е.
а
>
О,
а
*1
у
у
и
Ь
>
О.
Тогда
для
любого
числа
с,
такого,
что
О
х
а>О
с
>
О,
с
*
1,
существуют
logc
Ь
и
logc
а
а<О
и
верно
равенство
10
Ь
= logc
b
.
(1)
ga
logc
a
О
х
Примеры.
Рис.
1
Рис.
2
1
Вычислить:
а)
log!
32;
б)
lоg,JЗ
81'
2.
Если
D >
О,
то
график
квадратного
4 1
уравнения
пересекает
ось
Ох
в
точках
хl
и
Х2
(хl
<
Х2)'
которые
являются
корнями
I
Решение.
а)
Основание
логарифма
"4'
уравнения
ах
2
+
Ьх
+
с
=
О.
число
32.
Эти
числа
кратны
2,
поэтому
L
~
~-...J
17

г-----------T-----~----,
г----~-----------------,
I
удобно
перевести
логарифм
к
основанию
2
1
Ь
32 2
I
по
формуле
(1)
,
где
а
= -4; =
и
с
= .
I
log
32
5
I
Получим
10g.!
32
=
--2-1-
=
-2
=
-2,5,
I
4
10g
2
4"
т.
к.
2
5 =
32'
,
2-2
=.!.
.
4
Ответ:
-2,5.
1 3
б)
П
ере
ведем
1
og.j3
81
к
основанию
,
получим
1 1
1 _
lоg
з
81 =
(-4)
:
2"
=
-8.
log.j3 81 -
lоg
J3
з
Ответ:
-8.
Отметим
простые
следствия
формулы
перехода:
1 .
log
a
Ь
= log
а
'
b
log
a
Ь.
log
ak
Ь
=
-k-
,
log
1
Ь
=
-log
a
Ь
, (k =
-1).
а
--~---
I
Эти
точки
раЗбива~т
чис~овую
пря.мую
I
I
на
три
промежутка.
(-
00,
хl),
(Хl'Х2)'
I
(Х2;
+ 00). I
1·
Если
а
>
О,
то
решением
неравенства
I
будут
два
промежутка,
где
квадратный
I
трехчлен
положителен:
(-ОО;Хl)
и
I
I
(Х2;
+ 00)
(рис.
3); I
I •
Если
а
<
О,
то
решением
неравенства
будет
промежуток
(хl;
Х2)'
где
квадрат-
I
I
I
ный
трехчлен
положителен
(рис.
4). I
I
О
I
I
'
а
<
О
%, i
%,
%
m
*
Рис.
3
Рис.
4
3.
Если
D =
О,
то
график
квадратного
уравнения
касается
оси
Ох
в
точке
Хl'
I
являющейся
единственным
корнем
I
Ь
хl
= -
2а
уравнения
ах
2
+
Ьх
+
с
=
О.
I
Точка
хl
разбивает
числовую
прямую
на
I
два
промежутка:
(-ОО;Хl)
и
(Хl;+ОО),
I
•
Если
а
>
О,
то
решением
неравенства
I
будут
два
промежутка:
(-00;
хl)
и
(хl;
+00).
Так
как
неравенство
строгое,
то хl
исключается
из
решений
неравен
ства
(рис.
5).
•
Если
а
<
О,
то
неравенство
ах2
+
Ьх
+
с
>
О
не
имеет
решений
(рис.
6).
Рис.
а<О
l..
Рис.
6
-------
..J
18.
Свойства
функций
Монотонные
функции
Функция
{(х)
называется
возрастаю
щей
на
данном
числовом
промежутке
Х,
если
большему
значению
аргумента
х
Е
Х
соответствует
большее
значе
ние
функции
{(
х),
т.
е.
для
любых
хl
и
Х2
из
промежутка
Х,
таких, что
Х2
>
Хl'
выполняется
неравенство
{(Х2)
>
{(Хl)'
Функция
{(
х)
называется
убывающей
на
данном
числовом
промежутке
Х,
если
большему
значению
аргумента
х
Е
Х
соответствует
меньшее
значение функ·
ции
{(х),
т.
е.
для
любых
Хl
и
Х2 из
проме
жутка,
таких,
что
Х2
>
Хl'
выполняется
неравенство
{(Х2)
<
{(Хl)'
Функция
только
возрастающая
или
только
убывающая
на
данном
проме
жутке
называется
мокотоккой
на
этом
промежутке.
О
монотонности
функции
можно
судить
по
ее
графику.
Например,
функция,
гра
фик
которой
изображен
на
рис.
1,
возра
стает
при
всех
значениях
х.
Функция,
гра
фик
которой
изображен
на
рис.
2,
убывает
на
промежутке
(-00;
О]
и
возрастает
на
промежутке
[О;
+ 00).
+.*
Рис.
1
Рис.
2
Четиые
инечетные
функцин
Функция
у
=
{(
х)
называется
четкой,
если
для
любого
х
из
области
определения
функции
выполняется
равенство
f(
-х)
=
=
{(
х).
Примеры
четных
функций:
у
=
х
2
,
У
=
х
4
,
У
=
Ixl
'
у
=
сов
х.
Для
этих
функций
выполняется
усло
вие:
(-х)2
=
х
2
,
(-х)4
=
х
4
;
I-xj
=
Ixl;
сов
(-х)
=
сов
х.
Графики
четных
функций
симметрич
ны
относительно
оси
Оу
(рис.
3).
\1"/
+
L
Рис.
З
_
Функция
у
= {(
х)
называется
кечеm
кой,
если
для
любого
х
из
06ласти
опреде
ления
функции
выполняется
равенство
{(-х)
=
-f(x).
При
меры
нечетных
функций:
у
=
х
З
,
у
= sin
х,
у
=
tg
х,
У
=
ctg
х.
Для
этих
функций
выполняется
условие:
(-х)з
=
-х
З
,
sin
(-х)
=
-sin
х,
tg
(-х)
=
=
-tg
х,
ctg
(-х)
=
-ctg
х.
График
нечетной
функции
симметричен
относительно
начала
координат
(рис.
4).
'!;-q,
tr
Рис.
4
Заметим,
что
не
всякая
функция
явля
ется
четной
или
нечетной.
Например,
каж
дая
из
функций
у
=
12х
+ 1,
у
=
х
4
+
х,
У
=
(х
+
з)2
не
является
ни
четной,
ни
нечетной.
I-----~----
19.
Бесконечно
убывающая
I
геометрическая
прогрессия
I
Геометрическая
прогрессия
Сl' С2'
...,
Сп'
...,
знаменатель
которой
Iql
< 1
и
сl
*
О
,
на
~
зывается
бесконечно
убывающей
геомет
рической
nрогрессиеЙ.
Сумма
членов
бесконечно
убывающей
геометрической
прогрессии
вычисляется
по
формуле
8=~.
(1)
1-q
Пример
1.
Найдем
сумму
бесконечно
убывающей
геометрической
прогрессии
2 2 2
2,
3'
9'
27""
Решение.
В
данной
геометрической
про
1
грессии
q = 3.
Используя
формулу
(1),
получим
2
8=--1
=3.
1--
3
..l.
~
_..J
18
19
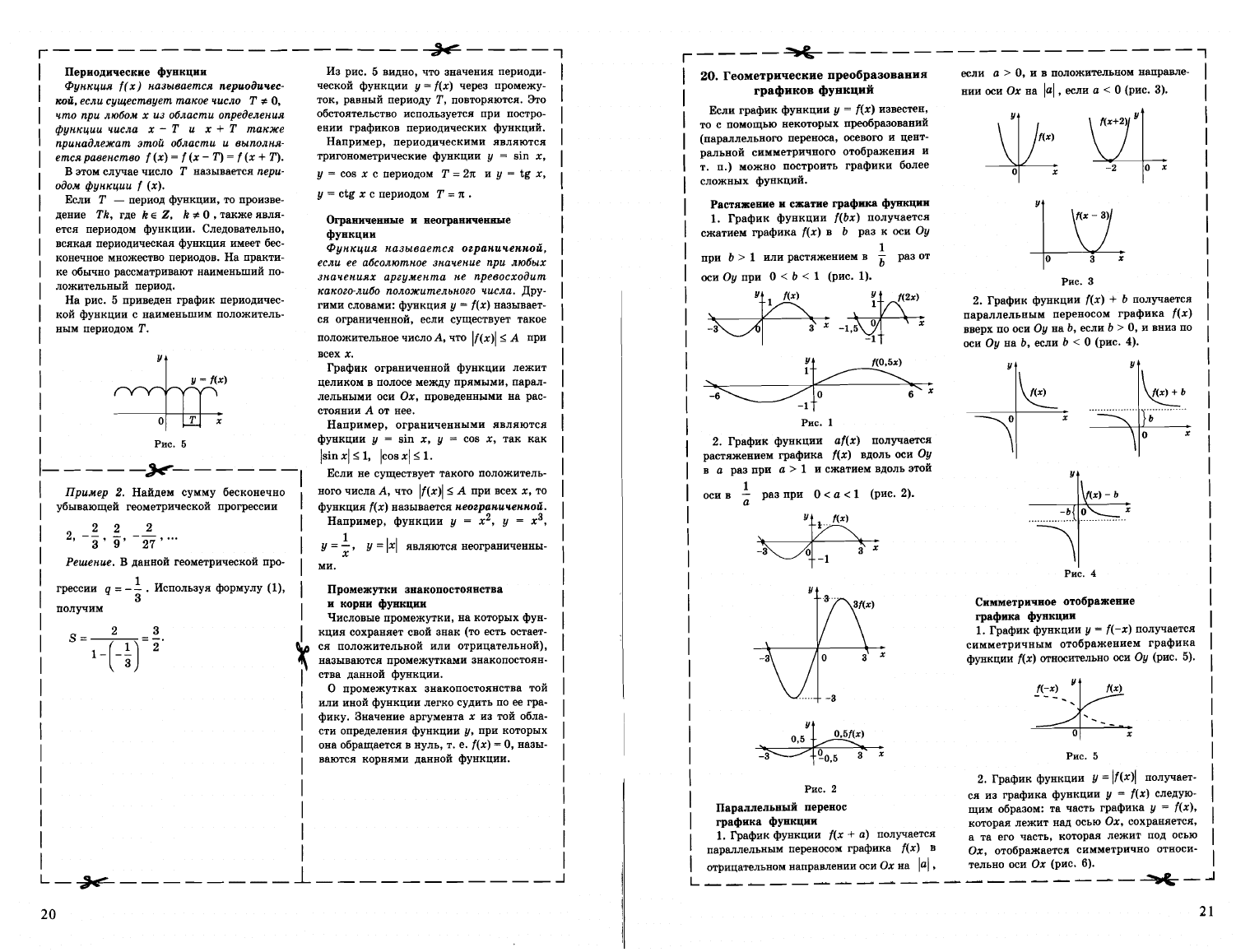
--
г-----------------~----I
г----~-----------------I
Периодические
функции
Из
рис.
5
видно, что
значения
периоди
если
а
>
О,
и
в
положительном
направле
20.
Геометрические преобразования
Фунжция
f(
х)
называется
nерuодUч'ес
ческой
функции
у
=
f(x)
через
промежу
графиков
функций
нии
оси
Ох
на
lal,
если
а
<
О
(рис.
3).
мй,
если
существует
такое
число
Т
1:-
О,
ток,
равный
периоду
Т,
повторяются.
Это
Если
график
функции
у
=
f{x)
известен,
что
при
любом
х
из
области
определения
обстоятельство
используется
при
постро
-2
О Х
то
с
помощью
некоторых
преобразований
\
Уl
функции
числа
х
-
Т
и
х
+
Т
также
ении
графиков
периодических
функций.
jf(X)
(параллельного
переноса,
осевого
и
цент
Например,
периодическими являются
принадлежат
этой
области
и
выполня
ральной
симметричного
отображения
и
---f-;
ется
равенство
f
(х)
= f
(х
-
Т)
= f
(х
+
Т).
тригонометрические
функции
у
= sin
х,
В
этом
случае
число
Т
называется
пери
у
=
cos
х
с
периодом
Т
=
2л
И
У
= tg
х,
т.
п.)
можно
построить
графики
более
сложных
функций.
I
I
I
I
I
I
I
I
I
I
I
I
I
I
I
I
I
1
одом
функции
f
(х).
у
= ctg
х
с
периодом
Т
= 1t •
Если
Т
-
период
функции,
то
произве
Растяжение
и
сжатие
графика
функции
у
дение
Tk,
где
k
Е
Z, k
1:-
О
,
также
явля
3)
(Х
-
1.
График
функции
f(bx)
получается
Ограниченные
инеограниченвые
ется
периодом
функции.
Следовательно,
сжатием
графика
f(x)
в
Ь
раз
к
оси
Оу
1
при
Ь
> 1
или
растяжением
в
Ь
раз
от
О
Х
функции
всякая
периодическая
функция
имеет
бес
Функция
называется
ОtраКUч'еккой,
конечное
множество
периодов.
На
практи
ке
обычно
рассматривают
наименьший
по
если
ее
абсолютное
значение
при
любых
оси
Оу
при
0<
Ь
< 1
(рис.
1).
значениях
аргумента
не
nревосходит
Рис.
3
ложительный
период.
какого-либо
положительного
числа.
Дру
На
рис.
5
приведен
график
периодичес
гими
словами:
функция
у
=
f(x)
называет
2.
График
функции
f(x)
+
Ь
получается
~
параллельным
переносом
графика
f(x)
~X-l~
оси
Оу
на
Ь,
если
Ь
<
о
(рис.
4).
i
-1
кой
функции
с
наименьшим
положитель
ным
периодом
Т.
ся
ограниченной,
если
существует
такое
~
вверх
по
оси
Оу
на
Ь,
если
Ь
>
О,
и
вниз
по
положительное
число
А, что
If(x)l:5:
А
при
всех
х.
i
r
~'();'X
-1
~x)
у
График
ограниченной
функции
лежит
целиком
в
полосе
между
прямыми,
парал
~
~
лельными
оси
Ох,
проведенными
на
рас
стоянии
А
от
нее.
~
\
Х
Рис.
1
Например,
ограниченными
являются
Х
О
функции
у
= sin
х,
у
=
cos
х,
так
как
2.
График
функции
af(x)
получается
Рис.
5
растяжением
графика
f(x)
вдоль
оси
Оу
Isin
xl
:5:
1,
ICOB
хl
:5:
1.
в
а раз
при
а
> 1
и
сжатием
вдоль
этой
у
-----~------I
Если
не
существует
такого
положитель
I
I
I
I
I
I
1
ного
числа
А,
что
If(x)l:5:
А
при
всех
х,
то
оси
в
а
раз
при
О
<
а
< 1
(рис.
2).
При
мер
2.
Найдем
сумму
бесконечно
'(Х)
-
ь
убывающей
геометрической
прогрессии
функция
f(x)
называется
кеоzраНUч'еккоЙ.
-ь~
10
Х
Например,
функции
у
=
х
2
,
У
=
х
3
,
2 2 2
2,
-3'
9'
\
1
-
27'
...
у
=
Ixl
являются
неограниченны
у
=
-,
-3
х
Решение.
в
данной
геометрической
про
грессии
q = _! .
Используя
формулу
(1),
3
получим
ми.
Рис.
4
Симметричное
отображение
и
корни
функции
Промежутки
знакопостоянства
графика
функции
Числовые
промежутки,
на
которых
фун
1.
График
функции
у
f(-x)
получается
кция
сохраняет
свой
знак
(то
есть
остает
s=~(
ся
положительной
или
отрицательной),
1-
1)=~'
=
симметричным
отображением
графика
*
Х
функции
f(x)
относительно
оси
Оу
(рис.
5).
называются
промежутками
знакопостоян
I
I
I
I
I
I
I
3
ства
данной
функции.
О
промежутках
знакопостоянства
той
или
иной
функции
легко
судить
по
ее
гра
фику.
Значение
аргумента
х
из
той
обла
сти
определения
функции
у,
при
которых
она
обращается
в
нуль,
т. е.
f(x)
=
О,
назы
ваются
корнями
данной
функции.
у
Х
Х
Рис.
5
2.
График
функции
У
=
lf(x)1
получает
Рис.
2
ся
из
графика
функции
у
=
f(x)
следую
Параллельиый
переное
щим
образом:
та
часть
графика
у
=
f(x),
графика
функции
которая
лежит
над
оеью
Ох,
сохраняется,
1.
График
функции
f(x
+
а)
получается
а
та
его
часть,
которая
лежит
под
осью
параллельныМ
переноеом
графика
f(x)
в
Ох,
отображаете"
симметрично
относи
I
отрицательном
направлении
оси
Ох
на
lal,
тельно
оси
Ох
(рис.
6).
I
I
I
I
L_~--------~-----------~
L
__
~
__
~~_~--_--
-~-~_~
20
21
