Филатов О.А. Шпаргалки по алгебре и геометрии
Подождите немного. Документ загружается.

г-----------T-----~----I
I
Окружностью
называется
множество
I
всех
точек
плоскости,
находящихся
на
заданном
расстоянии
от
некоторой
точки
I
плоскости,
называемой
центром
окруж
I
I
ности.
Радиусом
окружности
называется
отре
зок,
соединяющий
центр
окружности
с
I
любой
ее
точкой.
Отрезок,
соединяющий
две
точки
ок
I
ружности,
называется
хордой.
Хорда,
проходящая
через
центр
окруж
ности,
называется
диаметром.
Диаметр
равен
удвоенному
радиусу
окружности.
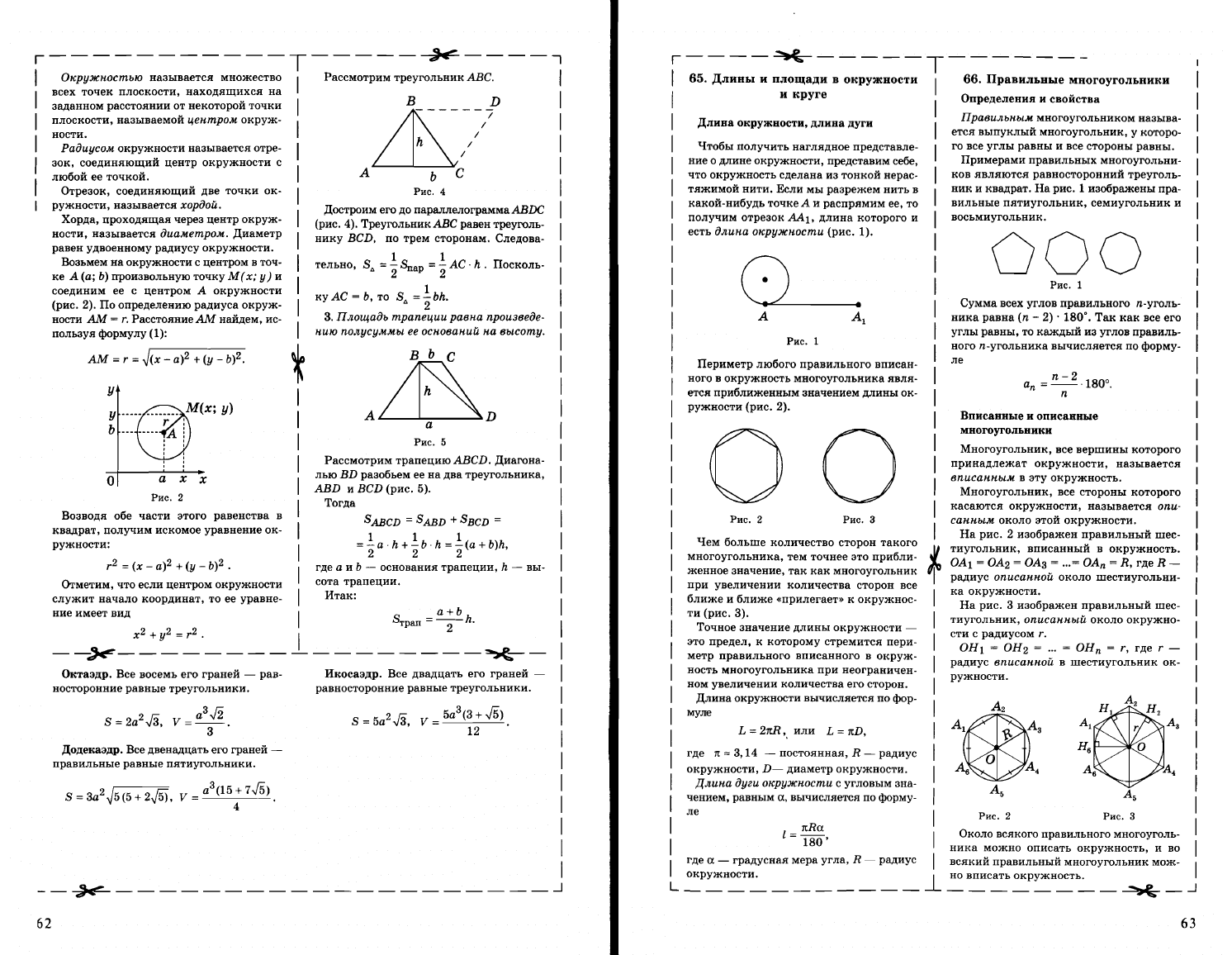
Возьмем
на
окружности
с
центром
в
точ
ке
А(а;
Ь)
произвольную
точку
М(х;
у)
и
соединим
ее
с
центром
А
окружности
(рис.
2).
По
определению
радиуса
окруж
ности
АМ
= r.
РасстояниеАМ
найдем,
ис
пользуя
формулу
(1):
АМ
=r =
~(x
-
а)2
+
(у
-
ь)2.
Y~
~M(X;
у)
ь---~
о а
Х Х
Рис.
2
Возводя
обе
части
этого
равенства
в
квадрат,
получим
искомое
уравнение
ок
ружности:
r
2
=
(х
-
а)2
+
(у
-
ь)2
.
Orметим,
что
если
центром
окружности
служит
начало
координат,
то
ее
уравне
ние
имеет
вид
х2
+
у2
=
r2
.
I
Рассмотрим
треугольник
АВС.
в
A&~'/
ь
с
Рис.
4
Достроим
его
до
параллелограмма
AВDC
(рис.
4).
Треугольник
АВС
равен
треуголь
нику
BCD.
по трем
сторонам.
Следов
а
1 1
тельно,
5" = 2
Sпар
= 2
АС·
h.
Посколь
ку
АС
=
Ь,
то
5" = 2
1
bh.
3.
Площадь
трапеции
равна
про
из
веде
нию
полусуммы
ее
оснований
на
высоту.
*
A~D
а
Рис.
Рассмотрим
трапецию
AВCD.
Диагона
лью
BD
разобьем
ее
на
два
треугольника,
AВD
и
BCD
(рис.
5).
Тогда
SAВCD
=
SAВD
+
SBCD
=
=
!
а
. h +!
ь
.h = !
(а
+ b)h
2 2 2 '
где
а
и
Ь
-
основания
трапеции,
h -
вы
сота
трапеции.
Итак:
STpan
=
а+Ь
h
2 .
--~--------~--------~
Октаэдр.
Все
восемь
его
граней
-
рав
Икосаэдр. Все двадцать
его
граней
-
носторонние
равные
треугольники.
равносторонние
равные
треугольники.
3
5а
3
(3
+
-Jб)
S=2a2J3,
v=a
.J2.
S =
5а
2
JЗ,
V
3
12
Додекаэдр.
Все
двенадцать
его
граней
-
правильные
равные
пятиугольники.
S=3a2~5(5+2J5),
v=a
3
(15+7.J5)
4
--~--------------------~
г----~-----T------
65.
Длины
и
площади
в
окружности
I
66.
Прав
ильные
многоугольники
и
круге
Определения
и
свойства
Длина
окружности,
длина
дуги
Правильны.м.
многоугольником
называ
ется
выпуклый
многоугольник,
у
которо
Чтобы
получить
наглядное
представле
го
все
углы
равны
и
все
стороны
равны.
ние
о
длине
окружности,
представим
себе,
что
окружность
сделана
из
тонкой
нерас
тяжимой
нити.
Если
мы
разрежем
нить
в
какой-нибудь
точке
А
и
распрямим
ее,
то
получим
отрезок
ААl,
длина
которого
и
есть
длина
окружности
(рис.
1).
О.
А
А
1
Рис.
1
Периметр
любого
правильного
вписан
ного
в
окружность
многоугольника
явля
ется
приближенным
значением
длины
ок
ружности
(рис.
2).
00
Рис.
2
Рис.
3
Чем
больше
количество
сторон
такого
многоугольника, тем
точнее
это
прибли
женное
значение,
так
как
многоугольник
при
увеличении
количества
сторон
все
ближе
и
ближе
«прилегает»
К
окружнос
ти
(рис.
3).
Точное
значение
длины
окружности
-
это
предел,
к
которому
стремится
пери
метр
правильного
вписанного
в
окруж
ность
многоугольника
при
неограничен
ном
увеличении
количества
его
сторон.
Длина
окружности
вычисляется
по
фор
муле
L =2rtR
'.
или
L =
1tD,
где
1t
'"
3,14
-
постоянная,
R -
радиус
окружности,
D-
диаметр
окружности.
Длина
дуги
окружности
с
угловым
зна
чением,
равным
а,
вычисляется
по
форму
ле
1tRa
l =
180'
где
а
-
градусная
мера
угла,
R -
радиус
окружности.
L___________
При
мерами
правильных
многоугольни
ков
являются
равносторонний
треуголь
ник
и
квадрат.
На
рис.
1
изображены
пра
вильные
пятиугольник,
семиугольник
и
восьмиугольник.
000
Рис.
1
Сумма
всех
углов
правильного
n-уголь
ника
равна
(n
- 2) .
180·.
Так
как
все
его
углы
равны,
то
каждый
из
углов
правиль
ного
n-угольника
вычисляется
по
форму
ле
n-2
а
n
=
--
.1800.
n
Вписаниые
и
описанные
многоугольники
Многоугольник,
все
вершины
которого
принадлежат
окружности,
называется
вписанным
в
эту
окружность.
Многоугольник,
все
стороны
которого
касаются
окружности,
называется
оnи·
~
санным
около
этой
окружности.
На
рис.
2
изображен
правильный
шес
тиугольник,
вписанный
в
окружность.
ОАl
=
ОА2
=
ОАз
= ...=
ОА
n
=
R,
где
R -
радиус
описанной
около
шестиугольни
ка
окружности.
На
рис.
3
изображен
правильный
шес
тиугольник,
описанный
около
окружно
сти
с
радиусом
r.
ОН
1 =
ОН
2 =
...
=
ОН
n = r,
где
r -
радиус
вписанной
в
шестиугольник
ок
ружности.
А
2
!A2H2
А!
r:
Аз
А~Аз
Н
6
О
А
6
1A
4
Aв~4
~
А
5
А
5
Рис.
2
Рис.
3
Около
всякого
правильного
многоуголь
ника
можно
описать
окружность,
и
во
I
всякий
правильный
многоугольник
мож
..l
но вписать
окружность.
_
~-~
63
62

г-----------T-----~------,
Центр
вписанной
вправильный
много-
I
Площадь
круга,
сектора,
сегмента
угольник
.?кружности
совпадает
с
центром
Площадь
круга
с
радиусом
R
вычисля
описаннои
около
правильного
многоуголь-
I
ется
по
формуле
ника
окружности;
эта
точка называется
I
2
центром
правильного
многоугольника.
На
S =
rtR
.
рис.
2
и
3
точка
О
-
центр
правильного
I
Круговым
сектором
называется
часть
шестиугольника.
Orpeзок
перпендикуляра,
проведеиного
из
центра
правильного
много
угольника
к
его
стороне,
называется
апо
фемой
правильного
многоугольника.
На
рис.
3
ОН1, ОН2,
...
ОН6-
апофемы
правильного
шестиугольника.
Вычисление
радиусов
вписанной
и
описанной
окружностей
В
правильном
n-угольнике
со
стороной
а
радиус
R
описанной
окружности
и
ра
диус
r
вписанной
окружности
вычисля
ются
по
формулам
а
r=
а
R =
1800'
2tg
1800 .
28in
-n
n
Используя
эти
формулы,
получим
следу
ющие
выражения.
Для
правильного
равностороннего
треу
гольника
со
стороной
а:
а а
R =
JЗ'
r =
2JЗ
.
Для
правильного
четырехугольника
(квадрата)
со
стороной
а:
а а
R=
J2'
r=2'
Для
правильного
шестиугольника
со
стороной
а:
аJЗ
R=a,
r=-2-'
ПЛощадь
правильиого
многоугольника
I
Площадь
правильного
n-угольника
рав
I
на
половине
произведения
его
периметра
на
радиус
вписанной
в
него
окружности:
I
1
S =2"Pr.
I
I
Площадь
правильного
n-угольника
мож
но
вычислить
и
через
радиус
R
описанной
I
около
него
окружности:
I
S =
.!.
R2
81'
3600
2
n
n--
n
I
I
I
I
L_~
64
круга,
лежащая
внутри
соответствующе
I
го
центрального
угла
(рис.
4).
(1)
Рис.
4
Площадь
кругового
сектора
вычисляет
ся
по
формуле
2
S = rtR
360
а,
где
а
-
градусная
мера
угла,
R -
радиус
*
круга.
Круговым
сегментом
называется
общая
часть
круга
и
полуплоскости,
граница
которой
содержит
хорду
этого
круга
(рис.
5
и
6).
®е
Рис.
5
Рис.
6
Площадь
кругового
сегмента,
не
равно
го
полукругу,
вычисляется
по
формуле
S=
1tR2
360
a±SA'
где
а
- градусная
мера
центрального
угла,
который
содержит
дугу
этого
кру
гового
сегмента,
а
SA
-
площадь
треу
гольника
с
вершинами
в
центре круга и
концах
радиусов,
ограничивающих
соот
ветствующий
круговой
сектор.
Знак
• -,)
надо
брать,
когда
а
<
180·
(рис.
5),
а
знак
•+» -
когда
а>
180·
(рис.
6).
~
~
г----~-----T--------------,
67.
Параллельиость
плоскостей
I
68.
Параллельиость
По
аксиоме
стереометрии
мы
знаем,
что
если
две
плоскости
имеют
общую
точку,
то
они
пересекаются
по
прямой.
Отсюда
следует,
что
две
плоскости
либо
пересека
ются
по
прямой
(рис.
1),
либо
не
пересека
ются,
т.
е.
не
имеют
ни
одной
общей
точ
ки
(рис.
2).
е
Рис.
1
Рис.
2
Определение.
Две
плоскости
называ
ются
nараллельными,
если
они
не
nере
секаются.
Представление
о
параллельных
плоско
стях
дают
пол
и
потолок
комнаты,
поверх
ность стола
и
плоскость
пола.
Параллельность
плоскостей
а
и
~
обо
значается
так:
all~.
Рассмотрим
признак
параллельности
двух
плоскостей.
Теорема.
Если
две
nересекающиеся
пря
мые
одной
плоскости
соответственно
параллельны
двум
прямым
другой
плос
кости,
то
эти
плоскости
параллельны.
~
Рис.
3
Доказательство.
Рассмотрим
две
плос
кости
а
и
~
(рис.
3).
В
плоскости
а
ле
жат
пересекающиеся
в
точке
М
прямые
а
и
Ь.
в
плоскости
~
-
прямые
а1
и
Ь1.
причем
q
11
щ
и
Ь
11
Ь:1.
Докажем,
что
all~
.
Прежде
всего
отметим,
что
по
признаку
параллельности
прямой
и
плоскости
alla
и
bll~.
Допустим,
что
плоскости
а
и
~
не
па
раллельны.
Тогда
они
пересекаются
по
не
которой
прямой
с.
Мы
получили,
что
плос
кость
а
проходит
через
прямую
а,
парал
лельную
плоскости
~,
и
пересекает
плоскость
~
по
прямой
с.
Теперь
восполь
зуемся
следующим
свойством:
если
nлос
прямой
и
плоскости
Плоскость
и
прямая,
не
при
надлежа
щая
этой
плоскости,
называются
nарал
лельными,
если
они
не
имеют
ни
одной
общей
точки.
Теорема.
Если
прямая,
не
лежащая
в
данной
плоскости,
параллельна
какой
нибудь
прямой,
лежащей
в
этой
плоско
сти,
то
она
nараллельnа
данной
плоско
сти.
Доказательство.
Для
доказательства
воспользуемся
леммой:
если
одна
из
двух
параллельных
прямых
пересекает
плос
кость, то
и
другая
прямая
тоже
пересека
ет
эту
плоскость.
Рассмотрим
плоскость
а
и
две
парал
лельные
прямые
с
и
Ь,
расположенные
так,
что
прямая
Ь
лежит
в
плоскости
а,
а
пря
мая
с
не
лежит
в
этой
плоскости
(см.
ри
сунок).
с
L
ь/
-----~
69.
Теорема
о
трех
перпеидикулярах
Прямая.
nроведенная
в
плоскости
че
рез
основание
наклонной
nерnендикуляр
но к
ее
nроекции
на
эту
плоскость,
nерnендикулярна
и
к
самой
наклонной.
I
I
Доказательство.
Обратимся
к
рисунку,
на
котором
отрезок
АН
-
перпендикуляр
к
плоскости
а,
АМ
-
наклонная,
а
-
пря
I
мая,
проведенная
в
плоскости
а
через
точ
I
ку
М
перпендикулярно
к
проекции
НМ
I
I
наклонной.
Докажем,
что
а
l..AМ.
Рассмотрим
плоскость
АМН.
Прямая
а
перпендикулярна
к
этой
плоскости,
так
I
как
она
перпендикулярна
к
двум
пересе
кающимся
прямым
АН
и
МН
(al..НM
по
L~~~ОХОд~~е~нну~ямую.~условиюиа~.так~АН~сю-~
65

г-----------T-----~----I
Докажем,
что
clla.
nараллельную
другой
плоскости,
и
nере
Допустим,
что
это
не
так.
Тогда
прямая
секает
эту
плоскость,
то
линия
nересе
с
пересекает
плоскость
а,
а
из
леммы
о
чения
плоскостей
параллельна
данной
пересечении
плоскости
параллельными
прямой.
прямыми
следует,
что
прямая
Ь
также
пе-
Отсюда
следует,
что
allc.
ресекает
плоскость
а.
Но
это
невозможно,
Но
плоскость
а
проходит
также
через
поскольку
прямая
Ь
лежит
в
плоскости
а.
прямую
Ь,
параллельную
плоскости
р.
По
Итак,
прямая
с
не
пересекает
плоскость
этому
bllc.
Таким
образом,
через
точку
М
а,
поэтому
она
параллельна
этой
плоско-
проходят
две
прямые
а
и
Ь,
параллельные
сти.
Теорема
доказана.
прямой
с.
Но
это
невозможно,
так
как
по
Приведем
еще
две
теоремы:
теореме
о
параллельных
прямых
через
точ
1.
Если
плоскость
nроведена
через
nря-
ку
М
проходит
только
одна
прямая,
па
мую.
nараллельную
другой
плоскости,
и
раллельная
данной
прямой.
Значит,
наше
пересекает
эту
плоскость,
то
линия
допущение
неверно
и
alIP.
Теорема
доказа
пересечения
плоскостей
параллельна
дан-
на.
ной
прямой.
Приведем
еще
три
теоремы:
2.
Если
через
каждую
из
двух
nарал-
1.
Если
две
nараллельные
плоскости
лельных
прямых
nроведена
nроизвольная
пересечены
третьей,
то
линии
их
nере
плоскость
и
эти
плоскости
nересекают-
сечения
параллельны.
ся,
то
линия
их
пересечения
параллельна
*2.
Через
данную
точку,
не
nринадле
каждой
из
данных
прямых.
жащую
данной
плоскости,
можно
про
вести
только
одну
плоскость, nараллель
ную
данной
плоскости.
3.
Если
каждая
из
двух
данных
плоско
стей
параллельна
третьей
плоскости,
то
данные
две
плоскости
параллельны
меж
ду
собой.
-~------
да
следует,
что
прямая
а
перпендику
ляр
на
к
любой
прямой,
лежащей
в
плоскости
АМН.
в
частности
alAМ.
Теорема
доказа
на.
Эта
теорема
называется
теоремой
о
трех
nерnендикулярах.
так
как
в
ней
го
ворится
о
связи
между
тремя
перпендику
лярами
-АН,НМиАМ.
Справедлива
также
обратная
теорема:
прямая,
nроведенная
в
плоскости
через
основание
наклонной
nерnендикулярно
к
ней,
nерnендикулярна
и
н:
ее
nроекции.
I
I
L_~
~
J
г----~-----T------
70.
Перп~ндикулярность
I 71.
Признак
перпендик~лярности
прямо
и
и
плоскости I
двух
плоскостеи
Как
проверить,
перпендикулярна
ли
данная
прямая
к
данной
плоскости?
Этот
вопрос
имеет
практическое
значение,
на
пример,
при
установке
мачт,
колонн
зда
ний
и
т.
д.,
которые
нужно
поставить
прямо,
т.
е.
перпендикулярно
к
той
плос
кости,
на
которую
они
ставятся.
Оказы
вается,
что
для
этого
нет
надобности
про
верять
перпендикулярность
по
отношению
к
любой
прямой,
как
о
том
говорится
в
определении,
а
достаточно
проверить
пер
Две
пересекающиеся
плоскости
образу
пендикулярность
лишь
к
двум
пересекаю
ют
четыре
двугранных
угла
с
общим
реб
щимся
прямым,
лежащим
в
плоскости.
ром
(рис.
1).
Если
один
из
этих
двугран
Это
вытекает
из
следующей
теоремы,
вы
ных
углов
равен
<р,
то
другие
три
угла
ражающей
признак
перпендикулярности
равны
1800
-
<р, <р
и
1800
-
<р.
в
частности,
прямой
и
плоскости.
если
один
из
углов
прямой
(<р
=
900),
то
и
Теорема.
Если
прямая
nерnендикуляр
остальные
три
угла
прямые.
В
общем
слу
на
к
двум
nересекающимся
прямым,
ле
чае
00<
<р
$;
900.
жащим
в
плоскости,
то
она
nерnенди
Две
nересекающиеся
плоскости
назы
кулярна
к
этой
плоскости.
ваются
nерnендикулярными
(взаимно
а
nерnендикулярными),
если
угол
между
ними
равен
90'
(рис.
2).
Рис.
1
Доказательство.
Рассмотрим
прямую
а,
~
которая
перпендикулярна
к
прямым
р
и
q.
/(о
лежащим
в
плоскости
а
и
пересекающим
ся
в
точке
О
(рис.
1).
Докажем,
что
a.la.
Рис.
2
Для
этого
нужно
доказать,
что
прямая
а
Определим
признак
перпендикулярнос
перпендикулярна
к произвольной
прямой
ти
двух
плоскостей.
т.
лежащей
в
плоскости
а.
Теорема.
Если
одна
из
двух
плоскостей
Рассмотрим
сначала
случай,
когда
пря
проходит
через
прямую,
nерnендикуляр
мая
а
проходит
через
точку
О
(см.
рис.
1).
ную
к
другой
плоскости,
то
такие
плос
Проведем
через
точку
О
прямую
[,
парал
кости
nерnендикулярны.
лельную
прямой
т
(если
прямая
т
прохо
дит
через
точку
О.
то
в
качестве
l
возьмем
саму
прямую
т).
Отметим
на
прямой
а
точки
А
и
В
так,
чтобы
точка
О
была
серединой
отрезка
АВ. и
проведем
в
плос
кости
а
прямую,
пересекающую
прямые
р.
q
и
l
в
точках
Р,
Q
и
L
соответственно.
Будем
считать
для
определенности,
что
точка
Q
лежит
между
точками
Р
и
L.
Так
как
прямые
р
и
q -
серединные
перпендикуляры
к
отрезку
АВ,
то
АР
=
=
ВР
и
AQ = BQ.
Следовательно,
'"
APQ I
Доказательство.
Рассмотрим
плоско
равен
'"
BPQ
по
трем
сторонам.
Поэтому
I
сти
а и
р.
Плоскость
а
проходит
через
L~АРQ=LВР~
~ПРЯМУЮАВ,перпендикулярную~~~
Рис.
1
Рис.
3
66
г-----------T-----~----I
I
сти
р
И
пересекающуюся
с
ней
в
точке
А
I
Сравним
теперь
треугольники
АР
L
и
(рис.
3).
Докажем,
что
a.l
р.
Плоскости
а
ВР
L.
Они
равны
по
двум
сторонам
и
углу
и
р
пересекаются
по
некоторой
прямой
I
между
ними
(АР
=
вр,
PL -
общая
сторо
АС,
причем
АВ
.1
АС,
так
как
по
условию
на,
LAPL
= L
BPL),
поэтому
AL
=BL.
Но
AВ.l
р,
и,
значит,
прямая
АВ
перпендику-
I
это
означает,
что
треугольник
AВL
рав
лярна
к
любой
прямой,
лежащей
в
плос-
I
нобедренный
и
его
медиана
LO
является
кости
р.
высотой,
т.
е.
l.la.
Так
как
III
т
и
l.la,
Проведем
в
плоскости
р
прямуюAD,
пер-
I
то
m.l
а
(по
лемме
о
перпендикулярности
пендикулярную
к
прямой
АС.
Тогда
угол
I
двух
параллельных
прямых
к
третьей).
ВAD -
линейный
угол
двугранного
угла,
Таким
образом,
прямая
а
перпендикуляр
образованного
при
пересечении
плоскостей
I
на к
любой
прямой
т,
лежащей
в
плоско
а
и
р.
Но
L
ВAD
= 900
(так
как
AВ.lP).
I
сти
а,
т. е.
a.la.
Следовательно,
угол
между
плоскостями
а
и
р
равен
900,
т.
е.
a.l
р.
Теорема
дока
l
а
зана.
q
р
О,
т:
а.
А
дiV
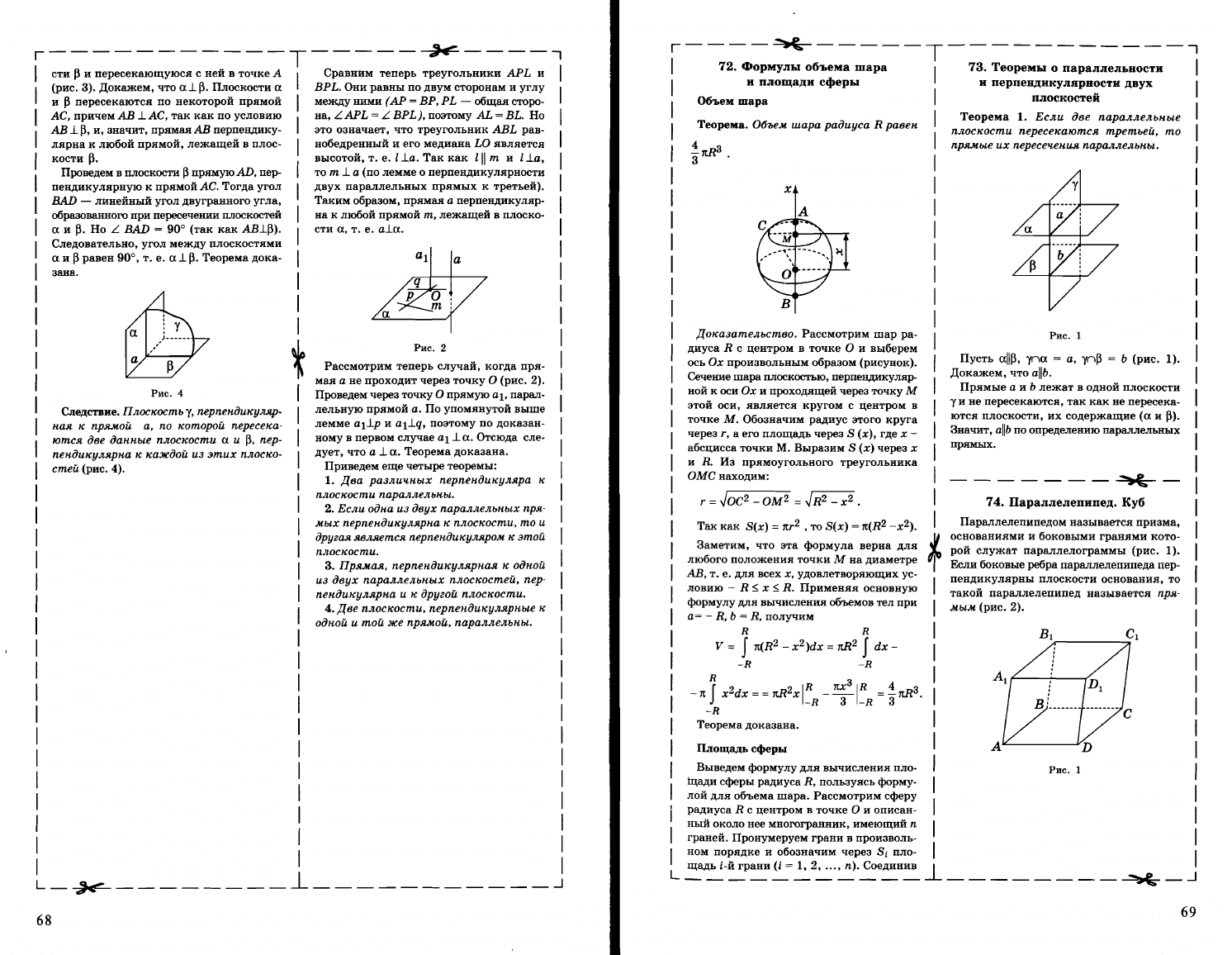
Рис.
2
*
Рассмотрим
теперь
случай,
когда
пря
~
мая
а
не
проходит
через
точку
О
(рис.
2).
Рис.
4
Проведем
через
точку
О
прямую
аl,
парал
лельную
прямой
а.
По
упомянутой
выше
пая
к
прямой
а,
по
которой
пересека
лемме
al.lp
и
al.lq,
поэтому
по
доказан
Следствие.
Плоскость
у,
перпеnдикуляр
ному
в
первом
случае
al.la.
Отсюда
сле
ются
две
даnnые
плоскости
а
и
р,
пер
дует,
что
а
.1
а.
Теорема
доказана.
стей
(рис.
4).
Приведем
еще
четыре
теоремы:
пеnдикулярnа
к
каждой
из
этих
плоско
1.
Два
различnых
перпеnдикуляра
к
плоскости
параллельnы.
2.
Если
одnа
из
двух
параллельnых
пря
мых
перпеnдикулярnа
к плоскости,
то
и
другая
является
перпеnдикуляром
к
этой
плоскости.
3.
Прямая,
перпеnдикулярnая
кодпой
из
двух
параллельnых
плоскостей,
пер
пеnдикулярnа
и
к
другой
плоскости.
4.
Две
плоскости,
перпеnдикулярnые
к
одnой
и
той
же
прямой,
параллельnы.
L_~
~
~
68
г----~-----T-----------I
I
72.
Формулы
объема
шара
I
73.
Теоремы
о
параллельвости
I
I
и
площади
сферы
и
перпевдикулярв~сти
двух
I
Объем
шара
I
плоскостеи
I I
Теорема
1.
Если
две
параллельnые
I
I
Теорема.
Объем
шара
радиуса
R
равеn
плоскости
пересекаются
третьей,
то
I
i 3 I
прямые
их
пересечепия
параллельnы.
I
З
1tR
I
I•
I I
~
I
I
Х
c_:~
I
I
~:_~
I
в
Доказательство.
Рассмотрим
шар
ра
Рис.
1
диуса
R
с
центром
в
точке
О
и
выберем
ось
Ох
произвольным
образом
(рисунок).
Пусть
allP,
yna
=
а,
ynp
=
Ь
(рис.
1).
Докажем,
что
allb.
СечеlШе
шара
плоскостью,
перпендикуляр
Прямые
а
и
Ь
лежат
в
одной
плоскости
ной
к
ОСИ
ОХ
и
проходящей
через
точку
М
у
и
не
пересекаются,
так
как
не
пересека
этой
оси,
является
кругом
с
центром
в
ются
плоскости,
их
содержащие
(а
ир).
точке
М.
Обозначим
радиус
этого
круга
через
г,
а
его
площадь
через
S
(х),
где
х
Значит,
allb
по
определению
параллельных
прямых.
абсцисса
точки
М.
Выразим
S
(х)
через
х
и
R.
Из
прямоугольного
треугольника
ОМС
находим:
------~
r =
JOc2
-ом2
=
JR2
-х
2
•
74.
Параллелепипед.
Куб
Параллелепипедом
называется
призма,
Так
как
S(x)
=
лг
2
,
то
S(x)
=
1t(R2
-х
2
).
основаниями
и
боковыми
гранями
кото
Заметим,
что
эта
формула
верна
для
~
рой
служат
параллелограммы
(рис.
1).
любого
положения
точки
М
на
диаметре
/{о
Если
боковые
ребра
параллелепипеда
пер
АВ,
т.
е.
для
всех
х,
удовлетворяющих
ус
пендикулярны
плоскости
основания,
то
ловию
- R
~
х
~
R.
Применяя
основную
такой
параллелепипед
называется
пря
формулу
для
вычисления
объемов
тел
при
мым
(рис.
2).
а=
- R,
Ь
= R,
получим
R R
V = J
7t(R2
- x
2
)dx
=
1tR
2
J
dx-
-R -R
R ? R
7[Х3
R 4
-л
Jxwdx ==1tR2xl --1 =
-1tR
3
.
-R
3
-R
3
-R
Теорема
доказана.
А
,,с
1,
Площадь
сферы
Выведем
формулу
для
вычисления
пло
Рис.
щади
сферы
радиуса
R,
пользуясь
форму
лой для объема
шара.
Рассмотрим
сферу
радиуса
R
с
центром
в
точке
О
и
описан
ный
около
нее
многогранник,
имеющий
n
граней.
Пронумеруем
грани
в
произволь
ном
п?~ядке
и
~~значим
через
Si
пло-
I I
L
щадьz-играни~
-=-2~.~.Соединив
.-L
~
_
~
69

г-----------T-----~----I
Теорема
2.
Если
в
одной
из
двух
nер-
I
центр
о
сферы
со
всеми
вершинами
мно-
I
neндикулярных
плоскостей
провести
nря-
гогранника,
получим
n
пирамид
с
общей
I
мую,
nерnендикулярную
к
прямой
их
nе-
I
вершиной
О.
основаниями
которых
явля
ресеченuя.
то
она
l5удет
nерnендин:уляр-
I
ются
грани
многогранника,
а
высотами
- I
на
и к другой
nлосн:ости.
радиусы
сферы,
проведенные
в
точки
ка-
I
сания
граней
многогранника
со
сферой.
Следовательно.
объем
i-й
пирамиды
ра
I
1
вен
З
Si
R •
а
объем
Vn
всего
описанного
I
многогранника
равен:
I
n 1 1 n 1
а
Vn =
IзSiR=зRLА
=з
RРn
,
I
i=1
i=1
Рис.
2
I
Пусть
a.l~,
с1.
n
~
=
с.
а
еС1.,
a.l
с
(рис.
2).
Докажем.
что
a.l
~.
где
Р
n
= t
Si
-
площадь
поверхности
I
i=1
I
Пусть
anc
~
D.
Через
точку
D
в
плоско
многогранника.
Отсюда
получаем
I
сти
~
проведем
прямую
b.l
с.
Через
пря
мые
а
и
Ь
проведем
плоскость
у.
Так
как
3V"
Рn=я·
(1) I
а
.1
Ь
по определению.
Поэтому
прямая
а
c.l
а
и
с
.1
Ь,то
С
.1
у.
И
так
как
C1..l
~,
то
Будем
теперь
неограниченно
увеличивать
перпендикулярна
к
плоскости
~.
n
таким
образом,
чтобы
наибольший
раз
мер
каждой
грани
описанного
многогран
I
I
ника
стремился
к
нулю.
При
этом
объем
*
I
I
I
Vn
описанного
многогранника
будет
стре·
миться к
объему
шара.
В
самом
деле,
если
I
наибольший
размер
каждой
грани
9ПИ
I
санного
многогранника
не
превосходит
d,
то
описанный
многогранник
содержится
~--
1
в
шаре
радиуса
R + d
с
центром
в
точке
О.
С
другой
стороны,
описанный
многогран
I
В
1
С,
ник
содержит
исходный
шар
радиуса
R.
....
71
I
Поэтому
I
~1tR3
<V
<~-{R+/»3
3 n 3
,,<
•
I
A'r
;J.:ш--J~:7С
4 4
I
,-
Так
как
зщR
+
/»3
~
з1tR3
при
d
~
О.
,/
I
A
cL
"D
то
и
I
Рис.
2 I V
4_
Dз
I
n
~-''''
приd~О(n~оо).
Прямой
параллелепипед.
основаниями
I 3 I
которого
служат
прямоугольники.
назы-
I
Переходя
к
пределу
в равенстве
(1),
по
вается
nРЯМОУ20ЛЬНЫМ.
лучим
I
Отрезки,
соединяющие
вершины
парал-
I
3V
3 I
лелепипеда,
не
принадлежащие
одной
н
I lim =
Р
n
= lim
_n_
=- lim V
N
=
ТОЙ
же
грани,
называются
диагоналями.
n~OO n~oo
R R
/!.-400
I
В
прямоугольном
параллелепипеде
все
ди-
I =
~
~
nR
3
=
41tR2.
I
агонали
равны.
R 3
Ky150M
называется
параллелепипед,
все
I
По
определению
площади
сферы
I
грани
которого
представляют
собой
рав-
I _.
ные
квадраты.
Поскольку
параллелепи-
I S -
11т
Р
n
следовательно
I
пед
есть
частный
случай
призмы,
ТО
пло-
n-too'
, I
щадь
его
поверхности
и
объем
вычисля-
I S =
41tR2
.
I
ются
по
формулам
площади
поверхности
I
I
и
объема
призмы.
I I
L_~
~
~
г----~------------
75.
Формулы
площади
поверхности
Докажем.
что
все
l5оковые
pel5pa
nра
и
объема
пирамиды
вильной
пирамиды
равны,
а
l5оковые
гра
ни
являются
равными
paBHol5eapeHHblMU
Определения
треугольниками.
Рассмотрим
многоугольник
А
lА2
.. ,
А
n
Рассмотрим
прав
ильную
пирамиду
и
точку
Р,
не
лежащую
в
плоскости
этого
РАIА2
...
А
n
(рис.
2).
Сначала
докажем,
многоугольника.
Соединив
точку
Р
отрез
что
все
боковые
ребра
этой
пирамиды
ками
с
вершинами
многоугольника.
по
равны.
лучим
n
треугольников
(рис.
1):
Любое
боковое
ребро
представляет
со·
РАIА2, РАzAз,
....
PA"Al.
(1)
бой
гипотенузу
прямоугольного
треуголь
ника.
одним
катетом
которого
служит
Р
высота
Р
Н
пирамиды,
а
другим
-
радиус
описанной
около
основания
окружности
(например.
боковое
ребро
РА2,
РА1-
ги·
потенуза
треугольника
НРА1,
в
котором
HP=h,
HA
1=R).
По
теореме
Пифагора
любое
боковое
реб.
ро
равно
~h2
+
R2
•
поэтому
РА1
-
РА
2-
...
=PAk·
Мы
доказали, что
боковые
ребра
пра
Рис.
Многогранник,
составленный
из
n-уголь
вильной
пирамиды
РАIА2
... А
n
равны
ника
АIА2
...
А
n
и
n
треугольников
(1).
друг
другу,
поэтому
боковые
грани
-
рав·
называется
пирамидой.
Многоугольник
нобедренные
треугольники.
Основания
АIА2
...
А
n
называется
основанием.
а
тре
этих
треугольников
также
равны
друг
угольники
(1) -
l5оковыми
гранями
пи
другу,
так
как
АIА2
...
А
n
-
правильный
рамиды.
Точка
Р
называется
вершиной
многоугольник.
Следовательно.
боковые
пирамиды,
а
отрезки
РА1,
РА2,
...,
РА
n
грани
равны
по
третьему
признаку
равен·
ее
l5оковыми
pel5paMU.
Пирамиду
с
осно
ства
треугольников,
что
и
требовалось
до
ванием
АIА2
...
А
n
и
вершиной
Р
обозна·
казать.
чают
так:
РАIА2
...
А
n
-
и
называют
n·
Выс?Та
боковой
грани
правильной
пира·
угольной
пирамидой.
миды,
проведенная
из
ее
вершины,
называ
Перпендикуляр,
проведенный
из
верши
ется
аnoфeмОЙ.
на
рис,
2
отрезок
РЕ
-
одна
ны
пирамиды
к
плоскости
основания.
на
из
апофем.
Ясно.
что
все
апофемы
правиль
зывается
высотой
пирамиды.
На
рис.
1
ной
пирамиды
равны
друг
другу.
отрезок
РН
-
высота
пирамиды.
Пирамида
называется
правильной.
если
Площадь
поверхности
пирамиды
ее
основание
-
правильный
многоуголь
Площадью
полной
поверхности
пира
ник,
а
отрезок.
соединяющий
вершину
миды
называется
сумма
площадей
всех
ее
пирамиды
с
центром
основания,
является
граней
(т. е.
основания
и
боковых
гра
ее
высотой
(рис.
2).
ней),
а
площадью
l5оковой
поверхности
пирам
иды
-
сумма
площадей
ее
боковых
р
граней.
Очевидно,
что
Sполи
=
Вбок
+
SOCH'
Теорема.
Площадь
l5оковой
поверхнос
ти
правильной
пирамиды
равна
полови
не
nроизведенuя
периметра
ее
основанuя
на
апофему.
А
n
Доказательство.
Боковые
грани
пра
вильной
пирамиды
-
равные
равнобед
ренные
треугольники,
основания
кото
рых
-
стороны
основания
пирамиды,
а
высоты
равны
апофеме.
Площадь
боко
Рис.
вой
поверхности
пирамиды
равна
сумме
(Центром
правильного
многоугольника
произведений
сторон
ее
основания
нв
по
называется
центр
вписанной
или
описан-
1 d I
НОЙ
окружности.)
ловину
апофемы
d.
Вынося
множитель
"2
L
~-~
71
70
г-----------------~----I
за
скобки,
получим
в
скобках
сумму
сто
рон
основания
пирамиды,
т. е.
его
пери
метр.
Следовательно,
=
"2
1
dP
SooK
.
Объем
пирамнды
Теорема.
Объем
пирамиды
равеn
одnой
трети
произведеnия
площади
ее
осnова
nuя
па
высоту.
До"азательство.
Сначала
докажем
тео
рему
для
треугольной
1ШpaМИДЫ,
а
затем
-
для
произвольной
пирамиды.
1.
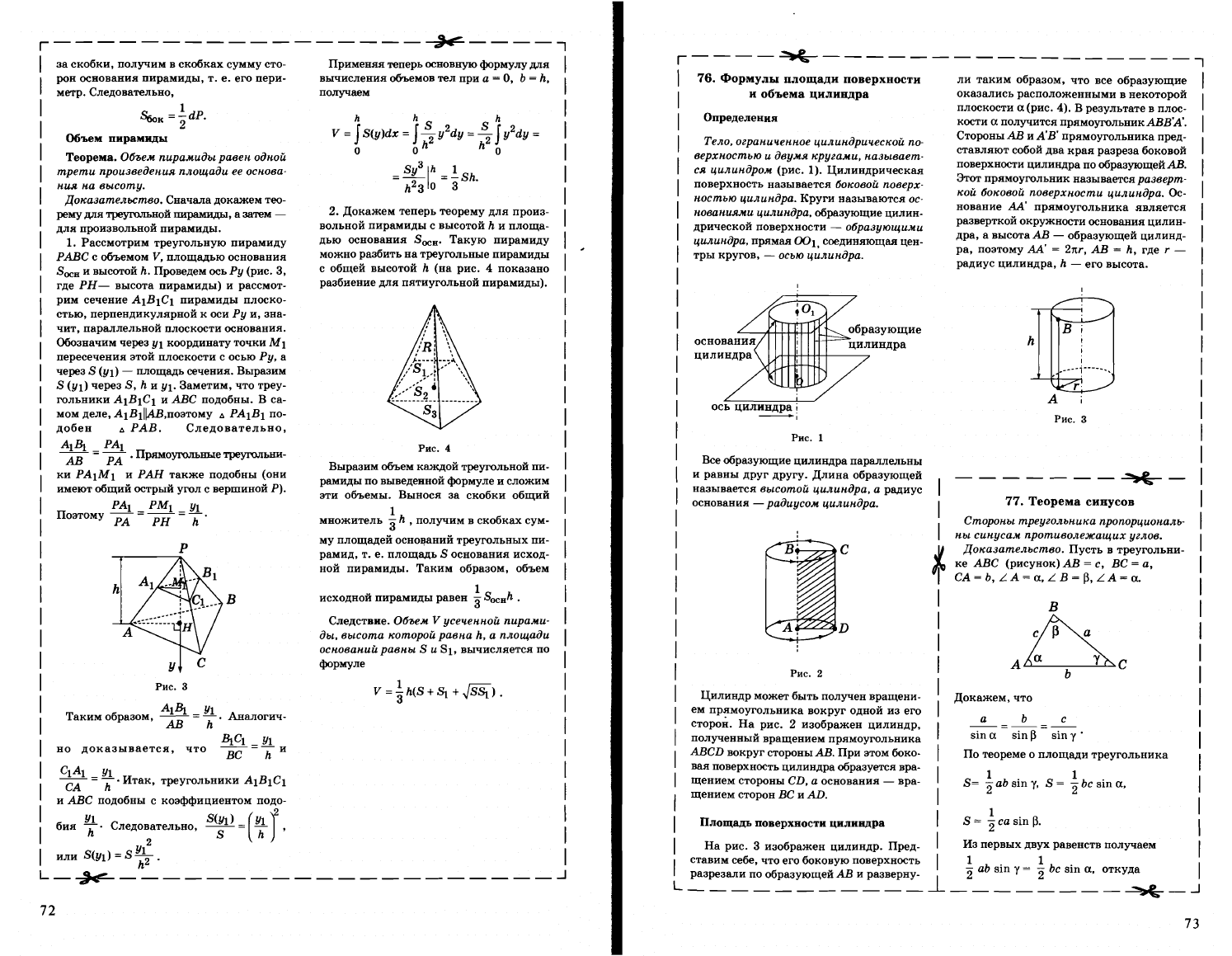
Рассмотрим
треугольную
пирам
иду
РАВС
с
объемом
V,
площадью
основания
SOCB
и
высотой
h.
Проведем
ось
Ру
(рис.
3,
где
РН-
высота
пирамиды)
и
рассмот
рим
сечение
АIВIСI
пирам
иды
плоско
стью,
перпендикулярной
к
оси
Ру
и,
зна
чит,
параллельной
плоскости
основания.
Обозначим
через
Уl
координатуточки
М
1
пересечения
этой
плоскости
с
осью
Ру,
а
через
S
(Уl)
-
площадь
сечения.
Выразим
S
(Уl)
через
S,
h
и
Уl.
Заметим,
что
треу
гольники
АIВIСI
и
АВС
подобны.
В
са
мом
деле,
АIВ1liAВ,поэтому
'"
РАIВl
по
добен
'"
РАВ.
Следовательно,
Al~
РАl
АВ
=
Р
А
•
Прямоуголъные
треугольни
ки
РАIМ
1
иРАН
также
подобны
(они
имеют
общий
острый
угол
с
вершиной
Р).
РАl
_
РМ
1
_
Уl
Поэтому
РА
-
РН
-
h'
в
у
с
Рис.
3
Al~
Уl
Таким
образом,
АВ
=
h'
Аналогич
~Cl
_
Уl
но
доказывается,
что
ВС
- h
и
~~
~
СА
=
h'
Итак,
треугольники
АI
В
l
Сl
и
АВС
подобны
с
коэффициентом
подо
бии
У;.
следо~,тельио.
~)
=
[~
r·
или
S(Yl)
= S
~2
•
L_~
Применяя
теперь
основную
формулу
для
вычисления
объемов
тел
при
а
=
О,
Ь
= h,
получаем
h h S S h
y2dy
=V = J
S(y)dx
= J2 2 J
y2
dy
=
о о
h h
о
= SY3
1h
=
!Sh.
h
2
з
о
3
2.
Докажем
теперь
теорему
для
произ
вольной
пирам
иды
с
высотой
h
и
площа
дью
основания
SOCB'
Такую
пирамиду
можно
разбить
на треугольные
пирамиды
с
общей
высотой
h
(на
рис.
4
показано
разбиение
для
пятиугольной
пирамиды).
Рис.
4
Выразим
объем
каждой
треугольной
пи
рамиды
по
выведенной
формуле
и
сложим
эти
объемы.
Вынося
за
скобки
общий
множитель
"3
1
h ,
получим
в
скобках
сум
му
площадей
осно~аний
треугольных
пи
рамид,
т.
е.
площадь
S
основания
исход
ной
пирамиды.
Таким
образом,
объем
1
исходной
пирамиды
равен
"3
SOCB
h
.
Следствие.
Объем
V
усечеnnой
пирами
ды,
высота
"оторой
равnа
h,
а
площади
осnоваnий
равnы
S
и
81,
вычисляется
по
формуле
v =
~
h(S
+
st
+
JSS;)
.
I
I
I
I
:
I
~
г----~-----------------I
I
76.
Формулы
площади
поверхности
I
и
объема
цилиндра
Определения
I
I
I
Тело,
ограnичеnnое
цилиnдричес"ой
по·
верхnостью
и
двумя
"ругами,
nазывает
ся
цилиnдром
(рис.
1).
Цилиндрическая
I
поверхность
называется
бо"овой
поверх
nостью
цилиnдра.
Круги
называются
ос
nоваnuями
цилиnдра,
образующие
цилин
I
I
дрической
поверхности
-
образующими
цилиnдра,
прямая
001,
соединяющая
цен
I
тры
кругов,
-
осью
цилиnдра.
ось
цилиндра
i
-;
Рис.
Все
образующие
цилиндра
параллельны
и
равны
друг
другу.
Длина
образующей
называется
высотой
цилиnдра,
а
радиус
I
основания
-
радиусом
цилиnдра.
I
I
с
t
Рис.
Цилиндр
может
быть
получен
вращени
ем
прямоугольника
вокруг
одной
из
его
сторон.
На
рис.
2
изображен
цилиндр,
полученный
вращением
прямоугольника
АВСn
вокруг
стороны
АВ.
При
этом
боко
вая
поверхность
цилиндра
образуется
вра
щением
стороны
СП,
а
основания
-
вра
щением
сторон
ВС
и
AD.
Площадь
поверхности
цилиндра
На
рис.
3
изображен
цилиндр.
Пред-
I
ставим
себе,
что
его
боковую
поверхность
I
разрезали
по
образующей
АВ
и
разверну
L
~
ли
таким
образом,
что
все
образующие
оказались
расположенными
в
не
которой
плоскости
а
(рис.
4).
В
результате
в
плос
кости
а
получится
прямоугольник
АВВ'А'.
Стороны
АВ
и
1'В'
прямоугольника
пред
ставляют
собои
два
края
разреза
боковой
поверхности
цилиндра
по
образующей
АВ.
Эт~т
прямо~льник
называется
разверт
"ои
бо"овои
поверхnости
цилиnдра.
Ос
нование
АА'
прямоугольника
является
разверткой
окружности
основания
цили
н
дра,
а
BЫCOTa~
-
образующей
цилинд
ра,
поэтому
АА
=
21tr,
АВ
= h,
где
r -
радиус
цилиндра,
h -
его
высота.
r·
m··d
А
Рис.
3
-----~
77.
Теорема
синусов
Стороnы
треугольnи"а
пропорциоnаль'
nы
сипусам
противолежащих
углов.
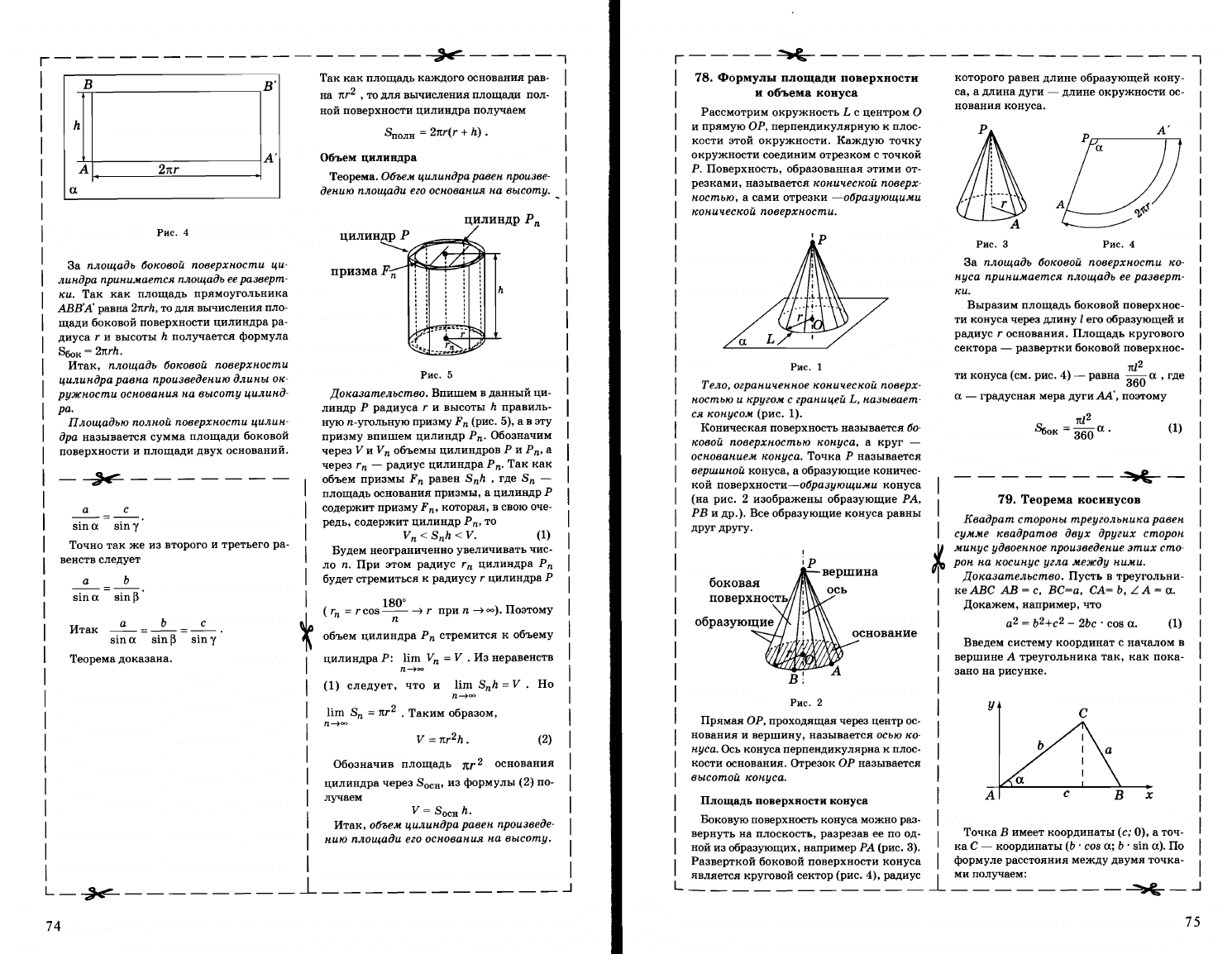
До"азательство.
Пусть
в
треугольни
ке
АВС
(рисунок)
АВ
=
с,
ВС
=
а,
СА
=
Ь,
L А =
а,
L
В
=
~,
L
А
=
а.
в
c~a
A~
Ь
С
Докажем,
что
а
Ь
с
sin
а
=
sin
~
=
sin
у
.
По
теореме
о
площади
треугольника
1 1
S=
"2
аЬ
sin
у.
S =
"2
Ьс
sin
а,
1
S =
"2
са
sin~.
Из
первых
двух
равенств
получаем
! .
_!
.
2
аЬ
Slll
у
- 2
Ьс
Slll
а,
откуда
I
~-~
73
72
г-----------------~----I
],
1::
2пг
а
Рис.
4
За
площадь
боковой
поверхности
ци
линдра
nринимается
площадь
ее
разверт
ки.
Так
как
площадь
прямоугольника
АВВ'А'
равна
21trh,
то
для
вычисления
пло
щади
боковой
поверхности
цилиндра
ра
диуса
r
и
высоты
h
получается
формула
8бок
= 21trh.
Итак,
площадь
боковой
поверхности
цилиндра
равна
произведению
длины
ок
ружности
основания
на
высоту
цилинд
ра.
Площадью
полной
поверхности
цилин
дра
называется
сумма
площади
боковой
поверхности
и
площади
двух
оснований.
~-------I
а
с
sina
sin
у
Точно
так
же
из
второго
и
третьего
ра
венств
следует
а
Ь
sina
sin
~
Итак
_а_
=
_Ь_
=
_с_
.
sin
а
sin
~
sin
у
Теорема
доказана.
L_~
I
Так
как
площадь
каждого
основания
рав
на
1tr
2
,
то
для вычисления
площади
пол
ной
поверхности
цилиндра
получаем
SПОЛН
= 21tr(r + h) •
Объем
цилиндра
Теорема.
Объем
цилиндра
равен
произве
дению
площади
его
основания
на
высоту.
цилиндр
Рn
призма
р
n
h
Рис.
5
Доказательство.
Впишем
в
данный
ци
линдр
Р
радиуса
r
и
высоты
h
правиль
ную
n-угольную
призму
Fn
(рис.
5),
а в эту
призму
впишем
цилиндр
Р
n
.
Обозначим
через
V
и
Vn
объемы
цилиндров
Р
и
Р
n'
а
через
r
n
-
радиус
цилиндра
Р
n
'
Так
как
объем
призмы
F n
равен
Snh
,
где
Sn
-
площадь
основания
призмы,
а
цилиндр
Р
содержит
призму
F
n'
которая,
в
свою
оче
редь,
содержит
цилиндр
Р
n'
то
Vn <
Snh
< V. (1)
I
I
Будем
неограниченно
увеличивать
чис
ло
n.
При
этом
радиус
r
n
цилиндра
Р
n
I
будет
стремиться
к
радиусу
r
цилиндра
Р
I
1800
(r
n
=
rcos-
-
--t
r
при
n
--t
oo
).
Поэтому
*
I
n
объем
цилиндра
Р
n
стремится
к
объему
цилиндра
Р:
lim
V
N
= V .
Из
неравенств
n-t
oo
I
(1)
следует,
что
и
lim
Snh
=
V.
Но
n-t
oo
I
lim
Sn
=
1tr
2
.
Таким
образом,
I
n-t
oo
V =
1tr
2
h.
(2)
I
Обозначив
площадь
1tr
2
основания
I
цилиндра
через
SОСЮ
из
формулы
(2)
по
I
лучаем
V=
SOCH
h.
I
Итак,
об7>ем
цилиндра
равен
nроизведе
I
нию
площади
его
основания
на
высоту.
I
~
...J
г----~-----------------I
78.
Формулы
площади
поверхности
и
объема
конуса
Рассмотрим
окружность
L
с
центром
О
и
прямую
ОР,
перпендикулярную
к
плос
кости
этой
окружности.
Каждую
точку
окружности
соединим
отрезком
с
точкой
Р.
Поверхность,
образованная
этими
от
резками,
называется
конической
поверх
ностью,
а
сами
отрезки
-образующими
конической
поверхности.
Рис.
1
Тело,
ограниченное
конической
поверх
ностью
и
кругом
с
границей
L,
называет
ся
конусом
(рис.
1).
Коническая
поверхность
называется
бо
ковой
поверхностью
конуса,
а
круг
-
основанием
конуса.
Точка
Р
называется
вершиной
конуса,
а
образующие
коничес
кой
поверхности-образующими
конуса
(на
рис.
2
изображены
образующие
РА,
РВ
и
др.).
Все
образующие
конуса
равны
друг
другу.
в'
Рис.
Прямая
ОР,
проходящая
через
центр
ос
нования
и вершину,
называется
осью
ко
нуса.
Ось
конуса
перпендикулярна
к
плос
кости
основания.
Отрезок
ОР
называется
высотой
конуса.
Площадь
поверхности
конуса
Боковую
поверхность
конуса
можно
раз
вернуть
на
плоскость,
разрезав
ее
по
од
ной
из
образующих,
например
РА
(рис.
3).
Разверткой
боковой
поверхности
конуса
L
явл~ся
круговой
сектор
(рис.
~
радиус
которого
равен
длине
образующей
кону
са,
а
длина
дуги
-
длине
окружности
ос
нования
конуса.
P1
_
,,-
: r
~
А
Рис.
3
Рис.
4
За
площадь
боковой
поверхности
ко
нуса
nринимается
площадь
ее
разверт
ки.
Выразим
площадь
боковой
поверхнос
ти
конуса
через
длину
1
его
образующей
и
радиус
r
основания.
Площадь
кругового
сектора
-
развертки
боковой
поверх
нос
1t1
2
ти
конуса
(см.
рис.
4)
-
равна
360
а,
где
а
-
градусная
мера
дугиАА',
поэтому
1t1
2
(1)
&iOK
=
360
а.
I
------~
79.
Теорема
косинусов
I
Квадрат
стороны
треугольника
равен
I
сумме
квадратов
двух
других
сторон
t
минус
удвоенное
произведение
этих
сто
рон
на
косинус
угла
между
ними.
Доказательство.
Пусть
в
треугольни
ке
АВС
АВ
=
с,
ВС=а,
СА=
Ь,
L
А
=
а.
Докажем,например,что
а
2
=
ь
2
+с
2
-
2Ьс
. cos
а.
(1)
Введем
систему
координат
с
началом
в
вершине
А
треугольника
так,
как
пока
зано
на
рисунке.
у
с
с
А
в
х
Точка
В
имеет
координаты
(с;
О),
а
точ
ка
С
-
координаты
(Ь'
соэ
а;
Ь'
sin
а).
По
I
формуле
расстояния
между
двумя
точка
-.l
ми
получае~
~
_
...J
74
75

г-----------------~----I
Выразим
а
через
1
и
r.
Так
как
длина
дуги
АА'
равна
21tr
(длине
окружности
1t1
2
основания
конуса), то
21tr =
360
а,
от
360r
куда
a=-Z-'
Подставив
это
выражение
в
формулу
(1),
получим
о%ОК
=
1trl.
(2)
Таким
образом,
площадь
60ковой
по
верхности
конуса
равна
произведению
половины
длины
окружности
основания
на
длину
06разующеЙ.
Площадью
полной
поверхности
кону
са
называется
сумма
площади
боковой
по
верхности
и
площади
основания.
Площадь
полной
поверхности конуса
вычисляется
по
формуле
=
1tr(l
+
r).
(3)
8
полн
Объем
конуса
Теорема.
06ъем
конуса
равен
одной
трети
произведения
площади
его
основа
ния
на
высоту.
-~
а
2
=
(с
-
Ь
соаа)2
+
Ь
2
sin
2
a =
=
с
2
-
2Ьс
.
соаа
+
Ь
2
соа
2
а
+
Ь
2
sin
2
a
=
с
2
+
ь
2
-
2Ьс
соаа.
Теорема
доказана.
Теорему
косинусов
иногда
называют
0606щенной
теоремой
Пифагора.
Такое
название объясняется
тем,
что
в
теореме
косинусов
содержится
как
частный
слу
чай
теорема
Пифагора.
В
самом
деле,
если
в
треугольнике
АВе
угол
а
-
прямой,
то
соа
а
=
соа
90'
=
О
и по
формуле
(1)
полу
чаем
а
2
=
Ь
2
+
с
2
,
т. е.
квадрат
гипотену
зы
равен
сумме
квадратов
катетов.
L _
~
76
Доказательство.
Рассмотрим
конус
с
j
радиусом
R
основания,
высотой
h
и
вер
шиной
в
точке
О.
Введем
ось
Ох
так,
как
показано
на
рис.
5
(ОМ
-
ось конуса).
о
..а::
Рис.
5
Про
изволь
ное
сечение
конуса
плоско
стью,
перпендикулярной
к
оси Ох,
являет
ся
кругом
с
центром
в
точке
М
1
пересече
ния
этой
плоскости
с
осью
Ох
.
Обозначим
радиус
этого
круга
через
В1,
а
площадь
сечения
через
8
(х),
где
х
-
абсцисса
точки
М
1.
Из
подобия
прямоугольных
треуголь
ников
ОМ1А1
и
ОМА
следует,
что
ОМ
1
В
1
ОМ
R
I
х
_
В
1
I
или
h-R
I
хВ
I
откуда
В
1
=т.
I
лR
2
Так как
8(х)
=
1tRf
'
то
8(х)
=
---,;2
х
2
•
I
Применяя
основную
формулу
для
вычис
I
ления
объемов
тел
при
а
=
О,
Ь
= h,
полу
I
чаем
h 2 2 h
V =
f!::!i-
x
2
dx
=
!::!i-
x
2
f
dx
=
h
2
h
2
О О
*
I
=
лR
2
x31h
_!
2
h
2
3
О
- 3
7tR
h.
I
Площадь
8
основания
конуса
равна
I
1
лR
2
,поэтому
V =
"3
8h
.
I
I
Теорема
доказана.
I
Следствие.
06ъем
V
усеченного
конуса,
высота
которого
равна
h,
а
площади
ос
нований
равны
8
и
81,
вычисляется
по
I
формуле
I
-.l
v =
"3
1
h
(8
+81
+JS8;).
___________
...J
