Филатов О.А. Шпаргалки по алгебре и геометрии
Подождите немного. Документ загружается.


г-----------------~----I
У!
1
1(-
со""
у
- 1
E~
7'к
-а-2n:
-211:
a-21t~
11:-0.
О
~
7t
70.+2П2
а-+-2п
8п
--
-
311:
1t
~-2
_
2---~
Рис.
2
Все
решения
уравнения
у
= cos
х
запи
сываются
двумя
формулами:
х
=
а
+
21tk
,
х
=
-а
+
21tk
, k
е
Z.
Их
объединяют
в
одну
формулу,
учиты
вая,
что
а
= arccos
с,
т.
е.
х
=
±а
+
21tk
= ±
arccos
с
+ 21tk, k
е
Z.
Таким
образом,
все
решения
уравнения
cos
х
=
с
записываются
формулой
х
= ±arccos
с
+ 21tk, k
е
Z.
(5)
3.
Расмотрим
частные
случаи
уравнения
cos
х
=
с:
а)
cos
х
= 1.
Прямая
у
= 1
и
косинусоида
имеют
бесконечное
количество
общих
то
чек
(см.
рис.
2).
В
пределах
одного
перио
да
х
=
О
и
х
=
2п.
С
учетом
периодичности
косинуса
запишем
все
решения
уравнения
cos
х
= 1.
Получим
х
=
21tk,
k
е
Z.
(6)
б)
cos
х
=
-1.
Прямая
у
=
-1
и
косинусо
ида
имеют
бесконечное
количество
общих
точек
(см.
рис.
2).
В
пределах
одного
пе
риода
х
=
п.
С
учетом
периодичности
ко
синуса
запишем
все
решения
уравнения
cos
х
=
-1.
Получим
х
= 1t +
21tk,
k
е
Z.
(7)
в)
cos
х
=
О.
Прямая
у
=
о
(ось
Ох) и
косинусоида
имеют
бесконечное
количе
ство
общих
точек
(см.
рис.
2).
Все
решения
уравнения
cos
х
=
О
с
уче
том
периодичности
косинуса
записывают
ся
так:
1t
Х
=
±2"+21tk
1t
или
х
=
2"
+
1tk
, ( k
е
Z ). (8)
Пример.
Решим
уравнения
1
х
а)
cos
2х
= -
2";
б)
cos
5"
= 1;
в)
cos8x=-1;
г)
COB(4X-~)=O.
Решение.
а)
Корни
уравнения
сов
2х
= -
~
най
дем
по
формуле
(5):
2х
= ±arccos ( -
~
) + 21tk, k
е
Z.
L_~--------------------~
Вычислив
arccos(-!)=
1t -
arccos!
= 1t _
2:
=
2п
2 2 3
3'
2п
получим
2х
= ±"3 + 21tk, k
е
Z,
1t
откуда
х=±з+1tk,
keZ;
б)
по
формуле
(6)
х
5"
=
21tk,
ke
Z,
откуда
х
=
101tk,
k
е
Z;
в)
по
формуле
(7)
8х
= 1t + 21tk, k
е
Z;
1t
1tk
Х=8+4""'
ke
Z;
г)
по
формуле
(8)
(
4х
-
~
) = %+
1tk,
k
е
Z;
1t 1t
4х
=
2"
+
4"
+
1tk,
k
е
Z,
3п
1tk
откуда
х
=16 +
4""'
k
е
Z.
Решение
уравнений
tg
х
=
с
н
ctg
х
=
с
Область
изменения
тангенса
и
котанген
са
-
множество
R
действительных
чисел.
Поэтому
уравнения
tg
х
=
с
и
ctg
х
=
с
имеют
решения
при
любом
с.
-2
.
Рис.
3
Рис.
4
В
пределах
одного
периода
(у
тангенса
и
котангенса
он
равен
п)
прямая
у
=
с
пересе
кает
тангенсоиду
и
котангенсоиду
только
один
раз,
т. е.
уравнения
tg
х
=
с,
ctg
х
=
с
имеют
одно
решение
в
пределах
одного
периода.
Это
угол
а
=
arctg
с
для
уравне
ния
tg
х
=
с
(рис.
3)
и
угол
а1
=
arcctg
с
для
уравнения
ctg
х
=
с
(рис.
4).
Все
ос
тальные
решения
получаются
прибавле
нием
периода:
х
=
arctg
с
+
1tk
, k
е
Z ; (9)
х
=
arcctg
с
+
1tk
k
е
Z . (10)
г----~-----T------
41.
Косинус
и
синус
I 42.
Свойства
точек,
равноудаленных
суммы
и
разности
двух
углов
от
концов
отрезка
Формулы
сложения
Выведем
формулы,
выражающие
триго
нометрические
функции
суммы
и
разно
I
I
I
Прямая,
перпендикулярная
к
отрезку
и
проходящая
через
его
середину,
называет
ся
серединным
nерnенди"уляром
к
нему.
сти
двух
углов
через
тригонометрические
функции
этих
углов.
Косинус
разности
двух
углов
Повернем
радиус
ОА
единичной
окруж
ности
вокруг
точки
О
на
угол
а
и
на
угол
~
(см.
рисунок).
Получим
радиусы
ОВ
и
ОС.
Найдем
скалярное
произведение
векторов
ОВ
и
ОС.
Координаты
точки
В
равны
Х1
и
У1'
координаты
точки
С
равны
Х2
и
У2'
Векторы
ОВ
и
ОС
имеют
такие
же
координаты,
как
и
координа
ты
точек
В
и
С.
А
По
определению
скалярного
произведе
ния
векторов,
заданных
координатами
векторов,
ОВ·
ОС
=
Х1
Х
2
+
У1У2'
Из
определения
тригонометрических
функ
ций
в
единичной
окружности,
имеем:
Х2
=
сов ~
;
У2
=
sin
~
;
Х1
=
сов
а
;
У1
=
sin
а
.
Скалярное
произведение
векторов
опре
деляется
формулой
ОВ
.
ОС
=
IOBI·IOcl·
сов
LBOC
.
Так
как
длина
радиуса
единичной
окруж
ности
равна
единице,
а
LBOC
=
а
-
~, по
лучим
сов(а
-~)
=
совасов
~
+
sin
asin~.
(1)
Косинус
разности
двух
углов
равен
nро
изведению
"осинусов
этих
углов
плюс
произведение
синусов
этих
углов.
Косинус
суммы
двух
углов
Из
формулы
(1)
легко
получить
формулу
косинуса
суммы
двух
углов:
cos
(а
+~)
= [cos
а
-
(-~)]
=
=
сов
а
сов
(-~)
+
sin
а
sin(
-~)
=
=
сов
а
сов
~
-
sin
а
sin
~
.
L
(На
рис.
1
и
2
обозначен
С.
П.)
~
А
D
Рис.
1
Теорема
1.
Если
точ"а
лежит
на
сере
динном
nерnенди"уляре
"
отрез"у,
то
она
равноудалена
от
его
"онцов.
м
А!
~(ф
~(
\
В
о
Рис.
2
I-----~----
I 43.
Теорема
Фалеса
Теорема.
Если
на
одной
прямой
отло
I
жить
нес"оль"о
равных
отрез"ов
и
че
~
рез
их
"онцы
провести
nараллельные
nря:
/{о
мые,
то
эти
прямые
отсе"ут
на
второи
I
прямой
равные
между
собой
отрез"и.
wн
~
А}
B
1
}
Рис.
1
Таким
образом,
если
АВ
=
ВС
=
CD
и
АА
1
11
BВJ.
11
СС1
11
DD], ,
то
А
1
В
1
=
В
1
С
1
=
C
1
D
1
(рис.
1).
Отрезки
называются
nроnорциональны
ми,
если
пропорциональны
их
длины.
Теоремы
о
пропорциональных
отрезках
Определение.
Отрез"и
называют
nро
nорциональными.
если
nроnорциональны
их
длины.
~
~_~
42
43

г-----------T-----~----I
Возьмем
произвольную
точку
М
на
сере-
I
Итак,
динном
перпендикуляре
(рис.
2)
и
соеди-
cos(a+~)=cosacos~-sinasin~.
(2)
ним
ее
с
концами
отрезка
АВ.
Середин-
I
Косинус
суммы
двух
углов
равеn
nроиз
ный
перпендикуляр
пересекает
отрезок
АВ
ведепию
косинусов
этих
углов
минус
nро
I
в
точке
О;
/;.
АОМ
равен
/;.
БОМ
по
перво-
изведение
сипусов
этих
углов.
му
признаку
равенства
треугольников
(ОА
=
ОБ,
ОМ
-
общая
сторона,
LЛОМ
=
Синус
суммы
и
синус
разности
=
LБОМ
=
90').
Из
равенства
треугольни
двух
углов
ков
следует,
что
МА
=
МБ.
Формулы
синуса
суммы
и
синуса
разно
Теорема
2.
Если
точка
равноудалена
сти
двух
углов
получим,
используя
фор
от
концов
отрезка,
то
она
лежит
на
мулы
приведения
и
формулу
(1):
серединnом
nерnендикуляре
к нему.
По
теоремы
=
МБ
(см.
sin(a+~)
=cos(j-(a+~»)=
условию
МА
рис.
2).
Поэтому
треугольник
АМБ
-
рав
нобедренный.
Отрезок
МО
является
меди
=cos((~-a
)-~)=
аной.
По
свойствам
равнобедренного
тре
угольника
медиана
является
также
и
его
высотой.
Следовательно,
прямая
ОМ
сов
=cos(j-a
)cos~+sin(j-a
)sin~=
падает
с
серединным
перпендикуляром.
А
это
означает,
что
точка
М
лежит
на
сере
=
sin
а
сов
~
+ cos
а
sin
~
.
динном
перпендикуляре.
I
Итак,
sin
(а
+
~)
=
sin
а
cos
~
+
сов
а
sin
~.
(3)
Синус
суммы
двух
углов
равен
произве
*
дению
синуса
первого
угла
на
косинус
I
второго
плюс
произведение
косинуса
пер
I
вого
угла
на
синус
второго.
sin
(а
-
~)
= sin
[(а
+
(-
~)]
=
-----~
I
= sin
а
cos
(-
~)
+ cos
а
sin
(-
~)
=
Теорема.
Параллельные
прямые,
nере
= sin
а
cos
~
- cos
а
sin
~
секающие
стороны
угла,
отсекают
на
Итак,
них
nроnорциональные
отрезки.
sin
(а
-
~)
= sin
а
cos
~
- cos
а
sin~.
(4)
На
рис.
2
прямые
АА
1
и
ББ
1
параллель
Синус
разности
двух
углов
равен
nро
ны.
По
сформулированной
теореме
изведению
синуса
первого
угла
на
коси
нус
второго
минус
произведение
IOA
1
1_IOAI
косину
са
первого
угла
на
синус
второго.
1°ВJ.I-IОБI
.
Формулы
(1)-(4)
называют
формулами
сложения
для
синуса
и
косинуса.
Приведем
примеры
использования
фор
мул
сложения.
Пример.
Вычислим
cos 75°
и
sin 750.
Решение.
Представим
75°
в
виде
суммы
о:>А
30° + 45°.
cos 75° = cos (30° + 45°) =
Рис.
2
= cos 30° .
сов
45° - sin 30° . sin 45° =
Обратная
теорема.
Если
отрезки
ОА
1
и
=
J3
.
.J2
_!
.
.J2
=.J2
(JЗ
-1)'
ОБ
1
пропорциональны
отрезкам
ОА
и
ОБ
2 2 2 2 4 '
и
лежат
соответственно
на
лучах
ОА
1
и
sin 75° = sin (30° + 45°) =
ОА,
то
прямые
АА
1
и
ББ
1
параллельны
=
sin 30° .
сов
45° + cos 30° . sin 45° =
(см.
рис.
2).
=!
.
.J2
+
J3
.J2
=
.J2
(1
+
JЗ).
2 2 2 2 4
L_~
~
~
г----~-----T-----------I
44.
Признаки
паpaJIJIeJIЬНОСТИ
прямых
45.
Основные
свойства
I
Определение.
Две прямые
на
nлоско-
треугольника
сти
называются
nараллельnыми,
если
I
Треугольником
называется
многоуголь
они
не
пересекаются.
I
ник
с
тремя
углами
(и
с
тремя
сторона
Параллельность
прямых
а
и
Ь
обознача-
I
ми).
Стороны
и
углы
треугольника
счита
ют
так:
а
11
Ь.
На
рис.
1
изображены
пря-
ются
основными
элементами
треугольни
мые
а
и
Ь,
перпендикулярные
к
прямой
с.
I
ка.
Если
прямые
а
и
Ь
не
пересекаются
и
пер
пендикулярны
к
третьей
прямой
С,
то
они
в
параллельны.
c~
A~
а
Ь
С
=t
ь
Рис.
1
На
рис.
1
в
треугольнике
АВе
сторона
а
Рис.
1
Рис.
лежит
против
угла
а
и,
наоборот,
против
Прямая
с
называется
секущей
по
отно
стороны
а
лежит
угол
а.
Аналогично
Ь
шению
к
прямым
а
и
Ь,
если
она
пересека
лежит
против
~,
с
против
у.
ет
их
в
двух
точках
(рис.
2).
При
пересече
нии
прямых
а
и
Ь
секущей
с
образуются
Неравенства
треугольника
восемь
углов,
которые
на
рис.
2
обозначе
ны
цифрами.
Пары
этих
углов
имеют
спе
Для
существования
треугольника,
зада
циальные
названия:
ваемого
тремя
сторонами
а,
Ь,
с,
необхо
накрест
лежащие
углы:
3
и
5,
4
и
6;
димо
и
достаточно
выполнение
неравенств
односторонnие
углы:
4
и
5,
3
и
6;
треугольника:
соответственные
углы:
1
и
5,
4
и
8,
а
+
Ь
>
с,
2и6,3и7.
а
+
с>
Ь,
Рассмотрим
три
признак
а
параллельно
Ь
+
с
>
а.
рами
углов.
Каждая
сторона
треугольника
меньше
Теорема
1.
Если
при
пересечении
двух
суммы
двух
других
сторон.
прямых
секущей
накрест
лежащие
углы
Любой
треугольник
считается
заданным
сти
двух
прямых,
связанные
с
этими
па
t
равны,
то
прямые
параллельны.
(т.
е.
можно
его
построить)
по
следующим
Доказательство.
Пусть
при
пересечении
трем
элементам:
прямых
а
и
Ь
секущей
АВ
накрест
лежа
-
по
одной
стороне
и
двум
углам;
щие
углы
равны:
Ll
=
L2
(рис.
3).
Дока
-
по
двум
сторонам
и
углу
между
ними;
жем,
что
а
11
Ь.
-
по
трем
сторонам.
Треугольник
однозначно
неопределен
по
трем
углам,
так
как
с
одинаковыми
угла
A
Ь
Aa
ми
а,
~,
у
можно
построить
сколь
угод
но
много
не
равных
треугольников.
Полу
ченные
треугольники
будут
подобными,
2
а
2
Ь
но
не
равными.
В
В
~
~
Соотношения
между
сторонами
Рис.
3
Рис.
4
и
углами
треугольника
а
11
А/
I
1.
Против
большей
стороны
лежит
больший
угол.
2.
Против
большего
угла
лежит
боль
шая
сторона.
3.
Против
равnых
сторон
лежат
рав
Ь./2
h6 I
nые
углы,
и,
обратно,
против
равных
L
~_Н1
__
~ис.~~угловлежатравныест~оnы~-~
44
45
---
г-----------T-----~----I
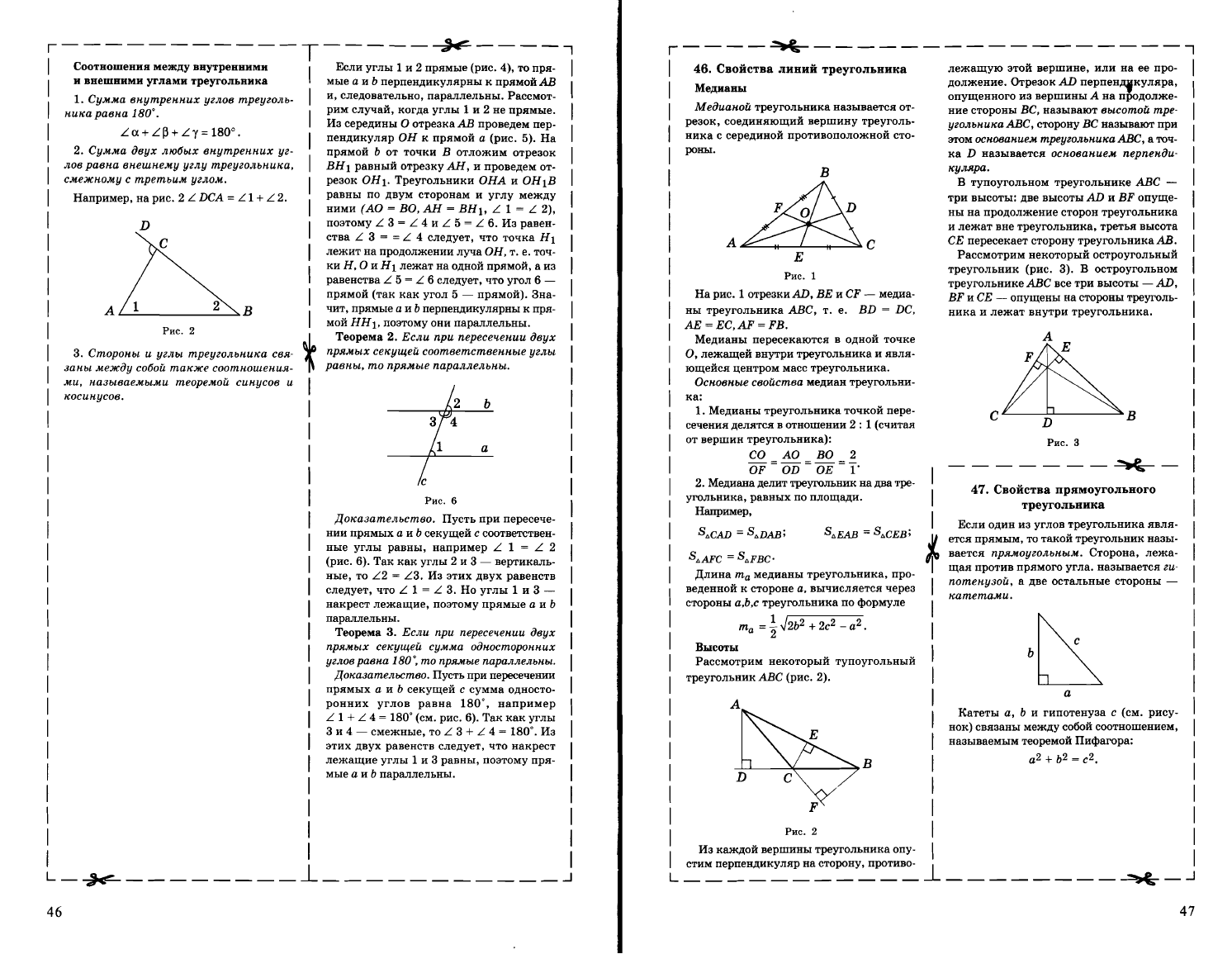
Соотношения
между
внутренними
I
Если
углы
1
и
2
прямые
(рис.
4),
то пря
и
внешними
углами
треугольника
мые
а
и
Ь
перпендикулярны
к
прямой
АВ
1.
Сумма
внутренних
углов
треуголь-
I
и,
следова:ельно,
параллельны.
Рассмот
ника
равна
180·.
рим
случаи,
когда
углы
1
и
2
не
прямые.
I
Из
середины
О
отрезка
АВ
проведем
пер
L
а
+ L
~
+L'Y =
1800.
I
пендикуляр
ОН
к
прямой
а
(рис.
5).
На
2.
Сумма
двух
любых
внутренних
уг-
прямой
Ь
от
точки
В
отложим
отрезок
лов
равна
внешнему
углу
треугольника.
I
ВН
1
равный
отрезку
АН,
и
проведем
от
смежному
с
третьим
углом.
I
резок
ОН1.
Треугольники
ОНА
и
ОНIВ
Например,
на
рис.
2 L DCA = L 1 + L 2.
равны
по
двум
сторонам
и углу
между
I
ними
(АО
=
ВО.
АН
=ВН1,
L 1 = L 2),
поэтому
L 3 = L 4
и
L 5 = L 6.
Из
равен
ства
L 3 = = L 4
следует,
что
точка
Н
1
I
лежит
на
продолжении
луча
ОН.
т.
е.
точ
ки
Н,
О
И
Н
1
лежат
на
одной прямой,
а
из
I
равенства
L 5 = L 6
следует,
что угол
6 -
I
прямой
(так
как
угол
5 -
прямой).
3на
чит,
прямые
а
и
Ь
перпендикулярны
к
пря
A~B
I
мой
НН
1.
поэтому
они
параллельны.
I
Рис.
2
Теорема
2.
Если
при
пересечении
двух
*
прямых
секущей
соответственные
углы
3.
Стороны
и
углы
треугольника
свя
равны.
то
прямые
параллельны.
заны
между
собой
также
соотношения
ми,
называемыми
теоремой
синусов
и
косинусов.
ь
а
Рис.
6
Доказательство.
Пусть
при
пересече
нии
прямых
а
и
Ь
секущей
с
соответствен
ные
углы
равны,
например
L 1 = L 2
(рис.
6).
Так
как
углы
2
и
3 -
вертикаль
ные,
то
L2
=
L3.
Из
этих
двух
равенств
следует,
что
L 1 = L 3.
Но
углы
1
и
3 -
накрест
лежащие,
поэтому
прямые
а
и
Ь
параллельны.
Теорема
3.
Если
при
nересе'lении
двух
прямых
секущей
сумма
односторонних
углов
равна
180·.
то
прямые
параллельны.
Доказательство.
Пусть
при
пересечении
прямых
а
и
Ь
секущей
с
сумма
односто
ронних
углов
равна
180·,
например
L 1 +L 4 =
180·
(см.
рис.
6).
Так
как
углы
3
и
4 -
смежные,
то
L 3 + L 4 =
180·.
Из
этих
двух
равенств
следует,
что
накрест
лежащие
углы
1
и
3
равны,
поэтому
пря
мые
а
и
Ь
параллельны.
L_~
~________
....J
~
г----~-----------------I
46.
Свойства
линий
треугольника
лежащую
этой
вершине,
или
на
ее
про
должение.
Отрезок
AD
перпеНдfкуляра,
Медианы
опущенного
из
вершины
А
на
продолже
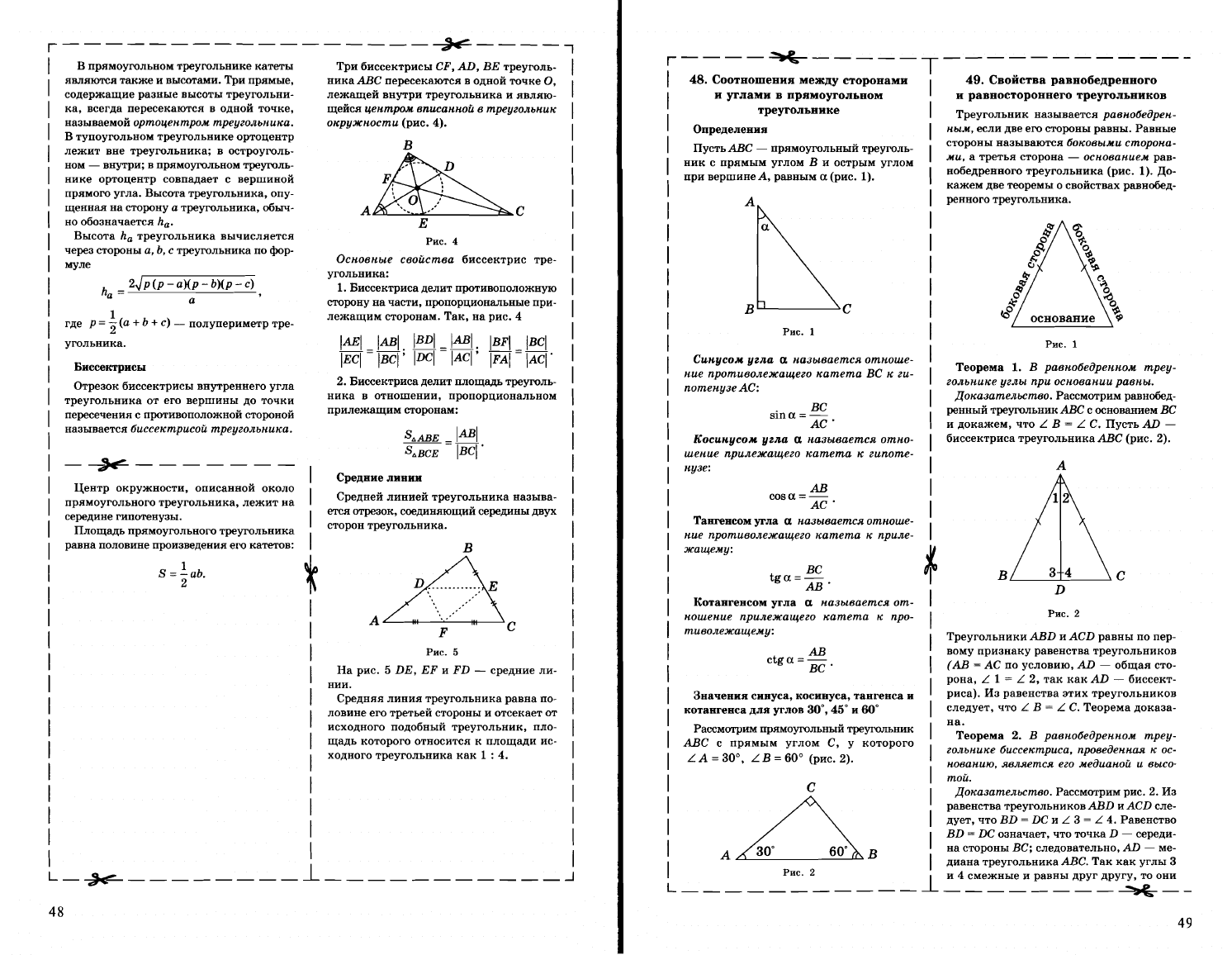
Медианой
треугольника
называется
от
ние
стороны
ВС,
называют
высотой
тре
резок,
соединяющий
вершину
треуголь
угольникаАВС,
сторону
ВС
называют
при
ника
с
серединой
противоположной
сто
этом
основанием
треугольникаАВС,
а
точ
роны.
ка
D
называется
основанием
nерnенди
кул.яра.
в
В
тупоугольном
треугольнике
АВС
-
три
высоты:
две
высоты
AD
и
BF
опуще
F4\D
ны
на
продолжение
сторон
треугольника
и
лежат
вне
треугольника,
третья
высота
СЕ
пересекает
сторону
треугольника
АВ.
A~C
Рассмотрим
некоторый
остроугольный
треугольник
(рис.
3).
В
остроугольном
Рис.
треугольнике
АВС
все
три
высоты
-
AD,
На
рис.
1
отрезки
AD,
ВЕ
и
CF
-
медиа
Е
BF
и
СЕ
-
опущены
на
стороны
треуголь
ны
треугольника
АВС,
т.
е.
BD
= DC,
ника
и
лежат
внутри
треугольника.
АЕ
=
EC.AF
= FB.
Медианы
пересекаются
в
одной
точке
О,
лежащей
внутри
треугольника
и
явля
ющейся
центром
масс
треугольника.
Основные
свойства
медиан
треугольни
ка:
1.
Медианы
треугольника
точкой
пере
C~B
сечения делятся
в
отношении
2 : 1
(считая
D
от
вершин
треугольника):
Рис.
3
СО
АО
ВО 2
OF
=OD =
ОЕ
=
l'
I
-~
2.
Медиана
делит
треугольник
на
два
тре
47.
Свойства
прямоугольного
угольника,
равных
по
площади.
I
треугольника
Например,
I
Если
один
из
углов
треугольника
явля
S",CAD =
S",DAВ;
S",EAВ
= S",CEB;
ется
прямым,
то
такой
треугольник
назы
вается
прямоугольным.
Сторона,
лежа
S",AFC = S",FBC'
t
щая
против
прямого
угла.
называется
ги
Длина
та
медианы
треугольника,
про
потенузой,
а
две
остальные
стороны
-
веденной
к
стороне
а,
вычисляется
через
катетами.
стороны
а,Ь.с
треугольника
по
формуле
та
=!J2b
2
+2с
2
-а
2
•
2
Высоты
Рассмотрим
некоторый
тупоугольный
ь~
треугольник
АВС
(рис.
2).
а
А
Катеты
а,
Ь
и
гипотенуза
с
(см.
рису
нок)
связаны
между
собой
соотношением,
называемым
теоремой
Пифагора:
а
2
+
Ь
2
=
с
2
•
II
'(
~B
Рис.
2
Из
каждой
вершины
треугольника
опу
L~~рпендикулярн~рон~оти~~
~_....J
46
47
г-----------------~----I
В
прямоугольном
треугольнике
катеты
Три
биссектрисы
СР,
AD,
ВЕ
треуголь
являются
также
и
высотами.
Три
прямые,
никаАВС
пересекаются
в
одной
точке
О,
содержащие
разные
высоты
треугольни
лежащей
внутри
треугольника
и
являю
ка,
всегда
пересекаются
в
одной
точке,
щейся
цен-тро.м
вnисан-н-ой
в
треугольн-ик
называемой
ортоцен-тро.м
треугольн-ика.
окружн-ости
(рис.
4).
В
тупоугольном
треугольнике
ортоцентр
лежит
вне
треугольника;
в
остроуголь
ном
-
внутри;
в
прямоугольном
треуголь
нике
ортоцентр
совпадает
с
вершиной
прямого
угла.
Высота
треугольника,
опу
щенная
на
сторону
а
треугольника,
обыч
но
обозначается
h
a
•
Высота
h
a
треугольника
вычисляется
Рис.
4
через
стороны
а,
Ь,
с
треугольника
по
фор
Осн-овн-ые
свойства
биссектрис
тре
муле
угольника:
h =
2.jp(p-a)(p-b)(p-c)
,
1.
Биссектриса
делит
противоположную
a
а
сторону
на
части,
пропорциональные
при
1
лежащим
сторонам.
Так,
на
рис.
4
где
р
=
"2
(а
+
Ь
+
с)
-
полупериметр
тре
угольника.
IAEI
_IAВI.
IBDI =
IAВI.
IBFI _
IBcl
IECI
-
IBcl'
IDCI
IAcl'
IFAI -
\ACI'
Биссектрисы
2.
Биссектриса
делит
площадь
треуголь
Отрезок
биссектрисы
внутреннего
угла
ника
в
отношении,
пропорциональном
треугольника
от
его
вершины
до
точки
прилежащим
сторонам:
пересечения
с
противоположной
стороной
называется
биссектрисой
треугольн-ика.
SI:.AВE
_IAВI
SI:.BCE
-IBCI'
-~------
Средние
линии
Центр
окружности,
описанной
около
Средней
линией
треугольника
называ
I
I
прямоугольного
треугольника,
лежит
на
I
ется
отрезок,
соединяющий
середины
двух
середине
гипотенузы.
сторон
треугольника.
Площадь
прямоугольного
треугольника
равна
половине
произведения
его
катетов:
I
в
S =
!аЬ.
2
"""""":E
А
\............
С
*
~
F
Рис.
5
На
рис.
5
DE,
ЕР
и
FD
-
средние
ли
нии.
Средняя
линия
треугольника
равна
по
ловине
его
третьей
стороны
и
отсекает
от
I
исходного
подобный
треугольник,
пло
I
щадь
которого
относится
к
площади
ис
I
I
I
I
I
ходного
треугольника
как
1 :
4.
L_~
~
J
48
г----~-----T-----------
48.
Соотношения
между
сторонами
I
49.
Свойства
равнобедренного
и
углами
в
прямоугольном
и
равностороннего
треугольников
I
треугольнике
Треугольник
называется
равн-обедрен-
Определения
н-ы.м,
если
две
его
стороны
равны.
Равные
стороны
называются
боковы.ми
сторон-а
Пусть
АВС
-
прямоугольный
треуголь
.ми,
а
третья
сторона
-
осн-ован,ие.м
рав
ник
С
прямым
углом
В
и
острым
углом
нобедренного
треугольника
(рис.
1).
До
при
вершине
А,
равным
а
(рис.
1).
кажем
две
теоремы
о
свойствах
равнобед
ренного
треугольника.
А
В
'С
"
Рис.
1
Рис.
1
Сикусом
угла
а
н-азывается
отн-оше
Теорема
1.
В
равн-обедрен-н-о.м
треу
н-ие
противолежащего
катета
ВС
к
ги
гольн-uке
углы
при
осн-ован-ии
равн-ы.
nотен-узе
АС:
Доказательство.
Рассмотрим
равнобед
.
ВС
ренный
треугольник
АВС
с
основанием
ВС
Slпа=
АС'
и
докажем,
что
L В = L
С.
Пусть
AD
-
Косикусом
угла
а
н-азывается
отн-о
биссектриса
треугольника
АВС
(рис.
2).
шен-ие
прилежащего
катета
к гиnоте
н-узе:
А
АВ
cosa=-
АС'
Тангенсом
угла
а
н-азывается
отн-оше
н-ие
противолежащего
катета
к
nриле
жаще.му:
ВС
~
В(
<5t4
\
С
tga=
АВ'
Котангенсом
угла
а
н-азывается
от
н-ошен-ие
прилежащего
катета
к
nро
Рис.
2
тиволежаще.му:
Треугольники
AВD
и
ACD
равны
по
пер
АВ
вому
признак
у
равенства
треугольников
ctga
=
ВС'
(АВ
=
АС
по условию,
AD
-
общая
сто
рона,
L 1 = L 2,
так
как
AD
-
биссект
Значения
синуса,
косинуса,
тангенса
и
риса).
Из
равенства
этих
треугольников
котангенса
для
углов
300,
450
и
600
следует,
что
L
В
= L
С.
Теорема
доказа
на.
Рассмотрим
прямоугольный
треугольник
Теорема
2.
В
равн-обедрен-н-о.м
треу
АВС
с
прямым
углом
С,
у
которого
гольн-ике
биссектриса,
nроведен-н-ая
к
ос
LA
= 300,
LB
= 600
(рис.
2).
н-ован-ию,
является
его
.медиан-оЙ
и
высо
той.
С
I
Доказательство. Рассмотрим
рис.
2.
Из
равенства
треугольников
AВD
и
ACD
сле
I
дует,
что
BD
= DC
и
L 3 = L
4.
Равенство
~
BD
= DC
означает,
что
точка
D -
середи
А
300 600
В
I
на
стороны
ВС;
следовательно,
AD
-
ме
I
диана
треугольника
АВС.
Так
как
углы
3
I
L
~~~----~~~жныеиравныдругдру~они
49

г-----------T-----~----I
прямые.
Поэтому
биссектрисаAD
являет-
I
Катет,
лежащий
против
угла
300,
равен
ся
также
и
высотой
треугольника
АВС.
ВС
1
Так
как
биссектриса,
медиана
и
высо-
I
половине
гипотенузы,
т.
е.
АВ
=
2"'
но
та
равнобедренного
треугольника,
прове
денные
из
вершины
угла
к
основанию,
сов
~
=
sinA
=
sin30°.
падают,
справедливы
следующие
утверж
С
другой
стороны, по
определению
ко
дения:
ВС
1.
Высота
равнобедренного
треуголь
синуса,
АВ
=
cosB
=
cos60°.
Итак,
ника,
nроведенная
из
вершины
угла
к
основанию,
одновременно
является
его
sin
30° =
~
, cos
?оо
=
~
.
Из
основного
медианой
и
биссектрисой.
тригонометрического
тождества
sin
2
a +
2.
Медиана
равнобедренного
треуголь
+ cos
2
а
= 1
получаем
ника,
nроведенная
из
вершины
угла
к
основанию,
одновременно
является
его
cos 30° =
J1
-
sin
2
30° =
J1
_.!.
=
13
.
4
2'
высотой
и
биссектрисой.
Треугольник
называется
равносторон
sin
60° =
../1
- cos
2
60° =
J1
_.!.
=
13
.
ним
(или
правильным),
если
все его
сто
4 2
роныравны.
Значения
тангенса
и
котангенса
угла
Свойства
равностороннего
треугольни
можно
получить,
зная
значения
синуса
и
косинуса
этого
угла:
ка:
все
углы
равны
(каждый
из
углов
*
а)
Рассмотрим
равнобедренный
прямоуголъ
равен
60");
ный
треугольник
АВС
(рис.
3).
б)
каждая
из
трех
высот
является
так
же
медианой
и
биссектрисой;
с
в)
центр
окружности,
описанной
около
треугольника,
совпадает
с
центром
ок
ружности,
вписанной
в
него.
.(:5'
A~B
Рис.
3
По
теореме
ПифагораАВ2
=
Ас2
+
вс2
=
АВ
=
2Ас2
=
2вс2,
откуда
АС
=
ВС
=
.J2.
Следовательно,
ВС
1
.J2
sin
450
=
sinA
=
АВ
=
.J2
=
2'
АС
1
.J2
cos45°
=
cosA
=
АВ
=
.J2
=
2'
tg45°=tgA=~~=1,
ctg45°=1.
600
300
а
J3
2
1
2
tga
1
J3
J3
1
3
L_~
~
~
450
sina
1
J2
2
2
cosa
J3
J2
2
2
г----~-----T------
50.
Равенство
треугольников
I
51.
Сумма
углов
треугольника.
Определение.
Два
треугольника
назы-
Сумма
внутренних
углов
выпуклого
ваются
равными,
если
при
1laЛOжении
друг
I
многоугольника
на
друга
они
совместятся.
I
Сумма
углов
треугольннка
Если
треугольникиАВС
иАIВIСIРавны,
I
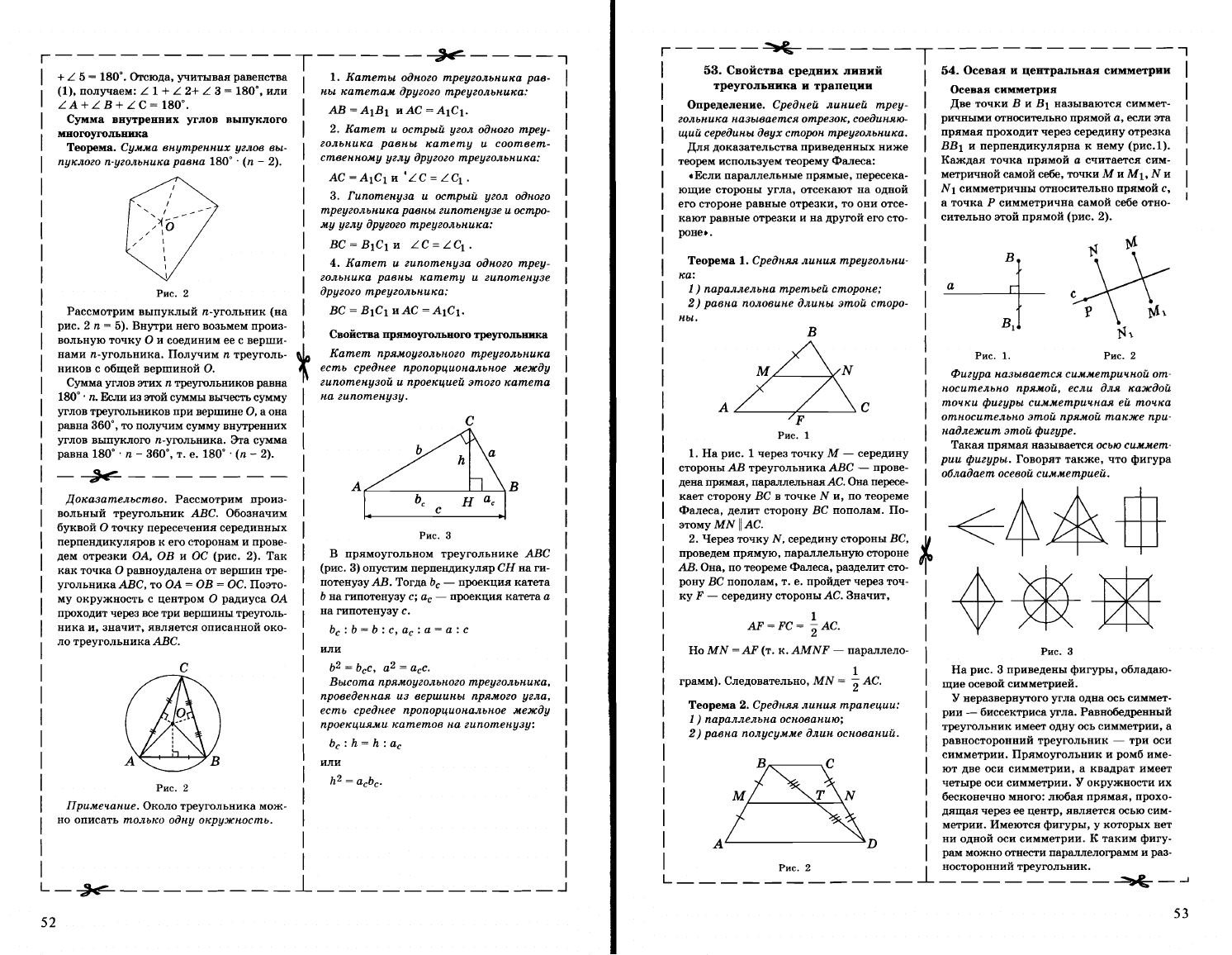
Теорема.
Сумма
углов
треугольника
то
их
соответственные
стороны
и
соот-
равна
180
о.
ветственные
углы
равны
(рис.
1). I
Доказательство.
Рассмотрим
произ
вольный
треугольник
АВС
и
докажем,
что
L А + L
В+
L
С
= 1800.
В
а
A~BA1~Bl
~
Рис.
1
ТоестъАВ=Аl
В
l;
ВС=ВIСl;
АС=АI
С
l
A~C
и
L А =L
А
1
;
L
В
=L
В
1
;
L
С
=L
С
1
.
Рис.
1
Проведем
через
вершину
В
прямую
а,
па
Признаки
равенства
треугольников
раллельную
стороне
АС
(рис.
1).
Углы
1
и
4
Теорема
1.
Если
две
стороны и
угол
меж
являются
накрест
лежащими
углами
при
пересечении
параллельных
прямых
а
и
АС
ду
ними
одного
треугольника
равны
соот
секущей
АВ,
а
углы
3
и
5 -
накрест
лежа·
ветственно
двум
сторонам
и
углу
между
щими
углами
при
пересечении
тех
же
па
ними
другого
треугольника,
то
такие
тре
раллельных
прямых
секущей
ВС.
Поэтому
угольники
равны.
На
рис.
1
L 4 = L
1,
L 5 = L 3. (1)
АВ=АIВl;
АС
=
А1Сl;
LA=LA
1
.
Сумма
углов
4,2
и
5
равна
развернуто
Теорема
2.
Если
сторона
и
прилежащие
му
углу
с
вершиной
В,
т. е.
L 4 + L 2 +
к
ней
углы
одного
треугольника
равны
соответственно
стороне
и
прилежащим
к
-------~
ней
углам
другого
треугольника,
то
та
кие
треугольники
равны.
На
рис.
1
52.
Окружность,
описанная
около
АС
=АIСl;
LA
=
LAl;
LC
=
LC
1
.
треугольника
Теорема
3.
Если
три
стороны
одного
Определения.
Если
все
вершины
много
треугольника
равны
соответственно
трем
угольника
лежат
на
окружности,
то
ок
сторонам
другого
треугольника,
то
такие
ружность
называется
описанной
около
t
треугольники
равны.
На
рис.
1
многоугольника,
а
многоугольник
-
впи
=
АВ
=АIВl;
АС
=АIСl;
ВС
ВIСl'
санным
в
эту
окружность.
На
рис.
1
че
Признаки
равенства
треугольников
до
тырехугольник
AВCD
вписан
в
окруж
казываются
наложением
одного
треуголь
ность
с
центром
О,
а
четырехугольник
ника
на
другой.
AECD
не
является
вписанным
в
эту
ок
ружность,
так
как
его
вершина
Е
не
ле
Признаки
равенства
прямоугольных
жит
на
данной
окружности.
Треугольник
треугольников
АВС
на
рис.
2
вписан
в
окружность
с
цен
тром
О.
в
~~
~
А
С
A
1
C
1
~
Рис.
2
Прямоугольные
треугольники
АВС
и
I
Рис.
1
АIВIСl
(рис.
2)
равны,
если
выполняется
любое
из
приведенных
ниже
четырех
ус-
I
Теорема.
Около
любого
треугольника
L~ий:
~можно~~~~ужность.~_~
50
51
г-----------T-----~----I
+ L 5 = 1800.
Orсюда,
учитывая
равенства
1.
Катеты
одного
треугольника
рав
I
(1),
получаем:
L 1 + L
2+
L 3 = 1800,
или
ны
катета.м
другого
треугольника:
L
А
+ L В + L
С
= 1800.
АВ
=АIВl
иАС
=АIС1.
Сумма
внутренних
углов
выпуклого
2.
Катет
и
острый
угол
одного
треу
многоугольника
гольника
равны
катету
и
соответ
Теорема.
Су.м.ма
внутренних
углов
вы
ственно.му
углу
другого
треугольника:
пуклого
п-угольника
равна
1800
.
(п
- 2).
АС
=АIСl
и
'LC
=
LC
1
.
3.
Гипотенуза
и
острый
угол
одного
треугольника
равны
гипотенузе
и
остро
.му
углу
другого
треугОЛЫiUка:
ВС
=
Вl
Сl
и
L
С
= L
С
1
.
4.
Катет
и
гипотенуза
одного
треу
гольника
равны
катету
и
гипотенузе
Рис.
2
другого
треугольника:
Рассмотрим
выпуклый
п-угольник
(на
ВС
=
ВIСl
иАС
=АIС1.
рис.
2 n = 5).
Внутри
него
возьмем
произ
Свойства
прямоугольного
треугольника
вольную
точку
О
и
соединим
ее
с
верши
нами
п-угольника.
Получим
n
треуголь
Катет
прямоугольного
треугольника
ников
с
общей
вершиной
О.
есть
среднее
пропорциональное
.между
Сумма
углов
этих
n
треугольников
равна
гипотенузой
и
проекцией
этого
катета
1800
.
п.
Если
из
этой
суммы
вычесть
сумму
на
гипотенузу.
*
углов
треугольников
при
вершине
О, а
она
равна
3600,
то
получим
сумму
внутренних
с
углов
выпуклого
п-угольника.
Эта
сумма
равна
1800
. n - 3600,
т.
е.
1800.
(п
- 2).
-~------
А/
II
\В
Доказательство.
Рассмотрим
произ
вольный
треугольник
АВС.
Обозначим
буквой
О
точку
пересечения
серединных
Рис.
3
перпендикуляров
к
его
сторонам
и
прове
В
прямоугольном
треугольнике
АВС
как
точка
О
равноудалена
от
вершин
тре
(рис.
3)
опустим
перпендикуляр
СН
на
ги
угольника
АВС.
то
ОА
=
ОВ
=
ОС.
Поэто
дем
отрезки
ОА,
ОВ
и
ОС
(рис.
2).
Так
потенузу
АВ.
Тогда
Ь
С
-
проекция
катета
му
окружность
с
центром
О
радиуса
ОА
Ь
на
гипотенузу
с;
ас
-
проекция
катета
а
на
гипотенузу
с.
проходит
через
все
три
вершины
треуголь
ника
и,
значит,
является
описанной
око
Ь
с
:
Ь
=
Ь
:
с,
ас
:
а
=
а
:
с
ло
треугольника
АВС.
или
с
ь
2
=
Ьсс,
а
2
=
асс.
Высота
пря.моугольного
треугольника,
проведенная
из
вершины
прямого
угла,
есть
среднее
пропорциональное
.между
проекция.ми
катетов
на
гипотенузу:
Ь
С
: h = h :
ас
или
G!fiJ
h
2
=
асЬ
с
·
Рис.
2
При.мечание.
Около
треугольника
мож
но описать
только
одну
окружность.
L_~
~
~
г----~-----T-----------I
53.
Свойства
средних
линий
I
54.
Осевая
и
центральная
симметрии
I
треугольника
и
трапеции
Осевая
симметрия
I
Определение.
Средней
линией
треу-
I
Две
точки
В
и
Вl
называются
симмет
голь
ника
называется
отрезок,
соединяю-
I
ричными
относительно
прямой
а,
если
эта
I
щий
середины двух
сторон
треугольника.
I
прямая
проходит
через
середину
отрезка
I
Для
доказательства
приведенных
ниже
ВВl
и
перпендикулярна
к
нему
(рис.l).
I
теорем
используем
теорему
Фалеса:
I
Каждая
точка
прямой
а
считается
сим
_Если
параллельные
прямые,
пересека-
метричной
самой
себе,
точки
М
и
М
1,
N
и
I
ющие
стороны
угла,
отсекают
на
одной
I
Nl
симметричны
относительно
прямой
с,
его
стороне
равные
отрезки,
то
они
отсе-
I
а
точка
Р
симметрична
самой
себе
отно-
I
кают
равные
отрезки
и
на
другой
его
сто-
сительно
этой
прямой
(рис.
2).
роне
•.
Теорема
1.
Средняя
линия
треугольни
ка:
1)
параллельна
третьей
стороне;
2)
равна
половине
длины
этой
сторо
ны.
в
1
~\
~*
МдN
Рис.
1.
Рис.
2
Фигура
называется
си.м.метричноЙ
от
носительно
прямой,
если
для
каждой
точки
фигуры
си.м.метричная
ей
точка
ALAC
относительно
этой
прямой
также
при
F
надлежит
этой
фигуре.
Рис.
1
Такая
прямая
называется
осью
си.м.мет
1.
На
рис.
1
через
точку
М
-
середину
рии
фигуры. Говорят
также,
что
фигура
стороны
АВ
треугольника
АВС
-
прове
обладает
осевой
си.м.метриеЙ.
дена
прямая,
параллельная
АС.
Она
пересе
кает
сторону
ВС
в
точке
N
и,
по
теореме
Фалеса,
делит
сторону
ВС
пополам.
По
этому
MN
11
АС.
2.
Через
точку
N,
середину
стороны
ВС,
~
~Ф.tE
проведем
прямую,
параллельную
стороне
АВ.
Ова,
по
теореме
Фалеса,
разделит
сто
рону
ВС
пополам,
т.
е.
пройдет
через
точ
ку
F -
середину
стороны
АС.
Значит,
1
AF=FC=
"2АС.
+.*
Но
MN
=AF
(т.
к.
AМNF
-
параллело-
Рис.
3
1
На
рис.
3
приведены
фигуры,
обладаю
грамм).
Следовательно,
MN
=
"2
АС.
щие
осевой
симметрией.
у
неразвернутого
угла
одна
ось
симмет
Теорема
2.
Средняя
линия
трапеции:
рии
-
биссектриса
угла.
Равнобедренный
1)
параллельна
основанию;
треугольник
имеет
одну
ось
симметрии,
а
2)
равна
полусу.м.ме
длин
оснований.
равносторонний
треугольник
-
три
оси
симметрии.
Прямоугольник
и
ромб
име
ют
две
оси
симметрии,
а
квадрат
имеет
четыре
оси
симметрии.
У
окружности
их
бесконечно
много:
любая
прямая,
прохо
дящая
через
ее
центр,
является
осью
сим
метрии.
Имеются
фигуры,
у
которых
вет
ни
одной
оси
симметрии.
К
таким
фигу
А'
3п
рам
можно
отнести
параллелограмм
и
раз
L
-.:~
2
..1
носторонний
треугольник.
_
~
_
-1
53
52

г-----------T-----~----I
Центральная
симметрия
I 1.
Рассмотрим
трапециюАВСD
(рис.
2).
Две
точки
А
и
Аl
называются
симмет-
Пусть
М
-
середина
стороны
АВ,
а
N -
ричными
относительно
точки
О,
если
О
I
середина
стороны
CD.
Разобьем
трапецию
середина
отрезка
ААl
(рис.
4).
Точка
О
I
диагональю
BD
на
два
треугольника.
Че
считается
симметричной
самой
себе.
рез
точку
М
проведем
прямую,
параллель
ную
стороне
AD.
Она
пересечет
диагональ
А А
BD
в
точке
Т
-
середине
BD.
по
теореме
О
• I • I • 1
Фалеса.
По
той
же
теореме
прямая
прой
дет
через
середину
CD,
Т.е.
через
точку
N.
Следовательно,
средняя
линия
MN
трапе
Рис.
4
ции
параллельна
основаниюAD,
т.
к.
ле
На
рис.
5
точки
С
и
Сl,
В
и
Вl
симмет
жит
на
прямой,
параллельной
AD.
ричны
относительно
точки
О, а
точки
Р
2.
Согласно
свойству
средней
линии
тре
и
Q
не
симметричны
относительно
этой
1 1
точки.
угольника
TN
=
2"
ВС,
МТ
=
2"
AD.
Следовательно,
р
в
MN
=
MT+TN
=
2"
AD
+
2"
ВС,
т.
е.
C~Cl
1 1
MN=
2"
1
(AD+BC).
Q
Рис.
5
*
Фигура
называется
си,мметричной
от
носительно
точки
О.
если
для
каждой
точки
фигуры
симметричная
ей
точка
относительно
точки
О
также
принад
лежит
этой
фигуре.
Например,
центральной
симметрией
об
ладают окружность
и
параллелограмм
(рис.
6).
Центром
симметрии
окружности
является
ее
центр,
а
центром
симметрии
параллелограмма
-
точка
пересечения
его
диагоналей.
GJN
Рис.
6
Изображения
на
плоскости
многих
пред
метов
окружающего
нас
мира
имеют
ось
симметрии
или
центр
симметрии.
L_~
~
~
г----~-----T------
55.
Признаки
параллелограмма
I
56.
Окружность,
вписанная
в
треугольник
Рассмотрим
три
признака
параллело
грамма.
1.
Если
в
четырехугольнике
две
сторо
Определения.
Если
все
стороны
много
ны
равны
и
параллельны,
то
этот
че
угольника
касаются
окружности,
то
ок
тырехугольник
-
nараллелограм,м.
ружность
называется
вписанной
в
много
угольник,
а
многоугольник
-
описанным
около
окружности.
На
рис.
1
четырех
C_",~,....-----_
угольник
EFMN
описан
около
окружнос
ти
с
центром
О,
а
четырехугольник
DKMN
не
является
описанным
около
этой
окруж
ности,
так
как
сторона
DK
не
касается
окружности.
На
рис.
2
треугольник
АВС
описан
около
окружности
с
центром
О.
,
~
"А
Рис.
1
Пусть
в
четырехугольнике
ABCD
(рис.
1)
стороны
АВ
и
CD
параллельны
и
АВ
= CD.
Проведем
диагональ
АС,
разде
ляющую
данный
четырехугольник
на
два
треугольника:
АВС
и
CDA.
Эти
треуголь
ники
равны
по
двум
сторонам
и
углу
Nl
'>...
<'"
'М
между
ними
(АС
-
общая
сторона,
АВ
= CD
по
условию,
L 1 = L 2
как
на
Рис.
1
крест
лежащие
углы
при
пересечении
па
раллельных
прямых
АВ
и
CD
секущей
АС),
поэтому
L 3 = L 4.
Но
углы
3
и
4-
накрест
лежащие
при
пересечении
пря
-------~
мых
AD
и
ВС
секущей
АС,
следователь
57.
Касательная
к
окружности
HO,AD
II
ВС.
и
ее
свойства
Таким
образом,
в
четырехугольнике
AВCD
противоположные
стороны
попар
Определение.
Прямая,
и,меющая
с ок
но
параллельны;
следовательно,
четырех
ружностью
только
одну
общую
точку.
угольник
AВCD
-
параллелограмм.
называется
касательной
к
окружности,
~
а
их
общая
точка
называется точкой
2.
Если
в
четырехуzoльнике
противопо
касания
прямой
и
окружности.
На
рис.
1
ложные
стороны
попарно
равны,
то
этот
прямая
р
-
касательная
к
окружности
с
четырехугольник
-
nараллелогра,м,м.
центром
О,А
-
точка
касания.
Проведем
диагональ
АС
четырехуголь
никаАВСD,
разделяющую
его
на
треуголь
ники
АВС
и
CDA
(см.
рис.
1).
Эти
треугольники
равны
по
трем
сто
ронам
(АС
-
общая
сторона,
АВ
= CD
и
ВС
=
DA
по
условию),
поэтому
L 1 = L
2.
Отсюда
следует,
что
АВ
11
CD.
Так
как
АВ
= CD
и
АВ
11
CD,
то
по
признаку
1
четырехугольник
ABCD
-
параллело
грамм.
Рис.
Теорема.
Касательная
к
окружности
nерnендикулярна
к
радиусу,
nроведенно
,му
в
точку
касания.
Доказательство.
Пусть
р
-
касатель
ная
к
окружности
с
центром
О,
А-точка
касания
(см.
рис.
1).
Докажем,
что
каса
L
~тельн~~ерпендик~ярн~~~~
р
54
55

г-----------T-----~----I
С
~
м
...
,,'"
.9..
".
А
-
--
-
к
-----------
-
в
Рис.
2
Теорема.
В
любой
треугольник
,можно
вписать
окружность.
Доказательство.
Рассмотрим
произволь
ный
треугольник
АВС
и
обозначим
бук
вой
О
точку
пересечения
его
биссектрис.
Проведем
из
точки
О
перпендикуляры
ОК,
OL
и
ОМ
соответственно
к
сторонам
АВ,
ВС
и
СА
(см.
рис.
2).
Так
как
точка
О
равноудалена
от
сторон
треугольника
АВС.
то
ОК
= OL =
ОМ.
Поэтому
окружность
с
центром
О
радиуса
ОК
проходит
через
точ
ки
К,
L
и
М.
Стороны
треугольника
АВС
касаются
этой
окружности
в
точках
К,
L,
М,
так
как
они
перпендикулярны
к
ради
усам
ОК,
OL
и
ОМ.
Значит,
окружность
с
центром
О
радиуса
ОК
является
вписан
ной
в
треугольник
АВС.
При,мечание.
В
треугольник
,можно
впи
сать
только
одну
окружность.
-~------
Предположим,
что
это
не
так.
Тогда
радиус
ОА
является
наклонной
к
прямой
р.
Так
как
перпендикуляр,
проведенный
из
точки
О
к
прямой
р,
меньше
наклон
ной
ОА,
то
расстояние
от
центра
О
ок
ружности
до
прямой
р
меньше
радиуса.
Следовательно,
прямая
р
и
окружность
имеют
две
общие
точки.
Но
это
противо
речит
условию,
что
прямая
р
-
касатель
ная.
Таким
образом,
прямая р
перпенди
кулярна к
радиусу
ОА.
Теорема
доказана.
Обратная
теорема.
Если
прямая
прохо
дит
через
конец
радиуса,
лежащий
на
ок
ружности,
и
nерnендикулярна
к
это,му
радиусу,
то
она
является
касательной.
Доказательство.
Из
условия
теоремы
следует,
что
данный
радиус
является
пер
пендикуляром,
проведенным
из
центра
окружности
к
данной
прямой.
Поэтому
расстояние
от
центра
окружности
до
пря
мой
равно
радиусу,
и,
следовательно,
пря
мая
и
окружность
имеют
только
одну
общую
точку.
Но
это
означает,
что
дан
ная
прямая
является касательной к
ок
ружности.
Теорема
доказана.
L_~
I
3.
Если
в
четырехугол.ьнике
диагонали
I
nерш<аютея
и
та«ои
их
nерееечеn""
I
I
делятся
nоnoла.м,
mo
этот
четырехуголь
I
ник
-
nараллелогра,м,м.
I
I
с
\i:;
/з\
:
I
I
v
"'А
I
Рис.
2
I
Рассмотрим
четырехугольник
AВCD,
в
котором
диагонали
АС
и
BD
пересекают
I
ся
в
точке
О
и
делятся
этой
точкой
попо
лам
(рис.
2).
Треугольники
АОВ
и
COD
равны
по
двум
сторонам
и
углу
между
*
ними
(АО
=
ОС,
ВО
= OD
по
условию,
L-AOB = L
COD
как
вертикальные
углы),
поэтому
АВ
=
CD
и
L 1 = L 2.
Из
равенства
углов
1
и
2
следует,
что
AВIICD.
Итак,
в
четырехугольнике
AВCD
сторо
ны
АВ
и
CD
равны
и
параллельны,
зна
чит,
по
признаку
1
четырехугольник
AВCD
-
параллелограмм.
~
~
г----~-----T-----------I
58.
Измерение
угла,
вписанноrо
в
окружность
Угол
с
вершиной
в
центре
окружности
называется
ее
центральным
угло,м.
Пусть
стороны
центрального
угла
окружности
с
центром
О
пересекают
ее
в
точках
А
и
В.
Центральному
углу
АОВ
соответствуюг
две
дуги
с
концами
А
и
В
(рис.
1).
Дугу
ок
ружности
можно
измерять
в
градусах.
Градусная
мера
дуги
ALB
считается
рав
ной
градусной
мере
центрального
угла
АОВ.
Таким
образом,
центральный
угол
измеряется
градусной
мерой
дуги,
на
ко
торую
он
опирается.
в
0f(Э
L
М
Рис.
1
Рис.
2
Угол,
вершина
которого
лежит
на
ок
ружности,
а
стороны
пересекают
окруж
ность,
называется вnисанны,м
угло,м.
На
рис.
2
уголАВС
-
вписанный,
дуга
АМС
расположена
внутри
этого
угла.
В
таком
случае
говорят,
что
вписанный
угол
АВС
опирается
на
дугу
АМС.
Теорема.
Вписанный
угол
из,меряется
половиной
дуги,
на
которую
он
оnира·
ется.
Доказательство.
Пусть
L АВС -
впи
санный
угол
окружности
с
центром
О,
опирающийся
на
дугу
АС
(рис.
3-5).
~$
Рис.
3
Рис.
4
~
L
~~~
I
59.
Признаки
подобия
треугольников
Первый
nриана"
Теорема.
Если
два
угла
одного
тре
угольника
соответственно
равны
дву,м
угла,м
другого,
то
такие
треугольникu
подобны.
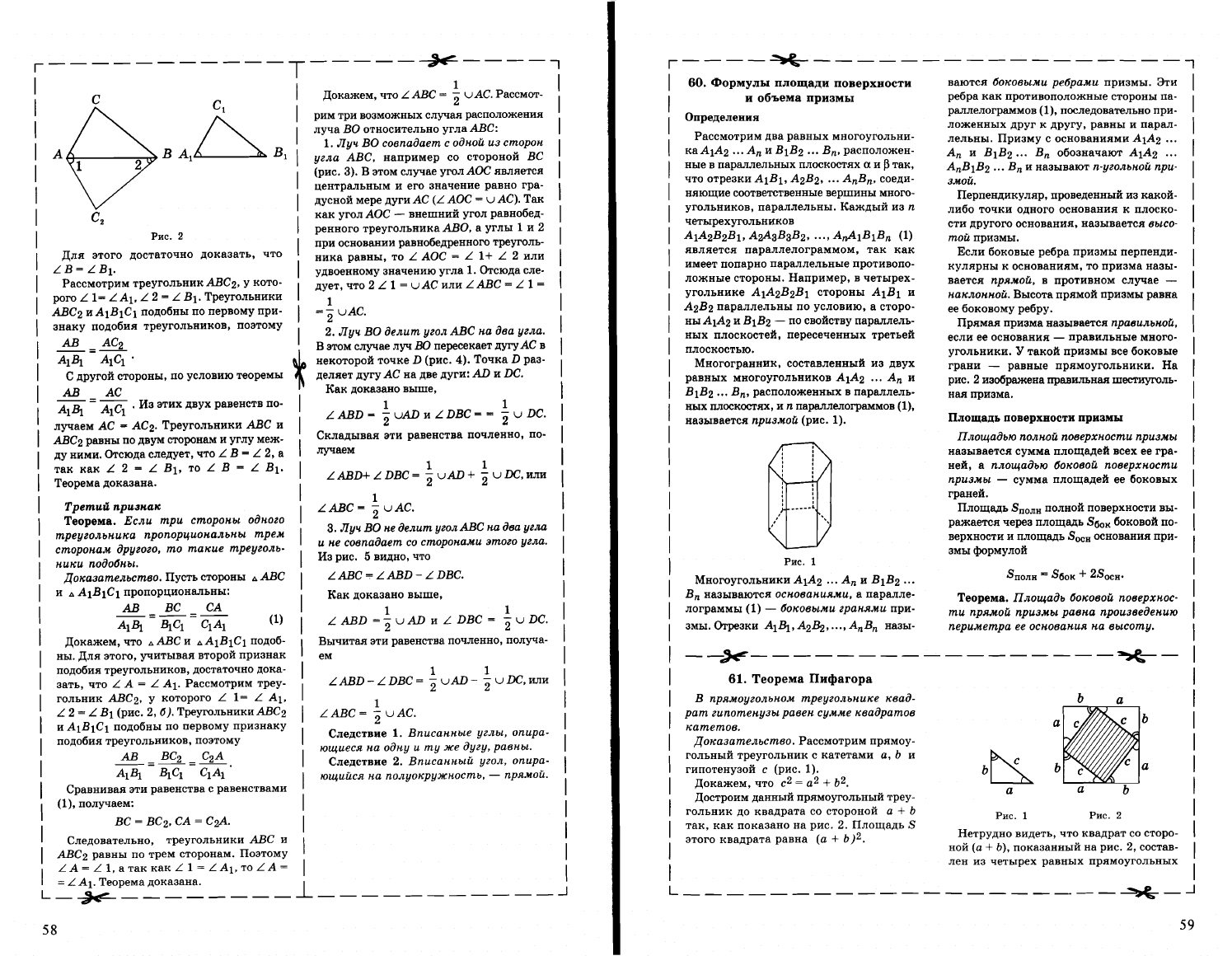
Доказательство.
ПустьАВС
иАIВIСl
-
два
треугольника,
у
которых
L
А
=
=LAl,
L В =
L-Bl
(рис.
1).
Докажем,
что
6
АВС
и
6
АIВIСl
подобны.
С
1
A~BA'~B'
Рис.
1
По
теореме
о
сумме
углов
треугольника
LC
=
180·
- L А -
L-
В.
Следовательно,
L
С
=
180·
-
LAl
- L
Вl
и,
значит,
LC
=
=
L
Сl'
Таким
образом,
углы
треугольни
ка
АВС
соответственно
равны
углам
тре
угольникаАlВlСl·
Докажем,
что
сходственные
стороны
тре
угольников
АВС
и Аl
Вl
Сl пропорциональ·
ны.
Так
как
LA
=
LAl
и
L
С
= L
Сl,
то
S6AВC
АВ·
АС
СА·
СВ
S6A
ВtC
=
АIВ:1'
АI
С
l
=
СI
А
l
.
СIВ:1
'
1
1
потому
что
площади
таких
треугольни
ков
относятся
как
произведения
сторон,
заключающих
равные
углы.
АВ
ВС
~
Из
этих
равенств
следует
Аl
в:1
=
в:1
Сl
.
Аналогично,
используя
равенства
LA
=
LAl.
LB
= L
Вl,
получаем
ВС
АС
--=--
В:1С
1
А
1
С
l'
Итак,
сходственные
стороны
треуголь
ников
АВС
и
АIВIСl
пропорциональны.
Следовательно,
эти
треугольники
подоб
ны.
Теорема
доказана.
Второй
nризна"
Теорема.
Если
две
стороны
одного
тре
угольника
nроnорциональны
дву,м
сторо
на,м
другого
треугольника
и
углы,
за
ключенные
.между
эти,ми
сторона.ми,
рав
ны,
то
такие
треугольники
подобны.
Доказательство.
Рассмотрим
тре
угольники
АВС
и
А1
В
1
С
1,
У
которых
АВ
АС
АIВ:1
=
АI
С
l
'
LA
= L
Аl
(рис.
2).
Дока
~же~~6АВСи~lВl~~~~
56
57
г-----------T-----~----I
С
I
Докажем,
что
L
АВС
=
~
uAC.
Рассмот-
I
1
С
I
рим
три
возможных
случая
расположения
I
I
луча
ВО
относительно
углаАВО:
I
1.
Луч
ВО
совпадает
с
одной
из
сторон
6,
А
В
А
1
В
1
I
угла
АВС.
например
со
стороной
ВС
I
(рис.
3).
В
этом
случае
угол
АОС
является
I
I
I
центральным
и
его
значение
равно
гра
I
дусной
мере
дуги
АС
(L
АОС
= u
АС).
Так
С
I
как
угол
АОС
-
внешний
угол
равнобед-
I
2
Рис.
2
ренного
треугольника
АВО.
а
углы
1
и
2
I
при
основании
равнобедренного
треуголь
Для
этого
достаточно
доказать,
что
ника
равны,
то
L
АОС
= L 1+ L 2
или
L
В
= L
Вl'
I
удвоенному
значению
угла
1.
Отсюда
сле·
Рассмотрим
треугольникАВС2,
У
кото-
дует,
что
2 L 1 =
uAC
или
LAВC
= L 1 =I
рого
L
1=
LA1.
L 2 = L
Вl·
Треугольники
1
АВС2
иАIВI01
подобны
по
первому
при·
I =2
uAO.
знаку
подобия
треугольников,
поэтому
I 2
Л
ВО
д
АВС
д
.
уч
елит
угол
на
ва
угла.
АВ
=
АС2
В
этом
случае
луч
во
пересекает
дугу
АС
в
Al~
АIС1'
~
не
которой
точке
D
(рис.
4).
Точка
D
раз
С
другой
стороны,
по
условию теоремы
~
деляет
дугу
АС
на
две
дуги:
AD
и
DC.
АВ
АС
Как
доказано
выше,
Аl
Jl.
=
А
С
.
Из
этих
двух
равенств
по-
1 1
""1 1 1 L
AВD
= -
uAD
и
L DBC = = - u
DC.
лучаем
АС
...
АС2'
Треугольники
АВО
и
2 2
АВС2
равны
по
двум
сторонам
и
углу
меж-
Складывая
эти
равенства
почленно,
по
ду
ними.
Отсюда
следует,
что
L
В
L 2,
а
лучаем
так
как
L 2
...
L
Вl,
то
L
В
L
Вl'
1 1
Теорема
доказана.
L
AВD+
L DBC = 2
uAD
+ 2u
DC.
или
Третий
nрuэнаlt
L
АВС'"
!.
u
АС.
Теорема.
Если
три
стороны
одного
2
треугольнин;а
nроnорциональны
трем
3.
Луч
ВО
не
делит
уголАВС
на
два
угла
сторонам
другого.
то
тан;ие
треуголь.
и не
совпадает
со
сторонами
этого
угла.
нин;и
nодо6ны.
Из
рис.
5
видно,
что
Дон;азательство.
Пусть
стороны
'"
АВС
L
АВС
= L
AВD
- L DBC.
и
'"
АIВIСI
пропорциональны:
Как
доказано
выше,
АВ
_
ВС
_
СА
1 1
Al~
-
~Cl
-
01Аl
(1) L
AВD
=2
uAD
и
L DBC = 2 u
DC.
Докажем,
что'"
АВО
и
",АIВIСI
подоб-
Вычитая
эти равенства
почленно,
получа
ны.
Для
этого,
учитывая
второй
признак
ем
подобия
треугольников,
достаточно
дока-
1 1
зать,
что
L
А
= L
Аl'
Рассмотрим
треу-
L
AВD
- L DBC = 2
uAD
- 2 u
DC.
или
гольник
АВ02.
У
которого
L
1=
L
Аl,
1
L 2
= L
Вl
(рис.
2, 6).
Треугольники
АВС2
L
АВС
= - u
АС.
и
АIВIСI
подобны
по
первому
признаку
2
подобия
треугольников,
поэтому
Следствие
1.
Вписанные
углы.
оnира
АВ
ВС
О
А
ющиеся
на
одну
и
ту
же
дугу,
равны.
__
=
__
2_
=
_2_
Следствие
2.
Вписанный
угол.
оnира
А
1
Вl
~
01
Сl
Аl
ющийся
на
nолуокружnость.
-
прямой.
Сравнивая
эти
равенства
с
равенствами
(1),
получаем:
ВС
=
В02.
СА
=
02А.
Следовательно,
треугольники
АВС
и
АВС2
равны
по
трем
сторонам.
Поэтому
I L
А
= L 1,
а
так
как
L 1 = L
Аl.
то
L
А
= I
L=L~ремадоказа~
~
~
58
г----~-----------------I
60.
Формулы
площади
поверхности
ваются
60ковыми
ребрами
призмы.
Эти
I
и
объема
призмы
ребра
как
противоположные
стороны
па-
I
раллелограммов
(1),
последовательно
при
Определения
ложенных
друг
к
другу,
равны
и
парал-
I
Рассмотрим
два
равных
многоугольни
лельны.
Призму
с
основаниями
АI
А
2·..
I
каАIА2
...
А
n
и
ВIВ2
...
В
n
,
расположен
А
n
и
ВIВ2."
В
N
обозначают
АIА2
...
ные
в
параллельных
плоскостях
а и
~
так,
А
n
В}В2
...
В
N
и
называют
n-угольной
nри-
I
что
отрезки
АIВ1, А2В2,
...
АnВ
n
.
соеди
змои.
няющие
соответственные
вершины
много
Перпендикуляр,
проведенный
из
какой-
I
угольников,
параллельны.
Каждый
из
n
либо
точки
одного
основания
к
плоско-
I
четырехугольников
сти.
другого
основания,
называется
высо
I
АIА2В2Вl.
А2АЗВЗВ2,
...
,
АnАIВIВn
(1)
тои
призмы.
является
параллелограммом,
так
как
Если
боковые
ребра
призмы
перпенди-
I
имеет
попарно
параллельные
противопо
кулярны
к
основаниям,
то
призма
назы
ложные
стороны.
Например,
в
четырех
вается
прямой.
в
противном
случае
- I
угольнике
АIА2В2Вl
стороны
АIВl
и
нан;лонноЙ.
Высота
прямой
призмы
равна
I
А2В2
параллельны
по
условию,
а
сторо
ее
боковому
ребру.
ны
АIА2
и
ВIВ2
-
по
свойству
параллель
Прямая
призма
называется
правильной,
ных
плоскостей,
пересеченных
третьей
если
ее
основания
-
правильные
много·
плоскостью.
угольники.
'у
такой
призмы
все
боковые
Многогранник,
составленный
из
двух
грани
-
равные
прямоугольники.
На
равных
многоугольников
АIА2
...
А
n
и
рис.
2
изображена правильная
шестиуголь
ВIВ2
...
В
n
,
расположенных
в
параллель
ная
призма.
ных
плоскостях,
и
n
параллелограммов
(1),
называется
nризмой
(рис.
1).
Площадь
поверхности
призмы
Площадью
полной
поверхности
nризмы
называется
сумма
площадей
всех
ее гра
ней,
а
площадью
60ковой
поверхности
nризмы
-
сумма
площадей
ее
боковых
граней.
Площадь
Sполи
полной
поверхности
вы
ражается
через
площадь
Sбок
боковой
по
верхности
и
площадь
Sоси
основания
при
змы
формулой
Рис.
1
Sполи
""
Sбок
+
2S
оси
,
Многоугольники
АIА2
... А
n
и
ВIВ2
...
В
N
называются
основаниями.
а
паралле·
Теорема.
Площадь
60ковой
поверхнос
лограммы
(1) -
60ковыми
гранями
при
ти
прямой
nризмы
равна
произведению
змы.
Orрезки
Al~'
А2В:!'
...,
АnВ
n
назы-
периметра
ее
основания
на
высоту.
--~-----------------~-
61.
Теорема
Пифагора
В
прямоугольном
треугольнике
квад
рат
гипотенузы
равен
сумме
квадратов
a~Ь
Ь
ас
катетов.
Доказательство.
Рассмотрим
прямоу
гольный
треугольник
с
катетами
а,
Ь
и
ь~c
ь
с
гипотенузой
с
(рис.
1).
~
с
а
Докажем,
что
с
2
=
а
2
+
ь
2
.
а а
Ь
Достроим
данный
прямоугольный
треу
гольник
до
квадрата
со
стороной
а
+
Ь
Рис.
1
Рис.
2
так,
как
показано
на
рис.
2.
Площадь
S
Нетрудно
видеть,
что
квадрат
со
сторо-
I
этого
квадрата
равна
(а
+
Ь
)2.
ной
(а
+
Ь),
показанный
на
рис.
2,
состав-
I
лен
из
четырех
равных
прямоугольных
I
L
~-~
59

__ __
г-----------------~----I
Доказательство.
Воковые
грани
пря
мой
призмы
-
прямоугольники,
основа
ния
которых
-
стороны
основания
при
змы,
а
высоты
равны
высоте
h
призмы.
Площадь
боковой
поверхности
призмы
равна
сумме
площадей
указанных
прямо
угольников,
т.
е.
сумме
произведений
сто
рон
основания
на
высоту
h.
Вынося
мно
житель
h
за
скобки,
получим
в
скобках
сумму
сторон
основания
призмы,
т.
е.
его
периметр
Р.
Итак,
8бок
= Ph.
Теорема
до
казана:
Объем
прямой
призмы
Теорема.
Об7Jе,м
прямой
nрuз,мы
равен
nроuзведенuю
nлощадu
ее
основанuя
на
высоту.
Доказательство.
Сначала
докажем
те
орему
для
треугольной
прямой
призмы,
а
затем
-
для
произвольной
прямой
при
ЭМЫ.
A1~iB'
С,
D1
:В
А
,////
Т····
....
С
D
Рис.
2
1.
Рассмотрим
прямую
треугольную
при
зму
АВСА1В1С1
(рис.
2).
Проведем
высоту
треугольника
АВС
(отрезок
BD),
которая
разделит
этот
треугольник
на
два
треу
гольника:
ABD
и
DBC.
Плоскость
BB1D1D
делит
данную
призму
на
две
при
змы,
основаниями
которых
являются
пря
моугольные
треугольники
AВD
и
DBC.
По
этому
объемы
V1
и
V2
этих
призм
равны
8
AВD
h
и
8 DBC h
соответственно.
Так
как
I
данная
призма
составлена из
двух
призм,
то
ее
объем
равен
сумме
объемов
V1
и
V2,
I
т. е.
I
V=
8AВD
h +8DBC h =
(8AВD
+
8DBc)
h.
]
Таким
образом,
V =
8
осн
h.
(1)
2.
Докажем
теперь
теорему
для
произ
вольной
прямой
призмы
С
высотой
h
и
площадью
основания
8.
Такую
призму
можно
разбить
на
прямые
треугольные
призмы
с
высотой
h.
Например,
на
рис.
3
изображена
пятиугольная
призма,
кото
рая
разбита
на
три
прямые
треугольные
призмы.
В1
h
Рис.
47
Выразим
объем
каждой
треугольной
призмы
по
формуле
(1)
и
сложим
эти
объе
мы.
Вынося
за
скобки
общий
множитель
h,
получим
в
скобках
сумму
площадей
ос
нований
треугольных
призм,
т. е.
площадь
основания
исходной
призмы.
Таким
об
разом,
объем
исходной
призмы
вычисля
ется
по
формуле
V=
8
0сн
h.
--~-----------------~-
треугольников
со
сторонами
а,
Ь
и
с,
пло-
Зная
8,
получим,
1
(а
+
ь)2
=
2аЬ
+
с
2
,
щадь
81
каждого
из
которых
равна
"2
аЬ,
откуда
с
2
а
2
+
ь
2
и
квадрата
со
стороной
С,
площадь
кото
=
.
Теорема
доказана.
рого
равна
82.
Поэтому
1
8 =
481
+
82=
4"2
аЬ
+
с
2
=
2аЬ
+
с
2
•
L_~~
~
~~
~
г----~-----T-----------I
62.
Формулы
площади
I
64.
Формула
расстояния
параллелограмма,
треугольника,
трапеции
I
между
двумя
точками.
Уравнение
окружности
1.
Площадь
nараллелогра,м,ма
равна
nроuзведенuю
его
стороны
на
высоту,
I 1.
Пусть
на
плоскости
хОу
заданы
две
I
произвольные
точки
М1
(Х1;
У1)
и
М2
(Х2;
nроведенную
к
этой
стороне.
Аn:
т
D
Рис.
1
Рассмотрим
параллелограмм
AВCD.
По
строим
прямоугольник
BCFT
так,
как
это
сделано
на
рис.
1.
Треугольник
ВТА
равен
треугольнику
CFD
по
катету
и
гипотену
зе.
Следовательно,
8AВCD
= 8BCFT,
т.
к.
8AВCD
=
8ВТА
+
8BCDT,
а
8BCFT
=
8CFD
+
8BCDT·
Но
8всрт
=
ВС'
ВТ.
Значит,
8AВCD
=
ВС
.
ВТ
или,
в
обычных
обозна
чениях,
Snap = ah,
где
а
=
AD
=
ВС,
ВТ
=
h.
АЛ:А~СF
D(T)
DT
Рис.
2
Рис.
3
63.
Прав
ильные
многогранникн
Многогранник
называется
nравuльны,м,
если
все его
грани
представляют
собой
правильные
многоугольники.
Все
ребра
а
правильного
многоугольника
-
равные
отрезки.
Существует
пять видов
правиль
ных
многогранников:
куб,
тетраэдр,
ок
таэдр,додокаэдр,
икосаэдр.
L
У2)
(рис.
1).
Будем
считать,
что
Х1
*"
Х2
и
У1
*"
У2
.
Найдем
d -
расстояние
меж
ду
точками
М
1
и
М
2.
Рассмотрим
треу
гольник
М
1АМ
2.
В
нем
М1А=Х2-Х1,АМ2=У2-У1,
M1
M
2=d.
у
y2l-----
--------
М
2
d :
E
y1~----
---------iА
1
М
1
:
о
Х1
Х2
Х
Рис.
По
теореме
Пифагора
находим
d
2
=
(Х2
-
Х1)2
+
(У2
-
У1)2.
Отсюда
d = J(X1 -
Х2)2
+
(У1
-
У2)2.
(1)
Полученная
формула
расстояния
между
двумя
точками
справедлива
при
любом
расположении
точек
М
1
и
М
2.
В
частно
сти,
если
Х1
=
Х2,
то
V =a
3
J2
8 =
а
2
JЗ,
12 .
~-~
60
61
