Филатов О.А. Шпаргалки по алгебре и геометрии

г-----------------~----I

г----~-----T-----------I

,У!

'Y=lf(x)1

~(x)

~

t

x

~

-v

-

Рис.

9

Рис,

6

3.

График

функции

у

= f

Ixl

получается

из

графика

функции

у

=

f(x)

следующим

образом:

при

х

~ О

график

функции

у

=

f(x)

сохраняется,

а

при

х

<

О

получен

ная

часть

графика

отображается

симмет

~

рично

относительно

оси

Оу

(рис.

7).

Рис,

10

У

11

\

У!

)Y-f(IХI)

~

Рис.

11

Рис.

7

Сохранив

часть

графика,

лежащую

над

Примеры

построеиия

графиков

осью

абсцисс

на

рис.

11,

а

часть

его,

ле

функции

жащую

под

осью

абсцисс,

отобразив

сим

При

м

е

р

1.

Построить

график

функ

метрично

этой

оси,

получим

график

функ

ции

у

=

IxI-

ции

у

=

Ilx

-11-11

(рис.

12).

Построим

график

функции

у

=

х.

Часть

этого

графика,

лежащую

над

осью

абс

11

цисс,

сохраним,

а

часть,

лежащую

под

осью

абсцисс,

отобразим

симметрично

этой

оси

(рис.

8).

х

...........

2

-1

~1/'

о

7г

Рис.

12

Рис.

8

При

м

е

р

2.

Построить

график

функ

ции

у

=

Ilx

-

11-

11

.

I

Последовательно

построим

графики

сле

I

дующих

функций:

у

=

х

- 1

(рис.

9),

I

у

=

Ix

-11

(рис.

10),

I

у

=

Ix

-11-

1

(рис.

11).

I

L_~--------------------~

22

21.

Логарифмирование

и

потенцирование

Теоремы

логарифмов

Теорема

1.

Логарифм

про

изведения

двух

положительных

чисел

равен

сумме

лога

рифмов

сомножителей.

Пусть

существуют

числа

loga

Ь

и

loga

с

,

т.

е.

а

>

О,

а

'#

1,

Ь

>

О

и

с

>

О.

Тогда

существует

число

loga(b·

с)

и

вер

но

равенство:

loga

(Ь

.

с)

=

logab

+

logac,

(1)

Теорема

2.

Логарифм

степени

равен

произведению

nоказателя

степени

на

логарифм

ее

основания.

Пусть

существует

число

loga

Ь

,

то есть

а

>

О,

а

'# 1

и

Ь

>

О.

Тогда

для

любого

числа

с

существует

число

loga

Ь

С

и

верно

равенство:

logabC =

с

logab,

(2)

Теорема

3.

Логарифм

частного

двух

положительных

чисел

равен

разности

логарифмов

делимого

и

делителя.

Пусть

существуют

числа

loga

Ь

и

loga

с

,

т. е.

а

>

О,

а

'# 1 ,

Ь

>

О

и

с

>

О.

Ь

Тогда существует

число

loga

ё

и

верно

равенство

ь

loga

ё

=

loga

b

-loga

c

,

(3)

Теорема

4.

Если

основание

а

логариф

ма

и

число

Ь,

стоящее

под

знаком

лога

рифма,

возвести

в

одну

и

ту

же

степень

с,

отличную

от

нуля,

то

значение

лога

рифма

не

изменится:

logab

=

loga

c

Ь

С

,

(4)

Например,

10g2

4 = log2

3

43;

6

logg

64

=

10g2

3

26

=

з1оg2

2 = 2.

Примеры.

Вычислим:

а)

10g12

4 +

10g12

3 =

10g12

4·3

=

10g12

12 =

1;

б)

log2 48

-10g2

3 = log2 3

48

=

= log2 16 = 4;

13

в)

19

13 -

19

130 =

19

- =

-1;

130

г)

lоgз

81 =

lоgз

92

=

21оg

з

9 =

2.2

=4.

L

I 22.

Производная

суммы

и

разности

двух

функций

I

Теорема.

Если

функции

и(

х)

и

и(

х)

I

имеют

nроизводные

во

всех

точках

ин

I

тервала

(а;

Ь),

то

I

[и

(х)

± v

(х)

r=

и'(х)

±

и'(х)

для

любого

х

Е

(а;

Ь).

Доказательство.

Пусть

{(х)

=

и(х)

+

и(х),

найдем

{'(х).

Вычислим

М(х)

=

f(x

+

~x)

-

f(x)

=

и

(х

+

~x)

+v

(х

+

~x)

-

[и (х)

+v

(х)]

=

и

(х

+

~x)

-

и

(х)

+v

(х

+

~x)

- v

(х)

=

~и

+

~и.

Найдем

отношение

М(х)

~и

+

~и ~и ~и

--=---=-+-.

~x

f

'(

) -

l'

м(х)

_

l'

(~и

~и)_

х

-

1т

---

1т

-+-

-

АХ--+О

~x

Ах--+О

~x ~x

Нт

~и

+

Нт

~и

=

и'(х)

+

и'(х).

АХ--+О

~x

АХ--+О

~x

I

'-----~----

I 23.

Производная

частного

двух

функций

I

Теорема.

Если

функции

и(х)

и

и(х)

~

имеют

nроизводные

во

всех

точках

ин

tjo

тервала

(а;

Ь),

причем

v

(х)

'#

О

для

лю

бого

х

Е

(а;

Ь)

,

то

u'(x)v

(х)

-

и

(х)

v'(x)

(

v(x)

v

2

(x)

и

J'

u'v

-

uv'

и(х»)'

Короче,

(

v =

--v-

2

-'

Доказательство.

и(х)

Пусть

f(x)

= v

(х)

.

Тогда

и(х)

=

и(х)

{(х).

Найдем

производную

функции

и(х)

по

правилу

дифференцирования

произведе

ния:

и'

=

(vf)'

=

и'!

+

vf'.

I

Найдем

из этой

формулы

(,

подставив

вместо

f

его

значение:

I

и

-и

-

и

~'

I f' =

и'

-

и'!

= v =

и'и

-

и'и

~

__

~

__

~

__

~-~

23

I

г----~-----------------I

г-----------T-----~----I

24.

Иррациоиальные

неравенства

Пример

1.

Таким

образом,

(и

±

v)'

=

u'(ж)

±

v'(ж)

. I

Логарифмирование

I

Определение

Решим

неравенство

~

х

2

-

3х

+ 2 > 2 -

х.

Производная

алгебраической

суммы

Прологарифмировать

алгебраическое

I

функций

равна

сумме

nроизводных

этих

I

выражение

-

значит

выразить

его

лога

Если

внеравенстве

присутствует

ирра-

Решение.

По

теореме

2

неравенство

заме

циональное

выражение,

то

такое

неравен-

ним

двумя

системами

неравенств:

фу/t/щий

(правило

справедливо

для

любо-

I

рифм

через

логарифмы

отдельных

чисел,

I

ство

называется

иррациональным.

>

О'

го

количества

слагаемых).

входящих

в это

выражение.

Это

можно

I

{2

_

Примеры:

I

сделать,

используя

теоремы

логарифмов.

Иррациональное

выражение

имеет

смысл

х

- ,

2/;

I

По

формуле

(3)

запишем:

I

19

х

=

19(5a

3

WЬ2)

-lg

[с

4

(а

+

ь)].

I

Логарифмы

произведений

заменим

сум

мой

логарифмов

по

формуле

(1):

I

10'

=[

195+lga'

+

10b~)

*

I

-[lgС

4

+lg(a+b)].

Выполним

преобразования

по

формуле

I

(2)

и

раскроем

скобки:

2

I

19

х

=

195

+

31g

а

+ S-lg

Ь

-

-41g

с

-lg(a

+

Ь).

-----k------,

I

Потенцирование

-

это

преобраЗОВ8ние,

и

J'

u'v - v'u

Следовательно,

(

v =

--v-

2

-.

I

обратное

логарифмированию.

I

Пример.

Дано:

Пример.

3

(х

3

)'

sin

х

- x

3

(sin

х)'

I

19

х

= 21g

а

- 51g

Ь

+

71g

с,

(э;:х

J

sin

2

х

I

где

а

>

О,

Ь

>

О,

с

>

О.

Найдем выражение

для

х.

зх

2

sin

х

-

х

3

соэ

х

I

Решение.

Используя

формулы

(2), (1)

и

sin

2

х

I

(3),

получим

I

19x

=lga

2

-lgb5

+lgc~

=

I

2

=

19[a

2

.

c~

J-lg

ь5

= 1

g

a

?f3

•

I

ь

5

I

Ответ:

х

= a

2

?f3

I

ь5

•

I

L_~--_-----~--_--

-_~

только

в

том

случае,

если

оно

положи-

х

2

-

3х

+

2>

(2 -

х)2;

(2х

3

+

3х

-1)'

=

(2х

3

)'

+

(3х)'

_ (1)' = I

Пример.

I

тельно

либо

равно

нулю.

Рассмотрим

че-

{2

_

х

<

О;

Прологарифмируем

выражение

<=>

=2(ж

3

)'+3(х)'-0=2.зх

2

+3=6х

2

+з;

I

з51:2

I

тыре

неравенства:

_

3х

+ 2

~

О.

5а "Ь"

1

Х=-4---'

а>О

Ь>О

с>О

I

~

х

2

+

х

+ 1 >

-2,

~

х

2

+ 1 >

-1,

х

2

(х3+/;)'=(х3)'+(/;)'=зх2+-.

I

с

(а+Ь)

, , ,

,

/;

<

О,

/;

$

-2.

I

т. е.

найдем

19

х

. I

[{

Х

>

2;

Первые

два

неравенства

справедливы

на

множестве

всех

действительных

чисел,

вторые

два

неравенства

не

имеют

реше

ний,

так

как

не

верны

при

любом

значе

нии

х

из

области

определения

(х

~

О).

Иррациональные

неравенства

по

теоре

мам

равносильных

преобразований

заме

няют

системой

или

совокупностью

сис

тем

неравенств,

и

решение

сводится

к

ре

шению

системы

неравенств.

Теоремы

равносильных

преобразований

'(х)

и

g(x)

-

функции

переменной

х.

Теорема

1.

j

f(X)

~

О;

~

<

g(x)

<=>

g(x)

>

О;

'(х)

<

g2(x).

Теорема

2.

g(X)

~

О;

~

>

g(x)

<=>

I

{

'(х)

>

g2

x

;

g(X)

<

О;

{

'(х)

~

О.

Теорема

3.

~

>

JiW

<=>

{f(X)

>

g(x);

g(x)

~

О.

Знак

<=>

обозначает,

что

выполняются

равносильные

преобразования.

Данные

теоремы

позволяют

установить

область

допустимых

значений

неизвестного,

учи

х

$2;

х

> 2'

{(х

-

;)(х

-

2)

~

О.

Видим,

что

первая система

равносиль

ной

совокупности

не

имеет

решения,

а

вторая

система

имеет

решения

(рис.

1)

при

х> 2.

~

2

х

~

2

х

Рис.

Ответ:

(2; + 00).

Пример

2.

Решим

неравенство

~x2

-

3х

-10

< 8 -

5х.

Решение.

По

теореме

1

неравенство

заме

ним

системой

неравенств:

-

3х

-10

~

О;

х

2

-

3х

-10

< (8 -

5х)2;

<=>

j

X

2

8

-5х

>

О.

[

Х

~

5;

х$-2;

х

~

5;

24х

2

- 77

х

+ 74 >

О;

х

$

-2;

8

<=>,

3

х<-·

х<1-.

5

тывая,

что

рассматриваются

только

ариф

Неравенство

24х

2

-

77

х

+ 74 >

О

имеет

метические

корни.

Затем

возводят

в

квад

отрицательный

дискриминант

(D

<

О),

сле

рат

правую

и

левую

части

неравенства,

довательно,

это

неравенство

справедливо

на

чтобы

освободиться

от

иррациональнос

R,

т.

е.

х

-

любое

действительное

число.

ти.

На

рис.

2

показаны

три

решения

систе

Необходимо

помнить,

что

при

возведе

мы

неравенств.

нии

в

степень

может

получиться,

что

об

ласть

значений

неизвестного

исходного

~з

С

неравенства

будет

только

частью

области

-2

15

значений

неизвестного

полученного

нера

Рис.

2

венства.

Поэтому

необходимо

всегда

про

водить

проверку

решения.

Получим

х

$

-2.

Ответ:

(_00; - 2].

L

~-~

3

Шпаргалки

по

алгебре

и

геометрии

24

25

г-----------------~----I

г----~-----T-----------I

I

Пример

3.

Решим

неравенство

Можно

выбрать

любое

значение

из

дан-

I

J9

-

х

2

+

Jбх

_

х

2

> 3

ного

промежутка.

I

.

Если

это

значение

удовлетворяет

нера

I

Решение:

Jбх

-

х

2

> 3 -

J9

-

х

2

.

венству,

то

и

все

остальные

значения

со-

I

Определим

область

определения

данного

ответствующего

промежутка

ему

удовлет-

I

неравенства:

воряют.

б

2

О

Если

проверяемое

значение

не

удовлет-

I

х

-

х

~

,

{=>

х

(б

-

х)

~

О,

{=>

воряет

неравенству,

то

и

никакое

другое

j

9 -

х

2

~

О.

{(3 -

х)(3

+

х)

~

О.

значение

из

проверяемого

промежутка

ему

0<

<

б

также

не

удовлетворяет.

-

х

- ,

{=>

0<

х

< 3

Пример.

Решим

неравенство

{

-3

~

х

~

3. - - .

~

2

Возведем

в

квадрат

правую

и

левую

ча-

х

10

-

х

>

х

-

б.

сти

неравенства,

получим

Решение:

~

1.

Находим

область

допустимых

значе

бх

-

х

2

> 9 -

б,,9

-

х

2

+ 9 -

х

2

,

ний

БJ9-х2

>18-бх;

J9-x

2

>3-х;

10-х

2

~O,

(.J10-х)(.J10+х)~0,

9 -

х

2

>

(3

-

х)2;

9 _

х

2

> 9 _

бх

+

х2,

-J1O

~

х

~

J1O.

2.

Решаем

уравнение

бх-2х

2

>0,

х(3-х»0,

откуда

xJ10-х2

=х2

-б,

1)

х

>

О

и

3 -

х

>

О,

значит

О

<

х

< 3;

2)

х

<

О

и

3 -

х

<

О,

не

имеет

решения.

х

2

(10 -

х

2

)

=

(х

2

-

б)2,

В

ответ

запишем

те

решения

неравен-

10х

2

-

х

4

=

х

4

-

12х

2

+ 36,

ства,

которые

входят

в

область

определе-

х

4

-

llх

2

+ 18 =

О,

х

2

= 2

и х

2

= 9,

т.

е.

ния

неравенства;

в

данном

случае

все

ре-

уравнение

имеет

четыре

корня:

шения

входят

в

область

определения

не-

х

= ±-/2

и

хз

4 = ±3.

равенства,

это

О

<

х

< 3.

1,2.

Ответ:

(О;

3).

Проверка

по

знаку

левой

и

правой

час

тей

уравнения

показывает,

что

корни

Решение

неравенств

методом

интервалов

+-/2

и

-3

-

посторонние,

т.

е.

уравнение

Рассмотрим

неравенство

f(x)

> g(x)

на

имеет

два

решения:

-J2

и

+

3.

[а;

Ь],

где

f(x)

и

g(x) -

непрерывные

функ

ции

на

отрезке

от

а

дО

Ь.

3.

На

отрезок

[-J1O;

+

J1O]

наносим

Из

рис.

3

очевидно,

что

неравенство

эти

корни

(рис.

4).

Выполняем

проверку

f(x)

> g(x)

выполняется

на

отрезках

[а;

хl)

неравенства.

и

(Х2;

Ь],

где

график

функции

f(x)

распо

. .

~

ложен

выше

графика

функции

g(x).

-110

--[2

3

+(IO

у

Рис.

4

g(x)

4.

Получены

три

промежутка.

Для

про

верки

удобно

взять

крайние

значения

про

межутков

и

О:

ах,

01

х,Ь

х

а)

при

х

=

-J1O

получим

О

> 4,

т.

е.

Рис.

3

неравенство

неверно;

б)

при

х

=

О

получим

О

>

-6,

т.

е.

Поэтому

решение

неравенства

выполня

неравенство

верно;

ем

по

следующему

алгоритму:

1.

Находим

область

допустимых

значе

в)

при

х

=

J10

получим

О

> 4,

т. е.

неравенство

неверно.

ний

неравенства:

[а;

Ь].

2.

Решаем

уравнение

f(x)

= g(x)

и

нахо

Итак,

есть

лишь

один

интервал,

в

кото

ром

выполняется

данное

неравенство.

дим

корни

уравнения,

исключив

посто

ронние.

Ответ:

(--/2;

3).

3.

Наносим

найденные

корни

на

полу

ченный

отрезок

области

допустимых

зна

чениЙ.

Найденные

корни

разбивают

отре

зок

на

промежутки.

4.

Выполняем

проверку

неравенства

на

каждом

из

полученных

промежутков.

L_~--------------------~

26

I 25.

Производная

'Произведения

I

двух

функций

Теорема.

Если

функции

и(х)

и

и(х)

I

имеют

nроиЗ80дные

80

всех

точках

ин

I

тервала

(а;

Ь),

то

[u(х)

v(x)

r=

u(х)

v'(x)

+

u'(х)

v(x)

I

для

любого

ХЕ

(а;

Ь).

Доказательство.

Пусть

f(x)

=

и(х)

и(х).

Тогда

М(х)

=

и(х

+.:lx)

и(х

+.:lx)

-

и(х)

и(х).

Заменим

и

(х

+.:lx)

=:

и(х)

+ .:lu(x)

и

v

(х

+ .:lx) = v

(х)

+

.:lv

(х).

Получим

М(х)

=

(и

(х)

+

.:lU(X»)

(и

(х)

+

.:lv

(х»)

-

-и(х)

и(х)

=

и

(x).:lv

(х)

+v

(x).:lu

(х)

+

+.:lu (x).:lv

(х).

М(х)

_ ( ).:lV

(х)

()

.:lu(x)

---их

--+их

--+

.:lx

.:lx.:lx

.:lu(x)

+~.:lv(x).

I

f

'()

l'

М(х)

х

=:

1т

-л-

=: I

ы~O

u.Х

.

.:lv

(Х).

.:lu(x) I

=:

11т

и(х)

~

+

11т

и(х)

-л- +

Ы~O

L.Ц

LlX~O

u.Х

I

.:lu(x)

+

Нт

~.:lv(x).

I

ы~O

L.Ц

По

определению

производной

I

Нт

.:lv(x) =:

и'.

Нт

.:lu(x) =:

и'

I

bl~O.:lx

'ДX~O.:lx

Третье

слагаемое

является

произведени

ем

двух

переменных

сомножителей,

веду

~

щих

себя

по-разному

при

.:lx

~

О:

. .:lu(x) ,

1

1т

~=:и,

а

.:lv~O,

ы~O

L.Ц

если

.:lx

~

О по

принципу

непрерывнос

ти.

Таким

образом,

третье

слагаемое

при

.:lx

~

О

стремится

к

нулю.

Подставив

по

лученные

значения

всех

трех

слагаемых,

получим

f'(x)

=

и

и'(х)

+

и'

v

(х).

Примеры.

[(х

+

3)(х

-

2)

r=

(х

+

3)'(х

- 2) +

+(х

+

3)(х

- 2)' = 1

(х

-

2)

+

(х

+ 3) .1 =

=

х

- 2 +

Х

+ 3 =

2х

+

1;

[(2х

-7)

х

2

J=

(2х

-7)'х

2

+

(2х

-7)(х

2

)'

=

2х

2

+

(2х

-7)·

2х

=

2х

2

+

4х

2

-14х

=

6х

2

-14х;

L

~

26.

Производные

I

элементарных

функций

I

Производная

степенной

функции

у

=

xn

I

Производную

степенной

функции

с

на

туральным

показателем

степени

можно

I

получить

по

правилу

дифференцирования

I

произведения.

Найдем

производную

функции

У

=

х

4

•

I

Представим

х

4

как

х

3

.х.

Тогда

I

(х

4

)'

=

(х

3

х)'

=

(х

3

)'х

+

х

3

(х)'

= I

=

зх

2

.

х

+

х

3

=

зх

2

+

х

3

=

4х

3

.

I

Таким

образом,

(х

4

)'

=:

4х

3

•

I

Общая

формула:

(хn)'

=

nхn-1

I

Примеры.

I

(х-

8

)'

=:

_8х-

8

-

1

=

-8х-

9

•

I

, I

(<tГ-;»'

[~]

3

~-1

3 _! 3

"х

3

=

х

4

=:

'4

х4

=:

'4

Х

4 =:

4fБ'

I

(x

100

)'

=:

100х

99

• I

Производвые

показательных

функций

I

Формулы

дифференцирования

Элементарная

ФУНКЦИЯ

ПрИ

УСЛОВИИ

и=х

Сложная

ФУНКЦИЯ

при

условии

и

=f

(х)

(аХ)'

=

аХ

lпа,

(а

И

)'

=

а

и

lпа·

и',

а>

О,

а

'*

1

а>

О,

а

'*

1

(е

Х

)'

=

е

Х

(е

и

)'

=

е

и

.

и'

Производвые

логарифмических

функций

Формулы

дифференцирования

Элементарная

ФУНКЦИЯ

ПрИ

условии

и=х

I

Сложная

ФУНКЦИЯ

при

условии

u

=f

(х)

(log

a

х)'

=

_1_

хlпа

'

и'

(loga

и)

=--

ulпа

(lg

х)'

=

0,4343

Ig

и

=

0,4343

и'

х

и

(1пх)'

=.!.

lnu

=.!..u'

х

и

~-~

27

__

г-----------T-----~----I

Пример.

Н~йдем

производные

следую-

I

(х

2

sin

х)'

=

(х

2

)'

sin

х

+ x

2

(sin

х)'

=

щих

функции:

a)y=x+lnx;

б)

у

= 5 19x;

в)

у

= log2x.

Решение:

а)

у'

= 1+

..!..

_

х

+1

х

-

-х

;

б)

у'

= (51g

х)'

= 5(1g

х)'

=

5·0,4343

2,1715

х

1

в) у'

=

xln2'

Производные

тригонометрических

функций

Формулы

дифференцирования

Элементарная

Сложная

функция

при

условии

u =х

при

условии

u

=f(x)

(sin

х)'

=cos

х

(sin

и)'

= cos

и

.

и'

(cosx)'

=

-sinx

(cos

и)'

=-

sin

u·

и'

1

(tg

х)'

=

--2-

cos

х

1

(tg

и)'

=

--2-и'

cos

и

(ctg

х)'

=

__

1_

sin

2

х

(ctgu)'

=

__

1_

u

,

sin

2

и

L_~

~

I

. 2

=2хsшх+х

cosx.

Вынесение

постоянного

множителя

за

звак

производной

I

Постоянный

множитель

можно

выно

сить

за

знак

производной:

[Cf(x)J =Cf'(x).

Применим

теорему

о

производной

про

изведения

к

выражению

С

{(х),

где

С

-

постоянное

число.

Получим

[СЛх)У

=С,!(х)

+

Cj'(x)

=

О·

лх)

+

Cj'(x)

=

Cj'(x).

Примеры.

х

2

J'

1 . 2

5 =

'5

(х

2

)'

=

'5

х

;

[

*

[х:

+2Х]'

~[x:]'

+(2х)'=

1

зх

2

=

в(х

3

)'

+

2(х)'

= 8 +2.

I

~

г----~-----T-----

27.

Уравнение

касательной

к

графику

функции

Геометрический

смысл

производной

Производная

фун"ции

в

точ"е

хо

рав

на

тангенсу

угла

на"лона

"асательной,

nроведенной

"

графи"у

фун"ции

в

точ"е

с

"оординатами

[хо;

{(Хо)]'

у

~#

~~

~~c.~%)

о

l(х

)i

z:y=J(;

:

м[%о;

1(%0)]

о

%0

х

Рис.

1

k =

tg

а

=

lim

~:

=

{'(х).

Лх---)о

u.л,

в

этом

заключается

геометрический

смысл

производной.

Число

k =

tga

называют

угловым

"0-

эффициентом

прямой,

а

угол

а

-

углом

между

этой

прямой

и

осью

Ох

(рис.

1).

1t

Если

k >

О,

то

О

<

а

<

2'

(рис.

2),

в

этом

случае

функция

у

= kx +

Ь

возрастает

и

говорят,

что

прямая

направлена

вверх.

1t

Если

k <

О,

то

-2' <

а

<

О

(рис.

3).

В

этом

случае

говорят,

что

прямая

направ

лена

вниз.

~

'f."1

..

~

'1)'

+Х

б

х

'f.+

.~

~

..

~

';-0

%

Рис.

2

Рис.

3

Пример.

Найдем

угол

между

касатель

ной

к

графику

функции

у

= sin

х

в

точке

(О;

О)

и

осью

Ох

(рис.

4).

1 .. +

==sinx

~

-1

Рис.

4

L

I 28.

Тригонометрические

функции

плоского

угла

I

Градусное

измерение

углов

I

Пусть

луч,

выходящий

из

точки

О,

за

нимает

исходное

положение

ОА. Сделав

I

определенный

поворот

из

этого

исходного

I

положения

против

часовой

стрелки,

он

займет

положение

ОБ

(рис.

1).

сэ

Рис.

1

Лучи

ОА

и

ОБ

образуют

плоский

угол

АОВ

(обозначается

аов).

Фигура,

состоящая

из

двух

различных

лучей

с

общим

началом

и

ограниченной

ими

частями

nлос"ости,

называется

плоским

углом.

Угол

называется

положительным,

если

он

образован

поворотом

луча

против

ча

совой

стрелки,

и

отрицательным,

если

он

образован

поворотом

луча

по

часовой

стрелке.

Плоские

углы

измеряются

либо

в

граду

сах,

либо

в

радианах.

Угол,

равный

10,

-

это

угол,

равный

1

360

части

полного

оборота луча

во,,

*

I

руг

своей

начальной

точ"и.

1

60

часть

градуса

называется

минутой

(обозначают

1').

I

1

60

часть

минуты

называется

се"ундой

I

(обозначают

1").

I

Если

стороны

угла

образуют

прямую,

то

такой

угол

называется

развернутым.

I

Значение

развернутого

угла

равно

1800.

I

Если

луч,

вращаясь

против

часовой

I

стрелки,

сделает

полный

оборот

(т.

е.

зай

мет

прежнее

место),

то

описанный

им

угол

называется

полным.

Значение

полного

угла

равно

3600.

I

При

вращении

от

начального

положе

I

ния

ОА

дО

любого

конечного

положения

(см.

рис.

1)

луч

может

совершить

несколь

I

ко

полных

положительных

или

отрица

I

тельных

поворотов,

т. е.

углы

по

абсо

лютной

величине

могут

быть

сколько

угод

I

но

большими.

~

~-~

28

29

г-----------T-----~----I

Два

угла

называются

равными,

если

Решение.

uНайдем

у~ловой

~оэффициент

I

равны

их

значения.

касательнои

к

кривои

У

=

SШ

х

в

точке

Радиаиное

измерение

углов

I

(О;

О),

т. е.

значение

производной

этой

Угол,

равный

1

радиану,

-

это

угол,

оnи-

функции

при

х

=

О.

рающийся

на

дугу

окружности, длина

КО-

I

Производная

функции

{(х)

= sin

х равна

торой

равна

радиусу

этой

окружности.

I

соэ

х.

tg

а

=

{'(О)

=

сов

О

=

1,

(~

1t

откуда

а

= arctg 1 = 4.

1t

Ответ:

а

=

4'

Выведем

уравнение

касательной

к

графи

~~:JA

ку

дифференцируемой

функции

{(х)

в

точ

ке

М

(см.

рис.

1).

Рис.

2

Если

у

= kx +

Ь

-

искомое

уравнение,

то

Радианная

мера

любого

угла

АОБ

есть

k =

tg

а

=

{'(хо),

т.

е.

уравнение

каса

отношение

длины

дуги

АВ,

описанной

тельной

имеет

вид

у

=

{'(хо)

+

Ь.

Так

как

про

из

вольным

радиусом

R

из

центра

О

и

касательная

проходит

через

точку

М

с

ко

заключенной

между

сторонами

угла,

к

ра

ординатами

[хо;

{(хо)]'

можно

записать

диусу

этой

дуги

(рис.

2).

равенство

Если

радиус

окружности

совершит

пол

*

{(хо)

=

{'(хо)хо

+

Ь,

2х

рад

(или

3600).

откуда

Ь

=

{(хо)

-

{'(хо)хо.

Итак,

уравнение

касательной

ный

оборот,

то

получится

угол,

равный

2х

1t

Радианная

мера

1

о

равна

360 = 180

(рад).

у

=

{'(хо)

х

+

{(хо)

-

{'(хо)

хо

Если

угол

а

задан

в

градусах,

то

его

или

радианная

мера

равна

у

=

(хо)

+

('(хо)(х

-

хо).

(1)

ах

Пример.

Найдем

уравнение

касательной

(1)

180

.

к

графику

функции

у

=

сов

х

в

точке

с

Если

угол

а

задан

в

радианах,

то

его

u 1t

градусная

мера

равна

абсциссои

хо

=

6"

.

а180

Решение.

Найдем

значения

функции

и

(2)

1t

Пример

1.

Найдем

радианную

меру

уг

ее

производной

в

точке

хо

=

~

.

лов

450, 600, -2250, 3000.

Решение.

По

формуле

(1)

рассчитаем

ра

1t

J3

{(хо)

=

СОВХо

=

СОВ6"

=

2'

дианную

меру

углов:

45х

1t

60х

1t

{

'()'

.

1t

1

ХО

=-вlllхо

=-Вlll6"

=-2"'

180

= 4

(рад);

180

=

3"

(рад);

Подставив

найденные

значения

в

фор

о

-225х

5х

-225

=

180

=

-"4

(рад);

мулу

(1),

получим

300х

5х

180

= 3

(рад).

y=~-~(x-~)

Пример

2.

Найдем

градусную

меру

уг-

или

1t 1t

1t

2х

I

лов

18;

9;

15;

3'

у=_!х+[JЗ

+~)

2 2

12'

Решение.

По

формуле

(2)

рассчитаем

гра

I

Ответ.

'Уравнение

касательной

I

дусную

меру

углов:

~

.

180

= 100.

~.

180

= 200.

у=_!х+[JЗ

+~)

I

18

1t

'9

1t ' 2 2

12'

~.

180

=

120.

2х.

180

=1200

I

15

1t

'3

1t •

I

L_~--------~-----------~

30

г----~-----T-----------I

29.

Тригонометрические

функции

I

30.

Свойства

функций

у

=

sin

х,

острого

угла

у

=

cos

х

и

их

графики

Определения

трнгоиометрических

I

Свойства

функции

у

= sin

х

функций

и

ее

график

I

Рассмотрим

единичную

окружность,

т.

е.

I

График

функции

у

=

sin

х

называют

окружность

с

центром

в

начале

коорди-

синусоидой

(рис.

1).

нат

и

радиусом,

равным

1.

Осями

коорди

нат

плоскость

и

окружность

делятся

на

четыре

четверти

(см.

рисунок).

II

У

1

-1\

01

С

/1

х

I

Рис.

1

1.

Область

определения

-

множество

R

всех

действительных

чисел.

-1

III

IV

2.

Область

изменения

(множество

зна

чений)

-

промежуток

[-1;

1],

значит,

Точка

А

имеет

координаты

(1;

О).

При

sin

х

-

функция

ограниченная.

повороте

на

угол

а

радиус

единичной

3.

Функция

нечетная:

sin

(-х)

= -

sin

х

окружности

переходит

из

положения

ОА

для

всех

х

Е

Н.

в

положение

ОБ.

4.

Функция

периодическая

с

наимень

В

зависимости

от

того,

в

какой

коор

шим

положительным

периодом

2х:

динатной

четверти

окажется

радиус

ОБ,

sin

(х

+

21tk)

=

sin

х,

угол

а

называют

углом

этой

четверти.

где

k

Е

Z

для

всех

х

Е

R .

Так,

если

00

<

а

< 900,

5.

Нули

функции:

то

а

-

угол

1

четверти;

sin

х

=

О

при

х

=

1tk,

k

Е

Z.

если

900 <

а

< 1800,

6.

Промежутки

знакоnостоянства:

то

а

-

угол

11

четверти;

sin

х

>

О

при

х

Е

(21tk;

1t +21tk), k

Е

Z,

если

1800 <

а

< 2700,

sin

х

<

О

при

х

Е

(х

+21tk;

2х

+

21tk),

то

а

-

угол

111

четверти;

если

2700 <

а

<

3600,

~

kE

Z.

7.

Монотонность

функции:

Очевидно,

что

при

прибавлении

к углу

то

а

-

угол

IV

четверти.

Функция

возрастает

от

-1

до

1

на

про

целого

числа

оборотов

получается

угол

той

межутках

же

четверти.

[-j + 21tk; j +

21tk

J.

k

Е

Z.

Например,

угол

4100

является

углом

1

четверти,

так

как

4100 = 3600 +

500

и

Функция

убывает

от

1

до

-1

на проме

00

<

500

< 900.

жутках

'Углы

00;

±90

0

; ±180

0

; ±270

0

; ±360

0

, ...

не

относятся

ни

к какой

четверти.

[

Х

3х

]

,

2"

+ 21tk; "2 +

21tk

k

Е

Z.

Пусть

при

повороте

вокруг

точки

О

на

8.

Наибольшее

значение

функции:

угол

а

начальный

радиус

ОА

перешел

в

положение

ОБ

(см.

рисунок).

sin

х

= 1

в

точках

х

= j +

21tk,

k

Е

Z.

Точка

Б

имеет

следующие

координаты:

Наименьшее

значение

функции:

х

=

locl,

у

=

IБсl·

.

3х

2 k

Sln

х

=

-1

в

точках

х

= "2 +

Х

,

Синусом

угла

а

называется

отноше

ние

ординаты

точки

Б

к

радиусу

единич

kE

Z.

ной

окружности.

9.

Функция

непрерывна

и

имеет

произ

Косинусом

угла

а

называется

отноше

водную при

любом

значении

аргумента:

(sin

х)'

=

соэ

х.

ние

абсциссы

точки

Б

к

радиусу

единич

L~~уж~ти.

~

~_~

31

г----~-----T-----------I

г-----------T-----~----I

Рис.

2

Свойства

функции

у

=

соэ

:r

Таnгеnсом

угла

а

называется

отно

и

ее

график

I

шение

ордипаты

точки

В

к

ее

абсциссе.

График

функции

у

=

сов

х

называют

I

Коmaшеnсом

угла

а

называется

отна

косинусоидой

(рис.

2).

шение

абсциссы

точки

В

к

ее

ординате.

I

Таким

образом,

I

sin

а

=

JL

=

у,

cos

а

=.!....

=

х,

R R

I

tg

а

=

J!....

=

sin

а,

ctg

а

=

~

=

c~s

а

.

I

х

cos

а

у

sш

а

I

Каждому

углу

а

соответствует

един

I

ственная

точка

В

(х;

у) и,

следовательно,

единственное

значение

синуса

и

косинуса

I

этого

угла.

Таким

образом,

sin

а

и

cos

а

,

1.

Область

оnределенUJl

-

множество

R

tg

а

и

ctg

а

являются

функциями

чис

всех

действительных

чисел.

I

лового

аргумента.

2.

Область

изменения

(множество

значений)

-

промежуток

[-1;

1],

значит,

Функция

tg

а

имеет

смысл

при

любом

cos

х

-

функция

ограниченная.

I

а

,

кроме

значений

±90

0

, ±270

0

, ±450

0

,

...

,

3.

Функция

четная:

cos

(-х)

= cos

х для

у

так

как

для

этих

углов дробь

х

не

имеет

всех

ХЕ

В.

График

функции

симметричен

отно

смысла.

сительно

оси Оу.

Функция

ctg

а

имеет

смысл

при

любом

4.

Функция

периодическая

с

наимень

*

а,

кроме

значений

00, ±180

0

, ±360

0

,

...

,

шим

положительным

периодом

2х:

х

cos

(х

+

21tk)

= cos

х,

k

Е

Z.

так

как для

этих

углов

дробь

у

не

имеет

5.

Нули

функции:

смысла.

1t

Каждому

допустимому

значению

а

со

cos

х

=

О

при

х

="2 +1tk, k

Е

Z.

ответствует

единственное

значение

триго

6.

Промежутки

знакоnостоянства:

нометрической

функции.

cos

х

>

О

для

всех

Значения

тригонометрических

XE(-~+21tk;~+21tk).

kEZ,

функций

cos

х

<

О

для

всех

Х

3х

)

х

Е

"2

+ 21tk; 2 +

21tk

; k

Е

Z.

(

7.

Монотонность

функции:

Функция

возрастает

от

-1

до

1

на

про

межутках

[-х

+ 21tk;

21tk],

k

Е

Z .

Функция

убывает

от

1

до

-1

на

проме

жутках

[21tk;

1t +

21tk],

k

Е

Z.

8.

Наu60льшее

значение

функции:

сов

х

= 1

в

точках

х

=

2м,

k

Е

Z .

Наименьшее

значение

функции:

сов

х

= - 1

в

точках

х

= 1t +

21tk,

k

Е

Z •

9.

Функция

nеnрерывна

и

имеет

произ-

I

водную

при

любом

значении

аргумента:

Аргумента

ФУНКЦИЯ

00

300 450 600 900

О

7t 7t

1t

6

4

3

"2

sina

О

1

J2

J3

"2

2 2

1

cosa

1

J3

J2

1

О

2 2

"2

tga

О

J3

1

J3

3

-

ctga

-

J3

1

J3

о

3

I

(cosx)'

=

-sinx.

Для

нахождения

значений

тригономет

I

рических

функций

углов,

кратных

900,

например

1800, 2700, 4500

и

т.

д.,

можно

I

использовать

единичную

окружность

(см.

I

рисунок).

I

L_~

~

31.

Свойства

функций

у

=

tg

х,

I

у

=

ctg

х

и

их

графики

Свойства

функции

у

=

tg:r

и

ее

rpафик

График

функции

у

=

tgx

называют

тан

I

генсоидой

(рис.

1). I

Рис.

1

1.

Область

определения

-

множество

всех

действительных

чисел,

кроме

чисел

1t

вида

X="2+1tk,

kE

Z.

2.

Область

изменения

-

множество

R

всех

действительных

чисел,

значит,

tg

х

функция

неограниченная.

3.

Функция

нечетная:

tg(-x)

=

-tg

х

для

всех

х

из

области

определения

функ

ции.

4.

Функция

периодическая

с

наимень

шим

положительным

периодом

х:

tg

(х

+

1tk)

=

tg

х

, k

Е

Z

для

всех

х

из

области

определения

функции.

5.

Нули

функции:

tg

х

=

О

при

х

= 1tk.

t

kE

Z;

6.

Промежутки

знакоnостояnства:

tg

х

>

О

при

х

Е

( 1tk;

~

+1tk). k

Е

Z;

tg

х

<

О

при

х

Е

( -

~

+ 1tk; 1tk). k

Е

Z.

7.

Монотонность

фуnкции:

Функция

возрастает

на

промежутках

(-~+1tk;~+1tk).

kEZ.

8.

Функция

nеnрерывна

и

имеет

произ

водную

при

любом

значении

аргумента

из

области

определения

функции:

, 1

(

tgx)

=--2-'

cos

х

L

~

32.

Соотношения

между

тригонометрическими

функциями

одного

и

того

же

угла

Основные

тригонометрические

тождества

Единичная

окружность

осями

коорди

нат

Ох

и

Оу

делится

на

четыре

части,

ко

торые

называют

четвертями

(или

н:вад

раnтами)

и

нумеруют

их

так же,

как

и

четверти

плоскости.

Пусть

при

повороте

радиуса

ОА

вокруг

точки

О

на

угол

а

получен

радиус

ОВ

(см.

рисунок).

у

А

III

:r

в

единичной

окружности

sin

а

=

у,

cos

а

=

х

,

где

х

-

абсцисса

точки

В,

у

-

ее

ордината.

Так

как

точка

В

принадлежит

окруж

ности

с

центром

в

начале

координат,

ра

диус

R

которой

равен

1,

то

ее

координа

ты

удовлетворяют

уравнению

х

2

+

у2

=

R2.

Подставив

значения

х

и

у,

получим

sin

2

а

+ cos

2

а

=

1.

(1)

Полученное

равенство

называется

основ

ным

тригонометрическим

тQждеством.

Тождество

справедливо

при

любых

зна

чениях

а.

В

единичной

окружности

tg

а

=

J!....

,

ctg

а

=

~

.

Подставив

значения

х

у

х

и

у,

получим

tga

=

sina

(2)

cosa;

ctga=

cosa

(3)

sina'

tg

а

=

_1_

.

tg

а.

.

ctg

а

= 1.

(4)

ctga

'

Равенство

(2)

верно

при

всех

значениях

а

,

при

которых

cos

а

"#

О.

а

равенство

(3)

верно

при

всех

значениях

а.

при

ко

торых

sin

а

"#

О.

~-~

32

33

г-----------T-----~----I

Равенство

(4)

показывает,

как

связаны

I

Свойства

функции

у

=

ctg

х

между

собой

тангенс

и

котангенс

угла

а.

и

ее

график

Оно

верно

при

всех

значениях

а,

при

ко-

I

График

функции

у

=

ctg

х

называют

торых

tg

а

и

ctg

а

имеют

смысл.

I

котан-ген-соидой

(рис.

2).

Выведем

формулы,

выражающие

соот

ношения

между

тангенсом и

косинусом,

а

также

между

котангенсом

и

синусом

од

ного

и

того

же

угла.

Разделив

обе

части

равенства

(1)

на

соэ

2

а

,

получим

sin

2

а

+ 1 =

__

1_,

т.

е.

соэ

2

а

соэ

2

а

1+

tg

2

a =

--2

1

-.

(5)

~

соэ

а

Рис.

2

Теперь

разделим

обе

части

равенства

(1)

на

sin

2

а

.

Получим

1.

Область

оnределен-ия

-

множество

всех

действительных

чисел,

кроме

чисел

1 +

соэ

2

а

1_

\lo

вида

х

= 1tk, k

Е

Z .

sin2

а

- sin2

а'

т.

е.

~

2.

Область

измен-ен-ия

-

множество

R

всех

действительных

чисел,

значит,

ctg

х

1

1 +

ctg

2

a =

-'-2

- . (6)

функция

н-еогран-ичен-н-ая.

sш

а

3.

Функция

н-ечетн-ая:

ctg

(-х)

= -

ctg

х

Равенства

(2)-(6)

также

являются

ос

для

всех

х

из

области

определения

функ

н-овн-ыми

тригон-ометрическими

тожде

ции.

ствами.

4.

Функция

периодическая

с

наимень

шим

положительным

периодом

п,

т.

е.

ctg

(х

+ 1tk) =

ctg

х,

k

Е

Z

для

всех

х

из

области

определения

функции.

5.

Нули

фун-кции:

1t

tg

х

=

О

при

х

= 2 +

1tk,

k

Е

Z .

6.

Промежутки

зн-акоnостоян-ства:

ctg

х

>

О

для

всех

х

Е

(

1tk

;

~

+

1tk

).

kE

z;

ctg

х

<

О

для

всех

х

Е

( -

~

+ 1tk;

1tk

).

kE

Z;

7.

Мон-отон-н-ость

фун-кции:

Функция

убывает

на

каждом

из

проме

жутков

(1tk

;

1t

+

1tk)

, k

Е

Z.

8.

Функция

н-еnрерывн-а

и

имеет

произ

водную

при

любом

значении

аргумента

из

области

определения

функции:

, 1

(ctg

х)

= -

sin

2

х

.

L_~

~ ~

~

г----~-----T-----------I

33.

Тригонометрические

функции

I 35.

Формулы

приведения

половинного

угла Тригонометрические

функции

углов

Формулы

для

тригонометрических

фун-

I

1t

31t

кций

половинного

угла

легко

получаются

I 2 ±

а,

1t

±

а,

2 ±

а

и

21t

±

а

могут

из

формул

двойного

угла:

I

быть

выражены

через

функции

угла

а

с

.

а

~1

-

соэ

а а

~1

+

соэ

а

помощью

формул,

которые

называют

фор

sш

2"

= ±

--2--;

соэ

2"

= ±

--2--;

I

мулами

nриведен-ия.

1t

sin(2:2 +

а)=

соэ

а

COS(-2

+

а)=

-sin

а

;t:

1t

(2k

+

1)

; k

Е

Z;

I

,

t

~

- +

/1

+

соэ

а

I

sш

.

(1t)

-

а

=

соэ

а,

соэ

(1t)

-

а

=

sш

а

2 2

.

с

g 2

--Vl-cosa'

a;t:21tk,

kE

Z.

В

этих

формулах

знак

перед

корнем

оп-

I

sin

(1t

-

а)

=

sin

а

,

соэ

(1t

-

а)

= - cos

а

ределяется по

знаку

четверти,

которой

I .

(31t) (31t)

.

а

sш 2 +

а

= -

соэ

а,

соэ

2 +

а

=

sш

а

принадлежит

угол

2"' I . (31t )

а

sina

sш

2-а

=-соэа

tg

2"

= 1 + cos

а'

a;t:

1t

(2k

+

1)

; k

Е

Z

tg~

=

1-cosa

31t

) .

cos 2 - а = -

sш

а

2

sina'

(

в

левой

части

a;t:

1t

(2k

+

1)

;

sin(21t +

а)

=sina

, cos(21t +

а)

=

cosa

в

правой

части

a;t:

21tk,

где

k

Е

Z.

sin(21t -

а)

=

-sina

, cos(21t -

а)

=

cosa

ctg

~

= 1 + cos

а

1t

2

sina'

1t

sш

2+

а соэа

в

левой

части

a;t:

21tk,

~

tg

(2

+

а)

= (1t ) = _

sin

а

= -

ctg

а

в

правой

части

a;t:

1tk, k

Е

Z.

cos 2 +

а

-----~----

ctg(1t +

а)

=

c~s(1t

+

а)

=

-c~sa

=

ctga.

34.

Тангенс

и котангенс

суммы

sш(1t

+

а)

-sша

и

разности

двух

углов

Все

формулы

приведения

сведем

в

две

таблицы,

поместив

в

таблице

1

формулы

Выведем

формулу

тангенса

суммы

двух

для

углов

1t

±

а

и

21t ±

а

,

а в

таблице

2 -

углов:

1t

31t

tg(a+~)=

sin(a+~)

~

I

для

углов

2±а

и

2±а

соэ(а

+~)

_

sin

а

cos

~

+

соэ

а

sin

~

-

cosacos~-sinasin~'

Разделим

числитель

и

знаменатель

этой

дроби

на

произведение

cosacos~,

предпо

лагая,

что

соэ

а

;t:

О и

соэ

~

;t:

О.

sin

а

соэ

~

+ cos

а

sin

~

t (

~)

=

соэ

а

соэ

~

соэ

а

соэ ~

g

а

+ cos

а

cos

~

sin

а

sin

~

cos

а

соэ ~

cos

а

соэ

~

tg

а

+

tg

~

=l-tgatg~·

Итак,

t

(а

+~)

=

tg

а

+

tg

~

,

g

1-tg

а

tg

~

1t 1t

а

;t:

2

(2k

+ 1),

~;t:

2 (2k + 1),

tg

atg

~

;t:

1; k

Е

Z.

L

~

ФУНК

ция

sin

х

cos х

tg

х

ctg

х

ФуНК

ция

sin

х

сов

х

tg

х

ctg

х

п+а

-sina

-сова

tga

ctga

1t

2+

а

cosa

-sina

-ctga

-tga

AuгvмeHTX

п-а

sina

-сова

-tga

-ctga

AuГVJ

1t

2-

а

сова

sina

ctga

tga

2п+а

sina

сова

tga

ctga

ент

Х

3п

т+

а

-cosa

sina

-ctga

-tga

Таблица

1

2п-а

-sina

сова

-tga

-ctga

Таблица

2

3п

т-а

-cosa

-sina

ctga

tga

~-~

34

35

г-----------T-----~----I

Правила

записи

формул

приведеиия

а

sina

По

табл.

1

и

2

легко

проследить

законо

ctg"2=I_cosa'

a;t27tk,

kEZ.

мерности,

имеющие

место

для

формул

при

В

формулах

знак

перед

корнем

берется

ведения.

Эти

закономерности

позволяют

а

так,

чтобы

он

совпадал

со

знаком

tg"2'

сформулировать

правила,

с

помощью

ко

а

торых

можно

записать

любую

формулу

т.

е.

ставится

знак .плюс.,

если

"2

приведения,

не

прибегая к таблицам:

угол

1

или

Ш

четверти,

и

знак

•

минус.

,

1.

Функция

в

правой

части

равенства

а

если

"2

-

угол

II

или

IV

четверти.

берется

с

тем

же

знаком,

какой

имеет

исходная

функция,

если

считать,

что

угол

Тригонометрические

функции

угла

мож

но

выразить

через

тангенс

половинного

а

является

углом

1

четверти;

угла:

2.

Для

углов

zt

±

а

и

2п

±

а

название

исходной

функции

сохраняется;

для

уг-

2tg~

sina

=

__

2_,

a;t

1t(2k+l),

kE

Z;

1t

3п

лов

"2

±

а

и

2 ±

а

название

исходной

l+tg

2

%

функции

изменяется

(синус

на

косинус,

1-

tg

2

~

cos

а

=

2,

a;t

1t

(2k

+ 1), k

Е

Z;

косинус

на

синус,

тангенс

на

котангенс,

котангенс

на

тангенс).

Пример

1.

l+tg

2

%

у

простим

выражение

tg

(З

2

п

-

а

).

~

2tg~

"

tga=-_2_,

a;t7t(2k+l),

kE

Z;

Решение.

I

l-tg2~

Угол

(З

2

п

-

а)

лежит

в

III

четверти

I

l-tg

2

~

окружности,

тангенс

угла

этой

четверти

ctga=~,

a;t7tk,

kEZ.

положителен,

поэтому

результат

берется

I

2tg-

со

знаком

.плюс

•.

Согласно

второму

пра

I 2

вилу,

название

функции

изменяется

с

тан

-----~-----

генса

на

котангенс.

Следовательно,

Аналогично

можно

доказать,

что

t

g

(3

1t

-а

)=ctga.

t _

tga-tg~

2

g

(а

-~)

- 1+

tg

atg

~'

Пример

2.

7t 7t

Упростим

выражение

cos

(п

-

а).

а

;t

"2

(2k

+ 1),

~;t"2

(2k

+1),

Решение.

tg

atg

~

;t

1;

k

Е

Z .

Угол

(п

-

а)

лежит

во

II

четверти.

Ко

синус

угла

второй

четверти

отрицателен,

Выполнив

преобразования,

аналогичные

приведенным

выше,

получим

формулы

для

нус

•.

Согласно

второму

правилу,

назва

котангенса

суммы

и

котангенса

разности

поэтому

результат

берется

со

знаком

.ми

двух

углов:

ние

функции

сохраняется.

Следовательно,

cos(7t -

а)

=

-cosa.

ctg

(а

+

~)

=

ctg

а

ctg

~

- 1 ,

ctga

+

ctg~

ct

(а

+

~)

=

ctg

а

ctg

~

-1

,

g

ctga

+

ctg

~

а

;t 7tk,

~;t

7tk,

a;t

-

~

+ 7tk, k

Е

Z.

а

;t

7tk

,

~;t

7tk,

a;t

~

+ 7tk, k

Е

Z.

L_~

~

36

г----~-----------------I

36.

Арксинус

и

арккосинус

Свойства

функции

у

=

arcsin

х

и

ее

график

Пусть

функция

f

монотонно

возрастает

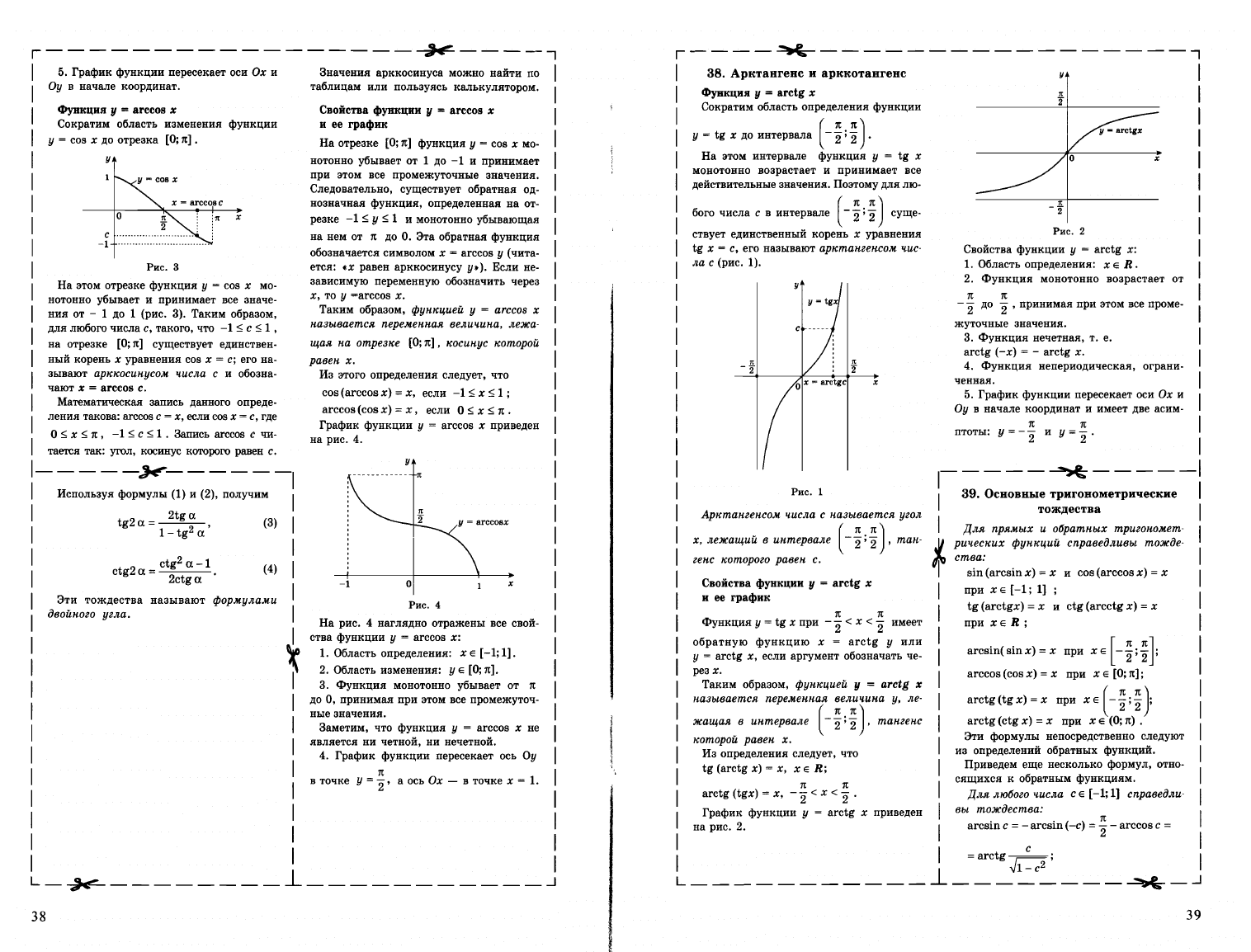
График

функции

у

= arcsin

х

приведен

(или

убывает)

на

промежутке

L,

а

число

с

на

рис.

2.

любое

из

зцачений,

принимаемых

функ

у

цией

на

этом

промежутке.

Тогда

уравне

ние

{(х)

=

с

имеет

единственный

корень

на

промежутке

L.

Функция

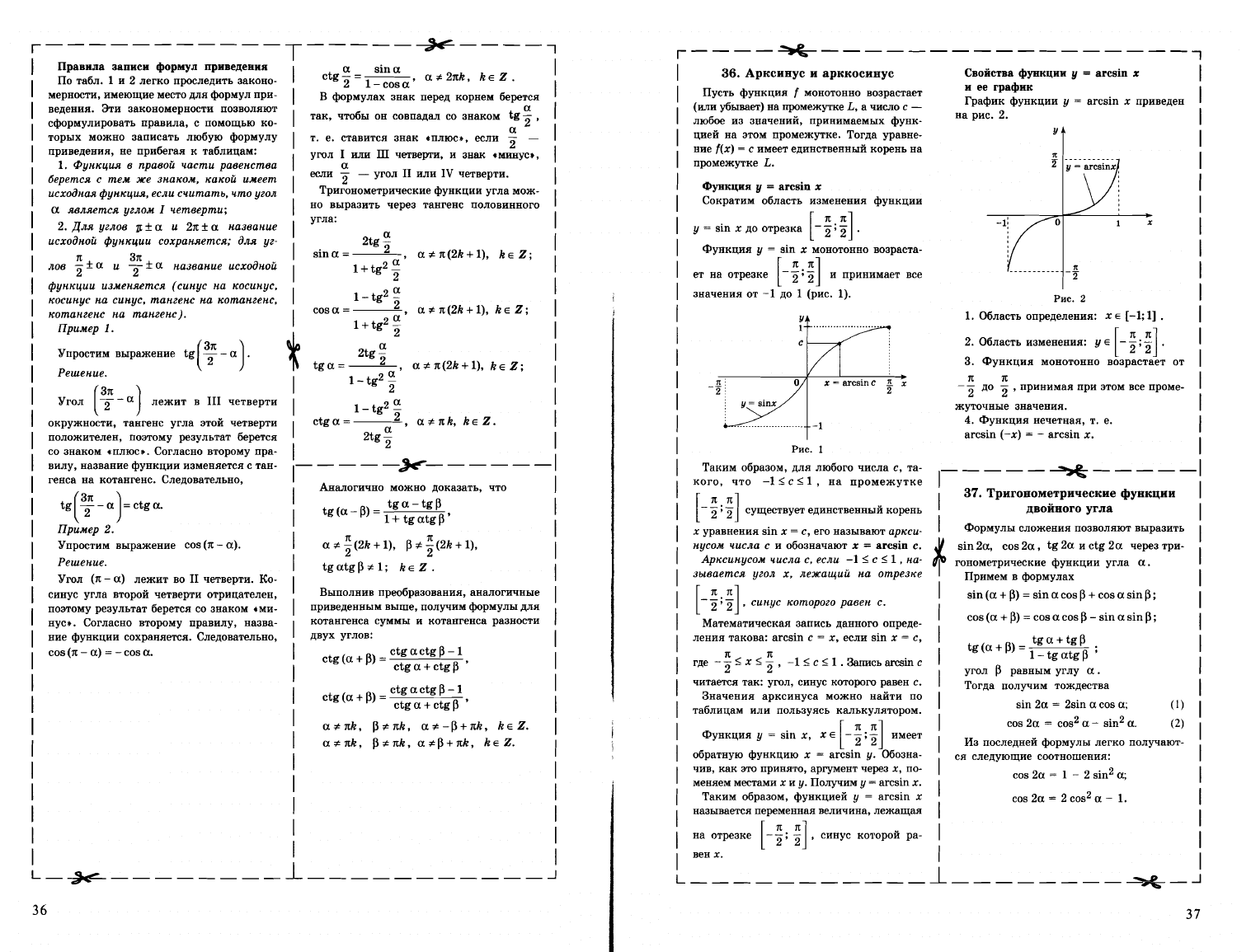
У

=

arcsin

х

Сократим

область

изменения

функции

х

-1:

у

= sin

х

до

отрезка

[-

~; ~]

.

Функция

у

= sin

х

монотонно

возраста

ет

на

отрезке

[-

~

;

~]

и

принимает

все

-2

1t

значения

от

-1

до

1

(рис.

1).

Рис.

2

у

1.

Область

определения:

х

Е

[-1;

1] .

1+·····················~

2.

Область

изменения:

у

Е

[ -

~

;

~]

•

3.

Функция

монотонно

возрастает

от

1t

Х

7t

-

2"

до

"2'

принимая

при

этом

все

проме

у

=

sinx

-i:

2

жуточные

значения.

4.

Функция

нечетная,

т.

е.

~··················-+-1

arcsin

(-х)

= - arcsin

х.

Рис.

1

Таким

образом,

для

любого

числа

с,

та

кого,

что

-1::;

с

::;

1,

на

промежутке

[-

~

;

~]

существует

единственный

корень

х

уравнения

sin

х

=

с,

его

называют

аркси

нусом

числа

с

и

обозначают

х

=

arcsin

с.

Арксинусом

числа

с,

если

-1::;

с::;

1,

на

зывается

угол

х,

лежащий

на

отрезке

[-

~;

~

] ,

синус

которого

равен

с.

cos

(а

+

~)

= cos

а

cos

~

-

sin

а

sin

~;

Математическая

запись

данного

опреде

ления

такова:

arcsin

с

=

х,

если

sin

х

=

С,

t

а

+ _

tg

а

+

tg

~

.

7t 7t

g (

~)

- 1-

tg

atg

~

,

где

-"2::;

х

::;

"2

'

-1::;

с

::;

1 .

Запись

arcsin

с

угол

~

равным

углу

а.

читается

так:

угол,

синус

которого

равен

с.

Тогда

получим

тождества

Значения

арксинуса

можно

найти

по

sin

2а

= 2sin

а

cos

а;

таблицам

или

пользуясь

калькулятором.

cos

2а

= cos

2

а

- sin

2

а.

Функция

у

= sin

х,

х

Е

[-~;~]

имеет

обратную

функцию

х

= arcsin

у.

Обозна

чив,

как

это

принято,

аргумент

через

х,

по

меняем

местами

х и

у.

Получим

у

=

aгcsin

х.

Таким

образом,

функцией

у

= arcsin

х

cos

2а

= 2 cos

2

а

- 1.

называется

переменная

величина,

лежащая

7t

п]

на

отрезке

-"2;

2"

'

синус

которои

ра

[

u

37

_______

_

г-----------------~----I

5.

График

функции

пересекает

оси

Ох

и

Оу

в

начале

координат.

Функция

у

=arccos

х

Сократим

область

изменения

функции

у

= cos

х

до

отрезка

[О;

л]

.

У

i

1t

х

-f1.·.·.·.·.·

· · -

·.·.·.~

Рис.

3

На

этом

отрезке

функция

у

= cos

х

мо

нотонно убывает

и

принимает

все

значе

ния

от

- 1

до

1

(рис.

3).

Таким

образом,

для любого

числа

С,

такого,

что

-1:5:

с:5:

1 ,

на

отрезке

[О;

л]

существует

единствен

ный

корень

х

уравнения

cos

х

=

С;

его на

зывают

арюсосинусом

числа

С

и

обозна

чают

х

= arccos

с.

Математическая

запись

данного

опреде

ления

такова:

arccos

С

=

х,

если

cos

х =

с,

где

0:5:

х

:5:

л,

-1:5:

С

:5:

1 .

Запись

arccos

С

чи

тается

так:

угол,

косинус

которого

равен

с.

-----:k------

I

Используя

формулы

(1)

и

(2),

получим

I

tg2a=~,

(3) I

1-

tg

2

а

I

2

ct

2a=ctg

a-1

(4) I

g

2ctga

Эти

тождества

называют

формулами

I

двойного

угла.

I

2.

Область

изменения:

у

Е

[О;

л].

3.

Функция

монотонно

убывает

от

1t

I

дО

О,

принимая

при

этом

все

промежуточ

*

ные

значения.

I

Заметим,

что

функция

у

= arccos

х

не

I

является

ни

четной,

ни

нечетной.

4.

График

функции

пересекает

ось

Оу

I

1t

В

точке

у

=

2'

а

ось

Ох

-

в

точке

х

= 1.

I

L_~--------~-----------~

Значения

арккосинуса

можно

найти

по

таблицам

или

пользуясь

калькулятором.

Свойства

функции

у

=arccos

х

и

ее

график

На

отрезке

[О;

л]

функция

У

=

соа

х

мо

нотонно

убывает

от

1

до

-1

и

принимает

при

этом

все

промежуточные

значения.

Следовательно,

существует

обратная

од

нозначная

функция,

определенная

на

от

резке

-1:5:

У

:5:

1

и

монотонно

убывающая

на

нем

от

1t

дО

О.

Эта

обратная

функция

обозначается

символом

х

= arccos

у

(чита

ется:

.х

равен

арккосинусу

у.).

Если

не

зависимую

переменную

обозначить

через

х,

то

у

=arccos

х.

Таким

образом,

фующией

у

=

arccos

х

называется

nеременная

величина,

лежа

щая

на

отрезн:е

[О;

л],

косинус

которой

равен

х.

Из

этого

определения

следует,

что

cos(arccosx)

=

х,

если

-1:5:

х:5:

1;

arccos (cos

х)

=

х,

если

0:5:

х

:5:

1t

•

График

функции

у

= arccos

х

приведен

на

рис.

4.

у

-1

о

х

Рис.

4

На

рис.

4

наглядно

отражены

все

свой

ства

функции

у

= arccos

х:

1.

Область

определения:

х

Е

[-1;

1] .

г----~-----------------I

38.

Арктангенс

и

арккотангенс

Функция

у

=

arctg

х

Сократим

область

определения

функции

у

=

tg

х

до

интервала

(-

j;j).

На

этом интервале

функция

у

=

tg

х

монотонно

возрастает

и

принимает

все

действительные

значения.

Поэтому

для

лю

бого

числа

с

в

интервале

(-

j;j)

суще

ствует

единственный

корень

х

уравнения

tg

х

=

с,

его

называют

арктангенсом

чис

ла

с

(рис.

1).

-~

Рис.

1

Арктангенсом

числа

с

называется

угол

х,

лежащий

в

интервале

(-

j ;

j),

тан

генс

которого

равен

с.

Свойства

функции

у

=

arctg

х

и

ее

график

1t 1t

Функция

У

=

tg

х

при

-2

<

х

< 2

имеет

обратную

функцию

х

=

arctg

у

или

у

=

arctg

х,

если

аргумент

обозначать

че

рез

х.

Таким

образом,

функцией

у

= arctg

х

называется

nеременная

величина

у,

ле

жащая

в

интервале

(-

j;

j

),

тангенс

которой

равен

х.

Из

определения

следует,

что

tg

(arctg

х)

=

х,

х

Е

R;

1t 1t

arctg

(tgx) =

х,

- 2 <

х

< 2 .

График

функции

у

=

arctg

х

приведен

на

рис.

2.

L

-2"

1t

Рис.

Свойства

функции

у

=

arctg

х:

1.

Область

определения:

х

Е

R.

2.

Функция

монотонно

возрастает

от

1t 1t

2

до

2 '

принимая

при

этом

все

проме

жуточные

значения.

3.

Функция

нечетная,

т. е.

arctg

(-х)

= -

arctg

х.

4.

Функция

непериодическая,

ограни

ченная.

5.

График

функции

пересекает

оси

Ох

и

Оу

в

начале

координат

и

имеет

две

асим

1t 1t

птоты:

у

= - 2

и

у

= 2 .

I-----~----

39.

Основные

тригонометрические

I

тождества

I

Для

прямых

и

обратных

тригономет

~

рических

функций

справедливы

тожде

/{о

ства:

sin

(arcsin

х)

=

х

и

соа

(arccos

х)

=

х

при

х

Е

[-1;

1]

tg

(arctgx)

=

х

и

ctg

(arcctg

х)

=

х

при

ХЕ

R ;

arcsin(

sin

х)

=

х

при

Х

Е

[ - j;jJ

arccos (cos

х)

=

х

при

х

Е

[О;

л];

arctg(tgx)=x

при

XE(-j;j}

arctg

(ctg

х)

=

х

при

х

Е

(О;

л)

.

Эти

формулы

непосредственно

следуют

из

определений

обратных

функций.

При

ведем

еще

несколько

формул,

отно

сящихся

К

обратным

функциям.

Для

любого числа

СЕ

[-1;1]

справедли

вы

тождества:

. . ( )

1t

arcsln

с

= -

arcsln

-с

= 2 - arccos

с

=

с

.

=шс,"

.)1-,2'

__

~_--!

..1

38

39

г-----------------~----I

г----~-----------------I

Функция

у

=

arcctg

х

Ар"котангенсом

числа

с

называется

40.

Простейmие

3х

Сократим

область

определения

функции

х

= 2 .

Учитывая

периодичность

синуса,

та

"ой

угол

х

из

интервала

(О;

п),

ко

тригонометрические

уравнения

у

=

ctg

х

до

интервала

(О;

х)

.

На

этом

тангенс

которого

равен

с.

Простейшими

тригонометрическими

интервале

функция

монотонно

убывает

от

запишем

все

решения

уравнения

sin

х

=

-1:

уравнениями

называют

уравнения

Свойства

функции

у

=

arcctg

х

+

00

до

-

00

и

принимает

все

действи

sin

х

=

с,

cos

х

=

с,

tg

х

=

с

и

ctg

х

=

с.

3л

и

ее

график

тельные

значения.

Поэтому

для

любого

х

= 2 +

21tk,

k

Е

Z.

(3)

числа

с

из

интервала

(О;

х)

существует

Функцией

у

=

arcctg

х

называется

пере

Решение

уравнения

sin

х

=

с

в)

sin

х

=

О.

Прямая

у

=

о

и

синусоида

единственный

корень

х

уравнения

ctg

х

=

с,

менная

величина,

лежащая

в

интервале

1.

Функция

у

=

sin

х

-

ограниченная,

имеют

бесконечное

количество

общих

то

его

называют

ар"котангенсом

числа

с

I

(О;

х)

,

котангенс

которой

равен

х.

так

как

область

ее

изменения

-

проме

i

чек

(см.

рис.

1).

(рис.

3).

График

функции

у

=

arcctg

х

приведен

жуток

[-1;

1],

поэтому

если

'сl

> 1

,то

урав

Решениями

уравнения

будут

О,

х, 2х,

на

рис.

4.

нение

sin

х

=

с

решений

не

имеет.

3х

,

...

общая

формула

которых

2.

Прямая

у

=

с

пересекает

синусоиду

"

21"

lI-arcСtg%

x=7tk,

kEZ.

(4)

бесконечное

количество

раз

(рис.

1).

Пример.

Решим

уравнения:

а)

sin3x

=

-~;

б)

sin2x

=

О;

2п

х

.

х

О

в)

SШ2"-1=

.

Решение.

а)

По

формуле

(1)

Рис.

1

Это

означает,

что

при

Icl

$1

уравнение

sin

х

=

с

имеет

бесконечное

количество

кор

Рис.

4

3х

=

(-1)k

arcsin(

-~)+

7tk,

kE

Z.

ней.

Так

как

функция

у

=

sin

х

имеет

Функция

у

=

arcctg

х

имеет

следующие

период

2х,

то

достаточно

найти

все

реше

свойства:

ния

в

пределах

этого

периода.

Из

рис.

1

Так

как

arcsin(

-~

)=

-~

,

то

1)

определена и

однозначна

на

всей

чис

Рис.

3

видно,

что

при

'сl

< 1

на

отрезке

[О;

2х]

ловой

прямой;

3X=(-1)k(_~)+7tk,

kE

Z;

2)

монотонно

убывает

от

1t

до

О,

прини

есть

два

числа,

синус

которых

равен

с,

мая

при

этом

все

промежуточные

значе

это

а

=

arcsin

с

и

7t

-

а

=

7t

-

arcsin

с.

Все

-----x------I

ния;

другие

решения

уравнения

sin

х

=

с

при

k (

п)

1tk

х

=

(-1)

- - +- k

Е

Z

18

3'

.

arccos

с

= 1t -

агссов

(-с)

= I

3)

не

является

ни

четной,

ни

нечетной,

Icl

< 1

получаются

из

двух

найденных

уг

Учитывая,

что

7t

3п

лов

прибавлением

периода.

7t

. t

с

I

так

как

arcctg

1 =

4"

'

а

arcctg

(

-1)

=4 ;

=

"2

-

агсsш

с

=

агс

g

~.

Итак,

пусть

а

= arcsin

с-

какое-либо

k (

х)

k 1t k+l

7t

4)

непериодическая,

ограниченная.

18

(-1)

--

=

(-1)

(-1)-

=

(-1)

-,

,,1-с

2

решение

уравнения

sin

х

=

с

при

'сl

< 1.

7t

I

График

функции

у

=

arcctg

х

пересекает

arctg

с

=

-arctg

(-с)

=

"2

-

arcctg

с

=

получаем х

= (_1)k+l ~ + 7tk, k

Е

Z;

Тогда

все

решения

этого

уравнения

полу

1t

18

3

с

.

I

ось

Оу

в

точке

у

="2

и

имеет

две

асимп-

чаются

по

формулам

б)

по

формуле

(4)

=

arcsin

J1

+

с

2

'

х

= arcsin

с

+ 27tk,

I

тоты: у

=

О

и

у

= 1t •

2х

=

7tk,

kE

Z;

х

=

1t

- arcsiIl

с

+ 21tk,

где

kE

Z.

7tk

1t

Эти

две

формулы

можно

объединить

в

Х=2'

kEZ;

arcctg

с

= 1t -

arcctg

(-с)

=

"2

-

arctg

с

=

I

одну:

x=(-1)k

arcs

inc+27tk,

kEZ.

(1)

в)

преобразуем

уравнение

к

виду

sш

2"

= 1

=мссо,

~1:

,2

;

~

. х

3.

Рассмотрим

частные

случаи

уравне

и

воспользуемся

формулой

(2):

.

7t

ния

sin

х

=

с:

агсsш

с

+ arccos

с

=

"2

;

~

= .:: + 21tk k

Е

z·

а)

sin

х

= 1.

Прямая

у

= 1

и

синусоида

2 2 ' ,

I

1t

имеют

бесконечное

количество

общих

то

x=1t+47tk,

kE

Z.

arctg

с

+

arctg

с

=

"2

.

I

чек

(см.

рис.

1).

Для

вычисления

значений

обратных

~

Решение

уравнення

cos

х

=

с

1t

тригонометрических

функций

при

отри

I

В

пределах

одного

периода

х

=

"2

.

Учи-

1.

Функция

у

= cos

х

-

ограниченная.

Так

же

как

и

в

предыдущем

случае,

полу

цательных

значениях

аргумента

исполь

I

ч

тывая

периодичность

синуса,

запишем

все

зуют

следующие

тождества:

чаем,

что

при

Icl

> 1

уравнение

cos

х

=

с

решения

уравнения

sin

х

= 1:

I

arcsin

(-с)

= -

arcsin

с

;

решения

не

имеет.

7t

arccos

(-с)

= 1t - arccos

с

;

х

=

"2

+27tk , k

Е

Z.

(2)

I

2.

При

Icl

$1

уравнение

имеет

беско

arctg

(

-с)

=

-arctg

с

;

б)

sin

х

=

-1.

Прямая

у

=

-1

и синусоида

нечное

количество

решений.

Из

рис.

2

вид

I

arctg

(-с)

= 1t -

arctg

с.

имеют

бесконечное

количество

общих

то

но,

что

в

пределах

одного

периода

уравне

I

чек

(см.

рис.

1).

В

пределах

одного

периода

ние

cos х =

а

имеет

два

корня:

а

и

-а.

L

~-~

L_~--_--~--~-----------~

40

41

Филатов О.А. Шпаргалки по алгебре и геометрии

Подождите немного. Документ загружается.