Федоров М.П. и др. Информационно-компьютерные технологии в строительстве. Применение программы SCAD для расчета сооружений на динамические воздействия
Подождите немного. Документ загружается.


60
67.409.0/42.0/1)/1(/
ɧɧ
2
ɧɧ
2
J JJ ZTJE
cc
ooo
PPPS ɬɫ = 45.813 ɤɇ.
ȼ ɫɨɨɬɜɟɬɫɬɜɢɢ ɫ ɩɪɚɜɨɣ ɱɚɫɬɶɸ ɜɵɪɚɠɟɧɢɹ (1.110) ɷɬɨ ɚɦɩɥɢɬɭɞɧɨɟ ɡɧɚɱɟɧɢɟ ɫɢɥɵ
ɞɨɥɠɧɨ ɛɵɬɶ ɜɡɹɬɨ ɫɨ ɡɧɚɤɨɦ «ɦɢɧɭɫ».
ɋɨɨɬɜɟɬɫɬɜɭɸɳɢɟ ɧɚɣɞɟɧɧɵɦ ɚɦɩɥɢɬɭɞɚɦ ɫɨɫɬɚɜɥɹɸɳɢɯ ɩɨɥɧɨɣ ɫɢɥɵ )(
tS ɚɦɩɥɢɬɭɞɵ
A
A
ccc
ɢ
ɫɨɫɬɚɜɥɹɸɳɢɯ ɩɨɥɧɨɝɨ ɩɟɪɟɦɟɳɟɧɢɹ
)(tu
ɢ ɚɦɩɥɢɬɭɞɵ
maxmax
ɢ MM
ccc
ɫɨɫɬɚɜɥɹɸɳɢɯ ɩɨɥɧɨɝɨ ɢɡɝɢɛɚɸɳɟɝɨ ɦɨɦɟɧɬɚ ɜ ɫɪɟɞɧɟɦ ɫɟɱɟɧɢɢ ɛɚɥɤɢ ɧɚɣɞɟɦ ɜ ɬɚɛɥɢɰɚɯ
«ɉɟɪɟɦɟɳɟɧɢɹ» ɢ «ɍɫɢɥɢɹ ɢ ɧɚɩɪɹɠɟɧɢɹ»:
ȿɞɢɧɢɰɵ ɢɡɦɟpɟɧɢɹ ɥɢɧɟɣɧɵɯ ɩɟpɟɦɟɳɟɧɢɣ: ɦɦ
------------------------------------------------------------------
| ɉȿɊȿɆȿɓȿɇɂə ɍɁɅɈȼ, ɦɦ |
------------------------------------------------------------------
| 1 2 3 |
------------------------------------------------------------------
| 5 - 1 ( ɝɚɪɦ1-ɪɟɡɨɧɚɧɫ) |
| 5 - 2 |
| Z 2.26 |
------------------------------------------------------------------
------------------------------------------------------------------
| ɍɋɂɅɂə /ɇȺɉɊəɀȿɇɂə/ ȼ ɗɅȿɆȿɇɌȺɏ, ɬɫ*ɦ |
------------------------------------------------------------------
| 2_ 1-1 1-2 2-1 2-2 |
------------------------------------------------------------------
| 5 - 1 ( ɝɚɪɦ1-ɪɟɡɨɧɚɧɫ) |
| 5 - 2 |
| M -9.33 -9.33 |
| 5 - S1 |
| M -9.33 -9.33 |
------------------------------------------------------------------
ɗɬɢ ɪɟɡɭɥɶɬɚɬɵ ɫɨɨɬɜɟɬɫɬɜɟɧɧɨ ɫɨɜɩɚɞɚɸɬ ɫ ɪɟɡɭɥɶɬɚɬɚɦɢ, ɩɨɥɭɱɟɧɧɵɦɢ ɜɵɲɟ ɪɚɫɱɟɬɨɦ
ɜɪɭɱɧɭɸ ɩɪɢ ɡɧɚɱɟɧɢɢ
0
ɧ
J
. ɋɨɜɩɚɞɟɧɢɟ ɪɟɡɭɥɶɬɚɬɨɜ ɩɨɥɭɱɚɟɬɫɹ ɩɪɢ ɢɫɩɨɥɶɡɨɜɚɧɢɢ
ɩɨɥɭɱɟɧɧɵɯ ɜɵɲɟ ɜɪɭɱɧɭɸ ɩɨ ɮɨɪɦɭɥɚɦ (1.111) ɫɢɥɚɦ
67.4ɢ0
cc
c
SS ɬɫ = 45.813 ɤɇ.
Ⱦɟɣɫɬɜɢɬɟɥɶɧɨ, ɢɫɩɨɥɶɡɭɹ ɮɨɪɦɭɥɵ (1.97)* ɢ (1.113) ɩɨɥɭɱɢɦ:
00226.0
)(ɫ)08.72(ɬ9.3
ɤɇ813.45
/;0
21-2
2
r
r Z
cc
r
cc
c
mSAA
ɦ = r 2.3 ɦɦ.
ɦɬɫ34.9)4/867.4()4/
ɛmaxmax
r r
cc
r
cc
lSMM = r 91.625 ɤɇ·ɦ.
ɉɨɷɬɨɦɭ ɢ ɜ ɫɥɭɱɚɟ, ɤɨɝɞɚ 1)/( ZT , ɫɭɦɦɚɪɧɵɟ ɜɟɥɢɱɢɧɵ ɞɥɹ ɩɪɨɝɢɛɚ ɢ ɢɡɝɢɛɚɸɳɟɝɨ
ɦɨɦɟɧɬɚ ɜ ɫɪɟɞɧɟɦ ɫɟɱɟɧɢɢ ɛɚɥɤɢ ɩɪɢ ɪɚɫɱɟɬɟ ɩɨ ɩɪɨɝɪɚɦɦɟ SCAD ɫɨɨɬɜɟɬɫɬɜɟɧɧɨ
ɫɨɜɩɚɞɚɸɬ ɫ ɩɪɢɜɟɞɟɧɧɵɦɢ ɜɵɲɟ ɪɟɡɭɥɶɬɚɬɚɦɢ ɪɚɫɱɟɬɚ ɜɪɭɱɧɭɸ.
ɇɚ ɪɢɫ. 1.26, ɚ, ɛ ɩɪɢɜɟɞɟɧɚ ɤɚɪɬɢɧɚ ɢɡɝɢɛɚ ɢ ɷɩɸɪɵ ɢɡɝɢɛɚɸɳɢɯ ɦɨɦɟɧɬɨɜ ɛɚɥɤɢ,
ɫɨɨɬɜɟɬɫɬɜɭɸɳɢɟ ɟɟ ɫɬɚɬɢɱɟɫɤɢɦ ɡɚɝɪɭɠɟɧɢɹɦ 1 ɢ 2. ɇɚ ɪɢɫ. 1.26, ɜ, ɝ ɚɧɚɥɨɝɢɱɧɵɟ
ɪɟɡɭɥɶɬɚɬɵ ɪɚɫɱɟɬɚ ɢɡɨɛɪɚɠɟɧɵ ɞɥɹ ɞɜɭɯ ɫɨɫɬɨɹɧɢɣ ɛɚɥɤɢ ɨɬ ɞɟɣɫɬɜɢɹ ɫɨɨɬɜɟɬɫɬɜɟɧɧɨ ɫɢɥ
ɬɫ17.0ɢɬɫ87.0
cc
c
SS , ɩɨɥɭɱɟɧɧɵɯ ɩɪɢ ɡɚɝɪɭɠɟɧɢɢ 3 ɞɢɧɚɦɢɱɟɫɤɨɣ ɫɢɥɨɣ
tPtP T sin)(
o
. ɇɚɩɪɚɜɥɟɧɢɹ ɫɢɥ SS
ccc
ɢ ɫɨɨɬɜɟɬɫɬɜɭɸɬ ɢɯ ɡɧɚɤɚɦ, ɩɪɢɧɹɬɵɦ ɜ ɩɪɨɝɪɚɦɦɟ
SCAD.

61
Ɋɢɫ. 1.26
4.8 ɬɫ·ɦ
0,6 ɬɫ/ɦ
ɚ)
– 1,4 ɦɦ
3,00 ɬɫ·ɦ
)ɛ
1,5 ɬɫ
– 0,7 ɦɦ
1,75 ɬɫ·ɦ
ɜ)
0,87 ɬɫ
0,42 ɦɦ
0,34 ɬɫ·ɦ
ɝ)
0,17 ɬɫ
0,08 ɦɦ
1,78 ɬɫ·ɦ
ɞ)
– 0,43 ɦɦ
9.58 ɬɫ·ɦ
6.02 ɬɫ·ɦ
17.13 ɬɫ·ɦ
1.53 ɬɫ·ɦ
ɟ)

62
ɇɚ ɪɢɫ. 1.26, ɞ ɩɪɢɜɟɞɟɧɵ ɷɩɸɪɵ ɪɚɫɱɟɬɧɵɯ ɚɦɩɥɢɬɭɞ A ɢ
max
M , ɩɨɞɫɱɢɬɚɧɧɵɯ
ɫɨɨɬɜɟɬɫɬɜɟɧɧɨ ɩɨ ɮɨɪɦɭɥɚɦ (1.98) ɢ (1.113), ɚ ɧɚ ɪɢɫ. 1.26, ɟ ɩɨɫɬɪɨɟɧɵ ɫɭɦɦɚɪɧɵɟ ɷɩɸɪɵ
ɢɡɝɢɛɚɸɳɢɯ ɦɨɦɟɧɬɨɜ ɩɪɢ ɡɚɞɚɧɧɨɦ ɜ ɩɪɢɦɟɪɟ ɫɨɨɬɧɨɲɟɧɢɢ ɭɝɥɨɜɵɯ ɱɚɫɬɨɬ 723.0)/( ZT
(ɫɩɥɨɲɧɵɟ ɥɢɧɢɢ) ɢ ɞɥɹ ɜɚɪɢɚɧɬɚ, ɤɨɝɞɚ
1)/( ZT (ɲɬɪɢɯɨɜɵɟ ɥɢɧɢɢ). Ɉɛɪɚɬɢɦ ɜɧɢɦɚɧɢɟ,
ɱɬɨ ɜɨ ɜɬɨɪɨɦ ɜɚɪɢɚɧɬɟ ɩɪɢ ɭɫɬɚɧɨɜɢɜɲɢɯɫɹ ɤɨɥɟɛɚɧɢɹɯ ɛɚɥɤɢ ɪɚɫɬɹɧɭɬɨɣ ɨɤɚɡɵɜɚɸɬɫɹ ɧɟ
ɬɨɥɶɤɨ ɟɟ ɧɢɠɧɹɹ ɫɬɨɪɨɧɚ, ɧɨ ɢ ɜɟɪɯɧɹɹ. Ɍɚɤ ɤɚɤ ɪɚɫɫɦɚɬɪɢɜɚɟɦɚɹ ɛɚɥɤɚ ɹɜɥɹɟɬɫɹ
ɠɟɥɟɡɨɛɟɬɨɧɧɨɣ, ɷɬɨ ɞɨɥɠɧɨ ɭɱɢɬɵɜɚɬɶɫɹ ɩɪɢ ɩɨɞɛɨɪɟ ɩɪɨɞɨɥɶɧɨɣ ɚɪɦɚɬɭɪɵ.
1.5. Ⱦɟɣɫɬɜɢɟ ɜɧɟɡɚɩɧɨ ɩɪɢɥɨɠɟɧɧɨɣ ɩɨɫɬɨɹɧɧɨɣ ɫɢɥɵ
ɉɭɫɬɶ ɧɚ ɪɚɫɱɟɬɧɭɸ ɫɯɟɦɭ ɛɚɥɤɢ ɜ ɜɢɞɟ ɧɟɜɟɫɨɦɨɝɨ ɭɩɪɭɝɨɝɨ ɫɬɟɪɠɧɹ ɫ
ɫɨɫɪɟɞɨɬɨɱɟɧɧɨɣ ɦɚɫɫɨɣ
m (ɫɦ. ɪɢɫ. 1.1,ɚ) ɜ ɦɨɦɟɧɬ ɜɪɟɦɟɧɢ 0 t ɦɝɧɨɜɟɧɧɨ
ɩɪɢɥɨɠɟɧɚ ɩɨɫɬɨɹɧɧɚɹ ɫɢɥɚ
o
P . (ɛɭɞɟɦ ɫɱɢɬɚɬɶ ɟɟ ɧɚɩɪɚɜɥɟɧɧɨɣ ɜɧɢɡ).
Ɉɩɪɟɞɟɥɢɦ ɩɟɪɟɦɟɳɟɧɢɟ ɦɚɫɫɵ (ɩɪɨɝɢɛ ɛɚɥɤɢ) ɩɪɢ ɪɚɡɥɢɱɧɨɣ ɞɥɢɬɟɥɶɧɨɫɬɢ
ɜɨɡɞɟɣɫɬɜɢɹ ɫɢɥɨɣ
o
P . ɉɪɢ ɷɬɨɦ ɛɭɞɟɦ ɩɪɟɞɩɨɥɚɝɚɬɶ, ɱɬɨ ɫɬɚɬɢɱɟɫɤɨɟ
ɩɟɪɟɦɟɳɟɧɢɟ ɨɬ ɜɟɫɚ ɦɚɫɫɵ ɪɚɫɫɦɨɬɪɟɧɨ ɨɬɞɟɥɶɧɨ ɢ ɜɫɟ ɩɟɪɟɦɟɳɟɧɢɹ,
ɜɵɡɜɚɧɧɵɟ ɦɝɧɨɜɟɧɧɨ ɩɪɢɥɨɠɟɧɧɨɣ ɫɢɥɨɣ
o
P
, ɨɬɫɱɢɬɵɜɚɸɬɫɹ ɨɬ ɨɫɢ ɛɚɥɤɢ ɫ
ɧɭɥɟɜɵɦɢ ɩɟɪɟɦɟɳɟɧɢɹɦɢ (ɫɦ. ɪɢɫ. 1,
ɚ).
ɋɢɥɚ ɞɟɣɫɬɜɭɟɬ ɛɟɫɤɨɧɟɱɧɨ ɞɨɥɝɨ. Ɋɚɫɫɦɨɬɪɢɦ ɜɚɪɢɚɧɬ,
ɤɨɝɞɚ
0
ɧ
J
Ɍɨɝɞɚ ɩɪɢ ɧɚɱɚɥɶɧɵɯ ɭɫɥɨɜɢɹɯ ɞɜɢɠɟɧɢɹ ɦɚɫɫɵ
0
ooo
uu
ɢɡ
ɢɧɬɟɝɪɚɥɚ Ⱦɸɚɦɟɥɹ (1.88) ɧɚɣɞɟɦ
³
WWZ
Z
t
o
dt
m
P
tu
0
)(sin)(
= )(
ɫɬ
tu
E
.
(1.114)
ɝɞɟ
)
2
cos1()(;/1;
2
ɫɬ
t
T
tmPu
o
S
EZ GG
.
(1.115)
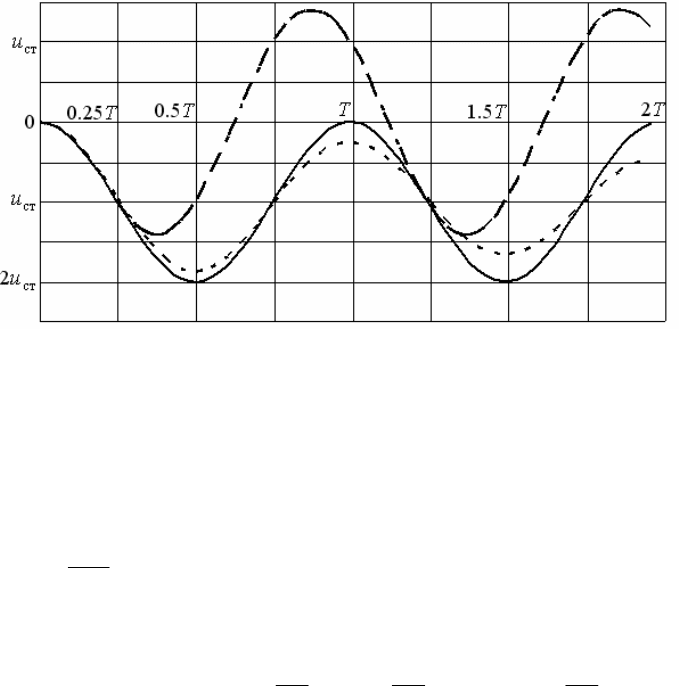
Ƚɪɚɮɢɤ ɢɡɦɟɧɟɧɢɹ ɩɟɪɟɦɟɳɟɧɢɹ (1.114) ɦɚɫɫɵ
m ɫ ɭɱɟɬɨɦ (1.115) ɜ
ɡɚɜɢɫɢɦɨɫɬɢ ɨɬ ɜɪɟɦɟɧɢ ɩɪɢ ɫɢɥɟ
o
P , ɧɚɩɪɚɜɥɟɧɧɨɣ ɜɧɢɡ, ɩɨɤɚɡɚɧ ɧɚ ɪɢɫ. 1.27
ɫɩɥɨɲɧɨɣ ɥɢɧɢɟɣ.
Ʉɚɤ ɜɢɞɧɨ, ɦɝɧɨɜɟɧɧɨ ɩɪɢɥɨɠɟɧɧɚɹ ɫɢɥɚ
o
P ɜɵɡɨɜɟɬ ɩɪɢ 0
ɧ
J
ɧɟɡɚɬɭɯɚɸɳɢɟ ɤɨɥɟɛɚɧɢɹ ɫɢɫɬɟɦɵ. ɉɪɢɱɟɦ ɜ ɦɨɦɟɧɬɵ ɜɪɟɦɟɧɢ k
T
T
t
2
/
,
ɝɞɟ
,...3,2,1 k , ɩɟɪɟɦɟɳɟɧɢɟ ɦɚɫɫɵ ɛɭɞɟɬ ɜ ɞɜɚ ɪɚɡɚ ɛɨɥɶɲɟ ɩɪɨɝɢɛɚ ɛɚɥɤɢ
G
o
Pu
ɫɬ
ɨɬ ɷɬɨɣ ɠɟ ɫɢɥɵ, ɩɪɢɥɨɠɟɧɧɨɣ ɫɬɚɬɢɱɟɫɤɢ. ɗɬɨ ɨɡɧɚɱɚɟɬ, ɱɬɨ
ɦɝɧɨɜɟɧɧɨɟ ɩɪɢɥɨɠɟɧɢɟ ɫɢɥɵ
o
P ɩɪɟɞɫɬɚɜɥɹɟɬ ɫɨɛɨɣ ɞɢɧɚɦɢɱɟɫɤɨɟ
ɜɨɡɞɟɣɫɬɜɢɟ. Ʉɨɷɮɮɢɰɢɟɧɬ ɞɢɧɚɦɢɱɧɨɫɬɢ ɜ ɭɤɚɡɚɧɧɵɟ ɦɨɦɟɧɬɵ ɜɪɟɦɟɧɢ
ɪɚɜɟɧ ɞɜɭɦ
( 2)(max E E t
t
).
63
Ɋɢɫ. 1.27
ȿɫɥɢ ɩɪɢ ɪɚɫɫɦɨɬɪɟɧɢɢ ɤɨɥɟɛɚɧɢɣ ɛɚɥɤɢ ɨɬ ɦɝɧɨɜɟɧɧɨɝɨ ɩɪɢɥɨɠɟɧɢɹ
ɫɢɥɵ ɭɱɟɫɬɶ ɜɥɢɹɧɢɟ ɫɢɥ ɧɟɭɩɪɭɝɨɝɨ ɫɨɩɪɨɬɢɜɥɟɧɢɹ, ɬɨ ɜ ɪɟɡɭɥɶɬɚɬɟ ɪɟɲɟɧɢɹ
ɢɧɬɟɝɪɚɥɚ Ⱦɸɚɦɟɥɹ (1.88) ɜɦɟɫɬɨ (1.114) ɢ (1.115), ɫ ɭɱɟɬɨɦ (1.79), ɩɨɥɭɱɢɦ:
³
WWZZJ
Z
t
dtt
m
P
tu
0
o
)(sin)5.0exp()(
ɧ
= )(
ɫɬ
tu E .
(1.116)
ɝɞɟ
»
¼
º
«
¬
ª
S
J
S
S
J E )
2
sin5.0
2
(cos)
2
5.0exp(1)(
ɧɧ
t
T
t
T
t
T
t .
(1.117)
Ƚɪɚɮɢɤ ɢɡɦɟɧɟɧɢɹ ɩɟɪɟɦɟɳɟɧɢɹ (1.116) ɫ ɭɱɟɬɨɦ (1.117) ɩɨɤɚɡɚɧ ɧɚ
ɪɢɫ. 1.27 ɲɬɪɢɯɨɜɨɣ ɥɢɧɢɟɣ. ȼɢɞɧɨ, ɱɬɨ ɩɪɢ 0
ɧ
zJ ɩɟɪɟɦɟɳɟɧɢɹ ɦɚɫɫɵ ɩɪɢ ɟɟ
ɤɨɥɟɛɚɧɢɹɯ, ɜɵɡɜɚɧɧɵɯ ɦɝɧɨɜɟɧɧɵɦ ɩɪɢɥɨɠɟɧɢɟɦ ɫɢɥɵ
o
P , ɫɨ ɜɪɟɦɟɧɟɦ ɛɭɞɭɬ
ɡɚɬɭɯɚɬɶ, ɩɪɢɛɥɢɠɚɹɫɶ ɤ ɡɧɚɱɟɧɢɸ ɩɟɪɟɦɟɳɟɧɢɹ
ɫɬ
u
. ɉɪɢ 2
/
T
t
ɢɡ (1.117)
ɩɨɥɭɱɢɦ ɦɚɤɫɢɦɚɥɶɧɵɣ ɞɢɧɚɦɢɱɟɫɤɢɣ ɤɨɷɮɮɢɰɢɟɧɬ:
)sin09.05.0(cos)09.05.0exp(1 SSS E
= 1+
1413.0
e = 1+0.87 = 1.87.
ɗɬɨ ɨɡɧɚɱɚɟɬ, ɱɬɨ ɪɚɫɱɟɬɧɨɣ ɫɢɥɨɣ ɞɥɹ ɛɚɥɤɢ ɹɜɥɹɟɬɫɹ ɫɢɥɚ
oomaxɪɚɫɱ
87.1 PPP E . Ɇɚɤɫɢɦɚɥɶɧɚɹ ɚɦɩɥɢɬɭɞɚ ɤɨɥɟɛɚɧɢɣ ɛɭɞɟɬ ɪɚɜɧɚ
ɫɬɫɬmaxmax
87.1 uuA E .
ɋɢɥɚ ɞɟɣɫɬɜɭɟɬ ɤɪɚɬɤɨɜɪɟɦɟɧɧɨ. Ɋɚɫɫɦɨɬɪɢɦ ɜɚɪɢɚɧɬ,
ɤɨɝɞɚ ɫɢɥɚ
o
P
ɜ ɦɨɦɟɧɬ ɜɪɟɦɟɧɢ 0
t
ɦɝɧɨɜɟɧɧɨ ɩɪɢɥɨɠɟɧɚ ɤ ɛɚɥɤɟ ɢ ɱɟɪɟɡ
ɧɟɛɨɥɶɲɨɣ ɩɟɪɢɨɞ ɜɪɟɦɟɧɢ
W
t
ɦɝɧɨɜɟɧɧɨ ɭɞɚɥɟɧɚ. ɑɬɨɛɵ ɩɨɞɫɱɢɬɚɬɶ
ɩɟɪɟɦɟɳɟɧɢɟ ɦɚɫɫɵ ɩɪɢ ɬɚɤɨɦ ɜɨɡɞɟɣɫɬɜɢɢ ɧɚ ɛɚɥɤɭ, ɪɚɫɫɦɨɬɪɢɦ ɫɥɟɞɭɸɳɢɟ
ɞɜɚ ɷɬɚɩɚ.
ɗɬɚɩ 1 (
Wd
t
). ɉɟɪɟɦɟɳɟɧɢɟ ɦɚɫɫɵ ɧɚ ɷɬɨɦ ɷɬɚɩɟ ɦɨɠɧɨ ɩɨɞɫɱɢɬɚɬɶ ɩɪɢ
0
ɧ
J
ɩɨ ɮɨɪɦɭɥɟ (1.114) ɫ ɭɱɟɬɨɦ (1.115) ɢɥɢ ɩɪɢ 0
ɧ
z
J
– ɩɨ ɮɨɪɦɭɥɟ (1.116)
ɫ ɭɱɟɬɨɦ (1.117). ɂɡ ɚɧɚɥɢɡɚ ɫɨɨɬɜɟɬɫɬɜɭɸɳɢɯ ɝɪɚɮɢɤɨɜ (ɫɦ. ɪɢɫ. 1.27) ɜɢɞɧɨ,
64
ɱɬɨ ɢ ɩɪɢ 0
ɧ
J
ɢ ɩɪɢ 0
ɧ
z
J
ɩɟɪɟɦɟɳɟɧɢɹ ɦɚɫɫɵ ɩɪɚɤɬɢɱɟɫɤɢ ɫɨɜɩɚɞɚɸɬ,
ɟɫɥɢ 2
/
T
t
d .
Ʉɪɨɦɟ ɬɨɝɨ, ɢɡ ɚɧɚɥɢɡɚ ɷɬɢɯ ɝɪɚɮɢɤɨɜ ɜɢɞɧɨ, ɱɬɨ ɟɫɥɢ ɭɞɚɥɢɬɶ ɫɢɥɭ ɜ
ɦɨɦɟɧɬ ɜɪɟɦɟɧɢ 4
/
T
d
W
, ɬɨ ɤ ɦɨɦɟɧɬɭ ɭɞɚɥɟɧɢɹ ɫɢɥɵ ɧɚ ɷɬɚɩɟ 1 ɩɟɪɟɦɟɳɟɧɢɟ
ɧɟ ɩɪɟɜɵɫɢɬ ɡɧɚɱɟɧɢɹ
ɫɬ
u , ɚ ɞɢɧɚɦɢɱɟɫɤɢɣ ɤɨɷɮɮɢɰɢɟɧɬ – ɡɧɚɱɟɧɢɹ 1
1
E .
ȿɫɥɢ ɠɟ ɭɞɚɥɢɬɶ ɫɢɥɭ ɜ ɦɨɦɟɧɬ ɜɪɟɦɟɧɢ 2
/
T
dW , ɬɨ ɧɚ ɷɬɚɩɟ 1
ɩɟɪɟɦɟɳɟɧɢɟ ɢ ɞɢɧɚɦɢɱɟɫɤɢɣ ɤɨɷɮɮɢɰɢɟɧɬ ɤ ɦɨɦɟɧɬɭ ɭɞɚɥɟɧɢɹ ɫɢɥɵ ɧɟ
ɩɪɟɜɵɫɹɬ ɫɨɨɬɜɟɬɫɬɜɟɧɧɨ ɡɧɚɱɟɧɢɣ 2
ɫɬ
u ɢ 2
1
E
.
ɗɬɚɩ 2 ( Wt
t
). ɇɚ ɜɬɨɪɨɦ ɷɬɚɩɟ (ɩɨɫɥɟ ɭɞɚɥɟɧɢɹ ɫɢɥɵ) ɛɭɞɭɬ
ɩɪɨɢɫɯɨɞɢɬɶ ɫɜɨɛɨɞɧɵɟ ɤɨɥɟɛɚɧɢɹ ɦɚɫɫɵ, ɩɟɪɟɦɟɳɟɧɢɟ ɤɨɬɨɪɨɣ ɩɪɢ
Wt
t
,
ɨɩɪɟɞɟɥɹɟɬɫɹ ɪɚɜɟɧɫɬɜɨɦ (1.18) ɢ ɡɚɜɢɫɢɬ ɨɬ ɧɚɱɚɥɶɧɵɯ ɭɫɥɨɜɢɣ ɫɜɨɛɨɞɧɵɯ
ɤɨɥɟɛɚɧɢɣ (1.16). ɗɬɢ ɧɚɱɚɥɶɧɵɟ ɭɫɥɨɜɢɹ ɫɜɹɡɚɧɵ ɫ ɜɪɟɦɟɧɟɦ
W
ɭɞɚɥɟɧɢɹ ɫɢɥɵ
(ɜɪɟɦɹ ɤɨɧɰɚ ɩɟɪɜɨɝɨ ɢ ɧɚɱɚɥɚ ɜɬɨɪɨɝɨ ɷɬɚɩɨɜ). ɂɡ (1.114) ɫ ɭɱɟɬɨɦ (1.115) ɷɬɢ
ɧɚɱɚɥɶɧɵɟ ɭɫɥɨɜɢɹ ɡɚɩɢɲɭɬɫɹ ɜ ɜɢɞɟ:
)
2
sin
2
);
2
cos1(
ɫɬ
oo
ɫɬ
o
W
S
S
W
S
T
T
uu
T
uu .
(1.118)
Ɍɨɝɞɚ ɜ ɫɨɨɬɜɟɬɫɬɜɢɢ ɫ (1.18) ɢ (1.21) ɩɨɥɭɱɢɦ:
t
u
tutu Z
Z
Z sincos)(
oo
o
2
=
)(
2ɫɬ
tu E
,
(1.119)
»
¼
º
«
¬
ª
S
W
S
S
W
S
E )
2
sin
2
sin
2
cos)
2
cos1()(
222
t
TT
t
TT
t ,
(1.120)
2
2
2
1
AAA =
2oo2o
)/()( Z uu = W
S
T
u sin2
ɫɬ
;
(1.121)
ɝɞɟ. W tt
2
.
Ɍɚɤ ɤɚɤ
>@
Atu
t
)(max
2
ɢ
>@
22
)(max
E
E
t
t ,
(1.122)
ɬɨ (1.119)
Tu
A W
S E sin2
ɫɬ
2
,
(1.123)
Ƚɪɚɮɢɤ ɫɜɨɛɨɞɧɵɯ ɤɨɥɟɛɚɧɢɣ ɦɚɫɫɵ )(
2
tu (1.119) ɫ ɭɱɟɬɨɦ (1.120)
ɢɡɨɛɪɚɠɟɧ ɧɚ ɪɢɫ. 1.27 ɲɬɪɢɯɩɭɧɤɬɢɪɧɨɣ ɥɢɧɢɟɣ ɞɥɹ ɜɚɪɢɚɧɬɚ, ɤɨɝɞɚ ɫɢɥɚ
o
P
ɭɞɚɥɟɧɚ ɜ ɦɨɦɟɧɬ ɜɪɟɦɟɧɢ 4
/
T
W . Ɍɨɝɞɚ, ɤɚɤ ɜɢɞɧɨ ɢɡ ɜɵɪɚɠɟɧɢɹ (1.123),
ɞɢɧɚɦɢɱɟɫɤɢɣ ɤɨɷɮɮɢɰɢɟɧɬ
2
E ɩɪɢ ɧɚɱɚɜɲɢɯɫɹ ɫɜɨɛɨɞɧɵɯ ɤɨɥɟɛɚɧɢɹɯ ɦɚɫɫɵ

65
ɧɚ ɜɬɨɪɨɦ ɷɬɚɩɟ ɞɨɫɬɢɝɧɟɬ ɦɚɤɫɢɦɚɥɶɧɨɝɨ ɡɧɚɱɟɧɢɹ 41.12
2
E , ɚ ɤɨɥɟɛɚɧɢɹ
ɦɚɫɫɵ ɛɭɞɭɬ ɩɪɨɢɫɯɨɞɢɬɶ ɨɬɧɨɫɢɬɟɥɶɧɨ ɩɨɥɨɠɟɧɢɹ ɛɚɥɤɢ ɫ ɧɭɥɟɜɵɦ ɩɪɨɝɢɛɨɦ.
ɉɪɢ ɭɞɚɥɟɧɢɢ ɫɢɥɵ
o
P ɜ ɦɨɦɟɧɬ ɜɪɟɦɟɧɢ 2
/
T
W – ɞɢɧɚɦɢɱɟɫɤɢɣ
ɤɨɷɮɮɢɰɢɟɧɬ ɭɫɩɟɟɬ ɞɨɫɬɢɱɶ ɡɧɚɱɟɧɢɹ 2
2
E . ɇɨ ɫɜɨɛɨɞɧɵɟ ɤɨɥɟɛɚɧɢɹ ɛɚɥɤɢ
ɩɨ-ɩɪɟɠɧɟɦɭ ɛɭɞɭɬ ɩɪɨɢɫɯɨɞɢɬɶ ɨɬɧɨɫɢɬɟɥɶɧɨ ɩɨɥɨɠɟɧɢɹ ɪɚɜɧɨɜɟɫɢɹ ɛɚɥɤɢ ɫ
ɧɭɥɟɜɵɦ ɩɪɨɝɢɛɨɦ (ɝɪɚɮɢɤ ɤɨɥɟɛɚɧɢɣ ɦɚɫɫɵ ɞɥɹ ɷɬɨɝɨ ɜɚɪɢɚɧɬɚ ɧɚ ɪɢɫ.1.27 ɧɟ
ɢɡɨɛɪɚɠɟɧ).
Ʉɪɚɬɤɨɜɪɟɦɟɧɧɭɸ ɧɚɝɪɭɡɤɭ ɨɛɵɱɧɨ ɧɚɡɵɜɚɸɬ ɢɦɩɭɥɶɫɢɜɧɨɣ, ɚ ɜɟɥɢɱɢɧɭ
W
o
PJ
p
– ɢɦɩɭɥɶɫɨɦ ɩɨɫɬɨɹɧɧɨɣ ɫɢɥɵ. Ɇɚɤɫɢɦɚɥɶɧɵɟ ɩɪɨɝɢɛɵ ɛɚɥɤɢ,
ɦɚɤɫɢɦɚɥɶɧɵɟ ɭɫɢɥɢɹ ɢ ɧɚɩɪɹɠɟɧɢɹ ɩɪɢ ɬɚɤɨɣ ɧɚɝɪɭɡɤɟ ɩɨɥɭɱɚɬɫɹ ɨɬ ɪɚɫɱɟɬɧɨɣ
ɫɢɥɵ
T
PPPP
ooo
W
S
WZ
WE W sin2
2
sin2)()(
2ɪɚɫɱ
,
(1.124)
ɡɧɚɱɟɧɢɟ ɤɨɬɨɪɨɣ, ɤɚɤ ɢ ɡɧɚɱɟɧɢɟ ɞɢɧɚɦɢɱɟɫɤɨɝɨ ɤɨɷɮɮɢɰɢɟɧɬɚ ɡɚɜɢɫɢɬ ɨɬ
ɜɪɟɦɟɧɢ
W
ɞɟɣɫɬɜɢɹ ɫɢɥɵ, ɬɨɱɧɟɟ – ɨɬ ɫɨɨɬɧɨɲɟɧɢɹ
T
/
W
.
ȿɫɥɢ ɢɦɩɭɥɶɫ ɫɨɡɞɚɟɬɫɹ ɫɢɥɨɣ, ɢɡɦɟɧɹɸɳɟɣɫɹ ɡɚ ɩɪɨɦɟɠɭɬɨɤ ɜɪɟɦɟɧɢ W ,
ɨɧ ɨɩɪɟɞɟɥɹɟɬɫɹ ɢɡ ɜɵɪɚɠɟɧɢɹ
³
W
0
)( dttPJ
p
,
(1.125)
ɝɞɟ
Ɉɲɢɛɤɚ! Ɉɛɴɟɤɬ ɧɟ ɦɨɠɟɬ ɛɵɬɶ ɫɨɡɞɚɧ ɢɡ ɤɨɞɨɜ ɩɨɥɟɣ ɪɟɞɚɤɬɢɪɨɜɚɧɢɹ.
)()( tfPtP
o
ɩɪɢ Wdd
t
0 ;
0
)
(
P
(1.126)
Ɏɭɧɤɰɢɹ )(
t
f
ɯɚɪɚɤɬɟɪɢɡɭɟɬ ɮɨɪɦɭ ɢɦɩɭɥɶɫɚ, ɩɪɢɱɟɦ ɦɚɤɫɢɦɭɦ
1)( tf .
Ʉɚɤ ɛɵɥɨ ɩɪɨɞɟɦɨɧɫɬɪɢɪɨɜɚɧɨ ɜ ɩɪɢɜɟɞɟɧɧɨɦ ɜɵɲɟ ɩɪɢɦɟɪɟ, ɪɟɚɤɰɢɹ
ɭɩɪɭɝɨɣ ɫɢɫɬɟɦɵ ɫ ɨɞɧɨɣ ɫɬɟɩɟɧɶɸ ɫɜɨɛɨɞɵ ɡɚɜɢɫɢɬ ɨɬ ɨɬɧɨɲɟɧɢɹ
T
/
W .
ȿɫɥɢ
T
1.0!W , ɩɪɢ ɪɚɫɱɟɬɟ ɫɨɨɪɭɠɟɧɢɹ ɧɚ ɢɦɩɭɥɶɫɢɜɧɭɸ ɧɚɝɪɭɡɤɭ
ɧɟɨɛɯɨɞɢɦɨ ɭɱɢɬɵɜɚɬɶ ɫɥɟɞɭɸɳɢɟ ɬɪɢ ɩɚɪɚɦɟɬɪɚ:
1) ɩɪɨɞɨɥɠɢɬɟɥɶɧɨɫɬɶ W ɢɦɩɭɥɶɫɚ; 2) ɮɨɪɦɭ )(
t
f
ɢɦɩɭɥɶɫɚ; 3)
ɧɚɢɛɨɥɶɲɭɸ ɨɪɞɢɧɚɬɭ
o
P ɝɪɚɮɢɤɚ ɧɚɝɪɭɡɤɢ )(
t
P
.
ȿɫɥɢ
T
1.0dW , ɢɦɩɭɥɶɫ ɧɚɡɵɜɚɸɬ ɦɝɧɨɜɟɧɧɵɦ. ɉɪɢ ɬɚɤɨɦ ɢɦɩɭɥɶɫɟ
ɨɫɧɨɜɧɵɦ ɩɚɪɚɦɟɬɪɨɦ ɩɪɢ ɪɚɫɱɟɬɟ ɫɨɨɪɭɠɟɧɢɹ ɫɱɢɬɚɟɬɫɹ ɡɧɚɱɟɧɢɟ
p
J ɫɚɦɨɝɨ
ɢɦɩɭɥɶɫɚ, ɚ ɟɝɨ ɮɨɪɦɚ )(
t
f
ɩɪɚɤɬɢɱɟɫɤɨɝɨ ɜɥɢɹɧɢɹ ɧɚ ɪɟɚɤɰɢɸ ɫɢɫɬɟɦɵ ɧɟ
ɨɤɚɡɵɜɚɟɬ.

66
ɉɪɢ ɞɟɣɫɬɜɢɢ ɦɝɧɨɜɟɧɧɨɝɨ ɢɦɩɭɥɶɫɚ ɩɪɟɞɩɨɥɚɝɚɟɬɫɹ ɩɪɢɦɟɪɧɨɟ
ɪɚɜɟɧɫɬɜɨ
T
T
/
/
sin SW|SW . Ɍɨɝɞɚ ɜɦɟɫɬɨ (1.123) ɢ (1.124) ɩɨɥɭɱɢɦ
ɫɨɨɬɜɟɬɫɬɜɟɧɧɨ ɜɵɪɚɠɟɧɢɹ (1.127) ɢ (1.128).
ZW
W
S|
W
S E
TTu
A
2sin2
ɫɬ
2
.
(1.127)
Z ZW
WZ
E W
p
JPPPP
oo2oɪɚɫɱ
2
sin2)(
.
(1.128)
ȼ ɩɪɨɝɪɚɦɦɟ SCAD ɩɪɟɞɩɨɥɚɝɚɟɬɫɹ ɡɚɞɚɧɢɟ, ɤɚɤ ɡɧɚɱɟɧɢɹ ɚɦɩɥɢɬɭɞɵ
o
P
ɫɢɥɵ, ɬɚɤ ɢ ɡɧɚɱɟɧɢɹ ɢɦɩɭɥɶɫɚ.
ɉɪɢɦɟɱɚɧɢɟ. ɋ ɛɨɥɟɟ ɞɟɬɚɥɶɧɵɦ ɢɫɫɥɟɞɨɜɚɧɢɟɦ ɜɨɩɪɨɫɚ ɨ ɪɚɫɱɟɬɟ ɫɢɫɬɟɦɵ ɫ ɨɞɧɨɣ
ɫɬɟɩɟɧɶɸ ɫɜɨɛɨɞɵ ɧɚ ɤɪɚɬɤɨɜɪɟɦɟɧɧɵɟ ɧɚɝɪɭɡɤɢ ɩɪɢ ɪɚɡɥɢɱɧɵɯ ɜɢɞɚɯ ɮɭɧɤɰɢɢ )(tf ɦɨɠɧɨ
ɨɡɧɚɤɨɦɢɬɶɫɹ ɜ ɫɩɪɚɜɨɱɧɢɤɟ [15] ɢ ɜ ɤɧɢɝɟ ɪɚɡɪɚɛɨɬɱɢɤɨɜ ɩɪɨɝɪɚɦɦɵ SCAD [23].
ȼ ɪɚɡɞɟɥɟ 5 ɫɩɪɚɜɨɱɧɢɤɚ [15] ɩɪɢɜɟɞɟɧɵ ɲɟɫɬɶ ɮɭɧɤɰɢɣ
)(tf ɢ ɫɨɨɬɜɟɬɫɬɜɭɸɳɢɯ ɢɦ
ɝɪɚɮɢɤɨɜ ɮɨɪɦ ɢɦɩɭɥɶɫɨɜ, ɧɚɢɛɨɥɟɟ ɱɚɫɬɨ ɜɫɬɪɟɱɚɸɳɢɯɫɹ ɜ ɩɪɚɤɬɢɤɟ ɪɚɫɱɟɬɨɜ. Ɍɚɦ ɠɟ
ɩɪɢɜɟɞɟɧɵ ɨɫɧɨɜɧɵɟ ɫɜɟɞɟɧɢɹ ɨ ɦɟɬɨɞɢɤɟ ɪɚɫɱɟɬɚ ɫɨɨɪɭɠɟɧɢɣ ɧɚ ɢɦɩɭɥɶɫɢɜɧɵɟ ɧɚɝɪɭɡɤɢ ɢ
ɪɟɡɭɥɶɬɚɬɵ ɪɹɞɚ ɢɫɫɥɟɞɨɜɚɧɢɣ, ɤɨɬɨɪɵɟ ɛɵɥɢ ɢɫɩɨɥɶɡɨɜɚɧɵ ɜ ɩɪɨɝɪɚɦɦɟ SCAD ɩɪɢ ɪɚɫɱɟɬɟ
ɫɨɨɪɭɠɟɧɢɣ ɧɚ ɢɦɩɭɥɶɫɢɜɧɵɟ ɧɚɝɪɭɡɤɢ [23].
Ɋɚɫɱɟɬ ɫɢɫɬɟɦɵ ɫ ɨɞɧɨɣ ɫɬɟɩɟɧɶɸ ɫɜɨɛɨɞɵ ɩɪɢ ɞɟɣɫɬɜɢɢ ɢɦɩɭɥɶɫɢɜɧɨɣ
ɧɚɝɪɭɡɤɢ ɞɨɫɬɚɬɨɱɧɨ ɩɪɨɫɬ ɞɥɹ ɟɝɨ ɜɵɩɨɥɧɟɧɢɹ ɜɪɭɱɧɭɸ. Ɉɞɧɚɤɨ, ɭɱɢɬɵɜɚɹ
ɧɚɩɪɚɜɥɟɧɧɨɫɬɶ ɭɱɟɛɧɨɝɨ ɩɨɫɨɛɢɹ, ɩɪɨɞɟɦɨɧɫɬɪɢɪɭɟɦ ɢɫɩɨɥɶɡɨɜɚɧɢɟ
ɩɪɨɝɪɚɦɦɵ SCAD ɢ ɧɚ ɫɨɨɬɜɟɬɫɬɜɭɸɳɢɯ ɩɪɨɫɬɵɯ ɩɪɢɦɟɪɚɯ.
ɉɪɢɦɟɪ 1. ɉɪɟɞɩɨɥɨɠɢɦ, ɱɬɨ ɠɟɥɟɡɨɛɟɬɨɧɧɚɹ ɛɚɥɤɚ, ɪɚɫɫɦɨɬɪɟɧɧɚɹ ɜ ɩɪɢɦɟɪɟ 4
ɩɨɞɪɚɡɞɟɥɚ 1.1 ɢ ɩɪɢɦɟɪɟ 1 ɩɨɞɪɚɡɞɟɥɚ 1.4, ɞɨ ɭɫɬɚɧɨɜɤɢ ɧɚ ɧɟɟ ɷɥɟɤɬɪɨɞɜɢɝɚɬɟɥɹ
ɩɨɞɜɟɪɝɥɚɫɶ ɜɨɡɞɟɣɫɬɜɢɸ ɢɦɩɭɥɶɫɢɜɧɨɣ ɧɚɝɪɭɡɤɢ, ɩɪɢɥɨɠɟɧɧɨɣ ɩɟɪɩɟɧɞɢɤɭɥɹɪɧɨ ɤ ɨɫɢ
ɛɚɥɤɢ ɜ ɫɟɪɟɞɢɧɟ ɟɟ ɩɪɨɥɟɬɚ.
ɂɦɩɭɥɶɫɢɜɧɭɸ ɧɚɝɪɭɡɤɭ ɡɚɞɚɞɢɦ ɜ ɜɢɞɟ ɩɨɫɬɨɹɧɧɨɣ ɫɢɥɵ 5.1
o
P ɬɫ, ɩɪɢɥɨɠɟɧɧɨɣ ɤ
ɛɚɥɤɟ ɜ ɦɨɦɟɧɬ ɜɪɟɦɟɧɢ
0 t
ɩɨ ɧɚɩɪɚɜɥɟɧɢɸ ɜɧɢɡ ɢ ɭɞɚɥɟɧɧɨɣ ɜ ɦɨɦɟɧɬ ɜɪɟɦɟɧɢ
Tt 5.0 W . ɂɧɵɦɢ ɫɥɨɜɚɦɢ, ɛɚɥɤɚ, ɧɚɯɨɞɹɳɚɹɫɹ ɩɨɞ ɞɟɣɫɬɜɢɟɦ ɫɨɛɫɬɜɟɧɧɨɝɨ ɜɟɫɚ, ɜ ɦɨɦɟɧɬ
ɜɪɟɦɟɧɢ
0 t
ɩɨɥɭɱɢɥɚ ɞɢɧɚɦɢɱɟɫɤɨɟ ɜɨɡɞɟɣɫɬɜɢɟ ɜ ɜɢɞɟ ɩɨɫɬɨɹɧɧɨɝɨ ɩɨ ɮɨɪɦɟ ɢɦɩɭɥɶɫɚ
TPJ
op
5.05.1 W ɩɪɨɞɨɥɠɢɬɟɥɶɧɨɫɬɶɸ T5.0 W . Ɂɞɟɫɶ ɩɨɞ ɩɚɪɚɦɟɬɪɨɦ
T
ɩɨɧɢɦɚɟɬɫɹ
ɩɟɪɢɨɞ ɫɨɛɫɬɜɟɧɧɵɯ ɤɨɥɟɛɚɧɢɣ ɛɚɥɤɢ ɤɚɤ ɫɢɫɬɟɦɵ ɫ ɨɞɧɨɣ ɫɬɟɩɟɧɶɸ ɫɜɨɛɨɞɵ. Ɍɚɤɚɹ
ɪɚɫɱɟɬɧɚɹ ɫɯɟɦɚ ɛɵɥɚ ɩɨɥɭɱɟɧɚ (ɫɦ. ɪɢɫ. 1.8) ɩɪɢ ɚɩɩɪɨɤɫɢɦɚɰɢɢ ɛɚɥɤɢ ɞɜɭɦɹ ɫɬɟɪɠɧɟɜɵɦɢ
ɤɨɧɟɱɧɵɦɢ ɷɥɟɦɟɧɬɚɦɢ ɬɢɩɚ 2 (ɩɨ ɤɥɚɫɫɢɮɢɤɚɰɢɢ ɩɪɨɝɪɚɦɦɵ SCAD).
Ȼɚɥɤɚ ɞɨ ɩɪɢɥɨɠɟɧɢɹ ɢɦɩɭɥɶɫɚ ɧɚɯɨɞɢɥɚɫɶ ɩɨɞ ɞɟɣɫɬɜɢɟɦ ɬɨɥɶɤɨ ɫɨɛɫɬɜɟɧɧɨɝɨ ɜɟɫɚ ɫ
ɢɧɬɟɧɫɢɜɧɨɫɬɶɸ ɧɚɝɪɭɡɤɢ ɜɞɨɥɶ ɨɫɢ ɛɚɥɤɢ
)ɦ24.0()ɬɫ/ɦ5.2(
23
ɛɛɛ
J Aq = 0.6 ɬɫ/ɦ =
= (0.6 ɬɫ/ɦ) · (9.81 ɦ/ɫ
2
) = 5.886 ɤɇ/ɦ. ɉɪɢ ɷɬɨɦ ɫɬɚɬɢɱɟɫɤɢɣ ɢɡɝɢɛɚɸɳɢɣ ɦɨɦɟɧɬ ɢ ɩɪɨɝɢɛ ɜ
ɫɪɟɞɧɟɦ ɫɟɱɟɧɢɢ ɛɚɥɤɢ ɨɬ ɟɟ ɫɨɛɫɬɜɟɧɧɨɝɨ ɜɟɫɚ ɭɠɟ ɢɡɜɟɫɬɧɵ ɢɡ ɩɪɢɦɟɪɚ 1 ɩɨɞɪɚɡɞɟɥɚ 1.4:
ɦɬɫ8.48/86.08/)(
22
ɛɛɛɫɬ
lqqM = 47.088 ɤɇ·ɦ.

67
ɦɦ1.4ɦ0.00145
384
51
)(
4
ɛɛ
8
0
ɛɫɬ
³
EI
lq
dxMM
EI
qu
p
.
Ʉɚɤ ɫɥɟɞɭɟɬ ɢɡ ɮɨɪɦɭɥ (1.123) ɢ (1.124), ɞɢɧɚɦɢɱɟɫɤɢɣ ɤɨɷɮɮɢɰɢɟɧɬ ɢ ɪɚɫɱɟɬɧɚɹ ɫɢɥɚ ɞɥɹ
ɨɩɪɟɞɟɥɟɧɢɹ ɪɚɫɱɟɬɧɵɯ ɩɟɪɟɦɟɳɟɧɢɣ ɢ ɭɫɢɥɢɣ ɜ ɛɚɥɤɟ ɩɪɢ ɭɞɚɥɟɧɢɢ ɫɢɥɵ 5.1
o
P ɬɫ ɜ
ɦɨɦɟɧɬ ɜɪɟɦɟɧɢ
Tt 5.0 W ɤ ɷɬɨɦɭ ɦɨɦɟɧɬɭ ɜɪɟɦɟɧɢ ɭɠɟ ɞɨɫɬɢɝɧɭɬ (ɛɟɡ ɭɱɟɬɚ ɜɥɢɹɧɢɹ ɫɢɥ
ɧɟɭɩɪɭɝɨɝɨ ɫɨɩɪɨɬɢɜɥɟɧɢɹ) ɫɨɨɬɜɟɬɫɬɜɟɧɧɨ ɦɚɤɫɢɦɚɥɶɧɵɯ ɡɧɚɱɟɧɢɣ
2
21
E E ɢ
32
oɪɚɫɱ
PP ɬɫ (ɫɦ. ɪɢɫ. 1.27). ɉɪɢ ɭɱɟɬɟ ɫɢɥ ɧɟɭɩɪɭɝɨɝɨ ɫɨɩɪɨɬɢɜɥɟɧɢɹ, ɤɚɤ ɷɬɨ ɩɨɤɚɡɚɧɨ
ɜɵɲɟ ɪɚɫɱɟɬɨɦ ɩɨ ɮɨɪɦɭɥɟ (1.117), ɷɬɢ ɡɧɚɱɟɧɢɹ ɫɨɨɬɜɟɬɫɬɜɟɧɧɨ ɛɭɞɭɬ ɧɟɫɤɨɥɶɤɨ ɦɟɧɶɲɟ:
87.1
21
E E ɢ 8.25.187.187.1
oɪɚɫɱ
PP ɬɫ (ɲɬɪɢɯɨɜɚɹ ɥɢɧɢɹ ɧɚ ɪɢɫ. 1.27).
Ɉɩɪɟɞɟɥɢɜ ɪɚɫɱɟɬɧɭɸ ɞɢɧɚɦɢɱɟɫɤɭɸ ɧɚɝɪɭɡɤɭ ɫ ɭɱɟɬɨɦ ɫɢɥɵ ɧɟɭɩɪɭɝɨɝɨ ɫɨɩɪɨɬɢɜɥɟɧɢɹ
ɜ ɜɢɞɟ ɫɨɫɪɟɞɨɬɨɱɟɧɧɨɣ ɫɢɥɵ, ɩɪɢɥɨɠɟɧɧɨɣ ɜ ɫɟɪɟɞɢɧɟ ɩɪɨɥɟɬɚ ɛɚɥɤɢ, ɧɚɣɞɟɦ ɪɚɫɱɟɬɧɨɟ
ɡɧɚɱɟɧɢɟ ɢɡɝɢɛɚɸɳɟɝɨ ɦɨɦɟɧɬɚ ɢ ɪɚɫɱɟɬɧɨɝɨ ɩɪɨɝɢɛɚ ɛɚɥɤɢ ɜ ɟɟ ɫɪɟɞɧɟɦ ɫɟɱɟɧɢɢ:
ɦɬɫ6.54/88.24/)(
ɛɪɚɫɱɪɚɫɱɪɚɫɱ
lPPM = 54.94 ɤɇ·ɦ.
ɦɦ1.3ɦ0.00138.2000484.0)(
ɪɚɫɱɪɚɫɱɪɚɫɱ
G PPu .
Ʉɚɤ ɜɢɞɧɨ (ɫɦ. ɪɢɫ. 1.27), ɩɪɢ ɢɦɩɭɥɶɫɟ
TPJ
op
5.05.1 W
, ɧɚɩɪɚɜɥɟɧɧɨɦ ɜɧɢɡ,
ɩɨɥɭɱɟɧɧɵɣ ɜ ɦɨɦɟɧɬ ɜɪɟɦɟɧɢ
Tt 5.0 ɦɚɤɫɢɦɚɥɶɧɵɣ (ɪɚɫɱɟɬɧɵɣ) ɞɢɧɚɦɢɱɟɫɤɢɣ
ɢɡɝɢɛɚɸɳɢɣ ɦɨɦɟɧɬ ɛɭɞɟɬ ɪɚɫɬɹɝɢɜɚɬɶ ɧɢɠɧɸɸ ɫɬɨɪɨɧɭ ɛɚɥɤɢ ɢ ɩɨɷɬɨɦɭ ɞɨɥɠɟɧɛɵɬɶ
ɩɪɨɫɭɦɦɢɪɨɜɚɧ ɫɨ ɫɬɚɬɢɱɟɫɤɢɦ ɢɡɝɢɛɚɸɳɢɦ ɦɨɦɟɧɬɨɦ, ɜɨɡɧɢɤɚɸɳɢɦ ɜ ɫɪɟɞɧɟɦ ɫɟɱɟɧɢɢ
ɛɚɥɤɢ ɨɬ ɟɟ ɫɨɛɫɬɜɟɧɧɨɝɨ ɜɟɫɚ. ȼ ɪɟɡɭɥɶɬɚɬɟ ɜ ɦɨɦɟɧɬ ɜɪɟɦɟɧɢ
Tt 5.0 ɩɨɥɭɱɢɦ ɫɭɦɦɚɪɧɵɣ
ɦɨɦɟɧɬ
ɦɬɫ4.106.58.4)()(
ɪɚɫɱɪɚɫɱɫɬɫ
PMqMM = 102.024 ɤɇ·ɦ.
Ⱥɧɚɥɨɝɢɱɧɨ (ɫɦ. ɪɢɫ. 1.27) ɩɪɢ ɢɦɩɭɥɶɫɟ TPJ
op
5.05.1 W , ɧɚɩɪɚɜɥɟɧɧɨɦ ɜɧɢɡ,
ɩɨɥɭɱɟɧɧɨɟ ɜ ɦɨɦɟɧɬ ɜɪɟɦɟɧɢ
Tt 5.0 ɪɚɫɱɟɬɧɨɟ ɞɢɧɚɦɢɱɟɫɤɨɟ ɩɟɪɟɦɟɳɟɧɢɟ ɬɚɤɠɟ ɛɭɞɟɬ
ɧɚɩɪɚɜɥɟɧɨ ɜɧɢɡ ɢ ɩɨɷɬɨɦɭ ɞɨɥɠɧɨ ɛɵɬɶ ɩɪɨɫɭɦɦɢɪɨɜɚɧɨ ɫɨ ɫɬɚɬɢɱɟɫɤɢɦ ɩɪɨɝɢɛɨɦ ɛɚɥɤɢ
ɨɬ ɟɟ ɫɨɛɫɬɜɟɧɧɨɝɨ ɜɟɫɚ. ȼ ɪɟɡɭɥɶɬɚɬɟ ɜ ɦɨɦɟɧɬ ɜɪɟɦɟɧɢ
Tt 5.0
ɩɨɥɭɱɢɦ ɫɭɦɦɚɪɧɵɣ ɩɪɨɝɢɛ
ɛɚɥɤɢ
ɦɦ7.2ɦɦ)3.1(ɦɦ)4.1()()(
ɪɚɫɱɪɚɫɱɛɫɬɫ
Puquu .
ɉɪɢ ɞɚɥɶɧɟɣɲɢɯ (ɭɠɟ ɫɜɨɛɨɞɧɵɯ ɩɨɫɥɟ ɭɞɚɥɟɧɢɹ ɫɢɥɵ
o
P ) ɤɨɥɟɛɚɧɢɹɯ ɛɚɥɤɢ, ɤɚɤ
ɫɢɫɬɟɦɵ ɫ ɨɞɧɨɣ ɫɬɟɩɟɧɶɸ ɫɜɨɛɨɞɵ, ɞɢɧɚɦɢɱɟɫɤɢɟ ɫɨɫɬɚɜɥɹɸɳɢɟ ɢɡɝɢɛɚɸɳɟɝɨ ɦɨɦɟɧɬɚ,
ɪɚɫɬɹɝɢɜɚɸɳɢɟ ɧɢɠɧɸɸ ɫɬɨɪɨɧɭ ɛɚɥɤɢ, ɢ ɩɪɨɝɢɛɚ ɛɚɥɤɢ ɩɨ ɧɚɩɪɚɜɥɟɧɢɸ ɜɧɢɡ ɩɪɢ ɭɱɟɬɟ ɫɢɥ
ɧɟɭɩɪɭɝɨɝɨ ɫɨɩɪɨɬɢɜɥɟɧɢɹ ɛɭɞɭɬ ɭɦɟɧɶɲɚɬɶɫɹ ɫ ɤɚɠɞɵɦ ɩɟɪɢɨɞɨɦ ɤɨɥɟɛɚɧɢɣ, ɩɪɢɛɥɢɠɚɹɫɶ
ɤ ɧɭɥɟɜɵɦ ɩɟɪɟɦɟɳɟɧɢɹɦ (ɫɦ. ɪɢɫ. 1.27).
Ɉɞɧɚɤɨ ɩɪɢ ɫɜɨɛɨɞɧɵɯ ɤɨɥɟɛɚɧɢɹɯ ɦɚɫɫɵ ɨɤɨɥɨ ɩɨɥɨɠɟɧɢɹ ɪɚɜɧɨɜɟɫɢɹ ɦɚɫɫɵ ɫ
ɧɭɥɟɜɵɦɢ ɩɟɪɟɦɟɳɟɧɢɹɦɢ ɩɟɪɟɦɟɳɟɧɢɟ ɦɚɫɫɵ ɜ ɦɨɦɟɧɬɵ ɜɪɟɦɟɧɢ
kTt , ɝɞɟ ,...3,2,1 k
(ɫɦ. ɪɢɫ.1.27) ɛɭɞɟɬ ɩɪɨɢɫɯɨɞɢɬɶ ɜɜɟɪɯ. Ɍɨɝɞɚ ɞɢɧɚɦɢɱɟɫɤɢɣ ɤɨɷɮɮɢɰɢɟɧɬ
)(kTE , ɚɦɩɥɢɬɭɞɚ
ɩɟɪɟɦɟɳɟɧɢɣ ɦɚɫɫɵ
)(kTA
ɢ ɢɡɝɢɛɚɸɳɢɣ ɦɨɦɟɧɬ
)(kTM
ɜ ɫɪɟɞɧɟɦ ɫɟɱɟɧɢɢ ɛɚɥɤɢ ɛɭɞɭɬ
ɢɦɟɬɶ ɡɧɚɤ «ɦɢɧɭɫ», ɬɚɤ ɤɚɤ ɛɚɥɤɚ ɛɭɞɟɬ ɜ ɭɤɚɡɚɧɧɵɟ ɦɨɦɟɧɬɵ ɜɪɟɦɟɧɢ ɩɪɨɝɢɛɚɬɶɫɹ ɜɜɟɪɯ ɨɬ
ɧɚɩɪɚɜɥɟɧɧɨɣ ɜɜɟɪɯ ɢɧɟɪɰɢɨɧɧɨɣ ɫɢɥɵ )(kTJ (ɫɦ. (1.31).
ȼɵɩɨɥɧɢɦ ɪɚɫɱɟɬ ɩɨ ɨɩɪɟɞɟɥɟɧɢɸ ɪɚɫɱɟɬɧɨɣ ɫɢɥɵ ɢ ɫɨɨɬɜɟɬɫɬɜɭɸɳɢɯ ɟɣ ɪɚɫɱɟɬɧɵɯ
ɡɧɚɱɟɧɢɣ ɩɟɪɟɦɟɳɟɧɢɹ ɛɚɥɤɢ ɢ ɢɡɝɢɛɚɸɳɢɯ ɦɨɦɟɧɬɨɜ ɜ ɫɪɟɞɧɟɦ ɫɟɱɟɧɢɢ ɩɨ ɞɥɢɧɟ ɛɚɥɤɢ ɫ

68
ɩɨɦɨɳɶɸ ɩɪɨɝɪɚɦɦɵ SCAD ɜ ɩɪɢɜɟɞɟɧɧɨɣ ɧɢɠɟ ɩɨɫɥɟɞɨɜɚɬɟɥɶɧɨɫɬɢ ɨɩɟɪɚɰɢɣ. ɉɪɢ ɷɬɨɦ
ɩɪɟɞɩɨɥɨɠɢɦ, ɱɬɨ ɪɚɫɱɟɬɧɚɹ ɫɯɟɦɚ ɛɚɥɤɢ ɤɚɤ ɫɢɫɬɟɦɵ ɫ ɨɞɧɨɣ ɫɬɟɩɟɧɶɸ ɫɜɨɛɨɞɵ ɞɥɹ ɟɟ
ɞɢɧɚɦɢɱɟɫɤɨɝɨ ɪɚɫɱɟɬɚ ɨɬ ɡɚɞɚɧɧɨɝɨ ɢɦɩɭɥɶɫɚ ɭɠɟ ɩɨɫɬɪɨɟɧɚ (ɫɦ. ɩɪɢɦɟɪ 4 ɜ ɩɨɞɪɚɡɞɟɥɟ
1.1).
1. ɉɨɫɥɟ ɩɨɥɭɱɟɧɢɹ ɜ ɪɚɡɞɟɥɟ «ɋɯɟɦɚ» ɪɚɫɱɟɬɧɨɣ ɫɯɟɦɵ ɆɄɗ ɞɥɹ ɛɚɥɤɢ
(ɫɦ. ɪɢɫ. 1.8, ɚ) ɨɬɤɪɵɜɚɟɦ ɪɚɡɞɟɥ «Ɂɚɝɪɭɠɟɧɢɹ».
2. ȼ ɨɬɤɪɵɜɲɟɣɫɹ ɢɧɫɬɪɭɦɟɧɬɚɥɶɧɨɣ ɩɚɧɟɥɢ ɚɤɬɢɜɢɡɢɪɭɟɦ ɤɧɨɩɤɭ
«Ⱦɢɧɚɦɢɱɟɫɤɢɟ ɜɨɡɞɟɣɫɬɜɢɹ» ɢ ɜ ɨɬɤɪɵɜɲɟɦɫɹ ɞɢɚɥɨɝɨɜɨɦ ɨɤɧɟ ɜɵɛɢɪɚɟɦ «ɋɨɡɞɚɧɢɟ ɧɨɜɨɝɨ
ɡɚɝɪɭɠɟɧɢɹ». ȼ ɪɟɡɭɥɶɬɚɬɟ ɨɬɤɪɵɜɚɟɬɫɹ ɩɟɪɜɚɹ ɫɬɪɚɧɢɰɚ ɞɜɭɯɫɬɪɚɧɢɱɧɨɝɨ ɞɢɚɥɨɝɨɜɨɝɨ ɨɤɧɚ
ɫ ɩɟɪɟɱɢɫɥɟɧɢɟɦ ɪɚɡɥɢɱɧɵɯ ɞɢɧɚɦɢɱɟɫɤɢɯ ɜɨɡɞɟɣɫɬɜɢɣ.
ɉɨɫɤɨɥɶɤɭ ɜ ɩɨɫɬɚɜɥɟɧɧɨɣ ɡɚɞɚɱɟ ɜɪɟɦɹ
T5.0 W ɜɨɡɞɟɣɫɬɜɢɹ ɩɨɫɬɨɹɧɧɨɣ ɫɢɥɵ
5.1
o
P ɬɫ ɧɚ ɛɚɥɤɭ ɫɜɹɡɚɧɨ ɫ ɩɟɪɢɨɞɨɦ
T
ɫɨɛɫɬɜɟɧɧɵɯ ɤɨɥɟɛɚɧɢɣ ɛɚɥɤɢ ɤɚɤ ɫɢɫɬɟɦɵ ɫ
ɨɞɧɨɣ ɫɬɟɩɟɧɶɸ ɫɜɨɛɨɞɵ, ɫɧɚɱɚɥɚ ɧɚɣɞɟɦ ɷɬɨɬ ɩɟɪɢɨɞ, ɬ. ɟ. ɫɧɚɱɚɥɚ ɜɵɩɨɥɧɢɦ
ɫɨɨɬɜɟɬɫɬɜɭɸɳɢɣ ɞɢɧɚɦɢɱɟɫɤɢɣ ɪɚɫɱɟɬ, ɧɚɡɜɚɧɧɵɣ ɜ ɩɪɨɝɪɚɦɦɟ SCAD ɤɚɤ «Ɇɨɞɚɥɶɧɵɣ
ɚɧɚɥɢɡ». ɗɬɚ ɡɚɞɚɱɚ ɞɥɹ ɡɚɞɚɧɧɨɣ ɛɚɥɤɢ ɛɵɥɚ ɪɟɲɟɧɚ ɜ ɩɪɢɦɟɪɟ 4 ɩɨɞɪɚɡɞɟɥɚ 1.1 ɞɥɹ ɛɚɥɤɢ,
ɤɨɝɞɚ ɧɚ ɧɟɟ ɛɵɥ ɩɨɫɬɚɜɥɟɧ ɷɥɟɤɬɪɨɞɜɢɝɚɬɟɥɶ ɜɟɫɨɦ gmG
ɞɞ
= (1.5 ɬ) ·(9.81 ɦ/ɫ
2
) =
= 14.715 ɤɇ = (14.715 ɤɇ) : (9.81 ɦ/ɫ
2
) = 1.5 ɬɫ. Ɍɚɦ ɛɵɥɚ ɩɨɥɭɱɟɧɚ ɭɝɥɨɜɚɹ ɫɨɛɫɬɜɟɧɧɚɹ
ɱɚɫɬɨɬɚ
08.72 Z ɫ
-1
ɢ ɩɟɪɢɨɞ ZS /2T = 0.087 ɫ.
ɉɪɢ ɨɬɫɭɬɫɬɜɢɢ ɞɜɢɝɚɬɟɥɹ, ɦɚɫɫɚ
2
m ɜɭɡɥɟ 2 ɪɚɫɱɟɬɧɨɣ ɫɯɟɦɵ ɭɦɟɧɶɲɢɬɫɹ ɢ ɛɭɞɟɬ ɪɚɜɧɚ
ɬɨɥɶɤɨ ɦɚɫɫɟ ɛɚɥɤɢ, ɩɪɢɜɟɞɟɧɧɨɣ ɤ ɭɡɥɭ 2, ɚ ɢɦɟɧɧɨ 2.4 ɬ (ɜɦɟɫɬɨ 3.9 ɬ ɩɪɢ ɧɚɥɢɱɢɢ ɜ ɷɬɨɦ
ɠɟ ɭɡɥɟ ɦɚɫɫɵ ɞɜɢɝɚɬɟɥɹ). ɂɡ ɮɨɪɦɭɥɵ (1.14) ɜɢɞɧɨ, ɱɬɨ ɫ ɭɦɟɧɶɲɟɧɢɟɦ ɦɚɫɫɵ ɭɝɥɨɜɚɹ
ɫɨɛɫɬɜɟɧɧɚɹ ɱɚɫɬɨɬɚ
Z
ɫɢɫɬɟɦɵ ɫ ɨɞɧɨɣ ɫɬɟɩɟɧɶɸ ɫɜɨɛɨɞɵ ɭɜɟɥɢɱɢɬɫɹ. Ⱦɟɣɫɬɜɢɬɟɥɶɧɨ, ɜ
ɪɚɫɫɦɚɬɪɢɜɚɟɦɨɣ ɜ ɞɚɧɧɨɦ ɩɪɢɦɟɪɟ ɫɢɫɬɟɦɵ ɫ ɨɞɧɨɣ ɫɬɟɩɟɧɶɸ ɫɜɨɛɨɞɵ ɩɨɥɭɱɢɦ:
88.91 Z
ɫ
-1
ɢ
T
0.068 ɫ.
Ɍɟɩɟɪɶ ɜ ɪɚɡɞɟɥɟ «Ɂɚɝɪɭɠɟɧɢɹ» ɫɧɨɜɚ ɧɚɠɢɦɚɟɦ ɤɧɨɩɤɭ
ɢ ɫɨɡɞɚɞɢɦ ɧɨɜɨɟ
ɞɢɧɚɦɢɱɟɫɤɨɟ ɡɚɝɪɭɠɟɧɢɟ ɨɬ ɡɚɞɚɧɧɨɝɨ ɢɦɩɭɥɶɫɧɨɝɨ ɜɨɡɞɟɣɫɬɜɢɹ ɧɚ ɛɚɥɤɭ (ɬɨɱɧɟɟ ɧɚ ɟɟ
ɪɚɫɱɟɬɧɭɸ ɫɯɟɦɭ ɜ ɜɢɞɟ ɫɢɫɬɟɦɵ ɫ ɨɞɧɨɣ ɫɬɟɩɟɧɶɸ ɫɜɨɛɨɞɵ).
3. ȼɵɛɢɪɚɟɦ ɜɢɞ ɜɨɡɞɟɣɫɬɜɢɹ «ɂɦɩɭɥɶɫ» ɢ ɡɚɞɚɟɦ ɨɬɪɚɠɚɸɳɟɟ ɫɭɬɶ ɪɚɫɱɟɬɚ ɢɦɹ
ɞɢɧɚɦɢɱɟɫɤɨɝɨ ɡɚɝɪɭɠɟɧɢɹ. ȼɵɯɨɞɢɦ ɢɡ ɩɟɪɜɨɣ ɫɬɪɚɧɢɰɵ ɞɢɚɥɨɝɨɜɨɝɨ ɨɤɧɚ ɧɚɠɚɬɢɟɦ ɜ ɟɝɨ
ɜɟɪɯɧɟɣ ɱɚɫɬɢ «ɂɦɩɭɥɶɫɧɵɟ ɢ ɭɞɚɪɧɵɟ ɜɨɡɞɟɣɫɬɜɢɹ
».
4. ɇɚ ɨɬɤɪɵɜɲɟɣɫɹ ɜɬɨɪɨɣ ɫɬɪɚɧɢɰɟ ɞɢɚɥɨɝɨɜɨɝɨ ɨɤɧɚ ɜɜɨɞɢɦ ɱɢɫɥɨ ɭɱɢɬɵɜɚɟɦɵɯ
ɫɨɛɫɬɜɟɧɧɵɯ ɮɨɪɦ ɤɨɥɟɛɚɧɢɣ (ɜ ɩɨɫɬɪɨɟɧɧɨɣ ɪɚɫɱɟɬɧɨɣ ɫɯɟɦɟ ɞɥɹ ɫɢɫɬɟɦɵ ɫ ɨɞɧɨɣ
ɫɬɟɩɟɧɶɸ ɫɜɨɛɨɞɵ ɜɜɨɞɢɦ ɰɢɮɪɭ 1) ɢ ɡɧɚɱɟɧɢɟ
09.0
ɧ
J
ɤɨɷɮɮɢɰɢɟɧɬɚ ɧɟɭɩɪɭɝɨɝɨ
ɫɨɩɪɨɬɢɜɥɟɧɢɹ ɠɟɥɟɡɨɛɟɬɨɧɧɨɣ ɛɚɥɤɢ. ɇɚɠɚɬɢɟɦ ɤɧɨɩɤɢ «ɈɄ» ɧɚ ɜɬɨɪɨɣ ɫɬɪɚɧɢɰɟ ɜɵɯɨɞɢɦ
ɢɡ ɞɢɚɥɨɝɨɜɨɝɨ ɨɤɧɚ.
5. ɇɚ ɢɧɫɬɪɭɦɟɧɬɚɥɶɧɨɣ ɩɚɧɟɥɢ ɚɤɬɢɜɢɡɢɪɭɟɦ ɤɧɨɩɤɭ
«ɂɧɟɪɰɢɨɧɧɵɟ
ɯɚɪɚɤɬɟɪɢɫɬɢɤɢ» ɢ ɜɵɛɢɪɚɟɦ ɜ ɨɬɤɪɵɜɲɟɦɫɹ ɫɩɢɫɤɟ «ɂɦɩɭɥɶɫɧɨɟ ɜɨɡɞɟɣɫɬɜɢɟ». Ɉɬɤɪɨɟɬɫɹ
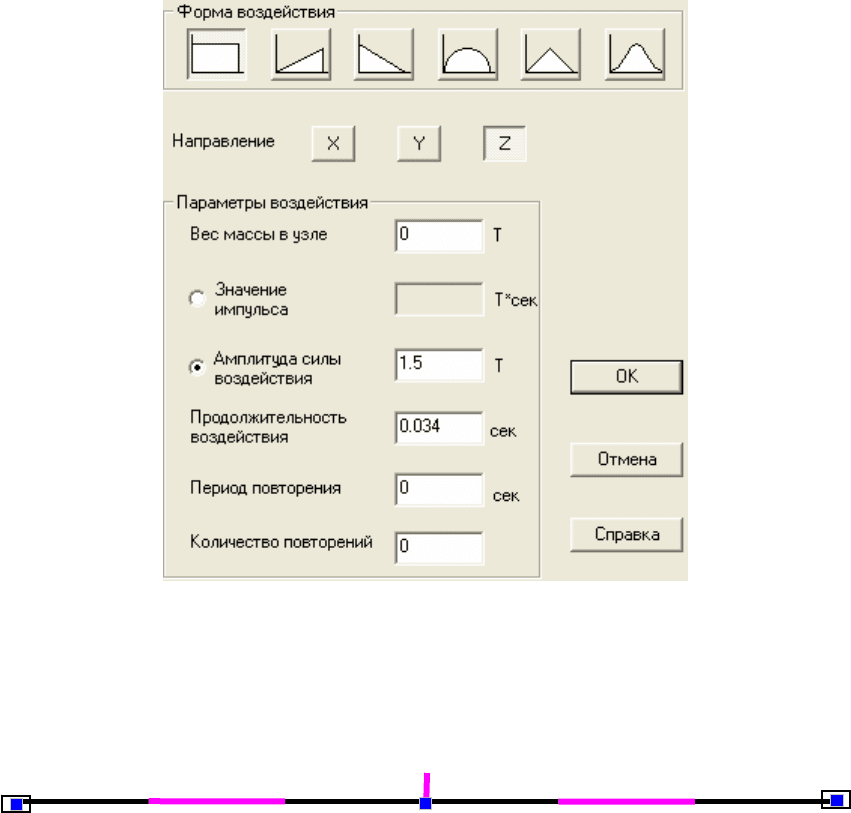
ɞɢɚɥɨɝɨɜɨɟ ɨɤɧɨ, ɨɫɧɨɜɧɚɹ ɱɚɫɬɶ ɤɨɬɨɪɨɝɨ ɩɪɢɜɟɞɟɧɚ ɧɢɠɟ.
ȼ ɨɤɧɟ ɜɜɨɞɹɬɫɹ ɭɤɚɡɚɧɧɵɟ ɬɚɦ ɯɚɪɚɤɬɟɪɢɫɬɢɤɢ ɡɚɞɚɧɧɨɝɨ ɢɦɩɭɥɶɫɢɜɧɨɝɨ ɜɨɡɞɟɣɫɬɜɢɹ
ɩɨɫɬɨɹɧɧɨɣ ɫɢɥɨɣ. ȼɵɛɪɚɧɧɵɟ ɟɞɢɧɢɰɵ ɢɡɦɟɪɟɧɢɹ ɜɜɨɞɢɦɵɯ ɜɟɥɢɱɢɧ ɩɪɢ ɨɬɤɪɵɬɢɢ ɩɪɨɟɤɬɚ
ɨɬɪɚɠɟɧɵ ɜ ɨɤɧɟ. Ɏɨɪɦɚ ɜɨɡɞɟɣɫɬɜɢɹ ɩɪɢɧɹɬɚ ɩɪɹɦɨɭɝɨɥɶɧɚɹ; ɧɚɩɪɚɜɥɟɧɢɟ ɜɨɡɞɟɣɫɬɜɢɹ – Z.
69
ȼɟɫ ɦɚɫɫɵ ɜ ɭɡɥɟ ɜɜɨɞɢɬɫɹ ɜ ɡɚɜɢɫɢɦɨɫɬɢ ɨɬ ɜɚɪɢɚɧɬɚ ɭɱɟɬɚ ɪɚɜɧɨɦɟɪɧɨ ɪɚɫɩɪɟɞɟɥɟɧɧɨɣ
ɦɚɫɫɵ ɛɚɥɤɢ.
ɉɪɢ ɢɫɩɨɥɶɡɨɜɚɧɢɢ ɜɬɨɪɨɝɨ ɜɚɪɢɚɧɬɚ (ɫɦ. ɩɪɢɦɟɪ 4 ɜ ɩɨɞɪɚɡɞɟɥɟ 1.1) ɜɜɨɞɢɦ ɜɟɫ ɦɚɫɫɵ
ɪɚɜɧɵɦ 0 ɤɇ (ɜ ɩɪɨɝɪɚɦɦɟ SCAD ɩɪɟɞɭɫɦɨɬɪɟɧɨ, ɱɬɨ ɪɚɜɧɨɦɟɪɧɨ ɪɚɫɩɪɟɞɟɥɟɧɧɚɹ ɦɚɫɫɚ
ɤɨɧɟɱɧɵɯ ɷɥɟɦɟɧɬɨɜ, ɩɨɞɯɨɞɹɳɢɯ ɤ ɭɡɥɭ, ɝɞɟ ɩɪɢɥɨɠɟɧ ɢɦɩɭɥɶɫ, ɦɨɠɟɬ ɛɵɬɶ ɜɜɟɞɟɧɚ
ɨɬɞɟɥɶɧɨ ɢ ɡɚɬɟɦ ɩɪɢɜɟɞɟɬɫɹ ɤ ɭɡɥɭ
2 ɪɚɫɱɟɬɧɨɣ ɫɯɟɦɵ ɜ ɜɢɞɟ ɫɨɫɪɟɞɨɬɨɱɟɧɧɨɣ ɩɪɢɜɟɞɟɧɧɨɣ
ɦɚɫɫɵ, ɪɚɜɧɨɣ 2.4 ɬ).
ɂɦɩɭɥɶɫɧɨɟ ɜɨɡɞɟɣɫɬɜɢɟ ɫɢɥɵ ɡɚɞɚɟɬɫɹ ɥɢɛɨ ɜ ɜɢɞɟ ɡɧɚɱɟɧɢɹ ɢɦɩɭɥɶɫɚ
W
op
PJ
ɜɤɇ·ɫ,
ɥɢɛɨ, ɤɚɤ ɩɨɤɚɡɚɧɨ ɜ ɞɢɚɥɨɝɨɜɨɦ ɨɤɧɟ, – ɜ ɜɢɞɟ ɚɦɩɥɢɬɭɞɵ ɫɢɥɵ ɜɨɡɞɟɣɫɬɜɢɹ:
ɤɇ14.715ɬɫ5.1
o
P . ɉɪɨɞɨɥɠɢɬɟɥɶɧɨɫɬɶ ɜɨɡɞɟɣɫɬɜɢɹ W ɨɩɪɟɞɟɥɟɧɚ ɡɚɞɚɧɢɟɦ:
034.05.0
W T ɫɟɤ.
ɉɪɟɞɩɨɥɚɝɚɟɬɫɹ, ɱɬɨ ɢɦɩɭɥɶɫ ɞɟɣɫɬɜɭɟɬ ɨɞɧɨɤɪɚɬɧɨ, ɩɨɷɬɨɦɭ ɩɟɪɢɨɞ ɩɨɜɬɨɪɟɧɢɹ ɢ
ɤɨɥɢɱɟɫɬɜɨ ɩɨɜɬɨɪɟɧɢɣ ɡɚɞɚɧɵ ɪɚɜɧɵɦɢ ɧɭɥɸ.
Ɂɚɞɚɧɧɨɟ ɜɨɡɞɟɣɫɬɜɢɟ ɨɬɧɨɫɢɦ ɤ ɭɡɥɭ 2 ɪɚɫɱɟɬɧɨɣ ɫɯɟɦɵ ɆɄɗ ɛɚɥɤɢ. ɉɪɢ ɷɬɨɦ ɧɚ
ɪɚɫɱɟɬɧɨɣ ɫɯɟɦɟ ɜ ɭɡɥɟ 2 (ɩɪɢ ɧɚɠɚɬɵɯ ɫɨɨɬɜɟɬɫɬɜɭɸɳɢɯ ɤɧɨɩɤɚɯ ɮɢɥɶɬɪɚ ɨɬɨɛɪɚɠɟɧɢɹ)
ɩɨɹɜɢɬɫɹ ɢɧɮɨɪɦɚɰɢɹ «D0» ɨ ɫɞɟɥɚɧɧɨɦ ɜɜɨɞɟ (ɪɢɫ. 1.28).
Ɋɢɫ. 1.28
Ɂɚɬɟɦ ɩɟɪɟɯɨɞɢɦ ɤ ɡɚɞɚɧɢɸ ɪɚɜɧɨɦɟɪɧɨ ɪɚɫɩɪɟɞɟɥɟɧɧɨɣ ɦɚɫɫɵ ɛɚɥɤɢ. Ⱦɥɹ ɷɬɨɝɨ ɫɧɨɜɚ
D0
D5.8860 ɤɇ = 0.6 ɬɫ
D5.8860 ɤɇ = 0.6 ɬɫ
2
1
3
