Федоров М.П. и др. Информационно-компьютерные технологии в строительстве. Применение программы SCAD для расчета сооружений на динамические воздействия
Подождите немного. Документ загружается.

10
1. ɋɂɋɌȿɆɕ ɋ ɈȾɇɈɃ ɋɌȿɉȿɇɖɘ ɋȼɈȻɈȾɕ
1.1. ɋɜɨɛɨɞɧɵɟ ɧɟɡɚɬɭɯɚɸɳɢɟ ɤɨɥɟɛɚɧɢɹ
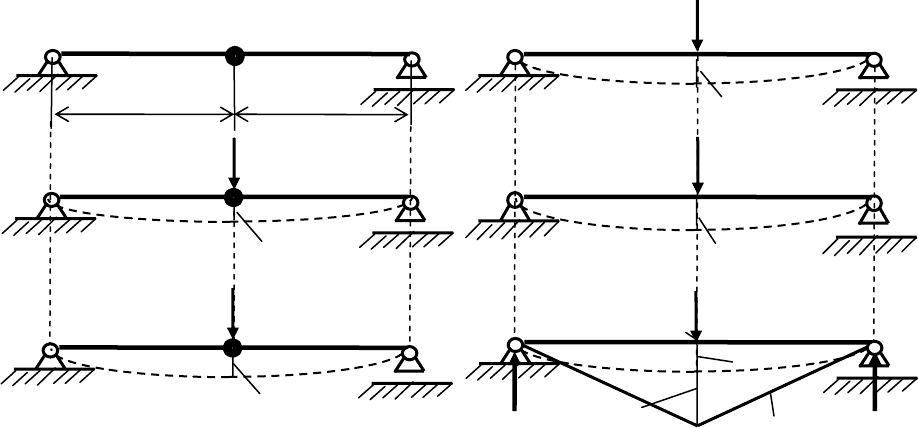
ɍɪɚɜɧɟɧɢɟ ɫɜɨɛɨɞɧɵɯ ɧɟɡɚɬɭɯɚɸɳɢɯ ɤɨɥɟɛɚɧɢɣ. Ɋɚɫɫɦɨɬɪɢɦ ɭɩɪɭɝɭɸ
ɥɢɧɟɣɧɨ ɞɟɮɨɪɦɢɪɭɟɦɭɸ ɫɢɫɬɟɦɭ ɜ ɜɢɞɟ ɛɚɥɤɢ (ɪɢɫ. 1.1,ɚ), ɜ ɫɟɪɟɞɢɧɟ ɩɪɨɥɟɬɚ
ɤɨɬɨɪɨɣ ɪɚɫɩɨɥɨɠɟɧɚ ɬɨɱɟɱɧɚɹ ɦɚɫɫɚ
m . ɉɭɫɬɶ ɩɚɪɚɦɟɬɪɵ ɛɚɥɤɢ ɢ ɦɚɫɫɵ
ɬɚɤɨɜɵ, ɱɬɨ ɜ ɪɚɫɱɟɬɧɨɣ ɫɯɟɦɟ ɦɨɠɧɨ ɫɱɢɬɚɬɶ ɫɚɦɭ ɛɚɥɤɭ ɛɟɡɦɚɫɫɨɜɨɣ
(ɧɟɜɟɫɨɦɨɣ). Ɍɚɤɚɹ ɫɢɫɬɟɦɚ ɩɪɢ ɩɨɩɟɪɟɱɧɵɯ ɤ ɨɫɢ ɛɚɥɤɢ ɤɨɥɟɛɚɧɢɹɯ ɦɚɫɫɵ
ɛɭɞɟɬ ɫɢɫɬɟɦɨɣ ɫ ɨɞɧɨɣ ɫɬɟɩɟɧɶɸ ɫɜɨɛɨɞɵ.
Ɋɢɫ. 1.1
ȼ ɫɩɨɤɨɣɧɨɦ ɫɨɫɬɨɹɧɢɢ ɦɚɫɫɚ m ɞɟɣɫɬɜɭɟɬ ɧɚ ɛɚɥɤɭ ɫɬɚɬɢɱɟɫɤɨɣ ɫɢɥɨɣ
ɜɟɫɚ
g
m
G
(ɪɢɫ. 1.1, ɛ), ɝɞɟ
g
– ɭɫɤɨɪɟɧɢɟ ɫɜɨɛɨɞɧɨɝɨ ɩɚɞɟɧɢɹ ɦɚɫɫɵ, ɢ
ɜɵɡɵɜɚɟɬ ɜ ɛɚɥɤɟ ɫɬɚɬɢɱɟɫɤɢɣ ɩɪɨɝɢɛ
G
'
ɢ ɫɨɨɬɜɟɬɫɬɜɭɸɳɢɟ ɫɬɚɬɢɱɟɫɤɢɟ,
ɭɫɢɥɢɹ, ɞɟɮɨɪɦɚɰɢɢ ɢ ɧɚɩɪɹɠɟɧɢɹ.
ɂɫɩɨɥɶɡɭɟɦ ɩɪɢɧɰɢɩ ɫɭɩɟɪɩɨɡɢɰɢɢ ɢ ɨɬɞɟɥɢɦ ɫɬɚɬɢɱɟɫɤɭɸ ɡɚɞɚɱɭ ɨɬ
ɞɢɧɚɦɢɱɟɫɤɨɣ ɡɚɞɚɱɢ ɨ ɫɜɨɛɨɞɧɵɯ ɤɨɥɟɛɚɧɢɹɯ, ɤɨɬɨɪɭɸ ɞɚɥɟɟ ɛɭɞɟɦ
ɪɚɫɫɦɚɬɪɢɜɚɬɶ. ȼ ɫɨɨɬɜɟɬɫɬɜɢɢ ɫ ɷɬɢɦ ɜ ɞɢɧɚɦɢɱɟɫɤɨɣ ɡɚɞɚɱɟ ɛɭɞɟɦ ɫɱɢɬɚɬɶ
ɩɨɥɨɠɟɧɢɟɦ ɪɚɜɧɨɜɟɫɢɹ ɛɚɥɤɢ ɩɪɹɦɨɥɢɧɟɣɧɭɸ ɨɫɶ ɛɚɥɤɢ (ɪɢɫ. 1.1,
ɚ).
G
ɫɬ
P
P
'
G
'
1
k
)(tJ
G
1
)(tu
)(tM
)(tM
C
)(5.0 tJ
)(5.0 tJ
)ɛ
)ɜ
)ɝ
)ɞ
A
B
m
l5.0
l5.0
)a
)ɟ
C
11
Ⱦɥɹ ɫɨɡɞɚɧɢɹ ɫɜɨɛɨɞɧɵɯ ɤɨɥɟɛɚɧɢɣ ɛɚɥɤɢ ɩɨɫɬɭɩɢɦ ɫɥɟɞɭɸɳɢɦ ɨɛɪɚɡɨɦ.
ɉɪɢɥɨɠɢɦ ɤ ɦɚɫɫɟ ɞɨɩɨɥɧɢɬɟɥɶɧɭɸ ɫɬɚɬɢɱɟɫɤɭɸ ɫɢɥɭ
ɫɬ
P (ɪɢɫ. 1.1, ɜ). Ɉɧɚ
ɜɵɡɨɜɟɬ ɭɩɪɭɝɭɸ ɫɬɚɬɢɱɟɫɤɭɸ ɞɟɮɨɪɦɚɰɢɸ ɛɚɥɤɢ ɢ ɨɬɤɥɨɧɢɬ ɦɚɫɫɭ ɨɬ
ɩɨɥɨɠɟɧɢɹ ɪɚɜɧɨɜɟɫɢɹ ɧɚ ɜɟɥɢɱɢɧɭ
P
' , ɤɨɬɨɪɭɸ ɦɨɠɧɨ ɨɩɪɟɞɟɥɢɬɶ ɫ ɩɨɦɨɳɶɸ
ɥɢɛɨ ɤɨɷɮɮɢɰɢɟɧɬɚ ɩɨɞɚɬɥɢɜɨɫɬɢ
G ɛɚɥɤɢ (ɪɢɫ. 1.1, ɝ), ɥɢɛɨ ɤɨɷɮɮɢɰɢɟɧɬɚ
ɠɟɫɬɤɨɫɬɢ
k ɛɚɥɤɢ (ɪɢɫ. 1.1, ɞ):
kPP
p
/
ɫɬɫɬ
G ' .
(1.1)
ɉɪɢ ɷɬɨɦ ɨɱɟɜɢɞɧɨ, ɱɬɨ
1;;
11
GG G
kkk .
(1.2)
ȼ ɨɬɤɥɨɧɟɧɧɨɦ ɩɨɥɨɠɟɧɢɢ ɦɚɫɫɚ ɛɭɞɟɬ ɧɚɯɨɞɢɬɶɫɹ ɜ ɪɚɜɧɨɜɟɫɢɢ ɩɨɞ
ɞɟɣɫɬɜɢɟɦ ɩɪɢɥɨɠɟɧɧɨɣ ɫɢɥɵ
P
kP '
ɫɬ
ɢ ɪɚɜɧɨɣ ɟɣ, ɧɨ ɩɪɨɬɢɜɨɩɨɥɨɠɧɨɣ ɩɨ
ɧɚɩɪɚɜɥɟɧɢɸ, ɭɩɪɭɝɨɣ «ɜɨɫɫɬɚɧɚɜɥɢɜɚɸɳɟɣ» ɫɢɥɵ
P
kK '
ɫɬ
, ɫɬɪɟɦɹɳɟɣɫɹ
ɜɨɡɜɪɚɬɢɬɶ ɦɚɫɫɭ ɜ ɩɨɥɨɠɟɧɢɟ ɪɚɜɧɨɜɟɫɢɹ, ɤɨɬɨɪɨɟ ɨɧɚ ɢɦɟɥɚ ɞɨ ɩɪɢɥɨɠɟɧɢɹ
ɫɢɥɵ
ɫɬ
P (ɫɦ. ɪɢɫ. 1.1, ɚ):
0
ɫɬɫɬ
KP
.
(1.3)
ȼ ɧɟɤɨɬɨɪɵɣ ɦɨɦɟɧɬ ɜɪɟɦɟɧɢ (ɡɚɮɢɤɫɢɪɭɟɦ ɟɝɨ, ɤɚɤ 0
t
) ɭɞɚɥɢɦ
(ɦɝɧɨɜɟɧɧɨ) ɫɢɥɭ
ɫɬ
P . ɋɬɚɬɢɱɟɫɤɨɟ ɪɚɜɧɨɜɟɫɢɟ ɦɚɫɫɵ ɧɚɪɭɲɢɬɫɹ, ɢ ɨɧɚ ɩɨɞ
ɞɟɣɫɬɜɢɟɦ ɭɩɪɭɝɨɣ ɜɨɫɫɬɚɧɚɜɥɢɜɚɸɳɟɣ ɫɢɥɵ
P
kK '
ɫɬ
ɛɚɥɤɢ ɧɚɱɧɟɬ
ɞɜɢɠɟɧɢɟ (ɩɟɪɟɦɟɳɟɧɢɟ) ɜ ɧɚɩɪɚɜɥɟɧɢɢ ɫɜɨɟɝɨ ɩɟɪɜɨɧɚɱɚɥɶɧɨɝɨ ɩɨɥɨɠɟɧɢɹ
(ɫɦ. ɪɢɫ. 1.1,
ɚ).
ɇɨ, ɜ ɫɨɨɬɜɟɬɫɬɜɢɢ ɫ ɡɚɤɨɧɨɦ Ƚɭɤɚ, ɤɚɤ ɬɨɥɶɤɨ ɩɪɨɝɢɛ ɛɚɥɤɢ ɭɦɟɧɶɲɢɬɫɹ,
ɩɪɨɩɨɪɰɢɨɧɚɥɶɧɨ ɭɦɟɧɶɲɢɬɫɹ ɢ ɫɜɹɡɚɧɧɚɹ ɫ ɩɪɨɝɢɛɨɦ ɭɩɪɭɝɚɹ
ɜɨɫɫɬɚɧɚɜɥɢɜɚɸɳɚɹ ɫɢɥɚ, ɬ.ɟ. ɨɛɟ ɜɟɥɢɱɢɧɵ ɛɭɞɭɬ ɹɜɥɹɬɶɫɹ ɮɭɧɤɰɢɹɦɢ
ɜɪɟɦɟɧɢ: )();(
t
K
K
t
uu . ɉɪɢ ɷɬɨɦ, ɤɚɤ ɢ ɜ ɫɬɚɬɢɱɟɫɤɨɣ ɡɚɞɚɱɟ, ɜ ɥɸɛɨɣ
ɦɨɦɟɧɬ ɜɪɟɦɟɧɢ ɩɪɢ ɩɟɪɟɦɟɳɟɧɢɢ ɦɚɫɫɵ ɛɭɞɟɬ ɫɨɛɥɸɞɚɬɶɫɹ ɡɚɜɢɫɢɦɨɫɬɶ
)()(
t
uk
t
K
.
(1.4)
Ɉɛɪɚɬɢɦ ɜɧɢɦɚɧɢɟ ɧɚ ɬɨ, ɱɬɨ ɧɚɱɚɥɶɧɚɹ ɫɤɨɪɨɫɬɶ ɞɜɢɠɟɧɢɹ ɦɚɫɫɵ ɜ
ɦɨɦɟɧɬ ɜɪɟɦɟɧɢ 0
t
ɛɵɥɚ ɪɚɜɧɚ ɧɭɥɸ. ɉɨɷɬɨɦɭ ɧɚɱɚɥɨ ɞɜɢɠɟɧɢɹ ɦɚɫɫɵ
ɫɜɹɡɚɧɨ ɫ ɩɪɢɞɚɧɢɟɦ ɟɣ ɫɢɥɨɣ )()(
t
uk
t
K
ɭɫɤɨɪɟɧɢɹ
0 t
u
.
Ⱦɚɥɶɧɟɣɲɟɟ ɞɜɢɠɟɧɢɟ ɦɚɫɫɵ ɤ ɩɟɪɜɨɧɚɱɚɥɶɧɨɦɭ ɩɨɥɨɠɟɧɢɸ ɪɚɜɧɨɜɟɫɢɹ
ɩɨɞ ɞɟɣɫɬɜɢɟɦ ɢɡɦɟɧɹɸɳɟɣɫɹ ɭɩɪɭɝɨɣ ɫɢɥɵ )()(
t
uk
t
K
ɬɚɤɠɟ ɛɭɞɟɬ
ɩɪɨɢɫɯɨɞɢɬɶ ɫ ɢɡɦɟɧɹɸɳɢɦɫɹ ɭɫɤɨɪɟɧɢɟɦ, ɬɚɤ ɤɚɤ ɩɨ ɜɬɨɪɨɦɭ ɡɚɤɨɧɭ ɇɶɸɬɨɧɚ
ɭɩɪɭɝɚɹ ɫɢɥɚ )(
t
K
, «ɬɨɥɤɚɸɳɚɹ» ɦɚɫɫɭ m ɫ ɭɫɤɨɪɟɧɢɟɦ )(
t
u
, ɤɪɨɦɟ ɜɵɪɚɠɟɧɢɹ
(1.4) ɦɨɠɟɬ ɛɵɬɶ ɩɪɟɞɫɬɚɜɥɟɧɚ ɬɚɤɠɟ ɡɚɜɢɫɢɦɨɫɬɶɸ:
12
)()(
t
um
t
K
.
(1.5)
ɉɪɢ ɷɬɨɦ ɢɡ (1.5) ɜɢɞɧɨ, ɱɬɨ ɢ ɫɢɥɚ )(
t
K
ɢ ɭɫɤɨɪɟɧɢɟ )(
t
u
ɛɭɞɭɬ ɢɦɟɬɶ
ɨɞɢɧɚɤɨɜɨɟ ɧɚɩɪɚɜɥɟɧɢɟ – ɤ ɩɟɪɜɨɧɚɱɚɥɶɧɨɦɭ ɧɟɞɟɮɨɪɦɢɪɨɜɚɧɧɨɦɭ
ɩɨɥɨɠɟɧɢɸ ɪɚɜɧɨɜɟɫɢɹ ɛɚɥɤɢ (ɫɦ. ɪɢɫ. 1.1,
ɚ).
Ʉɪɨɦɟ ɬɨɝɨ, ɩɪɢ ɞɜɢɠɟɧɢɢ ɦɚɫɫɵ ɫ ɭɫɤɨɪɟɧɢɟɦ ɧɚ ɛɚɥɤɭ ɛɭɞɟɬ
ɞɟɣɫɬɜɨɜɚɬɶ ɫɢɥɚ ɢɧɟɪɰɢɢ ɦɚɫɫɵ
)()(
t
um
t
J
,
(1.6)
ɤɨɬɨɪɚɹ, ɤɚɤ ɜɢɞɧɨ ɢɡ (1.6), ɧɚɩɪɚɜɥɟɧɚ ɜ ɫɬɨɪɨɧɭ ɩɪɨɬɢɜɨɩɨɥɨɠɧɭɸ
ɧɚɩɪɚɜɥɟɧɢɸ ɭɫɤɨɪɟɧɢɹ )(
t
u
.
ɋɨɩɨɫɬɚɜɥɟɧɢɟ (1.5) ɢ (1.6) ɩɨɡɜɨɥɹɟɬ ɡɚɩɢɫɚɬɶ ɭɪɚɜɧɟɧɢɟ
0
K
J
. (1.7)
Ɉɛɪɚɬɢɦ ɜɧɢɦɚɧɢɟ ɧɚ ɬɨ, ɱɬɨ ɭɩɪɭɝɚɹ ɫɢɥɚ
umuk
K
ɞɟɣɫɬɜɭɟɬ ɧɚ
ɦɚɫɫɭ ɨɬ ɛɚɥɤɢ, ɚ ɫɢɥɚ ɢɧɟɪɰɢɢ
um
J
ɞɟɣɫɬɜɭɟɬ ɧɚ ɛɚɥɤɭ ɨɬ ɦɚɫɫɵ. ɇɨ
ɭɪɚɜɧɟɧɢɟ (1.7) ɦɨɠɧɨ ɪɚɫɫɦɚɬɪɢɜɚɬɶ ɤɚɤ
ɭɪɚɜɧɟɧɢɟ ɪɚɜɧɨɜɟɫɢɹ ɦɚɫɫɵ ɜ ɥɸɛɨɣ
ɦɨɦɟɧɬ ɟɟ ɞɜɢɠɟɧɢɹ.
Ɍɚɤɨɟ ɩɪɟɞɫɬɚɜɥɟɧɢɟ ɩɪɟɞɥɨɠɟɧɨ Ⱦɚɥɚɦɛɟɪɨɦ ɢ
ɧɚɡɵɜɚɟɬɫɹ «ɉɪɢɧɰɢɩɨɦ Ⱦɚɥɚɦɛɟɪɚ».
ɉɨɞɫɬɚɜɢɜ ɜ (1.7) ɜɵɪɚɠɟɧɢɹ (1.4) ɢ (1.6), ɩɨɥɭɱɢɦ ɭɪɚɜɧɟɧɢɟ
0
kuum
, (1.8)
ɩɨɡɜɨɥɹɸɳɟɟ ɩɭɬɟɦ ɢɧɬɟɝɪɢɪɨɜɚɧɢɹ ɧɚɣɬɢ ɩɟɪɟɦɟɳɟɧɢɟ )(
t
uu ɦɚɫɫɵ
ɪɚɫɫɦɚɬɪɢɜɚɟɦɨɣ ɭɩɪɭɝɨɣ ɥɢɧɟɣɧɨ ɞɟɮɨɪɦɢɪɭɟɦɨɣ ɫɢɫɬɟɦɵ ɫ ɨɞɧɨɣ ɫɬɟɩɟɧɶɸ
ɫɜɨɛɨɞɵ ɛɟɡ ɭɱɟɬɚ ɜɥɢɹɧɢɹ ɫɢɥ, ɜɵɡɵɜɚɸɳɢɯ ɡɚɬɭɯɚɧɢɟ ɩɟɪɟɦɟɳɟɧɢɣ.
ȼɟɪɧɟɦɫɹ ɤ ɧɚɛɥɸɞɟɧɢɸ ɡɚ ɞɜɢɠɟɧɢɟɦ ɦɚɫɫɵ ɩɨɫɥɟ ɦɝɧɨɜɟɧɧɨɝɨ
ɭɞɚɥɟɧɢɹ ɫɬɚɬɢɱɟɫɤɨɣ ɫɢɥɵ
ɫɬ
P
. Ⱦɨɫɬɢɝɧɭɜ ɩɨɞ ɞɟɣɫɬɜɢɟɦ ɭɩɪɭɝɨɣ ɫɢɥɵ
ɝɨɪɢɡɨɧɬɚɥɶɧɨɝɨ ɩɟɪɜɨɧɚɱɚɥɶɧɨɝɨ ɩɨɥɨɠɟɧɢɹ (ɫɦ. ɪɢɫ. 1.1,
ɚ) ɦɚɫɫɚ m ɧɟ
ɨɫɬɚɧɨɜɢɬɫɹ, ɚ, ɧɚɨɛɨɪɨɬ, ɜ ɪɟɡɭɥɶɬɚɬɟ ɩɨɫɬɨɹɧɧɨɝɨ ɞɟɣɫɬɜɢɹ ɧɚ ɧɟɟ ɫɢɥɵ )(
t
K
(1.5), ɞɜɢɝɚɹɫɶ ɫ ɭɫɤɨɪɟɧɢɟɦ, ɞɨɫɬɢɝɧɟɬ ɦɚɤɫɢɦɚɥɶɧɨɣ ɫɤɨɪɨɫɬɢ ɢ ɩɨ ɢɧɟɪɰɢɢ
ɩɪɨɞɨɥɠɢɬ ɞɜɢɠɟɧɢɟ ɜɜɟɪɯ, ɢɡɝɢɛɚɹ ɛɚɥɤɭ ɫɢɥɨɣ ɢɧɟɪɰɢɢ (1.6).
ȼ ɫɨɨɬɜɟɬɫɬɜɢɢ ɫ ɡɚɤɨɧɨɦ Ƚɭɤɚ, ɩɪɨɝɢɛ ɛɚɥɤɢ, ɜɵɡɜɚɧɧɵɣ ɫɢɥɨɣ ɢɧɟɪɰɢɢ,
ɩɟɪɟɞɚɸɳɟɣɫɹ ɨɬ ɦɚɫɫɵ ɧɚ ɛɚɥɤɭ, ɜ ɥɸɛɨɣ ɦɨɦɟɧɬ ɜɪɟɦɟɧɢ ɦɨɠɟɬ ɛɵɬɶ
ɨɩɪɟɞɟɥɟɧ ɢɡ ɭɪɚɜɧɟɧɢɹ
)()(
t
J
t
u G .
(1.9)
ɋ ɭɱɟɬɨɦ (1.6) (ɫɤɨɛɤɢ ɫ ɧɟɡɚɜɢɫɢɦɨɣ ɩɟɪɟɦɟɧɧɨɣ
t
ɨɩɭɫɤɚɟɦ)
)(
umu
G
(1.10)
ɢɥɢ
0
G uum
.
(1.11)
13
Ʉɚɤ ɜɢɞɧɨ, ɭɪɚɜɧɟɧɢɹ (1.7), (1.8) ɢ (1.9) – (1.11) ɫɨɨɬɜɟɬɫɬɜɟɧɧɨ
ɩɪɟɞɫɬɚɜɥɹɸɬ ɞɜɟ ɮɨɪɦɵ ɡɚɩɢɫɢ ɭɪɚɜɧɟɧɢɹ ɞɜɢɠɟɧɢɹ ɦɚɫɫɵ, ɪɚɫɩɨɥɨɠɟɧɧɨɣ
ɧɚ ɭɩɪɭɝɨɣ ɥɢɧɟɣɧɨ ɞɟɮɨɪɦɢɪɭɟɦɨɣ ɫɢɫɬɟɦɟ. ȼ ɩɟɪɜɨɣ – ɢɫɩɨɥɶɡɨɜɚɧ
ɤɨɷɮɮɢɰɢɟɧɬ ɠɟɫɬɤɨɫɬɢ
k
ɛɚɥɤɢ, ɮɢɡɢɱɟɫɤɢ ɩɪɟɞɫɬɚɜɥɹɸɳɢɣ ɫɨɛɨɣ
ɫɬɚɬɢɱɟɫɤɭɸ ɫɢɥɭ, ɜɵɡɵɜɚɸɳɭɸ ɟɞɢɧɢɱɧɵɣ ɩɪɨɝɢɛ ɛɚɥɤɢ (ɫɦ. ɪɢɫ. 1.1,
ɞ). ɗɬɨɬ
ɤɨɷɮɮɢɰɢɟɧɬ ɨɩɪɟɞɟɥɹɟɬɫɹ ɩɪɢɟɦɨɦ ɢɡɜɟɫɬɧɵɦ ɢɡ ɦɟɬɨɞɚ ɩɟɪɟɦɟɳɟɧɢɣ
ɫɬɚɬɢɤɢ ɫɨɨɪɭɠɟɧɢɣ [21].
ȼɨ ɜɬɨɪɨɣ ɮɨɪɦɟ ɡɚɩɢɫɢ ɭɪɚɜɧɟɧɢɹ ɞɜɢɠɟɧɢɹ ɢɫɩɨɥɶɡɨɜɚɧ ɤɨɷɮɮɢɰɢɟɧɬ
ɩɨɞɚɬɥɢɜɨɫɬɢ
G ɛɚɥɤɢ, ɮɢɡɢɱɟɫɤɢ ɩɪɟɞɫɬɚɜɥɹɸɳɢɣ ɫɨɛɨɣ ɫɬɚɬɢɱɟɫɤɢɣ
ɩɪɨɝɢɛ ɛɚɥɤɢ, ɜɵɡɜɚɧɧɵɣ ɟɞɢɧɢɱɧɨɣ ɫɢɥɨɣ (ɫɦ. ɪɢɫ. 1.1,
ɝ). Ⱦɥɹ ɛɚɥɤɢ
ɷɬɨɬ ɤɨɷɮɮɢɰɢɟɧɬ ɦɨɠɟɬ ɛɵɬɶ ɨɩɪɟɞɟɥɟɧ ɫ ɩɨɦɨɳɶɸ ɮɨɪɦɭɥɵ
Ɇɚɤɫɜɟɥɥɚ-Ɇɨɪɚ [1, 2, 21].
Ɉɛɟ ɮɨɪɦɵ ɭɪɚɜɧɟɧɢɹ ɞɜɢɠɟɧɢɹ ɦɚɫɫɵ ((1.8) ɢ (1.11)) ɫ ɭɱɟɬɨɦ (1.2)
ɩɪɢɜɨɞɹɬɫɹ ɤ ɨɞɧɨɦɭ ɭɪɚɜɧɟɧɢɸ
0
2
Z uu
,
(1.12)
ɝɞɟ ɜɜɟɞɟɧɨ ɨɛɨɡɧɚɱɟɧɢɟ
mmk G Z 1
2
,
(1.13)
ɢɥɢ
mmk G Z 1.
(1.14)
ɂɡ ɞɜɭɯ ɮɨɪɦ ɪɟɲɟɧɢɹ ɡɚɞɚɱɢ ɜɵɛɢɪɚɸɬ ɬɭ, ɩɪɢ ɤɨɬɨɪɨɣ ɩɪɨɳɟ
ɩɪɚɤɬɢɱɟɫɤɚɹ ɪɟɚɥɢɡɚɰɢɹ ɡɚɞɚɱɢ (ɜ ɞɚɧɧɨɦ ɩɪɢɦɟɪɟ ɤɪɢɬɟɪɢɟɦ ɹɜɥɹɟɬɫɹ
ɩɪɨɫɬɨɬɚ ɨɩɪɟɞɟɥɟɧɢɹ ɜɟɥɢɱɢɧ Gɢɥɢk ).
Ⱥɧɚɥɢɡ ɪɟɲɟɧɢɹ ɭɪɚɜɧɟɧɢɹ ɫɜɨɛɨɞɧɵɯ ɧɟɡɚɬɭɯɚɸɳɢɯ ɤɨɥɟɛɚɧɢɣ.
ɉɨɥɭɱɟɧɧɨɟ ɭɪɚɜɧɟɧɢɟ (1.12) ɹɜɥɹɟɬɫɹ ɨɛɵɤɧɨɜɟɧɧɵɦ ɨɞɧɨɪɨɞɧɵɦ
ɞɢɮɮɟɪɟɧɰɢɚɥɶɧɵɦ ɭɪɚɜɧɟɧɢɟɦ ɜɬɨɪɨɝɨ ɩɨɪɹɞɤɚ ɫ ɩɨɫɬɨɹɧɧɵɦɢ
ɤɨɷɮɮɢɰɢɟɧɬɚɦɢ. ȿɝɨ ɪɟɲɟɧɢɟ ɢɡɜɟɫɬɧɨ ɢ ɦɨɠɟɬ ɛɵɬɶ ɡɚɩɢɫɚɧɨ ɜ ɜɢɞɟ:
tAtAu ZZ sincos
21
,
(1.15)
ɝɞɟ
21
ɢ AA – ɞɟɣɫɬɜɢɬɟɥɶɧɵɟ ɩɨɫɬɨɹɧɧɵɟ ɢɧɬɟɝɪɢɪɨɜɚɧɢɹ, ɨɩɪɟɞɟɥɹɟɦɵɟ ɢɡ
ɧɚɱɚɥɶɧɵɯ ɭɫɥɨɜɢɣ ɞɜɢɠɟɧɢɹ:
oo
0
o
0
; uuuu
tt
,
(1.16)
ɝɞɟ
ooo
ɢ uu – ɡɚɞɚɧɧɵɟ ɜ ɦɨɦɟɧɬ ɜɪɟɦɟɧɢ 0
t
ɧɚɱɚɥɶɧɵɟ ɫɨɨɬɜɟɬɫɬɜɟɧɧɨ
ɩɟɪɟɦɟɳɟɧɢɟ ɢ ɫɤɨɪɨɫɬɶ ɦɚɫɫɵ.
ɉɪɢɦɟɱɚɧɢɟ. ȼ ɬɨɥɶɤɨ ɱɬɨ ɪɚɫɫɦɨɬɪɟɧɧɨɦ ɩɪɢɦɟɪɟ ɩɪɢɱɢɧɨɣ ɧɚɱɚɥɚ ɞɜɢɠɟɧɢɹ ɦɚɫɫɵ
ɜ ɦɨɦɟɧɬ ɜɪɟɦɟɧɢ
0 t ɛɵɥɚ ɦɝɧɨɜɟɧɧɨ ɭɞɚɥɟɧɧɚɹ ɫɢɥɚ
ɫɬ
P , ɤɨɬɨɪɚɹ ɜɵɡɵɜɚɥɚ ɧɚɱɚɥɶɧɨɟ
ɩɟɪɟɦɟɳɟɧɢɟ ɦɚɫɫɵ
ɫɬ
o
Pu
P
G ' (ɩɟɪɜɨɟ ɧɚɱɚɥɶɧɨɟ ɭɫɥɨɜɢɟ). ɇɚɱɚɥɶɧɚɹ ɫɤɨɪɨɫɬɶ ɩɪɢ
14
ɭɞɚɥɟɧɢɢ ɫɢɥɵ ɛɵɥɚ ɧɭɥɟɜɨɣ, ɬ. ɟ. ɜ ɦɨɦɟɧɬ ɜɪɟɦɟɧɢ 0 t 0
oo
u (ɜɬɨɪɨɟ ɧɚɱɚɥɶɧɨɟ
ɭɫɥɨɜɢɟ).
ȼ ɨɛɳɟɦ ɫɥɭɱɚɟ (ɩɪɢ ɡɚɞɚɧɢɢ ɨɛɨɢɯ ɧɚɱɚɥɶɧɵɯ ɭɫɥɨɜɢɣ ɜ ɜɢɞɟ (1.16)) ɢɡ
ɩɟɪɜɨɝɨ ɭɫɥɨɜɢɹ ɩɨɥɭɱɚɟɦ
o
1
uA
. Ⱦɥɹ ɢɫɩɨɥɶɡɨɜɚɧɢɹ ɜɬɨɪɨɝɨ ɧɚɱɚɥɶɧɨɝɨ
ɭɫɥɨɜɢɹ ɧɟɨɛɯɨɞɢɦɨ ɡɚɩɢɫɚɬɶ ɜɵɪɚɠɟɧɢɟ ɞɥɹ ɫɤɨɪɨɫɬɢ ɦɚɫɫɵ:
tAtAu ZZZZ cossin
21
.
(1.17)
Ɍɨɝɞɚ, ɩɪɢɧɹɜ 0
t
, ɛɭɞɟɦ ɢɦɟɬɶ
2
oo
Au Z , ɢɥɢ Z
oo
2
uA .
ɉɨɞɫɬɚɜɢɜ ɷɬɢ ɧɚɣɞɟɧɧɵɟ ɩɨɫɬɨɹɧɧɵɟ ɜɟɥɢɱɢɧɵ ɜ (1.15), ɩɨɥɭɱɢɦ
ɜɵɪɚɠɟɧɢɟ ɞɥɹ ɩɟɪɟɦɟɳɟɧɢɹ ɦɚɫɫɵ ɜ ɜɢɞɟ
t
u
tuu Z
Z
Z sincos
oo
o
.
(1.18)
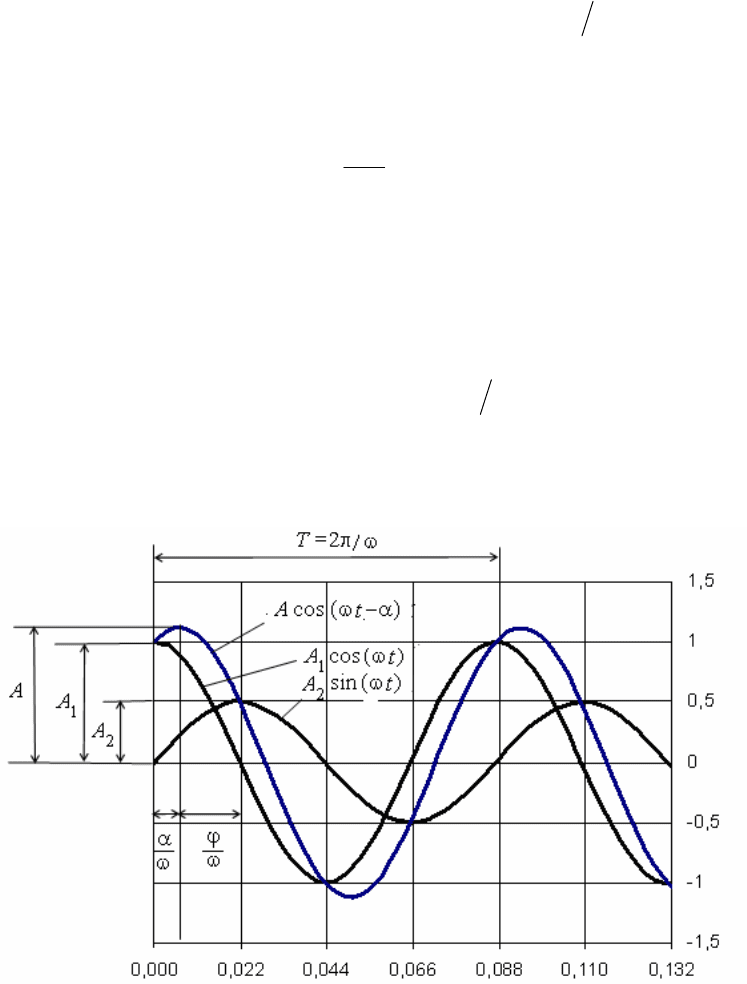
ȼɵɪɚɠɟɧɢɹ (1.15) ɢ (1.18) ɩɨɤɚɡɵɜɚɸɬ, ɱɬɨ ɫɜɨɛɨɞɧɨɟ ɩɟɪɟɦɟɳɟɧɢɟ
ɬɨɱɟɱɧɨɣ ɦɚɫɫɵ, ɪɚɫɩɨɥɨɠɟɧɧɨɣ ɧɚ ɭɩɪɭɝɨɣ ɥɢɧɟɣɧɨ ɞɟɮɨɪɦɢɪɭɟɦɨɣ ɛɚɥɤɟ,
ɩɪɟɞɫɬɚɜɥɹɟɬ ɫɨɛɨɣ ɫɭɦɦɭ ɞɜɭɯ ɧɟɡɚɬɭɯɚɸɳɢɯ ɝɚɪɦɨɧɢɱɟɫɤɢɯ ɤɨɥɟɛɚɧɢɣ.
ɉɟɪɜɨɟ ɩɪɨɢɫɯɨɞɢɬ ɩɨ ɡɚɤɨɧɭ ɤɨɫɢɧɭɫɚ ɢ ɢɦɟɟɬ ɚɦɩɥɢɬɭɞɭ
o
1
uA ,
ɜɬɨɪɨɟ – ɩɨ ɡɚɤɨɧɭ ɫɢɧɭɫɚ ɫ ɚɦɩɥɢɬɭɞɨɣ
Z
oo
2
uA .
ɂɡɦɟɧɟɧɢɟ ɷɬɢɯ ɫɨɫɬɚɜɥɹɸɳɢɯ ɩɟɪɟɦɟɳɟɧɢɹ ɦɚɫɫɵ m ɜɨ ɜɪɟɦɟɧɢ ɞɥɹ
ɧɚɝɥɹɞɧɨɫɬɢ ɩɪɟɞɫɬɚɜɥɟɧɨ ɝɪɚɮɢɱɟɫɤɢ ɧɚ ɪɢɫ. 1.2.
Ɋɢɫ. 1.2
ɉɪɢɦɟɱɚɧɢɟ ɤ ɪɢɫ. 1.2. Ƚɪɚɮɢɤɢ ɜɵɩɨɥɧɟɧɵ ɫ ɩɨɦɨɳɶɸ ɩɪɨɝɪɚɦɦɵ Mathcad ɩɪɢ
1
1
A
;
12
5.0 AA
; Z 72.08 1/ɫ.
ȼɵɪɚɠɟɧɢɹ (1.17) ɢ (1.18) ɫɜɹɡɵɜɚɸɬ ɬɚɤɠɟ ɫ ɜɪɚɳɟɧɢɟɦ ɫ ɪɚɜɧɨɦɟɪɧɨɣ
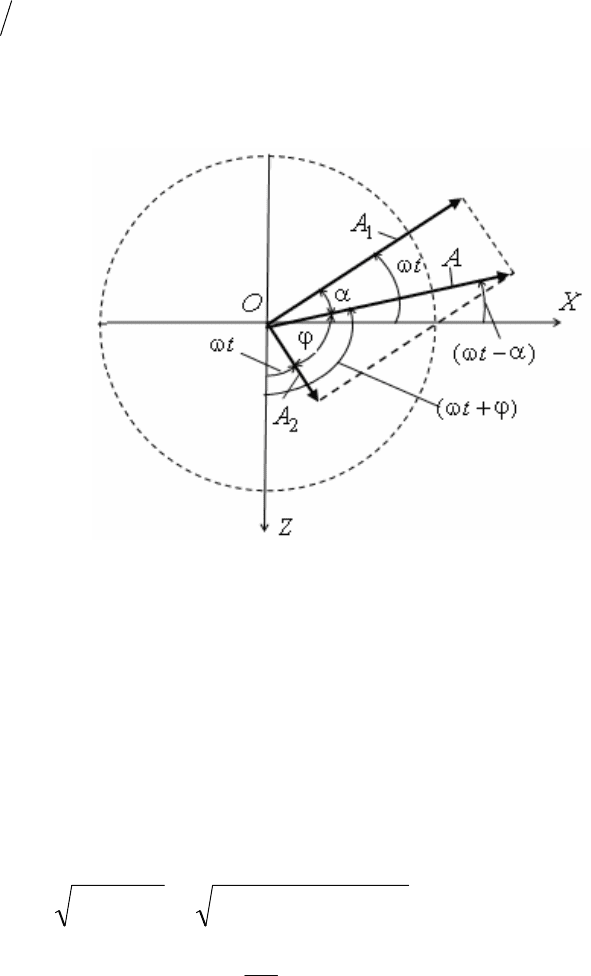
15
ɭɝɥɨɜɨɣ ɫɤɨɪɨɫɬɶɸ Z ɜɟɤɬɨɪɚ
o
1
uA ɢ ɨɬɫɬɚɸɳɟɝɨ ɨɬ ɧɟɝɨ ɧɚ ɭɝɨɥ 2
/
S
ɜɟɤɬɨɪɚ
Z
oo
2
uA (ɪɢɫ. 1.3) ɜɨɤɪɭɝ ɨɫɢ, ɩɪɨɯɨɞɹɳɟɣ ɱɟɪɟɡ ɬɨɱɤɭ O.
Ɋɚɡɦɟɪɧɨɫɬɶɸ Z ɹɜɥɹɟɬɫɹ ɪɚɞ/ɫ – ɫɤɨɪɨɫɬɶ ɪɚɜɧɨɦɟɪɧɨɝɨ ɜɪɚɳɟɧɢɹ ɩɪɢ
ɤɨɬɨɪɨɣ ɡɚ ɜɪɟɦɹ 1 ɫ ɫɨɜɟɪɲɚɟɬɫɹ ɩɨɜɨɪɨɬ ɜɟɤɬɨɪɨɜ ɧɚ ɭɝɨɥ 1 ɪɚɞ.
Ɋɢɫ. 1. 3
ɇɚ ɪɢɫ. 1.3 ɜɟɤɬɨɪɵ ɩɨɤɚɡɚɧɵ ɜ ɦɨɦɟɧɬ ɜɪɟɦɟɧɢ t (ɞɨ ɧɚɱɚɥɚ ɢɯ
ɜɪɚɳɟɧɢɹ ɨɧɢ ɫɨɜɩɚɞɚɥɢ ɫɨɨɬɜɟɬɫɬɜɟɧɧɨ ɫ ɨɫɹɦɢ OZOX ɢ ). ɂɯ
ɝɨɪɢɡɨɧɬɚɥɶɧɵɟ ɫɨɫɬɚɜɥɹɸɳɢɟ ɩɪɟɞɫɬɚɜɥɹɸɬ ɫɨɨɬɜɟɬɫɬɜɟɧɧɨ ɩɟɪɜɨɟ ɢ
ɜɬɨɪɨɟ ɫɥɚɝɚɟɦɵɟ ɩɟɪɟɦɟɳɟɧɢɹ ɬɨɱɟɱɧɨɣ ɦɚɫɫɵ ɜ (1.15) ɢ (1.18). ɉɪɢ ɷɬɨɦ
A
ɩɪɟɞɫɬɚɜɥɹɟɬ ɫɨɛɨɣ ɚɦɩɥɢɬɭɞɭ ɫɭɦɦɚɪɧɨɝɨ ɩɟɪɟɦɟɳɟɧɢɹ u , ɚ D – ɫɞɜɢɝ ɮɚɡɵ
ɩɨɥɧɨɝɨ ɤɨɥɟɛɚɧɢɹ ɩɨ ɨɬɧɨɲɟɧɢɸ ɤ ɮɚɡɟ ɤɨɥɟɛɚɧɢɹ, ɫɨɨɬɜɟɬɫɬɜɭɸɳɟɝɨ
ɩɟɪɜɨɦɭ ɫɥɚɝɚɟɦɨɦɭ:
2
2
2
1
AAA =
2oo2
1
o
)/()( Z uu ;
(1.19)
;arctg
1
2
A
A
D
(1.20)
D D sin;cos
21
AAAA .
(1.21)
ɋ ɭɱɟɬɨɦ (1.21) ɜɵɪɚɠɟɧɢɟ (1.15) ɦɨɠɧɨ ɩɪɟɞɫɬɚɜɢɬɶ ɜ ɜɢɞɟ
)(cos DZ
t
A
u .
(1.22)
Ʉɚɤ ɜɢɞɧɨ ɢɡ ɫɨɩɨɫɬɚɜɥɟɧɢɹ ɩɟɪɜɨɝɨ ɫɥɚɝɚɟɦɨɝɨ ɜ (1.15) ɢ ɜɵɪɚɠɟɧɢɹ
(1.22) (ɫɦ. ɬɚɤɠɟ ɪɢɫ. 1.2 ɢɪɢɫ.1.3), ɢɦɟɟɬ ɦɟɫɬɨ ɡɚɩɚɡɞɵɜɚɧɢɟ ɧɚ ɜɪɟɦɹ ZD
/
t
ɩɨɥɧɨɣ ɚɦɩɥɢɬɭɞɵ
A
ɩɨ ɨɬɧɨɲɟɧɢɸ ɤ ɚɦɩɥɢɬɭɞɟ
1
A .
Ɇɨɠɧɨ ɜɵɪɚɡɢɬɶ ɫɞɜɢɝ ɮɚɡɵ ɩɨɥɧɨɣ ɚɦɩɥɢɬɭɞɵ
A
ɩɨ ɨɬɧɨɲɟɧɢɸ ɤ ɮɚɡɟ
ɚɦɩɥɢɬɭɞɵ
2
A
ɫ ɩɨɦɨɳɶɸ ɜɟɥɢɱɢɧɵ

16
2
1
arctg
A
A
M .
(1.23)
Ɍɨɝɞɚ
;cos;sin
21
M M AAAA
(1.24)
)(sin MZ
t
A
u
(1.25)
Ʉɚɤ ɜɢɞɧɨ ɢɡ ɫɨɩɨɫɬɚɜɥɟɧɢɹ ɜɬɨɪɨɝɨ ɫɥɚɝɚɟɦɨɝɨ ɜ (1.15) ɢ ɜɵɪɚɠɟɧɢɹ
(1.25) (ɫɦ. ɬɚɤɠɟ ɪɢɫ. 1.2 ɢ ɪɢɫ.1.3), ɢɦɟɟɬ ɦɟɫɬɨ ɨɩɟɪɟɠɟɧɢɟ ɩɨ ɜɪɟɦɟɧɢ ɧɚ
ɜɟɥɢɱɢɧɭ
Z
M
/
t
ɩɨɥɧɨɣ ɚɦɩɥɢɬɭɞɵ
A
ɩɨ ɨɬɧɨɲɟɧɢɸ ɤ ɚɦɩɥɢɬɭɞɟ
2
A .
Ɉɱɟɜɢɞɧɨ, ɱɬɨ
2
/
)( S MD ɢ 4
/
2
/
)
/
/
(
T
t
ZS ZMZD .
(1.26)
ɉɪɨɰɟɫɫ ɩɟɪɟɦɟɳɟɧɢɹ ɦɚɫɫɵ ɩɪɢ ɫɜɨɛɨɞɧɵɯ ɩɨɩɟɪɟɱɧɵɯ ɤɨɥɟɛɚɧɢɹɯ
ɛɚɥɤɢ (ɫɦ. ɪɢɫ. 1.2 ɢ ɪɢɫ. 1.3) ɹɜɥɹɟɬɫɹ ɩɟɪɢɨɞɢɱɟɫɤɢɦ. Ɉɧ ɢɦɟɟɬ ɩɟɪɢɨɞ
ZS
/
2
T
(ɜɪɟɦɹ, ɫ, ɨɞɧɨɝɨ ɰɢɤɥɚ ɤɨɥɟɛɚɧɢɹ ɦɚɫɫɵ ɧɚ ɛɚɥɤɟ), ɪɚɜɧɵɣ ɩɟɪɢɨɞɭ
ɨɞɧɨɝɨ ɰɢɤɥɚ ɜɪɚɳɟɧɢɹ ɜɟɤɬɨɪɨɜ ɜɨɤɪɭɝ ɬɨɱɤɢ O ɫ ɪɚɜɧɨɦɟɪɧɨɣ ɭɝɥɨɜɨɣ
ɫɤɨɪɨɫɬɶɸ Z.
ȼɟɥɢɱɢɧɚ
SZ Q 2
/
/
1
T
1/ɫ (Ƚɰ) (1.27)
ɩɪɟɞɫɬɚɜɥɹɟɬ ɫɨɛɨɣ ɱɚɫɬɨɬɭ ɩɟɪɢɨɞɢɱɟɫɤɨɝɨ ɩɪɨɰɟɫɫɚ ɤɨɥɟɛɚɧɢɣ ɦɚɫɫɵ ɧɚ
ɛɚɥɤɟ ɢ ɩɟɪɢɨɞɢɱɟɫɤɨɝɨ ɩɪɨɰɟɫɫɚ ɜɪɚɳɟɧɢɹ ɜɟɤɬɨɪɨɜ, ɫɨɜɟɪɲɚɟɦɵɯ ɡɚ ɨɞɧɭ
ɫɟɤɭɧɞɭ ɜɪɟɦɟɧɢ. Ɍɚɤɭɸ ɱɚɫɬɨɬɭ ɢɧɨɝɞɚ ɧɚɡɵɜɚɸɬ ɬɟɯɧɢɱɟɫɤɨɣ ɱɚɫɬɨɬɨɣ.
Ɂɚ ɟɞɢɧɢɰɭ ɢɡɦɟɪɟɧɢɹ ɷɬɨɣ ɜɟɥɢɱɢɧɵ ɩɪɢɧɹɬɚ ɱɚɫɬɨɬɚ ɤɨɥɟɛɚɧɢɣ, ɩɪɢ
ɤɨɬɨɪɨɣ ɡɚ ɜɪɟɦɹ ɫ1 ɫɨɜɟɪɲɚɟɬɫɹ ɨɞɢɧ ɰɢɤɥ ɩɟɪɢɨɞɢɱɟɫɤɨɝɨ ɩɪɨɰɟɫɫɚ. ɗɬɨɣ
ɟɞɢɧɢɰɟ ɩɪɢɫɜɨɟɧɨ ɧɚɢɦɟɧɨɜɚɧɢɟ
ɝɟɪɰ (Ƚɰ) [19].
ȼ ɩɟɪɢɨɞɢɱɟɫɤɨɦ ɩɪɨɰɟɫɫɟ ɤɨɥɟɛɚɧɢɣ ɬɨɱɟɱɧɨɣ ɦɚɫɫɵ ɧɚ ɛɚɥɤɟ (ɫɦ. ɪɢɫ.
1.2) ɜɟɥɢɱɢɧɚ
QS S Z 2
/
2
T
ɪɚɞ/ɫ (1/ɫ) (1.28)
ɧɚɡɵɜɚɟɬɫɹ ɭɝɥɨɜɨɣ, ɤɪɭɝɨɜɨɣ ɢɥɢ ɰɢɤɥɢɱɟɫɤɨɣ ɱɚɫɬɨɬɨɣ, ɤɨɬɨɪɭɸ ɜ
ɫɨɨɬɜɟɬɫɬɜɢɢ ɫ (1.28) ɢ ɮɢɡɢɱɟɫɤɢɦ ɫɦɵɫɥɨɦ ɜɟɥɢɱɢɧ
T
ɢ Q ɨɛɵɱɧɨ
ɪɚɫɫɦɚɬɪɢɜɚɸɬ ɤɚɤ ɱɢɫɥɨ ɤɨɥɟɛɚɧɢɣ, ɫɨɜɟɪɲɚɟɦɵɯ ɡɚ ɜɪɟɦɹ, ɪɚɜɧɨɟ S2 ɫ
(ɫɦ. ɬɚɤɠɟ ɨɩɪɟɞɟɥɟɧɢɟ ɷɬɨɣ ɜɟɥɢɱɢɧɵ, ɞɚɧɧɨɟ ɜ [19]).
ɂɡ ɜɵɪɚɠɟɧɢɣ (1.15), (1.22) ɢ (1.25) ɩɨɥɭɱɚɸɬɫɹ ɜɵɪɚɠɟɧɢɹ ɞɥɹ ɫɤɨɪɨɫɬɢ
ɢ ɭɫɤɨɪɟɧɢɹ ɦɚɫɫɵ ɩɪɢ ɫɜɨɛɨɞɧɵɯ ɧɟɡɚɬɭɯɚɸɳɢɯ ɤɨɥɟɛɚɧɢɹɯ, ɚ ɬɚɤɠɟ ɞɥɹ ɫɢɥɵ
ɢɧɟɪɰɢɢ, ɞɟɣɫɬɜɭɸɳɭɸ ɧɚ ɛɚɥɤɭ, ɧɚɩɪɢɦɟɪ:
);(cos);(sin
2
DZZ DZZ tAutAu
(1.29)
)(cos)(cos)()(
o
2
DZ DZZ tJtAmtumtJ
,
(1.30)

17
ɝɞɟ
AmtJJ
t
2
o
)(max Z
(1.31)
ɩɪɟɞɫɬɚɜɥɹɟɬ ɫɨɛɨɣ ɚɦɩɥɢɬɭɞɭ (ɦɚɤɫɢɦɚɥɶɧɨɟ ɡɧɚɱɟɧɢɟ ɜɨ ɜɪɟɦɟɧɢ) ɫɢɥɵ
ɢɧɟɪɰɢɢ. Ɉɧɚ ɛɭɞɟɬ ɢɦɟɬɶ ɦɟɫɬɨ, ɤɨɝɞɚ 1)(cos
D
Z
t
, ɬ. ɟ. ɤɨɝɞɚ 0)( DZ
t
,
ɢɥɢ (ɫɦ. ɪɢɫ. 1.2) ɩɪɢ ZD
/
t
.
ɋɢɥɟ ɢɧɟɪɰɢɢ )(
t
J
(1.30) ɜ ɪɚɫɫɦɚɬɪɢɜɚɟɦɨɣ ɛɚɥɤɟ ɨɬɜɟɱɚɟɬ ɷɩɸɪɚ
ɢɡɝɢɛɚɸɳɢɯ ɦɨɦɟɧɬɨɜ )(
t
M
(ɪɢɫ. 1.1, ɟ) ɫ ɨɪɞɢɧɚɬɨɣ )(tM
C
ɜ ɫɟɱɟɧɢɢ, ɝɞɟ
ɩɪɢɥɨɠɟɧɚ ɫɢɥɚ. Ɇɚɤɫɢɦɚɥɶɧɨɦɭ ɜɨ ɜɪɟɦɟɧɢ ɡɧɚɱɟɧɢɸ
o
J (1.31) ɫɢɥɵ ɢɧɟɪɰɢɢ
ɫɨɨɬɜɟɬɫɬɜɭɟɬ ɢɡɝɢɛɚɸɳɢɣ ɦɨɦɟɧɬ
4/)(max
oo,
lJtMM
CtC
.
ȼ ɩɨɩɟɪɟɱɧɨɦ ɫɟɱɟɧɢɢ ɛɚɥɤɢ ɫ ɦɚɤɫɢɦɚɥɶɧɨɣ ɨɪɞɢɧɚɬɨɣ
o,C
M ɦɨɝɭɬ
ɛɵɬɶ ɨɩɪɟɞɟɥɟɧɵ ɦɚɤɫɢɦɚɥɶɧɵɟ ɢ ɦɢɧɢɦɚɥɶɧɵɟ ɡɧɚɱɟɧɢɹ ɧɨɪɦɚɥɶɧɵɯ
ɧɚɩɪɹɠɟɧɢɣ
CCCC
WM /
o,2,1
r V ɫɨɨɬɜɟɬɫɬɜɟɧɧɨ ɧɚ ɧɢɠɧɟɣ (ɪɚɫɬɹɧɭɬɨɣ) ɢ
ɜɟɪɯɧɟɣ (ɫɠɚɬɨɣ) ɫɬɨɪɨɧɚɯ ɫɟɱɟɧɢɹ.
Ⱥɧɚɥɨɝɢɱɧɨ ɦɨɝɭɬ ɛɵɬɶ ɨɩɪɟɞɟɥɟɧɵ ɢ ɩɨɩɟɪɟɱɧɵɟ ɫɢɥɵ ɜ ɫɟɱɟɧɢɹɯ ɛɚɥɤɢ
ɢ ɫɨɨɬɜɟɬɫɬɜɭɸɳɢɟ ɢɦ ɤɚɫɚɬɟɥɶɧɵɟ ɧɚɩɪɹɠɟɧɢɹ.
ɉɨɥɭɱɟɧɧɵɟ ɜɵɪɚɠɟɧɢɹ ɞɥɹ ɱɚɫɬɨɬ
f
ɢ
Z
, ɞɥɹ ɩɟɪɢɨɞɚ
T
, ɮɚɡɨɜɵɯ
ɯɚɪɚɤɬɟɪɢɫɬɢɤ
MD ɢ , ɩɟɪɟɦɟɳɟɧɢɣ u , ɫɤɨɪɨɫɬɢ u
, ɭɫɤɨɪɟɧɢɹ u
, ɫɢɥɵ
ɢɧɟɪɰɢɢ
J
ɹɜɥɹɸɬɫɹ ɨɛɳɢɦɢ ɞɥɹ ɥɸɛɵɯ ɫɢɫɬɟɦ ɫ ɨɞɧɨɣ ɫɬɟɩɟɧɶɸ ɫɜɨɛɨɞɵ.
Ɂɚɤɨɧ ɫɨɯɪɚɧɟɧɢɹ ɷɧɟɪɝɢɢ ɤɨɥɟɛɚɧɢɣ ɩɪɢ ɧɟɡɚɬɭɯɚɸɳɢɯ ɤɨɥɟɛɚɧɢɹɯ.
Ɉɞɧɨɜɪɟɦɟɧɧɨɟ ɡɚɞɚɧɢɟ ɦɚɫɫɟ ɧɚɱɚɥɶɧɵɯ ɭɫɥɨɜɢɣ ɞɜɢɠɟɧɢɹ (1.16) ɫɜɨɛɨɞɧɵɯ
ɤɨɥɟɛɚɧɢɣ ɫɢɫɬɟɦɵ ɫ ɨɞɧɨɣ ɫɬɟɩɟɧɶɸ ɫɜɨɛɨɞɵ ɫɨɨɬɜɟɬɫɬɜɭɟɬ ɩɨɥɭɱɟɧɢɸ
ɭɩɪɭɝɨɣ ɫɢɫɬɟɦɨɣ ɷɧɟɪɝɢɢ
ɨɨɨ
Ɍɉɗ .
(1.32)
ɋɥɚɝɚɟɦɵɟ ɜ (1.32) ɫɨɨɬɜɟɬɫɬɜɟɧɧɨ ɹɜɥɹɸɬɫɹ ɩɨɬɟɧɰɢɚɥɶɧɨɣ ɢ
ɤɢɧɟɬɢɱɟɫɤɨɣ ɷɧɟɪɝɢɹɦɢ
2oo2o
)(5.0;)(5.0 umɌukɉ
ɨɨ
.
(1.33)
ȼ ɩɪɨɰɟɫɫɟ ɤɨɥɟɛɚɧɢɣ ɩɨɬɟɧɰɢɚɥɶɧɚɹ ɢ ɤɢɧɟɬɢɱɟɫɤɚɹ ɷɧɟɪɝɢɢ
ɢɡɦɟɧɹɸɬɫɹ ɜɨ ɜɪɟɦɟɧɢ, ɧɨ ɩɨɫɤɨɥɶɤɭ ɪɚɫɫɦɚɬɪɢɜɚɟɬɫɹ ɜɚɪɢɚɧɬ ɤɨɥɟɛɚɧɢɣ ɛɟɡ
ɢɯ ɡɚɬɭɯɚɧɢɹ (ɛɟɡ ɩɨɬɟɪɢ ɷɧɟɪɝɢɢ ɤɨɥɟɛɚɧɢɣ), ɬɨ ɫɭɦɦɚɪɧɚɹ ɜɟɥɢɱɢɧɚ ɷɧɟɪɝɢɢ
22
5.05.0)()()( umkutɌtɉtɗ
(1.34)
ɜ ɥɸɛɨɣ ɦɨɦɟɧɬ ɜɪɟɦɟɧɢ ɨɫɬɚɟɬɫɹ ɩɨɫɬɨɹɧɧɨɣ.
Ⱦɟɣɫɬɜɢɬɟɥɶɧɨ, ɩɨɞɫɬɚɜɢɜ ɜ (1.34) ɜɵɪɚɠɟɧɢɹ (1.24) ɢ ɩɟɪɜɨɟ ɢɡ (1.29),
ɩɨɥɭɱɢɦ

18
)(sin5.0)(cos5.0)(
22222
DZZDZ tAmtkAtɗ .
(1.35)
ɢɥɢ ɫ ɭɱɟɬɨɦ (1.13)
ɨ
2222
5.0)](sin)([cos5.0)( ɗkAttkAtɗ DZDZ
.
(1.36)
ɋɭɦɦɚɪɧɚɹ ɷɧɟɪɝɢɹ ɧɟ ɢɡɦɟɧɹɟɬɫɹ ɢ ɩɪɢ ɩɪɨɯɨɠɞɟɧɢɢ ɦɚɫɫɨɣ
ɩɟɪɜɨɧɚɱɚɥɶɧɨɝɨ ɩɨɥɨɠɟɧɢɹ ɪɚɜɧɨɜɟɫɢɹ )0(
u
)5.05.0)()(;0)((
ɨ
2
2
2
max
ɗkAAmtɌtɌtɉ Z
(1.37)
ɢ ɩɪɢ ɩɪɨɯɨɠɞɟɧɢɢ ɦɚɤɫɢɦɚɥɶɧɨɝɨ ɨɬɤɥɨɧɟɧɢɹ ɦɚɫɫɵ ɧɚ ɚɦɩɥɢɬɭɞɭ (
A
u )
)0)(;5.0)((
2
max
tɌɗkAɉtɉ
ɨ
(1.38)
Ɍɚɤ ɤɚɤ ɷɧɟɪɝɢɹ ɧɟɡɚɬɭɯɚɸɳɢɯ ɤɨɥɟɛɚɧɢɣ (1.35) ɢɦɟɟɬ ɩɨɫɬɨɹɧɧɭɸ
ɜɟɥɢɱɢɧɭ, ɬɨ ɟɟ ɩɪɨɢɡɜɨɞɧɚɹ ɩɨ ɜɪɟɦɟɧɢ ɪɚɜɧɚ ɧɭɥɸ
0)(/)5.05.0(/)(/)(/)(
22
ukuumdtumkuddttdɌdttdɉdttdɗ
.
(1.39)
Ʉɚɤ ɜɢɞɢɦ, ɷɬɨ ɭɫɥɨɜɢɟ ɫɨɨɬɜɟɬɫɬɜɭɟɬ ɭɪɚɜɧɟɧɢɸ (1.8) ɫɜɨɛɨɞɧɵɯ
ɧɟɡɚɬɭɯɚɸɳɢɯ ɤɨɥɟɛɚɧɢɣ ɭɩɪɭɝɨɣ ɥɢɧɟɣɧɨ ɞɟɮɨɪɦɢɪɭɟɦɨɣ ɫɢɫɬɟɦɵ ɫ ɨɞɧɨɣ
ɫɬɟɩɟɧɶɸ ɫɜɨɛɨɞɵ.
Ɋɚɫɫɦɨɬɪɢɦ ɧɟɫɤɨɥɶɤɨ ɩɪɢɦɟɪɨɜ ɩɨ ɨɩɪɟɞɟɥɟɧɢɸ ɞɢɧɚɦɢɱɟɫɤɢɯ
ɯɚɪɚɤɬɟɪɢɫɬɢɤ
T
ɢ,
Q
Z
ɤɨɥɟɛɚɧɢɹ ɛɚɥɨɤ ɩɨ ɪɚɫɱɟɬɧɨɣ ɫɯɟɦɟ ɫɢɫɬɟɦɵ ɫ ɨɞɧɨɣ
ɫɬɟɩɟɧɶɸ ɫɜɨɛɨɞɵ.
ɉɪɢɦɟɪ 1. ɉɭɫɬɶ ɬɪɟɛɭɟɬɫɹ ɨɩɪɟɞɟɥɢɬɶ ɫɨɛɫɬɜɟɧɧɭɸ ɱɚɫɬɨɬɭ ɢ ɩɟɪɢɨɞ
ɧɟɡɚɬɭɯɚɸɳɢɯ ɤɨɥɟɛɚɧɢɣ ɭɩɪɭɝɨɣ ɥɢɧɟɣɧɨ ɞɟɮɨɪɦɢɪɭɟɦɨɣ ɫɢɫɬɟɦɵ ɫ ɨɞɧɨɣ ɫɬɟɩɟɧɶɸ
ɫɜɨɛɨɞɵ ɜ ɜɢɞɟ ɧɟɜɟɫɨɦɨɣ ɛɚɥɤɢ, ɧɟɫɭɳɟɣ ɧɚ ɫɟɛɟ ɬɨɱɟɱɧɭɸ ɦɚɫɫɭ ɜ ɫɟɪɟɞɢɧɟ ɩɪɨɥɟɬɚ (ɫɦ.
ɪɢɫ. 1.1, ɚ).
ȿɞɢɧɫɬɜɟɧɧɚɹ (ɩɟɪɜɚɹ) ɫɨɛɫɬɜɟɧɧɚɹ ɤɪɭɝɨɜɚɹ ɱɚɫɬɨɬɚ
Z, ɪɚɞ/ɫ, ɫɢɫɬɟɦɵ ɫ ɨɞɧɨɣ
ɫɬɟɩɟɧɶɸ ɫɜɨɛɨɞɵ, ɦɨɠɟɬ ɛɵɬɶ ɨɩɪɟɞɟɥɟɧɚ ɢɡ ɩɟɪɜɨɝɨ ɜɵɪɚɠɟɧɢɹ (1.14) ɫ ɩɨɦɨɳɶɸ
ɤɨɷɮɮɢɰɢɟɧɬɚ ɠɟɫɬɤɨɫɬɢ
k , ɥɢɛɨ ɢɡ ɜɬɨɪɨɝɨ ɜɵɪɚɠɟɧɢɹ (1.14) ɫ ɩɨɦɨɳɶɸ ɤɨɷɮɮɢɰɢɟɧɬɚ
ɩɨɞɚɬɥɢɜɨɫɬɢ
G . Ɋɚɫɫɦɨɬɪɢɦ ɨɛɚ ɩɭɬɢ ɪɟɲɟɧɢɹ.
1. ȼɟɥɢɱɢɧɭ
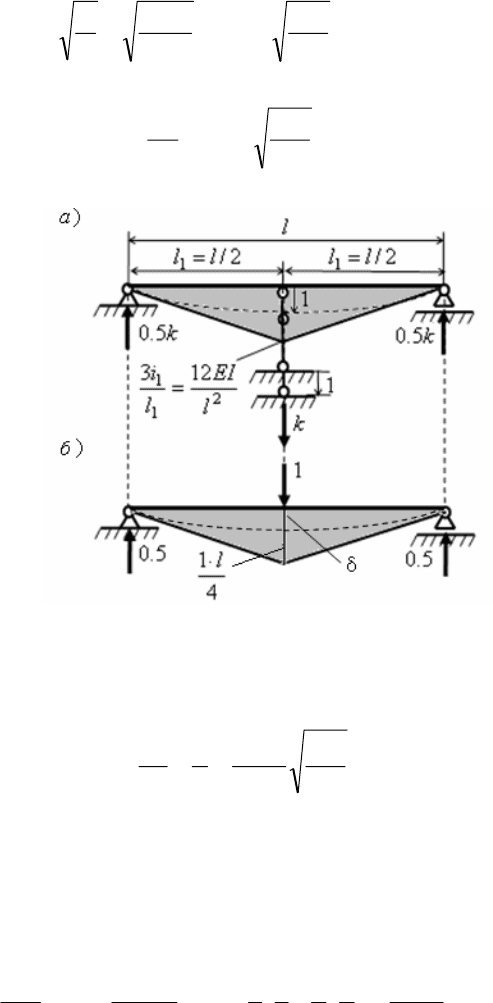
k ɞɥɹ ɛɚɥɤɢ ɧɚɣɞɟɦ ɩɪɢɟɦɨɦ, ɢɡɜɟɫɬɧɵɦ ɢɡ ɦɟɬɨɞɚ ɩɟɪɟɦɟɳɟɧɢɣ ɫɬɚɬɢɤɢ
ɫɨɨɪɭɠɟɧɢɣ (ɪɢɫ. 1.4,
ɚ) [1, 21].
ȼɜɟɞɟɦ ɠɟɫɬɤɭɸ ɫɜɹɡɶ, ɡɚɤɪɟɩɥɹɸɳɭɸ ɬɨɱɤɭ ɪɚɫɩɨɥɨɠɟɧɢɹ ɦɚɫɫɵ ɧɚ ɛɚɥɤɟ, ɢ ɡɚɬɟɦ
ɞɚɞɢɦ ɷɬɨɣ ɫɜɹɡɢ ɟɞɢɧɢɱɧɨɟ ɩɟɪɟɦɟɳɟɧɢɟ.
ȼ ɪɟɡɭɥɶɬɚɬɟ ɬɚɤɨɝɨ ɜɨɡɞɟɣɫɬɜɢɹ ɛɚɥɤɚ ɞɟɮɨɪɦɢɪɭɟɬɫɹ, ɢ ɜ ɧɟɣ ɜɨɡɧɢɤɧɭɬ ɭɫɢɥɢɹ, ɜ
ɱɚɫɬɧɨɫɬɢ, ɢɡɝɢɛɚɸɳɢɟ ɦɨɦɟɧɬɵ. ɂɯ ɷɩɸɪɚ ɫ ɨɪɞɢɧɚɬɨɣ ɜ ɫɟɪɟɞɢɧɟ ɩɪɨɥɟɬɚ ɪɚɜɧɚ [1, 21]:
2
1
1
12
3
l
EI
l
i
, ɝɞɟ
11
/ lEIi
(1.40)
Ɋɟɚɤɰɢɹ ɜɨ ɜɜɟɞɟɧɧɨɣ ɫɜɹɡɢ ɢ ɹɜɥɹɟɬɫɹ ɤɨɷɮɮɢɰɢɟɧɬɨɦ
k . Ɉɧɚ ɪɚɜɧɚ ɫɭɦɦɟ
ɩɨɩɟɪɟɱɧɵɯ ɫɢɥ
Q ɜ ɫɟɱɟɧɢɹɯ ɛɚɥɤɢ, ɩɨɞɯɨɞɹɳɢɯ ɤ ɫɜɹɡɢ ɫɥɟɜɚ ɢ ɫɩɪɚɜɚ:
32
48
]
2
/)
12
[(22
l
EIl
l
EI
Qk
.
(1.41)
Ɍɨɝɞɚ ɤɪɭɝɨɜɚɹ ɱɚɫɬɨɬɚ ɫɜɨɛɨɞɧɵɯ ɧɟɡɚɬɭɯɚɸɳɢɯ ɤɨɥɟɛɚɧɢɣ ɨɩɪɟɞɟɥɢɬɫɹ ɢɡ ɮɨɪɦɭɥɵ
19
1-
33
ɫɪɚɞ/ɫ,928.6
48
ml
EI
ml
EI
m
k
Z ,
(1.42)
ɚ ɱɚɫɬɨɬɚ ɤɨɥɟɛɚɧɢɣ, ɪɚɜɧɚɹ ɱɢɫɥɭ ɰɢɤɥɨɜ ɤɨɥɟɛɚɧɢɣ ɜ 1 ɫ (Ƚɰ), – ɢɡ ɮɨɪɦɭɥɵ
1-
3
ɫ103.1
2
ml
EI
S
Z
Q
.
(1.43)
Ɋɢɫ. 1.4
ɉɟɪɢɨɞ ɤɨɥɟɛɚɧɢɣ ɨɩɪɟɞɟɥɢɬɫɹ ɢɡ ɜɵɪɚɠɟɧɢɣ
ɫ
103.1
112
3
EI
ml
T
Q
Z
S
.
(1.44)
2. ɉɪɢ ɨɩɪɟɞɟɥɟɧɢɢ ɤɪɭɝɨɜɨɣ ɱɚɫɬɨɬɵ ɢɡ ɜɬɨɪɨɝɨ ɜɵɪɚɠɟɧɢɹ (1.14) ɧɟɨɛɯɨɞɢɦɨ
ɫɧɚɱɚɥɚ ɜɦɟɫɬɨ ɤɨɷɮɮɢɰɢɟɧɬɚ ɠɟɫɬɤɨɫɬɢ ɨɩɪɟɞɟɥɢɬɶ ɤɨɷɮɮɢɰɢɟɧɬ ɩɨɞɚɬɥɢɜɨɫɬɢ
G , ɤɨɬɨɪɵɣ
ɞɥɹ ɛɚɥɤɢ ɦɨɠɧɨ ɨɩɪɟɞɟɥɢɬɶ ɫ ɩɨɦɨɳɶɸ ɢɧɬɟɝɪɚɥɚ Ɇɚɤɫɜɟɥɥɚ – Ɇɨɪɚ [1, 2, 21]. ɉɪɢ ɭɱɟɬɟ
ɬɨɥɶɤɨ ɢɡɝɢɛɧɵɯ ɞɟɮɨɪɦɚɰɢɣ ɛɚɥɤɢ (ɷɩɸɪɚ M ɩɪɢɜɟɞɟɧɚ ɧɚ ɪɢɫ. 1.4, ɛ) ɢ ɜɵɱɢɫɥɟɧɢɢ
ɢɧɬɟɝɪɚɥɚ ɱɢɫɥɟɧɧɵɦ ɦɟɬɨɞɨɦ ɫ ɩɨɦɨɳɶɸ ɮɨɪɦɭɥɵ ɋɢɦɩɫɨɧɚ [1, 2, 21] ɩɨɥɭɱɢɦ
1
3
0
2
484488
40
62
2
»
¼
º
«
¬
ª
³
G k
EI
lllll
EI
l
dx
EI
M
l
.
(1.45)
Ʉɚɤ ɜɢɞɢɦ, ɫɨɛɫɬɜɟɧɧɚɹ ɤɪɭɝɨɜɚɹ ɱɚɫɬɨɬɚ
Z, ɪɚɞ/ɫ, ɫɨɛɫɬɜɟɧɧɚɹ ɱɚɫɬɨɬɚ Q , Ƚɰ, ɢ
ɫɨɨɬɜɟɬɫɬɜɭɸɳɢɣ ɢɦ ɩɟɪɢɨɞ
T
ɤɨɥɟɛɚɧɢɣ, ɫ, ɩɨɥɭɱɚɬɶɫɹ ɬɚɤɢɦɢ ɠɟ, ɤɚɤ ɢ ɩɪɢ ɨɩɪɟɞɟɥɟɧɢɢ
ɢɯ ɫ ɩɨɦɨɳɶɸ ɤɨɷɮɮɢɰɢɟɧɬɚ ɠɟɫɬɤɨɫɬɢ.
ɂɡ ɮɨɪɦɭɥ (1.14) ɜɢɞɧɨ, ɱɬɨ ɫ ɭɜɟɥɢɱɟɧɢɟɦ ɤɨɷɮɮɢɰɢɟɧɬɚ ɠɟɫɬɤɨɫɬɢ
k
(ɭɦɟɧɶɲɟɧɢɟɦ ɤɨɷɮɮɢɰɢɟɧɬɚ ɩɨɞɚɬɥɢɜɨɫɬɢ G ) ɛɚɥɤɢ ɢ ɧɟɢɡɦɟɧɧɵɦ ɡɧɚɱɟɧɢɟɦ ɬɨɱɟɱɧɨɣ
ɦɚɫɫɵ
m ɫɨɛɫɬɜɟɧɧɚɹ ɤɪɭɝɨɜɚɹ ɱɚɫɬɨɬɚ ɪɚɫɫɦɚɬɪɢɜɚɟɦɨɣ ɫɢɫɬɟɦɵ ɭɜɟɥɢɱɢɬɫɹ.
ɂɡɦɟɧɟɧɢɟ ɤɨɷɮɮɢɰɢɟɧɬɚ ɠɟɫɬɤɨɫɬɢ ɛɚɥɤɢ
k ɡɚɜɢɫɢɬ ɧɟ ɬɨɥɶɤɨ ɨɬ ɢɡɦɟɧɟɧɢɹ
ɩɚɪɚɦɟɬɪɨɜ
lIE ,, (ɫɦ. ɮɨɪɦɭɥɭ (1.41)), ɧɨ ɢ ɨɬ ɨɩɨɪɧɵɯ ɫɜɹɡɟɣ ɛɚɥɤɢ. Ɋɚɫɫɦɨɬɪɢɦ ɷɬɨ ɧɚ
ɞɜɭɯ ɫɥɟɞɭɸɳɢɯ ɩɪɢɦɟɪɚɯ.
ɉɪɢɦɟɪ 2. Ɉɫɬɚɜɢɦ ɪɚɫɫɦɚɬɪɢɜɚɟɦɭɸ ɜ ɩɪɟɞɵɞɭɳɟɦ ɩɪɢɦɟɪɟ ɛɚɥɤɭ ɢ ɦɚɫɫɭ ɛɟɡ
ɢɡɦɟɧɟɧɢɹ. ɂɡɦɟɧɢɦ ɬɨɥɶɤɨ ɯɚɪɚɤɬɟɪ ɨɩɢɪɚɧɢɹ ɛɚɥɤɢ: ɛɭɞɟɦ ɫɱɢɬɚɬɶ, ɱɬɨ ɜɦɟɫɬɨ ɲɚɪɧɢɪɧɵɯ
