Fattorini H.O., Kerber A. The Cauchy Problem

Подождите немного. Документ загружается.

5.2. The Neutron Transport Equation

277

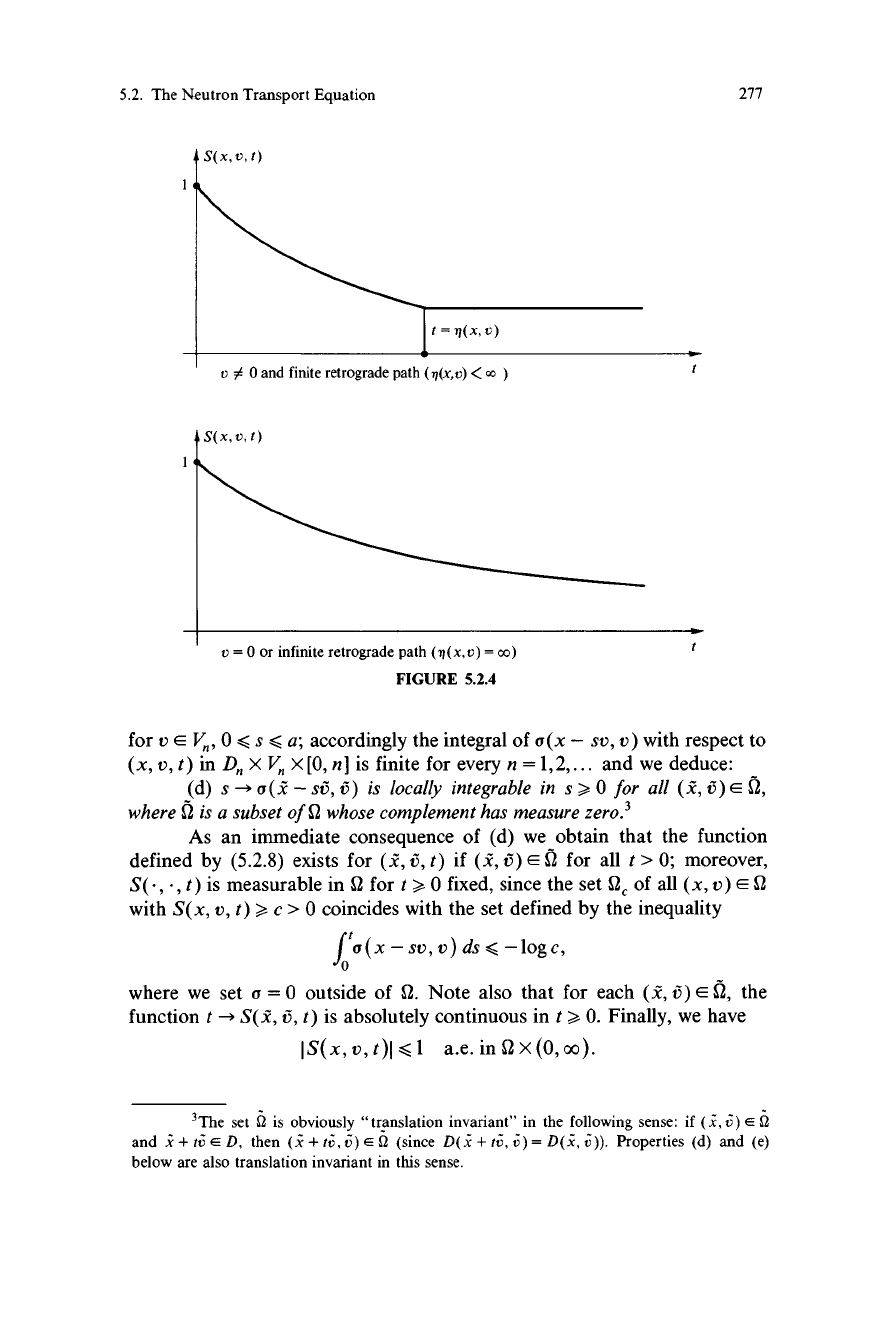
4S(x,v,1)

t=II(x,v)

v # 0 and finite retrograde path (n(x,v) < x )

v = 0 or infinite retrograde path (ri(x,v) = oo)

FIGURE 5.2.4

for v E V,,, 0 < s < a; accordingly the integral of a(x - sv, v) with respect to

(x, v, t) in D X V X [0, n] is finite for every n =1,2,... and we deduce:

(d) s - a(x - sv, v) is locally integrable in s >, 0 for all (z, v) E S2,

where C2 is a subset of 0 whose complement has measure zero.3

As an immediate consequence of (d) we obtain that the function

defined by (5.2.8) exists for (z, v, t) if (z, v) E S2 for all t > 0; moreover,

S(-, ,

t) is measurable in SZ for t >, 0 fixed, since the set SZc of all (x, v) E 2

with S(x, v, t) > c > 0 coincides with the set defined by the inequality

a(x-sv,v)ds<-logc,

where we set a = 0 outside of Q. Note also that for each (X, v) E S2, the

function t - S(z, v, t) is absolutely continuous in t > 0. Finally, we have

jS(x,v,t)I<1

a.e.in2x(0,oo).

3 The set S2 is obviously " translation invariant" in the following sense: if (z, v) E S2

and i + tv a D, then (z + tv, v) E fl (since D(z + tv, v) = D(z, V-)). Properties (d) and (e)

below are also translation invariant in this sense.

278

Perturbation and Approximation of Abstract Differential Equations

Define an operator C5 (t) (t > 0) in L"(S2) by the formula

(C5o(t)u)(x,v)=S(x,v,t)u(x-tv,v) (uEE), (5.2.9)

where we assume that u = 0 outside of 2. We have

I1(25 o(t) u11 < fuS(x, v, t)"I u (x - tv, v)IP dx dv

< f

Iu(x,v)I°dx) dv

<fV(fDI

u(x,v)IPdx)

dv=IIuIIP,

where the set D*(v, t) consists of all x E D with x + to E D. Hence

111250(t)11 <1 (t>-O)-

(5.2.10)

We show next that C5 is strongly continuous. Let u be a function

in the set ` used to prove the denseness of D(St ). It is easy to see that if

to >, 0, then

S(x, v, t) u (x - tv, v) - S(x, v, to) u (x - tov, v)

(5.2.11)

as t - to for all (z, v) E S2; in fact, (5.2.11) is immediate if to < 'q (x, v) or

to > q(x, v) (see the comments following (d)) and results for to = q(x, v)

observing that u (x - rt(x, v)v, v) = 0 since x - rl(x, v)v must be a boundary

point of D. We can then apply the dominated convergence theorem to

deduce that

II(5o(t)-so(to))uI -'0

(t-

to).

But in view of (5.2.10) and of the denseness of ¶, strong continuity follows

(see Theorem 1.1).

We consider now the operator

CS(X)b= fMe-AtCSO(t)bdt (ReX<O,bEE)

(5.2.12)

(integration understood in the vector sense). An argument very similar to

the one leading to (d) (but where the use of D, V is unnecessary due to the

fact that I)) (x, v) I P is integrable in D X V) yields:

(e) For any b E E, the function s - I b (x - sv, v) I P is integrable in s

for all (x, v) E S2, where Sl is a set of full measure in 0 and we have set b = 0

outside of 2. Plainly we may (and will) assume that the sets S2 in (d) and (e)

are the same.

Let q = qp(x, v) be an arbitrary smooth function of compact support,

thought of as an element of LP'(S2) (p-' + p'-' =1). Then

(9),t (A)b)= foo" e-Xt(9),C50(t)b)dt

=f,(0

5.2. The Neutron Transport Equation

279

It follows from this equality that there exists a set SZ of full measure in Sl

(which may be taken to coincide with the sets in (d) and (e)) such that, after

eventual modification of u in a null set,

u(x,v)= (0(X)b)(x,v)= o"(X,6)e-'sS(x,v,s)b(x-sv,v)ds

(5.2.13)

for (x, v) E 2 and x E D(x, 1b).4 Let now x be a point in the closure of some

component interval J of D(x, v) (we can take x to be the left endpoint if J

does not contain x - oov, in which case rl(x, v) = 0). Since rl(x + tv, v) =

n(x,v)+t, we obtain, after two elementary changes of variable, that if

0<t<r1(x,t3),then

u(x+tv,v)

{exp(-x(t-s)-J'(x+r)dr)}(x+s)ds

=ftX

so that (a) and (b) in the definition of D(s? [ o) are satisfied. Moreover,

Dtu(x+tv,v) = b(x+tv,v)

-(X+u(x+tv,v))u(x+tv,v)

hence u E D(WO) and

(XI-Wo)u=b.

(5.2.14)

If b = 0, it is not difficult to see from the boundary condition (b) and from

the fact that u (x - tv, v) must be absolutely continuous in t for almost all

(x, v) that any solution of (5.2.14) in LP(Sl) must be zero almost every-

where. Since (i(X) is bounded, we have shown that

C5(x)=R(x;1Co)

(Re)(>0),

which equality, in view of (5.2.12) and of Lemma 2.2.3 implies that

B E e+(1, 0) and that C ( ), defined by (5.2.9), is the propagator of

u'(t) = a 0u(t).

(5.2.15)

We study now the full equation (5.2.1). To apply the results in

Section 5.1 here, it is obviously sufficient to require that the integral

operator

u(x,v)= f K (x, v, v') u (x, v') dv'

(5.2.16)

4A continuity argument extends (5.2.13) to x in D(i, o), the closure of D(i, o). To see

this we observe that

v) and

o, t) can be extended to continuous functions in D(z, o);

on the other hand, t - b(x - to, o) belongs to LP.

280

Perturbation and Approximation of Abstract Differential Equations

be bounded in Lp(S2). A sufficient condition based on Holder's inequality is

p-1

sup f (fX, vv')IP/(P_1)dv')

dv<oo (5.2.17)

xED V

for the case p > 1 and

f ( sup sup IK(x, v, v')I) dv < oo (5.2.18)

V xEDv'EV

when p =1, both of which are satisfied if D and V are bounded and K is

measurable and bounded in 2. It must be pointed out, however, that

conditions like these may not be verified in some applications (see Larsen

[1975: 1]).

5.2.2 Theorem. Let D be an open set in R X, V a measurable set in

083,,, a a measurable, essentially bounded, nonnegative function in D X V, K a

nonnegative measurable function in D X V X V such that the operator A, in

(5.2.16) is bounded in LP(2) for some p, 1 S p < oo. Then the operator

A=% +A, (W 0 defined by (5.2.5) and following comments) belongs to

(1,11

) in Lp(S2) and the propagator of

u'(t) = 9fu(t) (5.2.19)

satisfies

C5(t)>' 0 (t>' 0). (5.2.20)

Theorem 5.2.2 immediately follows from Theorem 5.1.2; the result

on positivity of (2 is a consequence of Corollary 5.1.3, of the fact that

C50(t) is positive for all t > 0 (which results directly from its definition) and

from positivity of R, which is obvious since K is nonnegative.

The preceding treatment can be generalized in various ways; for

instance, the space Lp(1) can be replaced by Lp(I, It), where µ(dxdv) =

dx v(dv), the assumptions on a can be relaxed to boundedness from below

and integrability in 2, K need only be bounded below, and so on.

In studying (5.2.1) in the space C(S2) we stumble upon the following

difficulty: if rt is not continuous, the function C25o(t)u(x, v) defined by

(5.2.9) may not be continuous in (x, v) for some values of t even if u

satisfies the boundary condition (5.2.2). It is not difficult to surmise that

lack of continuity of q is related to lack of convexity of D. (See Figure 5.2.5).

We assume in what follows that D is open, convex, and bounded and

that V is closed and bounded. To begin with, we extend the function rl to all

x e D, adopting the convention that q = 0 if the set on the right-hand side

of (5.2.7) is empty. It is easy to extend Lemma 5.2.1 to show that q(x, v)

(with (x, v) roaming in SZ = D X V) is lower semicontinuous at any

(xo, vo) E D X V, where rl(xo, vo) > 0. (Of course, lower semicontinuity at

(xo, yo) is obvious if rl(xo, yo) = 0.) However, we can prove much more for

5.2. The Neutron Transport Equation 281

FIGURE 5.2.5

a convex set:

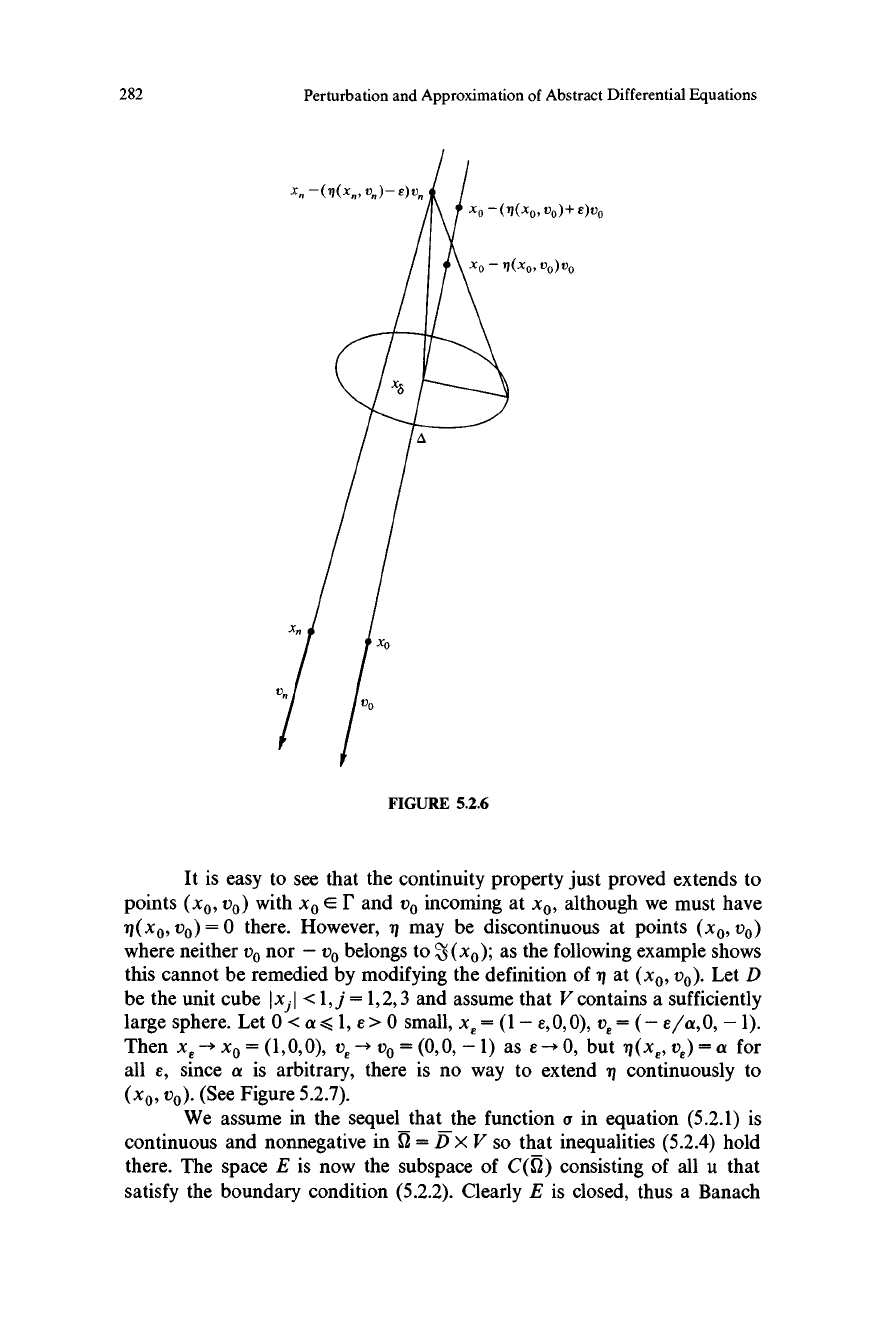
5.2.3 Lemma Let D be convex and let x0 E D, vo E V be such that

0 <,q(xo, vo) < oo. Then q is continuous at (xo, vo).

Note that q (xo, vo) > 0 if x0 E D and vo is any element of V; hence

as a particular case of Lemma 5.2.3, we obtain that i(x, v) is continuous in

2 if D is convex.

The proof of Lemma 5.2.3 runs as follows. Since q is lower semicon-

tinuous at the point in question, we only have to prove upper semicontinu-

ity. If q is not upper semicontinuous at (xo, vo) there exist e> 0 and two

sequences (xn) E D, (vn) EE V such that xn - x0, vn -. vo and

n(xnI vn) > n(xo, vo)+2e.

Let 0 < S < rt(xo, vo). Since the point xs = x0 - Svo belongs to D, there

exists a circular disk A contained in D with center at xs and perpendicular

to the line joining x0 and xs. On the other hand, xn -(q(xn, vn) - e)vn

belongs to D and approaches the half-line

(Y;Y=xo-tvo,'q(xo,vo)+e<t <00)

as n - oo. Using then the convexity of D as indicated in the next Figure

5.2.6, we deduce that x0 - tvo E D for ri(xo, vo) < t < q(xo, vo) + e, which is

absurd.

282

Perturbation and Approximation of Abstract Differential Equations

FIGURE 5.2.6

It is easy to see that the continuity property just proved extends to

points (xo, vo) with xo E I' and vo incoming at xo, although we must have

rl(xo, vo) = 0 there. However, rl may be discontinuous at points (x0, vo)

where neither vo nor - vo belongs to

(xo ); as the following example shows

this cannot be remedied by modifying the definition of q at (xo, vo). Let D

be the unit cube I xj I < 1, j =1, 2,3 and assume that V contains a sufficiently

large sphere. Let 0 < a < 1, e > 0 small, xE = (1- e, 0, 0), vE = (- a/a, 0, - 1).

Then xE - xo = (1,0,0), vE - vo = (0,0, - 1) as e - 0, but q(xe, ve) = a for

all e, since a is arbitrary, there is no way to extend n continuously to

(xo, vo). (See Figure 5.2.7).

We assume in the sequel that the function a in equation (5.2.1) is

continuous and nonnegative in Sl = D X V so that inequalities (5.2.4) hold

there. The space E is now the subspace of C(1) consisting of all u that

satisfy the boundary condition (5.2.2). Clearly E is closed, thus a Banach

5.2. The Neutron Transport Equation

283

FIGURE 5.2.7

space in its own right. The operator WO is again given by (5.2.5), its domain

described in the following way: u E E belongs to D(91o) if and only if for

every (x, v) E D X V the function s - u(x + sv, v) is continuously differen-

tiable in the closed interval J= D(x, v) 5, vanishes at the left endpoint and

the directional derivative (v, grad, u) belongs to E as a function of x and v.

For each t > 0 and u e E, extend u setting u = 0 outside of S2 and

define

(C5o(t)u)(x,v)=S(x,v,t)u(x-tv,v) (u EE)

(5.2.21)

(note that a, thus S, is defined in EX V). However, it is not immediately

obvious that C25o(t)u will be continuous in U X V; in fact, if 'Q(x, v) is

discontinuous

at (xo, vo),

then S(x, v, t) may be discontinuous at

(xo, vo,'q(xo, vo)). However, one may suspect that at these points the

possible discontinuity of S will be cancelled out by the boundary condition

satisfied by it. This is in fact the case, at least if we rule out isolated velocity

vectors be means of the following assumption:

(f) (i) Let v e V, v - 0, e > 0. Then, on every half line sufficiently close

to that determined by v there exist vectors v' E=- V with

lv'-v1 <E.

(ii) If 0 E V, 0 is an interior point of V.

We note that in problems of physical interest V has spherical

symmetry (if v E V and v' = I v 1, then v' (=- V) so that Assumption (f) is

trivially satisfied if 0 0 V.

5Here D(x, v) = D n t(x, v); since D is convex, D(x, v) consists of a single closed

interval.

284

Perturbation and Approximation of Abstract Differential Equations

The following result, which will be used in the proof of Lemma 5.2.5,

is well known.

5.2.4

Lemma.

Let D be open and convex, x E D, y E D. Then all

points in the segment joining x and y (except perhaps y itself) belong to D.

For a proof see Dunford-Schwartz [1958: 1, p. 413].

5.2.5 Lemma. Let u = u(x, v) be a continuous function in

SZ =

D X V that satisfies the boundary condition (5.2.2). Assume that D is convex,

open and bounded, that V is compact, and that Assumption (f) is satisfied.

Then the function u (x, v, t) _ (C5 0 (t) u)(x, v) defined by (5.2.21) is continu-

ous in 9 X [0, oo) = D X V X [0, oo).

To begin with, we note that if the point (x0, v0, t0) E D X V X [0, oo)

is such that

u (x0 - tovo, v0) = 0

(5.2.22)

(in particular, if x0 - t0vo E D), then continuity of u(x, v, t) at (x0, v0, to)

is a consequence of the continuity of u (x, v) regardless of behavior of S,

since u (x - tv, v) will be continuous as a function defined in R x X V x [0, 00)

at (x0, v0, to) (recall that u is extended outside of SZ setting u = 0 there).

We consider three separate alternatives, assuming for the moment

that v0 0.

(I) (x0, v0, to) E D X V X [0, oo) and q(xo, v0) > 0 (this happens if

and only if x0 E D or x0 E I' with - v0 incoming at x0). Clearly u will be

continuous at (x0, v0, to) if to < q(x0, v0) or if to > q(x0, v0); on the other

hand, if to ='q(x0, v0) the point x0 - t0vo belongs to the boundary I' and v0

is incoming at x0 - t0v0 so that (5.2.22) holds.

(II) (x0, v0, to) E F X V X [0, oo) with v0 incoming at x0. In this case,

u(x0,vo)=0

so that continuity of u(x, v, t) at to = 0 results from continuity of u(x, v).

Assume then that to > 0. Since v0 is incoming at x0, x0 + evo E D if e > 0 is

sufficiently small. Hence, if x0 - t0vo E U we deduce from Lemma 5.2.4 that

x0 E D, which is absurd. Accordingly, x0 - t0vo 14 D and (5.2.22) holds.

(III) (x0, v0, t) E I' X V X [0, oo) but neither v0 nor - v0 are incoming

at x0. Our objective is again to show that (5.2.22) holds, and we may assume

that

x0 - t0vo E F.

(5.2.23)

In fact, if x0 - t0v014 D, (5.2.22) is automatically satisfied; on the other

hand, if x0 - t0vo E D, the vector - v0 is incoming at x0 against the

hypotheses.

Let x be a point in D not in the line determined by x0 and v0. By

Lemma 5.2.4 the whole (two-dimensional) interior of the triangle de-

5.2. The Neutron Transport Equation

285

x0 - tovo

FIGURE 5.2.8

termined by the points x, xo and xo - tovo lies in D. Making use of

assumption (f) we deduce the existence of vectors v', arbitrarily close to vo

and such that v' is incoming at xo - tovo; since u(xo - tovo, v') = 0 it

follows from continuity of u that (5.2.22) holds.

The case vo = 0 is simple. If xo e D, q(xo, vo) = oo and we use

alternative (I). On the other hand, if x0 E IF, it follows from the second part

of Assumption (f) that there exist arbitrarily small incoming vectors at xo so

that u(xo, vo) = u(xo - tovo, vo) = 0 for any to >, 0 and (5.2.22) holds. This

ends the proof.

We can complete now the treatment of (5.2.1) in the space E by

slight modifications of the LP arguments. If u E E, we have shown in

Theorem 5.2.5 that

0(t)u is continuous in SZ X [0, oo), hence uniformly

continuous in each cylinder SZ X [0, a], a > 0. It is plain that C25o(t)u satisfies

(5.2.2) for all t if u does; hence (5.2.21) defines an operator in (E) for all

t > 0 and C25

() is strongly continuous in t > 0. Moreover,

II(25o(t)II < 1

(t>0)

since S is nonnegative and bounded by 1. Every A with Re A > 0 belongs to

p(9to) and

(R(A;

lf0)1))(x,v)=f'f(x'v)e-xtS(x,v,t)b(x-tv,v)dt

for all (x, v) E D X V; since b = 0 outside of D,

R(A;Ao)b= foo e-XtK o(t)bdt (ReX>0,teE)

as an (E)-valued integral, so that L o E e+(1, 0) and C25 0(t) = exp(t t o ),

t >, 0; again C25 o is positive for all t. Making use of Theorem 5.1.2 and

Corollary 5.1.3, we obtain:

5.2.6

Theorem.

Let D be open and bounded in R x, V a compact set

in R 3 satisfying Assumption (f ), a a nonnegative continuous function in D X V,

K a nonnegative continuous function in D X V X V making (5.2.16) a bounded

operator in E. T h e n It = W o + A belongs to e+(1, I

I A I I) and exp(t fit) is positive

for all t > 0.

286

Perturbation and Approximation of Abstract Differential Equations

We note that R maps E into E if K is continuous in D X V X V and

K(x,v,v')=O (xEF,vE,s(x),v'EV). (5.2.24)

In some treatments of the transport equation it is assumed that the

neutrons belong to velocity groups characterized by I v I = k, > 0, i =1, ... , M.

The C(Sl) treatment applies fully to this case; here V is the union of the

spheres V = (v: I v I = k;). For the L n treatment the appropriate space is

LP(D x V x

X V,,,) with measure µ = dxdu1

do,,,, da; the area dif-

ferential in V. Note that assumption (f) is satisfied.

5.2.7

Example.

(i) Let D be a bounded domain, V a measurable set such

that

IvI, c> 0 (v E V).

Then there exists to > 0 such that

go(t)=O (t,to).

(5.2.25)

(5.2.26)

(ii) If the operator 9 in (5.2.16) is compact, then Ca(t) is compact

and continuous in the norm of (E) in LP(12) (1 < p < oo) for t, to (this

follows from (5.2.26) and the perturbation series (5.1.19)).

(iii) The same conclusion holds in C(S2) (here we assume D open,

convex, and bounded and V closed, bounded, and satisfying (5.2.25)).

Example 5.2.7 makes possible to obtain information on the spectral

behavior of W using Example 4.10.3:

5.2.8

Example.

Under the assumptions above, a(%1), the spectrum of fit,

is empty or consists of a (finite or infinite) sequence X,

X21... of eigenval-

ues such that Re Ak - - oo if the sequence is infinite. The generalized

eigenspaces corresponding to each eigenvalue (Section 3) are finite dimen-

sional.

5.3. PERTURBATION RESULTS FOR OPERATORS

IN a+(1,0) AND IN 9

In the perturbation theorems considered in Section 5.1, no hypotheses were

made on P except that P should be "dominated by A" in the sense specified

there. In Theorem 5.1.2 the hypothesis on P is quite stringent; this is

perhaps not the case with those in Theorem 5.1.1, but (5.1.2) is not easy to

verify as it involves rather complete knowledge of S(t). Note also that when

A-= (2, the assumptions in Theorems 5.1.1 and 5.1.2 coincide; if (5.1.2)

holds, then, for t > 0 and u E E,

IIPull=IIPS(t)S(-t)uII <a(t)IIS(-t)uII <Ca(t)e`jjuII

so that P must be bounded.