Fattorini H.O., Kerber A. The Cauchy Problem

Подождите немного. Документ загружается.

Chapter 5

Perturbation and Approximation of

Abstract Differential Equations

Many differential equations of importance in applications (such as the

Schrodinger equation) are of the form u'(t) = (A + P)u(t), where the

operator A is known to belong to E+ or to a subclass thereof and P is

a perturbation operator. It is then of interest to determine conditions

on P that guarantee that A + P belongs to the same class.

Two results of this kind are proved in Sections 5.1 and 5.3, the

first for the class (3+ and the second for m-dissipative operators; there

are also theorems for the class i and for the case where P is bounded.

Applications to the neutron transport equation in Section 5.2 and to

the Schrodinger and Dirac equations with potentials in Section 5.4 are

examined in detail; also, it is shown in Section 5.5 how to relax some

of the assumptions imposed on second order elliptic operators in

Chapter 4. Symmetric hyperbolic operators, last seen in Chapter 3,

reappear in Section 5.6; the objective is to study the Cauchy problem

in Sobolev spaces generalizing the results pertaining to the constant

coefficient case in Chapter 1.

A basic problem in the numerical treatment of the abstract

differential equation u'(t)=Au(t) is that of approximating its solu-

tions by those of the equation u;, (t) =A,, u (t), where A -A in a

suitable sense, or by those of a difference equation like u(t + T) =

u. (t). Sections 5.7 and 5.8 contain a study of this problem,

with applications to a parabolic equation.

267

268

Perturbation and Approximation of Abstract Differential Equations

5.1.

A PERTURBATION RESULT

It was already observed in Section 2.1 that direct application of Theorem

2.1.1 is difficult in general, except perhaps in the dissipative case treated in

Chapter 3. It is many times useful to have at our disposition perturbation

results, that is, theorems of the type "if A belongs to e, (or to e, (2'*, ()

and P belongs to a certain class of operators 6P(A), then A + P belongs to

6+ (or to e. (2°°, 9). A straightforward but useful result in that direction is

the following.

5.1.1 Theorem.

Let A E C+, S(t) = S(t; A) the propagator of

u'(t) = Au(t) (t >,0). (5.1.1)

Let P be a closed, densely defined operator such that D(P) D D(A) and

II PS(t)uII s a(t)IIuII (u E D(A), t > 0), (5.1.2)

where a is a finite, measurable function with

f ta(t)dt<oo.

(5.1.3)

Then A + P (with domain D(A + P) = D(A)) belongs to 3+.

Proof.

Since we wish to show that A + P E e+, we must deal with

the equation

u'(t) = (A+P)u(t)=Au(t)+Pu(t).

(5.1.4)

Formally, we can solve (5.1.4) with initial condition

u(0) = uo (5.1.5)

by means of the following successive approximation scheme: let u0(t)

S(t) uo and the solution of

(t>,0)

(5.1.6)

uo. (5.1.7)

Then u(t) = lim

will be a solution of (5.1.4), (5.1.5). The initial value

problem (5.1.6), (5.1.7) can of course be solved by means of the theory

developed in Section 2.4; in view of (2.4.3) we must have

(n>l)

so that

u=(S+S*PS+S*(PS)*2+ ...)uo, (5.1.8)

where * indicates convolution product and * n the n-th convolution power.

To justify formula (5.1.8) directly would be cumbersome, thus we will only

take it as a heuristic guide.

5.1. A Perturbation Result 269

In what follows f, g, h,... will be (E)-valued functions defined and

strongly continuous in t > 0 such that I I f 11,

11 g l1.

. . .

are integrable near zero.

(Note that, by the uniform boundedness theorem, 11f 11

is bounded on

compact subsets of t > 0; also, since 11f(t)II = sup{llf(t)ull; Ilull < 1), II! 11 is

lower semicontinuous, hence measurable). We denote by 5 the space of all

such functions.

The convolution off and g E 5 is defined by the familiar formula

(f *g)(t)u= f `f(t-s)g(s)uds. (5.1.9)

The following properties of the convolution are either well known or easily

deduced and left to the reader.

(a) If f, g E f, then f* g E 1 and

11(f*g)(t)II<(I1f11*I1g11)(t)

(t>o). (5.1.10)

(b)

f*(g*h)=(f*g)*h.

Clearly we can use (5.1.10) combined with Young's Theorem 8.1 to

estimate convolution powers: if f E F, f*" = f * f * . . . * f and

f °°llf(t)lldt=Y<oo,

(5.1.11)

then

llf*n(t)Ildt<Yn<00

(n>, 1).

(5.1.12)

If g is bounded,

plainly we have

Ilg(t)11 < C (t>0)1

II(g*f*")(t)II<Cy"

(n>,l,t>0).

5.1.13)

We apply these observations to our perturbation problem. It follows

from (5.1.2) that for each t > 0, PS(t)-which is in principle only defined in

D(A)-admits an (E)-valued extension PS(t) that satisfies

IlPS(t)111"(t)

(t>0).

(5.1.14)

Since

PS(t)=PS(t0)S(t - t0),

(5.1.15)

it is clear that PS(-) is strongly continuous in t > 0; in view of (5.1.14), PS

belongs to 5. On the other hand, it also follows from (5.1.15) that

11PS(t)Il

<Ca(t0)e-'toewt

> t0)

where C, w are constants such that

llS(t)Il <Cewt

(t >, 0). (5.1.16)

270

Perturbation and Approximation of Abstract Differential Equations

We choose now w'> w so large that

f0°°e - -"JJ TS(t)II dt = y < 1

(5.1.17)

and avail ourselves of the equality

exp(-(o't)(f* g)=exp(-w't)f*exp(-w't)g

to estimate

S*(PS)" = exp(w't){exp(- w't)S *exp(- w't)(PS)*"),

making use of (5.1.16), (5.1.17), and (5.1.13). We obtain

II S*(PS)*n(t)II S

Cynew't

i 0).

(5.1.18)

This clearly means that the series

S1(t) _ i S*(PS)*"(t) (5.1.19)

n=0

converges in (E) uniformly on compact subsets of t >, 0 and

IISi(t)II,<C(1-y)-lew.t

(t>,0). (5.1.20)

Since reiterated applications of (c) show that every term of (5.1.19) is

strongly continuous in t > 0, S,(t) is likewise strongly continuous in t > 0.

Let now f be a function in 5 growing at most exponentially at

infinity and assume that w'> w is so large that exp(- w't )I I f (t )I I is summa-

ble in t >, 0. Let $ f be the Laplace transform of f,

ef(A)u= f 00

which exists in Re A > w'. It can be shown just as in the scalar case that if g

is another function

in 6 with exp(- w't)IIgII E L'(0, oo),

then

exp(- w't)ll.f * gll E L'(0, oo) as well and

(ReX>w'). (5.1.21)

On the other hand, it follows from Lemma 3.4 and an approximation

argument that

L(PSu)=PLS(A)u=PR(A)u (ReX>w',uEE).

(5.1.22)

Let Re A > w'. Multiply the series (5.1.19) by exp(- A t). In view of (5.1.18),

the resulting series will converge uniformly in t > 0, the partial sums being

bounded in norm by a constant times exp(- (Re A - w')t). We can then

integrate term by term and make use of (5.1.21) and (5.1.22) to obtain

Q(A)=CS1(A)=R(A) (PR(A))" (ReA>w'),

n=0

the series convergent in (E). Clearly Q(X)E C R(A)E = D(A) = D(A + P)

5.1. A Perturbation Result

271

and

(Al- A- P)Q(A)

(PR(A))n - Fr (PR(A)) n = l;

n=0 n=1

in applying Al - A and P term by term to the series, we make use of the

fact that both operators are closed. On the other hand, if u E D(A),

Q(A)(AI- A- P)u = R(A) 2 (PR(A))n(XI - A- P)u

n=0

00 00

_ E (R(A)P)nu- E (R(X)P)nu=u

n=0 n=1

so that Q(A) = R(A; A + P). The proof of Theorem 5.1.1 follows now from

the fact that Q(A) = eS,(A) and from Lemma 2.2.3.

A particularly interesting case of Theorem 5.1.1 is that where P is

everywhere defined and bounded (all the hypotheses are then automatically

satisfied). Since some additional precision can be gained, we prove this case

separately.

5.1.2

Theorem.

Let A E C+(C, w) and let P be a bounded operator.

ThenA+PEe+(C,w+CIIPII).

Proof. By virtue of Theorem 2.1.1, R(A)= R(A; A) exists for,\ > w

and

IIR(A;A)nll5C(A-w)-n

(A>w,n>, 1).

(5.1.23)

In particular, if

X>w+CIIPII,

then

IIPR(A)II < CIIPII(A - w)-' < 1,

(5.1.24)

hence the series

Q(A) = R(A) E (PR(A))n

n=O

is convergent in (E). It can be proved exactly as in Theorem 5.1.1 that

Q(A) = R(A; A + P).

We estimate the powers of R(A; A + P). We have

R(X)

R(A; A+ P)m

, (PR(A))nl

n=0

R(A)(PR(A))n

X R(A)(PR(A))J2... R(X)(PR(X)) j-.

272

Perturbation and Approximation of Abstract Differential Equations

Now, in view of (5.1.23) and (5.1.24),

IIR(X;A+P)mll<

1-CIIPII(X-w)-'

=C(X-((0+CIIPII))-m (A>w+CIIPII),

which, in view of Theorem 2.1.1 as modified by Remark 2.1.4, ends the

proof.

The following result relates Theorem 5.1.1 and Theorem 5.1.2 with

the results in Section 3.7.

5.1.3 Corollary. Let E be a Banach lattice, A E C+, and assume

that S(t) = S(t; A) is positive for all t > 0. Let P be an operator satisfying the

conditions in Theorem 5.1.1 and let P itself be positive (or, more generally,

assume there exists a constant /3 such that

Pu>-$u (uED(A),u>,0)).

(5.1.25)

Finally, assume that E+ n D(A) is dense in E+ (E+ is the set of nonnegative

elements of E). Then S(t; A + P) is positive for all t.

Proof.

Assume P is positive (/3 = 0 in (5.1.25)). Then PS(t)u >, 0 if

u E E+ n D(A). The hypothesis on E+ n D(A) and the fact that E+ is

closed implies that PS(t) is positive for all t. Using again the closedness of

E+ we see that S * PS, S * (PS)*2,

... are

positive for all t and thus the same

is true of S(t; A + P), sum of the series (5.1.19). If P is not positive but only

satisfies (5.1.25), we only have to apply the previous comments to P + /31

and use the formula S(t; A + P) = e - 8`S(t; A + (P +,01)).

We note that when P is bounded and everywhere defined the

hypothesis that E+ n D(A) be dense in E+ can be discarded.

To close this section we note the following result, that can be easily

obtained applying Theorem 5.1.2 to A and - A:

5.1.4

Corollary. Let A E C (C, w) and let P be bounded. Then

A+PE(2(C,w+CIIPID

5.2. THE NEUTRON TRANSPORT EQUATION

As an application of the results in the previous section, we consider the

neutron transport equation

8t+(v,g adXu)+a(x,v)u=JK(x,v,v')u(x,v ,t)dv .

(5.2.1)

Here x = (x1, x2, x3), v = (vt, v2, v3), and u = u(x, v, t). This equation

5.2. The Neutron Transport Equation

273

describes the migration and multiplication of neutrons in a body occupying

a domain D of x-space: the nonnegative function u is the density at time t

of neutrons of velocity v at x. The nonnegative function a represents the

absorption coefficient at x for neutrons of velocity v, whereas the integral

operator on the right-hand side of (5.2.1) describes the production of

neutrons at x by scattering and nuclear fission. We shall assume that D is

open and connected in x-space R

(although connectedness is not essential)

and that the velocities v belong to some measurable set V in v-space UB;,.

Let x E t = boundary of D, and v E V. We say that v is incoming at x

(in symbols, v E

(x)) if and only if there exists e> 0 with

x + tv E D (0 < t < s).

v incoming at x

FIGURE 5.2.1

The solution of (5.2.1) is assumed to satisfy the following boundary condi-

tion:

u(x,v,t)=0 (xEI',vEZ (x),t>0).

(5.2.2)

Physically, this simply means that no neutrons enter the domain D from

outside. This is natural if D is a convex region in empty space of if D is

surrounded with absorbing material so that neutrons abandoning D are

captured and unable to reenter. The initial neutron density is given:

u(x,v,0)=uo(x,v)

(x ED,vEV).

(5.2.3)

Let SZ = D X V. In view of the interpretation of it as a density, it is

clear that the space E = L'(SZ)R is the natural setting to study (5.2.1) as an

abstract differential equation. However, since no additional difficulties

appear, we shall take E = L'(Q)R with 1 < p < oo. With some additional

restrictions on D we shall also consider the case where E is a suitable

274

Perturbation and Approximation of Abstract Differential Equations

subspace of C(Sl)R. Since only nonnegative solutions of (5.2.1) have physi-

cal meaning, it will be essential in each case to show that the solution

remains nonnegative if the initial datum (5.2.3) is nonnegative.

We examine first (5.2.1) when K=O in the space E = L"(SI),

1 < p < oo. We assume that a is measurable and

0<a(x,v)<C a.e.inSZ. (5.2.4)

Define

9lou (x, v) = - (v, grad.,u (x, v))- a(x, v)u (x, v). (5.2.5)

The domain of W

is described as follows. For each x E R x, v e R 3,,, let

D(x,v)=Dnl(x,v),

where l;(x, v) is the line (y; y = x + sv, - oo < s < oo). Since D is open,

D(x, v) is open in J(x, v), thus we can express D(x, v) as the union of a

finite or countable family of disjoint open intervals,

D(x, v) = J, U J2 U ,

which we call component intervals of D(x, v). A function u E LP(1) belongs

to D(WO) if and only if for almost all (x, v) in St = D X V

(a) The function

f(s;x,v)=u(x+sv,v)

can be extended in each component interval J of D(x, v) to a function

FIGURE 5.2.2

5.2. The Neutron Transport Equation

275

absolutely continuous in the closure In (locally absolutely continuous in fn if J

is infinite). (Note that if two intervals have a common endpoint, the two

extensions may not coincide there.)

(b)

f=0

at the left endpoint of each component interval of D(x, v) (except if the left

endpoint is x - oov).

f'(s) = (v, gradxu) (5.2.6)

belongs to E = LP(S2) (as a function of x and v).

Note that the expression on the right-hand side of (5.2.6) for the

directional derivative is purely formal, since we do not assume the existence

of the partial derivatives. Also, in view of (a), for almost all (x, v) the

derivative (5.2.6) exists almost everywhere in D(x, v), so that (5.2.6) is

defined almost everywhere in S2.

If T is, say, an infinitely differentiable function of x with support

contained in D and 4i

is a function in LP(V), it

is immediate that

9)(x)/ (v) E D(Wo ). But the set Z of linear combinations of such functions

is dense' in LP(2) so that D(uf o) is dense as well. We compute next the

resolvent of Wo. To this end, we define a function rt = (x, v) in S2 as

follows:

n(x,v)=sup(t>0;x-svED,0<s<t)2.

(5.2.7)

Since D is open, ij(x, v) > 0 for all (x, v) E 9 and, if rl(x, v) < co, x - tv

belongs to D for t < rl(x, v) but not for t = q(x, v). In more intuitive terms,

q(x, v) is the time taken by the point x - tv to abandon D (for the first

time) starting at t = 0.

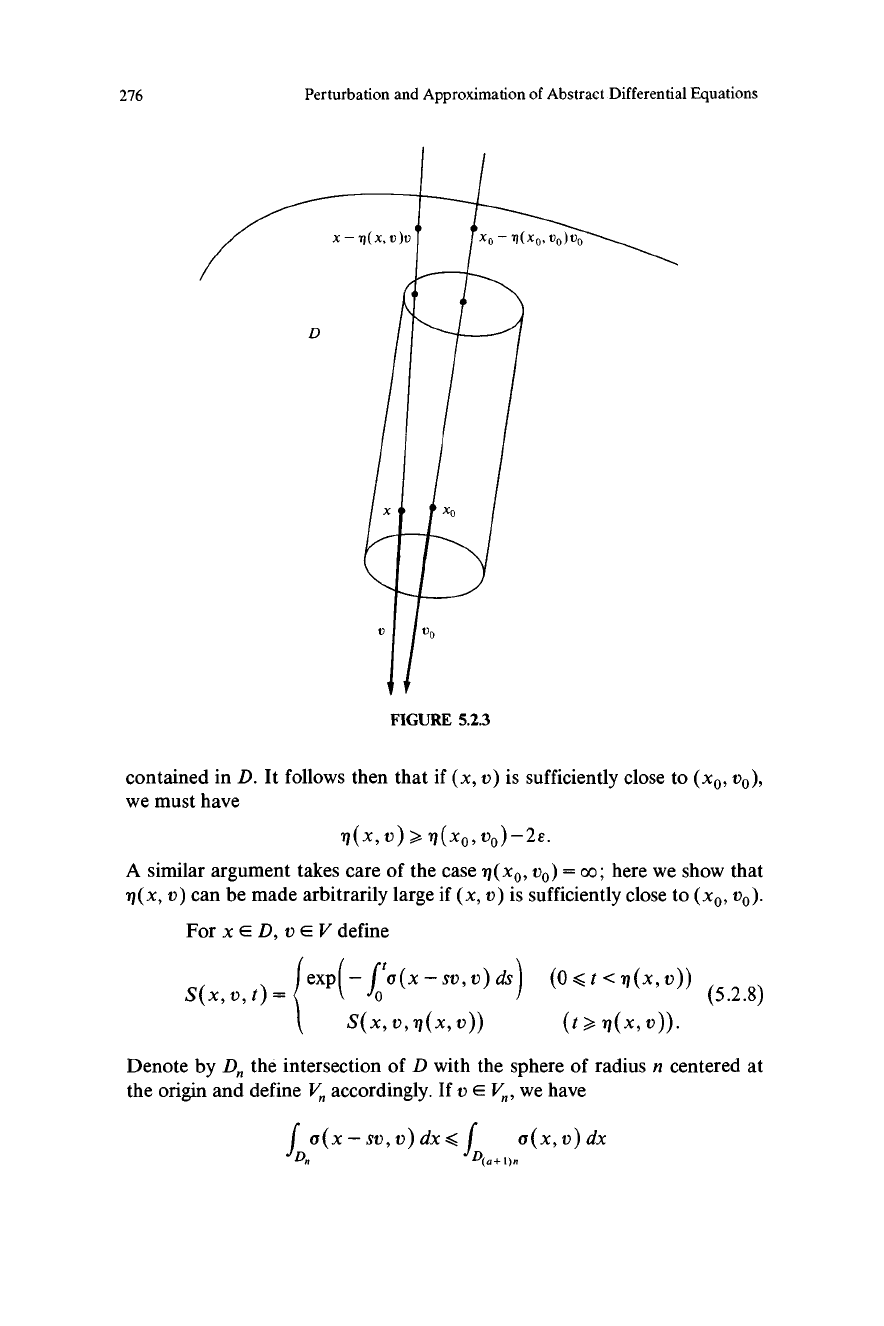
5.2.1 Lemma. rf is lower semicontinuous in U.

Proof Let (xo, vo) E SZ with q(xo, vo) < oo. Since xo - tvo E D for

0 < t < q(xo, vo), a continuity argument can used to show that, given e > 0

there exists 6 > 0 such that the circular cylinder consisting of all the points

x - tvo with x roaming over the disk of radius S centered at xo and

perpendicular to the line (xo, vo), and - 6 < t <,q(xo, vo)- e is entirely

'It is obviously sufficient to show that 6D(D) is dense in LP(D) and that linear

combinations of functions f(x)g(x) (f e LP(D), g e LP(V)) are dense in LP(D X V). The

final result can be proved with the help of mollifiers and the second by the Stone-Weierstrass

theorem (Adams [1975: 1, p. 10]).

2We do not define 11 for x tt Sl, in particular for x e T. We shall do so later, however

(see p. 280) .

276

Perturbation and Approximation of Abstract Differential Equations

FIGURE 5.2.3

contained in D. It follows then that if (x, v) is sufficiently close to (xo, vo),

we must have

'q(x, v) % n (xo, vo)-2e.

A similar argument takes care of the case rl (xo, vo) = oo ; here we show that

rl(x, v) can be made arbitrarily large if (x, v) is sufficiently close to (xo, vo).

For x E D, v E V define

S(x,v,t)-

exp(- fta(x-sv,v)ds)

(0<t<q(x,v))

(5.2.8)

S(x,v,,q (X, V))

(t>n (x,v)).

Denote by D the intersection of D with the sphere of radius n centered at

the origin and define V accordingly. If v E V,,, we have

Df a(x-sv,v)dx<

4(a

a(x,v)dx

+ pn