Fattorini H.O., Kerber A. The Cauchy Problem

Подождите немного. Документ загружается.

3.2. Ordinary Differential Operators in the Whole Line

127

have to be extended later. We take D(A0) = 6l

c, the space of complex-

valued Schwartz test functions.

3.2.2 Lemma.

The operator Ao is dissipative in LP (1<p < oo) if

a(x)>0, c(x)+P(a"(x)-b'(x))<0 (-oo<x<oo). (3.2.8)

The first inequality (3.2.8) is necessary in all cases; the second is necessary

when p =1.

Proof

Recall that the only duality map 0: LP -

-1 +P-1

1)is

0(u)=IIuII2-PIu(x)IP-2u(x)(u_0).It

is easy to see that if p>2and

u E 6D, then 0(u) is continuously differentiable and

IIuIIP-20(u),(x)=

(p-2)IuIP-4Re(au')u+IuIP-2u',

while, on the other hand,

(I uIp)'= PI

uI'-2(UIU,

+ u2u2)

(3.2.9)

= pIulV-2Re(uu').

Performing two integrations by parts we obtain

(3.2.10)

IIuII°-2Re(0(u), Aou) = Ref ((au')'+(b-a')u'+cu)IuIP-2udx

= -(p

-2)f alul'-4(Re(uu'))2dx

-f alulP-21u'l2dx

+ 1 f(a"-b'+pc)IuIPdx<0

(3.2.11)

under hypotheses (3.2.8).

In the case I < p < 2, a technical difficulty appears; even if u E 6D, it is not

clear how 0(u) behaves at "non-analytic" zeros of u,-that is, at points x0 where all

the derivatives of u vanish but where u itself fails to vanish identically in any

neighborhood of x0.

To remedy this, we introduce the class of piecewise analytic, twice

continuously differentiable complex valued functions with compact support in

- oo < x < oo. If U E

6ye(2), it is clear that

I uIP - 2 u is infinitely differentiable

between zeros of u, thus we only have to examine the behavior of its derivative

(IuIP-2u),=(p_2)IuIP a(uiu1+u2u'2)u+IuIP-2u,

near an isolated zero x0. Assuming that u is analytic at x0, let in > 0 be an integer

such that u(x)

U(m -1)(0)

= 0, u(m)(0) * 0. It follows from Taylor's formula

that

/ /

I0(u)'(x)I

-O(Ix-xolm(P-1)-')

128 Dissipative Operators and Applications

near x0, where m(p -1) > 0. If the point x0 is an endpoint of some of the intervals

where u is analytic, we simply use two one-sided estimations. It follows that 9(u)(x)

is absolutely continuous and then that the basic inequality (3.2.11) holds for

1 < p < 2 and u E e121. To see that the first two terms on the right-hand side add

up to a non-positive number, we only have to notice that I Re(uu') I < I u I

I u'. To

check that Re(O(u), Aou) < 0 for u E 61 , we take a sequence in

such that

the supports of the u are contained in a bounded set and u -

u, u -+ u', u;; --> u"

uniformly in (- oo, oo), and notice that Aou

Aou and (passing if necessary to a

subsequence) 8(u) weakly in LP'. Of course we may avoid this last step by

simply defining D(A0) =

(2) when p < 2, which does not modify at air the

ensuing theory.

We deal finally with the case p =1. For p > 1 we will denote by Bp in

the next few lines the unique duality map 6p: LP -* Li'. It is plain that if

u E 61 and 0(u) E L°° is the duality set of u as an element of L', we have

plim+ 9p(u)(x) = u*(x) E O(u)

(3.2.12)

almost everywhere in the support of u, whereas 9p(u)(x) (say, for 1 < p < 2)

is uniformly bounded. It follows then from the dominated convergence

theorem that

f u*(x)Aou(x) dx = lim f 00(u)(x)Aou(x) dx, (3.2.13)

pl+

which, by virtue of inequality (3.2.11), shows Re<u*, Aou) < 0 if conditions

(3.2.8) hold with p = 1. That this inequality must hold for any u* E O(u) is

obvious from the fact that two elements of 0(u) coincide where u

The necessity of the first condition (3.2.8) for p > 1 follows from

3.2.3

Example. Let f, g be real-valued continuous functions, and let p > 1. As-

sume that

f (fui2lulp-2+glulp)dx>0

(3.2.14)

for all u E 61. R (or u E P(R with support in some interval Q. Then

f(x)>0 (x(=- 0).

In fact, we only have to apply the result above to f (x) = (p -1) a (x ), g(x) _

- p - '(a"- Y+ pc).

Finally, we show the necessity of conditions (3.2.8) for dissipativity

of A0 in L'. Let u be a function in 6 DR with support in an interval [a, /3] and

such that u < 0 in (a, xo),u > 0 in (xo, a) for some x0 E (a, /3). Assuming

for simplicity that 1lull1=1, if u* E 0(u), then u*(x) _ -1 in (a, x0),

u*(x) =1 in (xo, a). Since u'(a) = u'(f3) = 0, we have

(u*, Auo) = f s((au')'+(b - a')u'+ cu)u*(x) dx

_ -2a(xo)u'(xo)+

f 0(a"- b'+ c)l ul dx,

(3.2.15)

3.2. Ordinary Differential Operators in the Whole Line

129

and it is clear that we can manipulate a, a, u in such a way as to make

(3.2.15) positive if either condition (3.2.8) is violated at some point.

3.2.4

Example. The second inequality 3.2.8 is not necessary for dissipa-

tivity of A0 if p > 1.

An important role will be subsequently played by the formal adjoint

of A0, defined in the same domain as A 0 by the familiar expression

A'u=(au)"-(bu)'+cu

= au"+(2a'- b)u'+(a"- b'+ c)u

=au"+bu'+cu.

The operator Ao satisfies the Lagrange identity

f (Aou)vdx= f uAovdx

(u,vEi l ), (3.2.16)

(and is uniquely determined by it). Clearly

(A'0)'=A0.

It is easy to see that the two inequalities (3.2.8) are satisfied for an operator

A0 in LP if and only if they are satisfied for the adjoint A'oin LP' (in Co if

p=1).

We examine now the problem of extending A0 in such a way that

dissipativity is preserved and that (3.1.8) holds for some a > 0 (in other

words, the problem of finding m-dissipative extensions of AO) in the spaces

under consideration. We begin with the case E = LP, 1 < p < oo. Let, as

usual, p'-' + p -' =1 and, given A > 0, denote by `3Cp,, . the subspace of

LP'(- no, oo) consisting of all elements of the form a9 - A' OT ((p E 6D). If A'0

is dissipative in Lv', it follows from the fundamental inequality (3.1.9) that

Ilrolip' <

IlXro - A'opIip' (

E 6D),

hence the functional

1D(Aqp-A'0q)=(v,,p)

(cED),

where v is a fixed element of L p, is well defined and 11 4D I I < A-' I I v I I P.

By the

Hahn-Banach theorem this functional can be extended to LP without

increasing its norm; accordingly, there exists a u E LP with

(u,Xgp-A'p)_(v,q)) ((pE6l)

(3.2.17)

and

Ilullp < Ilvllp.

(3.2.18)

It is clear from the general definition of adjoint operators that (3.2.17)

implies that u e D((A')*) and

(XI - (Ao)*)u = v. (3.2.19)

130 Dissipative Operators and Applications

This proves that (Al -(A' )*)D((A')*) = E. In view of (3.2.18), if we could

prove that Al -(A' )* is one-to-one, it would follow that A belongs to

p((A')*) and that

IIR(A)II<X

(A>0),

(3.2.20)

in other words, that (A' )* is m-dissipative. In order to do this we need more

precise information about (A' )* and its domain. This information is

contained in the following result, where no use is made of the dissipativity

of A0 or A'; however, we assume from now on that

a(x)>0 (-oo<x<oo).

(3.2.21)

3.2.5

Lemma.

(a) Let f be a function that belongs to Lf.., in an open

interval 0, 1 < p < oo. Let u be a locally summable function that satisfies

au"+bu'+cu= f (3.2.22)

in the sense of distributions, that is,

f uAogi dx = f f qq dx

(qp E

(Q))

Then u coincides with a function in W1

' and satisfies (3.2.22) almost

everywhere. If f is continuous, then u coincides with a twice continuously

differentiable function in Q. (b) Let v be a locally finite Borel measure in 2,

and assume that a locally finite Borel measure µ satisfies

ap"+ bµ'+ c,s = v (3.2.23)

in the sense of distributions, that is,

f gpdv

(T E=- 6D (Q)).

Then µ coincides with a continuous function in R.

The proof depends upon solving (3.2.22) by means of the usual

" variation of constants" formula (Coddington [ 1961: 1, p. 68]). In fact, if u1

and u2 are two linearly independent solutions of the homogeneous equation

au"+ bu'+ cu = 0 and W(i) = W(u1, u2; ) is their Wronskian, let G(x, E)

_ (u1()u2(x)- u1(x)u2(E))/W(E). Then (3.2.22) has a solution v given by

v(x) = f .G(x, E)f(E)

where x0 is an arbitrary fixed point in Q. Since G is twice continuously

differentiable in x and G(x, x) = 0, then v belongs to W1a if f belongs to

L fem. If u is the solution of (3.2.22) postulated in (a), then u - v satisfies the

homogeneous equation in the sense of distributions (f (u - v)Aop dx = 0 for

all q) e 6D) and (a) will follow if we can prove that u - v must coincide with

an ordinary solution of the homogeneous equation. For a proof of this, see

Dunford-Schwartz [1963: 1, p.

1291]; although infinitely differentiable

3.2. Ordinary Differential Operators in the Whole Line

131

coefficients are required there, the argument can be easily extended.

In case (b) we take

v(x) f xG(x, )µ(df),

which is immediately seen to be continuous, and argue as in (a).

Lemma 3.2.6 allows us to identify readily the adjoint of A'; u E

D((A')*) if and only if u E W1a (- oo, cc)f1 LP(- oo, oo) and (Ao)*u =

au" + bu'+ Cu E LP( - oo, oo). The converse part of this assertion follows

from Lemma 3.2.6, while the direct half is obtained integrating by parts.

In order to study the uniqueness of the solution of (3.2.19) a further

result is needed.

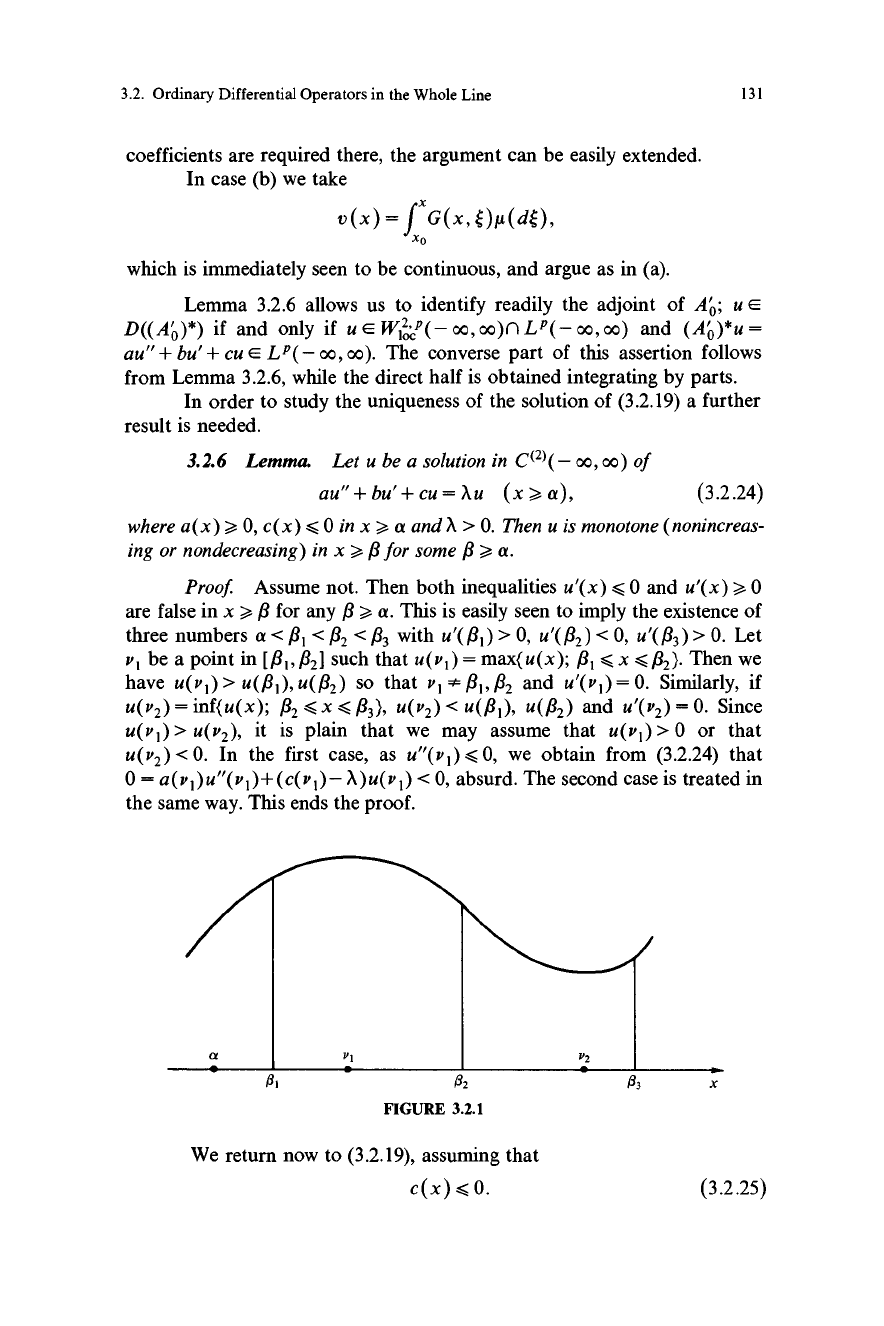
3.2.6 Lemma. Let u be a solution in C(2)(- 00, 00) of

au"+bu'+cu=Xu (x>a), (3.2.24)

where a(x) > 0, c(x) < 0 in x > a and X > 0. Then u is monotone (nonincreas-

ing or nondecreasing) in x > $ for some / > a.

Proof Assume not. Then both inequalities u'(x) < 0 and u'(x) > 0

are false in x > Q for any Q > a. This is easily seen to imply the existence of

three numbers a < #, <

N2 < $3

with u'(/31) > 0, u'(fl2) < 0, u'($3) > 0. Let

v, be a point in [/31,$21 such that u(v1)= max(u(x); ,B, <x <$2). Then we

have u(v1) > u($,), u($2) so that v, -

R1,

x(32 and u'(v1) = 0. Similarly, if

u(v2) = inf(u(x); $2 < x < R3), u(v2) < u($1), u($2) and u'(v2) = 0. Since

U(PI) > u (v2 ), it is plain that we may assume that u(PI) > 0 or that

u(v2) < 0. In the first case, as u"(v 1) < 0, we obtain from (3.2.24) that

0 = a(v1)u"(v,)+(c(v1)- X)u(v1) < 0, absurd. The second case is treated in

the same way. This ends the proof.

We return now to (3.2.19), assuming that

c(x) <0.

(3.2.25)

132

Dissipative Operators and Applications

If u,, u2 are two solutions of (3.2.19) in LP, u = u, - u2 satisfies (Ao)*u = Au.

Making use of Lemma 3.2.5, we see that u is twice continuously differentia-

ble and satisfies the equation

au" + bu' + cu = Au

(3.2.26)

in (- oo, oo). It follows from Lemma 3.2.6 applied to the real and imaginary

parts of u(x) and u( - x) that they are monotonic for large Ixl; since u

belongs to LP, this can only be possible if

lim Iu(x)I = 0,

lXI -i 00

which shows that u belongs to the domain of the operator Ao in Co. We

obtain then from (3.2.26), from the fact that A0 is dissipative in C. and from

inequality (3.1.9) that u = 0. This completes the proof that (A')* is m-

dissipative in LP.

We examine next the case E = Co(- oo, oo), under assumptions

(3.2.21) and (3.2.25). By Lemma 3.2.1 these conditions imply dissipativity of

A0 in Co. Our first concern is to show that A0 (with D(A0) defined as in

Lemma 3.2.1) is closed. In order to do this we consider the operator Ao in

L', with domain 6D. Its adjoint (A')* is a closed operator in L°° and it is not

difficult to see with the help of Lemma 3.2.5(a) that A0 is just the restriction

of (A' )* to the space of all u E D((A0)*)fl Co such that (A' )*u E Co and is

therefore closed.

We are forced to assume now that Ao is dissipative in LP' for some

P'> 1. In view of the comments following (3.2.16), it suffices to assume that

the second inequality (3.2.8) holds for some p > 1.

Let v be an element of Co with compact support. We can employ the

argument previously used in the LP case to produce a solution of (3.2.19)

with A = 1. By Lemma 3.2.5 u must then belong to C(2) and satisfy the

homogeneous equation (3.2.26) for

I x I

large enough, and it follows once

again that Iu(x)I -' 0 as I x I - oo. Hence u E D(A0) and satisfies

(I-A0)u=v. (3.2.27)

If v is an arbitrary element of CO, we take a sequence (vn) in Co such that

the v,, have compact support and converge to v in Co. If u,, is the solution of

(I - A0)un = vn constructed in the previous comments, we obtain from

dissipativity of A0 in Co that

Ilun-umlis1I(I-Ao)(un-um)ll-Ilvn-vml1

so that (un) is convergent to some u E CO; since A0 is closed, u E D(A0) and

(3.2.27) holds. It follows then that A0 is m-dissipative.

We have proved parts (a) and (b) of the following result.

3.2.7 Theorem. (a) Let the coefficients of the operator A0 satisfy

a(x)>0, c(x)<0 (-oo<x<oo) (3.2.28)

and assume Ao is dissipative in LP' for some p'> 1 (for which a sufficient

3.2. Ordinary Differential Operators in the Whole Line 133

condition is

c(x)+ p(a"(x)-b'(x))<0 (-oo<x<oo) (3.2.29)

for some p > 1). Let A be the operator defined by

Au(x) = a(x)u"(x)+b(x)u'(x)+c(x)u(x),

(3.2.30)

where D(A) is the set of all u E C(2) fl Co such that (3.2.30) belongs to Co.

Then A is m-dissipative in Co.

(b) Let 1 < p < oo. Assume inequalities (3.2.28) hold, and suppose A'0

is dissipative in

LP,

(for which (3.2.29) is a sufficient condition). Let A be the

operator defined by (3.2.30), where D(A) is the set of all u E Wi' fl LP such

that the right-hand side belongs to LP. Then A is m-dissipative in LP.

a"(x)-b'(x)+c(x) <0 (-oo <x <oo).

(3.2.31)

Then the operator A defined as in (b) with p =1 is m-dissipative in L'.

Part (c) follows from (a) through an application of the duality theory

in Section 2.2. In fact, the assumptions on the coefficients of A0 are

equivalent to

a(x)>O, c(x) <0, a"(x)-b'(x)+c(x) <0

(3.2.32)

in (- no, oo). Adding the second inequality to the third, we obtain a"(x)-

b'(x)+2c(x) < 0; hence we are within the assumptions in (a) and the

operator Ao (with the domain corresponding to the space Co) is m-dissipa-

tive in Co. We apply now Theorem 2.2.11; in order to do this we have to

identify Co = D((A')*) c C0* = E(- no, oo) (see Section 7) and the operator

(A')#. Assume µ E E= Co belongs to the domain of (A')*. Then there

exists v E E such that

f Aorp(x)µ(dx) = f 9,(x)v(dx)

for all test functions 4p E'l

It follows from Lemma 3.2.5(b) that µ(dx) _

u(x) dx, where u is a continuous function in R. Hence any element of

D((A')*) must be a continuous function. Conversely, it is obvious that if u

belongs to 6D, then u E D((A')*) (and (Ao)*u = Aou). Accordingly, the

closure of D((A' )*) in the topology of E must be L' (recall that if

µ(dx) = u(x) dx, then IIµIIE = IIull1). We have then shown that

E#=L'.

The operator (A')# (which is obviously an extension of AO) must be

m-dissipative in L'. A precise characterization of (A')' can now be

obtained. By definition of the #-adjoint and by Lemma 3.2.5, every

u E D((A' ) #) must belong to the domain of the operator A defined in (c)

134

Dissipative Operators and Applications

and satisfy (Ao)#u = Au; in other words,

(A')# C A.

Take now uo E D(A); since (A')# is m-dissipative there exists u, E

D((A0)#) c D(A) with (I - A)u, _ (I -(A' )#)u1 = (I - A) uo. Then u =

u, - uo is a solution of (3.2.26) with X = 1. It follows from Lemma 3.2.5 that

u E 02) and from Lemma 3.2.6 that u, being in L', must belong to CO, a

fortiori to D(Ao) in Co. But the hypotheses in (c) imply that A0 is

dissipative in CO, hence u = 0. We have then shown that (A')# = A and in

this way completed the proof of Theorem 3.2.7.

We note that in (a) it is sufficient to assume that Ao - cI is dissipa-

tive in LP' for some c: we only have to take A sufficiently large in (3.2.19)

(see also Remark 3.4.4)

Some additional information on the operators A in Theorem 3.2.8

can be gleaned under supplementary hypotheses by making further use of

the duality theory in Section 4. In fact, let p > 1 and let A 0 satisfy the

assumptions in (c). It is plain that A0 satisfies the hypotheses in (b) as an

operator in LP and Ao satisfies the same hypotheses in Li'. Applying

Theorem 3.2.7, we see that (A' )* is a m-dissipative extension of A0 in LP

and Ao is a m-dissipative extension of Ao in LP'. However, it follows from

Theorem 3.1.14 that A** is also m-dissipative, and, since Ao D Ao,

Ao = Ao* C (Ao)*.

Since p(Ao*)f1 p((A')*) is not empty (both resolvent sets must contain the

half plane Re X > 0), an argument similar to the one closing the proof of

Lemma 2.3.9 shows that

A= (A' )* = Ao. (3.2.33)

We note finally the particularly interesting case where A 0 is formally

self-adjoint,

Aou = (au')'+ cu, (3.2.34)

where the hypotheses in any of the three cases in Theorem 3.2.7 (hence also

the ones leading to (3.2.33)) reduce to

a(x) > 0,

c(x) < 0.

It is easy to check that throughout all the theory in this section we

have not actually used the fact that a (=- C(2) and b E C0), but only that

a (=- C(') and a'- b E 0). Because of this, it is perhaps more convenient to

write A

in variational form,

A0 = (au')'+ bu'+ cu (3.2.35)

with the requirement that a, b (=- 0), c E Coo). The whole theory unfolds in

the same way with some simplifications in the writing of adjoints and

dissipativity conditions.

3.2. Ordinary Differential Operators in the Whole Line

135

3.2.8 Example.

The dissipativity condition (3.2.2) in Co has the same

form for (3.2.35) as for (3.2.1). The dissipativity conditions (3.2.8) in LP,

1 < p < oo, become

a(x)>,0, c(x)-

6(x)<0 (-oo<x<oo). (3.2.36)

3.2.9

Example. Let A = Ap be the operator in LP defined in Theorem

3.2.7(b). Denote by A' the operators corresponding to the formal adjoint

A'. Then

A;,=Ap (1<p<00)

(3.2.37)

with p'-' + p -' =1. (We adopt here the hypotheses in (c)).

3.3. ORDINARY DIFFERENTIAL OPERATORS IN

A CLOSED INTERVAL. SEMI-INFINITE INTERVALS

We examine here the operator A0 in a semi-infinite closed interval, which we

may assume without loss of generality to be [0, oo). The treatment makes use

essentially of the same technical tools employed in the previous section. The

main novelty is that, in order to obtain a domain where the operator is

m-dissipative, we will be forced to impose a boundary condition at the left

endpoint.

We assume for the coefficients a, b, c the same degree of smoothness

as in the previous section; a is twice continuously differentiable, b is

continuously differentiable, and c is continuous in x >, 0.

The boundary condition at the origin will be of one of the following

two forms:

(I)

u'(0) = yu(0) (3.3.1)

(where y is an arbitrary real number) or

(II)

u(0) = 0. (3.3.2)

We begin by considering spaces of continuous functions. If the boundary

condition is of type (I), the space is E = Co[0, oo) (which consists of all

continuous functions in x >, 0 with lim,,.. Iu(x) I = 0). When the boundary

condition is (3.3.2), however, the use of the same space will prevent the

domain of our differential operator from being dense in E. We use instead

E = Co,o[0, oo), that is, we require all the functions in the space to satisfy the

boundary condition (II). (See Section 7).2

Let $ denote one of the boundary conditions (3.3.1) or (3.3.2). The

operator Ao($) is defined by

A0($)u(x) = a(x)u"(x)+b(x)u'(x)+c(x)u(x),

(3.3.3)

2Following strictly the notational conventions of Section 7 the correct notation would

be Co.(o). We shall ignore, here and in other places, the distinction.

136

Dissipative Operators and Applications

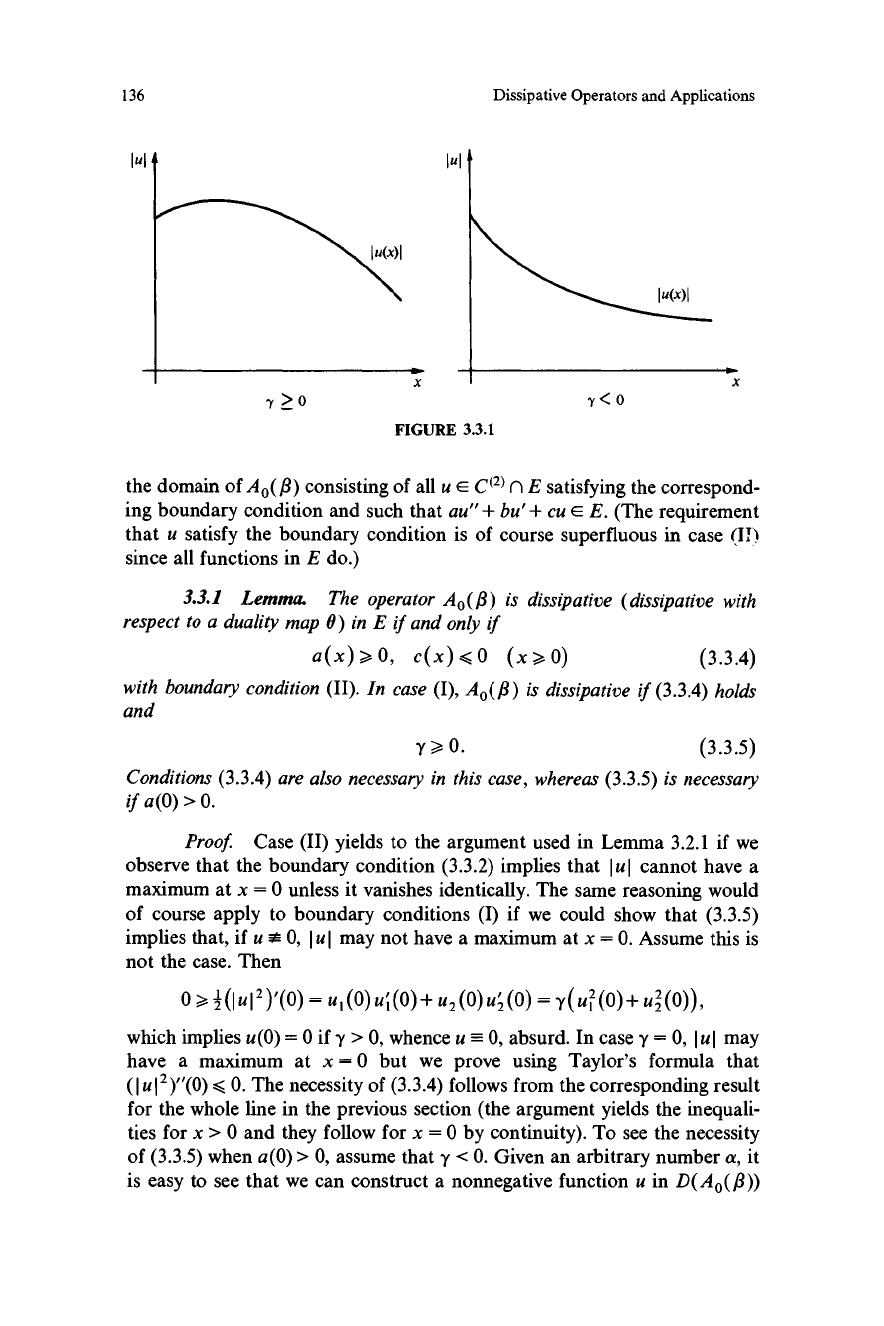
lul

y>0

y<0

FIGURE 3.3.1

the domain of A0(/3) consisting of all u E C(2) n E satisfying the correspond-

ing boundary condition and such that au" + bu' + cu E E. (The requirement

that u satisfy the boundary condition is of course superfluous in case (IT)

since all functions in E do.)

3.3.1

Lemma.

The operator A0(/3) is dissipative (dissipative with

respect to a duality map 0) in E if and only if

a(x) >, 0,

c(x) < 0

(x >_ 0)

(3.3.4)

with boundary condition (II). In case (I), A0(/3) is dissipative if (3.3.4) holds

and

Y>, 0. (3.3.5)

Conditions (3.3.4) are also necessary in this case, whereas (3.3.5) is necessary

if a(0) > 0.

Proof.

Case (II) yields to the argument used in Lemma 3.2.1 if we

observe that the boundary condition (3.3.2) implies that

I u I cannot have a

maximum at x = 0 unless it vanishes identically. The same reasoning would

of course apply to boundary conditions (I) if we could show that (3.3.5)

implies that, if u E0 0,

1 u I may not have a maximum at x = 0. Assume this is

not the case. Then

0 %

(luI2)'(0) = u1(0)ui(0)+ u2(0)u2(0) = Y(u1(0)+ u2(0)),

which implies u (0) = 0 if y > 0, whence u = 0, absurd. In case y = 0,

1 u I may

have a maximum at x = 0 but we prove using Taylor's formula that

(I u 2)"(0) S 0. The necessity of (3.3.4) follows from the corresponding result

for the whole line in the previous section (the argument yields the inequali-

ties for x > 0 and they follow for x = 0 by continuity). To see the necessity

of (3.3.5) when a(0) > 0, assume that y < 0. Given an arbitrary number a, it

is easy to see that we can construct a nonnegative function u in D(Ao(/l3))