Fattorini H.O., Kerber A. The Cauchy Problem

Подождите немного. Документ загружается.

Chapter 3

Dissipative Operators and Applications

If we restrict our attention to equations u'(t) = Au(t) having solutions

whose norm does not increase with time, the theory of the Cauchy

problem in Chapter 2 becomes simpler and more incisive. The result-

ing theory of dissipative operators is treated in Sections 3.1 and 3.6,

with applications to second order ordinary differential operators and

to symmetric hyperbolic operators in the rest of the chapter.

Section 3.7 develops a theory whose main application is to

study partial differential (and more general) equations that possess the

property of conserving nonnegative solutions.

3.1.

DISSIPATIVE OPERATORS

As pointed out in Section 2.1, direct application of Theorem 2.1.1 is in

general difficult, since it involves verification of the infinite set of inequali-

ties (2.1.11), or at least of their "real" counterparts (2.1.29). When C = 1,

however, only the first inequality needs to be checked. Since A - wI E @ (1, 0)

if and only if A E (2 (1, w) (this can be seen observing that solutions of

u' = Au are mapped into solutions of v' = (A - wI )v through v(t) =

e - "tu(t)), we may restrict ourselves to the case w = 0. We state the resulting

particular case of Theorem 2.1.1.

117

118

Dissipative Operators and Applications

3.1.1 Theorem.

The closed, densely defined operator A belongs to

(2+(1,0) if and only if (0, oo) c-p(A) and

IIR(X)II<1/A (A>0).

(3.1.1)

We note that the solution operator S(.) of

u'(t) = Au(t) (3.1.2)

satisfies

IIS(t)II<l

(t>10).

(3.1.3)

The semigroup S(.) is called a contraction semigroup. If (3.1.2) is a model

for a physical system and 11.11 measures, say, the energy of the states, then

(3.1.3) means that as a state evolutions in time, its energy decreases (or at

least, does not increase). This situation is of course common in practice.

The result corresponding to the Cauchy problem in (- no, oo) is

3.1.2 Theorem.

The closed, densely defined operator A belongs to

(2(1,0) if and only if (- oo,0)U(0, oo) c p(A), and, for A real,

IIR(A)II <l/IAI

(A *0).

(3.1.4)

Note that in the case covered by Theorem 3.1.1, a(A) must be

contained in the left half plane Re A < 0, whereas if A satisfies the hypothe-

ses of Theorem 3.1.2, a(A) is a subset of the imaginary axis.

Theorem 3.1.1 can be cast in a considerably more convenient (and

intuitive) form by using the notion of dissipative operator, which we define

below after some preparatory work.

For u e E define the duality set of u as

O(u) = {u* E E*; Ilu*112

= IIu112 = (u*, u)).

Clearly 0(0) = (0). It follows from the material in Section 2 (Corollary 2.3)

that 0(u) is nonempty for all u. It is also true that each 0(u) is a closed

convex set. Closedness is immediate. On the other hand, let ui , u2 E O(u)

and u* = au* +(1- a)u** with 0 < a < 1. Then (u*, u) = IIu112, while Ilu*II <

(lull. It follows that Ilu*II = (lull and thus that u* E 0(u).

3.1.3 Example.

Let E* be strictly convex (llu*+ v*ll <2 if 11011 =11v*11

1, u* - v*). Then 0 is single-valued.

3.1.4

Example.

Assume in addition that E* is uniformly convex (if (u*),

(v,*) are such that Ilu*ll = Ilvn ll = 1, Ilu* + v,*11-, 2 implies IIu - v, II -+ 0).

Then O is continuous.

3.1.5

Example. Assume there exists a map 9: E -* E* such that 9(u) E

O(u) and 9 is conjugate linear (0(Au*+µv*)=A9(u*)+µ9(v*) for u*,v*

E E* and complex A, it). Then E is a Hilbert space. (Hint:

Define

2(u, v) = (0(v), u) + (9(u), v).) The converse is of course true.

3.1. Dissipative Operators

119

3.1.6

Example.

Let 2 be a Borel subset of Euclidean space, and let

E = LP(2) (1 <p <oo). Then:

(a) If 1 < p < oo, 0 is single-valued and, if u - 0,

0(u)(x) = II

uIIP-PIu(x)IP-zu(x)

(where we make the convention that Iu(x)IP-2u(x) if

u(x) = 0).

(b) If p = 1, u :s- 0, 0(u) consists of all u* E L°°(SZ) with

u*(x) = IIuII1(u(x)I -'u(x) (u(x) - 0),

lu*(x)I < Ilulli a.e.

(u(x)=O).

FIGURE 3.1.1

3.1.7

Example. (a) Let K be a compact subset of Euclidean space R m,

and let E = C(K) (Section 7). If u e C(K), let

m(u) = (x E K; I u(x)I

= IIuhI).

Then m (u) is nonempty and E )(u) consists of all measures p E E(K )

supported by m(u) and such that

f u(x) t(dx)>0

for every Borel set e E m(u) (i.e., such that u(x)p(dx) is a positive measure)

and

f JAI(dx)

= Ilull.

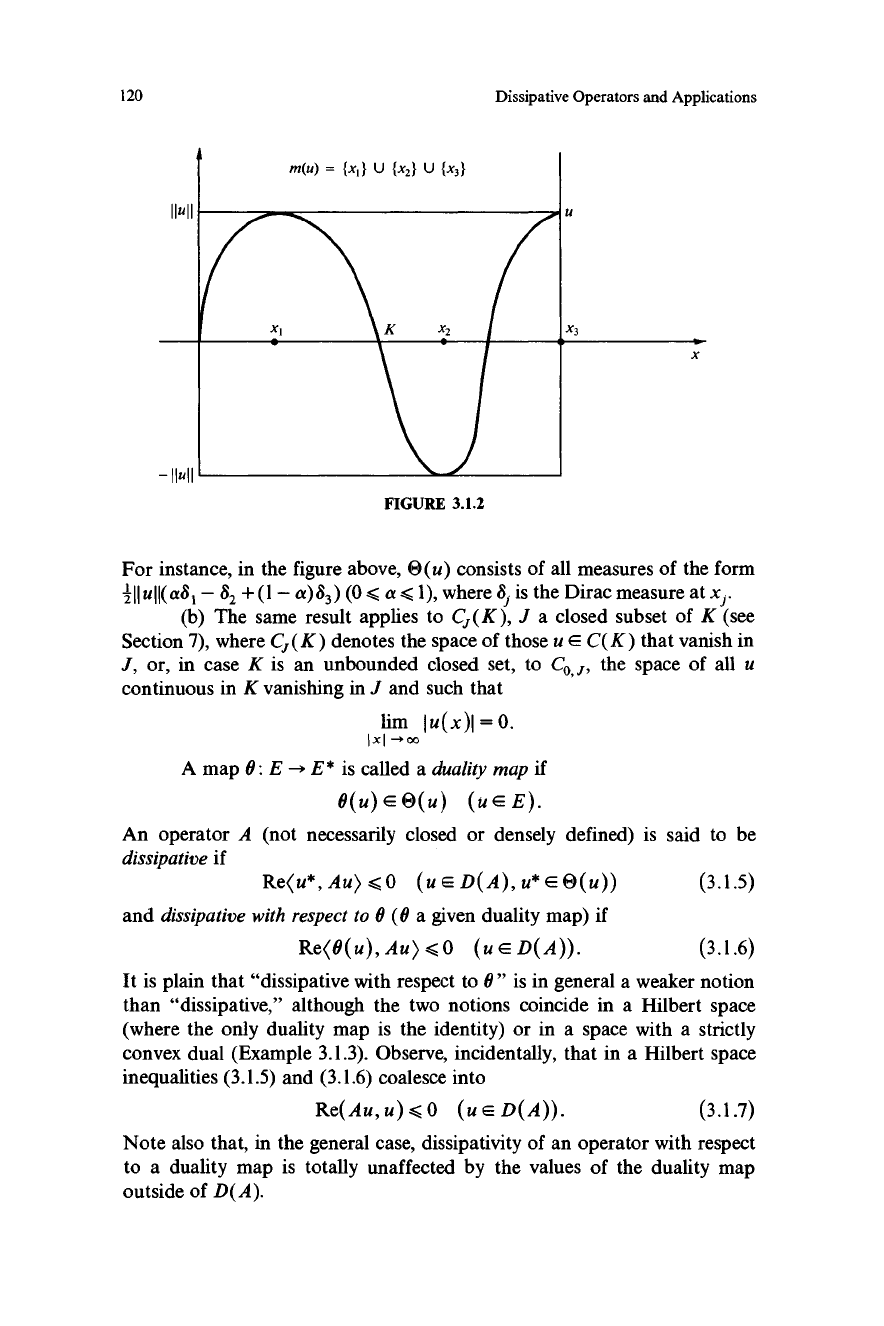
120

Dissipative Operators and Applications

m(u) = {X1} U {X2} U {x3}

-hull

FIGURE 3.1.2

For instance, in the figure above, O(u) consists of all measures of the form

i I I u I I(aS t - S2 + (1- a)83) (0 < a < 1), where Sj is the Dirac measure at xj.

(b) The same result applies to Cj(K), J a closed subset of K (see

Section 7), where C1(K) denotes the space of those u E C(K) that vanish in

J, or, in case K is an unbounded closed set, to Co, j, the space of all u

continuous in K vanishing in J and such that

lim

I u(x)I = 0.

1xI--ao

A map 0: E -* E* is called a duality map if

0(u) E O(u)

(u E E).

An operator A (not necessarily closed or densely defined) is said to be

dissipative if

Re(u*, Au) <O (u E D(A), u* E ©(u))

(3.1.5)

and dissipative with respect to 0 (0 a given duality map) if

Re(0(u), Au) <0 (u E D(A)). (3.1.6)

It is plain that "dissipative with respect to 0" is in general a weaker notion

than "dissipative," although the two notions coincide in a Hilbert space

(where the only duality map is the identity) or in a space with a strictly

convex dual (Example 3.1.3). Observe, incidentally, that in a Hilbert space

inequalities (3.1.5) and (3.1.6) coalesce into

Re(Au, u) < 0

(u E D(A)). (3.1.7)

Note also that, in the general case, dissipativity of an operator with respect

to a duality map is totally unaffected by the values of the duality map

outside of D(A).

3.1. Dissipative Operators

121

Before considering examples of dissipative operators we justify their

introduction in the context of the Cauchy problem.

3.1.8

Theorem.

Let A E C2+(1,0). Then A is dissipative and

(AI - A)D(A) = E (A> 0). (3.1.8)

Conversely, let A be densely defined, dissipative with respect to some duality

map 0, and let (3.1.8) be satisfied for some A0 > 0. Then A E (2+(1,0).

Proof.

Let A E e+(1,0), S the evolution operator of (3.1.2), u E

D(A), u* E O(u). We have

hence

Re(u*, S(h)u) < Ilu*II IIS(h)II Ilull < IIu112

(h > 0),

Re(u*,

h(S(h)u-u))=ReI (u*,S(h)u)-

IIIUI12<0.

Letting h - 0, inequality (3.1.5) follows. That (3.1.8) holds is evident, since

every positive A must belong to p(A).

To prove the converse, let A > 0 and u E D(A). Write

Then

v=Au - Au.

(0(u), v) = A(0(u), u) - (0(u), Au)

so that in view of (3.1.6),

AIIUII2 =A(0(u), U) =ReA(0(u), u)

<Re(0(u), v) < I10(u)II Ilvll

= (lull Ilvll

If u - 0, it follows that Allull < Ilvll (the inequality is obviously true if u = 0).

Hence

Ilull < XII(AI- A)uhl

(u E D(A)). (3.1.9)

Inequality (3.1.9) plainly implies that (Al - A) - ' exists and is a bounded

operator, although it does not follow that (Al - A) -' is everywhere defined.

(We do not yet know that (Al -A) D(A) = E.) However, since (3.1.8) is

assumed to hold for A = A0, it results that (A0I - A)-' is everywhere

defined, then A0 E p(A) and IIR(A0)II < 1/A0. By virtue of the results in

Section 3, R(A) must then exist in IA - A0I < A0, and, again because of

(3.1.9),

I I R (A )I I <1/A there; making use of the same argument for A, =

3A0/2, A2 = 5A0/2,..., we see that R(A) exists for every A > 0 and satisfies

IIR(A)ll < 1/A

(A > 0),

which places A under the hypotheses of Theorem 3.1.1. This completes the

proof of Theorem 3.1.8.

The result corresponding to the Cauchy problem in (-

oo, oo) is

3.1.9 Theorem.

Let A E (2 (1, 0). Then

Re(u*, Au) = 0

(u E D(A), u* E O(u))

(3.1.10)

122

Dissipative Operators and Applications

and (3.1.8) holds for all real X, A - 0. Conversely, assume that A is densely

defined, that (3.1.10) is satisfied, and that (3.1.8) holds for some A0 > 0 as well

as for some AI < 0. Then A E e(1,0).

The proof follows immediately from Theorem 3.1.8 and from the fact

(already used in the previous chapter) that A E e (C, w) if and only if

A, - A E C'+(C, w). We note that the fact that llS(t)ll < 1 in - oo < t < oo

actually implies that each S(t) is an isometry:

IIS(t)ull =1Iull

(-oo<t<cc).

(3.1.11)

In fact, if (3.1.11) is false for some u E E and some to, we would have

(lull = IIS(- t0)S(t0)ull < IIS(to)ull < Ilull, which is a contradiction.

3.1.10

Example.

Let A E @+(C, (o). Then the space E can be renormed

(with a norm equivalent to the original one) in such a way that A E e+(1, co).

(Hint:

If w = 0, use IIuhl'= sup(IIS(t)ull; t >, 0)). The same result holds in

(2 (C, co).

In many of the future applications of Theorem 3.1.8, the operator A

will be at first defined in a set of smooth functions, where verification of

dissipativity usually reduces to integration by parts in one way of another.

However, equality 3.1.8 may not hold, and in order to remedy this it will be

necessary to extend the domain of definition of A; the crucial step is to

show that dissipativity is not lost in the extension. The following result will

be useful in this connection.

3.1.11

Lemma. Let A0 be densely defined and dissipative with re-

spectto a duality map 00: D(A0) - E*. Then (a) A0 is closable. (b) Let

A = A0. Then there exists a duality map 0: D(A) -* E* whose restriction to

D(A0) coincides

with

00 such that A is

dissipative

with respect

to 0.

Proof. We begin by observing that if is a sequence in D(A0)

such that u - u E E and such that

is E-weakly convergent to some

u* E E* (which can always be achieved by passing to a subsequence; see

Theorem 5.3),' then

Ilu*ll <

limllunll = 11U11-

On the other hand,

(u*, u) = lim(00(un),

limlIunll2

= Ilull2.

These two equalities imply that Ilu*Il = (lull and that u* E 8(u).

'Strictly speaking a subnet, unless E is separable (see Corollary 5.3). The same

observation applies to subsequent arguments.

3.1. Dissipative Operators

123

We prove first that A0 is closable. Assume this fails to be the case.

Then there exists a sequence such that u - 0, A0u - v * 0. Choose

u E D(A0) such that

Ilu - vll < Hull

(3.1.12)

and let ' be an arbitrary complex number. Making use of the considerations

at the beginning of the proof, we may assume that 00(u +

u* E 0 (u). Then

Re(u*, v) = limRe(0(u +

A0(u

S 0.

Since

is arbitrary, we must have

(u*, v) = 0. (3.1.13)

However (u*, v) = (u*, u) + (u*, v - u), which contradicts the previous

equality since, in view of (3.1.12), I (u*, v - u) I < Ilull2

Let A be the closure of A0. We extend 00 to D(A) as follows: if

u E D(A0), set 0(u) = 00(u); if u E D(A)\ D(A0), select a sequence

D(A0) such that u - u, A0u - Au and

is weakly convergent to

some u* in E*, and define 0(u) = u* (we have already noted that u* must

belong to 0(u)). Then

(0(u), Au) = lim(00(un), A0u ),

which plainly shows that A is dissipative with respect to 0. (The extension of

00 outside of D(A0) is of course far from unique in general.) This ends the

proof of Lemma 3.1.11.

For future reference, densely defined dissipative operators satisfying

(3.1.8) for some A > 0 (or, equivalently, operators in (2+(1,0)) will be called

m-dissipative.

3.1.12 Remark. Let A be a closed, densely defined dissipative operator. It

follows from the fundamental inequality (3.1.9) that (Al - A)D(A) is

closed. This shows that, in order to establish (3.1.8) we only have to prove

that (XI - A)D(A) is dense in E, that is,

XI - A D A = E. (3.1.14)

Condition (3.1.14) can be given yet another equivalent form. Clearly

(XI - A)D(A) fails to be dense in E if and only if there exists a u* E E*,

u* $ 0 such that

(u*, Au - Au) = 0 (u E D(A)). (3.1.15)

But (3.1.15) is in turn equivalent to: u* E D(A*) and

(XI-A*)u*=0 (3.1.16)

so that (3.1.8) holds if and only if the equation (3.1.16) has no nontrivial

solutions. A sufficient condition for this to happen is that A* itself be

124

Dissipative Operators and Applications

dissipative with respect to some duality map 0*: D(A*) - E**, for in this

case inequality (3.1.9) for A* shows that (3.1.16) implies u* = 0. Note that it

is not necessary here to require that D(A*) be dense in E*.

If A is not closed, the preceding remarks can be applied to its closure

(which exists because of Lemma 3.1.10). It follows that, if A. is densely

defined and dissipative and (AI - A0)D(A) is dense in E, then A = A0 is

m-dissipative, that is, A E e+(1,0).

3.1.13 Remark. In many applications (say, in the theory of the heat

equation) it is natural to consider spaces of real-valued rather than

complex-valued functions. Since the theory heretofore developed works in

complex spaces, we indicate how to fit real spaces in the complex theory.

Let E be a real Banach space. The complexification of E is the set Ec

("E (D iE ") of all pairs (u, v) (" u + iv ") of elements of E. Addition and

multiplication by complex scalars A _ + in are defined by (u v,)+

(u2, v2) = (u1 + u2, VI + v2) and rl)(u, v) =

rev, rlu + iv), whereas

the norm is any of the usual product norms. The following modifications to

the various results must be made.

Theorem

2.1.1. The statement is the same, except that inequalities (2.1.11)

are replaced by their real counterparts. Necessity is shown in the same way

(except that A > w is real). To prove sufficiency, we introduce an operator

A. in E. by

Ac (u, v) _ (Au, Av), (3.1.17)

with D(Ac) = D(A)X D(A); clearly Ac is densely defined in E. since A is

densely defined in E. If I (resp. Ic) is the identity operator in E (resp. Ec)

and A is real, then (XI, - Ac)(u, v) = ((Al - A)u,(AI - A)v), hence it

follows that p(A) = p(Ac)fR, R(1,; Ac)(u, v) _ (R(1\; A)u, R(1\; A)v)

and the real inequalities (2.1.29) for Ac follow from the corresponding

inequalities for A (with the same constants C, w). It follows then that

Ac E(2+(C,w) in Ec. Since

is a solution of u' (t)=

Au(t) if and only if u ( ), v(-) are solutions of u'(t) = A u(t ), we deduce

that A E C,(C, w) as well.

Lemma 2.3.5, Lemma 2.3.9, Theorem 3.1.1, Theorem 3.1.2.

Same state-

ments and proofs.

Theorem 2.2.1.

The statement and proof are the same, except that in-

equalities (2.2.3) are replaced by their real counterparts

IIR(µ)"II < C(IµI - w)-"

(IµI > w, n >,1).

(3.1.18)

Lemma 2.2.3, Theorem 2.2.9, Theorem 2.2.11, Theorem 2.3.1, Theorem

2.3.3. No change in statements or proofs.

Theorems 2.3.2, 2.3.4.

Statements and proofs are the same but inequalities

(2.3.13) and (2.3.15) are replaced by their real counterparts.

3.2. Ordinary Differential Operators in the Whole Line 125

In a real Banach space, an operator A is dissipative if

(u*, Au) <0 (uED(A), u*E8(u)) (3.1.19)

and dissipative with respect to 9 (6 a given duality map) if

(B(u), Au) < 0

(u E D(A)). (3.1.20)

Theorems 3.1.8, 3.1.9, Lemma 3.1.11.

Same statements and proofs.

In the future, we shall mostly (but not always) consider complex

spaces and leave it to the reader the formulation of the real counterparts of

subsequent results (whenever applicable); in most instances the complex

setting yields additional information.

We close this section with an observation about adjoints that is an

immediate consequence of Theorem 3.1.8 and of the duality theory in

Section 2.2, especially Theorems 2.2.9 and 2.2.11; the formulation and

proofs are identical in the real or the complex case.

3.1.14

Theorem.

Let A be m-dissipative in E. Then the Phillips

adjoint A# defined in Theorem 2.2.11 is m-dissipative in E#. If E is reflexive,

A* = A* is m-dissipative in E* = E#.

3.1.15

Example (Bishop-Phelps [1961: 1]; see also Ekeland [1979: 1]). If

E is an arbitrary Banach space, the set 0 = U{0(u); u e E} is dense in E*.

3.1.16 Example (James [1963: 11).

The Banach space E is reflexive if

and only if

0 = E*.

3.1.17 Example.

Check Theorem 3.1.8 for the operators in Example 2.2.7.

Check Theorem 3.1.9 for the operators in Examples 2.2.4 and 2.2.5.

3.2.

ORDINARY DIFFERENTIAL OPERATORS IN THE

WHOLE LINE

As an illustration of the theory in the preceding section, we examine the

ordinary differential operator

Aou(x) = a(x)u"(x)+b(x)u'(x)+c(x)u(x).

(3.2.1)

The coefficients a, b, c are real-valued. We shall consider A0 in the complex

spaces Lt, Co, c; although this is not always called for in applications, it will

yield important additional information about A0. Since all spaces under

consideration are complex, we eliminate the subscript C throughout.

Our standing assumptions on the coefficients a, b, c are: a is twice

continuously differentiable, b is continuously differentiable, c is continuous

in - oo < x < oo.

126

Dissipative Operators and Applications

We begin by considering the space E = Co(- oo, oo) and define

D(AQ) there as the set of all twice continuously differentiable u such that

Aou E Co.

3.2.1

Lemma. The operator A0 is dissipative (dissipative with re-

spect to a duality map 0) in Co if and only if

a(x)>,O, c(x)<O (-oo<x<oo).

(3.2.2)

Proof.

Let u E D(Ao), u 0,

m(u)_(xE9t; lu(x)l=1lu11).

(3.2.3)

We have already seen (Example 3.1.7) that 0(u) consists of all measures

µ E E supported by m(u), such that u(x) t(dx) is a positive measure in

m(u) and f l µ1(dx) = (lull. We have

(µ, Aou)

= f Aou(x)µ(dx)

M(U)

u(x)-'(a(x)u"(x)+b(x)u'(x)+c(x)u(x))u(x)µ(dx).

(3.2.4)

m(u)

Write u = ul + iu2 with u,, u2 real. Since

l u l2 = u + u2 reaches its maxi-

mum in m(u), we must have there 1(Iul2)"=

u1u'I' + u2u'2 + u12 + u' < 0. Accordingly, if x E m(u),

u-'u'=illull-2(u,u'-u;u2),

(3.2.5)

Ilull

2(uIu +u2u2)+illull

-2(u1u2-ui'u2),

(3.2.6)

where

u1u'1'+u2u2<-(ui2+u2 ).

(3.2.7)

Replacing (3.2.5) and (3.2.6) into (3.2.4) and making use of inequality

(3.2.7), we obtain

Re(µ, Aou) = <

-fU)

(Ilull -2a(x)lu'(x)12 - c(x))u(x) t(dx) < 0

if inequalities (3.2.2) hold. To prove the converse let x0, a, $ be three

arbitrary real numbers. If a > 0, /3 < 0 it is immediate that there exists a

nonnegative function u E D(A0) having a single maximum at x0 and such

that u(xo) = a, u"(xo) _ /3. Then 0(u) = (a8o), where So is the Dirac mea-

sure at x0. We have

(So, Aou) = a(xo)$ + c(xo)a.

If one of the conditions (3.2.2) fails to hold, it is clear that we can find a, /3

making (So, Aou) positive. This ends the proof of Lemma 3.2.1.

We consider next the operator A0 in the spaces E = LP(- cc, cc),

1 < p < cc. In this case the definition of D(A0) is not critical since A0 will