Фарзане Н.Г., Илясов Л.В. Технологические измерения и приборы
Подождите немного. Документ загружается.


51
погрешность, которая линейно возрастает (или убывает) с увеличением
измеряемой величины.
Графически появление мультипликативной погрешности
интерпретируется поворотом реальной функции преобразования относительно
номинальной (рис. 2.7, в). Если мультипликативная погрешность является
случайной, то реальная функция преобразования представляется полосой,
показанной на рис. 2.7, г. Причиной возникновения мультипликативной
погрешности обычно является изменение коэффициентов преобразования
отдельных элементов и узлов измерительных устройств.
На рис. 2.7, д показано взаимное расположение номинальной и реальной
функций преобразования измерительного устройства в случае, когда отличие
этих функций вызвано нелинейными эффектами. Если номинальная функция
преобразования линейная, то вызванную таким расположением реальной
функции преобразования систематическую погрешность называют
погрешностью линейности. Причинами данной погрешности могут быть
конструкция (схема) измерительного устройства и нелинейные искажения
функции преобразования, связанные с несовершенством технологии про-
изводства.
Наиболее существенной и трудноустранимой систематической
погрешностью измерительных устройств является погрешность гистерезиса
(от греч. hysteresis — запаздывание), или погрешность обратного хода,
выражающаяся в несовпадении реальной функции преобразования
измерительного устройства при увеличении (прямой ход) и уменьшении
(обратный ход) измеряемой величины (рис. 2.7, е). Причинами гистерезиса
являются: люфт и сухое трение в механических передающих элементах,
гистерезисный эффект в ферромагнитных материалах, внутреннее трение в
материалах пружин, явление упругого последействия в упругих
чувствительных элементах, явление поляризации в электрических,
пьезоэлектрических и электрохимических элементах и др. Существенным при
этом является тот факт, что форма получаемой петли реальной функции
преобразования зависит от предыстории, а именно от значения измеряемой
величины, при котором после постепенного увеличения последней начинается
ее уменьшение (на рис. 2.7, е это показано пунктирными линиями).
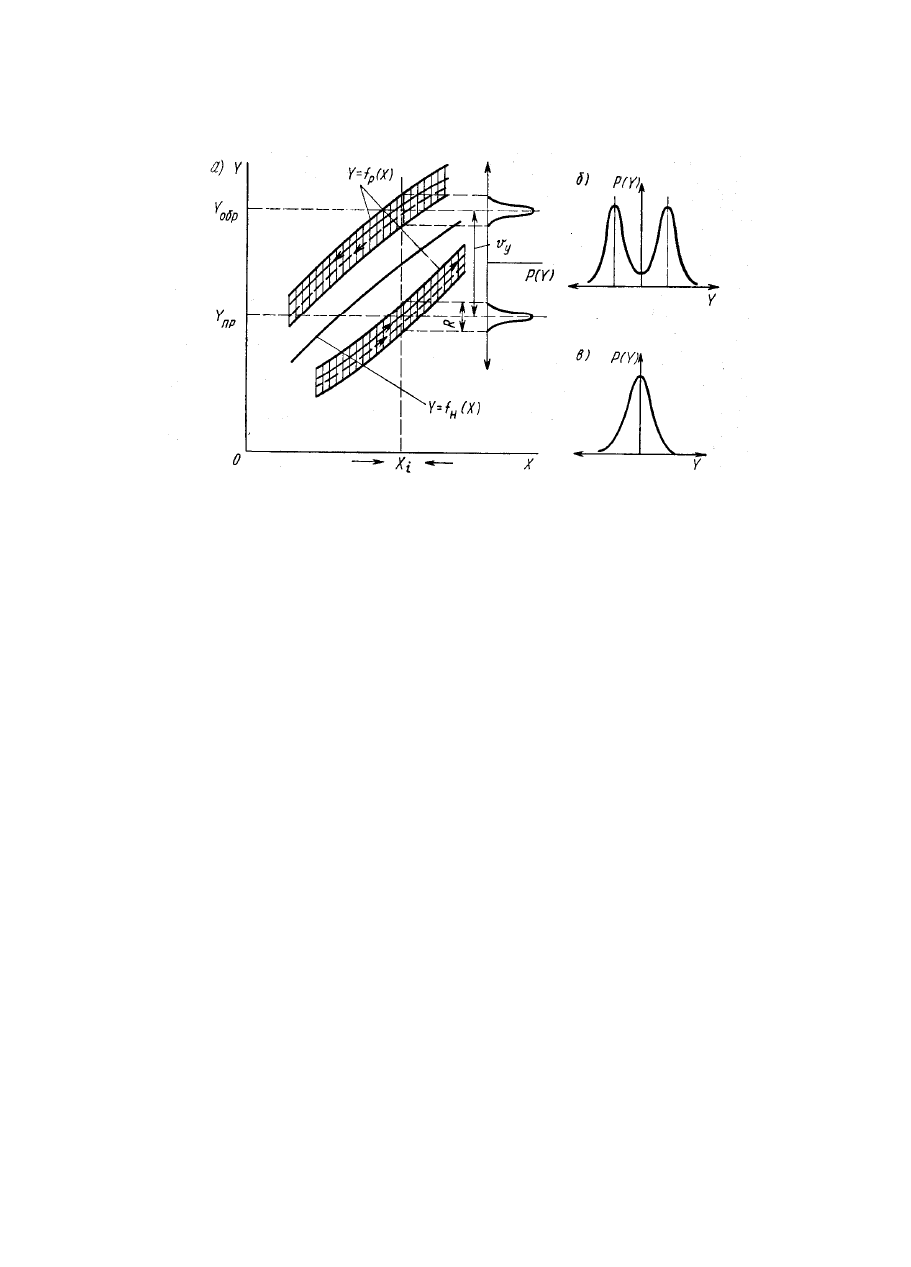
Для количественной оценки погрешности гистерезиса обратимся к рис.
2.8. Здесь показан фрагмент взаимного расположения реальной и номинальной
функций преобразования измерительного устройства, обладающего
погрешностью гистерезиса. Под действием влияющих величин реальная
функция преобразования изменяет свое расположение и форму. На рис. 2.8, а
для примера показаны два ее расположения, нанесенные сплошной и
пунктирной линиями. При нормальных условиях эксплуатации измерительного
устройства все изменения формы реальной функции преобразования не
выходят за пределы заштрихованных на рис. 2.8, а полос как для верхней, так и
для нижней ее ветвей. Если влияющие величины,
52
вызывающие изменения положения и формы функции преобразования, при
измерении не выявляются, то рассматриваемое явление определяется как
невоспроизводимость и характеризует случайную погрешность измерительного
устройства. При этом используют понятие «размах» и «вариация».
Рис. 2.8. Взаимное расположение реальной и номинальной функций пре-
образования измерительного устройства, обладающего погрешностью
гистерезиса
Размахом (непостоянством) 7? выходного сигнала измерительного
преобразователя (показаний измерительного прибора) называют разность
между наибольшим и наименьшим значениями выходного сигнала,
соответствующими одному и тому же значению измеряемой величины и
полученными при многократном и одностороннем подходе к этому значению,
т. е. при постепенном увеличении или уменьшении измеряемой величины
(только при прямом или только при обратном ходе).
Размах характеризует ширину заштрихованных на рис. 2.8, а полос,
определяющих случайную погрешность при значении измеряемого параметра,
равном XL
Вариацией v
y
выходного сигнала измерительного преобразователя
(показаний измерительного прибора) называют среднюю разность между
значениями выходного сигнала, соответствующими одному и тому же
значению измеряемой величины, полученными при многократном и
двустороннем подходе к этому значению, т. е. при постепенном увеличении и
последующем уменьшении измеряемой величины (иначе говоря, при прямом и
обратном ходе).
Как видно из рис. 2.8, а, при одном и том же значении измеряемой
величины X
i
закон распределения выходного сигнала измерительного

53
устройства при наличии вариации является двухмодальным. Если размахи для
нижней и верхней ветвей функции преобразования перекрываются, то закон
распределения выходного сигнала имеет вид, показанный на рис. 2.8, б. Формы
функций преобразования с законами распределения (рис. 2.8, а, б) являются
наиболее типичными для рабочих измерительных устройств, в том числе для
устройств, используемых при технологических измерениях., В частном случае
при отсутствии вариации закон распределения выходного сигнала является
одномодальным или нормальным (рис. 2.8,в).
Абсолютное значение вариации определяется для измерительных
приборов v
x
и преобразователей v
y
соответственно из выражений:
обрпрx
XX −=ν
(2.28)
обрпрy
YY
−
=
ν
(2.29)
где Х
пр
и Х
обр
— показания измерительного прибора при прямом и обратном
ходах;
Y
пр
и Y
обр
— выходной сигнал измерительного преобразователя при прямом и
обратном ходах.
Приведенное значение вариации обычно определяется для из-
мерительных приборов W
x
и преобразователей W
y
соответственно из
выражений:
100100
НВ
обрпр
НВ
x
x
XX
XX
XX
W
−
−
=
−
=
ν
(2.30)
100100
НВ
обрпр
НВ
y
x
YY
YY
YY
W
−
−
=
−
=
ν
(2.31)
т. е. определяется как отношение абсолютного
значения вариации к диапазону измерения по
входу или по выходу измерительного устройства.
Использование приведенных представлений
о номинальной и реальной функциях
преобразования позволяет наглядно отразить
изменения погрешностей измерительных устройств
под действием влияющих величин (рис. 2.9).
Предположим, что при эксплуатации некоторого
измерительного устройства в нормальных условиях
его реальная функция преобразования имеет вид
петлеобразной кривой 1, где заштрихованная

54
полоса определяет случайную погрешность, вызванную изменением влияющих
величин в допустимых нормальными условиями пределах. При этом обычно
для измерительного устройства устанавливается значение основной
погрешности. На рис. 2.9 это показано графически в виде полосы шириной ±Δ.
Если измерительное устройство эксплуатируется в рабочих условиях, когда
значение одной или нескольких влияющих величин выходит за пределы,
соответствующие значениям при нормальных условиях, функция преобразо-
вания выходит за установленное для данного измерительного устройства
значение полосы основной погрешности (петлеобразная кривая 2 на рис. 2.9), т.
е. появляется дополнительная погрешность.
§ 2.6. Нормирование метрологических характеристик измерительных
устройств
Все рассмотренные в § 2.3 — 2.5 характеристики измерительных
устройств принято называть метрологическими, так как они влияют на
точность осуществляемых с помощью этих устройств измерений.
Средства измерений, в том числе и измерительные устройства,
допускаются к применению только в том случае, если установлены нормы —
нормированы их метрологические характеристики. Сведения о последних
приводятся в технической документации на средства измерений.
Для удобства использования, анализа и нормирования метрологических
характеристик средств измерений их удобно классифицировать на группы,
приведенные в табл. 2.2.
Посредством нормирования метрологических характеристик
обеспечивается взаимозаменяемость средств измерений и единство измерений в
государственном масштабе. Реальные значения метрологических характеристик
средств измерений определяются при их изготовлении, а затем периодически
проверяются в процессе эксплуатации. При наличии отклонений хотя бы одной
нормированной метрологической характеристики от нормы средство измерений
регулируется, подвергается ремонту или бракуется и изымается из обращения.
Выбор нормируемых метрологических характеристик из числа
приведенных в табл. 2.2 зависит от вида средства измерений и осуществляется
в процессе разработки, освоения производства и аттестации средства
измерений данного типоразмера (см. § 2.9).
Общий подход при нормировании метрологических характеристик
состоит в том, что для всех нормируемых функций и значений устанавливаются
номинальные функции и номинальные значения и пределы допустимых
отклонений (например, номинальная функция преобразования, номинальная
функция влияния, номинальное значение информативного параметра на
выходе, номинальное значение постоянной времени и т. п.). Для остальных
характеристик

55
Таблица 2.2
Метрологические характеристики измерительных устройств
Группа
метрологических
характеристик
Метрологические характеристики
Характеристики,
предназначенные для
определения результата
измерений
Функция преобразования, коэффициент преобразования цена
деления, чувствительность, диапазон измерений, верхний и
нижний пределы измерений, диапазон показаний, конечное и
начальное значени
я шкалы
Характеристики
погрешности
Систематическая погрешность, случайная погрешность,
основная погрешность, динамическая погрешность, порог
чувствительности, мультипликативная погрешность,
аддитивная погрешность, погрешности линейности, вариация,
абсолютная, относительная и приведенная погрешности
Характеристики
чувствительности к
влияющим величинам
Функции влияния, дополнительная погрешность, изменение
показаний, изменение коэффициента изменение
коэффициента преобразований, значения неинформативного
параметра выходного сигнала
Динамические
характеристики
Дифференциальное уравнение, передаточная функция,
комплексная частотная функция, переходная характеристика,
импульсная переходная характеристика, амплитудно-фазовая
характеристика, постоянная времени, время реакции,
амплитудно-частотная характеристика, фазочастотная
характеристика, полоса пропускания и др.
Характеристики
взаимодействия с
подключаемыми
средствами измерения
Входной импеданс, выходной импеданс
устанавливаются пределы допустимых значений (например, пределы
допускаемой основной погрешности, пределы допускаемой вариации и т. п.).
Определенную специфику имеет нормирование характеристик,
определяющих точность измерений, выполняемых с помощью данного
средства измерений (основная и дополнительная погрешности, размах,
вариация).
Основная погрешность устройства для технологических измерений
нормируется путем установления предела допускаемой абсолютной,
относительной или приведенной погрешности:
a
±
=
∆
(2.32)

56
c
X
±=
∆
±
=
1000
δ
(2.33)
b
X
N
±=
∆
±
=
1000
γ
(2.34)
где X — входной сигнал измерительного устройства.
Нормирующее значение X
N
в выражении (2.34) принимают равным
диапазону измерений (для многих измерительных устройств, в том числе для
большинства устройств, используемых для технологических измерений),
конечному значению шкалы, длине шкалы, если последняя имеет резко
изменяющееся деление.
Способ задания пределов допускаемой основной погрешности для
измерительных приборов и преобразователей определяется зависимостью их
погрешности от значения измеряемой величины и требованиями простоты.
Если у измерительных устройств данного типоразмера после соответствующей
их регулировки погрешность практически не зависит от значения измеряемой
величины, т. е. является аддитивной, то предел допускаемой основной
погрешности нормируется абсолютной погрешностью, определяемой по
формуле (2.32), либо приведенной погрешностью, определяемой по формуле
(2.34).
Если погрешность измерительных устройств данного типоразмера
является мультипликативной и пропорциональна значению измеряемой
величины (
X
c
100
±=δ
) то предел допускаемой основной погрешности удобно
нормировать через относительную погрешность, определяемую по формуле
(2.33), так как норма определяется одним числом:
cX
X
c
±=±=
100
100
δ
(2.35)
Значение предела относительной или приведенной погрешности
определяется из ряда предпочтительных чисел:
[1; 1,5 (1,6); 2; 2,5 (3); 4; 5; 6] 10
n
(2.36)
Числа 1,6 и 3 допускаются к применению, но не рекомендуются. Значение
п принимается равным: +1, 0, –1, –2 и т. д. Причем при одном значении п
допускается устанавливать не более пяти различных пределов допускаемой
погрешности для измерительных устройств конкретного вида.
При нормировании основной погрешности учитывается тот факт, что
положение реальной функции преобразования в пределах полосы,
определяемой пределом допускаемой основной погрешности, изменяется (см.
рис. 2.8, а) за счет действия влияющих величин, что вызывает случайную
погрешность, определяемую размахом R. Обычно допускаемое значение
размаха принимается меньшим половины предела допускаемой погрешности:
∆
≤
5.0R
(2.37)

57
Для нормирования вариации измерительных устройств исполь-1 зуют
формулы (2.28), (2.29), (2.30) или (2.31), т. е. выражают ее абсолютным или
приведенным значением. Значение же предела допускаемой вариации
принимается в виде дольного (кратного) значения предела допускаемой
основной погрешности обычно из следующих соотношений:
∆÷= )5,10,1(
y
ν
(2.38)
γ
)5,10,1(
÷
=
y
W
(2.39)
Так как значение вариации всегда меньше удвоенного значения основной
погрешности, то для некоторых измерительных устройств вариация не
нормируется.
Дополнительная погрешность нормируется в тех случаях, когда при
измерении влияющих величин в рабочей области основная погрешность
превышает установленный для нее предел. Дополнительная погрешность
нормируется: в виде постоянного значения Δ
доп
для всей рабочей области
влияющей величины или по отдельным интервалам этой области; путем
указания отношения предела допускаемой дополнительной погрешности,
принятой для регламентируемого интервала влияющей величины, к значению
этого интервала, т. е. Δ
доп
/Δξ (Δξ — регламентируемый интервал влияющей
величины |); путем указания зависимости предела допускаемой дополнительной
погрешности от влияющей величины, т. е.
Δ
доп
= E(ξ)
Пределы допускаемой дополнительной погрешности, как правило,
устанавливают в виде дольного (кратного) значения предела допускаемой
основной погрешности.
Измерительные устройства принято разделять на классы точности.
В настоящее время класс точности Λ трактуется как обобщенная
характеристика средств измерений, определяемая пределами допускаемых
основной и дополнительной погрешностей, а также рядом других свойств,
влияющих на точность осуществляемых с их помощью измерений.
Связь между пределами основной и дополнительной погрешностей, а
также с другими свойствами средств измерений обычно регламентируется
соответствующими стандартами на отдельные виды средств измерений.
Классы точности не устанавливаются только для тех средств измерений,
для которых отдельно нормируется систематическая и случайная составляющие
погрешности, а также для средств измерений, для которых нормируется и имеет
существенное значение динамическая погрешность.
Обозначение классов точности Λ производится в зависимости от
способов задания пределов допускаемой основной погрешности. Если
последняя выражается приведенной (2.34) или относительной (2.33)
погрешностью, применяются соответственно следующие
58
обозначения: 1,5 и
1.5
(обозначения приведены для класса точности 1,5). В
рассмотренных (наиболее распространенных) случаях обозначение класса
точности дает информацию о пределе допускаемой основной погрешности.
Числовые значения для классов точности выбирают из приведенного ряда
(2.36).
Для измерительных приборов и преобразователей, применяемых для
технологических измерений, как правило, нормальные условия эксплуатации
выбирают такими, что в большинстве случаев исключается необходимость
нормирования дополнительной погрешности. Поэтому класс точности
однозначно определяет точность этих средств измерений.
§ 2.7. Структурные схемы и метрологические характеристики
измерительных систем
Для измерительных систем можно выделять некоторые общие
структурные схемы.
На рис. 2.10 показаны структурные схемы измерительных систем,
используемых для автоматического контроля, регулирования и управления
технологическими процессами. Измерительная система, построенная по схеме
2.10, а, обеспечивает одновременное измерение и регистрацию всех величин
объекта измерения, а измерительная система, построенная по схеме 2.10, б,—
поочередно измерение и регистрацию.
Измерительная информация в приведенных измерительных системах
формируется с помощью первичных измерительных преобразователей / и
посылается в виде сигналов в канал связи 4.
Рис. 2.10. Структурные схемы измерительных систем
В зависимости от типа измеряемой физической величины, принципа
действия первичного измерительного преобразователя и расстояния, на которое
необходимо передать информацию, в состав измерительной системы могут
быть включены помимо первичных измерительных преобразователей
промежуточный 2 (рис. 2.10, а) и передающий 3 измерительные
преобразователи. При этом измерительный преобразователь может
располагаться территориально около первичного или около прибора 5,
измеряющего сигнал, поступающий
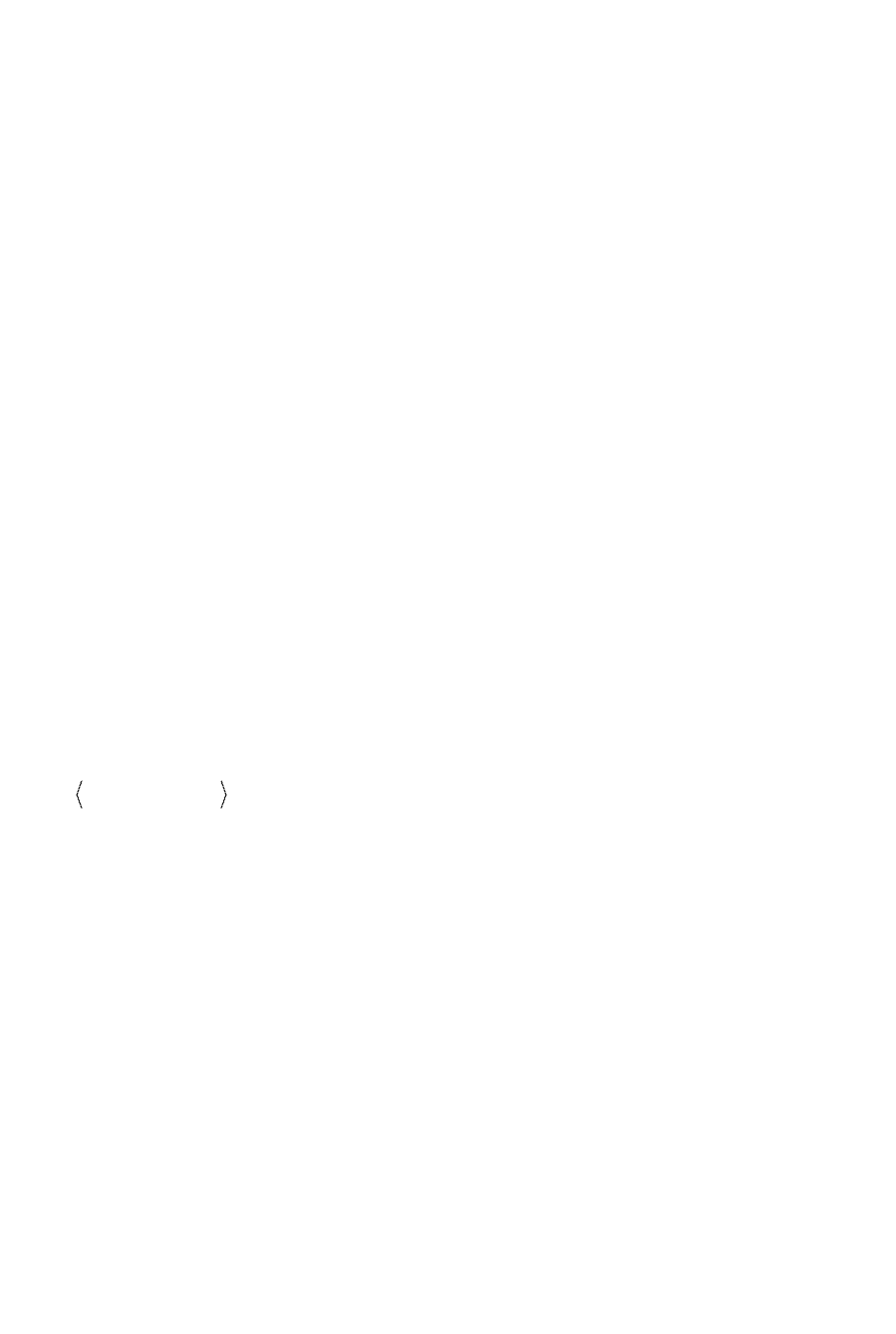
59
из канала связи, представляющего последний в форме, удобной для восприятия
человеком, и осуществляющего регистрацию. Измерительный прибор 5
называют вторичным прибором, считая при этом, что все измерительные
преобразователи, работающие с ним в комплекте, являются первичными
приборами.
В измерительной системе (рис. 2.10, б) с поочередным подключением
первичных измерительных преобразователей к прибору 5 применяется
коммутатор 6, который следует рассматривать как вспомогательное устройство.
Для простоты на рис. 2.10, б показана измерительная система, в составе
которой имеются только первичные измерительные преобразователи 1. В
общем случае в нее могут быть включены промежуточные и передающие
измерительные преобразователи. При этом выходные сигналы преобразова-
телей всех измеряемых величин в отличие от системы, построенной по схеме
рис. 2.10, а, должны быть одинаковыми по природе и диапазону измерений.
Последнее необходимо для обеспечения возможности их измерения и
регистрации одним и тем же прибором 5.
В структурных схемах рассмотренных измерительных систем можно
выделить цепочки, состоящие из измерительных преобразователей, каналов
связи и вторичных приборов. Если для каналов связи нормированы те же
характеристики, что и для измерительных преобразователей и приборов
измерительной системы, то можно рассматривать последнюю как
последовательное соединение нескольких преобразователей.
Функция преобразования измерительной системы через известные
функции преобразования отдельных преобразователей может быть в общем
случае записана в виде
[
]
{
}
)(...
123
XffffY
n
=
(2.40)
Если функции преобразования указанных преобразователей линейны,
функция преобразования измерительной системы имеет вид
XKY
n
i
i
=
∏
=1
(2.41)
где K
i
— коэффициент преобразования i-ro преобразователя.
Динамические свойства измерительной системы определяются
динамическими свойствами входящих в ее состав преобразователей. С позиций
теории автоматического регулирования измерительную систему можно
рассматривать как последовательное соединение ряда динамических звеньев.
Поэтому ее передаточную функцию можно представить произведением
передаточных функция
преобразователей:
)()(
1
pWpW
n
i
i∏
=
=
(2.41)

60
Для измерительных систем обычно нормируются те же метрологические
характеристики, что и для измерительных устройств. В то же время следует
подчеркнуть, что до сих пор не найдено теоретически обоснованное и
практически целесообразное решение задачи нормирования метрологических
характеристик измерительных систем.
При выполнении технологических измерений имеется лишь информация
о метрологических характеристиках измерительных устройств, входящих в
измерительную систему. Обычно эта информация представляется в виде класса
точности, что для измерительных устройств, используемых для
технологических измерений, соответствует пределу допускаемой приведенной
погрешности. Поэтому для приближенной оценки приведенной погрешности
измерительной системы из п включенных последовательно преобразователей с
линейными функциями преобразования используют выражение:
∑
=
=
n
i
i
1
γγ
(2.43)
где γ
i
— приведенная погрешность i-ro преобразователя.
Оценка погрешности измерительных систем, полученная с помощью
выражения (2.43), является максимальной, так как предполагает одновременное
появление максимальных погрешностей одного знака при любых значениях
измеряемой физической величины у всех измерительных преобразователей,
составляющих конкретную измерительную систему. Для получения более
реальной погрешности измерительных систем суммирование приведенных
погрешностей преобразователей осуществляется вероятностным методом, т. е.
используют выражение [6, 10]:
∑
=
=
n
i
i
1
2
γγ
(2.44)
При этом предполагается, что погрешности всех преобразователей
независимы, закон распределения погрешностей для каждого из
преобразователей является равномерным (см. рис. 1.9, а), а значение предела
допускаемой приведенной погрешности определяет границы этого
распределения. Если функции преобразования измерительных устройств,
входящих в измерительную систему, нелинейны, то для оценки ее приведенной
погрешности используют выражение
∑
=
=
n
i
ii
W
1
2
γγ
(2.45)
где W
i
— коэффициент влияния для i-ro преобразователя.
Определение коэффициентов влияния W, осуществляется так же, как и
при обработке результатов косвенных измерений (см. гл. 3).
