Farin G. Curves and Surfaces for CAGD. A Practical Guide
Подождите немного. Документ загружается.


4>12 Chapter 22 Coons Patches
n
The third building block, gi25 is simply the interpolating tensor product
surface
m n
The Gordon surface g now becomes
g = gi + g2-gi2- (22.13)
It is left as an exercise to verify that (22.13) in fact interpolates to all given
curves. Note that for the actual computation of g, we do not have to use the
Lagrange polynomials. We only have to be able to solve the univariate polynomial
interpolation problem, for example, by using the Vandermonde approach.
We have derived Gordon surfaces as based on polynomial interpolation. Much
more generality is available. Equation (22.13) is also true if we use interpolation
methods other than polynomial interpolation. The essence of (22.13) may be
stated as follows: take a univariate interpolation scheme, apply it to all curves
g(w, vj) and to all curves
g(M^,
t/), add the resulting two surfaces, and subtract
the tensor product interpolant that is defined by the univariate scheme. We
may replace polynomial interpolation by spline interpolation, in which case we
speak of spline-blended Gordon surfaces. The basis functions of the univariate
interpolation scheme are called blending functions,
22.8 Boolean Sums
Our development of Coons patches was quite straightforward, yet it is slightly
flawed from a geometric viewpoint. When we derived (22.3), we added the two
surfaces r^ and r^ as an intermediate step. This is illegal—the sum of two surfaces
would depend on the choice of a coordinate system (see the discussion in Section
2.1).
Although the situation is straightened out by subtracting the bilinear surface
r^^, one might ask for a cleaner development. It is provided by the use of Boolean
sums.
Let us define an operator V\ that, when applied to a rectangular surface x,
returns the ruled surface through
X(M,
0) and x(«, 1):
[Vxx\{u, v) = {\- v)x(u, 0) + vx(u, 1).

22.8 Boolean Sums 413
Similarly, we define Vi to return the ruled surface through x(0, v) and x(l, v):
[ViAiu, v) = {l- u)x(0, v) + wx(l, v).
In terms of Section 22.1, Pj and Vi yield the surfaces r^ and rj.
We would like to formulate the bilinearly blended Coons patch—which we
now call Px—in terms of Vi and Vi,
Let us take P^x as a first building block for the Coons patch. Since V\S.
interpolates only on two boundaries, we will try to add another surface to it,
such that the final result will interpolate to all four boundaries. Such a correction
surface must interpolate to all four boundaries of the error surface x
—
V\x.^ It
may be obtained by applying Vi to the error surface. We then obtain
Px = 7^ix + p2(x-7^ix).
This expression for the bilinearly blended Coons patch may be shortened by
showing only the involved operators:
V = Vi +
V2{l-Vi),
(22.14)
where X is the identity operator. This means of obtaining one operator 'P as a
combination of two operators V\^ Vi is called a Boolean sum and is often written
^ = ^10^2. (22.15)
Of course, we may also multiply out the terms in (22.14). We then obtain
J>
= p^^V2 = Vi + V2- V{P2'
We now see that, even with the use of an operator calculus, we still have the
same old Coons patch as defined by (22.3): the term V{P2 is simply the bilinear
interpolant to the patch corners.
Let us summarize the essence of the Boolean sum approach: an interpolant
to the given data is built by applying Pj. A second operator V2 is then applied
to the "failures" of P^, and the result is added back to the output from Vi. The
interpolant V2 may actually be of a simpler nature than V^, since it has to act on
only zero data where Vi was "successful." We can illustrate this for the example
of univariate cubic Hermite interpolation: we define Vi to be the (point-valued)
linear interpolant between two points
XQ
and x^ and V2 to be the (vector-valued)
5 Note that this error surface is vector valued, since both x and Vix are point valued.

414 Chapter 22 Coons Patches
cubic Hermite interpolant to a data set 0,
HIQ,
mi, 0. Then Vi
0
P2 is the standard
cubic Hermite interpolant.
A note on the notation used in this section: the letter
V
that we used to denote
our building-block interpolants is due to the term projector, A projector is an
operator, which,
if
applied to its own output, will not change the result.^ For
example,
Vix
is
a
ruled surface, and V{PiX is the same ruled surface. Operators
with the property of being projectors are also called idempotent.
It was W. Gordon who realized the underlying algebraic structure
of
Coons
patches. That discovery then led him to the generalization that now bears his
name (Section 22.7). Boolean sums may be used
in
the development
of
many
surface interpolation schemes, for an excellent survey, see Barnhill [21].
22.9 IV'iangular Coons Patches
Just as triangular Bezier patches provide an alternative to the rectangular variety,
we may devise a triangular version of Coons patches. Several solutions have been
proposed through the years; we will briefly explain the ones by Barnhill,
Birkhoff,
and Gordon [26] and by Nielson
[443].
The C^ Barnhill,
Birkhoff,
and Gordon (BBG) approach can be explained as
follows. Suppose we are given three boundary curves, as shown in Figure 22.7.
We seek
a
surface that interpolates
to
all three
of
them, that is,
a
transfinite
triangular interpolant. The construction follows the standard Coons patch de-
velopment in that it consists of several building blocks, which are then combined
in
a
clever way.
Let us denote^ the three boundary curves by x(0, z/, w)^ x(w, 0, w/), x(w, z/, 0).
We define three building blocks, each being
a
ruled surface that interpolates
to
two boundary curves:
Pix(u)
=
(1
-
r)x(^, 0, w)
+
rx(^, v, 0); r =
^,
V2x(u)
=
a-s)x(u,v,0)+sx(0,v,w); 5=^,
(22.16)
P3x(u)
=
(1
-
t)x(u, 0, w)
+
^x(0, v,w);
t
=
^.
Several combinations
of
these surfaces yield
an
interpolant
Vx to
all three
boundaries: the Boolean sum of any two—for example,
V
= V\®
V^—will
have
that property.
6 The term comes from geometry:
if
a 3D object is projected into
a
plane, we may then
repeat that projection, yet it will not change the image.
7 We use the concept of barycentric coordinates as outlined in Section 3.5.

22.9 Triangular Coons Patches
415
Figure
22.7
BBG interpolation: three boundary curves
are
given, left. Three ruled surfaces
are
con-
structed from them (only one shown,
middle).
They are combined to yield the
final
surface,
right.
Another possibility
is to
define
P as a
convex combination
of the
threelP^:
Vx
= uV\x
-h
VV2X
H-
WVT,X,
(22.17)
The building blocks that
are
used
in
(22.16)
are
rational
in
w,
^',
w, but
they
are linear
in r, s, t,
liwt w^ere
to
incorporate cross-boundary derivative data, that
is,
to
build
a C^
BBG interpolant, v^e w^ould define P^,
7^2?
^3
^^
be
cubic Hermite
interpolants
in r, s, t:
Pix(u)
=
H^(r)x(w,
0, w) +
Hl(r)xi(u,
0, w)
+ Hl(r)x^(u,
V,
0) +
H|(r)x(w,
v, 0),
P2x(u)
=
Hl{s)x(u,
V,
0) +
H^^(s)x2(^,
V,
0)
+
H|(S)X2(0,
V,
w) + H^(s)x(0,1/, w),
V^xiu) =
H^(Ox(0,
zy,
w) +
H^\0x3(0,
^, u/)
+ Hlit)x2(u,
0, u/) +
Hl{t)x(u,
0, ^).
(22.18)
The terms
x^ are
shorthand
for
directional derivatives
of x
taken
in a
direction
parallel
to
edge
/;
more precisely:
Xi(u)
= (1/ +
W/)De2_e3X(u),
X2(U)
= (W +
W/)De3_elX(u),
X3(u)
= (w +
Z/)De2-elX(u).

416 Chapter 22 Coons Patches
Figure 22.8 Nielsen's side vertex method: three boundary curves are given, left. Three ruled surfaces
are constructed from them (only one shown, middle). They are combined to yield the final
surface, right.
The factors {v
-\-w)^
and so on, appear because cubic Hermite interpolation is
sensitive to interval lengths. A reminder: the terms el, e2, e3 refer to points, not
to edges!
Again, a Boolean sum of any tw^o of the preceding operators will provide a
solution—provided the cross-boundary derivatives are compatible (v^hich typi-
cally they won't be!).
A different approach is due to G. Nielson
[443].
He considers—for a C^
interpolant—radial curves, connecting a patch vertex with a point on the op-
posite edge, as shown in Figure 22.8. We have
Pix(u) = wx(l, 0, 0) + (1 - w)x(0, r, 1 - r); r = ^
V -\-w
'P2x(u) = i/x(0,1,0) + (1 - zy)x(l - s, 0, s); s = ^^, (22.19)
u-\-w
p3x(u) = w/x(0,0,1) + (1 - M/)x(^
1-^0);
t= —^.
u-{-v
The final interpolant may then be written as a triple Boolean sum:
=
7^1
+ ^2 + ^3
- V{P2 - V{P^ - V2V3
+ V{P2Vy
To make this scheme C\ we again replace the linear interpolants in (22.19)
by cubic Hermite interpolants, now with directional derivatives supplied in the
radial directions.

22.10 Problems 417
For more literature on triangular Coons-type interpolants, consult the follow-
ing: Barnhill [20], Barnhill and Gregory [33], [32], Gregory and Charrot
[292],
Marshall and Mitchell
[420],
Lacombe and Bedard
[367],
and Nielson
[444].
22.10 Problems
1 Show that the bilinearly blended Coons patch is not in the convex hull of
its boundary curves. Is this a good or a bad property.'*
2 Verify the caption to Figure 22.2 algebraically.
3 Equation (22.9) generates tangent ribbons from the given boundary curve
network. Verify that the resulting surface does not suffer from twist incom-
patibilities.
* 4 Translational surfaces have zero twists. Show that the inverse statement is
also true: every surface with identically vanishing twists is a translational
surface.
* 5 Show that the bilinearly blended Coons patch, when applied to cubic
boundary curves, yields a bicubic patch.
*6 Show that Adini's twist from Section 16.3 is the twist of the bilinearly
blended Coons patch for the four boundary cubics.
* 7 As we have seen, two adjacent bihnearly blended Coons patches are not
C^ in general. What are the conditions for the boundary curves of the two
patches such that the Coons patches are C^?
PI Use the data set car.dat. Interpolate all four boundaries using uniform
B-spline interpolation. Then compute the bilinearly blended Coons patch.
Next, experiment with different blending functions and discuss how they
change the shape of the surface.
This Page Intentionally Left Blank

Shape
w e discussed many methods for curve and surface generation. In this chapter,
we shall discuss some ways to inspect the geometric quality of those curves and
surfaces, and develop a few ideas on how to remove shape imperfections. There
is a growing interest in this area; see for example, the collection of Sapidis
[532].
25.1 Use of Curvature Plots
A spline curve is typically obtained in one of two
ways:
as a curve that interpolates
to given data points, or as the result of interactive manipulation of a B-spline
polygon. In both cases, it is hard to tell from the display on the screen if the
shape of the curve is acceptable or not: two curves may look identical on the
screen, yet reveal significant shape differences when plotted to full scale. Such
plots are both expensive and time consuming—one needs a tool to analyze curve
shape at the CAD terminal.
The most commonly used tool for this task is provided by the curvature plot
of the curve. For a given curve, we can plot curvature versus arc length or versus
the parameter. The resulting graph is the curvature plot. We have already used
curvature plots in Chapter 9. All three curves from Figures 9.8, 9.10, and 9.12
look very similar, yet their curvature plots reveal substantial differences. The
same is true for Figures 9.16 and 9.18. What actually constitutes a "substantial"
difference depends on the application at hand, of course.
419

420 Chapter 23 Shape
The curvature of a space curve is nonnegative by definition (10.7).^ Very
often, we are interested in the detection of inflection points of the current planar
projection, that is, the points of inflection of the curve as it appears on the screen.
If we introduce signed curvature by
x{u)y{u) ~ y{u)x{u)
'^(^)
= 7 ^i
^TTTT?
23.1
[(x(«))2 + (y(^))2]3/2'
where
;c,
y are the two components of the curve, it is easy to point to changes
in the sign of curvature, which indicate inflection points. (Those sign changes
can be marked by special symbols on the plot.) Signed curvature is used in all
examples in this book.
We now go one step further and use curvature plots for the definition of fair
curves: a curve is fair if its curvature plot is continuous and consists of only a
few monotone pieces? Regions of monotone curvature are separated by points
of extreme curvature. The number of curvature extrema of a fair curve should
thus be small—curvature extrema should occur only where explicitly desired by
the designer, and nowhere else!
This definition of fairness (also suggested by Dill
[169],
Birkhoff [64], and Su
and Liu [583] in similar form) is certainly subjective; however, it has proved to
be a practical concept. Once a designer has experienced that "flat spots" on the
curve correspond to "almost zero" curvature values and that points of inflection
correspond to crossings of the zero curvature line, he or she will use curvature
plots as an everyday tool.
An interesting alternative to plain curvature plots are plots of the logarithm
of curvature; see [99]. Such plots highlight "flat" areas on a curve. Tiny changes
in curvature have a significant effect in these regions, and they are magnified by
the use of logarithms.
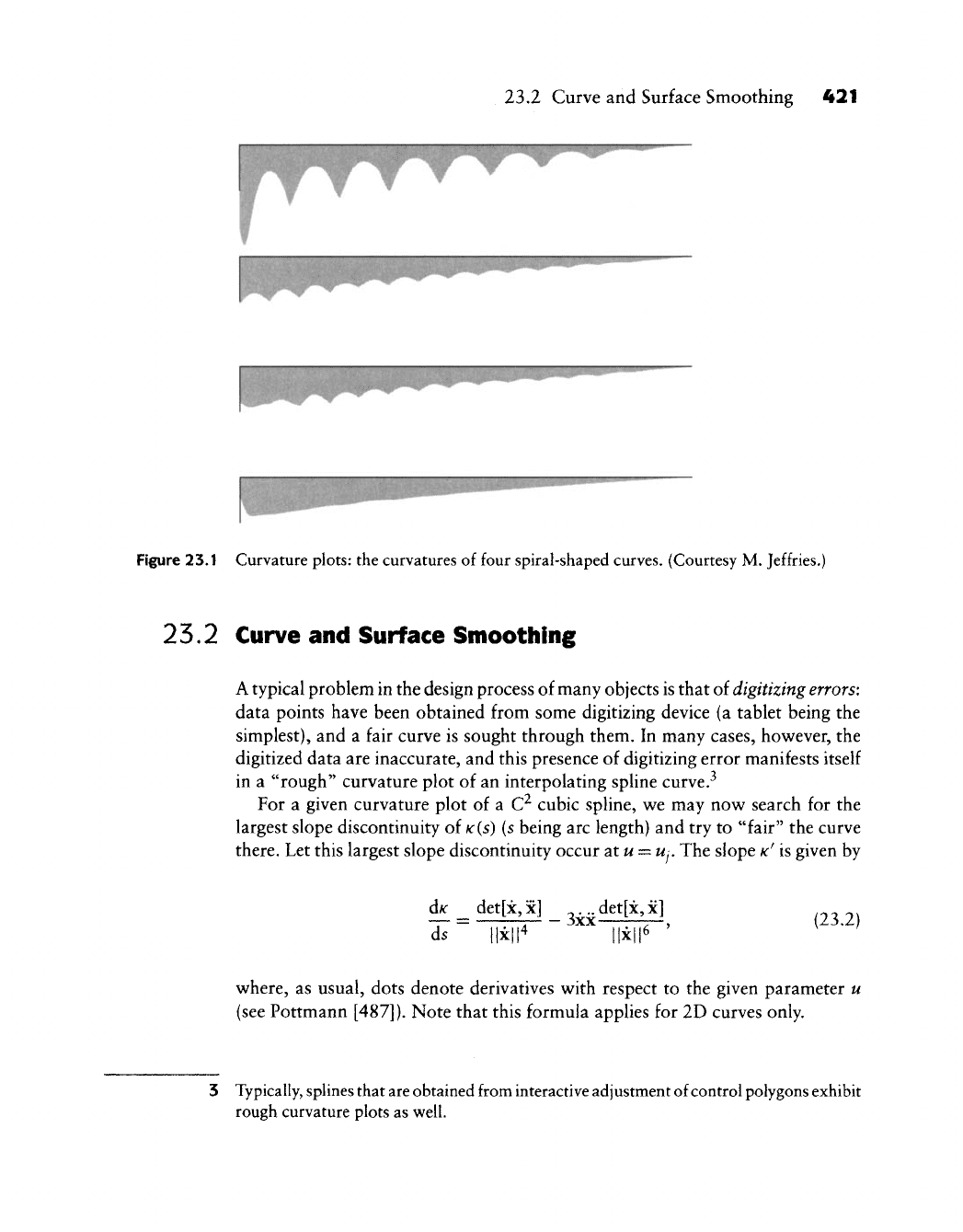
Figure 23.1 shows several curvature plots. They are obtained from the curves
in Figures 9.1 through 9.4. Note how "bumpy" the cubic case with only nine
intervals is.
1 See also the Problems at the end of Chapter 13.
2 M. Sabin
has
suggested that "a frequency analysis of the radius of curvature plotted against
arc length might give some measure of fairness—the lower the dominant frequency, the
fairer the curve." Quoted from Forrest
[240].
23.2 Curve and Surface Smoothing 421
4?^^^t-
:
>-^
7:--^x
^^is^^
;Cpj3:i;^^S;^ '^'.
Figure 23.1 Curvature plots: the curvatures of four spiral-shaped curves. (Courtesy M. Jeffries.^
25.2 Curve and Surface Smoothing
A typical problem in the design process of many objects is that of digitizing errors:
data points have been obtained from some digitizing device (a tablet being the
simplest), and a fair curve is sought through them. In many cases, however, the
digitized data are inaccurate, and this presence of digitizing error manifests itself
in a "rough" curvature plot of an interpolating spline curve.^
For a given curvature plot of a C^ cubic spline, we may now search for the
largest slope discontinuity of
K(S)
(S
being arc length) and try to "fair" the curve
there. Let this largest slope discontinuity occur atu =
Uj.
The slope
K'
is given by
d^
ds
det[x, x]
3xx
. det[x, x]
(23.2)
where, as usual, dots denote derivatives with respect to the given parameter u
(see Pottmann [487]). Note that this formula applies for 2D curves only.
3 Typically, splines that
are
obtained from interactive adjustment of control polygons exhibit
rough curvature plots as well.
