Farin G. Curves and Surfaces for CAGD. A Practical Guide
Подождите немного. Документ загружается.


402 Chapter
22
Coons Patches
+ [x(^,0) x(«,l)]P^''l (22.4)
^ ^Lx(l,0) x(l,l)J[
V J
It
is
left
as an
exercise
to
verify that (22.4) does indeed interpolate
to all
four
boundary curves.
We can now justify the name bilinearly blended
for
the preceding Coons patch:
a ruled surface "blends" together the two defining boundary curves; this blending
takes place
in
both directions. However,
the
Coons patch
is not
generally itself
a bilinear surface—the name refers purely
to the
method
of
construction.
The functions
1—w, u and 1—f, v are
called blending functions,
A
close
inspection
of
(22.4) reveals that many other pairs
of
blending functions,
say,
/i(w),
fiiu)
and
g\{v)^
giip)^
could also
be
used
to
construct
a
generalized Coons
patch.
It
would then
be of the
general form
x{u,v)=[h{u) /2(«)][^J5;^J]
+ [x(«,0) x(«,l)]|^jij|;jl (22.5)
Ihiu) f2(«)][^(i^o) x(l,l)JLg2(t^)J-
There
are
only
two
restrictions
on the d and gi:
each pair must
sum to
one identically: otherwise,
we
would generate nonbarycentric combinations
of
points (see Section 2.1). Further, we must have /^(O)
=
^^(O)
=
1,
fi(l) =
gi(l)
= 0
in order
to
actually interpolate.
The
shape
of the
blending functions
has a
predictable effect
on
the shape
of
the resulting Coons patch. Typically,
we
require
fi
and gi to be
monotonically decreasing; this produces surfaces
of
predictable
shape,
but is not
necessary
for
theoretical reasons.
22.2 Coons Patches: Partially Bicubically Blended
The bilinearly blended Coons patch solves
a
problem
of
considerable importance
with very little effort,
but we pay for
that
by an
annoying drawback. Consider
Figure
22.2: it
shows
two
bilinearly blended Coons patches, defined over
u e

22.2 Coons Patches: Partially Bicubically Blended 403
Figure 22.2 Coons
patches:
the input
curves
for two neighboring patches may
have
C^
boundary curves
(left),
yet the
tw^o
Coons patches determined
by
them do not form
a
smooth surface (right).
[0,2],
V G
[0,1].
The boundary curves v = 0 and v=\^ both composite curves, are
differentiable. How^ever, the cross-boundary derivative is clearly discontinuous
along
w
= 1; also see Problems."^
Analyzing this problem, w^e see that it can be blamed on the fact that cross-
boundary tangents along one boundary depend on data not pertaining to that
boundary. For example, for any given bilinearly blended Coons patch, a change
in the boundary curve x(l,i/) w^ill affect the derivatives across the boundary
x(0,i/).
How^ can w^e separate the derivatives across one boundary from information
along the opposite boundary.^ The answer: use different blending functions,
namely, some that have zero slopes at the endpoints. Striving for simplicity, as
usual, v^e find tv^o obvious candidates for such blending functions: the cubic
Hermite polynomials H^ and H| from Section 7,5^ as defined by (7.14).
Let us investigate the effect of this choice of blending functions: w^e have set
f\=g\
= ^0 ^^^ /2 = g2
=
say,
w
= 0, now^ becomes:
H|
in (22.5). The cross-boundary derivative along.
x„(0,t^) = [x„(0,0) x„(0,l)] (22.6)
2 We also see that bilinearly blended Coons patches suffer from a shape defect: each of the
two patches is too "flat." This effect of Coons patches has been studied by Nachman
[436].

404 Chapter 22 Coons Patches
all other terms vanish since d/dwH|.(0) = d/dwH|.(l) = 0 for / = 0 and / = 1.
Thus,
the only data that influence x^ along
w
= 0 are the two tangents x^(0, 0)
and x^(0,1)—^we have achieved our goal of making the cross-boundary derivative
along one boundary depend only on information pertaining to that boundary.
With our new blending functions, the two patches from Figure 22.2 would now
beCi.
Unfortunately, we have also created a new problem. At the patch corners,
these patches often have "flat spots." The reason; partially bicubically blended
Coons patches,^ constructed as before, suffer from zero corner twists:
x^^(ij)
= 0;
/,/€{0,l}.
This is easily verified by simply taking the wi/-partial of (22.5) and evaluating at
the patch corners.
The reason for this poor performance lies in the fact that we use only two
functions,
HQ
and H3 from the full set of four Hermite polynomials. Both have
zero derivatives at the interval endpoints, and pass that property on to the surface
interpolant.
We will now modify the partially bicubically blended Coons patch in order to
avoid the flat spots at the corners.
22.5 Coons Patches: Bicubically Blended
Cubic Hermite interpolation needs more input than positional data—first deriva-
tive information is needed. Since our positional input consists of whole curves,
not just points, the obvious data to supply are derivatives along those input
curves. Our given data now consist of
x(w,0),
x(w, 1), x(0,i/), x(l,i/)
and
x^(w,0), x^(w, 1), x^(0,i/), x^(l,i/).
We can think of the now prescribed cross-boundary derivatives as "tangent
ribbons," illustrated in Figure 22.3 (only two of the four "ribbons" are shown
there).
3 We use the term
partially
bicubically blended since only a part of all cubic Hermite basis
functions is used.

22.3 Coons Patches: Bicubically Blended 405
Figure 22.3 Coons patches: for the bicubically blended case, the concept of the lofted surface is
generalized. In addition to the given boundary curves, cross-boundary derivatives are
supplied.
The derivation of the bicubically blended Coons patch is analogous to the
one in Section 22.1: we must simply generalize the concept of a ruled surface
appropriately. This is almost trivial; we obtain
h,(u,
V)
= H^Wx(0,
V)
+ Hi^(w)x^(0,
V)
+ H|(w)x^(l, v) + H|(W)X(1, V)
for the w-direction (this surface is shown in Figure 22.3) and
h^(t/,
V)
= H^(i/)x(w, 0) + Hl{v)^y{u, 0) + Hl(v)x^(u, 1) + HI(V)X(U, 1).
Proceeding as in the bilinearly blended case, we define the interpolant to the
corner data. This gives the tensor product bicubic Hermite interpolant h^j from
Section 15.5:
hcj(«, v) =
[H^iu) Hl(u) Hliu) Hliu)]
•x(0,0) x,(0,0) x^(0,l) x(0,l)
x^(0,0) x^^(0,0) x^,(0,l) x^(0,l)
x^(l,0) x^,(l,0) x^^(l,l) x^(l,l)
L x(l, 0) x,(l, 0) x,(l, 1) x(l, 1) J
L
Hliv) J
The bicubically blended Coons patch now becomes
H^v)
(22.7)
X
= h^ + hj - h
^cd-
(22.8)
Before closing this section, we need to take a closer look at the h^j part of
(22.8).
On closer inspection, we find that it wants data that we were not willing

406 Chapter 22 Coons Patches
(or able) to provide in our initial problem description, namely, the central "twist
partition" of the 4x4 matrix in (22.7). The bicubically blended Coons patch
needs these quantities as input, and this has caused CAD software developers
many headaches since Coons proposed his surface scheme in 1964. The most
popular "solution" seems to be simply to define each of the four corner twists
to be the zero vector. The drawbacks of that choice were already discussed in
Section 14.10, but alternatives are pointed out in that section, too.
22.4 Piecewise Coons Surfaces
We will now apply the bicubically blended patch to the situation for which it was
intended: we assume that we are given a network of curves as shown in Figure
22.6 and that we want to fill in this curve network with bicubically blended
Coons patches. The resulting surface will be C^.
To apply (22.8), we must create twist vectors and cross-boundary derivatives
(tangent ribbons) from the given curve network. As a preprocessing step, we
estimate a twist vector ^^y{ui^
Vj)
at each patch corner. This can be done by using
any of the twist vector estimators discussed in Section 16.3. In that section, we
assumed that the boundary curves of each patch were cubics; that assumption
does not affect the computation of the twist vectors at all, however.
Having found a twist vector for each data point, we now need to create cross-
boundary derivatives for each boundary curve. Let us focus our attention on
one patch of our network, and let us assume for simplicity (but without loss of
generality!) that the parameters u and v vary between 0 and 1. We shall now
construct the tangent ribbon x^(w, 0). We have four pieces of information about
x^(w, 0): the values of ^y{u^ 0) at u = 0 and at
w
= 1, and the derivatives with
respect to u there—these are the twists that we made up earlier, namely, x^j;(0,0)
andx^^(l,0).
We therefore have the input data for a univariate cubic Hermite interpolant,
and the desired tangent ribbon assumes the form
x,(u,
0) = x,(0, O)Ho^(^) + x^,(0,0)Hliu)
+ x^,(l, 0)Hl(u) + x,(l, 0)Hl(u), (22.9)
The remaining three tangent ribbons are computed analogously.
We have thus found a way to pass a C^ surface through a C^ network of curves.
All we needed was the ability to estimate the twists at the data points.

22.5 Two Properties 407
22.5 IWo Properties
Coons patches are twist minimizing in the sense that
xLdS (22.10)
Js"""'
is minimal exactly for the Coons patch (S being the domain).
If we apply the minimum principle to the discrete Coons patch, we have that
m—ln—1
i=0 j=0
is minimal if the hjj form a discrete Coons patch.
Coons patches satisfy a permanence principle: let two points
(WQ?
^O)
^^^
(^1,
vi) define a rectangle R in the domain of a Coons patch. The four boundaries
of this subpatch will map to four curves on the Coons patch. You may ask what
the Coons patch to those four boundary curves is. The answer: the original Coons
patch, restricted to the rectangle R^ In this sense. Coons patches are self-similar!
We can apply this principle to a 3 x 3 grid of a discrete Coons patch. Such a
grid is given by
b/-l,/+l b^-,;+l b/^l,;+l
b/-i,;-i b^-,/-i b^+i,;-i
As a consequence of the permanence principle,
1
^(b.,;+i +
b,_i,^-
+
b,,.!,^-
+
b,,_i).
(22.11)
We could thus obtain the discrete Coons patch as the solution to a Unear
system of equations. This is not practical for the construction of a rectangular
control net, but offers a basic construction principle for more complex surfaces.
For more details, see
[207].
4 The term
permanence principle
for Coons patches was coined by R. Barnhill in a slightly
different context around 1980.

408 Chapter 22 Coons Patches
22.6 Compatibility
It is an obvious requirement for the bilinearly blended Coons patch that the four
prescribed boundary curves meet at the corners; in other words, we must exclude
data configurations as shown in Figure 22.4. This condition on the prescribed
data is known as a compatibility condition. An incompatibility of that form can
usually be overcome by adjusting boundary curves so that they meet at the patch
corners.
The bicubically blended Coons patch suffers from a more difficult compat-
ibility problem. It results from the appearance of the twist terms in the tensor
product term h^j in (22.7). The problem was not recognized by Coons, and only
later did R. Barnhill and J. Gregory discover it; see Gregory
[288].
From calculus, we know that we can usually interchange the order of
dif-
ferentiation when taking mixed partials: we can set
x^^^
= x^;^ if x(«, v) is twice
continuously differentiable. Unfortunately, this simplification does not apply to
our situation. Let us examine why: at x(0,0), two given "tangent ribbons" meet.
We can obtain the twist at x(0,0) by differentiating the "ribbon"
yiy{u^
0) with
respect to u:
Xi;„(0,0) = lim —x^(w, 0),
M-^0 du
or the other way around:
x«t;(0,0) = lini —x„(0, v).
v-^0 dv
Figure 22.4 Compatibility problems: in the case of a bilinearly blended Coons patch, compatible
boundary curves must be prescribed. Data as shown lead to ill-defined interpolants.

22.6 Compatibility 409
Figure 22.5 Compatibility problems: we show the example of tangent ribbons that are represented in
cubic Bezier form. Note how we obtain two different interior Bezier points, and thus two
different corner twists.
If the two twists x^^(0, 0) and x^^(0, 0) are equal, there are no problems: enter
this twist term into the matrix in (22.7), and the bicubically blended Coons patch
is well defined.
However, as Figure 22.5 illustrates, these two terms need not be equal. Now
we have a serious dilemma: entering either one of the two values yields a surface
that only partially interpolates to the given data. Entering zero twist vectors only
aggravates matters, since they will in general not agree with even one of the two
twists.
There are two ways out of this dilemma. One is to try to adjust the given data
so that the incompatibilities disappear. Or, if the data cannot be changed, we
can use a method known as Gregory's square. This method replaces the constant
twist terms in the matrix in (22.7) by variable twists. The variable twists are
computed from the tangent ribbons:
x^,(0,0) =
x^,(0,1) -
x^^(l, 1) =
^|;X^(Q,0)+l/|^X,(0,0)
u-\-v
-^|;x,(0,l) + (i;-l)|^x,(0,l)
—u
+ v
—
1
a-u)ix^a,o)
+ vix,a,o)
l
—
U
+ P
(M-1)|;X„(1,1) + (Z;-1)|-X^(1,1)
u-l+v-1

410 Chapter 22 Coons Patches
The resulting surface does not have a continuous twist at the corners. In fact,
it is designed to be discontinuous: it assumes two different values, depending
on from where the corner is approached. If we approach x(0,0), say, along the
isoparametric line
w
= 0, we should get the w-partial of the given tangent ribbon
x^(w, 0) as the twist x^^(0, 0). If we approach the same corner along z/ = 0, we
should get the i/-partial of the given ribbon x^(0, v) to be x^^(0,0).
An interesting application of Gregory's square was developed by Chiyokura
and Kimura
[112]:
suppose we are given four boundary curves of a patch in cubic
Bezier form, and suppose that the cross-boundary derivatives also vary cubically.
Let us consider the corner x(0,0) and the two boundary curves that meet there.
These curves define the Bezier points boy and
b^o-
The cross-boundary derivatives
determine by and
b^j.
Note that bn is defined twice! This situation is illustrated
in Figure 22.5. Chiyokura and Kimura made b^ a function of u and v:
bii = bii(w, V) = • ,
where hii(u) denotes the point b^ that would be obtained from the cross-
boundary derivative x^(0, v), and so on. Similar expressions hold for the remain-
ing three interior Bezier points, all following the pattern of Gregory's square.
Although a solution to the posed problem, we should note that Gregory's
square (or the Chiyokura and Kimura application) is not free of problems. Even
with polynomial input data, it will produce a rational patch. Written in rational
Bezier form, its degree is seven in both u and v and the corner weights are
zero (see [202]). The resulting singularities are removable, but require special
attention. In situations where we are not forced to use incompatible cross-
boundary derivatives, it is therefore advisable first to estimate corner twists and
then to use (22.9) as a cross-boundary derivative generator.
22.7 Gordon Surfaces
Gordon surfaces are a generalization of Coons patches. They were developed
in the late 1960s by W. Gordon
[281], [283], [280], [282],
who was then
working for the General Motors Research labs. He coined the term transfinite
interpolation for this kind of surface.
It is often not sufficient to model a surface from only four boundary curves. A
more complicated (and realistic) situation arises when a network of curves is pre-
scribed, as shown in Figure 22.6. We will construct a surface g that interpolates
to all these curves—they will then be isoparametric curves g(w/, t/); / = 0,..., m
and g(M, Vj)\j = 0,...,
w.
We shall therefore refer to these input curves in terms
of the final surface g. The idea behind the construction of this Gordon surface
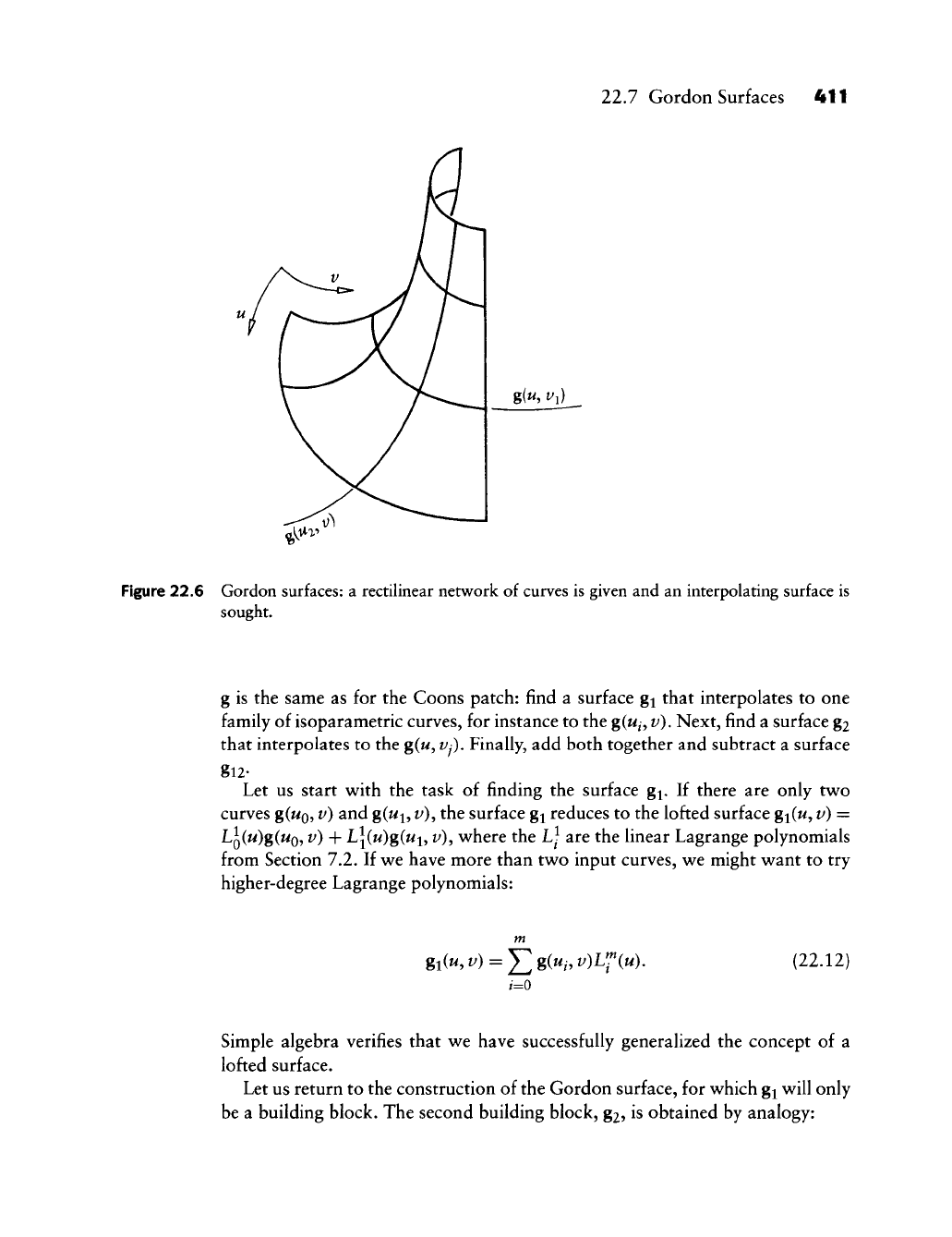
22.7 Gordon Surfaces 411
Figure 22.6 Gordon surfaces: a rectilinear network of curves is given and an interpolating surface is
sought.
g is the same as for the Coons patch: find a surface gj that interpolates to one
family of isoparametric curves, for instance to the g(w/, v). Next, find a surface g2
that interpolates to the
g(M,
Vj),
Finally, add both together and subtract a surface
gl2-
Let us start vv^ith the task of finding the surface gj. If there are only two
curves
gC^o?
^) ^^^ g(^i5
^)y
the surface gi reduces to the lofted surface gi(w, v) =
Lliu)g{uQ^ v)
-\-
Lj(w)g(wi, f), v^here the L\ are the linear Lagrange polynomials
from Section 7.2. If we have more than two input curves, we might want to try
higher-degree Lagrange polynomials:
%Mv) =
Y,%{Ui,v)Vl^{u).
{IIAI)
i=0
Simple algebra verifies that we have successfully generalized the concept of a
lofted surface.
Let us return to the construction of the Gordon surface, for which gj will only
be a building block. The second building block, g2, is obtained by analogy:
