Farin G. Curves and Surfaces for CAGD. A Practical Guide
Подождите немного. Документ загружается.


432 Chapter 24 Evaluation of Some Methods
A flexible system should have both: interpolation and interactive manipula-
tion. The interpolation process may of course be formulated in terms of B-splines.
Since many designers do not favor interactive manipulation of control polygons,
w^e should allow them to generate curves using interpolation. Subsequent curve
modification may also take place without display of a control polygon: for in-
stance, the designer might move one (interpolation) point to a new position. The
system could then compute the B-spline polygon modification that would pro-
duce exactly that effect. So a user might actually work with a B-spline package,
but a system that is adapted to his or her needs might hide that fact. See Section
9.3 for details.
We finally note that every C^ B-spline curve may be generated as an interpolat-
ing spline curve: read off junction points, end tangent vectors, and knot sequence
from the B-spline curve. Feed these data into a C^ cubic spline interpolator, and
the original curve will be regenerated.
24.5 The Monomial or the Bezier Form?
We have made the point in this book that the monomial form^ is less geometric
than the Bezier form for a polynomial curve. A software developer, however,
might not care much about the beauty of geometric ideas—in the workplace,
the main priority is performance. Since the fundamental work by Farouki and
Rajan
[224], [225], [220],
one important performance issue has been resolved:
the Bezier form is numerically more stable than the monomial form. Farouki
and Rajan observed that numerical inaccuracies, unavoidable with the use of
finite precision computers, affect curves in the monomial form significantly more
than those in Bezier form. More precisely, they show that the condition number
of simple roots of a polynomial^ is smaller in the Bernstein basis than in the
monomial basis. If one decides to use the Bezier form for stability reasons, then
it is essential that no conversions be made to other representations; these will
destroy the accuracy gained by the use of the Bezier form. For example, it is not
advisable from a stability viewpoint to store data in the monomial form and to
convert to Bezier form to perform certain operations. More details are given in
Daniel and Daubisse
[132].
Figure 24.1 shows a numerical example, carried out using the routine bez__to_
pow
with single precision arithmetic. A degree 18 Bezier curve (top) was converted
1 This form is also called the power
basis
form.
2 This number indicates by how much the location of a root is perturbed as a result of a
perturbation of the coefficients of the given polynomial.
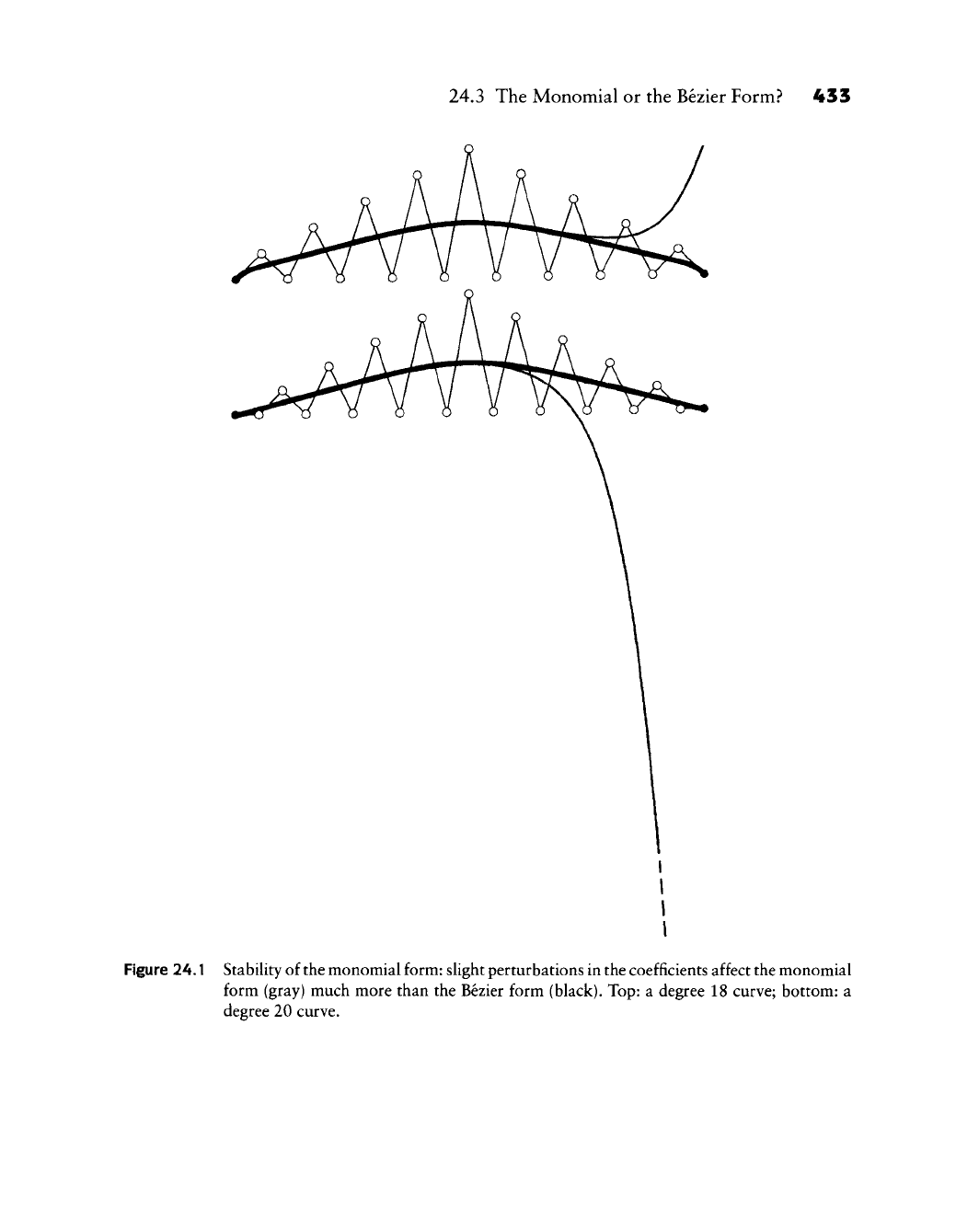
24.3 The Monomial or the Bezier Form? 433
Figure 24.1 Stability of the monomial form: slight perturbations in the coefficients affect the monomial
form (gray) much more than the Bezier form (black). Top: a degree 18 curve; bottom: a
degree 20 curve.

434 Chapter 24 Evaluation of Some Methods
Figure 24.2 A piecewise monomial surface: the patches miss the points (1,1) due to
roundoff.
to the monomial form. Then, the coefficients of the Bezier and of the monomial
form were perturbed by a random error, less than 0.001 in each coordinate. (The
x-values of the control polygon extend from 0 to 20.) The Bezier curve shows
no visual sign of perturbation, whereas the monomial form is not very reliable
near t = 1, The experiment was then repeated for a degree 20 curve (bottom)
with even more disastrous results. Although degrees like 18 or 20 look high, we
should not forget that such degrees already appear in harmless-looking tensor
product surfaces: for example, the diagonal u = v oi a patch with n = m = 9 is
of degree 18!
As a consequence of its numerical instability, the monomial form is not very
reliable for the representation of curves or surfaces. For the case of surfaces.
Figure 24.2 gives an illustration (in somewhat exaggerated form). Since the
monomial form is essentially a Taylor expansion around the local coordinate
(0,0) of each patch, it is quite close to the intended surface there. Farther
away from (0,0), however, roundoff takes its toll. The point (1,1) is computed
and therefore missed. For an adjacent patch, the actual point is stored as a
patch corner, thus giving rise to the discontinuities shown in Figure 24.2. The
significance of this phenomenon increases dramatically when curves or surfaces
of high degrees are used.
Let's not forget to mention the main attraction of the monomial form: speed.
Horner's method is faster than the de Casteljau algorithm; it is also faster than the
routine hornbez. There is a tradeoff therefore between stability and speed. (Given
modern hardware, things are not quite that clear-cut, however: T. DeRose and
T. Flolman [166] have developed a multiprocessor architecture that hardwires
the de Casteljau algorithm into a network of processors and now outperforms
Horner's method.)

24.5 Triangular or Rectangular Patches? 435
24.4 The B-Spline or the Hermite Form?
Cubic B-spline curves are numerically more stable than curves in the piecewise
cubic Hermite form. This comes as no surprise, since some of the Hermite
basis functions are negative, giving rise to numerically unstable nonconvex
combinations. However, there is an argument in favor of the piecev^ise Hermite
form: it stores interpolation points explicitly. In the B-spline form, they must be
computed. Even if this computation is stable, it may produce
roundoff.
A significant argument against the use of the Hermite form points to its
lack of invariance under affine parameter transformations. Everyone who has
programmed the Hermite form has probably experienced the trauma resulting
from miscalculated tangent lengths. A programmer should not be burdened with
the subtleties of the interplay between tangent lengths and parameter interval
lengths.
An important advantage of the B-spline form is storage. For B-spline curves,
one needs a control point array of length L + 2 plus a knot vector array of length
L + 1 for a curve with L data points, resulting in an overall storage requirement
of 4L -h 7 reals.^ For the piecewise Hermite form, one needs a data array of
length IL (position and tangent at each data point) plus a knot vector of length
L -h 1, resulting in a storage requirement of 7L + 1 reals. For surfaces (with
same degrees in u and v for simplicity), the discrepancy becomes even larger:
3(L + 2)^ + 2(L + 1) versus 12L^ + 2(L + 1) reals. (For the Hermite form, we
have to store position, u- and i/-tangents, and twist for each data point.)
When both forms are used for tensor product interpolation, the Hermite form
must solve three sets of linear equations (see Section 15.5) while the B-spline form
must solve only two sets (see Section 15.4).
24.5 Triangular or Rectangular Patches?
Most of the early CAD efforts were developed in the car industry, and this is per-
haps the main reason for the predominance of rectangular patches in most CAD
systems; the first applications of CAD methods to car body design were to the
outer panels such as
roof,
doors, and hood. These parts basically have a rectan-
gular geometry, hence it is natural to break them down into smaller rectangles.
These smaller rectangles were then represented by rectangular patches.
Once a CAD system had been successfully applied to a design problem, it
seemed natural to extend its use to other tasks: the design of the interior car
3 We are not storing knot multiplicities. We would then be able to represent curves that are
only C^, which the cubic Hermite form is not capable of.

436 Chapter 24 Evaluation of Some Methods
body panels, for instance. Such structures do not possess a notably rectangular
structure, and rectangular patches are therefore not a natural choice for modeling
these complicated geometries. However, rectangle-based schemes already existed,
and the obvious approach
w^as
to make them v^ork in "unnatural" situations also.
They do the job, although w^ith some difficulties, w^hich arise mainly in the case
of degenerate rectangular patches.
Triangular patches do not suffer from such degeneracies and are thus better
suited to describe complex geometries than are rectangular patches. It seems
obvious, therefore, to advise any CAD system developer to add triangular patches
to the system.
The French car company Citroen used triangular patches in the early 1960s,
but later abandoned their use. In the middle 1980s, Evans and Sutherland used
triangular patches as the backbone of their CDDRS system—they were subse-
quently replaced by B-spline surfaces. More recently, NVIDIA uses triangular
patches to fill in holes in rectangular topologies.

Quick Reference
of Curve and
Surface Terms
ab initio design Latin: from the beginning. Used to describe design processes
in which the designer inputs his or her ideas directly into the computer, without
constraints such as interpolatory constraints.
Affine combination Same as a barycentric combination.
Affine invariance A property of a curve or surface generation scheme: the same
resuh is obtained if computation of a point on a curve or surface occurs before
or after an affine map is apphed to the input data.
Affine map Any map comprising translations, rotations, scalings, and shears.
Maps parallels to parallels. Leaves ratios of collinear points unchanged.
Approximation Fitting a curve or surface to given data. As opposed to interpo-
lation, the curve or surface approximation only has to be close to the data.
Barycentric combination A weighted average where the sum of the weights
equals one.
Barycentric coordinates A point in E^ may be written as a unique barycentric
combination of three points. The coefficients in this combination are its barycen-
tric coordinates.
Basis function Functions form linear spaces, which have bases. The elements
of these bases are the basis functions.
Bernstein polynomial The basis functions for Bezier curves.
Beta-spline curve A G^ piecewise cubic curve that is defined over a uniform
knot sequence.
Bezier curve A polynomial curve that is expressed in terms of Bernstein poly-
nomials.
437

438 Appendix A Quick Reference of Curve and Surface Terms
Bezier polygon The coefficients in the expansion of a Bezier curve in terms of
Bernstein polynomials are points. Connected according to their natural number-
ing, they form the Bezier polygon.
Bilinear patch A patch that is ruled in two directions. Or: a hyperbolic para-
boloid.
Blossom A multivariate polynomial that is associated v^ith a given polynomial
through the process of blossoming.
Blossoming The procedure of applying n (the polynomial degree) de Casteljau
algorithm steps or n de Boor steps to a polynomial (or to a segment of a spline
curve),
but each one for a different parameter value.
B-spline A piecev^ise polynomial function. It is defined over a knot partition,
has local support, and is nonnegative. If a spline curve is expressed in terms of
B-splines, it is called a B-spline curve.
B-spline polygon The coefficients in the expansion of a B-spline curve in terms
of B-splines are points. Connected according to their natural numbering, they
form the B-spline polygon. Also called de Boor polygon.
Breakpoint Same as a knot.
Butterfly scheme An interpolatory recursive subdivision scheme that creates
smooth surfaces from a given set of triangulated points.
CAGD Computer aided geometric design.
Catmull-Clark Surfaces Subdivision surfaces that are bicubic spline surfaces
v^hen the input mesh is rectangular.
C^ A smoothness property of curves or surfaces: being r times differentiable w^ith
respect to the given parametrization.
Chord length parameters In many curve interpolation problems, data points
need to be assigned parameter values. If these are spaced relative to the spacing
of the data points, we have chord length parameters.
Collinear Being on a straight line.
Compatibility For some interpolation problems, the input data may not be
arbitrary but must satisfy some consistency constraints, called compatibility
conditions.
Conic section The intersection curve between a cone and a plane. Or: the
projective image of a parabola. A nondegenerate conic is an ellipse, a parabola,
or a hyperbola.
CONS Curve on surface.
Control polygon See Bezier polygon or B-spline polygon.

Quick Reference of Curve and Surface Terms 439
Control vector For rational curves, a Bezier or B-spline control point that has
degenerated to a vector, implying a zero weight.
Convex curve A planar curve that is a subset of the boundary of its convex hull.
Convex hull The smallest convex set that contains a given set.
Convex set A set such that the straight line segment connecting any tv^o points
of the set is completely contained within the set.
Coons patch A patch that is fitted between four arbitrary boundary curves.
Coplanar Being on the same plane.
Cross plot Breaking down the plot of a parametric curve into the plots of each
coordinate function.
Cross ratio A quantity computed from four coUinear points, invariant under
projective maps. A generalization of affine ratios.
Curvature At a point on a curve, curvature is the inverse of the radius of the
osculating circle. Also: curvature measures by how much a curve deviates from
a straight line at a given point.
Curve The path of a point moving through space. Or: the image of the real line
under a continuous map.
de Boor algorithm The algorithm that recursively computes a point on a
B-spline curve.
de Casteljau algorithm The algorithm that recursively computes a point on a
Bezier curve.
Decimation Reducing the number of triangles in a triangulation while staying
close to the initial geometry.
Delaunay triangulation A triangulation that maximizes the minimal angle of
all triangles. Or: the dual of the Dirichlet tessellation.
Developable surface A ruled surface whose Gaussian curvature vanishes ev-
erywhere.
Direct
G^
splines G^ piecewise cubics that are generated by specifying a control
polygon and some Bezier points.
Dirichlet tessellation A partition of E^ or E^ into convex tiles. Each tile is
associated with a given data point such that all of its points are closer to "its"
data point than to any other data point.
Domain The preimage of a curve or surface.
Doo-Sabin surfaces Subdivision surfaces that are biquadratic spline surfaces
when the input mesh is rectangular.

440 Appendix A Quick Reference of Curve and Surface Terms
End condition In cubic spline curve interpolation, one has to supply an extra
condition at each of the two endpoints. Examples of such end conditions: pre-
scribed tangents or zero curvature.
Four-point sciieme An interpolatory curve subdivision scheme.
Frenet frame At each point of a (nondegenerate) curve, the first, second, and
third derivative vectors are linearly independent. Applying Gram-Schmidt or-
thonormalization to them yields the Frenet frame of the curve at the given point.
Functional curve or surface A curve of the form y = f{x) or a surface of the
form z =
f{x^y),
C^ spline curve A C^ piecewise cubic curve that is twice differentiable with
respect to arc length.
y-spline A G^ spline that is C^ over a given knot sequence.
Geometric continuity Smoothness properties of a curve or a surface that are
more general than its order of differentiability.
Gordon surface A generalization of Coons patches. Interpolates to a rectilinear
network of curves.
Hermite interpolation Generating a curve or surface from data that consist of
points and first and/or higher derivatives.
Hodograph The first derivative curve of a parametric curve.
Homogeneous coordinates A coordinate system that is used to describe ra-
tional curves and surfaces in terms of projective geometry, where they are just
polynomial.
Horner's scheme An efficient method to evaluate a polynomial in monomial
form by nested multiplication.
IGES Initial Graphics Exchange Specification. A popular data specification for-
mat, aiming at unifying geometry descriptions.
Infinite control point Same as control vector.
Inflection point A point on a curve where the tangent intersects the curve. Often
corresponds to points with zero curvature.
Interior Bezier points For curves, those Bezier points that are not junction
points. For surfaces, those Bezier points that are not boundary points.
Interpolation Finding a curve or surface that satisfies some imposed constraints
exactly. The most common constraint is the requirement of passing through a set
of given points.
Junction point A spline curve comprises segments. The common point shared
by two segments is called the junction point. See also knot.

Quick Reference of Curve and Surface Terms 441
Knot A spline curve is defined over a partition of an interval of the real line. The
points that define the partition are called knots. If evaluated at a knot, the spline
curve passes through a junction point.
Knot insertion Adding a new knot to the knot sequence of a B-spline curve
without changing the graph of the curve.
Lagrange interpolation Finding a polynomial curve through a given set of data
points.
Least squares An approximation process that aims at minimizing the devia-
tions of given data points from a desired curve or surface.
Linear precision A property of many curve schemes: if the curve generation
scheme is applied to data read off from a straight line, that straight line is
reproduced.
Local control A curve or surface scheme has the local control property if a
change in the input data only changes the curve or surface in a region near the
changed data.
Lofting Creating a ruled surface between two given curves.
Minmax box Smallest 2D or 3D box with edges parallel to the coordinate axes
that completely contains a given object.
Monomial form A polynomial is in monomial form if it is expressed in terms
of the monomials 1, ^, ^^,.. ..
Multiresolution Breaking down an object into a sequence of approximations
with increasing accuracy.
Node A term that is used inconsistently in the literature: it sometimes refers to
a knot, sometimes to a control point.
NURB Nonuniform rational B-spline curve or surface.
y-spline An interpolating G spline curve that is C^ over a given knot sequence.
Osculating circle At a given point, the osculating circle approximates the curve
"better" than any other circle.
Osculating plane The plane that contains the osculating circle of a curve at a
given point. This plane is spanned by the given point and the curve's first and
second derivative vectors.
Oslo algorithm The process of simultaneously inserting several knots into a
B-spline curve.
Parametrization Assigning parameter values to junction points in spline curves.
Also used with a different meaning: the function that describes the speed of a
point traversing a curve.
