Фафурин В.А., Терюшов И.Н. Автоматизация технологических процессов и производств

Подождите немного. Документ загружается.

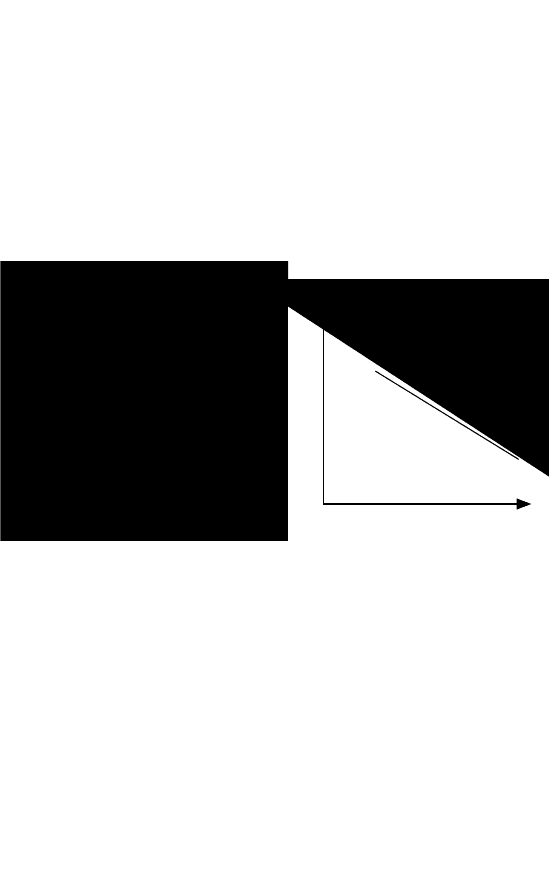
τJτ





где ∆τ - величина, определяемая по формуле (69).

2.6.Проводим аналогичные расчеты



и при других значениях

величин

maxx

измx

, изменяющихся в пределах (67) и (68) с

любым удобным для расчетов шагом: var (∆

maxx

) при

измx

=соnst

и var (

измx



) при

maxx

= const .

2.7. Результаты расчетов представляем в виде графиков

i max

i изм

и делаем выводы о влиянии величин

maxx

измx

на период

опроса датчика



. Результаты необходимо объяснить.

Задача 2. Фильтрация измеряемых величин от помех. Выбор и

расчет фильтров.

Исходные данные:

1. Параметры случайного процесса и искажающий полезный

сигнал помехи:

1.1. Дисперсия случайного процесса

хх

σD 

1.2. Коэффициент экспоненты, аппроксимирующей

корреляционную функцию случайного процесса, α.

1.3. Параметры помехи k и m (см. таблицу 1.3).

2. Период опроса датчика



Требуется:

Выбрать тип фильтра и рассчитать его настроечный параметр n

или γ, обеспечивающий минимальную погрешность фильтрации при

заданных параметрах помехи k и m.

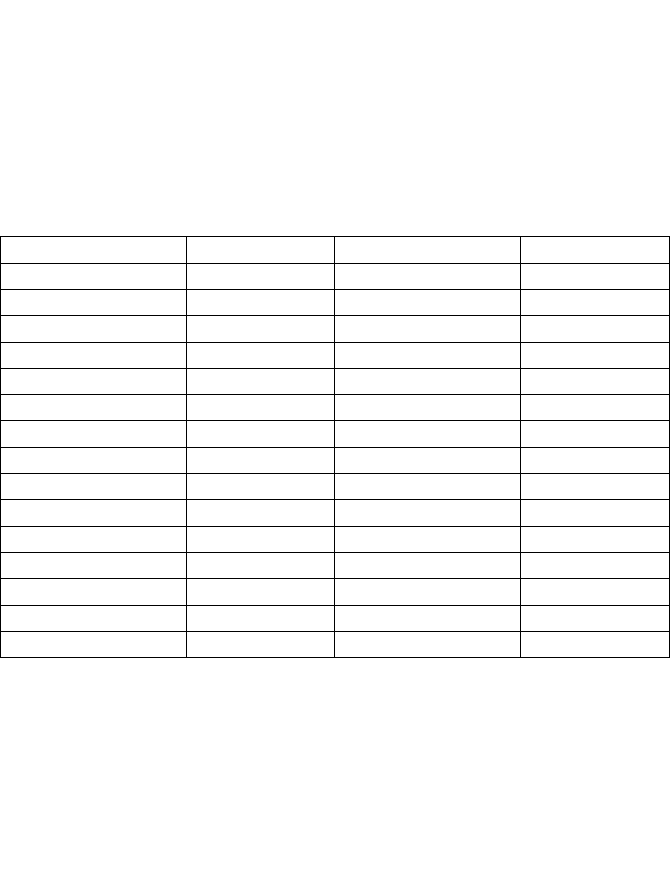
Таблица 1.3

k m k m

0,40 6,0 2,05 6,0

1,25 8,0 2,60 5,5

0,60 5,0 3,50 8,0

0,50 2,5 1,25 6,0

1,20 6,5 0,95 7,4

0,90 7,0 1,50 5,6

1,50 5,0 2,42 6,5

2,05 4,5 1,75 7,2

1,60 8,6 1,90 5,4

2,10 3,0 2,05 8,3

1,42 4,0 1,95 7,4

3,05 5,0 0,46 6,2

2,56 7,0 0,65 5,4

1,65 6,2 2,15 7,6

2,04 5,6 1,20 6,3

Порядок расчета

1. По полученной корреляционной функции при расчете периода

опроса датчика





определяем дисперсию D

случайного процесса

и коэффициент α экспоненты, аппроксимирующей эту

корреляционную функцию.

Дисперсию D

определяем как значение корреляционной

функции при



= 0 (см. рис.1.8).

Для определения коэффициента α аппроксимируем исходную

корреляционную функцию экспонентой. С этой целью проводим

следующие построения:

- на графике корреляционной функции находим точку перегиба,

т.е. точку максимальной скорости спада корреляционной функции, где

значение производной

 

max

τd

τdK



На графике, приведенном на рис.1.8, это будет точка А:

- проводим касательную ab в этой точке и находим постоянную

времени T экспоненты, аппроксимирующей исходную

корреляционную функцию*;

- находим коэффициент экспоненты α по формуле



 

1

минс

2. По диаграмме k(m), приведенной на рис.1.3, выбираем тип

фильтра** (скользящего среднего или экспоненциального

сглаживания), обеспечивающий требуемое качество фильтрации при

заданных параметрах помехи K и m.

3. Определяем параметры настройки выбранного типа фильтра.

Для фильтра скользящего среднего параметром настройки будет

величина n - число ординат усреднения случайного процесса.

Значение n обычно ищут на интервале 2 ≤ n ≤ 10 с шагом ∆n = 1.

Для фильтра экспоненциального сглаживания параметром

настройки будет величина γ- коэффициент экспоненциального

сглаживания. Значение γ ищут на интервале 0 < γ < 1 с шагом ∆γ =

0,05 (0,1).

Программы расчета оптимальных настроечных параметров

фильтров скользящего среднего и экспоненциального сглаживания

приведены ниже.

____________________________________________________________

*Нахождение точки перегиба А и проведение касательной ab можно

осуществить с достаточно высокой точностью, используя метод нормалей,

описанный в книге О.Б.Власова-Власюка «Экспериментальные методы в

автоматике». М.; Машиностроение. 1989. 412 с.

**Так как задачи фильтрации в АСУТП решаются программным

путем, то выбирать следует дискретные варианты фильтров.

Задача 3. Проверка исходной информации на достоверность и

коррекция результатов измерений.

Исходные данные:

1. Объект автоматизации, контролируемые параметры и схема

автоматизации контроля этих параметров.

2. Уравнение связи между измеряемыми параметрами

(материального или теплового и др.).

3. Измеренные значения параметров контроля.

4. Допустимые погрешности выполнения уравнений связи

(соблюдения материального, теплового балансов и др.).

5. Допустимые погрешности измерения параметров.

Весовые коэффициенты P

, позволяющие учесть различия в

классах точности измерительной аппаратуры (среднеквадратичные

погрешности измерения).

В нашей работе методику выявления метрологических отказов и

коррекции результатов измерений рассмотрим на примере

технологической системы, приведённой на рис.1.9, в которой

контролируются расходы четырёх потоков – трёх индивидуальных

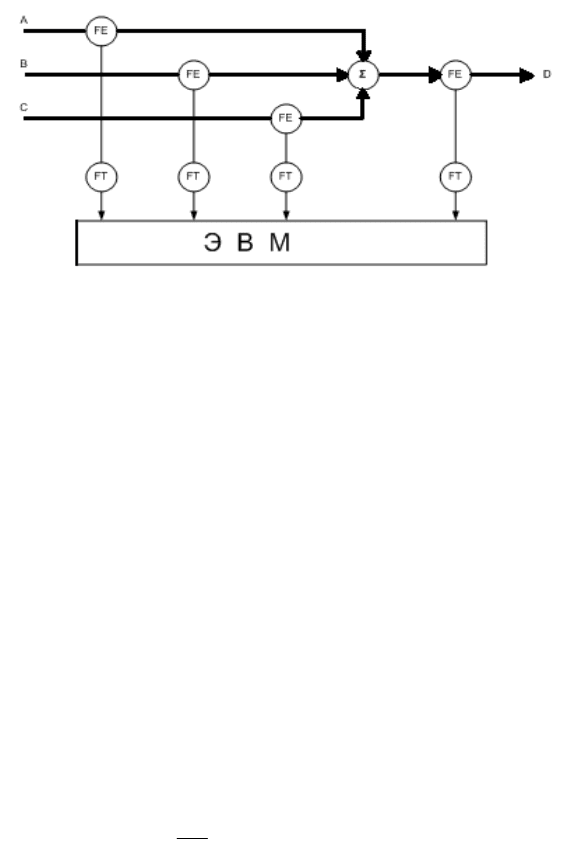
Рис.1.9. Схема автоматизации контроля расходов

технологических потоков: FE, FT датчики расхода; ∑ - сливной

коллектор

, F

и суммарного (коллекторного) потока F

связанных между собой согласно технологической схеме уравнением

материального баланса

+ F

= F

(70)

Указанные расходы контролируются соответствующими

расходомерами, информация с которых подается на ЭВМ, где

вычисляются скорректированные значения расходов потоков А, В и С

и проверяется условие соблюдения материального баланса (70). В

случае его несоблюдения компьютер по предлагаемой в этой работе

методике вычисляет погрешности измерения расходов F

, F

и корректирует их значения с целью сведения материального

баланса (70).

Требуется

1. Проверить условие соблюдения материального баланса (70).

2. В случае его невыполнения рассчитать оценки погрешностей

расходомеров ∆F

i ,

4,1i

и осуществить коррекцию их показаний с

целью сведения материального баланса (70).

Коррекцию показаний расходомеров осуществить по формуле

= x

- ∆x

(71)

где x

– измеренные значения расходов,

4,1i

;

∆x

- погрешности

измерения; x

- скорректированные значения расходов.

Порядок расчета

Исходные данные для расчета (по вариантам) и порядок расчета

погрешностей измерения ∆x

с коррекцией результатов измерений

приведены в методическом пособии [3], которое необходимо

использовать при выполнении этой работы.

Расчеты погрешностей ∆x

выполнить с использованием

микрокалькулятора. Проверку расчетов осуществить с

использованием компьютерной программы «DIAGNOSTICA»,

приведенной в приложении 1.

В этой программе X(i) ,

4,1i

- измеренные значения

расходов; ℓ - допустимая погрешность выполнения уравнения

материального баланса (70); dX(i) - допустимые погрешности

измерения; sigma (i) - среднеквадратичные погрешности измерения;

sx - погрешность выполнения уравнения связи (70) согласно

исходным данным по расходу потоков A,B,C,D; sdx - алгебраическая

сумма искомых погрешностей измерения; K - искомая константа; P(i)

- весовые коэффициенты;

 

iР



; i – число измерительных каналов.

Задача 4. Коррекция показаний датчиков при отклонении

условий измерения от расчетных (градуировочных).

4.1 Расходомеры переменного перепада давления

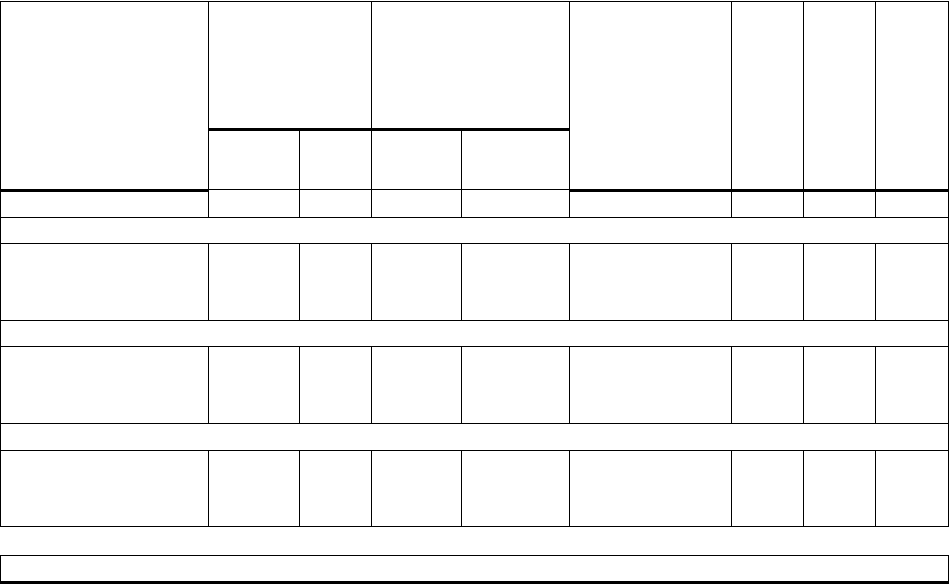
Таблица 1.4

Исходные данные для расчета скорректированных значений расходов

Технологический

поток

Параметры

технологичес

кого потока в

рабочем

состоянии

Расчетные

значения

параметров

Плотность

технологичес

кого потока

при расчетных

условиях



, кг/

АЦП

max

АЦП

max

Р, кгс/

см



атм

,К

1 2 3 4 5 6 7 8 9

Задание 1

Насыщенный пар

Газ

Перегретый пар

3,2

3,0

14,0

120

210

2,0

293

1,96

2,84

320

384

448

1024

630

500

320

Задание 2

Насыщенный пар

Газ

Перегретый пар

3,6

2,5

16,0

160

240

2,0

293

1,80

3,05

1536

1920

1056

4096

400

800

630

Задание 3

Насыщенный пар

Газ

Перегретый пар

4,0

3,6

12,0

160

200

2,0

293

1,96

2,76

384

320

256

1024

250

160

400

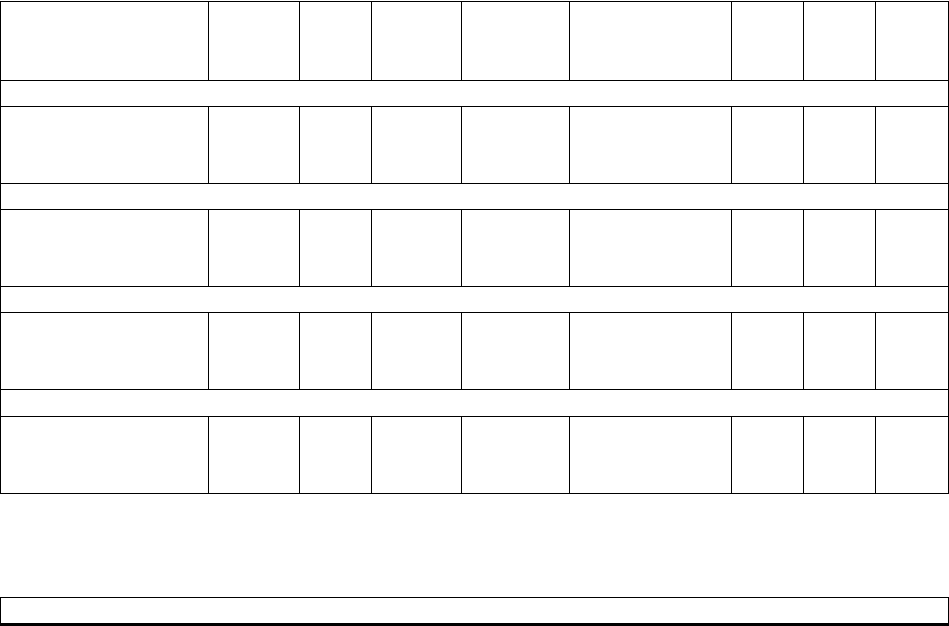
Продолжение таблицы 1.4

Задание 4

Насыщенный пар

Газ

Перегретый пар

3,4

4,0

15,0

200

220

2,0

293

1,96

2,90

430

320

384

1024

200

500

630

Задание 5

Насыщенный пар

Газ

Перегретый пар

6,0

3,2

16,4

220

250

2,0

293

2,24

3,02

256

1024

288

1024

4096

1024

250

800

630

Задание6

Насыщенный пар

Газ

Перегретый пар

5,5

4,0

15,6

230

240

2,0

293

2,78

3,00

320

448

288

1024

630

125

1000

Задание 7

Насыщенный пар

Газ

Перегретый пар

5,0

4,6

10,5

240

230

2,0

293

2,56

3,00

384

1536

283

1024

4096

1024

500

630

800

Задание 8

Насыщенный пар

Газ

Перегретый пар

5,2

4,0

8,0

260

240

2,0

293

2,62

3,20

288

384

1588

1024

630

1250

800

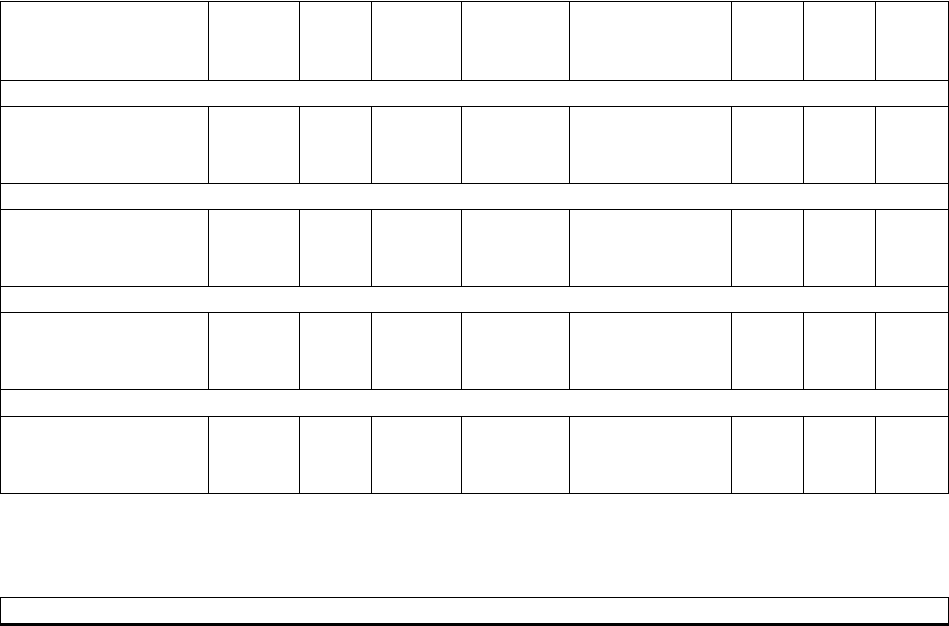
Продолжение таблицы 1.4

Задание 9

Насыщенный пар

Газ

Перегретый пар

3,8

3,6

12,9

220

240

2,0

239

2,06

3,05

352

1984

336

1024

4096

1024

800

1600

630

Задание 10

Насыщенный пар

Газ

Перегретый пар

6,2

3,9

10,6

250

2,0

293

2,64

3,04

368

256

1952

1024

4000

630

800

Задание 11

Насыщенный пар

Газ

Перегретый пар

3,0

4,2

16,5

240

200

2,0

293

2,08

3,06

256

1930

272

1024

4096

1024

400

630

800

Задание 12

Насыщенный пар

Газ

Перегретый пар

5,0

4,0

14,6

250

240

2,0

293

2,45

3,05

272

1962

304

1024

4096

1024

6300

800

5000

Задание 13

Насыщенный пар

Газ

Перегретый пар

4,6

5,2

12,4

120

208

2,4

293

2,08

2,84

320

384

448

1024

630

320

500

Продолжение таблица 1.4

Задание 14

Насыщенный пар

Газ

Перегретый пар

3,9

4,0

12,7

165

240

3,0

293

1,96

3,04

1056

1920

1536

4096

800

400

630

Задание15

Насыщенный пар

Газ

Перегретый пар

3,2

5,8

10,6

180

260

2,8

293

2,26

4,20

1410

416

1950

4096

1024

4096

630

800

1600

Задание 16

Насыщенный пар

Газ

Перегретый пар

4,6

5,0

14,2

220

270

3,4

293

1,86

4,35

360

2020

380

1024

4096

1024

630

800

400

Задание 17

Насыщенный пар

Газ

Перегретый пар

3,8

4,5

10,3

160

200

3,2

293

2,14

3,86

460

2040

2260

1024

4096

250

800

1600

Задание 18

Насыщенный пар

Газ

Перегретый пар

5,3

4,2

10,0

220

240

3,6

293

2,7

4,50

2400

524

4096

1024

630

800

400

Продолжение таблицы 1.4

Задание 19