Everitt B.S. The Cambridge Dictionary of Statistics

Подождите немного. Документ загружается.

different slopes intersecting the ordinate corresponding to zero dose of the stimuli. The

relative potency of these stimuli is obtained by taking the ratio of the estimated slopes of the

two lines. [Bioassay, 2nd edition, 1984, J. J. Hubert, Kendall-Hunt, Dubuque.]

Slutsky, Eugen (1 880^1 948): Born in Yaroslaval province, Slutsky entered the University of

Kiev as a student of mathematics in 1899 but was expelled three years later for revolutionary

activities. After studying law he became interested in political economy and in 1918

received an economic degree and became a professor at the Kiev Institute of Commerce.

In 1934 he obtained an honorary degree in mathematics from Moscow State University, and

took up an appointment at the Mathematical Institue of the Academy of Sciences of the

Soviet Union, an appointment he held until his death. Slutsky was one of the originators of

the theory of

stochastic processes

and in the last years of his life studied the problem of

compiling tables for functions of several variables.

Slutsky’stheorem:If X

; X

...; X

are a sequence of random variables such that

lim

n!1

PðX

 xÞ¼PðX  xÞ for some random variable x for which PðX  xÞ is continuous

everywhere, then for any continuous function g: lim

n!1

P½gðX

Þy¼P½gðX Þy

Slutsky ^ Y ule effect: The introduction of correlations into a

time series

by some form of

smoothing. If, for example, fx

g is a

white noise sequence

in which the observations are

completely independent, then the series fy

g obtained as a result of applying a

moving

average

of order 3, i.e.

¼ðx

t1

þ x

tþ1

Þ=3

consists of correlated observations. The same is true if fx

gis operated on by any

linear ﬁlter

[TMS Chapter 2.]

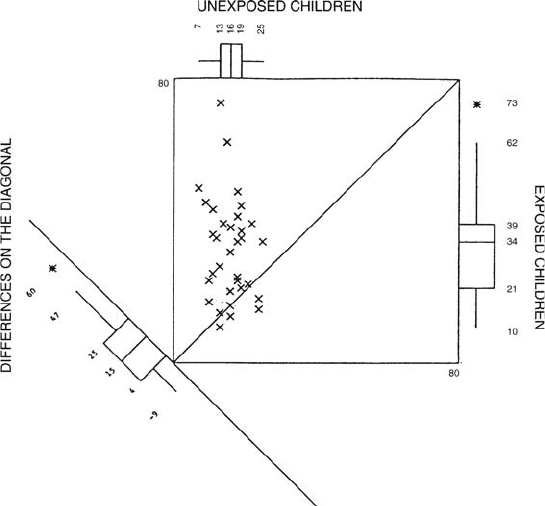
Fig. 127 An example of a sliding square plot for blood lead levels of matched pairs of children.

399

Small area estimation: The application of model-based or indirect estimators to link survey

outcome variables such as disease or substance use available for a national or regional

study, for example, a

census

, to local area predictors such as countydemographic and

socioeconomic variables, to estimate local area disease or substance use prevalence rates.

The ‘areas’ in small area estimation may be deﬁned by geographical domains such as a state

or county and by socio-demographic characteristics such as income, race, age, or gender

subgroups. Such an approach can be applied to cases where the number of area-speciﬁc

sample observations is not large enough to produce reliable direct estimates. [Small Area

Estimation, 2003, J. N. K. Rao, Wiley, New York.]

Small expected frequencies: A term that is found in discussions of the analysis of

contingency

tables

. It arises because the derivation of the

chi-squared distribution

as an approximation for

the distribution of the

chi-squared statistic

when the hypothesis of independence is true, is

made under the assumption that the expected frequencies are not too small. Typically this

rather vague phrase has been interpreted as meaning that a satisfactory approximation is

achieved only when expected frequencies are ﬁve or more. Despite the widespread accept-

ance of this ‘rule’, it is nowadays thought to be largely irrelevant since there is a great deal of

evidence that the usual chi-squared statistic can be used safely when expected frequencies

are far smaller. See also STATXACT.[The Analysis of Contingency Tables, 2nd edition,

1992, B. S. Everitt, Chapman and Hall/CRC Press, London.]

Smear-and-sweep: A method of adjusting death rates for the effects of confounding variables. The

procedure is iterative, each iteration consisting of two steps. The ﬁrst entails ‘smearing’ the

data into a two-way classiﬁcation based on two of the confounding variables, and the second

consists of ‘sweeping’ the resulting cells into categories according to their ordering on the

death rate of interest. [Encyclopedia of Statistical Sciences, 2006, eds. S.Kotz, C. B. Read,

N.Balakrishnan and B.Vidakovic, Wiley, New York.]

Smirnov, Nikolai Vasil’yevich ( 1 900^1 966): Born in Moscow, Russia, Smirnov graduated

from the University of Moscow in 1926 and then taught at Moscow University, Timoryazev

Agricultural Academy and Moscow City Pedagogical Institute. In 1938 he obtained his

doctorate with his dissertation, ‘On approximation of the distribution of random variables’.

From 1938 until his death Smirnov worked at the Steklov Mathematical Institute of the

USSR Academy of Sciences in Moscow making signiﬁcant contributions to the distribu-

tions of statistics used in

nonparametric tests

and the limiting distributions of

order statistics

He died on June 2nd, 1966 in Moscow.

Smith , Cedri c Aust en Bardel l ( 1 917^2002): Born in Leicester, UK, Smith won a scholarship

to Trinity College, Cambridge, in 1935 from where he graduated in mathematics with ﬁrst-

class honours in 1938. He then began research in statistics under

Bartlett

, J. Wishart and

Irwin

, taking his doctorate in 1942. After World War II Smith became Assistant Lecturer at

the Galton Laboratory, eventually becoming Weldon Professor in 1964. It was during this

period that he worked on linkage analysis, introducing ‘lods’ (log-odds) to linkage studies

and showing how to compute them. Later he introduced a Bayesian approach to such

studies. Smith died on 16 January 2002.

Sm ooth ingmet h ods: A term that could be applied to almost all techniques in statistics that involve

ﬁtting some model to a set of observations, but which is generally used for those methods

which use computing power to highlight unusual structure very effectively, by taking

advantage of people’s ability to draw conclusions from well-designed graphics. Examples

of such techniques include kernel methods, spline functions, nonparametric regression

and locally weighted regression. [TMS Chapter 2.]

400

Smoothlyclippedabsolutedeviation: A method for estimating the parameters in a regression

model and simultaneously selecting important variables consistently, whilst producing

parameter estimates that are as efﬁcient as if the true model was known. The method is

particularly important for

high-dimensional data

. See also lasso and sure screening meth-

ods.[Biometrika, 2007, 94, 553–568.]

SMR: Acronym for standardized mortality rate.

S^N cu rve: A curve relating the effect of a constant stress (S) on the test item to the number of cycles

to failure (N). [Statistical Research on Fatigue and Fracture, 1987, edited by T. Tanaka,

S. Nishijima and M. Ichikawa, Elsevier, London.]

Snedecor, George Waddel (1881^1974): Born in Memphis, Tennessee, USA, Snedecor

studied mathematics and physics at the Universities of Alabama and Michigan. In 1913 he

became Assistant Professor of Mathematics at Iowa State University and began teaching the

ﬁrst formal statistics course in 1915. In 1927 Snedecor became Director of a newly created

Mathematical Statistical Service in the Department of Mathematics with the remit to provide

a campus-wide statistical consultancy and computation service. He contributed to design of

experiments, sampling and

analysis of variance

and in 1937 produced a best selling book

Statistical Methods, which went through seven editions up to 1980. Snedecor died on 15

February 1974 in Amherst, Massachusetts.

Snedecor’s F-distribution: Synonym for F-distribution.

Snow, Joh n ( 1 813^1 858): Born in York, England, Snow was, at the age of 14, apprenticed to a

surgeon in Newcastle and later worked as a colliery surgeon. Snow was a pioneer in

epidemiology and his investigation of a cholera outbreak in Soho, a district of London, in

1854 in which he plotted the number of deaths in different streets and identiﬁed the popular

water pump in Broad Street as the source of the infection, probably saved many lives;

Snow’s ﬁndings also demonstrated that the ‘miasma’ (bad air) theory of how cholera was

spread to be wrong. Snow died in London on the 16th June, 1858.

Snowball sampling: A method of sampling that uses sample members to provide names of other

potential sample members. For example, in sampling heroin addicts, an addict may be asked

for the names of other addicts that he or she knows. Little is known about the statistical

properties of such samples. See also respondent driven sampling (RDS).[International

Journal of Epidemology, 1996, 25, 1267–70.]

Snowflak es: Synonymous for star plots.

Sobel and We i ss st o pping rul e: A procedure for selecting the ‘better’ (higher probability of

success, p) of two independent

binomial distributions

. The observations are obtained by a

play-the-winner rule

in which trials are made one at a time on either population and a success

dictates that the next observation be drawn from the same population while a failure causes a

switch to the other population. The proposed stopping rule speciﬁes that play-the-winner

sampling continues until r successes are obtained from one of the populations. At that time

sampling is terminated and the population with r successes is declared the better. The

constant r is chosen so that the procedure satisﬁes the requirement that the probability of

correct selection is at least some pre-speciﬁed value whenever the difference in the P-values

is at least some other speciﬁed value. See also play-the-winner rule.[Biometrika, 1970, 57,

357–65.]

So ft meth ods: Statistical modelling often needs to make qualitative and subjective judgements

that cannot be easily translated into precise probability values. Such judgements give rise to

401

a number of different types of uncertainty which classical statistics may not be equipped

to deal with. Soft methods are a range of powerful techniques developed in the area of

artiﬁcial intelligence

that attempt to address these problems when the encoding of subjective

information is unavoidable. See also belief functions and imprecise probabilities.

[Soft Methods in Probability, Statistics and Data Analysis, 2002, P. Grzegorzewski,

O. Hryniewicz and M. A. Gil, Springer, New York.]

So journ time: The total time spent in a condition or state. Often used in medicine for the interval during

which a particular condition is potentially detectable but not yet diagnosed. [Statistics in

Medicine, 1989, 8, 743–56.]

SO LAS: Software for

multiple imputation

. [Statistical Solutions, 8 South Bank, Crosse’s Green, Cork,

Ireland.]

SO LO: A computer package for calculating sample sizes to achieve a particular power for a variety of

different research designs. See also nQuery advisor. [Statistical Solutions, 8 South Bank,

Crosse’s Green, Cork, Ireland.]

So mer’ sd: A measure of association for a

contingency table

with ordered row and column categories

that is suitable for the asymmetric case in which one variable is considered the response and

one explanatory. See also Kendall’s tau statistics .[The Analysis of Contingency Tables ,

2nd edition, 1992, B. S. Everitt, Chapman and Hall/CRC Press, London.]

Sortedbinary plot: A graphical method for identifying and displaying patterns in

multivariate data

sets. [Technometrics, 1989, 31,61–7.]

Sources of data: Usually refers to reports and government publications giving, for example,

statistics on cancer registrations, number of abortions carried out in particular time periods,

number of deaths from AIDS, etc. Examples of such reports are those provided by the World

Health Organization, such as the

World Health Statistics Annual

which details the seasonal

distribution of new cases for about 40 different infectious diseases, and the

World Health

Quarterly

which includes statistics on mortality and morbidity.

Space ^ ti me cl uste ring: An approach to the analysis of epidemics that takes account of three

components:

the time distribution of cases;

the space distribution;

a measure of the space–time interaction.

The analysis uses the simultaneous measurement and classiﬁcation of time and distance

intervals between all possible pairs of cases. [Statistics in Medicine, 1995, 14, 2383–92.]

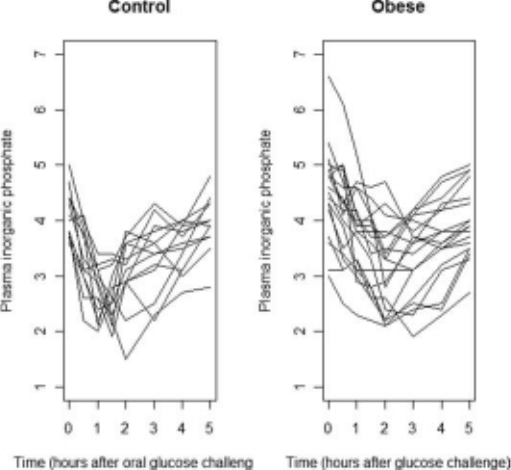
Spaghetti plot: A name occasionally used for a plot of individual subjects’ proﬁles of response

values in a longitudinal study. An example for data consisting of plasma inorganic phosphate

measurements obtained from 13 control and 20 obese patients 0.5, 1,1.5, 2 and 3 hours after

an oral glucose challenge is given in Figure 128 Such plots quickly become ‘messy’ as the

number of subjects increases.

Sparsity-of-effect principle: The belief that in many industrial experiments involving several

factors the system or process is likely to be driven primarily by some of the main effects and

low-order interactions. See also response surface methodology.

Spatial autocorrelation: See autocorrelation.

Spa tial automod e ls:

Spatial processes

whose probability structure is dependent only upon con-

tributions from neighbouring observations and where the conditional probability

402

distribution associated with each site belongs to the

exponential family

.[Graphical Models

and Image Processing, 1996, 58, 452–463.]

Spatial cumulative distribution function: A random function that provides a statistical

summary of a random ﬁeld over a spatial domain of interest. [Journal of the American

Statistical Association, 1999, 94,86–97.]

Spati al data: A collection of measurements or observations on one or more variables taken at speciﬁed

locations and for which the spatial organization of the data is of primary interest. [Spatial Data

Analysis by Example, Volume 1, 1985, G. Upton and B. Fingleton, Wiley, Chichester .]

Spati alexper i ment: A comparative experiment in which experimental units occupy ﬁxed locations

distributed throughout a region in one-, two- or three-dimensional space. Such experiments

are most common in agriculture. [Biometrics, 1991, 47, 223–239.]

Spatial med ian: An extension of the concept of a median to

bivariate data

.Deﬁned as the value of 

that minimizes the measure of scatter, T ðÞ, given by

TðÞ¼

 j

where jjis the

Euclidean distance

and x

; x

; ...; x

are n bivariate observations. See also

bivariate Oja median.[Journal of the Royal Statistical Society, Series B, 1995, 57,565–74.]

Spatial process: The values of random variables deﬁned at speciﬁed locations in an area. [Spatial

Data Analysis by Example, Volume 1, 1985, G. Upton and B. Fingleton, Wiley, Chichester.]

Spatial randomness: See complete spatial randomness.

Spearman ^ Brown prophesy formula: A formula arising in assessing the reliability of meas-

urements particularly in respect of scores obtained from psychological tests. Explicitly if

Fig. 128 Spaghetti plots for glucose challenge data obtained from control and obese groups.

403

each subject has k parallel (i.e. same true score, same standard error of measurement)

measurements then the reliability of their sum is

1 þðk  1ÞR

where R is the ratio of the true score variance to the observed score variance of each

measurement. [Statistical Evaluation of Measurement Errors: Design and Analysis of

Reliability Studies, 2004, G. Dunn, Arnold, London.]

Spea r m a n, Ch arl es Edward (1863^1945 ): Born in London Spearman attended private

schools where he showed strong interests in mathematics and science. On leaving school

he served as an army ofﬁcer in India for almost 15 years. During this time he read much

philosophy and psychology and after resigning from the army he went to Germany to study

experimental psychology. In 1906 Spearman obtained his Ph.D. He is now most remem-

bered for his early and pioneering work on correlation and

factor analysis

used in testing his

two-factor theory of human ability. He died in London on September 17

, 1945.

Spearman ^ Kärberest i mato r: An estimator of the

median effective dose

bioassays

having

a binary variable as a response. [Communications in Statistics – Theory and Methods,

1991, 20, 2577–88.]

Spearman’srho: A

rank correlation coefﬁcient

. If the ranked values of the two variables for a set of

n individuals are a

and b

, with d

¼ a

 b

, then the coefﬁcient is deﬁned explicitly as

 ¼ 1 

i¼1

 n

In essence ρ is simply Pearson’s product moment correlation coefﬁcient between the

rankings a and b. See also Kendall’s tau statistics. [SMR Chapter 11.]

Specif icity: An index of the performance of a

diagnostic test

, calculated as the percentage of

individuals without the disease who are classiﬁed as not having the disease, i.e. the

condi-

tional probability

of a negative test result given that the disease is absent. A test is speciﬁcif

it is positive for only a small percentage of those without the disease. See also sensitivity,

ROC curve and Bayes’ theorem. [SMR Chapter 14.]

Specif ic vari ates: See factor analysis.

Spectral analysis: A procedure for the analysis of the frequencies and periodicities in

time series

data. The time series is effectively decomposed into an inﬁnite number of periodic compo-

nents, each of inﬁnitesimal amplitude, so the purpose of the analysis is to estimate the

contributions of components in certain ranges of frequency, ω, i.e. what is usually referred to

as the spectrum of the series, often denoted hðωÞ. The spectrum and the

autocovariance

function

, γðkÞ, are related by

hðωÞ¼

k¼1

γðkÞcosðkωÞp  ω  p

The implication is that all the information in the autocovariances is also contained in the

spectrum and vice versa. Such an analysis may show that contributions to the ﬂuctuations in

the time series come from a continuous range of frequencies, and the pattern of spectral

densities may suggest a particular model for the series. Alternatively the analysis may

suggest one or two dominant frequencies. See also harmonic analysis, power spectrum

and fast Fourier transform. [TMS Chapter 7.]

404

Spectral density matrix: See multiple time series.

Spectral radius: A term sometimes used for the size of the largest eigenvalue of a

variance–

covariance matrix

Spectrum: See spectral analysis.

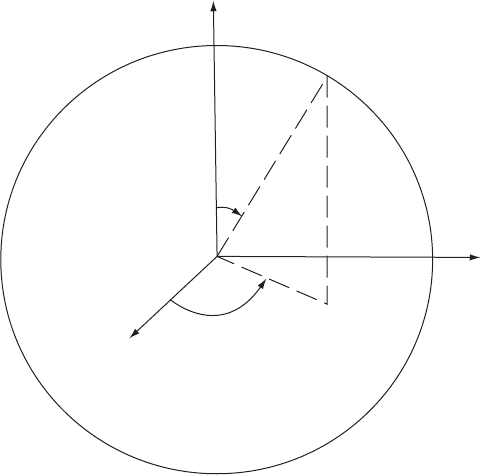
Spherical variable: An angular measure conﬁned to be on the unit sphere. Figure 129 shows a

representation of such a variable. [Multivariate Analysis, 1979, K. V. Marda, J. T. Kent and

J. B. Bibby, Academic Press, London.]

Sphericity: See Mauchly test.

Sphericity test: Synonym for Mauchly test.

Spiegelman, M ortimer ( 1 901^1 969): Born in Brooklyn, New York, Spiegelman received a

masters of engineering degree from the Polytechnic Institute of Brooklyn in 1923 and a

masters of business administration degree from Harvard University in 1925. He worked for

40 years for the Metropolitan Life Insurance Ofﬁce and made important contributions to

biostatistics particularly in the areas of

demography

and public health. Spiegelman died on

25 March 1969 in New York.

Spi neplot: An alternative to the

bar chart

for graphically representing categorical data; in this type of

plot the category count is represented by the width of the bar rather than by the height. An

example showing the number of failures and non-failures of the O-rings in space shuttle ﬂights

against temperature is shown in Figure 130. [Computational Statistics, 1996, 11,23–33.]

Spl ici ng: Areﬁned method of smoothing out local peaks and troughs, while retaining the broad ones,

in data sequences contaminated with noise.

Fig. 129 An illustration of a spherical variable.

405

Spline function: A smoothly joined piecewise polynomial of degree n. For example, if t

; t

; ...; t

are a set of n values in the interval a,b, such that a

 t

t

 b, then a cubic

spline is a function g such that on each of the intervals ða; t

Þ; ðt

; t

Þ; ...; ðt

; bÞ, g is a cubic

polynomial, and secondly the polynomial pieces ﬁt together at the points t

in such a way that

g itself and its ﬁrst and second derivatives are continuous at each t

and hence on the whole of

a, b. The points t

are called knots. A commonly used example is a cubic spline for the

smoothed estimation of the function g in the following model for the dependence of a

response variable y on an explanatory variable x

y ¼ f ðxÞþ

where  represents an error variable with expected value zero. The starting point for the

construction of the required estimator is the following minimization problem; ﬁnd f to

minimize

i¼1

ðy

 f ðx

ÞÞ

þ l

1

½f

ðuÞ

where primes represent differentiation. The ﬁrst term is the residual sum of squares which is

used as a distance function between data and estimator. The second term penalizes rough-

ness of the function. The parameter l  0 is a smoothing parameter that controls the trade-

off between the smoothness of the curve and the bias of the estimator. The solution to the

minimization problem is a cubic polynomial between successive x-values with continuous

ﬁrst and second derivatives at the observation points. Such curves are widely used for

interpolation for smoothing and in some forms of regression analysis. See also Reinsch

spline.[Journal of the Royal Statistical Society, Series B, 1985, 47,1–52.]

Split -half method: A procedure used primarily in psychology to estimate the reliability of a test.

Two scores are obtained from the same test, either from alternative items, the so-called

yes

fail

temperature

0.0

0.2 0.4 0.6 0.8 1.0

Fig. 130 Spineplot of space shuttle O-ring data.

406

odd–even technique, or from parallel sections of items. The correlation of these scores, or

some transformation of them gives the required reliability. See also Cronbach’s alpha.

[Statistical Evaluation of Measurement Errors: Design and Analysis of Reliability Studies,

2004, G. Dunn, Arnold, London.]

Spl it -lot desig n: A design useful in experiments where a product is formed from a number of

distinct processing stages. Each factor is applied to one and only one of the processing

stages with at each of these stages a split-plot structure being used. [Technometrics, 1998,

40, 127–40.]

Spl it -plot design: A term originating in agricultural ﬁeld experiments where the division of a testing

area or ‘plot’ into a number of parts permitted the inclusion of an extra factor into the study.

In medicine similar designs occur when the same patient or subject is observed at each level

of a factor, or at all combinations of levels of a number of factors. See also longitudinal data

and repeated measures data. [MV2, Chapter 13.]

S-P L US: A high level programming language with extensive graphical and statistical features that can

be used to undertake both standard and non-standard analyses relatively simply. [Insightful,

5th Floor, Network House, Basing View, Basingstoke, Hampshire, RG21 44G, UK;

Insightful Corporation, 1700 Westlake Avenue North, Suite 500, Seattle, Washington, WA

98109-3044, USA; www.insightful.com]

Spread: Synonym for dispersion.

Spreadsheet: In computer technology, a two-way table, with entries which may be numbers or text.

Facilities include operations on rows or columns. Entries may also give references to other

entries, making possible more complex operations. The name is derived from the sheet of

paper employed by an accountant to set out ﬁnancial calculations, often so large that it had to

be spread out on a table. [Journal of Medical Systems, 1990, 14, 107–17.]

SPSS: A statistical software package, an acronym for Statistical Package for the Social Sciences. A

comprehensive range of statistical procedures is available and, in addition, extensive

facilities for ﬁle manipulation and re-coding or transforming data. [SPSS UK, St

Andrew’s House, West St., Woking, Surrey, GU21 6EB, UK; SPSS Inc., 233 S.Wacker

Drive, Chicago, Illinois 60606-6307, USA; www.spss.com.]

Spuri ous correlatio n: Commonly used for a correlation between two variables that disappears when it

is ‘controlled’ for a third variable but is also used for the introduction of correlation due to

computing rates using the same denominator . Speciﬁcally if two variables X and Yare not related,

then the two ratios X/Z and Y/Z will be related, where Z is a further random variable. [Causality,

Models, Reasoning and Inference, 2000, J. Pearl, Cambridge University Press, Cambridge.]

Spurious precision: The tendency to report results to too many signi ﬁcant ﬁgures, largely due to

copying ﬁgures directly from computer output without applying some sensible

rounding