Everitt B.S. The Cambridge Dictionary of Statistics
Подождите немного. Документ загружается.

Kuiper’s test: A test that a circular random variable has an
angular uniform distribution
. Given a
set of observed values,
1
;
2
; ...;
n
the test statistic is
V
n
¼ D
þ
n
þ D
n
where
D
þ
n
¼ maxðj=n x
j
Þ; j ¼ 1; ...; n
D
n
¼ max
x
j
j 1
n
; j ¼ 1; ...; n
and x
j
¼
j
=2p. V
n
ffiffiffi
n
p
has an approximate standard normal distribution under the hypo-
thesis of an angular uniform distribution. See also Watson’s test. [MV2 Chapter 14.]
K u llback^ Lei bl er in f o rmati o n: A function, I,defined for two probability distributions, f(x)
and g(x) and given by
Iðf : gÞ¼
Z
1
1
f ðxÞlog
f ðxÞ
gðxÞ
dx
Essentially an asymmetric distance function for the two distributions.
Jeffreys’s distance
measure is a symmetric combination of the Kullback–Leibler information given by
Iðf ; gÞþIðg; f Þ
See also Bhattacharya ’s distance and Hellinger distance. [MV2 Chapter 11.]
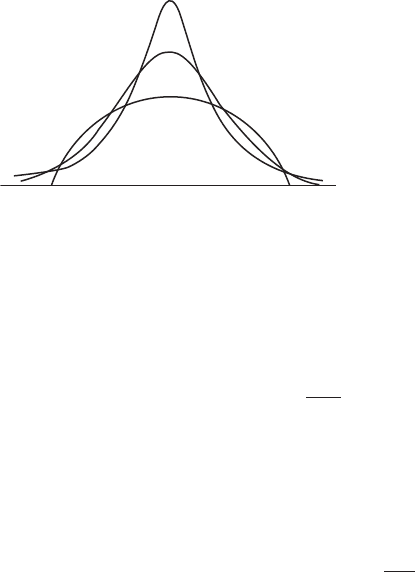
Kurtosis: The extent to which the peak of a unimodal probability distribution or frequency distri-
bution departs from the shape of a normal distribution, by either being more pointed
(leptokurtic)orflatter (platykurtic). Usually measured for a probability distribution as
4
=
2
2
where
4
is the fourth central
moment
of the distribution, and
2
is its variance.
(Corresponding functions of the sample moments are used for frequency distributions.)
For a normal distribution this index takes the value three and often the index is redefined
as the value above minus three so that the normal distribution would have a value zero.
(Other distributions with zero kurtosis are called mesokurtic.) For a distribution which is
leptokurtic the index is positive and for a platykurtic curve it is negative. See Fig. 82.
See also skewness. [KA1 Chapter 3.]
Kurtosis procedure: See many-outlier detection procedures.
Kwiatkowski-Phillips-Schmidt-Shin test (KPSS test): A test of the hypothesis that
a
time series
is
stationary
around a deterministic trend. [Journal of Economics, 1992, 54,
159–178.]
C
A
B
Fig. 82 Curves with differing degrees
of kurtosis: A, mesokurtic; B, platykurtic;
C, leptokurtic.
239

L
L’Abbe
´
plot: A plot often used in the
meta-analysis
of
clinical trials
where the outcome is a binary
response. The event risk (number of events/number of patients in a group) in the treatment
groups are plotted against the risk for the controls of each trial. If the trials are fairly
homogeneous the points will form a ‘cloud’ close to a line, the gradient of which will
correspond to the pooled treatment effect. Large deviations or scatter would indicate
possible heterogeneity. [Annals of Internal Medicine, 1987, 107, 224–33.]
Labour force survey: A survey carried out in the UK on a quarterly basis since the spring of 1992.
It covers 60 000 households and provides labour force and other details for about 120 000
people aged 16 and over. The survey covers not only unemployment, but employment, self-
employment, hours of work, redundancy, education and training.
Lackof memory property: A property possessed by a random variable Y, namely that
PrfY x þ y jY yg¼PrfY xg
Variables having an
exponential distribution
have this property, as do those following a
geometric distribution
.[A Primer on Statistical Distributions, 2003, N. Balakrishnan and
V. B. Nevzorov, Wiley, New York.]
Ladder of re-expression: See one-bend transformation.
Lagging indicators: Part of a collection of economic
time series
designed to provide information
about broad swings in measures of aggregate economic activity known as business cycles.
Used primarily to confirm recent turning points in such cycles. Such indicators change after
the overall economy has changed and examples include labour costs, business spending and
the unemployment rate.
Lagrange multipliers: A method of evaluating maxima or minima of a function of possibly several
variables, subject to one or more linear constraints. [Optimization, Theory and Applications,
1979, S. S. Rao, Wiley Eastern, New Delhi.]
Lagrange multiplier test: Synonym for score test.
Lancaster,HenryOliver(1913^2001): Born in Kempsey, New South Wales, Lancaster intended
to train as an actuary, but in 1931 enrolled as a medical student at the University of Sydney,
qualifying in 1937. Encountering Yule’s Introduction to the Theory of Statistics, he became
increasingly interested in statistical problems, particularly the analysis of 2 × 2 × 2
tables. After World War II this interest led him to obtain a post as Lecturer in Statistics at
the Sydney School of Public Health and Tropical Medicine. In 1948 Lancaster left Australia
to study at the London School of Hygiene and Tropical Medicine under
Bradford Hill
,
returning to Sydney in 1950 to study trends in Australian mortality. Later he undertook more
theoretical work that led to his 1969 book, The Chi-squared Distribution. In 1966 he was
made President of the Statistical Society of Australia. Lancaster died in Sydney on 2
December 2001.
240

Lancast ermod els: A means of representing the
joint distribution
of a set of variables in terms of the
marginal distributions
, assuming all interactions higher than a certain order vanish. Such
models provide a way to capture dependencies between variables without making the
sometimes unrealisitic assumptions of total independence on the one hand, yet having a
model that does not require an unrealistic number of observations to provide precise
parameter estimates. [Statistical Pattern Recognition, 1999, A. Webb, Arnold, London.]
Landmark an alysis: A term applied to a form of analysis occasionally applied to data consisting of
survival times in which a test is used to assess whether ‘treatment’ predicts subsequent
survival time among subjects who survive to a ‘landmark’ time (for example, 6 months post-
randomization) and who have, at this time, a common prophylaxis status and history of all
other covariates. [Statistics in Medicine, 1996, 15, 2797–812.]
Lan dma r k-based shape an alys i s: An approach to quantifying the shape and shape differences
of widely-spaced landmarks (coordinate points) that allows visualization of these differ-
ences between groups. [Statistical Shape Analysis, 1998, I. Dryden and K. V. Mardia, Wiley,
New York.]
Landmark registrat i on: A method for aligning the profiles in a set of
repeated measures data
, for
example
human growth curves
, by identifying the timing of salient features such as peaks,
troughs, or inflection points. Curves are then aligned by transforming individual time so that
landmark events become synchronized. [The Annals of Statistics, 1992, 16,82–112.]
Lapl a ce ap pr ox im a tion: An approach to approximating the integral of a function ∫ f(x)dx by fitting
a multivariate normal density at the maximum
^
x of f(x) and computing the volume under
the density. The covariance matrix of the fitted
multivariate normal distribution
is deter-
mined by the
Hessian matrix
of log f(x) at the maximum
^
x. The term is also used
for approximating the
posterior distribution
with a multivariate normal centered at the
maximum a posteriori estimate. [Bayesian Data Analysis, 2004, A.Gelman, J. B. Carlin,
H. S. Stern and D. B. Rubin, Chapman and Hall/CRC, Boca Raton.]
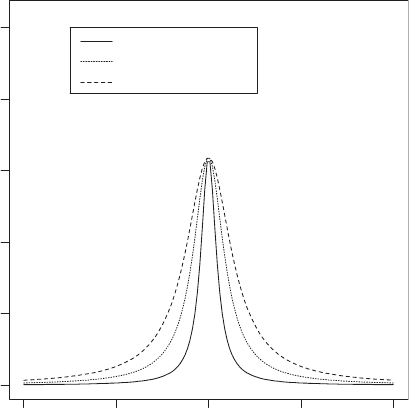
Lapl a ce distrib utio n: The probability distribution, f (x), given by
f ðxÞ¼
1
2
1
exp
jx j
4
0; 1
5
x
5
1
Can be derived as the distribution of the difference of two independent random variables
each having an identical
exponential distribution
. Examples of the distribution are shown in
Fig. 83. The mean, variance,
skewness
and
kurtosis
of the distribution are as follows:
mean ¼
variance ¼ 2
2
skewness ¼ 0
kurtosis ¼ 6
Also known as the double exponential distribution. [STD Chapter 22.]
Laplace, Pie rre-Si mon , M arq u is de ( 1749^1 827): Born in Beaumont-en-Auge near to Caen
where he first studied, Laplace made immense contributions to physics, particularly astron-
omy, and mathematics. Became a professor at the École Militaire in 1771 and entered the
Académie des Sciences in 1773. Most noted for his five-volume work Traité de Mécanique
Céleste he also did considerable work in probability including independently discovering
Bayes’ theorem
, ten years after Bayes’ essay on the topic. Much of this work was published
in Théorie Analytique des Probabilités. Laplace died on 5 March 1827, in Paris.
241
Large samplemethods: Methods for evaluating the performance of estimators and statistics as the
sample size tends to infinity. See also asymptotic distribution .
Lasagna’slaw: Once a
clinical trial
has started the number of suitable patients dwindles to a
tenth of what was calculated before the trial began. [British Medical Journal, 2001, 322,
1457–62.]
Lasso: A penalized
least squares regression
method that can be used for variable selection on high-
dimensional data. For a
multiple linear regression
model of the form
y
i
¼ x
0
i
β þ
i
The lasso estimator of β is the value that minimizes
X
n
i¼1
ðy
i
x
0
i
βÞ
2
þ l
X
q
j¼1
jβ
j
j
where q is the number of variables and λ is the penalty parameter. The estimator minimizes
the usual sum of squared errors but has a bound on the sum of the absolute values of these
coefficents. When the bound is large enough the constraint has no effect and the solution is
simply that of multiple regression. When however the bound is smaller the parameter
estimates are ‘shrunken’ versions of the least squares estimates. [Journal of the Royal
Statistical Society, Series B, 1996, 58, 267–288.]
Last observation carried forward: A method for replacing the observations of patients who
drop out of a
clinical trial
carried out over a period of time. It consists of substituting for each
missing value
the subject’s last available assessment of the same type. Although widely
applied, particularly in the pharmaceutical industry, its usefulness is very limited since it
makes very unlikely assumptions about the data, for example, that the (unobserved) post
drop-out response remains frozen at the last observed value. See also imputation.[Statistics
in Medicine, 1992, 11, 2043–62.]
x
f(x)
–20 –10 0 10 20
0.0 0.1 0.2 0.3 0.4 0.5
alpha = 0, beta = 1
alpha = 0, beta = 2
alpha = 0, beta = 3
Fig. 83 Laplace
distributions for α =0;
β =1,2,3.
242
Latent c lass analys i s: A method of assessing whether a set of observations involving q categorical
variables, in particular , binary variables, consists of a number of dif ferent groups or classes within
which the variables are independent. Essentially a
finite mixture model
in which the component
distributions are the product of q Bernoulli distributions, one for each of the binary variables in
the data. Parameters in such models can be estimated by
maximum likelihood estimation
via the
EM algorithm
. Can be considered as either an analogue of
factor analysis
for categorical
variables, or a model of
cluster analysis
for such data. See also grade of membership model.
[An Introduction to Latent Variable Models, 1984, B. S. Everitt, Chapman and Hall, London.]
Latent c lass i dentif i ab ility d i s pl a y: A graphical diagnostic for recognizing weakly identified
models in applications of
latent class analysis
.[Biometrics, 2000, 56, 1055–67.]
Latent period: The time interval between the initiation time of a disease process and the time of the
first occurrence of a specifically defined manifestation of the disease. An example is the
period between exposure to a tumorigenic dose of radioactivity and the appearance of
tumours. [The Mathematical Theory of Infectious Diseases and its Applications, 1975,
N. T. J. Bailey, Arnold, London.]
Latent root d istributions: Probability distributions for the latent roots of a square matrix whose
elements are random variables having a
joint distribution
. Those of primary importance arise
in multivariate analyses based on the assumption of
multivariate normal distributions
. See
also Bartlett’s test for eigenvalues.[An Introduction to Multivariate Statistics, 1979, M. S.
Srivastava and C. G. Khatri, North Holland, New York.]
Latent roots: Synonym for eigenvalues.
Latent var iabl e: Avariable that cannot be measured directly, but is assumed to be related to a number
of observable or manifest variables. Examples include racial prejudice and social class. See
also indicator variable.[An Introduction to Latent Variable Models, 1984, B. S. Everitt,
Chapman and Hall/CRC Press, London.]
Latent vectors: Synonym for eigenvectors.
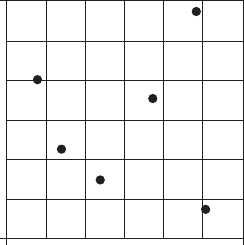
Latin hypercube sampling (LHS): A stratified random sampling technique in which a sample of
size N from multiple (continuous) variables is drawn such that for each individual variable
the sample is (marginally) maximally stratified, where a sample is maximally stratified when
the number of strata equals the sample size N and when the probability of falling in each of
the strata equals N
−1
. An example is shown in Fig. 84, involving two independent uniform
[0,1] variables, the number of categories per variable equals the sample size (6), each row or
each column contains one element and the width of rows and columns is 1/6. [Reliability
Engineering and System Safety, 2003, 81,23–69.]
Latin sq uar e: An experimental design aimed at removing from the experimental error the variation
from two extraneous sources so that a more sensitive test of the treatment effect can be
achieved. The rows and columns of the square represent the levels of the two extraneous
factors. The treatments are represented by Roman letters arranged so that no letter appears
more than once in each row and column. The following is an example of a 4 × 4 Latin square
ABCD
BCDA
CDAB
DABC
See also Graeco-Latin square.[Handbook of Experimental Methods for Process
Improvement, 1997, D. Drain, Chapman and Hall, London.]
243
Lattice designs: A class of
incomplete block designs
introduced to increase the precision of treat-
ment comparisons particularly in agricultural crop trials. [The Design of Experiments, 1988,
R. Mead, Cambridge University Press, Cambridge.]
Lattice distribution: A class of probability distributions to which most distributions for discrete
random variables used in statistics belong. In such distributions the intervals between values
of any one random variable for which there are non-zero probabilities are all integral
multiples of one quantity. Points with these coordinates thus form a lattice. By an approx-
imate linear transformation it can be arranged that all variables take values which are
integers. [Univariate Discrete Distributions, 2005, N. I. Johnson, A. W. Kemp and
S. Kotz, Wiley, New York.]
Lattice square: An
incomplete block design
for ν =(s − 1)s treatments in b = rs
blocks
, each
containing s − 1 units. In addition the blocks can be arranged into r complete replications.
[Biometrics, 1977, 33, 410–13.]
Law of large numbers: A ‘law’ that attempts to formalize the intuitive notion of probability
which assumes that if in n identical trials an event A occurs n
A
times, and if n is very
large, then n
A
/n should be near the probability of A. The formalization involves translating
‘identical trials’ as
Bernoulli trials
with probability p of a success. The law then states that as
n increases, the probability that the average number of successes deviates from p by more
then any preassigned value where
4
0 is arbitrarily small but fixed, tends to zero.
[An Introduction to Probability Theory, Volume 1, 3rd edition, 1968, W. Feller, Wiley,
New York.]
Law o flikelih ood: Within the framework of a statistical model, a particular set of data supports one
statistical hypothesis better than another if the
likelihood
of the first hypothesis, on the data,
exceeds the likelihood of the second hypothesis. [Likelihood, 1992, A. W. F. Edwards,
Cambridge University Press, Cambridge.]
Law of primacy: A ‘law’ relevant to work in market research which says that an individual for
whom, at the moment of choice, n brands are tied for first place in brand strength chooses
each of these n brands with probability 1/n.[Marketing Research: State of the Art
Perspectives, edited by C. Chakrapani, 2000, American Marketing Association, Chicago.]
Law of truly large numbers: The law that says that, with a large enough sample, any outrageous
thing is likely to happen. See also coincidences.
LD50: Abbreviation for lethal dose 50.
B
A
0
0
1
1
Fig. 84 Latin hypercube sampling.
244
LDUtest: A test for the rank of a matrix A using an estimate of A based on a sample of observations.
[Journal of the American Statistical Association, 1996, 91, 1301–9.]
Leadt im e: An indicator of the effectiveness of a screening test for chronic diseases given by the length
of time the diagnosis is advanced by screening. [International Journal of Epidemiology,
1982, 11, 261–7.]
Lead timeb ias: A term used particularly with respect to cancer studies for the bias that arises when the
time from early detection to the time when the cancer would have been symptomatic is added
to the
survival time
of each case. [Journal of the National Cancer Institute, 1968, 41,665–81.]
Leaps-and-bounds algorithm: An algorithm used to find the optimal solution in problems that
may have a very large number of possible solutions. Begins by splitting the possible
solutions into a number of exclusive subsets and limits the number of subsets that need to
be examined in searching for the optimal solution by a number of different strategies. Often
used in
all subsets regression
to restrict the number of models that have to be examined.
[ARA Chapter 7.]
Least absolute deviation reg ression: An alternative to
least squares estimation
for determin-
ing the parameters in
multiple regression
. The criterion minimized to find the estimators of
the regression coefficients is S, given by;
S ¼
X
n
i¼1
j y
i
β
0
X
q
j¼1
β
j
x
ij
j
where y
i
and x
ij
; j ¼ 1; ...; q are the response variable and explanatory variable values for
individual i. The estimators, b
0
; b
1
; ...; b
q
of the regression coefficients, β
0
; β
1
; ...; β
q
are
such that the median(b
i
Þ¼β
i
(median unbiased) and are
maximum likelihood estimators
when the errors have a
Laplace distribution
. This type of regression has greater power than
that based on least squares for asymmetric error distributions and heavy tailed, symmetric
error distributions; it also has greater resistance to the influence of a few outlying values of
the dependent variable. [Transformation and Weighting in Regression, 1988, R. J. Carroll
and D. Ruppert, Chapman and Hall/CRC Press, London.]
Least significant difference test: An approach to comparing a set of means that controls the
familywise error rate
at some particular level, say α. The hypothesis of the equality of the
means is tested first by an α-level
F-test
. If this test is not significant, then the procedure
terminates without making detailed inferences on pairwise differences; otherwise each
pairwise difference is tested by an α-level,
Student’s t-test
.
Least squares cross-validation: A method of cross validation in which models are assessed by
calculating the sum of squares of differences between the observed values of a sub-set of the
data and the relevant predicted values calculated from fitting a model to the remainder of the
data. [ Biometrika, 1984, 71, 353–60.]
Least sq ua r es esti m ation: A method used for estimating parameters, particularly in regression
analysis, by minimizing the difference between the observed response and the value predicted
by the model. For example, if the expected value of a response variable y is of the form
E ð yÞ¼α þ βx
where x is an explanatory variable, then least squares estimators of the parameters α and β
may be obtained from n pairs of sample values ðx
1
; y
1
Þ; ðx
2
; y
2
Þ; ...; ðx
n
; y
n
Þ by minimizing
S given by
245

S ¼
X
n
i¼1
ðy
i
α βx
i
Þ
2
to give
^
α ¼
y
^
β
x
^
β ¼
P
n
i¼1
ðx
i
xÞðy
i
yÞ
P
n
i¼1
ðx
i
xÞ
2
Often referred to as ordinary least squares to differentiate this simple version of the
technique from more involved versions such as,
weighted least squares
and
iteratively
reweighted least squares
. [ARA Chapter 1.]
Leave-one-out estimator: See error-rate estimation.
LeCam, Lucien (1924^2000): Born in Felletin, France, LeCam studied at the University of Paris
and received a Licence en Sciences (university diploma) in 1945. His career began with
work on power and hydraulic systems at the Electricité de France, but in 1950 he went to
Berkeley at the invitation of
Jerzy Neyman
. LeCam received a Ph.D. from the university in
1952. He was made Assistant Professor of Mathematics in 1953 and in 1955 joined the new
Department of Statistics at Berkeley. He was departmental chairman from 1961 to 1965.
LeCam was a brilliant mathematician and made important contributions to the asymptotic
theory of statistics, much of the work being published in his book Asymptotic Methods in
Statistical Decision Theory, published in 1986.
Left-censored: See censored observations.
Lehmann, Erich Leo (1917^2009): Lehmann obtained his MA and PhD from the University of
California, Berkeley where he worked from 1942. During the Second World War he worked
as an analyst for the US Air Force. In the early 1950s Lehmann worked at Columbia,
Princeton and Stanford universities, before returning to Berkeley. Erich Lehmann made
numerous important contributions to mathematical statistics, particularly to estimation
theory and the theory of hypothesis testing. He served as editor of The Annals of
Mathematical Statistics, was president of the Institute of Mathematical Statistics, and an
elected member of the American Academy of Arts and Sciences and the US National
Academy of Science. Erich Lehmann died on September 12th 2009.
Length -b iased data: Data that arise when the probability that an item is sampled is proportional to
its length. A prime example of this situation occurs in
renewal theory
where inter-event time
data are of this type if they are obtained by sampling lifetimes in progress at a randomly
chosen point in time. [Biometrika, 1996, 83, 343–54.]
Length-biased sampling: The bias that arises in a sampling scheme based on patient visits, when
some individuals are more likely to be selected than others simply because they make more
frequent visits. In a
screening study
for cancer, for example, the sample of cases detected is
likely to contain an excess of slow-growing cancers compared to the sample diagnosed
positive because of their symptoms. [Australian Journal of Statistics, 1981, 23,91–4.]
Lenth’smethod: An objective method for deciding which effects are active in the analysis of
unreplicated experiments, when the model is saturated and hence there are no degrees of
freedom for estimating the error variance. [Technometrics, 1989, 31, 469–473.]
Lepagetest: A
distribution free test
for either location or dispersion. The test statistic is related to that
used in the
Mann–Whitney test
and the
Ansari–Bradley test
. [NSM Chapter 5.]
246

Leptokurtic curve: See kurtosis.
Les lie matr ix mo del: A model often applied in demographic and animal population studies in
which the vector of the number of individuals of each age at time t, N
t
, is related to the initial
number of individuals of each age, N
0
, by the equation
N
t
¼ M
t
N
0
where M is what is known as the population projection matrix given by
M ¼
B
0
B
1
B
2
B
v1
B
v
P
0
00 00
0 P
1
0 00
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
000 P
v1
P
v
0
B
B
B
B
B
@
1
C
C
C
C
C
A
where B
x
equals the number of females born to females of age x in one unit of time that
survive to the next unit of time, P
x
equals the proportion of females of age x at time t that
survive to time t + 1 and v is the greatest age attained. See also population growth model.
[Bulletin of Mathematical Biology, 1995, 57, 381–99.]
Lethal dose 50: The administered dose of a compound that causes death to 50% of the animals
during a specified period, in an experiment involving toxic material. [Modelling Binary
Data, 2nd edition, 2003, D. Collett, Chapman and Hall/CRC Press, London.]
Levene test: A test used for detecting heterogeneity of variance, which consists of an
analysis of
variance
applied to
residuals
calculated as the differences between observations and group
means. [ Journal of the American Statistical Association, 1974, 69, 364–7.]
Leverage poi nts: A term used in regression analysis for those observations that have an extreme
value on one or more explanatory variables. The effect of such points is to force the fitted
model close to the observed value of the response leading to a small residual. See also hat
matrix, influence statistics and Cook’s distance. [ARA Chapter 10.]
Le
´
vy concentrationfunction: A function Q(x; λ) of a random variable X defined by the equality
QðX ; lÞ¼
sup
x
Prðx X x þ lÞ
for every l 0; QðX ; lÞ is a non-decreasing function of λ satisfying the inequalities
0 QðX ; lÞ1 for every l 0. A measure of the variability of the random variable that
is used to investigate convergence problems for sums of independent random variables.
[Concentration Functions, 1973, W. Hengarner and R. Theodorescu, Academic Press, New
York.]
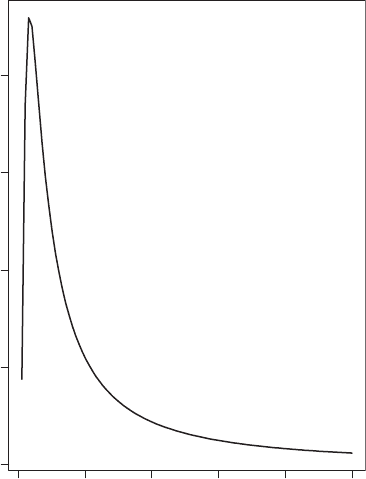
Le
´
vy distribution: A probability distribution, f(x), given by
f ðxÞ¼ð2pÞ
1
2
exp½
1
2x
x
3
2
; 0 x
5
1
None of the moments of the distribution exist. An example of such a distribution is given in
Fig. 85. [KA1 Chapter 4.]
Le
´
vy, Paul-Pierre (1886^1971): Born in Paris, Lévy was educated at the Ecole Polytechnique
between 1904 and 1906. His main work was in the calculus of probability where he
introduced the
characteristic function
, and in
Markov chains
,
martingales
and
game theory
.
Lévy died on 15 December 1971 in Paris.
247
Le
´
vy process: A
stochastic process
that has independent and stationary increments and a stochasti-
cally continuous sample path. Such processes provide a natural generalization of the sum of
independent and identically distributed random variables. [Journal of Financial Economics,
2004, 71,113–141.]
Lexian d ist ri butio ns:
Finite mixture distributions
having component
binomial distributions
with
common n.[Univariate Discrete Distributions, 2005, N. I. Johnson, A. W. Kemp and
S. Kotz, Wiley, New York.]
Lexicostatistics: A term sometimes used for investigations of the evolution times of languages,
involving counting the number of cognate words shared by each pair of present-day
languages and using these data to reconstruct the ancestry of the family. [Statistique
Textuelle, 1994, L. Lebart and A. Salem, Dunod, Paris.]
Lexisdiagram: A diagram for displaying the simultaneous effects of two time scales (usually age and
calendar time) on a rate. For example, mortality rates from cancer of the cervix depend upon
age, as a result of the age-dependence of the
incidence
, and upon calendar time as a result of
changes in treatment, population screening and so on. The main feature of such a diagram is
a series of rectangular regions corresponding to a combination of two time bands, one from
each scale. Rates for these combinations of bands can be estimated by allocating failures to
the rectangles in which they occur and dividing the total observation time for each subject
between rectangles according to how long the subjects spend in each. An example of such a
diagram is given in Fig. 86.[Statistics in Medicine, 1987, 6, 449–68.]
Lexis,Wilhelm (1837^1914): Lexis’s early studies were in science and mathematics. He graduated
from the University of Bonn in 1859 with a thesis on analytic mechanics and a degree in
mathematics. In 1861 he went to Paris to study social science and his most important
statistical work consisted of several articles published between 1876 and 1880 on population
and
vital statistics
.
x
f(x)
0246810
0.0 0.1 0.2 0.3 0.4
Fig. 85 An example of a Lévy
distribution.
248
