Everitt B.S. The Cambridge Dictionary of Statistics

Подождите немного. Документ загружается.

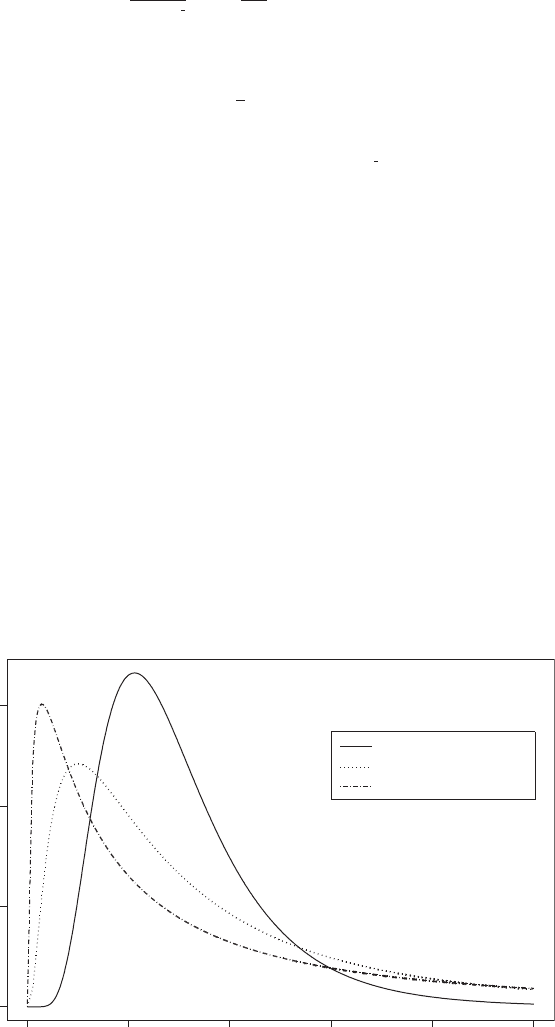
Lognormal distri bution: The probability distribution of a random variable, X, for which ln (X) has

a normal distribution with mean µ and variance σ

. The distribution is given by

f ðxÞ¼

xð2pÞ

exp 

2

ðln x  Þ



0  x

The mean, variance,

skewness

and

kurtosis

of the distribution are

mean ¼ expð þ



variance ¼ expð2 þ

Þðexpð

Þ1Þ

skewness ¼ðexpð

Þþ2Þðexpð

Þ1Þ

kurtosis ¼ expð4

Þþ2 expð3

Þþ3 expð2

Þ3

For small σ the distribution is approximated by the normal distribution. Some examples of

the distribution are given in Fig. 90. [STD Chapter 25.]

Logrank test: A test for comparing two or more sets of

survival times

, to assess the null hypothesis

that there is no difference in the survival experience of the individuals in the different groups.

For the two-group situation the

test statistic

U ¼

j¼1

ðd

 e

where d

is the number of deaths in the ﬁrst group at t

(j)

, the jth ordered death time,

j ¼ 1; 2; ...; r, and e

is the corresponding expected number of deaths given by

¼ n

where d

is the total number of deaths at time t

(j)

, n

is the total number of individuals at risk at

this time, and n

the number of individuals at risk in the ﬁrst group. The expected value of U

is zero and its variance is given by

f(x)

0246810

0.0 0.1 0.2 0.3

mu = 1.0, sigma = 0.5

mu = 1.0, sigma = 1.0

mu = 1.0, sigma = 1.5

Fig. 90 Lognormal distributions for µ = = 1.0; σ = 0.5, 1.0, 1.5.

259

V ¼

j¼1

where

ðn

 d

ðn

 1Þ

Consequently U=

ﬃﬃﬃﬃ

can be referred to a standard normal distribution to assess the

hypothesis of interest. Other tests use the same test statistic with different values for the

weights. The Tarone–Ware test, for example, uses w

ﬃﬃﬃ

and the Peto-Prentice test uses

i¼1

 d

þ 1

[SMR Chapter 13.]

LOGXACT: A specialized statistical package that provides exact inference capabilities for

logistic

regression

. [Cytel Software Corp., 675 Massachusetts Avenue, Cambridge, MA 02139

USA.]

Lomb periodogram: A generalization of the

periodogram

for unequally spaced

time series

[Biological Rhythm Research, 2001, 32, 341–5.]

Lo ngini ^ K oopman mode l: In

epidemiology

a model for primary and secondary infection, based

on the characterization of the

extra-binomial variation

in an infection rate that might arise

due to the ‘clustering’ of the infected individual within households. The assumptions

underlying the model are:

a person may become infected at most once during the course of the epidemic;

all persons are members of a closed ‘community’. In addition each person belongs to a

single ‘household’. A household may consist of one or several individuals;

the sources of infection from the community are distributed homogeneously through-

out the community. Household members mix at random within the household;

each person can be infected either from within the household or from the community.

The probability that a person is infected from the community is independent of the

number of infected members in his or her household;

The probability that exactly k additional individuals will become infected for a household

with s initial susceptibles and j initial infections is

Pðkjs; jÞ¼



Pðkjk; jÞB

ðskÞ

ðjþkÞðskÞ

k ¼ 0; 1; ...; s  1

Pðsjs; jÞ¼1 

s1

k¼0

Pðkjs; kÞ

where B is the probability that a susceptible individual is not infected from the community

during the course of the infection, and Q is the probability that a susceptible person escapes

infection from a single infected household member . [Statistics in Medicine, 1994, 13, 1563–74.]

Lo ngit u dinaldata: Data arising when each of a number of subjects or patients give rise to a vector of

measurements representing the same variable observed at a number of different time points.

Such data combine elements of multivariate data and

time series

data. They differ from the

former, however, in that only a single variable is involved, and from the latter in consisting of

a (possibly) large number of short series, one from each subject, rather than a single long

260

series. Such data can be collected either prospectively, following subjects forward in time, or

retrospectively, by extracting measurements on each person from historical records. This

type of data is also often known as repeated measures data, particularly in the social and

behavioural sciences, although in these disciplines such data are more likely to arise from

observing individuals repeatedly under different experimental conditions rather than from a

simple time sequence. Special statistical methods are often needed for the analysis of this

type of data because the set of measurements on one subject tend to be intercorrelated. This

correlation must be taken into account to draw valid scientiﬁc inferences. The design of most

such studies speciﬁes that all subjects are to have the same number of repeated measure-

ments made at equivalent time intervals. Such data is generally referred to as balanced

longitudinal data. But although balanced data is generally the aim, unbalanced longitudinal

data in which subjects may have different numbers of repeated measurements made at

differing time intervals, do arise for a variety of reasons. Occasionally the data are unbal-

anced or incomplete by design; an investigator may, for example, choose in advance to take

measurements every hour on one half of the subjects and every two hours on the other half.

In general, however, the main reason for unbalanced data in a longitudinal study is the

occurrence of

missing values

in the sense that intended measurements are not taken, are lost

or are otherwise unavailable. See also Greenhouse and Geisser correction, Huynh–Feldt

correction, compound symmetry, generalized estimating equations, Mauchly test,

response feature analysis, time-by-time ANOVA and split-plot design.[Analysis of

Longitudinal Data, 2nd edition, 2002, P. J. Diggle, P. J. Heagerty, K.-Y. Liang and

S. Zeger, Oxford Scientiﬁc Publications, Oxford.]

Lon gitu dinal stu dies: Studies that give rise to

longitudinal data

. The deﬁning characteristic of

such a study is that subjects are measured repeatedly through time.

Long memory processes: A

stationary stochastic process

with slowly decaying or long-range

correlations. See also long-range dependence.[Statistics for Long Memory Processes,

1995, J. Beran, Chapman and Hall/CRC Press, London.]

Long -range dependence: Small but slowly decaying correlations in a stochastic process. Such

correlations are often not detected by standard tests, but their effect can be quite strong.

[Journal of the American Statistical Association, 1997, 92, 881–93.]

Lord, Frederic Mather ( 1 912^2000): Born in Hanover, New Hampshire, Lord graduated from

Dartmouth College in 1936 and received a Ph.D. from Princeton in 1952. In 1944 he joined the

Educational Testing Service and is recognized as the principal developer of the statistical

machinery underlying modern mental testing. Lord died on 5 February 2000 in Naples, Florida.

Lo r d’sparadox: The fact that estimates of treatment effects using

change scores

, where (posttest–

pretest) is regressed on treatment, differ from

analysis of covariance

, where the posttest is

regressed on both treatment and pretest. [ Sociological Methodology, 1990, 20,93–114.]

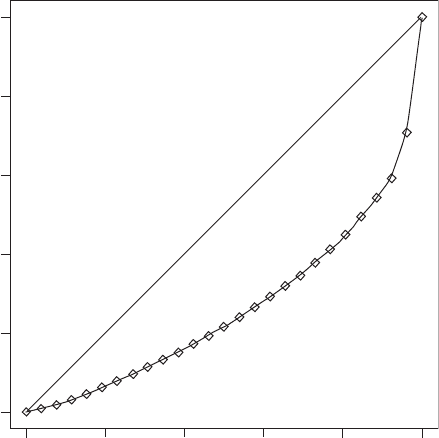
Lorenz curve: Essentially a graphical representation of the cumulative distribution of a variable,

most often used for income or wealth. If the risks of disease are not monotonically increasing

as the exposure becomes heavier, the data have to be rearranged from the lowest to the highest

risk before the calculation of the cumulative percentages. Associated with such a curve is the

Gini index deﬁned as twice the area between the curve and the diagonal line. This index is

between zero and one, with larger values indicating greater variability while smaller ones

indicate greater uniformity. The further the Lorenz curve lies below the line of equality, the

more unequal is the distribution of, in Figure 91 for example, income. [KA1 Chapter 2.]

Loss function: See decision theory.

261

Lotteri es: See national lotteries.

Low-dose extrapolation: The estimation of the potential risks associated with a low dose of, for

example, a suspected carcinogen, for observed data on individuals exposed to moderately

high levels of the agent of interest. One approach is to rely on an assumed mathematical

function relating risk to exposure, for example the

probit

logit

. In many cases however it is

possible to postulate different models that ﬁt the observed data equally well, but which

provide point estimates of risk at low exposures that differ by several orders of magnitude.

See also detection limits and dose-response curve .[Communications in Statistics:

Simulation and Computation, 1988, 11,27–45.]

Lower triangular matrix: A matrix in which all the elements above the main diagonal are zero. An

example is the following,

L ¼

1000

2300

1130

1567

LSD: Abbreviation for least signiﬁcant difference.

LST: Abbreviation for large simple trial.

L-statistics: Linear functions of order statistics often used in estimation problems because they are

typically computationally simple. [Statistics in Civil Engineering, 1997, A. V. Metcalfe,

Edward Arnold, London.]

Lugann i and Rice formu la: A

saddlepoint method

approximation to a probability distribution

from a corresponding

cumulant generating function

. [KA1 Chapter 11.]

0.0

0.2

0.4

0.6

0.8

1.0

0.2 0.4

Income

Total income

0.6

0.8

1.0

Fig. 91 Example of Lorenz curve and Gini index.

262

L yapunov exponent: A measure of the experimental divergence of trajectories in chaotic systems

[Fractal Geometry, 1990, K. Falconer, Wiley, Chichester.]

Lynden^Bell method: A method for estimating the

hazard rate

, or probability distribution of a

random variable observed subject to data truncation. It is closely related to the

product-limit

estimator

for censored data. [Monthly Notices of the Royal Astronomical Society, 1987, 226,

273–80.]

263

Machine learning: A term that literally means the ability of a machine to recognize patterns that

have occurred repeatedly and to improve its performance based on past experience. In

essence this reduces to the study of computer algorithms that improve automatically

through experience. A computer program is said to learn from experience E with respect

to some class of tasks T and performance measure P, if its performance at tasks in T,as

measured by P, improves with experience E. Machine learning is inherently a multi-

disciplinary ﬁeld using results and techniques from probability and statistics, computa-

tional complexity theory,

information theory

etc; it is closely related to

pattern recognition

and

artiﬁcial intelligence

and is widely used in modern

data mining

.[Introduction to

Machine Learning, 2004, E. Alpaydin, MIT Press, Boston.]

Mack^Wolfe te st: A

distribution free test

for one way designs for testing a null hypothesis of

equality against an alternative specifying an

umbrella ordering

. [NSM Chapter 6.]

MAD: Abbreviation for median absolute deviation .

MADAM: Abbreviation for mean and dispersion additive model.

M ahalanobis D

: A measure of the distance between two groups of individuals given by

¼ð







1







where



and



are the mean vectors of the two groups and S is a weighted average of the

variance–covariance matrices

of the two groups, S

and S

, i.e.

S ¼

þ n

where n

and n

are the sample sizes in the two groups. See also Hotelling’s T

test. [MV1

Chapter 4.]

M ahalanobis, Pransanta Chandra ( 1 893^1 972): Born in Calcutta, India, Mahalanobis ﬁrst

studied physics in Calcutta and then in Cambridge where he was elected a senior research

scholar in 1915. He eventually returned to India to teach at the Presidency College in

Calcutta. Mahalanobis made major contributions to many areas of statistics. His D

statistic

arose from work on anthropometric problems. Mahalanobis’ work on ﬁeld experiments led

to a close friendship with

Fisher

. In 1931 he founded the Indian Statistical Institute.

Mahalanobis was made a Fellow of the Royal Society in 1945 and given one of his country’s

highest awards the Padma Vibhushan. He died on 28 June 1972 in Calcutta.

Mahalonobis-Taguchi system: A diagnostic and predictive method for analyzing patterns in

multivariate data

. The system is reported to make accurate forecasts using small, correlated

data sets. [Concurrent Engineering, 2006, 14, 343–354.]

Main effect: An estimate of the independent effect of usually a factor variable on a response variable

analysis of variance

. [SMR Chapter 12.]

264

Mainframes: High speed, large and expensive computers with a very large storage capacity and

capable of supporting thousands of users simultaneously. Mainframes support more simul-

taneous programs than

supercomputers

, but the latter can execute a single program faster.

Mainland, Donald (19 02^19 85): Mainland graduated in medicine at Edinburgh University and

in 1930 he became Professor and Chairman of the Department of Anatomy at Dalhousie

University. He later developed an interest in measurement issues and statistics, publishing a

book on statistics in medicine in 1937. In 1950 Mainland became Professor of Medical

Statistics at New York University. A proliﬁc writer on statistical issues, Mainland died in

July 1985 in Kent, Connecticut.

Majority rule: A requirement that the majority of a series of

diagnostic tests

are positive before

declaring that a patient has a particular complaint. See also unanimity rule.[Statistics in

Medicine, 1987, 7, 549–557.]

Mallows’ C

statistic: An index used in

multiple regression analysis

as an aid in choosing the

‘best’ subset of explanatory variables. The index is deﬁned as

i¼1

ðy



ðkÞ

 n þ 2p

where n is the number of observations, y

is the observed value of the response variable for

individual i,

ðkÞ

is the corresponding predicted value from a model with a particular set of k

explanatory variables and s

is the residual mean square after regression on the complete set

of p explanatory variables. The model chosen is the one with the minimum value of C

. See

also Akaike’s information criterion and all subsets regression. [ARA Chapter 7.]

Malthus, Thomas Rober t (1 766^183 4): Malthus studied history, poetry, modern languages,

classics and mathematics at Jesus College, Cambridge. After being elected to a Fellowship at

Jesus in 1793 he became a curate in a small town, Albury in 1798, the year in which he

published the ﬁrst version of his famous work, Essay on the Principle of Population as it

affects the Future Improvement of Society. Malthus was a strong advocate of statistical

investigation and was a founder member of the Statistical Society of London. He died in

December 1834 in Bath, UK.

Malthusian parameter: The rate of increase that a population would ultimately attain if its age-

speciﬁc birth and death rates were to continue indeﬁnitely. Explicitly the parameter λ in the

exponential equation of population growth, NðtÞ¼N

, where N

is the initial population

size (t=0) and t is the elapsed time. See also population growth model.[Proceedings of the

National Academy of Science, USA, 1996, 93, 276–8.]

M a ndel , J oh n ( 1914^2007): Born in Antwerp, Belgium, Mandel received a master ’s degree in

chemistry from the University Libre de Bruxelles in 1937 and worked as a chemist in

Belgium up to 1940 when he was forced to ﬂee to France and then Portugal before travelling

to the United States. In New York he again worked as a chemist, studying mathematics at

night at Brooklyn College. In 1965 Mandel received a doctorate in mathematical statistics

from the Eindhoven University of Technology in the Netherlands. Mandel then spent

40 years as a statistician at the National Institute of Standards and Technology in

Washington and became an internationally recognized authority on the application of

mathematical and statistical methods in the physical sciences. He received many honours

including the Shewhart Medal and the American Statistical Association’s W. J. Youden

Award. Mandel died on the 1st October 2007 in Silver Springs, USA.

Manhattan distance: Synonym for city block distance.

265

M ani fest variable: A variable that can be measured directly, in contrast to a

latent variable

M ann ^ Whitney test: A

distribution free test

used as an alternative to the

Student’s t-test

for

assessing whether two populations have the same median. The test statistic

is calculated

from comparing each pair of values, one from each group, scoring these pairs 1 or 0

depending on whether the ﬁrst group observation is higher or lower than that from the

second group and summing the resulting scores over all pairs. In the case of no ties then

U ¼ W  nðn þ 1Þ=2

where

is the number of observations in the smaller group and

is the rank sum statistic

associated with

Wilcoxon’s rank sum test

. The two tests are thus equivalent. Tables giving

critical values of the test statistic are available, and for moderate and large sample sizes, a

normal approximation can be used. [SMR Chapter 6.]

MANOVA: Acronym for multivariate analysis of variance.

Mantel, Nathan (19 19 ^20 02): Born in New York, Mantel graduated from City College in 1939

with a major in statistics. His career as a statistician began in 1940 in the War Production

Board. After the war Mantel joined the National Cancer Institute where he remained until his

retirement. Mantel made substantial contributions to biostatistics and epidemiology, includ-

ing the

Mantel–Haenszel estimator

. He died on 26 May 2002, in Potomac, Maryland.

M ant el^ Haenszel esti mato r: An estimator of the assumed common

odds ratio

in a series of

two-by-two contingency

tables arising from different populations, for example, occupation,

country of origin, etc. Speciﬁcally the estimator is deﬁned as

ω ¼

i¼1

where k is the number of two-by-two tables involved and a

are the four counts in the

ith table. [Case-Control Studies: Design, Conduct, Analysis, 1982, J. J. Schlesselman, Oxford

University Press, Oxford.]

M any-outl ier detection procedures: Procedures for detecting multiple

outliers

in a sample of

n observations, x

; x

; ...; x

. Generally based on assuming that k of the observations

; x

; ...; x

are outliers distributed normally with mean  þ l

; j ¼ 1; ...; k and variance



, while the remaining n-k observations are normally distributed with mean µ and again

variance 

. Three such procedures are:

1. The extreme standardized deviate (ESD), given by

ESD

¼jx

ðS

1Þ





xðS

i1

Þj=sðS

i1

Þ; i ¼ 1; ...; k

where x

ðS

1Þ

is the observation farthest away from the mean



xðS

i1

Þ in the subset

i–1

,and

ðS

i1

Þ¼

niþ1

j¼1

½x

ðS

i1

Þ



xðS

i1

Þ

=ðn iÞ

¼fx

; x

; ...; x

g and subsets S

; i ¼ 1; ...; k  1 are formed by deleting an

observation farthest from the mean of the subset S

i-1

2. The standardized range procedure (STR):

STR

¼½x

ðS

i1

Þx

ðS

i1

Þ=sðS

i1

Þ; i ¼ 1; ...; k

where x

ðS

i1

Þ is the largest observation in the subset S

i-1

, and x

ðS

i1

Þ is the smallest

observation in the subset S

i-1

266

3. The kurtosis procedure (KUR):

KUR

¼ðn  i þ 1Þ

niþ1

j¼1

½x

ðS

i1

Þ



xðS

i1

Þ

=½

niþ1

j¼1

ðS

i1

Þ



xðS

i1

Þ

;

i ¼ 1; ...; k

Sample values of any of these statistics are compared with the corresponding critical

values for i=k. If a sample value is found to be greater than the corresponding critical

value, k outliers are declared to be present in the sample; otherwise, similar compar-

isons are made for i ¼ k  1; ...; 1 until for a particular value of i=l, the sample value

is greater than the corresponding ordeal value in which case l outliers are declared to

be present in the sample. If for i=1 the sample value of the statistics is less than or

equal to the corresponding critical value, no outliers are detected. [Technometrics,

1975, 17, 221–7.]

MAPestimate: Abbreviation for maximum a posteriori estimate.

Maple: A computer system for both mathematical computation and computer algebra. See also

Mathematica [http://www.maplesoft.com/]

Mardia’ s multivariate normality test: A test that a set of

multivariate data

arise from a

multivariate normal distribution

against departures due to

kurtosis

. The test is based on

the following multivariate kurtosis measure

2;q

i¼1

fðx





xÞ

1

ðx





xÞg

where q is the number of variables, n is the sample size, x

is the vector of observations for

subject i,



x is the mean vector of the observations, and S is the sample

variance–covariance

matrix

. For large samples under the hypothesis that the data arise from a multivariate normal

distribution, b

2,q

, has a normal distribution with mean q(q þ2) and variance 8qðq þ 2Þ=n.

[Multivariate Analysis, 1979, K. V. Mardia, J. T. Kent and J. M. Bibby, Academic Press,

London.]

MAREG: A software package for the analysis of marginal regression models. The package allows the

application of

generalized estimating equations

and

maximum likelihood methods

, and

includes techniques for handling

missing values

.[Statistical Software Newsletter in

Computational Statistics and Data Analysis, 1997, 24, 237–41 and http://www.stat.uni-

muenchen.de/sfb386/software/mareg/winmareg.html]

Marginal distribution: The probability distribution of a single variable, or combinations of vari-

ables, in a multivariate distribution. Obtained from the multivariate distribution by integrat-

ing over the other variables. [KA1 Chapter 1.]

Marginal homogeneity : A term applied to

square contingency tables

when the probabilities of

falling in each category of the row classiﬁcation equal the corresponding probabilities for the

column classiﬁcation. See also Stuart–Maxwell test.

Marginal likelihood: See likelihood.

M a rg i na l matching: The matching of treatment groups in terms of means or other summary

characteristics of the matching variables. Has been shown to be almost as efﬁcient as the

matching of individual subjects in some circumstances. [Work, Employment and Society,

1994, 8, 421–31.]

267

Marginal models: See population averaged model.

Marginal structural model (MSM): A model for estimation of the causal effect of a time-

dependent exposure in the presence of

time-dependent covariates

that may simultaneously

be confounders and intermediate variables. Inverse-probability-of-treatment weighting esti-

mators (extensions of the

Horvitz-Thompson estimator

) are used to estimate causal effects

based on the concept of potential outcomes (see

Neyman-Rubin causal framework

). A

simpler but more limited approach than using a

structural nested model

.[Epidemiology,

2000, 11, 550–560.]

Marginal totals: A term often used for the total number of observations in each row and each column

of a

contingency table

Markers of disease progression: Quantities that form a general monotonic series throughout

the course of a disease and assist with its modelling. In general such quantities are highly

prognostic in predicting the future course. An example is CD4 cell count (cells per µl),

which is generally accepted as the best marker of HIV disease progression. [Chemical and

Biological Interactions, 1994, 91, 181–6.]

Market model: A

linear regression

model of the form

¼ α þ βm

þ 

where r

represent the returns of the stock and of the market in period t; 

is the error term

which is uncorrelated to the market return in period t. This model is widely used in modern

portfolio management. [Mathematical Finance, 1997, 7, 127–55.]

M a rk ov, Andrey And reyevic h ( 1856^1922): Born in Ryazan, Russia, Markov studied at

St Petersburg where he became professor in 1893. In 1905 he left for self-imposed exile

in the town of Zaraisk. A student of

Chebyshev

, he worked on number theory and probability

theory. Best remembered for the concept of a

Markov chain

which has found many

applications in physics, biology and linguistics.

Markov chain: A

stochastic process

, fX

g; t ¼ 0; 1; 2; ... where X

takes values in the ﬁnite set

S ¼f1; 2; ...; Ng, and is such that

PrðX

¼ i

; ...; X

n1

¼ i

n1

Þ¼PrðX

¼ i

n1

¼ i

n1

(Strictly this deﬁnes a discrete time Markov chain; if the set S contains an uncountable number

of elements then a continuous time Markov chain results.) The equation given implies that to

make predictions about the future behaviour of the system it sufﬁces to consider only its

present state and not its past history. The probability PrðX

¼ i

n1

¼ i

n1

Þ is known as a

one step transition probability. The more general transition probability,PrðX

¼ ijX

¼ jÞ

satisﬁes the famous Chapman–Kolmogorov equation given by

PrðX

¼ ijX

¼ jÞ¼

PrðX

¼ kjX

¼ jÞPrðX

¼ ijX

¼ kÞ m

A time-homogeneous Markov chain is one for which the transition probabilities depend only

on the difference n − m rather than on n or m. In particular, the one-step transition probability,

PrðX

¼ ijX

n1

¼ jÞ can be written as simply p

. The N×Nmatrix, P, with ijth element p

a stochastic matrix, i.e.

0  p

 1; 1  i; j  N

j¼1

¼ 1; 1  i  N

268