Есипов Ю.В., Самсонов Ф.А., Черемисин А.И. Мониторинг и оценка риска систем защита - объект

Подождите немного. Документ загружается.

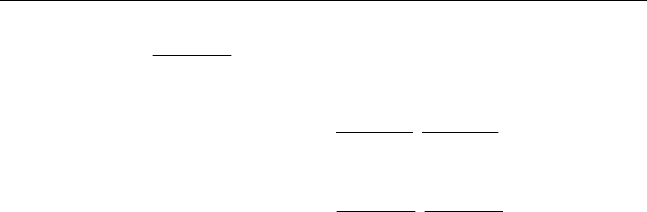
Определение возможностной меры реализации происшествий 91

0114

0223

20114

02 23

30223

(04)

(014)min( )min

( 023) min( ) min

SrSr

B, ,;

Sr Sr

B, ,;

πππ

∩

Δ+Δ

⎛⎞

∩

== =

⎜⎟

Δ+Δ Δ+Δ

⎝⎠

⎛⎞

∩∩

== =

⎜⎟

Δ+Δ Δ+Δ

⎝⎠



(3.70)

801122334

( 01234) min( )B,,,.

ππππ

Далее, объединяя формулы (3.69), (3.70), зависимость (3.68) предста-

вим в виде:

min( max ( ( )))

,B,

πππ

−

= (3.71)

где

— возможностная мера действия на объект внешнего фактора;

() ( )

iiSSNr

BS,S,,,r,

ππ

=ΔΔΔ

— возможностная мера существования

параметрической цепочки

0 iN

−

− .

Действуя по индукции, зависимость (2.28) преобразуем к виду:

()Pos(()1)

max (min( max ( ( ))))

звых

вых

вых SN

ttm

tT m

N,Т ,f y Т

,B,

ππ

−

⊂

(3.72)

где возможностные аргументы

()

раскрываются по формулам (2.23),

(2.27), (3.70).

Таким образом, получена точная компактная формула возможностной

меры отказа объекта как функции от ВМ отказа элементов с учётом их

связности.

Осуществим преобразование формулы (3.72) для двух случаев:

а) если в объекте связность и накопление по отказам элементов отсутст-

вуют, тогда:

( ) max (min( ( )))

()

Вых tt Вых

N,T,f ,ON

πππ

⊂

= ; (3.73)

б) если связность и каналирование в объекте однократные, вида:

Раздел 3

(0 ) 1 1

Вых Вых

iN ,i ,N ,

−

−=−

тогда:

( ) max (min( max ( ( ))))

Вых

()

Вых ttВых

tT i

N,Т ,f , OiN .

πππ

−

⊂=

= (3.74)

Формула (3.73) определяет ВМ отказа объекта только по отказу его

выходного (критического) элемента, инициированного действием внеш-

них факторов, принадлежащих к множеству видов

Т .

В свою очередь, формула (3.74) описывает ВМ отказа критического

элемента объекта, инициированного однократными действиями вторич-

ных факторов от каждого его ПОЭ, отказавшего при действии внешних

факторов, при условии принадлежности внешних и вторичных факторов к

множеству видов

Т .

И, наконец, если искусственно предположить, что внешние факторы в

среде возникают с мерой

,t T

∀∈ , тогда получим формулу возмож-

ностной меры возникновения «собственного» отказа объекта при одно-

кратном действии его вторичных факторов:

( ) max ( max ( ( )))

NВых

(C)

Вых Вых

tT ш

N,T,f tiN ,tT

ππ

−

⊂=

∈ . (3.75)

Таким образом, полученные зависимости (3.73)–(3.75) доказывают

универсальность формулы (3.72) и при адекватном множественно-

параметрическом представлении техногенных (экологических) систем

относительно сопоставимого исхода аварийной (чрезвычайной) ситуации

могут быть использованы для сравнения их опасности (безопасности).

3.7. Определение возможностной меры

реализации параметрической предпосылки

по границам размытости и уровням

различимости

В большинстве практических случаев эксперты могут получить с не-

которой степенью уверенности исходные данные о модели отказа в виде

границ ядер и носителей нечетких величин [21, 47, 49], но не о виде их

функций принадлежности, что затрудняет применение общего подхода

[11]. В таких условиях важным оказывается обоснование видов функций

принадлежности по отношению ко всему

диапазону изменения исходных

данных [39, 42].

Определение возможностной меры реализации происшествий 93

В свою очередь, при отыскании значений меры отказа от 0,03 и ниже

большое значение приобретает как анализ краевых условий задачи, так и

анализ их влияния на результат её решения.

Рассматривается задача об определении условий существования ре-

шения и нахождении меры реализации критерия отказа t: s > r, если пара-

метры s, r — нечеткие величины

, ядра которых заданы, а границы их но-

сителей установлены на уровне

-среза. При отсутствии статистических

данных о параметрах системы «факторы — объект» оценка меры опреде-

ленности отказа в ней может быть произведена только по величине воз-

можностной меры [39]. При этом оказывается важным выяснение усло-

вий, для которых решение такой задачи осуществимо в интересуемых для

практики диапазонах изменения параметров системы.

3.7.1. Постановка задачи

Рассматривается

уникальная система «ОВФ — ПОО — СМЗ». Про-

изведем оценку её безопасности путем построения параметрической мо-

дели «нечеткое воздействие s — нечеткая чувствительность r», на основе

которой установим меру определенности реализации критерия «воздейст-

вие фактора превышает чувствительность объекта, t: s > r». Статистиче-

ские данные о разбросе нечетких параметров отсутствуют, но экспертным

путем установлены:

области

для ядер нечетких величин s, r, обозначаемых в виде:

⎯s

∈ [0,

⎯

∈ [r

⎯

]

;

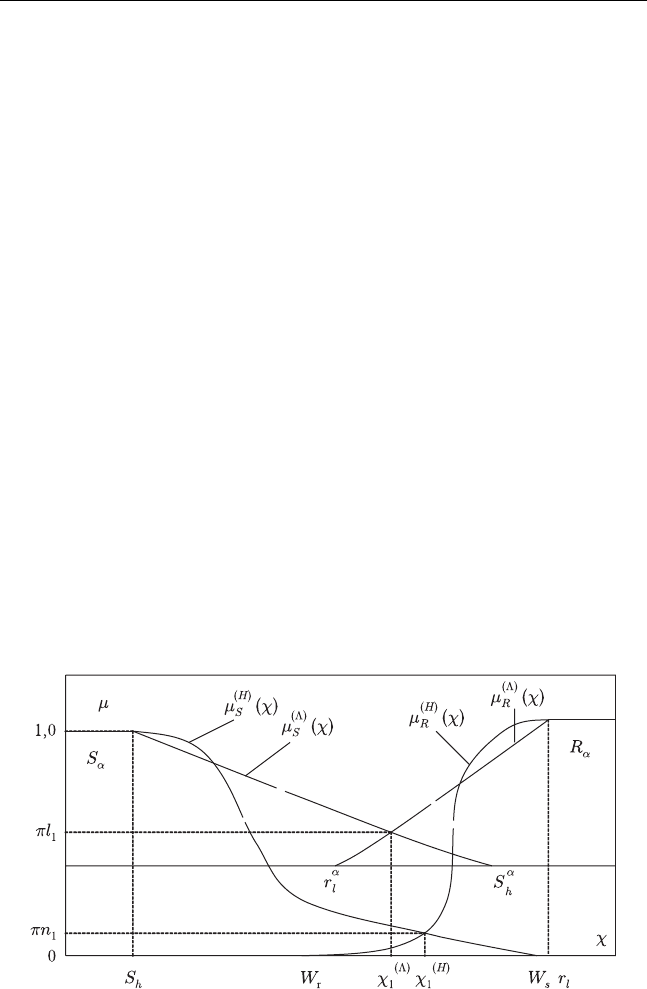
области для носителей этих величин на уровне их

-среза [11], рис. 3.8:

Раздел 3

Рис. 3.8

= {

∈

(

) ≥

: r

⎯

}; (3.76)

= {

∈

(

) ≥

⎯

= 0,

⎯

, s

}. (3.77)

Причем в зависимостях (3.76) и (3.77) под границами r

, s

носите-

лей R

, S

будем подразумевать «ничтожно» возможные значения нечет-

ких величин r и s, которые эксперты различают со степенью уверенности,

равной 1 −

, где

— уровень различимости этих границ. Отметим, что

для решения задачи в рамках указанной модели вполне достаточно для

«верхней»

⎯

и «нижней»

⎯

границ ядер задать условие:

⎯

<⎯

С учетом априорной информации о размытости величин s, r предпо-

ложим, что их функции принадлежности являются монотонными функ-

циями.

В частности, рассмотрим линейную

xxxviii

(л)

(

) (рис. 3.9) и гауссову

(нормальную)

(н)

(

) (рис. 3.8) функции принадлежности. Известно, что

такие функции принадлежности описывают варианты либо полного не-

знания характера размытости, либо «нормальной» размытости величин

[11, 21].

Требуется найти асимптотическое значение меры определенности от-

каза как функции от 1) границ⎯r

,⎯s

ядер, 2) границ r

, s

носителей не-

четких параметров r, s, а также от 3) уровня

различимости этих границ.

3.7.2. Решение задачи для трех вариантов

граничных условий

Рассмотрим решение задачи для трёх вариантов (условий) соотноше-

ния границ «ничтожно» возможных значений параметров воздействия и

чувствительности:

1) r

< s

; 2) r

= s

; 3) r

> s

. (3.78)

Рассмотрим первый вариант соотношения границ и определим воз-

можностную меру в линейной аппроксимации функций принадлежности

нечетких параметров s и r на уровне

-среза (рис.3.9).

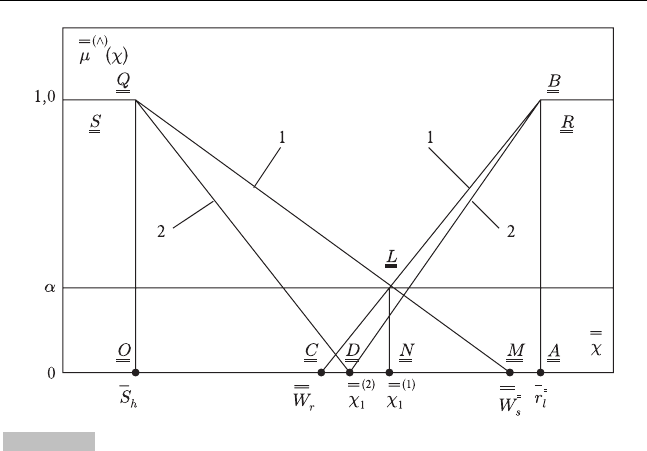
Определение возможностной меры реализации происшествий 95

Рис. 3.9

xxxix

Для этого случая, как показано в п. 3.5, возможностная мера

отка-

за есть отношение длины интервала пересечения [r

, s

] носителей к

сумме длин областей размытости

, взятых по

-срезу параметров

модели отказа:

= (s

−

) / (

) = 1

−

zb / (

) = 1

−⎯

, (3.79)

где длины «практических» областей размытости определяются по зависи-

мостям:

= s

−

⎯

=⎯r

− r

. (3.80)

Параметры zb =

⎯

−⎯s

⎯

= zb/

называются, соответст-

венно, абсолютный и приведенный параметрические «запасы безопасно-

сти».

Из формулы (3.80) следует, что если ⎯zb

= 1, т. е. если

⎯

−⎯s

тогда

= 0.

Следовательно, в линейном приближении возможностная мера отказа

равна нулю, если сумма областей размытости равна и больше параметри-

ческого запаса безопасности, а решение существует, если⎯zb

≤ 1.

Кроме того, как видно из рис.3.8 и 3.9, существование неполной раз-

личимости границ с уровнем

> 0 обуславливает наличие неустранимой

погрешности в определении меры отказа, которая в линейной аппрокси-

мации равна уровню различимости:

Раздел 3

С другой стороны, если будет считаться, что

> 0, хотя в действи-

тельности имеет место вариант 2 или 3 зависимости (3.78), см. ветви (2)

на рис. 3.9, то это может привести к «ложному решению» — к принятию

варианта (1) в условии (3.78) задачи.

Если будут выявлены «абсолютно невозможные» величины w

, w

, ко-

торые соответствуют уровню различимости

= 0, рис. 3.8, то потенци-

альная ошибка нахождения

равна (стремится к) нулю.

Исследуем влияние уровня

-различимости границ параметров моде-

ли отказа на аргумент ⎯zb

в предположении о том, что их функции при-

надлежности линейны вплоть до нуля, рис. 3.9. Выразим длины интерва-

лов размытости

(2)

−⎯s

⎯

−

(2)

, взятые по уровню

= 0

(точка D в ветвях (2) функций принадлежности

(

) и

(

)), через длины

интервалов

ветвей (1), рис. 3.9, и значение

-уровня. Из рассмот-

рения двух пар подобных треугольников OQM, NLM и ABC, NLC на об-

ласти значений 0 ≤

≤ 0,1 можно получить следующие соотношения:

/ (1

−

);

/ (1

−

). (3.81)

Просуммировав соответствующие левые и правые части соотноше-

ний (4.91) и разделив их на zb, в результате несложных преобразований

получим:

⎯

−

);

⎯

≈⎯

(1 +

). (3.82)

Как следует из зависимости (3.82), приведенный параметрический

запас

⎯

линейно зависит от уровня

3.7.3. Возможностная мера при гауссовой аппроксимации

ФП параметров

Определим возможностную меру при нормальной (гауссовой) аппрок-

симации функций принадлежности нечетких параметров s и r:

(

) = exp (

−

0,5 ((

−⎯

) /

)

);

(

) =

= exp (

−

0,5 ((

−

⎯

) /

)

), (3.83)

где

(

) — характеристика размытости соответственно параметров s, r,

связанная с практической областью размытости Δ

(Δ

) соотношением:

Δ = k∗σ, где k — коэффициент нормальной размытости, которому при k =

3; 4; 5 соответствует квантиль доверия 1 − ν: 0,9968; 0,999968; 0,9999997

[26].

Определение возможностной меры реализации происшествий 97

По определению [11], возможностная мера превышения s над r есть

значение функций принадлежности в их точке пересечения

. Тогда, как

видно из рис. 3.8:

(

(н)

) =

(

(н)

). (3.84)

После подстановки (3.83) в (3.84), с учетом обозначений в формулах

(3.79) и (3.80), получим следующую зависимость «нормальной» аппрок-

симации возможностной меры:

= exp (

−

((

⎯

−⎯s

) / (

))

) = exp (

−

⎯

), (3.85)

где k

= k/2, а значения коэффициента k

= 4,5; 8; 12,5 соответствуют зна-

чениям коэффициента k = 3; 4; 5 в формуле (3.83).

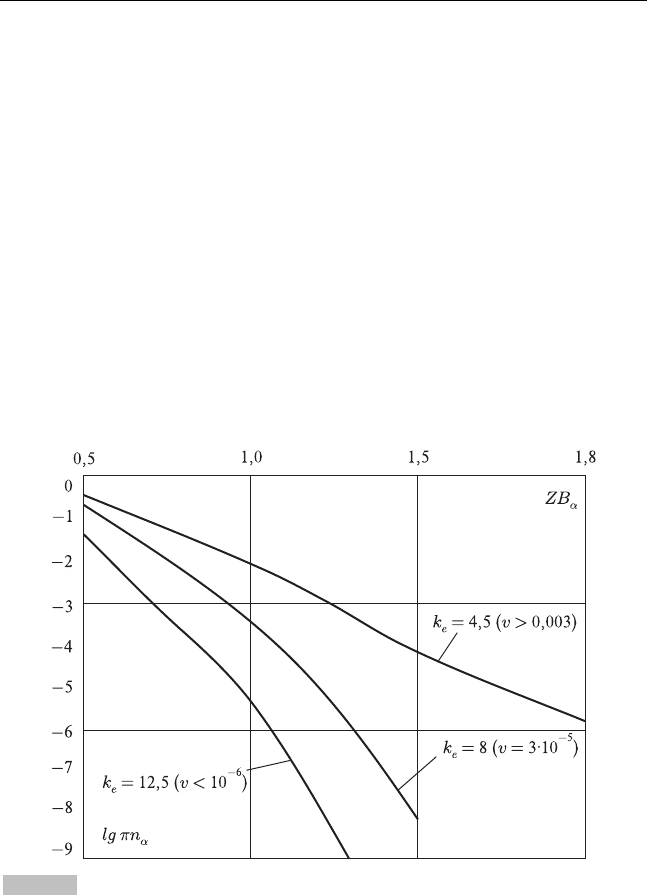
Результаты численного решения зависимости (3.85) представлены на

рис.3.10. Как видно из рис. 3.10, влияние аргумента ⎯zb

на функцию

слабее, нежели влияние коэффициента k

. При изменении k

от 4,5 до 12,5

происходит изменение πn

на несколько порядков.

Рис. 3.10

Из сравнения полученных аппроксимаций возможностных мер, фор-

мулы (3.79), (3.85), следует, что они имеют инвариантный аргумент. Это

позволяет объединить рассмотрение функций

на одной оси абс-

цисс ⎯zb

и выявить области их практического применения.

Раздел 3

Как следует из анализа рис. 3.8, 3.10, применение формулы (3.85) по-

зволяет найти решение вариантов (2, 3) задачи, указанных в зависимости

(3.78). Причем с практической точки зрения достаточно рассмотреть сле-

дующие области изменения аргументов:

∈

[ 10

–5

, 10

–1

∈ [ 1, 2 ].

Таким образом, для нахождения меры определенности в диапазоне [0,

0,02] необходимо выбирать нормальную зависимость возможностной ме-

ры, а на области zb

≥ 1 необходимо учитывать как квантиль «недоверия»

, так и уровень

различимости границ.

Дополнительно исследуем влияние уровня

на потенциальную по-

грешность

в определении возможностной меры отказа. С учетом фор-

мулы (3.82), (3.85) представим z$b

как требуемое значение запаса, а по-

тенциальную погрешность

запишем в виде:

(

) =

n (z$b

)

−

n(z$b

) =

n (1)

−

n (1 +

). (3.86)

С учетом аппроксимаций

с коэффициентом k

= 4,5; 8 из зависи-

мости (3.86) можно получить следующие соотношения:

= 4,5)

≈

0,1

;

= 8)

≈

0,004

. (3.87)

3.7.4. Установление потенциальной погрешности

определения ВМ

Применим зависимости (3.86), (3.87) для установления потенциаль-

ной погрешности в определении возможностной меры отказа при условии,

что уровень различимости

параметров воздействия и чувствительности

не ниже 0,001. Для этого возьмем значения

= 0,001; 0,01 и учтем, что

для k

= 4,5 и 8 соответствующие квантили «недоверия» равны

= 0,003 и

0,00003. Результаты расчета потенциальной погрешности

сведем в

табл. 3.1, из анализа которых сделаем следующие выводы:

1. Чтобы оценивать и различать меру отказа на уровне значений от 0,001

и выше достаточно различать границы нечетких параметров модели

отказа на уровне 0,01 и выше.

2. Чтобы оценивать и различать меру отказа на уровне значений от

0,00001 и выше при уровне различимости границ нечетких

парамет-

ров равно и выше 0,001, необходимо использовать их нормальную

аппроксимацию, характеризуемую квантилем доверия не ниже

0,99997.

Определение возможностной меры реализации происшествий 99

Таблица 3.1

Коэффициент,

Квантиль

недоверия,

Уровень

различимости,

Потенциальная

погрешность

π n

4,5 0,003 0,01/0,001 0,001/0,0001

8 0,00003 0,01/0,001

⋅

−5

⋅

−6

3.7.5. Примеры нахождения ВМ и достижимого уровня

её различимости

Рассматривается уникальная система «нерегламентированные факто-

ры — потенциально опасный объект», предпосылки к отказам в которой

можно выразить в виде унифицированного критерия: «если воздействие

любого фактора превысит заданную чувствительность объекта, то это

приведет к несанкционированному срабатыванию или отказу объекта».

Экспертами установлены границы области

размытости нечеткого воздей-

ствия [s$

, s

] и нечеткой чувствительности [r

⎯

], где s

, r

− «ничтож-

но» возможные (на уровне различимости

) значения параметров,

⎯

— соответственно верхняя и нижняя границы «абсолютно» воз-

можных (с уверенностью, равной единице) значений параметров s и r.

Пусть известно, что

⎯

= 10, s

= 20, r

= 15,

⎯

= 18.

Пример № 1. Требуется оценить асимптотическое значение меры оп-

ределенности возникновения отказа, если априорной информации о ха-

рактере размытости параметров нет.

Решение примера № 1. Поскольку априорной информации о характе-

ре размытости параметров s, r нет, то асимптотическое значение меры оп-

ределенности возникновения отказа d следует определять по линейной

аппроксимации возможностной

меры, формула (3.79).

В результате получим: d =

l = 1 –

⎯

zb = 1

−

0,6154 = 0,3846.

Пример № 2. Решить пример № 1 при условии, что априорная размы-

тость параметров s, r характеризуется как «нормальная».

Решение примера № 2. Асимптотическое значение меры определен-

ности d с учетом дополнительной информации, приведенной в условии,

определим по нормальной зависимости возможностной меры. Обращаясь

к формуле (3.85) или к рис.3.10 и выбирая k

= 4,5, которому соответствует

квантиль «недоверия»

ν ≥

0,003, при

⎯

= 0,6154 получим:

d =

n = exp (

−

⎯

) = 0,1819 (k

= 4,5).

Раздел 3

100

Пример № 3. Оценить значение приведенного запаса

безопасности

⎯

и уровень различимости

, обеспечивающие для «нор-

мально» размытых s, r различение и оценку величины возможностной

меры отказа в диапазоне:

1) 0,003

≤

1; 2) 0,001

≤

Решение примера № 3. Воспользуемся результатами, приведенными в

табл. 4.1.

xli

Из таблицы следует, что для решения задачи в обоих случаях

достаточно достичь уровня различимости границ

≤ 0,01. Однако в пер-

вом случае корректную оценку

достаточно провести с величиной

квантиля «недоверия»

≤

0,003. Тогда как для оценки

в диапазоне

0,001

≤

πn

≤

1 необходимо уменьшать

. Поэтому для решения первого

варианта задачи достаточно обусловить применение формулы (3.85) с ко-

эффициентом k

= 4,5, а для решения второго варианта задачи необходимо

уточнение аппроксимации, например до k

= 8.

Тогда с помощью формулы (3.85) получим:

⎯

1(2)

= (0,222(0,125) ln (1 / πn))

0,5

. Откуда

⎯

= 1,1361;

⎯

= 0,9292.

Для выяснения физического смысла полученных результатов примера

№ 3 раскроем выражение

⎯

= (r$

− s$

) / (

), из которого следует,

что для выполнения решений

⎯

1(2)

необходимо, чтобы параметрический

запас безопасности (r

−⎯s

) превышал в 1,1361 (0,9292) раза сумму длин

интервалов размытости воздействия и чувствительности, различаемых на

уровне

= 0,01.

Таким образом, нахождение асимптотического значения меры воз-

никновения отказа в уникальной системе достижимо на основе построе-

ния модели вида «нечеткое воздействие — нечеткая чувствительность» и

установления границ размытости параметров этой модели. При этом

асимптотическое значение меры отказа можно определить по формулам

возможностной меры (3.79), (3.85), которые представляют собой функции

от инвариантного аргумента, выраженного

в виде отношения области пе-

ресечения носителей к сумме длин областей размытости, взятых по

срезу нечетких параметров модели отказа.

Чтобы оценивать и различать меру отказа на уровне значений от 0,001

и выше достаточно различать границы нечетких параметров модели отка-

за на уровне 0,01 и выше. Чтобы оценивать и различать меру отказа на

уровне значений от 0,00001 и выше, при уровне различимости границ не-

четких параметров равно и

выше 0,001, необходимо использовать нор-

мальную аппроксимацию нечетких параметров модели, характеризуемую

квантилем доверия не ниже 0,99997 (коэффициентом их размытости k

≥

4).

Есипов Ю.В., Самсонов Ф.А., Черемисин А.И. Мониторинг и оценка риска систем защита - объект - среда

Подождите немного. Документ загружается.