Есипов Ю.В., Самсонов Ф.А., Черемисин А.И. Мониторинг и оценка риска систем защита - объект

Подождите немного. Документ загружается.

Определение возможностной меры реализации происшествий 81

2) если явления исследованы экспериментально-теоретическими мето-

дами, то форма ФП параметров модели определяется на основе функ-

ций вероятности;

3) если явления исследованы теоретически, например с помощью воз-

можностного анализа, то вид ФП определяется из класса гипотетиче-

ских функций.

При этом из нескольких гипотез о формах ФП

(

)

{

}

по правилу

суммирования алгебры Заде определяется одна:

(

)

(

)

(

)

(

)

l l , l ...

μμμ

∪

= . (3.44)

Если же имеется ФП как самое слабое свидетельство о распределе-

нии возможности проявления нечеткой величины, например, для

R ,

()

, такое что:

(

)

(

)

μμ

∪

, (3.45)

означающее, что данная функция

(

)

«поглощает» все остальные вари-

анты распределения параметра

R (все другие слагаемые в зависимости

(3.45)), то для анализа достаточно остановиться на ее рассмотрении и оп-

ределении характеристик ее формы.

При рассмотрении форм ФП

(

)

∪

могут иметься следующие

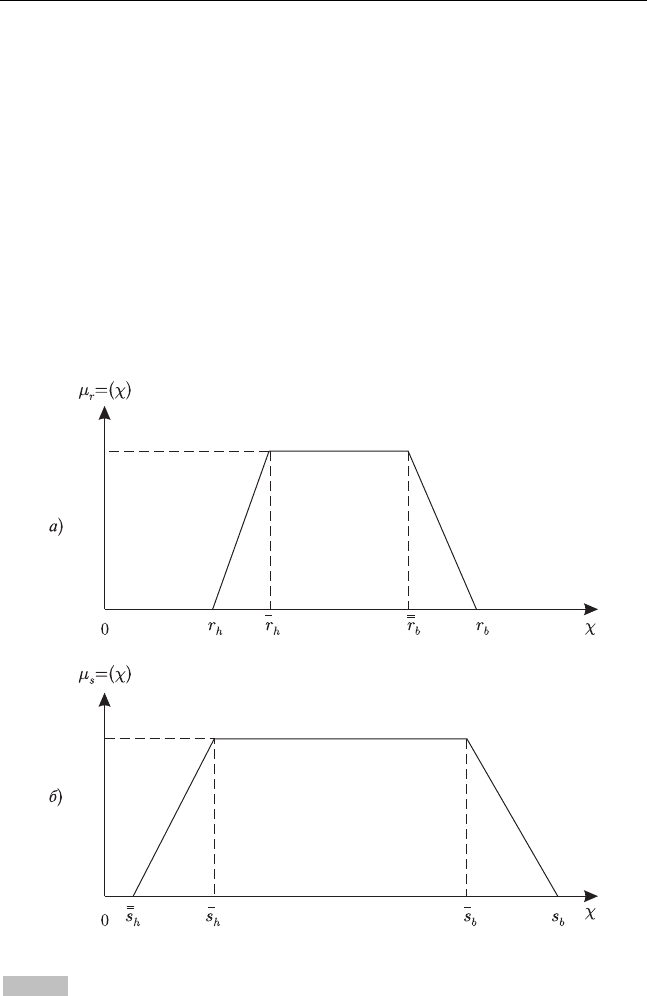
«крайние» и «средний» варианты, иллюстрируемые на примере (рис. 3.3),

где цифрами обозначены: 1 — функция Гаусса, 2 — ступенчатая функция,

3 — линейная функция, представляющие функции распределений случай-

ной величины, соответственно, нормального, равновероятного и Симпсо-

на.

xxxi

Прад и Дюбуа использовали линейную форму ФП нечеткой величины

в виде формы трапеций [11]. Действительно, физически всегда оправдано,

что возможность появления значения

R , например, на самой нижней гра-

нице

R весьма мала и стремится к нулю:

(

)

→ , тогда как

возможность появления значения

R вблизи ядра (

R ) приближается к

единице:

()

=→.

Аналогичные рассуждения можно привести для других вариантов не-

четкой величины

R и для других нечетких величин.

Таким образом, в предположении о существовании одной «погло-

щающей» формы функции принадлежности нечеткой величины, которая

выражается нормальной трапецией, для однозначного задания ее сторон

достаточно найти значения границ ядра и носителя.

Раздел 3

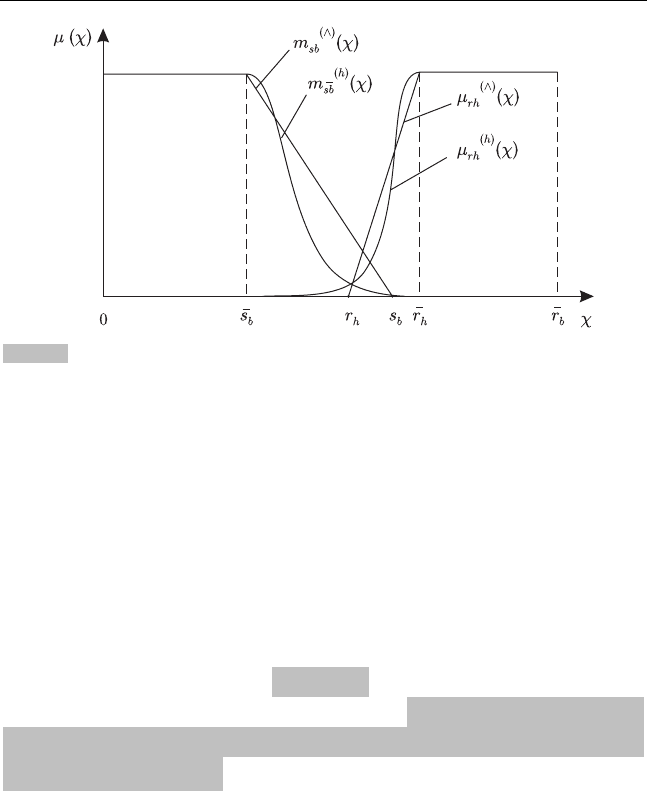
Связывая проведенные рассуждения с зависимостями (3.42), (3.43),

легко получить следующие теоретические формы ФП параметров

S и R

(рис. 3.4).

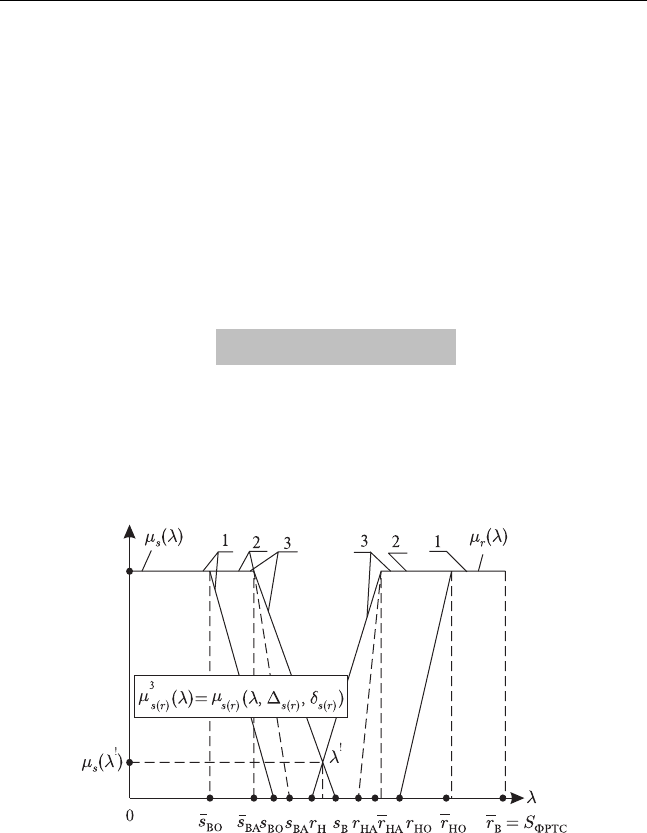
Однако в практике параметрического анализа отказа объекта чаще

всего интересует область возможного перекрытия (пересечения) парамет-

ров

S и R . Это можно описать прямоугольными трапециями вида

рис. 3.5, где нижнее значение ядра воздействия равно



, верхнее зна-

чение ядра восприимчивости объекта к воздействию равно максимально-

му физически реализуемому его значению в системе:

2 pp

RS=



, и, вследст-

вие неопределенности информации, возможно превышение верхнего зна-

чения

S параметра воздействия над нижним значением

R параметра

восприимчивости, т. е. могут перекрываться функции

(

)

(

)

Рис. 3.4

Определение возможностной меры реализации происшествий 83

Рис. 3.5

3.6.3. Детальное описание нечеткой модели системы

Перейдем к детальному описанию модели «нечеткое воздействие —

нечеткая восприимчивость». Пусть каждая составляющая этой модели

представлена одним параметром, причем эти параметры одной размерно-

сти, так что

R,S,i R∈ , где каждый параметр есть размерная переменная,

заданная на области действительных чисел

R . Графически представим

модель так, чтобы рассмотреть все физически возможные варианты пере-

крытия нечетких величин (см. п. 3.3). Предположим, что области измене-

ния воздействия и восприимчивости (носители нечетких величин) сле-

дующие: [

,S ], [

maxH

r,r ], и что их ядра представлены отрезками:

[ 0

,S ], [

maxB

r,r ] (рис.3.5), где

S ,

xxxii

— соответственно верхнее зна-

чение ядра и носителя нечеткой величины S ,

r — нижнее значение но-

сителя нечеткой величины r ,

r и

r — нижнее и верхнее значения ядра

нечеткой величины r

xxxiii

, причем

max pp

rs=

, что означает: максимальная

восприимчивость объекта к отказу выражается через значение физически

реализуемого воздействия, непосредственно прикладываемого к нему.

Таким образом, нечеткие величины

S и R описаны в виде функций при-

надлежности

()

(

)

и представлены на рис. 3.5.

Требование полноты анализа в рамках принятой модели сводится к

перебору следующих вариантов типов изменения параметров:

constr,s−

, 1)

const varr,s

−

, 1.1)

const var

s,s

−

− ,

1.2)

var

s,s− , 2)

const vars,r

−

, 2.1)

const var

r,r

−

− ,

Раздел 3

2.2)

var

r,r − , 3) varr,s

−

, 3.1) const var

HB BH

s,r ,s,r

−

− ,

3.2)

var const

HB BH

s,r ,s,r−−, 3.3) var const

HBH B

s,s,r ,r

−

− ,

3.4)

var const

BHB H

s,r,r ,s−−, 3.5) var

HBHB

s,s,r,r− .

Выше было показано, формулы (3.44), (3.45), что в рамках возможно-

стной оценки допустимо использовать самую общую форму ФП. Поэтому

рассмотрение всех возможных вариантов соотношения нечетких величин

r и

(требование полноты анализа) может быть сведено к анализу вари-

анта 3.5, рис. 3.6. Достоверность

D оценки безопасности однопарамет-

рического объекта представляет собой функцию от возможностной меры

работоспособного состояния объекта и вероятностной меры ошибок 1 и 2

рода [25, 56, 58]:

xxxiv

(

)

(

)

DSR

=<⋅−−

∏

, (3.46)

где на основе свойства дополнения ВМ

(

)

(

)

SR O<=− Λ≥

∏∏

. (3.47)

Рис. 3.6

При отсутствии ошибки 1 рода, 0

, пренебрегая бесконечно ма-

лыми 2 порядка малости, из (3.46), (3.47) получим:

(

)

=− − Λ≥

∏

. (3.48)

Определение возможностной меры реализации происшествий 85

При однопараметрическом представлении выражение (3.48) связыва-

ет показатель достоверности существования безопасного состояния сис-

темы с возможностными мерами активного отказа

(

)

OΛ≥

∏

xxxv

и необ-

наруженного активного отказа

. Как следует из (3.48), рассматриваемые

события образуют «псевдополную» группу событий, характеризуемую

квазитождеством:

(

)

+Λ≥=

∏

, что согласуется с краевыми

условиями рассматриваемой задачи.

3.6.4. Вывод зависимости возможностной меры отказа

в однопараметрической системе

3.6.4.1. Общее решение

Из общей постановки задачи, формула (3.38), следует, что в случае

однопараметрической системы требуется определить зависимость:

()

(

)

(

0var min max

Pl f , r,s , ,

ηθ β θ

≥= − → → , (3.49)

где

br s

∩ ,

b,r,s,l R

∈

— характеристики прямоугольно-трапецеидальной формы ФП пара-

метров

и r , устанавливаемые для

(

)

l:s,d

, для

(

)

rHr

l:r,d

d,d — начальный диапазон неопределенности величин

и r (длина

абсциссы стороны трапеции

), d

= s

–⎯ s ; d

=⎯ r – r

;

— характеристики составляющих погрешности получения информации

о параметрах

и r , представленных формулами (3.40), (3.41).

Требование учета максимального значения погрешностей представ-

ления составляющих модели на всем диапазоне их определения,

max

→ , сводится к следующему:

1) выбирается такая сторона трапеции

()

, которая образована пере-

носом значения

S из-за аддитивной погрешности

вправо (в сто-

рону увеличения):

BA BO S

+Δ , (3.50)

где

S , S

ВА

— соответственно «действительное» и неточное, из-за адди-

тивной ошибки, значения верхней границы параметра

S ,

Раздел 3

2) аддитивная погрешность

величины r в функции

(

)

учитыва-

ется путем переноса стороны трапеции

(

)

влево (в сторону

уменьшения)

AHO r

+Δ (3.51)

где

r , r

НА

— действительное и неточное значения нижней границы па-

раметра

r ,

3) мультипликативная погрешность

(

) величины

(r ) в функ-

ции

()

(

)

) учитывается путем изменения наклона стороны

трапеции, вызванного переносом верхней границы

(

r ) вправо

(влево):

(

)

BBO s

=+,

()

HO s

=−, (3.52)

4) предполагается, что аддитивная и мультипликативная погрешности

независимы.

Описанные здесь условия, раскрывающие требование

max

→ , ил-

люстрируются на рис. 3.6.

Тогда с учетом граничных условий (3.50)–(3.52) и условия о том, что

аддитивная

и мультипликативная

погрешности независимы, урав-

нения функций принадлежности имеют вид:

()

ssBOs

so s BO

lsl

με

++Δ−

, (3.53)

() ()

()

rHOHBOr

ro r HO

llrs

με

−− −Δ

. (3.54)

Из уравнений (3.53), (3.54) выразим параметрический критерий опас-

ности и запас безопасности системы. Действительно, отказ не произойдет,

если:

BO s BO s HO r HO r

ss rr

+Δ < − −Δ . (3.55)

Обозначая параметрический запас безопасности как:

OBO

PZB r s

− , (3.56)

из условия (3.55) выразим параметрический критерий возможности отказа

из-за наличия ошибок и нечеткого представления информации в виде:

Определение возможностной меры реализации происшествий 87

sBO rHO s R

rPZB

+Δ +Δ ≥ . (3.57)

Если нечеткие величины и привнесенные погрешности их представ-

ления таковы, что критерий (3.57) выполняется, то возможно выполнение

условия

r≥ . Тогда, опуская промежуточные выкладки, общее реше-

ние системы уравнений (3.53), (3.54) получим в виде:

() ( )

r s BO HO rO BO sO HO s BO rO r HO sO

s r ds dr s d rd

εε ε ε

++++−

(

)

(

)

r r s r HO s s BO r

dd r s

εε

−Δ + Δ − Δ

, (3.58)

где

rssBOrHO

dd s r

++ + .

Точка

l есть точка пересечения функций принадлежности

(

)

(

()

) (см. рис. 3.6), в ней возможностная мера отказа максимальна.

В частности, если диапазон неопределенности параметров равен ну-

лю:

= , а аддитивные и мультипликативные погрешности равны:

Δ=Δ,

BO r HO

= , то точка пересечения ФП находится по формуле:

(

)

rsBOHO

BO r HO

εε

. (3.59)

В этом случае аддитивные погрешности параметров

и r компенси-

рует друг друга, поэтому в выражении (3.59) они отсутствуют.

Подставляя решение (3.58) или (3.59) в зависимость ФП, например

()

, получим зависимость возможностной меры отказа элемента от ха-

рактеристик погрешностей однопараметрического представления воздей-

ствия и восприимчивости:

()

(

)

()

(

)

!! !

ss sBOs

ssBO

Pl l s l

με

=++Δ−

. (3.60)

3.6.4.2. Определение возможностной меры по интегральной

аддитивной погрешности параметров R и S.

Пусть все погрешности параметров

S и R представлены интеграль-

ными аддитивными погрешностями в виде:

SB r H

SS; rr,Δ= − Δ=−

(3.61)

Раздел 3

где

S,r,S ,r — соответственно верхнее и нижнее значения ядер и границ

нечётких параметров воздействия и восприимчивости.

Параметрический запас безопасности по отказу в данной модели обо-

значим:

brS,

−

причём, как и ранее, считается, что

Δ+Δ

Требуется определить возможностную меру отказа как функцию вида

xxxvi

!f( ,,Zb).

ΔΔ

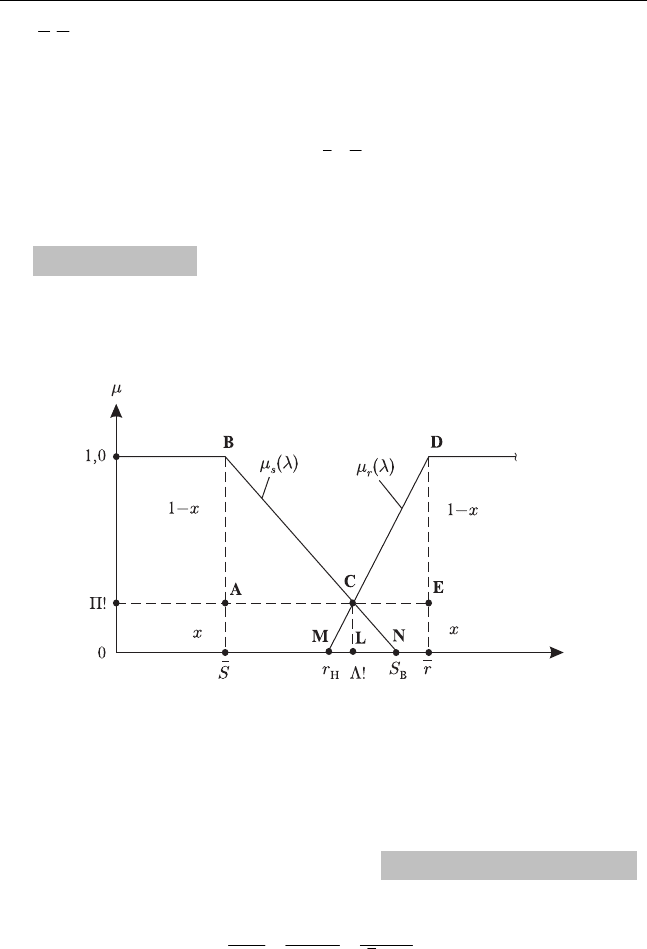
Решение. Представим нечёткие величины

S и r функциями принад-

лежности

(),()

λμλ

в виде трапеций (рис. 3.7) и рассмотрим тре-

угольники ABC, CDE, CLN, CLM.

Рис. 3.7

Очевидно, что они образуют следующие пары подобных треугольни-

ков:

BC,CLN ; CDE,CLM .

Обозначим стороны треугольников как 1aCL x, AB x, ! y.

==− =

Из подобия треугольников следует:

Syyr

xyS

−

−−

−

(3.62)

Выражение (3.62) преобразуем к виду:

Определение возможностной меры реализации происшествий 89

()()()()

Syry yryS,−−=− −

из которого получим:

Sr rS

−

Δ+Δ

(3.63)

Вернёмся к выражению (3.62) и запишем

()(1)( )

yS xS y.−=− −

Из последнего выражения найдём

()

xS y

−Δ. (3.64)

После подстановки (3.63) в выражение (3.64) и несложных преобра-

зований получим формулу возможностной меры отказа в виде:

Sr Sr

−

==−

+Δ Δ +Δ

. (3.65)

На основании произведенного вывода можно сформулировать сле-

дующие утверждения:

1. В параметрической модели предпосылок опасности «нечеткое воз-

действие

s — нечеткая восприимчивость r» при условии максимума

её полноты и достоверности и с учётом выбора максимально небла-

гоприятного варианта сочетания погрешностей представления этих

параметров возможностная мера реализации предпосылки есть

от-

ношение

интервала пересечения нечётких параметров воздействия s

и восприимчивости r к суммарной абсолютной погрешности

Δ+Δ их представления.

2. Возможностная мера реализации предпосылки опасности есть

раз-

ность

между суммарной абсолютной погрешностью представления

характеризующих опасность параметров и параметрическим запасом

безопасности,

отнесённая к этому запасу.

3. При представлении нечетких параметров воздействия, восприимчи-

вости и инициирования как

ограниченных сверху множеств реализа-

ция предпосылки опасности невозможна, если суммарная абсолют-

ная погрешность этих параметров меньше его

xxxvii

параметрическо-

го запаса безопасности

+Δ <

Раздел 3

3.6.4.3. Уст а н овл ени е аналитического выражения возможностной

меры реализации критической функции опасности

Используя полученную формулу (3.65) для ВМ реализации элемен-

тарной предпосылки, на основе операций сигнатуры алгебры нечетких

множеств

произведем гомоморфное преобразование функции связно-

сти элементов относительно критического элемента объекта (2.29) в фор-

мулу возможностной меры отказа объекта как функции от ВМ отказа эле-

ментов. То есть при следующих условиях преобразования:

Pos( ( ) 1) ( );

Pos( 1 ;

Pos( 1) ( ) 1

ВЫХ RM

to to

ttt ttstrtt

y Т T

Zex s,r,, e

⎫

⎪

⎬

⎪

== ΔΔ =

⎪

⎭

(3.66)

требуется определить зависимость вида:

() ( ( ) )

ВЫХ З

NStoSrm

Т f,s,r,,B,tT

πππ

=ΔΔ∈

, (3.67)

где

— условная запись функции связности возможностных мер отказа

элементов, заданной на сигнатуре

S алгебры Заде.

Решение. По аналогии с выводом зависимости (2.28) решим задачу

методом индукции. Для этого применим к зависимости (2.23) условия

преобразования (3.66) и получим:

Pos( 1) Pos( 1 ( ) 1) min( ( ))

yy ,

== =∧ ==. (3.68)

В свою очередь, запишем, что:

{

}

()max

(b ) ,

ππ

=

(3.69)

где по формуле (2.24)

B — есть упорядоченный булеан, причём его эле-

менты с учётом формулы (3.65) определяются в виде:

Есипов Ю.В., Самсонов Ф.А., Черемисин А.И. Мониторинг и оценка риска систем защита - объект - среда

Подождите немного. Документ загружается.