Eschrig H. Topology and Geometry for Physics
Подождите немного. Документ загружается.

e ¼ð/
b
ðpÞÞ
1
; and in the second equality the action of G on a principal fiber
bundle was employed. Finally, w
1
a
ððx; eÞw
ab
ðxÞÞ ¼ w
1
a
ðx; eÞw
ab
ðxÞ¼s
a
ðxÞw
ab
ðxÞ:
The canonical section s
a
is a mapping of the manifold U
a
into the manifold P;
hence it may be pushed forward to a linear mapping s
a
of the tangent spaces
T
x
ðMÞ into the tangent spaces T
s
a
ðxÞ
ðPÞ: Likewise, the mapping w
ab
of the manifold
U
a
\ U
b
into G may be pushed forward to a linear mapping w
ab
from the spaces
T
x
ðMÞ into the spaces T
w
ab
ðxÞ
ðGÞ: Since these push forwards are differentials
(Sect. 3.5), the Leibniz rule applies to the above displayed relation: For every
tangent vector X
x
2 T
x
ðMÞ; x 2 U
a
\ U
b
;
s
b
ðX
x
Þ¼s
a
ðX
x
ÞRðw
ab
Þþðs
a
ðxÞÞ
w
ab
ðX
x
Þ;
where R is the representation of G by right action onto the vector space
T
s
a
ðxÞ
ðPÞ; ðR
g
Þ
ðYÞ¼YRðgÞ; and ðs
a
ðxÞÞ
is the push forward of s
a
ðxÞ; for fixed x
considered as a mapping G 3 g 7!s
a
ðxÞg 2 P; to a linear mapping from T
w
ab
ðxÞ
ðGÞ
into T
s
b
ðxÞ
ðPÞ with s
b
ðxÞ¼s
a
ðxÞw
ab
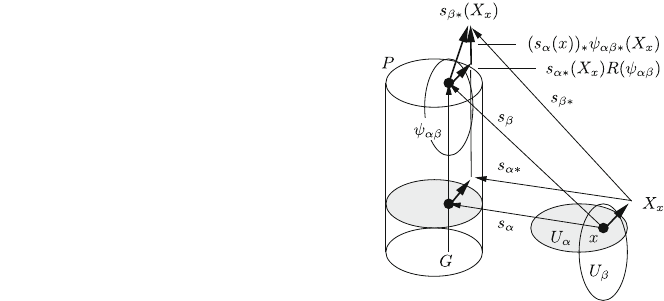
ðxÞ; cf. Fig. 7.4.
Let fE
i
ji ¼ 1; ...; dim Gg be a fixed base in g and let x ¼
P
i
x
i
E
i
be a con-
nection form on P: Then, as x
i
p
2 T
p
ðPÞ; hx
i
s
b
ðxÞ
; s
b
ðX
x
Þi is a real number and, if x
is varied through U
b
; it is a smooth real function on U
b
: Hence,
P
i
hx
i
s
b
ðxÞ
; s
b
ðX
x
ÞiE
i
is a smooth vector valued function on U
b
with values in g: It is denoted by
x
b
and is the pull back of x
i
2D
1
ðPÞ to D
1
ðU
b
Þ by s
b
: hx
i
b
; X
x
i¼hx
i
s
b
ðxÞ
; s
b
ðX
x
Þi ¼ hs
b
ðx
i
s
b
ðxÞ
Þ; X
x
i; that is, x
b
¼ s
b
ðxÞ: Applying x on both sides of the
above displayed Leibniz rule one obtains for X 2XðU
a
\ U
b
Þ
hx
b
; Xi¼hðAdðw
1
ab
Þx
a
Þ; Xiþh#
ab
; Xi; x
a
¼ s
a
ðxÞ;#
ab
¼ w
ab
ð#Þ;
ð7:4Þ
where # is the canonical Maurer–Cartan 1-form (p. 176) of G and the g-valued
1-forms x
a
¼ s
a
ðxÞ are called local connection forms. They are pull backs of
Fig. 7.4 Local sections
s
a
and s
b
with transition
function w
ab
and push
forwards
7.3 Connections on Principle Fiber Bundles 217
the connection form x from the canonical local section s
a
ðU
a
ÞP to U
a
M:
The first term on the right hand side was transformed with the property 2 of
connection forms: hx; s
a
ðXÞRðw
ab
Þi ¼ hx; ðR
w
ab
Þ
ðs
a
ðXÞÞi ¼ hððR
w
ab
Þ
xÞ; s
a
ðXÞi ¼ hððR
w
ab
Þ
xÞ
a
; Xi¼hðAdðw
1
ab
ÞxÞ
a
; Xi¼hðAdðw
1
ab
Þx
a
Þ; Xi: The last step
realizes the independent linear action of AdðgÞand of s
a
on X :
P
j
Adðw
1
ab
Þ
i
j
x
j
a
¼
P
j
Adðw
1
ab
Þ
i
j
x
j
a
: As regards the second term on the right hand side of (7.4), consider
the left invariant vector field Y on G which for g ¼ w
ab
ðxÞ equals w
ab
ðX
x
Þ2
T
ðx;w
ab
ðxÞÞ
ððU
a
\ U
b
ÞGÞ and apply the canonical Maurer–Cartan 1-form:
h#; w
ab
ðX
x
Þi ¼ h#; Yi¼Y
e
: The isomorphism G p
1
ðxÞ translates Y
into a fundamental vector field Y
e
¼ R
ðY
e
Þ on P; the value of which at p ¼
s
a
ðxÞw
ab
ðxÞis ðs
a
ðxÞÞ
w
ab
ðX
x
Þ: Now, hx; ðs
a
ðxÞÞ
w
ab
ðX
x
Þi ¼ hx; R
ðY
e
Þi ¼ Y
e
¼
h#; w
ab
ðX
x
Þi ¼ hðw
ab
ð#ÞÞ; X
x
i:
The transition formula (7.4) from U
a
to U
b
for the local connection forms of a
connection form x; that is, from x
a
to x
b
looks quite involved. Consider the
important special case where G is Glðn; KÞ or a subgroup thereof, that is, where
both G and g T
e
ðGÞ consist of n n-matrices. Recall that w
ab
ðxÞ2G and
hx; Xi2g: The relation (7.4) becomes a matrix equation and reads
hx
b
; Xi¼w
1
ab
hx
a
; Xiw
ab
þ w
1
ab
w
ab
ðXÞ:
The first expression is due to the definition of the adjoint representation of G in this
case, and in the second expression w
1
ab
pulls back the vertical vector w
ab
ðXÞ2
T
ðx;w
ab
ðxÞÞ
ððU
a
\ U
b
ÞGÞ to a vertical vector of T
ðx;eÞ
ððU
a
\ U
b
ÞGÞg:
Recall, that w
ab
is the differential of w
ab
:
There is a one–one correspondence of connection forms x on P and families of
local connection forms x
a
on M obeying (7.4). The correspondence is expressed
by the second relation (7.4).
A local connection form x
a
is a connection form on the trivial bundle U
a
G:
It is easily seen that on a trivial bundle M G the lifts Q
ðx;gÞ
of the tangent spaces
Q
ðx;eÞ
on the reduced bundle M feg; that is, all tangent spaces on all submani-
folds M fgg; form a connection. It is called the canonical flat connection.
(Later it becomes clear why it is called flat.) Since all manifolds are supposed to
be paracompact, the technique of partitioning of unity (Sect. 2.4) can be used to
show that on every principal fiber bundle any local connection may be continued
to a global connection [1, vol. I, Sect. II.2].
A connection exists on every principal fiber bundle.
Let ðLðMÞ; M; p; Glðm; RÞ; m ¼ dim M be the frame bundle over M: A con-
nection form x on LðMÞ is called a linear connection. (There is a modification
compared to the general case which is explained in more detail at the end of Sect.
7.7.) A linear connection is a glðm; RÞ-valued 1-form x ¼
P
ij
x
i
j
E
j
i
with
218 7 Bundles and Connections

properties 1 and 2 on p. 215, where fE
j
i
ji; j ¼ 1; ...; mg is a fixed base in glðm; RÞ ;
for instance given by the real m m-matrices E
j
i
having a unit entry in the ith row
and jth column and zeros otherwise, ðE
j
i
Þ
l
m
¼ d
l
i
d
j
m
: Recall from Sect. 7.2 that a
linear frame is an ordered base ðX
1
; ...; X
m
Þ of T
x
ðMÞ; and LðMÞ3p ¼
ðx; X
1
; ...; X
m
Þ:
Consider a local trivialization of LðMÞ by an open cover f U
a
g of M and
introduce local coordinates u
a
: U
a
! U
a
R
m
: x 7!
P
k
x
k
e
k
; where fe
k
g is the
base of R
m
introduced in Sect. 7.2. As was done there, consider again the linear
bijection uðpÞ : R
m
! T
pðpÞ
ðMÞ; uðpgÞ¼uðpÞg and find local coordinates
w
a
ðpÞ¼ðx
k
ðpÞ; u
k
i
ðpÞÞ on U
a
Glðm; RÞLðMÞ and w
a
ðpgÞ¼ðx
k
ðpÞ; u
k
j
ðpÞg
j
i
Þ;
where u
k
i
ðpÞ is a real non-degenerate m m-matrix. Therefore, the coordinate
expression of a tangent vector is
T
p
ðLðMÞÞ 3 X
p
¼
X
k
X
k
ðpÞ
o
ox
k
þ
X
ik
X
k
i
ðpÞ
o
ou
k
i
¼
h
X
p
þ
v
X
p
:
While the first coordinate expression has no component tangent to the fiber and hence
belongs to the horizontal space
h
X
p
only, the second one may, depending on the
connection, belong partially to both
h
X
p
and
v
X
p
: Nevertheless, the horizontal space
must be m-dimensional since it is isomorphic to T
x
ðMÞand the vertical space must be
m
2
-dimensional since it is isomorphic to glðm; RÞ: The canonical local section is
s
a
: x 7!w
1
a
ðx
k
a
ðxÞ; d
k
i
Þ and s
b
ðxÞ¼w
1
a
ðx
k
a
ðxÞ; d
k
i
Þw
ab
¼ w
1
a
ðx
k
a
ðxÞ; ðw
ab
Þ
k
i
Þ:
Let h be the R
m
-(vector)-valued 1-form on LðMÞ; defined as
hh
p
; X
p
i¼u
1
ðp
ðX
p
ÞÞ; X
p
2 T
p
ðLðMÞÞ; ð7:5Þ
where p
: T
p
ðLðMÞÞ ! T
pðpÞ
ðMÞ is the push forward of p as previously which
projects any tangent vector X
on the bundle space LðMÞ to the tangent space on
the base space M; and u ¼ uðpÞ : R
m
! T
pðpÞ
ðMÞ is the linear bijection as above
and in Sect. 7.2 which transforms the orthonormal standard base of the R
m
into the
frame p: u
1
then represents the vector X
x
¼ p
ðX
p
Þ in the frame p: h is called the
canonical form on LðMÞ (sometimes called the soldering form which ‘solders’
structural objects of the points of LðMÞ like tangent vectors to the base space M).
If X
p
is vertical, then p
ðX
p
Þ¼0 (pðpðtÞÞ has zero derivative at t where
the tangent vector X
pðtÞ
to the curve pðtÞ is vertical) and hence hh
p
; X
p
i¼0 for
vertical X
p
: In the case of a general X
p
a group action yields hðR
g
ðh
pg
ÞÞ; X
p
i¼
hh
pg
; R
g
ðX
p
Þi ¼ ðugÞ
1
ðp
ðR
g
ðX
p
ÞÞÞ ¼ g
1
u
1
ðp
ðX
p
ÞÞ ¼ g
1
hh
p
; X
p
i: (Since
R
g
ðX
p
Þ is in the same fiber as X
p
; p
ðR
g
ðX
p
ÞÞ ¼ p
ðX
p
Þ:) Hence, R
g
ðhÞ¼g
1
h:
Now, since Q
p
R
m
; let B be a linear mapping of R
m
3 X into the space
HðLðMÞÞ 3 BðXÞ of horizontal vector fields on LðMÞ; BðXÞ
p
2 Q
p
; defined by
hx; BðXÞi ¼ 0; hh; BðXÞi ¼ X: ð7:6Þ
7.3 Connections on Principle Fiber Bundles 219
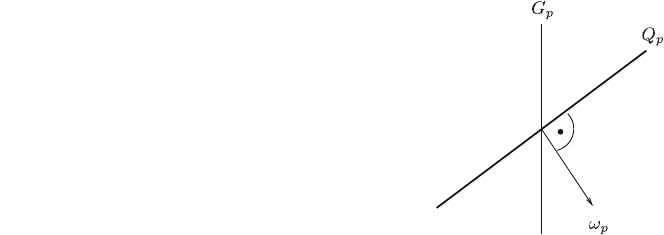
The first relation ensures that
v
BðXÞ¼0 while the second relation spells out
as p
ðBðXÞ
p
Þ¼ðuðpÞÞðXÞ; and, since Q
p
T
pðpÞ
ðLðMÞÞ; BðXÞ is uniquely defined
by (7.6). It is called the standard horizontal vector field corresponding to X:
There are m
2
linearly independent fundamental vertical vector fields, which are
independent of the connection x; and m linearly independent standard horizontal
vector fields, which depend on the choice of the connection x by the first relation
of (7.6) (Fig. 7.5).
7.4 Parallel Transport and Holonomy
The connection C on a principal fiber bundle ðP; M; p; GÞ is used to define the
parallel transport of fibers on the base space M: Let F : I ! M; I ¼½0; 1R; be
a path in M from x
0
¼ Fð0Þ to x
1
¼ Fð1Þ: A (horizontal) lift F
of the path F is a
path F
: I ! P which is projected to F so that p F
¼ F and which has
a horizontal tangent vector in every of its points F
ðtÞ; t 2 I: If X 2XðMÞ is a
tangent vector field on M and if F is an integral curve of X; then F
is obviously an
integral curve in P of the lift X
of X: Since there is a one–one correspondence of
tangent vector fields X on M and their lifts X
on P; which was stated on p. 216,
and since there is a unique maximal integral curve of X
through every point p 2 P
by Frobenius’ theorem, there is precisely one lift F
of the path F starting at a
given point p
0
2 p
1
ðx
0
Þ: In other words, for every p
0
2 p
1
ðx
0
Þ there is a
uniquely defined lift F
which transports p
0
to a point p
1
2 p
1
ðx
1
Þ; for given x
1
on F uniquely defined by F and p
0
: This is written as p
1
¼
~
Fðp
0
Þ: Obviously,
~
Fðp
0
gÞ¼
~
Fðp
0
Þg; since ðR
g
Þ
ðX
Þ¼X
for every horizontal vector field. Hence,
~
F : p
1
ðx
0
Þ!p
1
ðx
1
Þ is a Lie group isomorphism. It is called the parallel
transport of the fiber along the path F from x
0
to x
1
:
If F is a path in M; then F
; F
ðtÞ¼Fð1 tÞ is the inverse path, and
~
F
¼
~
F
1
is the inverse isomorphic mapping of fibers. If F is a path from x
0
to x
1
and F
0
is a path from x
1
to x
2
; then the concatenation (p. 182) F
00
¼ F
0
F is a path from x
0
Fig. 7.5 Example of vertical
space G
p
and horizontal space
Q
p
of a two-dimensional
tangent space T
p
ðPÞ (drawing
plane), showing how the
connection form x; x
p
2
T
p
ðPÞ; determines Q
p
with
G
p
independently given
220 7 Bundles and Connections
to x
2
(not necessarily smooth at x
1
; but this does not pose a problem in the present
context, piecewise smooth paths may be allowed). Obviously,
~
F
00
¼
~
F
0
~
F:
If F is a loop with base point x; then
~
F is an automorphism of p
1
ðxÞ: Every loop
F yields such an automorphism. Let L
x
be the family of all loops in M with base
point x: From the last paragraph it follows that all automorphisms due to the loops of
L
x
form a group, the holonomy group H
x
of the connection C with base point x: If
L
0
x
is the family of all null-homotopic loops with base point x; then the corresponding
subgroup of the holonomy group is the restricted holonomy group H
0
x
:
Take a loop F based on x; and take any point p 2 p
1
ðxÞ: It is parallel trans-
ported by the loop to p
0
¼
~
FðpÞ2p
1
ðxÞ; and, since G acts transitively from the
right on p
1
ðxÞ; there is g
F
2 G so that
~
FðpÞ¼pg
F
: Clearly,
g
F
0
FðpÞ¼pg
F
g
F
0
¼
R
g
F
0
g
F
ðpÞ: This provides a homomorphism from the holonomy group H
x
of auto-
morphisms of p
1
ðxÞ into the right action R of the structure group G of P; and,
since G acts freely on p
1
ðxÞ; into G itself. The image of this homomorphism in G
is a subgroup of G; it is called the holonomy group H
p
with reference point p:
The restricted holonomy group H
0
p
with reference point p is likewise defined. If the
reference point is changed within a fiber from p to pg; then
g
F
0
FðpgÞ¼pgg
F
g
F
0
¼
pðgg
F
g
1
gg
F
0
g
1
Þg ¼
g
F
0
FðpÞg: Hence, the holonomy group H
p
with reference
point p is changed into H
pg
¼ gH
p
g
1
(and H
0
p
is changed into gH
0
p
g
1
).
Observe, that by the above definitions the holonomy group H
x
is a subgroup of
Autðp
1
ðxÞÞ AutðGÞ; while H
p
is a subgroup of G itself. Let F and F
0
be two
loops with base point x ¼ pðpÞ and so that p
0
g
F
6¼ p
0
g
F
0
for some p
0
2 p
1
ðxÞ; that
is the automorphisms corresponding to F and F
0
are not the same. Then, since G
acts freely on p
1
ðxÞ; p
0
g
F
6¼ p
0
g
F
0
for all p
0
2 p
1
ðxÞ: Hence, F and F
0
yield two
different elements in every H
p
0
; which means that the homomorphism from H
x
to
H
p
0
G is injective. H
p
and H
x
for x ¼ pðpÞ are isomorphic.
More generally, let p and p
0
be two points (not necessarily of the same fiber)
which may be parallel transported into each other by a lift of some path F from
pðpÞ to pðp
0
Þ; p
0
¼
~
FðpÞ: Then, for every loop F
x
2L
x
ðL
0
x
Þ with base point x ¼
pðpÞ there is a loop F
x
0
¼ FF
x
F
2L
x
0
ðL
0
x
0
Þ with base point x
0
¼ pð p
0
Þ: Let p
F
x
¼
~
F
x
ðpÞ¼pg
F
x
; that is, g
F
x
2 H
p
: Then, p
0
F
x
0
¼ð
~
F
~
F
x
~
F
1
Þðp
0
Þ¼
~
Fð
~
F
x
ðpÞÞ ¼
~
Fðpg
F
x
Þ¼
~
FðpÞg
F
x
¼ p
0
g
F
x
: In the last but one equality, it was used that
~
F is a Lie
group isomorphism from p
1
ðxÞ to p
1
ðx
0
Þ: Hence, g
F
x
2 H
p
0
; too:
If p can be parallel transported to p
0
; then H
p
¼ H
p
0
and H
0
p
¼ H
0
p
0
:
It can be proved [1, vol. I, Sect. II.3] that
if M is pathwise connected (and paracompact), then for every p 2ðP; M; p; GÞ
the holonomy group H
p
is a Lie subgroup of G whose connected component of
unity is H
0
p
; while H
p
=H
0
p
is countable.
As a very simple example reconsider the universal covering of S
1
by R of
Fig. 6.1 on p. 181. At the end of Sect. 7.1 the universal covering of a connected
7.4 Parallel Transport and Holonomy 221
manifold was considered as a principal fiber bundle, in the present case
ðR; S
1
; p; p
1
ðS
1
ÞÞ where the bundle projection is p : R 3 t 7!/ ¼ e
it
2 S
1
; and
p
1
ðS
1
ÞZ is the fundamental group of the circle S
1
: Since this is a discrete Lie
group, its Lie algebra is trivial, and there are no vertical vector fields. Like the
whole bundle P ¼ R; the horizontal space is one-dimensional and coincides with
R at every point p ¼ t; which is likewise the tangent space on S
1
at every point
x ¼ e
it
: A lift of the loop based on / ¼ 1 and running once around S
1
is an interval
½2pn; 2pðn þ1Þ 2 R; n 2 Z: Hence, the holonomy group H
t
¼ Z for every t 2
R ¼ P; while H
0
t
¼ 0 (both groups in additive writing). If a loop F from / ¼ 1
returns to / ¼ 1 without running around S
1
; then F
from 2pn returns to 2pn:
H
t
¼ H
t
=H
0
t
¼ Z is a countable discrete Lie subgroup of G ¼ p
1
ðS
1
Þ; which in this
case coincides with G itself.
The reader easily verifies that the holonomy group H
p
for every point p of the
Möbius band is fe; Ig; while H
0
p
is again trivial.
Less trivial examples of holonomy groups will be considered later.
7.5 Exterior Covariant Derivative and Curvature Form
Like the g-valued 1-form x; the connection form with property 2 on p. 215,
consider more generally g-valued r-forms r ¼ðr
1
; ...; r
dim G
Þ; so that hr
i
; X
1
^
^X
r
i; X
j
2XðPÞ; are real functions on P and
ðR
g
Þ
r ¼ Adðg
1
Þr for every g 2 G: ð7:7Þ
Such a form is called a pseudo-tensorial r-form of type ðAd; gÞ: It is said to be
horizontal, if hr
i
p
; ðX
1
Þ
p
^^ðX
r
Þ
p
i¼0 whenever at least one of the tangent
vectors ðX
j
Þ
p
at p 2 P is vertical (tangent to the fiber). A horizontal pseudo-
tensorial r-form is called a tensorial r-form. Note that a connection form x is
vertical in this sense, it is a pseudo-tensorial 1-form of type ð Ad; gÞ; but not a
tensorial 1-form.
For every pseudo-tensorial r-form r; a tensorial r-form
h
r may be uniquely
defined by
h
h
r; X
1
^^X
r
i¼hr;
h
X
1
^^
h
X
r
i: ð7:8Þ
Indeed, because of the r-linearity of r;
h
r is uniquely defined by the above
relation, and together with r it is of type ðAd; gÞ: Furthermore, it vanishes
whenever at least one of the vectors X
j
is vertical, which means that
h
X
j
vanishes.
For a connection form x always
h
x ¼ 0 holds.
The exterior covariant derivative D of a pseudo-tensorial r-form r is defined
as
222 7 Bundles and Connections
Dr ¼
h
ðdrÞ: ð7:9Þ
It is a linear mapping from pseudo-tensorial r-forms to tensorial ðr þ 1Þ-forms.
Indeed, by the linearity of the exterior derivative, together with r the exterior
derivative dr is a pseudo-tensorial form.
The tensorial 2-form
X ¼ Dx ð7:10Þ
is called the curvature form of the connection C given by the connection form x:
This name derives from the geometric meaning in the case of the Riemannian
geometry (Chap. 9). Recall that there is no angle between a vector and a covector,
both living in different spaces, nevertheless one often speaks of orthogonality, if a
covector annihilates a vector, h x; Xi¼0: Likewise, there is no radius of curvature
of a manifold not having gotten a metric. Nevertheless, the curvature form mea-
sures the deviation of parallel transport between two points along distinct paths,
and the manifold is said to be flat (see below), if the curvature form vanishes.
Let X ¼
h
X and Y ¼
h
Y be two horizontal tangent vectors at p 2 P: Then, (7.8)
yields h
h
r; X ^ Yi¼hr; X ^ Yi for any pseudo-tensorial 2-form r: Hence,
hdx; X ^ Yi¼hX; X ^ Yi in this case. Now, let X ¼
h
X further be horizontal and
Y
0
¼
v
Y
0
be vertical. Continue X to a horizontal vector field on P and Y
0
to the
uniquely defined (vertical) fundamental vector field Y
¼ R
ðYÞ; equal to Y
0
at p
and corresponding to Y 2 g: First of all, according to (3.37), ½X; Y
¼½Y
; X¼
lim
t!0
ðð/
t
Þ
ðXÞXÞ=t where the 1-parameter group /
t
created by Y
is a
subgroup of G and therefore it leaves the horizontal vector field X horizontal.
Hence, ½X; Y
is a horizontal vector field. Now, (4.49) yields hdx; X ^ Y
i¼
L
X
hx; Y
iþL
Y
hx; Xihx; ½X; Y
i ¼ 0: The first Lie derivative vanishes since
hx; Y
i¼hx; R
ðYÞi ¼ Y is constant, in the second and third hx; ...i¼0 since the
argument is horizontal. Finally, if both X
0
and Y
0
are vertical and X
and Y
are the
corresponding fundamental vector fields, then hdx; X
^ Y
i¼hx; ½X
; Y
i ¼
½X; Y ¼ ½hx; X
i; hx; Y
i: Again the two Lie derivatives vanish as derivatives
of a constant, and in the remaining term hx; X
i¼X was used twice.
Let X; Y 2 T
p
ðPÞ be two arbitrary tangent vectors, decompose them into their
horizontal and vertical components and continue them into tangent vector fields as
above. By virtue of the bilinearity of the 2-form dx; E. Cartan’s structure
equations for a connection x on a principal fiber bundle,
hdx; X ^ Yi ¼ ½hx; Xi; hx; Yi þ hX; X ^ Yi; ð7:11Þ
are obtained. In symbolic writing they are often expressed as dx ¼½x; xþX:
Eq. 7.11 is a g-valued equation consisting of dim G real equations. They may be
obtained by introducing a base fE
i
ji ¼ 1; ...; dim Gg in g with corresponding
structure constants c
k
ij
: Then, x ¼
P
i
x
i
E
i
; X ¼
P
i
X
i
E
i
and from the left AdðgÞ
invariance of x and (6.3) one has
7.5 Exterior Covariant Derivative and Curvature Form 223

dx
i
¼
1
2
X
jk
c
i
jk
x
j
^ x
k
þ X
i
: ð7:12Þ
(In addition the obvious relation
P
c
i
jk
x
j
x
k
¼
P
ð1=2Þc
i
jk
x
j
^ x
k
following from
the properties of the structure constants was used, observe that each vector com-
ponent dx
i
of the g-vector is a 2-form in K
2
ðT
p
ðPÞÞ; and the wedge-product of 1-
forms is such a 2-form.)
A word on notation. In exterior calculus the convention
½x; r
i
1
...i
rþs
¼ðx
i
1
...i
r
r
i
rþ1
...i
rþs
r
i
rþ1
...i
rþs
x
i
1
...i
r
Þð7:13Þ
is used. If x and r are matrices, then the matrix element ðx
i
1
...i
r
r
i
rþ1
...i
rþs
Þ
k
l
may not
be the same as ðr
i
rþ1
...i
rþs
x
i
1
...i
r
Þ
k
l
; and one of them may even not be defined
according to the concatenation rule for matrices. Then, ½x; r would not exist.
However, in general ½x; x¼x ^x for a 1-form, while ð½r; xþ½x; rÞ
ij
¼
ðr
i
x
j
x
j
r
i
þ x
i
r
j
r
j
x
i
Þ need not vanish for general 1-forms, and hence
generally it may be that ½r; x 6¼½x; r: In analogy to the derivation of (7.11),
the exterior covariant derivative of a tensorial 1-form r may be obtained as
Dr ¼ dr þð½r; xþ½x; rÞ=2:
Like the local connection forms x
a
of a connection form x; local curvature
forms hX
i
a
; X
x
^ Y
x
i¼hX
i
s
a
ðxÞ
; s
a
ðX
x
Þ^s
a
ðY
x
Þi ¼ hs
a
ðX
i
s
a
ðxÞ
Þ; X
x
^ Y
x
i on open
sets U
a
M of local bundle trivializations may be introduced with the help of the
canonical local sections s
a
; that is, X
a
¼ s
a
ðXÞ are pull backs of the curvature form
on P to U
a
M: However, since X is a tensorial form with the property (7.7) and
since w
ab
ð
h
XÞ vanishes, the transition relations are simply
X
b
¼ Adð w
1
ab
ÞX
a
or X
b
¼ w
1
ab
X
a
w
ab
; ð7:14Þ
where the second relation again holds, if G is a subgroup of Glðn; KÞ in matrix
notation. Since a pull back is a homomorphism of exterior algebras commuting
with the exterior differentiation, one immediately has dx
a
¼½x
a
; x
a
þX
a
:
Taking the exterior derivative of (7.12), one finds 0 ¼ ddx
i
¼
P
c
i
jk
dx
j
^
x
k
þ dX
i
as an equation of 3-forms. Let X; Y; Z be three horizontal tangent vectors
at p 2 P: Since x
k
annihilates horizontal vectors, it follows that hdX
i
; X ^ Y ^
Zi¼0: In view of (7.8, 7.9), this may be expressed as
DX ¼ 0: ð7:15Þ
These are the Bianchi identities for the curvature form. Alternatively, for any
pseudo-tensorial r-form DDr ¼ D
h
ðdrÞ¼
h
ðddrÞ; and D
2
¼ 0 is inherited from
d
2
¼ 0; hence (7.15) immediately follows from (7.10).
224 7 Bundles and Connections
On p. 218 the canonical flat connection of a trivial principal fiber bundle
P ¼ M G was introduced. Consider the canonical Maurer–Cartan form # of G
and the projection p
2
: M G ! G: Then,
x ¼ p
2
ð#Þð7:16Þ
is the canonical flat connection form. Indeed, the #
i
g
form a dual base to a base in
T
g
ðGÞ and hence p
2
ð#Þ¼ðp
2
#Þ
¼ #
p
2
pulls any vector X 2 T
ðx;gÞ
ðPÞ first
back to T
g
ðGÞ and then isomorphically to T
e
ðGÞ: Hence, hx; Xi¼0; iff the pull
back of X to T
g
ðGÞ vanishes, that is, iff X is tangent to M fgg (cf. Fig. 7.5).
Now, dx ¼ dðp
2
ð#ÞÞ ¼ p
2
ðd#Þ¼p
2
ð½#; #Þ ¼ ½ p
2
ð#Þ; p
2
ð#Þ ¼ ½x; x;
and hence X ¼ 0: In the third equality the Maurer–Cartan equations of a Lie group
where used.
A connection in a general principal fiber bundle ðP; M; p; GÞ is called a flat
connection, if every point x 2 M has a neighborhood U for which there exists an
isomorphism F : p
1
ðUÞ!U G mapping horizontal spaces on p
1
ðUÞto tangent
spaces on U fgg: Since the above considerations were local ones, it is clear that
X ¼ 0 for a flat connection. However, the reverse is also true, which is the result of
three theorems presented here without proof (see for instance [1, vol. I, Chap. II]).
Reduction theorem: Let ðP; M; p; GÞ be a principal fiber bundle, let M be
pathwise connected (and paracompact), and let C be a connection on P with
connection form x and curvature form X: For every p 2 P; denote PðpÞ the set of
all points p
0
2 P which may be parallel transported to p. Then; PðpÞ is a reduced
fiber bundle with the reduction of the structure group from G to H
p
: Let F :
PðpÞ!P be the corresponding bundle homomorphism with the push forward
F
: h
p
! g; and let C
0
be a connection on PðpÞ with connection form x
0
and
curvature form X
0
: Then, F
ðx
0
Þ¼F
ðxÞ; F
ðX
0
Þ¼F
ðXÞ; where F
pulls x
i
and X
i
back from DðPÞ to DðPðpÞÞ; however, still forming vectors of g:
Ambrose–Singer theorem on holonomy: In the settings and notation of the
previous theorem, the Lie algebra h
p
is generated by all those elements of g which
may be expressed as h X
p
0
; X
p
0
^ Y
p
0
i; where X
p
0
and Y
p
0
are arbitrary horizontal
vectors in T
p
0
ðPÞ:
Theorem on flat connections: A connection on a principal fiber bundle is a flat
connection, iff the corresponding curvature form vanishes.
Let C be a flat connection on ðP; M; p; GÞ; X ¼ 0; and let M be connected. Let
p 2 P be arbitrary and consider the holonomy bundle through p: Denote it
~
M ¼
PðpÞ: In view of the Ambrose–Singer theorem, h
p
is trivial. Hence, h
0
p
is also
trivial, and, since H
0
p
is a connected Lie subgroup of G and hence uniquely defined
by h
0
p
; it is also trivial. Consequently, H
p
¼ H
p
=H
0
p
is countable and therefore
discrete. It follows that
~
M is a covering space of M: In particular, if M is simply
connected, then P is isomorphic to the trivial bundle M G and C is isomorphic to
the canonical flat connection of the latter.
7.5 Exterior Covariant Derivative and Curvature Form 225
The theory of principal fiber bundles forms the base of the theory of more
special and important vector bundles considered in the following sections. How-
ever, it also yields immediately the mathematics of gauge field theories and, more
generally, of geometric phases (Berry phases) in quantum physics, which will be
considered in the next chapter.
7.6 Fiber Bundles
Before more general covariant derivatives of parallel transport of vector and tensor
fields are considered with the help of a connection, as a further step more special
structure is introduced into fiber bundles.
A general bundle over M is a triple ðE; M; pÞ of two topological spaces, E and
M and a smooth surjective mapping p : E ! M: In a fiber bundle ðE; M; p
E
; F; GÞ;
M is a manifold (locally homeomorphic to R
m
for some m ¼ dim M), and all
spaces p
1
E
ðxÞ; x 2 M are isomorphic to each other and isomorphic to a manifold
F; the typical fiber. Moreover, there is a Lie group G of transformations of F
which introduces more structure into F (for instance the group Glðn; KÞ; n ¼
dim F introduces the structure of a K-vector space into F) and which in physics
often has the meaning of a symmetry group. In a principle fiber bundle the typical
fiber is the group G itself which acts on itself from the right. In order to adjust the
action of G to the fiber bundle ðE; M; p
E
; F; GÞ; it is incorporated by a principle
fiber bundle ðP; M; p; GÞ:
A fiber bundle ðE; M; p
E
; F; GÞ; or in short E; consists of
1. a principal fiber bundle ðP; M; p; GÞ;
2. G acts on F from the left, that is, G F ! F : ðg; f Þ¼gf; g 2 G; f 2 F; is a
linear mapping and hence a representation of the Lie group G;
3. E ¼ P
G
F; that is, ðp; f Þ¼ðpg; g
1
f Þ is an equivalence relation R in P F;
and E ¼ðP FÞ = R; the elements of E are denoted pðf Þ;
4. p
E
: E ! M : pðf Þ7!pðpÞ;
5. every local diffeomorphism p
1
ðUÞU G; U M; induces a local diffeo-
morphism p
1
E
ðUÞU F:
Item 3 may be understood as a mapping p : F ! p
1
E
ðxÞE; x 2 M : f 7!pðf Þ of
the typical fiber F into E: In this respect, an isomorphism of fibers is a mapping
p p
0
1
: p
1
E
ðx
0
Þ!p
1
E
ðxÞ where x
0
¼ pðp
0
Þ; x ¼ pðpÞ: Since x
0
¼ x implies p
0
¼
pg
1
for some g 2 G; p p
0
1
¼ p g p
1
in this case, the group of automor-
phisms of a fiber p
1
E
ðxÞ is isomorphic to the structure group itself. Item 5 fixes the
topology in E in such a way that for every local trivialization of p
1
ðUÞ in P there
is a local trivialization of p
1
E
ðUÞ in E: Of course, this is only possible, if there
exists a bijection between p
1
E
ðUÞ defined by the previous items and U F:
Consider ðU G FÞ=R ¼ ffðx; gg
0
; g
0
1
f Þjg
0
2 Ggg: Choosing g
0
¼ g
1
; any
226 7 Bundles and Connections
