Eschrig H. Topology and Geometry for Physics
Подождите немного. Документ загружается.


Chapter 8
Parallelism, Holonomy, Homotopy
and (Co)homology
This chapter is devoted to most topical and important applications of topology and
geometry in physics: gauge field theory and the physics of geometric phases which
vastly emerges from the notion of the Aharonov–Bohm phase and later more
generally from the notion of a Berry phase (see [1, 2]) and even penetrates
chemistry and nuclear chemistry. The central notion in these applications is hol-
onomy. Since holonomy is based on lifts of integral curves of tangent vector fields
on the base manifold M of a bundle, and maximal integral curves may end in
singular points of tangent vector fields, non-singularity of tangent vector fields
plays its role. Non-zero tangent vector fields can be expressed as sections of the
‘punctured tangent bundle’ on M: This is a subject of the interrelation of holonomy
with homotopy of fiber bundles, an important issue by itself. Therefore the chapter
starts with two sections on homotopy of fiber bundles before gauge fields and
finally geometric phases in general are considered. All these issues fall also into
the vast realm of characteristic classes and index theory. In a first reading the first
two sections may be skipped.
8.1 The Exact Homotopy Sequence
Let a fiber bundle ðE; M; p
E
; F; GÞ associated with a principal fiber bundle
ðP; M; p; GÞ be given. (In particular E may be P itself.) So far (horizontal) lifts of
paths in M to E were considered. Now the goal is to lift homotopy classes of
mappings of n-dimensional spheres into M: Recall, that a special intermediate
bijective mapping P of n-spheres S
n
to one point compactified cubes I
n
was needed
in order to define a group structure on the sets of homotopy classes (Sect. 2.5,in
particular Fig. 2.8). In the following, I
n
; I denote the n-cube, unit interval closed in
the ordinary Euclidean topology,
I
n
:
I denote their interior, and I
n
as previously
denotes the one-point compactification of
I
n
:
H. Eschrig, Topology and Geometry for Physics, Lecture Notes in Physics, 822,
DOI: 10.1007/978-3-642-14700-5_8, Ó Springer-Verlag Berlin Heidelberg 2011
247

Let
e
U : I
n
! M be a mapping with
e
UðoI
n
Þ¼x
0
2 M; where oI
n
¼ x
1
is the
boundary of the unit cube I
n
which is defined to be the point x
1
of the one-point
compactification of the open cube
I
n
to I
n
: Then, U ¼
e
U P is the mapping of the
n-sphere S
n
into M which in Sect. 2.5 was considered for a general topological
space X instead of a manifold M, and for which Uðs
0
Þ¼x
0
: The part of the
homotopy class of U with the mapping s
0
7!x
0
fixed is ½U¼fU
H
: I S
n
!
M jU
H
ð0; Þ ¼ U; U
H
ðt; s
0
Þ¼x
0
for t 2 Ig: It corresponds to ½
e
U¼f
e
U
H
: I I
n
!
M j
e
U
H
ð0; Þ ¼
e
U;
e
U
H
ðI oI
n
Þ¼fx
0
gg:
As in Sect. 5.5, all continuous mappings from a closed simplex (or a cube) of
R
k
into M may be arbitrarily closely uniformly approximated (in the metrics of R
k
and of coordinate neighborhoods U
a
of M) by smooth mappings of some neigh-
borhood of the simplex (cube) into M: In this sense all mappings are again sup-
posed to be smooth in the following.
Let D
k
be a (sufficiently smoothly bounded) domain in R
k
: A general lift of
U : D
k
! M to E is a (smooth) function U
: D
k
! E with p
E
U
¼ U:
Let U : I I
n
! M be given and let Q ¼ðf0gI
n
Þ[ðI oI
n
Þ: Let U
Q
: Q !
E be a general lift of the restriction Uj
Q
of U to Q: Then, there exists a general lift
U
: I I
n
! EofU with U
j
Q
¼ U
Q
:
Proof Consider first the case that UðI I
n
Þ lies in a trivializing coordinate
neighborhood U of the base space M of E, so that p
1
E
ðUÞU F: Then,
U
Q
j
f0gI
n
maps x 2 I
n
to ðUðxÞ; /ðxÞÞ, where / is some mapping from I
n
to the
typical fiber F: Consider U as a homotopy of Uj
I
n
and take any homotopy of / in F
to obtain a general lift of U:
Next, take a homeomorphism q of I I
n
onto itself which maps f0gI
n
onto Q: Such a homeomorphism exists, it can explicitly be constructed in the
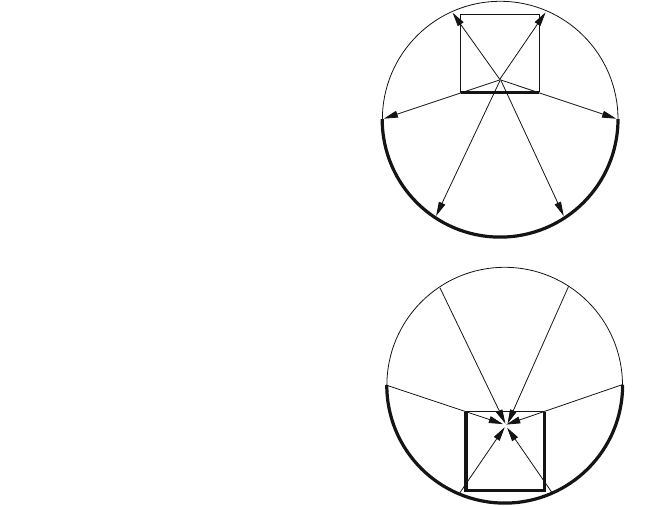
following way (Fig. 8.1). Map I
n
homeomorphically into an n-ball B
n
and hence
I I
n
into a spherical cylinder I B
n
: Then, in a first step (a), embed
the domain I B
n
(n ¼ 1 in the figure) into a large enough ball B
nþ1
, and then
stretch it homogeneously along the drawn arrows from some inner point in such
a way that the domain f0gB
n
(thick line of the figure) is mapped onto the
lower half-sphere of the boundary of the ðn þ1Þ-ball (thick arc). This is a
homeomorphic map of I B
n
onto the ball B
nþ1
: Next, shift the ðn þ 1Þ-ball
upwards as shown in part (b) of the figure and shrink it homogeneously along
the drawn arrows to I B
n
which after going back to I I
n
maps the lower half-
sphere to Q: The composition of all homeomorphisms yields the sought map q
from I I
n
to I I
n
mapping f0gI
n
to Q: (Is the mapping from I
n
to B
n
necessary in this construction?) The mapping
e
U ¼ U q maps I I
n
to U, and
e
Uj
f0gI
n
¼ Uj
Q
q.
e
U
Q
¼ U
Q
q is a general lift of
e
Uj
f0gI
n
: It was seen in the
previous paragraph that it has an extension to a lift
e
U
of
e
U. U
¼
e
U
q
1
is
now the wanted general lift of U: On the trivializing neighborhood U the
statement holds in an elementary way also for n ¼ 0:
248 8 Parallelism, Holonomy, Homotopy and (Co)homology
Now, the general case is reduced to the just considered by subdividing I I
n
into N
nþ1
small cubes of equal size, small enough that each of them is mapped by
U into a trivializing coordinate neighborhood in M: In a first step, I of the
homotopy is replaced by the interval ½0; 1=N, and then, step by step the contin-
uation is performed to all I: Start at the small cube with corner ð0; ...; 0Þ and scan
lexicographically with respect to the coordinates of the corner closest to the origin
through the cubes. At any stage, U
is determined on the n-face of the cube with
x
1
¼ const. and on some of the n-faces sharing an ðn 1Þ-face with the latter. An
n
0
-face is an n
0
-cube, and the above extension procedure can be applied to it,
provided U
is already defined on all its ðn
0
1Þ-faces sharing ðn
0
2Þ-faces with
the n-face x
1
¼ const.: In case of necessity one has further to go down with n
0
at
most to n
0
¼ 0 in which case the above continuation of U
(from a point to an
interval) is always possible. Stepping from there upwards again with n
0
finally
extents U
to the whole ðn þ1Þ-cube, and one can proceed to the next. U
is finally
established on I I
n
: h
As seen from the given proof, in the above statement the cube I
n
may be
replaced by any domain which is homeomorphic to a ball, in particular also by an
n-simplex. Even more generally, it may even be replaced by any polyhedron jcj
(see p. 141 f), when oI
n
is replaced by any subpolyhedron jc
0
j of jcj: By definition,
a subpolyhedron of jcj is a polyhedron which is also a subset of the skeleton of
some complex realizing the polyhedron jcj:
(a)
(b)
Fig. 8.1 The mapping q in
two steps for n ¼ 1: See text
for explanation
8.1 The Exact Homotopy Sequence 249
Let M be contractible, and let U : I M ! M be given with Uð0; xÞ¼x
0
fixed
for all x 2 M and Uð1; xÞ¼x: Let
0
2 E be some point. The just mentioned
generalization of the above lifting proposition says that there is a general lift U
of
U, and for Uð1; Þ this is a (global) section of E: Hence, every fiber bundle with a
contractible base space has a section. This is also true for principal fiber bundles,
for which it was shown in Sect. 7.1 that a principal fiber bundle P which has a
section is trivial (that is, P M G). By the very definition of fiber bundles
associated with principal fiber bundles, triviality transfers also to the former:
A fiber bundle with contractible base space is trivial.
With the help of the lifting proposition a group homomorphism
d : p
n
ðM; x
0
Þ!p
n1
ðF; f
0
Þ; n [ 1, between homotopy groups may be con-
structed. Given a group element of p
n
ðM; x
0
Þ, a representing mapping U : I
n
!
M; UðoI
n
Þ¼fx
0
g is chosen. Lift x
0
to any point
0
¼fðp
0
g; g
1
f
0
Þg 2 p
1
E
ðx
0
Þ:
This can be extended to a general lift of U to U
: I
n
! E which lifts Uj
Q
; Q ¼
oI
n
nf1gðI
n1
Þ
to
0
: Since Uðf1gI
n1
Þ¼fx
0
g, it holds that U
ðf1g
I
n1
Þp
1
E
ðx
0
Þ: Moreover, oðf1gI
n1
ÞQ; and hence U
j
f1gI
n1
represents a
group element of p
n1
ðF; f
0
Þ: Let U
0
: I
n
! M; U
0
ðoI
n
Þ¼fx
0
g be a mapping
homotopic with U: That means that there is a mapping
e
U : I I
n
! M with
e
Uj
f0gI
n
¼ U;
e
Uj
f1gI
n
¼ U
0
: This can be lifted to
e
U
with
e
U
j
f0gI
n
¼ U
and
hence yields a homotopy in F between U
and
e
U
j
f1gI
n
: Hence, the constructed
correspondence between representatives of group elements of p
n
ðM; x
0
Þ
and p
n1
ðF; f
0
Þ yields a correspondence between the group elements themselves
independent of the chosen representatives (Fig. 8.2). Taking the construction (2.35),
it is easy to see that the just constructed mapping d from p
n
ðM; x
0
Þto p
n1
ðF; f
0
Þis a
group homomorphism for n [ 1: For n ¼ 1 it is still a well defined mapping from the
fundamental group p
1
ðM; x
0
Þ to p
0
ðF; f
0
Þ: Only p
0
ðF; f
0
Þ is not in general a group.
It is a set in bijective relation to the pathwise connected components of F:
The exact homotopy sequence is
!
d
p
n
ðF; f
0
Þ!
i
p
n
ðE;
0
Þ!
p
E
p
n
ðM; x
0
Þ!
d
p
n1
ðF; f
0
Þ!
i
ð8:1Þ
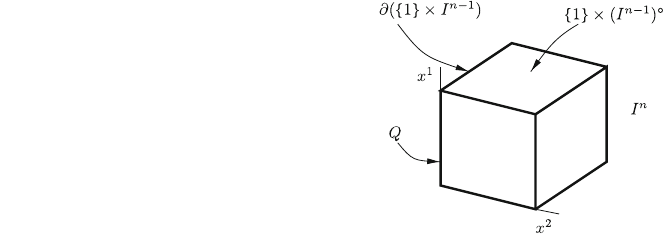
Fig. 8.2 A cube I
n
; n ¼ 3. Q
is its surface without the
interior of its upper face
(open box). oðf1gI
n1
Þ
consists of the edges of the
upper face
250 8 Parallelism, Holonomy, Homotopy and (Co)homology
where i is the inclusion mapping of F onto the fiber through
0
¼fðp
0
g; g
1
f
0
Þg 2
p
1
E
ðx
0
Þ in E; p
E
is the bundle projection, and both mappings are pushed forward to
the corresponding homotopy groups.
Proof of the exactness of the sequence The elements of p
n
ðF; f
0
Þ are homotopy
classes of mappings from the cube I
n
into F with oI
n
mapped to f
0
: The inclusion
mapping i maps these mappings to mappings of the same cube into the fiber of E
containing
0
, and hence the images of these mappings are projected by p
E
to
constant mappings of the cube I
n
to the point x
0
¼ p
E
ð
0
Þ, which represent the zero
element of p
n
ðM; x
0
Þ: Hence Im i
Ker p
E
:
The elements of p
n
ðE;
0
Þ are homotopy classes of mappings U
of the cube I
n
into E with oI
n
mapped to
0
: By p
E
they are projected to mappings p
E
U
of I
n
into M with oI
n
mapped to x
0
: Then, d maps the latter to the restriction to f1g
I
n1
of any general lift ðp
E
U
Þ
which maps f0gI
n1
to f
0
: If one takes U
as
such a general lift, it maps f1gI
n1
to ff
0
g which belongs to the zero of
p
n1
ðF; f
0
Þ: Hence Im p
E
Ker d:
Finally, the elements of p
n
ðM; x
0
Þ are homotopy classes of mappings U of the
cube I
n
into M with oI
n
mapped to x
0
. d puts them to the homotopy classes of the
restriction U
j
f1gI
n1
of a general lift U
with U
j
f0gI
n1
¼f
0
g, which means
that U
j
f1gI
n1
is null-homotopic. Hence Im d Ker i
:
To prove exactness, the reverse inclusions have also to be demonstrated.
Suppose that the homotopy class of U
: I
n
! E belongs to Ker p
E
, that is, that
p
E
U
is null-homotopic in M: Lift the homotopy between U
0
x
0
and p
E
U
to
e
U
: I
nþ1
! E: It shows that U
is homotopic to a mapping of I
n
into p
1
E
ðx
0
Þ
and thus belongs to Im i
: Hence Im i
Ker p
E
:
Suppose that the homotopy class of U : I
n
! M belongs to Ker d: That means
that U can be chosen so that Uðf1gI
n1
Þp
1
E
ðx
0
Þ and Uðf0gI
n1
Þ¼f
0
g:
This can be lifted to U
belonging to p
n
ðE;
0
Þ: Hence Im p
E
Ker d:
The last step is a little bit more elaborate. Let U
: I
n1
! F; U
ðoI
n1
Þ¼
ff
0
g belong to Ker i
: This means that there exists a mapping (homotopy)
e
U
P :
I S
n1
! E with
e
U
Pj
f1gS
n1
¼ i U
P;
e
U
Pðf0gS
n1
Þ¼f
0
g and
e
U
PðI fs
0
gÞ ¼ f
0
g: This implies
e
U
: I I
n1
! E with
e
U
j
f1gI
n1
¼ i
U
;
e
U
ðf0gI
n1
Þ¼f
0
g and
e
U
ðI oI
n1
Þ¼f
0
g: Now it is easily seen that
U ¼ p
E
e
U
represents an element of p
n
ðM; x
0
Þ which by d is mapped to the
element of p
n1
ðF; f
0
Þ represented by U
. Hence Im d Ker i
h
If one defines the ‘zero’ of the set p
0
ðX; x
0
Þ to correspond to the pathwise
connected component of X containing x
0
, then it is easy to see that (8.1) extends to
n ¼ 0: If one further defines p
n
ðF; f
0
Þ¼p
n
ðE;
0
Þ¼p
n
ðM; x
0
Þ¼0 for n\0 and
dðp
0
ðM; x
0
ÞÞ ¼ f0g, then the exact homotopy sequence extends infinitely in both
directions as an exact sequence.
The exact homotopy sequence can amply be used to compute homotopy groups.
Let, for instance, p
n
ðM; x
0
Þ¼0 for some n: This implies Ker p
E
¼ p
n
ðE;
0
Þ and
8.1 The Exact Homotopy Sequence 251
hence, by exactness of the homotopy sequence, that i
is surjective. If now
additionally p
nþ1
ðM; x
0
Þ¼0, then Im d ¼ 0 in p
n
ðF; f
0
Þ and hence i
is also
injective, which means that
if p
n
ðM; x
0
Þ¼p
nþ1
ðM; x
0
Þ¼0, then p
n
ðF; f
0
Þp
n
ðE;
0
Þ:
In the same way one obtains
if p
n1
ðF; f
0
Þ¼p
n
ðF; f
0
Þ¼0, then p
n
ðE;Þp
n
ðM; x
0
Þ;
in particular, for n ¼ 0,
If F and M are (pathwise) connected, so is E,
and
if p
n1
ðE;
0
Þ¼p
n
ðE;
0
Þ¼0, then p
n
ðM; x
0
Þp
n1
ðF; f
0
Þ:
If X is a discrete topological space, then p
n
ðX; x
0
Þ¼0 for all n [ 0: Hence it
follows from the second of the above conclusions that
if the fiber F is discrete, then p
n
ðE;
0
Þp
n
ðM; x
0
Þ for all n [ 1:
For instance, since SUð2Þ is a twofold cover of SOð3Þ, it can be considered as a
principal fiber bundle with base space SOð3Þ and the discrete structure group
G ¼ F
2
¼ðZ mod 2Þ consisting of two elements. On the other hand, according to
(6.35), the elements of SUð2Þ are represented by matrices
A ¼
x
1
þ ix
2
x
3
þ ix
4
x
3
þ ix
4
x
1
ix
2
; det A ¼ x
2
1
þ x
2
2
þ x
2
3
þ x
2
4
¼ 1; ð8:2Þ
and therefore SUð2Þ is homeomorphic to S
3
: Hence, p
n
ðSOð3ÞÞ p
n
ðSUð2ÞÞ
p
n
ðS
3
Þ for all n [ 1: (See also p. 226 f for more details.)
As another example (by taking E ¼ P and F ¼ G), consider the principal fiber
bundle ðR; S
1
; p; 2pZÞ with pðt 2 RÞ¼expðitÞ2S
1
; already discussed previously.
It follows that p
n
ðS
1
Þp
n
ðRÞ¼0 for all n [ 1, which is intuitively clear since an
n-sphere with n [ 1 cannot continuously be wound around S
1
: Since SOð2Þ is
homeomorphic to S
1
, also p
n
ðSOð2ÞÞ ¼ 0 holds for n [ 1:
As yet another example, consider the principal fiber bundle ðSOð3Þ;
S
2
; p; SOð2ÞÞ with bundle space SOð3Þ, base space S
2
and structure group SOð2Þ:
(Any SOð3Þ-transformation corresponds bijectively to a directed rotation axis, that
is, a point of S
2
and a rotation in the mathematically positive sense around this
axis, which rotations are in bijective correspondence to SOð2Þ-transformations.
More generally, it can be shown that ðSOðnÞ; S
n1
; p; SOðn 1ÞÞ is a principal
fiber bundle, [3, Section 9.3]). Now, since p
n
ðSOð2ÞÞ ¼ 0 for n [ 1, the second of
the above conclusions from the exact homotopy sequence yields p
n
ðSOð3ÞÞ
p
n
ðS
2
ÞÞ and hence also p
n
ðS
3
Þp
n
ðS
2
Þ for n [ 2: This implies the Hopf theorem
p
3
ðS
2
Þp
3
ðS
3
ÞZ as a special case (cf. the end of Sect. 2.5).
Suppose that there exists a section s : M ! E in the fiber bundle E: Then,
p
E
s ¼ Id
M
and hence p
E
s
¼ Id
p
n
ðM;x
0
Þ
, where the pushes forward from the
spaces to their homotopy groups are considered. Therefore, every ½U2p
n
ðM; x
0
Þ
252 8 Parallelism, Holonomy, Homotopy and (Co)homology
is the image of some ½U
2p
n
ðE;
0
Þ : Im p
E
¼ p
n
ðM; x
0
Þ: Because of the
exactness of (8.1) this means p
n
ðM; x
0
Þ¼Ker d, which is the same as d 0:
If E has a section, then
0 ! p
n
ðF; f
0
Þ!
i
p
n
ðE;
0
Þ!
p
E
p
n
ðM; x
0
Þ!0 for all n; ð8:3Þ
that is, p
n
ðM; x
0
Þ¼p
n
ðE;
0
Þ=p
n
ðF; f
0
Þ:
8.2 Homotopy of Sections
The construction of (global) sections in a fiber bundle is a case of interrelation
between homotopy and homology. In this section it will be presupposed that the base
space M is a compact manifold (of dimension m as always in this text), which is
homeomorphic to a polyhedron jc
M
j embedded into some R
n
; n m: (Section 5.6;
recall that every polyhedron of dimension m may be embedded into the R
2mþ1
;
hence, besides M being compact, the presupposition is not really restrictive.)
Let an abstract complex c
M
corresponding to the polyhedron jc
M
j be fixed, and
let c
r
be the rth skeleton of c
M
¼ c
m
: For simplicity it will now further be assumed
that p
0
ðFÞ¼0, that is, the typical fiber F is assumed to be pathwise connected. By
smoothness, a section through
0
¼ p
0
ðf
0
Þ¼fðp
0
g; g
1
f
0
Þg consists of points
2 E, represented (for g ¼ e)byðp; f Þ, where f stays in the pathwise connected
component of f
0
for all x 2 M,ifM is pathwise connected. Hence, for pathwise
connected M, instead of a bundle ðE
0
; M; p
E
0
; F
0
; PÞ the subbundle ðE; M; p
E
; F; GÞ
may be considered in the general case with F being the pathwise connected
component of f
0
2 F
0
:
Next, assume that a section on jc
l
j is given for some l\m and that p
k
ðFÞ¼0
for all k\l: (Recall that for a pathwise connected space F; p
k
ðF; f
0
Þ¼p
k
ðFÞ does
not depend on the point f
0
:) Try to extend the section to jc
lþ1
j: If this is done,
induction in l can be used, since p
0
ðF; f
0
Þ¼0, and jc
0
j consists of discrete points
(vertices) only for which the existence of a section is trivial.
Consider first a trivial fiber bundle E ¼ M F:
Take a (regular) simplex given by c
lþ1
i
2 c
lþ1
: As any regular ðl þ1Þ-simplex,
jc
lþ1
i
j is homeomorphic to the ðl þ 1Þ-ball. Its boundary belongs to the lth skeleton,
oc
lþ1
i
2 c
l
, and joc
lþ1
i
j is homeomorphic to the l-sphere S
l
: A section s on joc
lþ1
i
j is
homotopic to a mapping s : S
l
! F and hence defines an element g
s
ðc
lþ1
i
Þ of the
homotopy group p
l
ðFÞ: It is easily seen that the section s can be extended to all of
jc
lþ1
i
j, iff g
s
ðc
lþ1
i
Þ¼0: (For instance by contracting the values of s on S
l
to one
point when contracting S
l
to its center.)
Consider the ðl þ1Þ-chain module C
lþ1
ðc
M
; ZÞ generated by the ðl þ1Þ-sim-
plices of c
lþ1
: Any section s on joc
lþ1
j gives rise to a mapping of each simplex c
lþ1
i
of c
lþ1
to some element g
s
ðc
lþ1
i
Þ of p
l
ðFÞ: Since the homotopy group p
l
ðFÞ is
Abelian, this mapping may be extended by linearity to a mapping hs; c
lþ1
m
i :
8.1 The Exact Homotopy Sequence 253
C
lþ1
ðc
M
; ZÞ!p
l
ðFÞ; where c
lþ1
m
¼
P
i
m
i
c
lþ1
i
; m
i
integer. All these mappings for
all sections form a cochain module C
lþ1
ðc
M
; p
l
ðFÞÞ with coefficients in the ho-
motopy group p
l
ðFÞ: If the cochain hs; i is trivial (zero-dimensional), then every
section on jc
l
j may be extended to a section on jc
lþ1
j: Therefore, the cochain hs; i
is called the obstruction cochain to the extension of the section s to jc
lþ1
j: It is
obviously constant under continuous (homotopic) deformations of s:
With the help of the lifting proposition on p. 248, it can be demonstrated that all
sections on jc
l1
j are mutually homotopic as long as all homotopy groups p
k
ðFÞ
are trivial for all k\l: To see this, take two arbitrary sections s and s
0
and construct
a homotopy of their restrictions to jc
0
j, which is always possible since jc
0
j consists
of isolated points. By means of the lifting proposition, extend this homotopy to a
homotopy of sj
c
1
with some s
1
on jc
1
j which coincides with s
0
on joc
1
j:
If p
1
ðFÞ¼0, all sections on jc
1
j coinciding on joc
1
j are homotopic, and hence s
1
may be homotopically deformed into s
0
j
c
1
: These two steps may be repeated until
jc
l1
j is reached.
Given two sections s and s
0
on jc
l
j which coincide on joc
l
j; for each simplex jc
l
i
j
the mapping /
s;s
0
: S
l
! F is considered, which maps the upper hemisphere of S
l
homeomorphically to the simplex and composes this mapping with s, maps the
lower hemisphere of S
l
again homeomorphically to the simplex and composes with
s
0
, in such a way that both mappings coincide on the equator of S
l
which is mapped
onto joc
l
i
j: The homotopy class of this mapping is denoted by h/
s;s
0
; c
l
i
i and forms
by linear extension a cochain of the module C
l
ðc
M
; p
l
ðFÞÞ: It is called the dif-
ference cochain between s and s
0
: Clearly h/
s;s
0
; i ¼ 0, iff s and s
0
are homotopic.
From the construction of both cochains it is clear that
hd/
s;s
0
; i ¼ hs; i hs
0
; i; hd/
s;s
0
; c
lþ1
m
i¼h/
s;s
0
; oc
lþ1
m
i: ð8:4Þ
Indeed, two arbitrary sections s and s
0
on jc
l
j are homotopic to sections s and
~
s
0
which coincide on jc
l1
j since on jc
l1
j all sections are homotopic. Putting /
s;s
0
¼
/
s;
~
s
0
; /
s;s
0
is defined for all sections s and s
0
on jc
l
j: Moreover, (2.35) in additive
writing for the group operation implies the left relation (8.4), if hd/
s;s
0
; i is defined
by the right relation. (Note that by the above construction the coordinate x
1
of
(2.35) runs in the opposite direction for s
0
, hence the minus sign.)
Since o
2
¼ 0; the second relation (8.4) implies d
2
¼ 0: Take s
0
to be the con-
stant section s
0
for which hs
0
; i ¼ 0, and obtain hs; i ¼ hd/
s;s
0
; i, that is, the
obstruction cochain is a coboundary (and also a cocycle, since d
2
¼ 0).
If l ¼ m, there are no ðl þ1Þ-simplices in jc
M
jM: By extension of the second
relation (8.4) to this case, h/
s;s
0
; i may be considered to be a cocycle on c
m
n c
m1
(hd/
s;s
0
; i ¼ 0), and there are no non-trivial m-boundaries. It follows that, if
p
k
ðFÞ¼0 for all k\m, then the set of homotopy classes of sections of M F is in
bijective correspondence with the cohomology group H
m
ðc; p
m
ðFÞÞ:
So much for a trivial bundle M F: If E is not a trivial fiber bundle, then an
abstract complex for M is to be considered which corresponds to a subdivision of
254 8 Parallelism, Holonomy, Homotopy and (Co)homology
the polyhedron jc
M
jM into simplices fine enough so that each simplex lies
within a trivializing coordinate neighborhood U of M: Instead of F, now a fiber
above some point x
i
2 U
i
is to be taken, which is isomorphic to F as a fiber.
However, instead of f
0
each m-simplex has now its own reference point
0
, and
instead of p
k
ðF; f
0
Þ, now the set of isomorphic groups p
k
ðp
1
E
ðx
i
Þ;
i
Þ is to be
considered, which leads to cochains with values in local groups. The technicalities
are considered in [3, Section 11.4]. The definition of corresponding (co)homology
groups of M is straightforwardly transfered to the new situation.
The obstruction cochain and the difference cochain are now defined to have
coefficients in the local homotopy groups, which are all isomorphic and connected
by group isomorphisms as transition functions. The relations (8.4) as local rela-
tions remain valid. In particular, from the very definition of difference cochains it
is clear, that for a given section s of E, the mapping h/
s;s
0
; i into the cochain
module is surjective. Indeed, given l and a section s on the l-skeleton of c
M
, take
any simplex c
l
i
of the l-skeleton. By the definition of the homotopy group
p
l
ðp
1
e
ðx
i
ÞÞ; x
i
2jc
l
i
jÞ; for any predefined group element g
i
there is a mapping
e
U
i
: jc
l
i
j!p
1
E
ðx
i
Þ; U
i
j
joc
l
i
j
¼
i
representing g
i
: It is homotopic to a mapping
U
i
: jc
l
i
j!p
1
E
ðx
i
Þ; U
i
j
joc
l
i
j
¼ sj
joc
l
i
j
since on the skeleton c
l1
all sections are
homotopic. Let s
0
be the section on the l-skeleton which on jc
l
i
j is equal to U
i
: It is
a section because on joc
l
i
j it coincides with the section s and hence it is continuous
(and thus homotopic to a smooth section). Consequently, for every predefined
cochain there exists a section s
0
of jc
l
j so that h/
s;s
0
; i is mapped to that cochain.
However, since on a non-trivial bundle a constant section does not necessarily
exist, obstruction cochains are not necessarily coboundaries any more. Only, for
any obstruction cochain hs
0
; i and any coboundary hd/; i , the cochain hs; i ¼
hs
0
; i þ hd/; i is again an obstruction cochain. Moreover, as long as p
k
ðFÞ¼0 for
k\l, every hs; i is a cocycle: hds; c
lþ1
m
i¼hs; oc
lþ1
m
i¼0: (h s; oc
lþ1
m
i maps to
p
l1
ðp
1
E
ðx
i
Þ;
i
Þp
l1
ðFÞ¼0 by assumption.) Hence, the obstruction cochains
form a certain cohomology class corresponding to an element h
lþ1
ðEÞ of the
cohomology group H
lþ1
ðc;
~
p
l
ðFÞÞ ¼ Z
lþ1
ðc;
~
p
l
ðFÞÞ=B
lþ1
ðc;
~
p
l
ðFÞÞ; where
~
p
l
ðFÞ
means the set of local homotopy groups connected by transition isomorphisms. This
cohomology class h
lþ1
ðEÞ is called a characteristic class of the fiber bundle E:
The fiber bundle ðE; M; p
E
; F; GÞ admits a section over the ðl þ 1Þ-skeleton, iff
the characteristic class is h
lþ1
ðEÞ¼0; h
lþ1
ðEÞis defined, iff all h
k
ðEÞ¼0 for k l:
Characteristic classes will be considered in more detail later. As seen from
above, they provide a measure of ‘non-triviality’ of a fiber bundle.
As a simple application, consider the problem of singular points of tangent
vector fields on compact manifolds M: Consider the punctured tangent bundle
T
ðMÞ¼ðT
ðMÞ; M; p
T
; R
m
nf0g; Glðm; RÞÞ: Its typical fiber F ¼ R
m
nf0g is
homotopy equivalent to the sphere S
m1
: It was mentioned at the end of Sect. 2.5
that p
k
ðS
m1
Þ¼0 for k\m 1 and p
m1
ðS
m1
Þ¼Z: (See [3, Section 7.1] for an
outline of a proof.) Therefore, there is always a non-zero tangent vector field on
8.2 Homotopy of Sections 255
the ðm 1Þ-skeleton of any polyhedron jc
M
jM: The attempt to extend it to M
will run into an obstruction, if h
m
ðT
ðMÞÞ is non-zero.
h
m
ðT
ðMÞÞ is an element of the cohomology group H
m
ðM; ZÞ: If M is con-
nected and orientable, then, since Poincaré’s duality (5.61) holds also for K ¼ Z
instead of R; one has H
m
ðM; ZÞH
0
ðM; ZÞ¼Z; and h
m
ðT
ðMÞÞ is an integer
depending on M (since the typical fiber F was fixed).
Isolated nodes of a tangent vector field are called singularities. Let x 2 M be a
singular point of a tangent vector field X: Put a small sphere S
m1
around that point,
so that no other singularity is enclosed and the enclosed ball is inside a single
coordinate neighborhood of M: Then, Xj
S
m1
can be considered as a mapping from
S
m1
to R
m
: Composing it with the central projection R
m
nf0g!S
m1
; a mapping
of S
m1
to itself is obtained. The degree of such a mapping was defined on p. 47.
This degree is called the index of the singular point of the tangent vector field.
Replacing the enclosed ball by a homeomorphic simplex, it is easily seen that the
index of the singularity is the obstruction to continue the non-zero tangent vector
field X from the boundary of the ball (sphere) into the whole ball. The obstruction in
the given case is an element of the homotopy group p
m1
ðS
m1
ÞZ:
Next, consider a decomposition of M into simplices small enough that each
simplex contains at most one singularity. Take the non-zero vector field X on the
ðm 1Þ-skeleton of this decomposition, and let n define the characteristic class of
T
ðMÞ, which is the obstruction to continue the non-zero X to all M: It is clear that
n is the sum of all indices of all singularities of X:
The sum of the indices of all singularities of a tangent vector field does not
depend on X, it only depends on M and is a topological invariant of M:
This is a simple case of an index theorem. By taking a sufficiently simple
tangent vector field for which the index sum is easy to compute, one can show that
n is Euler’s characteristic in that case. (For instance the gradient vector field of a
real function on M provided with a metric can be analyzed by means of Morse
theory (Sect. 5.8).) Since the only non-zero Betti numbers of a sphere S
m
are
b
0
ðS
m
Þ¼b
m
ðS
m
Þ¼1 (cf. (5.60)), Euler’s characteristic of an even dimensional
sphere is 2 and of an odd dimensional sphere is 0. Hence, an even dimensional
sphere cannot have a non-zero tangent vector field without singularities. (In two
dimensions: ‘every hedgehog has a vortex’; in fact it has at least one vortex of
index 2 or two vortices of index 1.) Odd dimensional spheres have non-singular
tangent vector fields. In fact, again by Poincaré’s duality, this is true for any odd-
dimensional compact orientable manifold.
8.3 Gauge Fields and Connections on R
4
The theory of connections on principal fiber bundles and gauge field theory
describe the same situation in different languages; for several decades they were
developed in parallel and largely independently.
256 8 Parallelism, Holonomy, Homotopy and (Co)homology
