Eschrig H. Topology and Geometry for Physics

Подождите немного. Документ загружается.

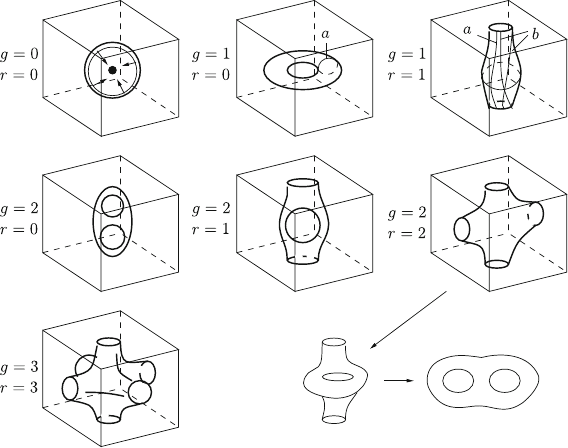
is shown where again all loops are contractible in T

which means r ¼ 0: Next, a

pretzel is shown of which one hole is again inside T

and the other one coincides

with one hole of T

(that one closing the top and bottom face). There is only one

type of loops not contractible in T

and hence r ¼ 1: Why the last picture in this

row shows a pretzel with two holes in T

is indicated in the sketches below, where

ﬁrst the left and right faces are closed and then the top and bottom faces. Here

there are two types of loops on FS, one from bottom to top and one from left to

right, which are not contractible in T

: Hence, F



ðp

ðFSÞÞ ¼ Z

and r ¼ 2:

Finally, in the bottom row only the case r ¼ 3 for a FS which is a pretzel with tree

holes and hence g ¼ 3 is shown. As an exercise the reader may draw sketches for

FS with any g [ 2 for cases r ¼ 0; 1; 2; 3:

The conjecture from these consideration is

r 3; r g:

It was already shown by the homomorphism argument for F



that r 3 and that

g ¼ 0 implies r ¼ 0, hence r [ 0 implies g [ 0: That means that only the second

inequality for r ¼ 2; 3 remains to be proved. To that goal, the homology groups H

of FS and of T

are considered. Suppose that a single FS sheet is a boundary in the

Fig. 5.15 Genus g and rank r of Fermi surface sheets. The Brillouin zone T

is shown as a cube

of which opposite faces have to be identiﬁed. Further explanations are given in the text

5.9 Examples from Physics 167

Brillouin zone. The alternative is considered below. Here, the push forward of the

embedding F is another homomorphism F



: H

ðFS; RÞ!H

ðT

; RÞ; which is

trivial, F



ðH

ðFS; RÞÞ ¼ 0; since FS is a boundary in T

: Therefore, for any closed

2-form x; dx ¼ 0,onT

the bilinear form

x ¼h½x; ½FSi ¼

1

dx ¼ 0

(cf. (5.40), o

1

FS is the domain in T

to which FS is the boundary), which implies

that the pull back F



: H

ðT

Þ!H

ðFSÞ is also trivial. Moreover, since Z



ðp

ðFSÞÞ ¼ F



ðH

ðFS; ZÞÞ; there are r mutually non-homologous cycles cðFSÞ

(not combined into boundaries) on FS which remain non-homologous on T

: Again

exploiting the non-degeneracy of (5.40), there must be r linearly independent

cohomology classes ½r of closed 1-forms r on T

so that h½r; ½cðFSÞi 6¼ 0: Hence,



ðH

ðT

; RÞÞ ¼ R

 H

ðFSÞ¼R

: Now, in R

a symplectic structure may

be introduced with the non-degenerate closed 2-form x ¼

i¼1

^ dp

(cf. p. 113), where q

and p

may be, roughly speaking, local coordinates along the

cycles a

and b

of Fig. 5.8. Assume for some i that dq

and dp

are both pull-backs of

some closed 1-forms r

; s

on T

: Then, F



ð½r

^ s

Þ  F



ðH

ðT

ÞÞ ¼ 0 which

contradicts the non-degeneracy of x: Hence, at most one of each pair of 1-forms in

the symplectic form x can be a pull-back of a closed 1-form on T

; and consequently

2r 2g: (Accordingly, in Fig. 5.15 at least one of the cycles a

; b

for each pretzel

hole of the FS is contractible in the Brillouin zone T

Note that in these considerations a central point was that the considered single

FS sheet is a boundary. The only alternative is a pair of corrugated planes ‘in

average’ parallel to each other which are not pathwise connected in T

but which

only together form a boundary. For that reason they must always appear in pairs,

since the total FS is necessarily a boundary as shown earlier. According to their

orientation, the two partners have homology classes opposite to each other. They

are heuristically seen to form two 2-tori ðg ¼ 2Þ with r ¼ 2 each, which also can

be proved formally.

On Fig. 5.16, the development of a real Fermi surface of YCo

under increasing

pressure is shown where sheets of all ranks except r ¼ 3 appear. In the third upper

panel there are small sheets with g ¼ r ¼ 0 centered at the top and bottom faces of

the Brillouin zone while in the lower panels the emergence under pressure of a

sheet with g ¼ r ¼ 0 around the center of the Brillouin zone is shown. In the

second upper panel there are small sheets (tori) with g ¼ 2; r ¼ 0 centered on the

edges of the hexagonal faces. The sheet of the left upper panel is a corrugated

cylinder with g ¼ r ¼ 1: The large sheet of the second panel has g ¼ 3; r ¼ 1: the

six holes around the vertical edges of the hexagonal Brillouin zone yield, after

closing the sides of the Brillouin zone as shown in Fig. 5.14 on p. 162, two holes

centered at the points AEC and DBF of Fig. 5.14 (each of the six holes belongs to

three zones). Cycles around these holes are, however, obviously contractible (into

the above mentioned points) in T

: Hence the only non-contractible class of

trajectories appears due to closing the top and bottom face of the Brillouin zone

168 5 Integration, Homology and Cohomology

into a torus, like in the ﬁrst band arising from trajectories parallel to the hexagonal

axis. The monster like Fermi surface sheet of the third panel has g ¼ 7; r ¼ 2: the

two holes centered on the hexagonal axis and the tree holes centered on the edges

of the hexagonal faces (one from two opposite edges) all yield contractible cycles

in T

: The only two relevant holes are those appearing by closing the two unin-

terrupted horizontal edge lines of the Fermi surface sheet around the mantle of the

Brillouin zone as in Fig. 5.14. They yield two classes of cycles non-contractible in

; from trajectories in three directions in the hexagonal plane two of which are

linearly independent. No trajectory perpendicular to the hexagonal plane remains

non-contractible.

The rank r of a Fermi surface is deﬁned to be equal to the maximal rank of its

sheets. Why is the rank of a Fermi surface interesting? It for instance governs the

magneto-resistivity of pure samples at low temperatures in strong magnetic ﬁelds.

In this case the dynamics of the electrons can be treated quasi-classically. If no

voltage is applied, the equations of motion are

ðpÞ¼

 B



½v

 B

;

¼ v

; ð5:105Þ

Fig. 5.16 Real Fermi surface of two majority spin conduction bands of hexagonal YCo

under

increasing pressure from left, 0 GPa, to right, about 25 GPa (courtesy of H. Rosner)

5.9 Examples from Physics 169

where e is the electron charge and c is the velocity of light. B is a spatially

homogeneous applied magnetic ﬁeld and v

is the Fermi velocity of a Bloch

electron on the Fermi surface of band m: The motion in quasi-momentum space is

all the time perpendicular to the Fermi velocity, hence the Bloch electron stays all

the time at constant energy on the Fermi surface. If Cartesian coordinates are

introduced in both the quasi-momentum space and the position space with the

z-axis in B-direction, then the projection of the motion onto the x; y-plane in

quasi-momentum space is geometrically similar with the motion in position space

rotated by 90



in the mathematically positive direction (due to the negative

sign of e) as compared to the motion in quasi-momentum space. While p

const.; dz=dt ¼ v

ðp

ðtÞÞ is a periodic function of p

which in the simplest model

case of a Fermi sphere is a constant. Recall, however, that in general v is an

arbitrary function of p; and both are in general not collinear.

While in the considered case with a homogeneous magnetic ﬁeld the motion in

quasi-momentum space is always on closed orbits, the position space is a torus

only in the idealized model of an inﬁnite perfect crystal. In reality the distance of a

unit cell from a boundary of a sample is measurable, and hence the physical

motion is in the universal covering space R

: Then, the trajectory of the Bloch

electrons through the crystal is a closed orbit, if the corresponding trajectory in

the Brillouin zone is contractible. It is running through the whole crystal as an

open trajectory, if the corresponding trajectory in the Brillouin zone is not con-

tractible, which can be the case in r linearly independent directions for each

Fermi surface sheet the rank r of which is non-zero. The directions are given by

the generators ðn

; n

Þ; j ¼ 1; ...; r of the subgroup F



ðp

ðFSÞÞ  p

ðT

Þ; that

is, by the reciprocal lattice vectors G

¼ n

þ n

: Only in the case of

pairs of corrugated planes there are open trajectories in all directions on those

planes.

If the mean scattering time of Bloch electrons (deﬁned by the purity of the

crystal and by the temperature) is s, then the length of the trajectory in quasi-

momentum space between two scattering events is on average Dp ¼jðev

=cÞBsj

where v

is the average Fermi velocity. Strong magnetic ﬁelds are those for which

Dp  hjb

j; but l

Bohr

B  e

in order that the quasi-classical treatment applies. If

only closed trajectories in position space are present, then the conductivity tensor r

and the resistivity tensor q are [8]



2

1

2

1

; q



while, if open trajectories are present, then



2

1

; q



170 5 Integration, Homology and Cohomology

The ﬁeld direction is assumed to be the z-direction and in the second case the

direction of open trajectories in the quasi-momentum space is the x-direction. The

entries a

and b

in the matrices mean that these components stay constant in the

limit B !1of the quasi-classical theory. The quotient q

=B ¼ R is the Hall

constant.

Further analysis now needs for a given Fermi surface to ﬁnd the directions of

magnetic ﬁeld B with respect to the reciprocal lattice for which open trajectories

may occur. This task can again be solved with topological methods [9, Chapter 2].

Even if r ¼ 1 there need not be directions for the ﬁeld so that open orbits appear: if

the ‘corrugated cylinder’ is a spiral shaped tube, there may be no plane intersecting

it in open trajectories.

References

1. Warner, F.W.: Foundations of Differentiable Manifolds and Lie Groups. Springer, New York

(1983)

2. Pontryagin, L.S.: Foundations of Combinatorial Topology. Dover, London (1996)

3. Thirring, W.: A Course in Mathematical Physics, 2nd ed., vol. 1. Springer, Wien (1992)

4. Scheck, F.: Mechanics, 2nd corrected and enlarged ed. Springer, Berlin (1994)

5. t’Hooft, G. (ed.): 50 Years of Yang-Mills Theory. World Scientiﬁc, Singapore (2005)

6. Thirring, W.: A Course in Mathematical Physics, 2nd ed., vol. 2. Springer, New York (1986)

7. Kato, T.: Perturbation Theory for Linear Operators. Springer, Berlin (1966)

8. Lifshits, I.M., Azbel, M.Y., Kaganov, I.M.: Electron Theory of Metals. Nauka, Moscow

(1971) (Translated: Consultants Bureau, New York, 1973)

9. Monastyrsky, M.I.: Topology in Condensed Matter. Springer, Berlin (2006)

5.9 Examples from Physics 171

Chapter 6

Lie Groups

6.1 Lie Groups and Lie Algebras

A Lie group is a smooth manifold that is also a group. Lie groups play a central

role in the geometry of manifolds and in the theory of invariants of dynamical

systems in physics. They are named in honor of S. Lie, their theory was much

developed by E. Cartan.

A Lie group G is a smooth manifold with a group structure such that for all

g; h 2 G the mapping G G ! G : ðg; hÞ7!gh

1

is smooth. Then, the mapping

h 7!h

1

is also smooth, since it can be considered as a case of the previous

mapping with g ¼ e; the unit element of the group. The composition of these two

mappings yields the mapping ðg; hÞ7!gh; which hence is also smooth. In sum-

mary, all group operations are smooth as a consequence of the smoothness of

ðg; hÞ7!gh

1

Since a Lie group is a special case of a topological group, all the arguments

used on p. 46 for topological groups are valid. In particular, if the group consists of

more than one pathwise connected component as a topological space, then each

pathwise connected component is diffeomorphic to the pathwise connected com-

ponent G

containing the unit element e of the group, and G=G

¼ p

ðGÞ; the

zeroth homotopy group of G whose elements are in one–one correspondence with

the pathwise connected components of G:

A simple case of a Lie group is R

with its usual topology and vector addition

as group operation. It is Abelian and additively written. The product G G

two Lie groups G and G

with the product manifold structure (p. 60) and the

direct product group structure (Compendium C.1) is a Lie group. For instance

¼ R R (n factors).

Let fa

; ...; a

g be a base of the vector space R

; and consider the lattice

L ¼f

i¼1

2 Zg: L is a subgroup of the Lie group R

: The quotient group

¼ R

=L is also a topological space with the quotient topology. T

is a Lie

group and is called the n-torus group. The 1-torus group can be viewed as the

multiplicative group S

¼fe

i2pt

jt 2 Rg: Then, T

 S

S

(n factors).

H. Eschrig, Topology and Geometry for Physics, Lecture Notes in Physics, 822,

DOI: 10.1007/978-3-642-14700-5_6, Ó Springer-Verlag Berlin Heidelberg 2011

173

Write the points of R

as real n n-matrices A; and consider the subset of R

of non-singular matrices, det A 6¼ 0; with the relative topology from R

: Since

det A is a polynomial and hence a smooth function on R

; Glðn; RÞ¼fA jdet A 6¼

0g is an open subset of dimension n

of R

and hence an n

-dimensional smooth

submanifold. It becomes a Lie group under matrix multiplication where AB

1

is a set

of rational functions with non-zero denominators and hence smooth. It is called the

general linear group of n dimensions (linear transformations of the vector space

). In particular Glð1; RÞ¼R nf0g is the multiplicative group of non-zero real

numbers. It consists of two pathwise connected components, the positive and the

negative real numbers. Likewise, the points of C

 R

(p. 21) may be written as

complex n n-matrices C; and the submanifold Glðn; CÞ¼fC jdet C 6¼ 0g forms

the complex general linear group of n dimensions. In particular Glð1; CÞ¼

C nf0g is the multiplicative group of non-zero complex numbers. It is pathwise

connected but not simply connected.

Consider the product manifold Glðn; RÞR

; but instead of the ordinary

direct product group structure deﬁne the group operations by ðA; xÞðA

; x

Þ¼

ðAA

; Ax

þ xÞ: This is the Lie group of afﬁne motions or afﬁne linear trans-

formations of R

: By deﬁning the action of the group elements ðA; xÞ on any point

y 2 R

by ðA; xÞy ¼ Ay þ x; any group element performs an afﬁne motion of R

and group multiplications correspond to compositions of afﬁne motions (exercise).

Formally, ðA; xÞ may be represented by a special ðn þ 1Þðn þ1Þ-matrix for

which the group operation is now the matrix product:

ðA; xÞ7!

A x



;

A x



þ x



The action on y 2 R

becomes a matrix multiplication by appending an n þ1st

unit element to y:

Returning to the general theory, every element g 2 G deﬁnes mappings l

h 7!gh and r

: h 7!hg of G into itself. They are called left and right translations

by g: If H is a subset of G; then l

ðHÞ¼gH; r

ðHÞ¼Hg: These mappings are

injective: gh ¼ gk yields h ¼ k after left translation by g

1

: They are also sur-

jective: any element k 2 G is gðg

1

kÞ and hence image of some element g

1

k 2 G

with respect to the left translation by g: These simple considerations apply likewise

to right translations. Being group operations the translations are smooth trans-

formations of the manifold G:

Let X 2XðGÞ be a tangent vector ﬁeld on the manifold G: At every point h 2 G

it deﬁnes a tangent vector X

2 T

ðGÞ: Let G be n-dimensional and let xðh

Þ¼

ðx

ðh

Þ; ...; x

ðh

ÞÞ be a local coordinate system centered at h, xðhÞ¼0: For every

smooth real function F : G ! R it yields X

F ¼

ðhÞðoF=ox

x¼0

: For

every h 2 G; a left translation by g induces as a push forward a mapping l

g

ðGÞ!T

ðGÞ: A tangent vector ﬁeld X is called a left invariant vector ﬁeld,if

g

ðX

Þ¼X

; that is, the tangent vector at h is pushed forward into the tangent

174 6 Lie Groups

vector at gh of the same tangent vector ﬁeld. Right invariant vector ﬁelds are

deﬁned analogously.

Let g be the set of all left invariant vector ﬁelds on the Lie group G: Then,

1. g is a real vector space isomorphic to T

ðGÞ by the isomorphism p : X 7!X

Consequently, dim g ¼ dim T

ðGÞ¼dim G:

2. X 2 g is smooth.

3. X; Y 2 g )½X; Y2g; that is, g is a Lie algebra (p. 68).

4. Let fX

; ...; X

g be a base of the vector space g; then there are constants c

such that

½X

; X

¼

k¼1

; c

þ c

¼ 0;

ðc

þ c

Þ¼0: ð6:1Þ

These constants are uniquely deﬁned by G and the base fX

g of g:

Proof Linear combinations of left invariant vector ﬁelds are clearly left invariant

vector ﬁelds, hence g is a subspace of the real vector space XðGÞ: p is injective,

since pðXÞ¼pðYÞ)X

¼ Y

) X

¼ Y

for all g 2 G due to left invariance. p is

also surjective, since for every X

2 T

ðGÞ there is X 2XðGÞ with X

¼ l

g

ðX

Þ:

Hence, p is an isomorphism of vector spaces.

Smoothness of left invariant vector ﬁelds is traced back to smoothness of the

group operations of Lie groups and properties of the push forward, analyzed in

(3.29, 3.30) on the basis of the commutative diagram on p. 73. In the present case,

h 2 U

; l

ðhÞ¼gh 2 U

and local coordinates x

¼ u

ðhÞ2U

and y

ðghÞ2U

are to be considered, where smoothness of the group operations

means that the coordinates y

¼ðl

ðx

Þ are smooth functions of the coordinates

for all admissible charts ðU

; u

Þ and ðU

; u

Þ: Equation 3.30 with F ¼ l

now

reads l

g

ðo=ox

Þ¼

ðoðl

=ox

Þðo=oy

Þ: The ﬁrst factor of the last expression

is the jth component of the vector ﬁeld at y

and, as the derivative of the smooth

function ðl

; is a smooth function of the x

If X and Y are l

-related (p. 78), then ½X; Y is l

-related, and hence Lie products

of left invariant vector ﬁelds are left invariant vector ﬁelds. From that, the exis-

tence and uniqueness of the constants c

follows. Their properties are a direct

consequence of the properties (3.17) of the Lie product. h

Depending on context both isomorphic Lie algebras g and T

ðGÞ are called the

Lie algebra of the Lie group G: The relevance of this Lie algebra lies in the fact

that it locally, and in the important case of pathwise connected, simply connected

Lie groups also globally, completely determines the Lie group. In physics one

speaks of the elements of the Lie algebra as of the inﬁnitesimal generators of the

Lie group. The constants c

are called the structure constants of the Lie group G:

Let x 2D

ðGÞ be an r-form on G: At each point h 2 G; x

is an element of

ðT



Þ (cf. (4.32)). A left translation l

induces as a pull back a mapping l



g;h

ðT



ðGÞÞ ! K

ðT



ðGÞÞ: The r-form x is called a left invariant r-form,if

6.1 Lie Groups and Lie Algebras 175



g;h

ðx

Þ¼x

; that is, the r-form at gh is pulled back to its own value at h: Left

invariant r-forms form the vector space D

inv

ðGÞ and the exterior algebra

inv

ðGÞ¼

r¼0

inv

ðGÞ; n ¼ dim G: ð6:2Þ

Like the case of tangent vector ﬁelds, here due to a property of pull back,

smoothness of r-forms is a consequence of left invariance. Right invariant r-forms

are deﬁned analogously.

The left invariant 1-forms, which in local coordinates are

ðhÞdx

; are

called the Maurer–Cartan forms.

Left invariant r-forms have the following properties:

1. They are smooth.

2. D

inv

ðGÞ is a subalgebra of DðGÞ: By the isomorphism p



: x 7!x

; D

inv

ðGÞ is

isomorphic to KðT



ðGÞÞ; in particular D

inv

ðGÞ is isomorphic to T



ðGÞ and

hence dual to g:

3. x 2D

inv

ðGÞ and X 2 g )hx; Xi¼const. on G:

4. x 2D

inv

ðGÞ and X; Y 2 g )hdx; X ^ Yi¼hx; ½X; Yi:

5. If #

inv

ðGÞ and f#

; ...;#

g is the base dual to fX

; ...; X

g; then the

Maurer–Cartan equations or structure equations

¼

1 j\k n

^ #

; c

¼h#

; ½X

; X

i ð6:3Þ

hold.

The isomorphism of 2 is proved analogously to the case of vector ﬁelds, and 3 is

a direct consequence. 4 follows from (4.49) where the second line vanishes due to

3, and 5 follows from the duality h#

; X

i¼d

together with (4.22, 6.1) and 4. Let

# ¼

; then h#

; i maps T

ðGÞ isomorphically onto g: The tangent-vector

valued 1-form # is called the canonical Maurer–Cartan form.

Depending on context, in the whole concept of Lie algebra of Lie groups

sometimes right invariant vector ﬁelds and forms are used, mainly for the sake of

convenience of notation. Since in both cases the Lie algebra g is isomorphic to the

same T

ðGÞ and D

inv

ðGÞ is isomorphic to the same KðT



ðGÞÞ; the buildings in both

cases are isomorphic to each other. However, the composition of two right

translations is r

: h 7!hgg

and hence r

¼ r

: This contravariant behavior

transfers to the push forward r

g

; and therefore the Lie product ½X; Y of left

invariant vector ﬁeld corresponds to the Lie product ½Y; X of right invariant

vector ﬁelds. Correspondingly, the structure constants of both cases differ by a

sign while all the above given relations remain valid for both cases.

For an Abelian Lie group (like for instance R

) left and right invariant vector

ﬁelds coincide, hence all structure constants vanish and the corresponding Lie

algebra is also Abelian: all Lie products are zero.

176 6 Lie Groups