Escher J., Guidotti P., Hieber M. et al. (editors) Parabolic Problems: The Herbert Amann Festschrift

Подождите немного. Документ загружается.

678 S. Shimizu

n−1

j,k=1

− g)

+ g(

−

tjk

)

∂

∂ξ

n−1

j,k=1

− g)∂

+ g(∂

−∂

tjk

)

∂u

∂ξ

n−1

j,k=1

− g

)

∂

g + g

(

−

tjk

)∂

g + g

tjk

(∂

g −∂

)

2gg

∂u

∂ξ

Since

g

−g

1−1/q

(Γ)

≤ C



∇



α

−1/q

(Γ)





∇



+ u

+ v) dτ

(Ω)

+∇



α

1−1/q

(Γ)





∇



+ u

+ v) dτ 

(Ω)



≤ CT

1/p



(2M + R)M,

g

−g

∞

((0,T ),W

1−1/q

(Γ))

≤ CT

1/p



(2M + R)M,



tjk

−



∞

((0,T ),W

1−1/q

(Γ))

≤ CT

1/p



(2M + R)M,

g,

tjk



∞

((0,T ),W

1−1/q

(Γ))

≤ CM,

and for example

(g

− g)

∇



+ u

+ v)

((0,T ),W

−1/q

(Γ))

≤ Cg

−g

∞

((0,T ),W

1−1/q

(Γ))

×



∞

((0,T ),W

1−1/q

(Γ))

∇



+ u

+ v)

((0,T ),L

(Ω))

≤ CT

1/p



(2M + R)

we have

(Δ

− Δ

Γ(t)

)(u

+ u

+ v)

((0,T ),W

−1/q

(Γ))

≤ CT

1/p



(2M + R)

Therefore we obtain

(m −Δ

)

−1

ν ·(Δ

−Δ

Γ(t)

)(u

+ u

+ v)

((0,T ),W

2−1/q

(Γ))

≤ Cν

1−1/q

(Γ)

(Δ

− Δ

Γ(t)

)(u

+ u

+ v)

((0,T ),W

−1/q

(Γ))

≤ CT

1/p



(2M + R)

. (6.34)

Finally we consider the term: (m − Δ

)

−1

ν ·

(t)ξ. By a direct calculation with

Γ(t)



n−1

j=1



∂

tj

−

∂

tj

−

tj

∂

−

tj

∂

tj

∂



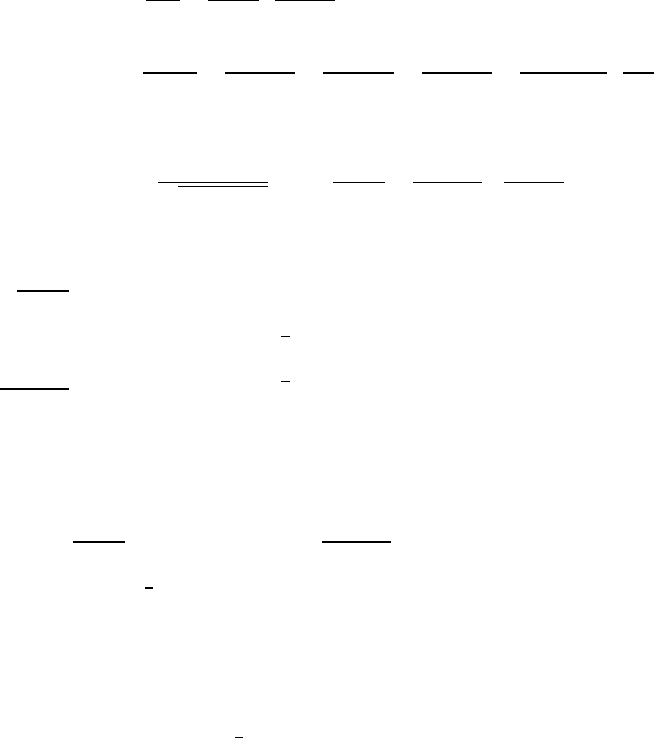
Local Solvability of Free Boundary Problems 679

Γ(t)

n−1

j,k=1



tjk

−

tjk



∂

∂ξ

n−1

j,k=1



∂

tjk

−

∂

tjk

−

tjk

∂

−

tjk

∂

tjk

∂



∂α

∂ξ

it holds that

ν ·

(t)ξ =



1+|∇



α|

n−1

j,k=1



∂

tjk

−

tjk

∂



∂

∂ξ

(6.35)

(cf. [24]). Since, from (6.9),

∂

tjk

((0,T ),W

−1/q

(Γ))

≤C∇



α

−1/q

(Γ))

∇



+ u

+ v)

((0,T ),L

(Ω))

≤CT

(2M + R)M,

tjk

∂

((0,T ),W

−1/q

(Γ))

≤CT

(2M + R)M

we have

(m − Δ

)

−1

ν ·

(t)ξ

((0,T ),W

2−1/q

(Γ))

≤ C

∂

tjk

((0,T ),W

−1/q

(Γ))

tjk

∂

((0,T ),W

−1/q

(Γ))

α

3−1/q

(Γ)

≤ C((2M + R)t

. (6.36)

Therefore from (6.27), (6.33), (6.34) and (6.36), we obtain

G(u

+ u

+ v)+ν ·(u

+ u

) ∈ L

((0,T),W

2−1/q

(Γ)),

G(u

+ u

+ v)+ν ·(u

+ u

)

((0,T ),W

2−1/q

(Γ))

≤ C{T

(2M + R)M

+ T

1/p



(2M + R)

}. (6.37)

Step 3 (Estimate of H

and H

). Next we estimate the right-hand side of the

boundary condition H

and H

. From the deﬁnition of H

1,1/2

q,p

(Ω ×R), we have to

extend not only u

and v but also



∇(u

+ u

+ v) dτ to the whole time R.To

do this, we use Lemma 6.3 and the following lemma.

Lemma 6.8 (Lemma 2.4 in [20]). Let 2 <p<∞ and n<q<∞.Set

1,1

q,p

(

Ω ×I)={f ∈ W

1,1

q,∞

(

Ω × I):∂

f ∈ L

(I,W

(

Ω))}.

Let 0 <T ≤ 1. Then, there exist linear operators F

: W

(Ω) →

1,1

q,p

(Ω × R),

: W

2,1

q,p

(Ω × (0, 2)) →

1,1

q,p

(Ω × R), F

: W

2,1

q,p,0

(Ω × (0,T)) →

1,1

q,p

(Ω × R),

680 S. Shimizu

such that

z(ξ,t)=



∇z(ξ,τ) dτ, 0 ≤ t ≤ T,

z =0 for t ∈ [0, 2T ],

F

z

∞

(R,W

(Ω))

≤ CTz

(Ω)

∂

z)

∞

(R,L

(Ω))

≤ Cz

(Ω)

∂

z)

(R,W

(Ω))

≤ Cz

(Ω)

F

z

∞

(R,W

(Ω))

≤ CT

1/p



z

2,1

q,p

(Ω×I

)

for j =2, 3,

∂

z)

∞

(R,L

(Ω))

≤ Cz

2,1

q,p

(Ω×I

)

for j =2, 3,

∂

z)

(R,W

(Ω))

≤ Cz

2,1

q,p

(Ω×I

)

for j =2, 3,

where I

=(0, 2), I

=(0,T),andC is independent of z and T .

We recall that

[[ H

(u)]] = −[[ Π(Π

− Π)(μD(u)ν

)+Π(μD(u)(ν

− ν)) + ΠΠ

(Q(u)ν

)]],

where Q(u) is deﬁned in (1.6). We consider the term H

+Ev) instead of

+ u

+ v) with time integral F

+ F

v,becausewehavetoestimate

the norm of H

1,1/2

q,p

(Ω × R). Since

(

−1

)

= δ

+ B





∇



dτ,...,



∇



j−1

dτ,



∇



j+1

dτ,...,



∇



dτ



(6.38)

where B

is some polynomial such as B

(0,...,0) = 0 (cf. (A.5) Appendix in

[20]), we can write

−1

ν = ν + B





∇udτ



ν,

where (j, k) component of B is given by B

in (6.38). Therefore we obtain

−1

ν|

ν + B(



∇udτ)ν

|ν + B(



∇udτ)ν|

, (6.39)

−ν =

Bν

|(I + B)ν|

−ν

ν · Bν + Bν ·(I + B)ν

|ν||(I + B)ν|(|(I + B)ν| + |ν|)

, (6.40)

∂

Bν

|(I + B)ν|

−

(I + B)ν(I + B)ν) · ∂

Bν

|(I + B)ν|

. (6.41)

By (6.4) and (6.5), we obtain

B(F

+ F

∞

(R,W

(Ω))

≤ CT

1/p



(2M + R), (6.42)

Local Solvability of Free Boundary Problems 681

and by (6.4), (6.40)–(6.42) and (6.18), we obtain

˜ν

t(u

+Ev)



∞

(R,W

(Ω))

≤ CM, (6.43)

ν

t(u

+Ev)

−ν

∞

(R,W

(Ω))

≤B

∞

(R,W

(Ω))

ν

(Ω)

≤ CT

1/p



(2M + R)M. (6.44)

Here and hereafter ν

and ν denote again the extension of ν

and ν, respectively,

on Γ to Ω. By

∂

B(F

+ F

∞

((0,T ),L

(Ω))

≤ Cu

+ E

+ Ev

∞

(R,W

(Ω))

≤ C(2M + R), (6.45)

∂

B(F

+ F

((0,T ),W

(Ω))

≤ Cu

+ E

+ Ev

(R,W

(Ω))

≤ C(2M + R), (6.46)

and (6.4), (6.16), (As.3), (5.1), (5.3), we have

∂

t(u

+Ev)



∞

(R,L

(Ω))

≤ Cu

+ E

+ Ev

∞

(R,W

(Ω))

≤ C(2M + R),

(6.47)

∂

t(u

+Ev)



(R,W

(Ω))

≤ Cu

+ E

+ Ev

(R,W

(Ω))

≤ C(2M + R).

(6.48)

To estimate the norm of H

1,1/2

q,p

(Ω × R), we use the following lemma.

Lemma 6.9 (Lemma 2.6 in [20]). Let 1 <p<∞, n<q<∞ and 0 <T ≤ 1.

Let

1,1

q,p

(Ω × R) bethesamespaceasinLemma6.8.Iff ∈

1,1

q,p

(Ω × R), g ∈

1,1/2

q,p

(Ω × R) and f vanishes when t ∈ [0, 2T ], then we have

fg

1,1/2

q,p

(Ω×R)

≤

p,q

[f

∞

(R,W

(Ω))

(q−n)/(pq)

f



(1−n/(2q))

∞

(R,L

(Ω))

f



n/(2q)

(R,W

(Ω))

]g

1,1/2

q,p

(Ω×R)

Proposition 2.8 in [20] and Lemma 6.3 yield the following lemma.

Lemma 6.10. Let 1 <p,q<∞.Foru

∈ W

2,1

q,p

(Ω×(0, 2)) and v ∈ W

2,1

q,p

(Ω×(0,T)),

there exists a constant C

p,q

> 0 such that

E



1/2

(R,W

(Ω))

≤ C

p,q

u



2,1

q,p

(Ω×(0,2))

Ev

1/2

(R,W

(Ω))

≤ C

p,q

v

2,1

q,p

(Ω×(0,T ))

By (4.2), it holds that

(Π − Π

)d =(d, ν

)ν

−(d, ν)ν =(d, ν

)(ν

− ν)+(d, ν

−ν)ν. (6.49)

Setting f = ν

t(u

+Ev)

and g = D(u

+ E

+ Ev), and applying Lemma 6.9,

we have from (6.44), (6.47), (6.48) and Lemma 6.10,

D(u

+ E

+ Ev)ν

t(u

+Ev)



1,1/2

q,p

(Ω×R)

≤ C(2M + R)M. (6.50)

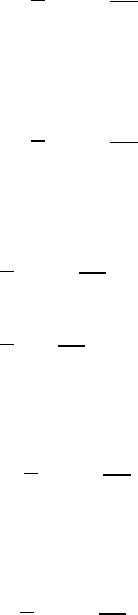
682 S. Shimizu

Setting f = ν

t(u

+Ev)

− ν and g =(D(u

+ E

+ Ev)ν

t(u

+Ev)

t(u

+Ev)

), and applying Lemma 6.9, we have from Lemma 6.10,

(D(u

+ E

+ Ev)ν

t(u

+Ev)

,ν

t(u

+Ev)

)

×(ν

t(u

+Ev)

− ν)

1,1/2

q,p

(Ω×R)

≤ C(T



M + T

q−n

)(2M + R)

. (6.51)

Combining (6.49), (6.50) and (6.51) we have

Π(Π − Π

)μD(u

+ E

+ Ev)ν

+Ev



1,1/2

q,p

(Ω×R)

≤ C(T



M + T

q−n

)(2M + R)

. (6.52)

In a similar manner we obtain

ΠμD(u

+ E

+ Ev)(ν

t(u

+Ev)

− ν)

1,1/2

q,p

(Ω×R)

≤ C(T



M + T

q−n

)(2M + R)

, (6.53)

ΠΠ

Q(u

+ E

+ Ev)ν

t(u

+Ev)



1,1/2

q,p

(Ω×R)

≤ C(T



+ T

q−n

)(2M + R)

. (6.54)

Therefore by (6.52), (6.53), and (6.54) we obtain

+ E

+ Ev) ∈ H

1,1/2

q,p

(Ω × R),

H

+ E

+ Ev)

1,1/2

q,p

(Ω×R)

≤ C(T



M + T

q−n

)(2M + R)

. (6.55)

From the deﬁnition of H

1,1/2

q,p

(Ω ×(0,T)), we see that

+ u

+ v) ∈ H

1,1/2

q,p

(Ω × (0,T)),

H

+ u

+ v)

1,1/2

q,p

(Ω×(0,T ))

≤ C(T



M + T

q−n

)(2M + R)

. (6.56)

Finally we consider the term H

. We recall that

[[ H

(u, π)]] = [[ν · S(u, π)(ν − ν

) − ν ·Q(u)ν

]]

+[[ρ]] c



dτ ν ·ν

+[[ρ]] c

ν · (ν

−ν)

− 2σ



∇



udτ



∇

· ν + σm



ν · udτ.

We consider the term H

+ E

+ Ev, π

+¯π

θ) instead of H

+ u

v, π

+ π

+ θ) with time integral F

+ F

v,becausewehavetoestimate

the norm of H

1,1/2

q,p

(Ω × R). Similar to the way we estimated H

+ E

+ Ev),

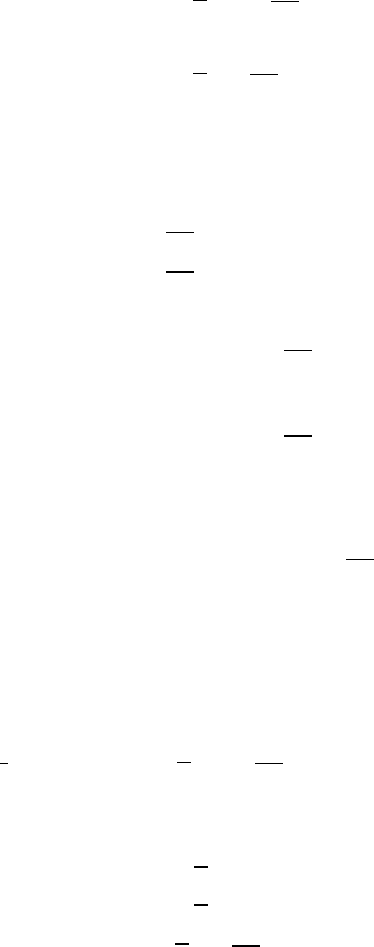
Local Solvability of Free Boundary Problems 683

we have

ν ·(S(u

+ E

+ Ev,π

+¯π

θ)(ν −ν

t(u

+Ev)

)

1,1/2

q,p

(Ω×R)

≤ C(T



M + T

q−n

)(2M + R)

, (6.57)

ν ·Q(u

+ E

+ Ev)ν

t(u

+Ev)



1,1/2

q,p

(Ω×R)

≤ C(T



+ T

q−n

)(2M + R)

. (6.58)

Let χ(t) be a function in C

∞

(R) such that χ(t)=1for|t|≤1andχ(t)=0

for |t|≥2. Setting f = ν

t(u

+Ev)

− ν and g = χ(t)ξ

ν, and applying Lemma

6.9, we have

(ν

t(u

+Ev)

− ν)χ(t)ξ

ν

1,1/2

q,p

(Ω×R)

≤ C(T

1/p



M + T

q−n

)(2M + R)χ(t)ξ

ν

(R,W

(Ω))

≤ C(T

1/p



M + T

q−n

)(2M + R)M

By the deﬁnition of H

1,1/2

q,p

(Ω × (0,T)), we see that

(ν

t(u

+v)

−ν)ξ

ν

1,1/2

q,p

(Ω×(0,T ))

≤ C(T

1/p



M + T

q−n

)(2M + R)M

. (6.59)

By (6.7) we have

(∇

·ν)∇



udτ

1,1/2

q,p

(Ω×(0,T ))

≤ C(T

1/p



M + T

q−n

)(2M + R)M

. (6.60)

Therefore from (6.57), (6.58), (6.7), (6.59) and (6.60), we obtain

+ u

+ v, π

+ π

+ θ) ∈ H

1,1/2

q,p

(Ω × (0,T)),

H

+ u

+ v, π

+ π

+ θ)

1,1/2

q,p

(Ω×(0,T ))

≤ C(T

1/p



M + T

q−n

)(2M + R)M

(6.61)

Step 4. Combining (6.37), (6.56), (6.61), we have

V 

2,1

q,p

(Ω×(0,T ))

+ Θ

((0,T ),

(Ω))

+ 

Θ

1,1/2

q,p

(Ω×(0,T ))

+ ∂

Y 

((0,T ),W

2−1/q

(Γ))

+ Y 

((0,T ),W

3−1/q

(Γ))

≤ C{T

(2M + R)M

+(T



M + T

q−n

)(2M + R)

}. (6.62)

Here we also use

Div Q(u

+ u

+ v),R(u

+ u

+ v)∇(π

+ π

+ θ)

((0,T ),L

(Ω))

≤ CT



(2M + R)

E(u

+ u

+ v)

((0,T ),W

(Ω))

≤ CT



(2M + R)



E(u

+ u

+ v)

((0,T ),L

(Ω))

C(T



+ T

q−n

)(2M + R)

684 S. Shimizu

(cf. §2 in [20]). For given M deﬁned by (6.2), we choose R>0andT>0such

that the right-hand member of (6.62) is less than R, then by (6.62) we have

V 

2,1

q,p

(Ω×(0,T ))

+ Θ

((0,T ),

(Ω))

+ 

Θ

1,1/2

q,p

(Ω×(0,T ))

(6.63)

+ ∂

Y 

((0,T ),W

2−1/q

(Γ))

+ Y 

((0,T ),W

3−1/q

(Γ))

≤ R.

Moreover from the deﬁnition of E(u

+ u

+ v),

E(u

+ u

+ v), H

+ u

+ v)

and H

+ u

+ v, π

+ π

+ θ), we see that

E(u

+ u

+ v)|

t=0

E(u

+ u

+ v)|

t=0

=0,

+ u

+ v)|

t=0

= H

+ u

+ v, π

+ π

+ θ)|

t=0

=0.

Therefore for the map Φ(v, θ,

θ, η)=(V,Θ,

Θ,Y)itmapsI

R,T

into itself.

Now we show that Φ is a contraction map. To do this, given (v

,θ

,η

) ∈

R,T

(i =1, 2), we set

, Θ

)=Φ(v

,θ

,η

),i=1, 2.

From (6.3), we see that V

− V

,Θ

− Θ

and Y

−Y

satisfy the linear equation

∂

− V

) − Div S(V

−V

, Θ

−Θ

)=DivQ(u

+ u

+ v

)

− Div Q(u

+ u

+ v

)+R(π

+ π

+ θ

) − R(π

+ π

+ θ

)inΩ,t>0,

div (V

−V

)=E(u

+ u

+ v

) −E(u

+ u

+ v

)

=div

E(u

+ u

+ v

) − div

E(u

+ u

+ v

)inΩ,t>0,

∂

−Y

) −ν · (V

−V

)=G(u

+ u

+ v

) − G(u

+ u

+ v

)onΓ,t>0,

[[ ΠD(V

−V

)ν]] = [[ H

+ u

+ v

) − H

+ u

+ v

)]] on Γ,t>0,

[[ ν ·S(V

−V

, Θ

− Θ

)ν]] + σ(m − Δ

)(Y

− Y

)

=[[H

+ u

+ v

,π

+¯π

)

−H

+ u

+ v

,π

+¯π

)]] on Γ,t>0,

[[ V

− V

]] = 0 o n Γ ,t>0,

− V

t=0

=0inΩ, (Y

− Y

t=0

=0onΓ. (6.64)

Applying the same argument as in the proof of (6.63), we can show that

V

− V



2,1

q,p

((0,T )×Ω)

+ Θ

− Θ



((0,T ),

(Ω))

+ 

−



1,1/2

q,p

(Ω×(0,T ))

+ Y

− Y



((0,T ),W

2−1/q

(Γ))

≤C{T

+(T



+ T

q−n

)(2M + R)M

}

v

− v



2,1

q,p

((0,T )×Ω)

+ θ

−θ



((0,T ),

(Ω))

+ 

−



1,1/2

q,p

(Ω×(0,T ))

+ η

− η



((0,T ),W

2−1/q

(Γ))

. (6.65)

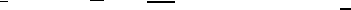
Local Solvability of Free Boundary Problems 685

Choosing T>0sosmallthat

C{T

+(T



+ T

q−n

)(2M + R)M

}≤

in (6.65), we see that Φ is a contraction map on I

R,T

. Therefore Φ has the ﬁxed

point (V,Θ,

Θ,Y) which solves (6.3). This completes the proof of Theorem 6.1.

Acknowledgment

The author is grateful to Professor Yoshihiro Shibata for the proof of Lemma 2.3

and Proposition 6.7. She is also grateful to the referee for valuable suggestions

which improved the presentation of this paper.

References

[1] H. Abels, On general solutions of two-phase ﬂows for viscous incompressible ﬂuids,

Interfaces Free Boud., 9 (2007) 31–65.

[2] G. Allain, Small-time existence for the Navier-Stokes equations with a free surface,

Appl. Math. Optim., 16 (1987) 37–50.

[3] H. Amann, Linear and Quasilinear Parabolic Problems, Vol I Abstract Linear Theory,

Monographs in Math. Vol. 89, Birkh¨auser Verlag, Basel·Boston·Berlin, 1995.

[4] H. Amann, Nonhomogeneous linear and quasilinear elliptic and parabolic boundary

value problems, Teubner-Texte Math., 133 (1993) 9–126.

[5] J.T. Beale, Large time regularity of viscous surface waves, Arch. Rat. Mech. Anal.,

84 (1984) 307–352.

[6] J.T. Beale and T. Nishida, Large time behavior of viscous surface waves,Lecture

Notes in Numer. Appl. Anal., 8 (1985) 1–14.

[7] J. Bourgain, Vector-valued singular integrals and the H

-BMO duality, in: Probabil-

ity Theory and Harmonic Analysis, D. Burkholder (ed.). Marcel Dekker, New York

(1968), 1–19.

[8] A.P. Calder´on, Lebesgue spaces of diﬀerentiable functions and distributions,Proc.

Symp. in Pure Math., 4 (1961), 33–49.

[9] I.V. Denisova, A priori estimates for the solution of a linear time-dependent problem

connected with the motion of a drop in a ﬂuid medium,TrudyMat.Inst.Steklov.,

188 (1990) 3–21 (in Russian); English transl.: Proc. Steklov Inst. Math., 188 (1991)

1–24.

[10] I.V. Denisova, Problem of the motion of two viscous incompressible ﬂuids separated

by a closed free interface, Acta Appl. Math., 37 (1994) 31–40.

[11] I.V. Denisova and V.A. Solonnikov, Solvability in H¨older spaces of a model initial-

boundary value problem generated by a problem on the motion of two ﬂuids,Zap.

Nauchn. Sem. Leningrad. Otdel. Mat. Inst. Steklov. (LOMI), 181 (1991) 5–44 (in

Russian); English transl.: J. Math. Sci., 70 (1994) 1717–1746.

[12] I.V. Denisova and V.A. Solonnikov, Classical solvability of the problem on the motion

of two viscous incompressible ﬂuids, Algebra i Analiz, 7 (1995) 101–142 (in Russian);

English transl.: St. Petersburg Math. J., 7 (1996) 755–786.

686 S. Shimizu

[13] R. Denk, M. Hieber and J. Pr¨uss, R-boundedness, Fourier multipliers and problems

of elliptic and parabolic type, Memoirs of AMS, Vol. 166, No. 788, 2003.

[14] G.P. Galdi, An introduction to the mathematical theory of the Navier-Stokes equa-

tions Volume I, Linearised steady problems, Springer Tracts in Natural Philosophy,

38, Springer-Verlag, New York, Berlin, Heidelberg, 1994.

[15] S.G. Mihlin, On the multipliers of Fourier integrals (Russian), Dok. Akad. Nauk.,

109 (1956), 701–703.

[16] S.G. Mihlin, Fourier integrals and multiple singular integrals (Russian), Vest.

Leningrad Univ. Ser. Mat., 12 (1957), 143–145.

[17] J. Pr¨uss and G. Simonett, Analysis of the boundary symbol for the two-phase Navier-

Stokes equations with surface tension, Proc. Banach Center Publ., 86 (2009), 265–

285.

[18] J. Pr¨uss and G. Simonett, On the two-phase Navier-Stokes equations with surface

tension, Interfaces Free Bound., 12 (2010), 311–345.

[19] J. Pr¨uss and G. Simonett, Analytic solutions for the two-phase Navier-Stokes equa-

tions with surface tension and gravity,preprint.

[20] Y. Shibata and S. Shimizu, On some free boundary problem for the Navier-Stokes

equations, Diﬀerential Integral Equations, 20 (2007), 241–276.

[21] Y. Shibata and S. Shimizu, On the L

-L

maximal regularity of the Neumann problem

for the Stokes equations in a bounded domain, J. reine angew. Math., 615 (2008),

157–209.

[22] Y. Shibata and S. Shimizu, Report on a local in time solvability of free surface

problems for the Navier-Stokes equations with surface tension, Applicable Analysis,

12 (2011), 201–214.

[23] Y. Shibata and S. Shimizu, On the L

-L

maximal regularity of the two-phase Stokes

equations; Model problems,preprint.

[24] V.A. Solonnikov, Lectures on evolution free boundary problems: classical solutions,

L. Ambrosio et al.: LNM 1812, P.Colli and J.F.Rodrigues (Eds.), (2003) 123–175,

Springer-Verlag, Berlin, Heidelberg.

[25] A. Tani, Small-time existence for the three-dimensional incompressible Navier-Stokes

equations with a free surface, Arch. Rat. Mech. Anal., 133 (1996) 299–331.

[26] A. Tani and N. Tanaka, Large time existence of surface waves in incompressible

viscous ﬂuids with or without surface tension, Arch. Rat. Mech. Anal., 130 (1995)

303–314.

[27] N. Tanaka, Global existence of two phase non-homogeneous viscous incompressible

ﬂuid ﬂow, Commun. P.D.E., 18 (1993) 41–81.

[28] L. Weis, Operator-valued Fourier multiplier theorems and maximal L

-regularity,

Math. Ann., 319 (2001) 735–758.

Senjo Shimizu

Department of Mathematics

Shizuoka University

Shizuoka 422-8529, Japan

e-mail: ssshimi@ipc.shizuoka.ac.jp

Progress in Nonlinear Diﬀerential Equations

and Their Applications, Vol. 80, 687–704

 2011 Springer Basel AG

Inversion of the Lagrange Theorem

in the Problem of Stability of Rotating

Viscous Incompressible Liquid

V.A. Solonnikov

Dedicated to Professor H. Amann on the occasion of his jubilee

Abstract. The paper contains analysis of the spectrum of a linear problem

arising in the study of the stability of a ﬁnite isolated mass of uniformly ro-

tating viscous incompressible self-gravitating liquid. It is assumed that the

capillary forces on the free boundary of the liquid are not taken into account.

It is proved that when the second variation of the energy functional can take

negative values, then the spectrum of the problem contains ﬁnite number of

points with positive real parts, which means instability of the rotating liquid

in a linear approximation. The proof relies on the theorem on the invari-

ant subspaces of dissipative operators in the Hilbert space with an indeﬁnite

metrics.

Mathematics Subject Classiﬁcation (2000). 76E07, 47B50.

Keywords. Rotating liquid, stability, dissipative operators.

1. Formulation of main result

This paper is devoted to the problem of stability of a ﬁnite mass of a viscous

incompressible liquid of a unit density uniformly rotating about a ﬁxed axis (x

axis). The liquid is subject to the forces of self-gravitation; the surface tension on

the free boundary is not taken into account. The velocity and the pressure of the

rotating liquid are given by

V (x)=ω(e

×x),P(x)=



+ p

, (1.1)

where ω is the angular velocity of rotation, e

=(0, 0, 1),x



=(x

, 0), p

const. The domain F occupied by the liquid (the equilibrium ﬁgure) is deﬁned by