Escher J., Guidotti P., Hieber M. et al. (editors) Parabolic Problems: The Herbert Amann Festschrift
Подождите немного. Документ загружается.

xPreface
Herbert Amann has been a steady source of new ideas, and he has influenced
many researchers. His unwavering dedication to research and teaching has been
an example to all of his colleagues and students, in particular to his 24 doctoral
students. In 2001 he became foreign corresponding member of the Real Academia
de Ciencias Exactas, F´ısicas y Naturales, Madrid, and, one year later, received a
Doctor Honoris Causa from the Universidad Complutense, Madrid. As of 2004,
Herbert Amann is Professor Emeritus of the Universit¨at Z¨urich.
During his long and ongoing career he has enjoyed the invaluable support of
his wife, Gisela Amann.
The present volume contains original research papers and reflects the wide-
ranging scientific interests of Herbert Amann. It is inspired by the conference
“Nonlinear Parabolic Problems: In honor of Herbert Amann” held May 10–16,
2009, at the Banach Center in Bedlewo, Poland.
We are grateful to all the participants of the conference and all the contrib-
utors of this volume.
References
[1] H. Amann. Monte-Carlo-Methoden und lineare Randwertprobleme. Z. Angew. Math.
Mech. 48 (1968), 109–116.
[2] H. Amann.
¨
Uber die n¨aherungsweise L¨osung nichtlinearer Integralgleichungen. Nu-
mer. Math. 19 (1972), 29–45.
[3] H. Amann. Lusternik-Schnirelman theory and non-linear eigenvalue problems. Math.
Ann. 199 (1972), 55–72.
[4] H. Amann, S.A. Weiss. On the uniqueness of the topological degree. Math. Z. 130
(1973), 39–54.
[5] H. Amann. Saddle points and multiple solutions of differential equations. Math. Z.
169 (1979), no. 2, 127–166.
[6] H. Amann. On the number of solutions of nonlinear equations in ordered Banach
spaces. J. Functional Analysis 11 (1972), 346–384.
[7] H. Amann. Existence and multiplicity theorems for semi-linear elliptic boundary
value problems. Math. Z. 150 (1976), no. 3, 281–295.
[8] H. Amann. Periodic solutions of semilinear parabolic equations. Nonlinear analysis
(collection of papers in honor of Erich H. Rothe), pp. 1–29, Academic Press, New
York, 1978.
[9] H. Amann. Multiple positive fixed points of asymptotically linear maps. J. Functional
Analysis 17 (1974), 174–213.
[10] H. Amann, M.G. Crandall. On some existence theorems for semi-linear elliptic equa-
tions. Indiana Univ. Math. J. 27 (1978), no. 5, 779–790.
[11] H. Amann. Fixed point equations and nonlinear eigenvalue problems in ordered Ba-
nach spaces. SIAM Rev. 18 (1976), no. 4, 620–709.
[12] H. Amann, P. Hess. A multiplicity result for a class of elliptic boundary value prob-
lems. Proc. Roy. Soc. Edinburgh Sect. A 84 (1979), no. 1-2, 145–151.
Preface xi
[13] H. Amann, E. Zehnder. Nontrivial solutions for a class of nonresonance problems
and applications to nonlinear differential equations. Ann. Scuola Norm. Sup. Pisa
Cl.Sci.(4)7 (1980), no. 4, 539–603.
[14] H. Amann. Parabolic evolution equations and nonlinear boundary conditions. J. Dif-
ferential Equations 72 (1988), no. 2, 201–269.
[15] H. Amann. Existence and regularity for semilinear parabolic evolution equations.
Ann. Scuola Norm. Sup. Pisa Cl. Sci. (4) 11 (1984), no. 4, 593–676.
[16] H. Amann. Parabolic evolution equations in interpolation and extrapolation spaces.
J. Funct. Anal. 78 (1988), no. 2, 233–270.
[17] H. Amann. Dynamic theory of quasilinear parabolic equations. I. Abstract evolution
equations. Nonlinear Anal. 12 (1988), no. 9, 895–919.
[18] H. Amann. Dynamic theory of quasilinear parabolic equations. II. Reaction-diffusion
systems. Differential Integral Equations 3 (1990), no. 1, 13–75.
[19] H. Amann. Dynamic theory of quasilinear parabolic systems. III. Global existence.
Math. Z. 202 (1989), no. 2, 219–250.
[20] H. Amann. Nonhomogeneous linear and quasilinear elliptic and parabolic bound-
ary value problems. Function spaces, differential operators and nonlinear analysis
(Friedrichroda, 1992), 9–126, Teubner-Texte Math., 133, Teubner, Stuttgart, 1993.
[21] H. Amann. Coagulation-fragmentation processes. Arch. Ration. Mech. Anal. 151
(2000), no. 4, 339–366.
[22] H. Amann. Operator-valued Fourier multipliers, vector-valued Besov spaces, and ap-
plications. Math. Nachr. 186 (1997), 5–56.
[23] H. Amann. Compact embeddings of vector-valued Sobolev and Besov spaces. Dedicated
to the memory of Branko Najman. Glas. Mat. Ser. III 35 (55) (2000), no. 1, 161–177.
[24] H. Amann. Elliptic operators with infinite-dimensional state spaces. J. Evol. Equ. 1
(2001), no. 2, 143–188.
[25] H. Amann. Multiplication in Sobolev and Besov spaces. Nonlinear analysis, 27–50,
Sc. Norm. Super. di Pisa Quaderni, Scuola Norm. Sup., Pisa, 1991.
[26] H. Amann. On the strong solvability of the Navier-Stokes equations. J. Math. Fluid
Mech. 2 (2000), no. 1, 16–98.
[27] H. Amann. Stability of the rest state of a viscous incompressible fluid. Arch. Rational
Mech. Anal. 126 (1994), no. 3, 231–242.
[28] H. Amann. Time-delayed Perona-Malik type problems. Acta Math. Univ. Comenian.
(N.S.) 76 (2007), no. 1, 15–38.
[29] H. Amann. Maximal regularity and quasilinear parabolic boundary value problems.
Recent advances in elliptic and parabolic problems, 1–17, World Sci. Publ., Hacken-
sack, NJ, 2005.
[30] H. Amann. Ordinary differential equations. An introduction to nonlinear analysis.
Translated from the German by Gerhard Metzen. de Gruyter Studies in Mathemat-
ics, 13. Walter de Gruyter & Co., Berlin, 1990. xii+438 pp.
[31] H. Amann. Linear and quasilinear parabolic problems. Vol. I. Abstract linear the-
ory. Monographs in Mathematics, 89. Birkh¨auser Boston, Inc., Boston, MA, 1995.
xxxvi+335 pp.
xii Preface
[32] H. Amann, J. Escher. Analysis. I. Translated from the 1998 German original by
Gary Brookfield. Birkh¨auser Verlag, Basel, 2005. xiv+426 pp.
[33] H. Amann, J. Escher. Analysis. II. Translated from the 1999 German original by
Silvio Levy and Matthew Cargo. Birkh¨auser Verlag, Basel, 2008. xii+400 pp.
[34] H. Amann, J. Escher. Analysis. III. Translated from the 2001 German original by
Silvio Levy and Matthew Cargo. Birkh¨auser Verlag, Basel, 2009. xii+468 pp.
[35] H. Amann. Anisotropic function spaces and maximal regularity for parabolic prob-
lems. Part 1:Functionspaces.Jindrich Necas Center for Mathematical Modeling
Lecture Notes, Prague, Volume 6, 2009.
Joachim Escher
Leibniz Universit¨at Hannover
Patrick Guidotti
University of California, Irvine
Matthias Hieber
Technische Universit¨at Darmstadt
Piotr Mucha
Warsaw University
Jan Pr¨uß
Martin-Luther-Universit¨at
Halle-Wittenberg
Yoshihiro Shibata
Waseda University
Gieri Simonett
Vanderbilt University
Christoph Walker
Leibniz Universit¨at Hannover
Wojciech Zajaczkowski
Polish Academy of Sciences
Progress in Nonlinear Differential Equations
and Their Applications, Vol. 80, 1–20
c
2011 Springer Basel AG
Double Obstacle Limit for a
Navier-Stokes/Cahn-Hilliard System
Helmut Abels
Dedicated to Herbert Amann on the oc casion of his 70th birthday
Abstract. We consider the double obstacle limit for a Navier-Stokes/Cahn-
Hilliard type system. The system describes a so-called diffuse interface model
for the two-phase flow of two macroscopically immiscible incompressible vis-
cous fluids in the case of matched densities, also known as Model H. Starting
with a suitable class of singular free energies, which keep the concentration
strictly inside the physically reasonable interval [a, b], we analyze a certain
singular limit, where the equation for the chemical potential converges to
a differential inclusion related to the subgradient of the indicator function
of [a, b].
Mathematics Subject Classification (2000). Primary 76T99; Secondary 76D27,
76D03, 76D05, 76D45, 35B40, 35B65, 35Q30, 35Q35,
Keywords. Two-phase flow, diffuse interface model, mixtures of viscous fluids,
Cahn-Hilliard equation, Navier-Stokes equation, double obstacle problem.
1. Introduction and main result
In the present contribution we study a system describing the flow of viscous incom-
pressible Newtonian fluids of the same density, but different viscosity. Although
it is assumed that the fluids are macroscopically immiscible, the model takes a
partial mixing on a small length scale measured by a parameter ε>0intoac-
count. Therefore the classical sharp interface between both fluids is replaced by an
interfacial region and an order parameter related to the concentration difference
of both fluids is introduced. This makes it possible to describe the flow beyond the
occurrence of topological singularities of the separating interface (e.g., coalescence
or formation of droplets), cf. Anderson and McFadden [5] for a review on that
topic.

2H.Abels
This model, also known as “model H”, cf. Hohenberg and Halperin [10] and
Gurtin et al. [9], leads to a coupled Navier-Stokes/Cahn-Hilliard system:
∂
t
v + v ·∇v − div(ν(c)Dv)+∇p = −ε div(∇c ⊗∇c)inΩ×(0, ∞), (1.1)
div v =0 inΩ× (0, ∞), (1.2)
∂
t
c + v ·∇c = mΔμ in Ω ×(0, ∞), (1.3)
μ = ε
−1
φ(c) − εΔc in Ω ×(0, ∞). (1.4)
Here v is the mean velocity, Dv =
1
2
(∇v + ∇v
T
), p is the pressure, c is an or-
der parameter related to the concentration of the fluids (e.g., the concentration
difference or the concentration of one component), and Ω is a suitable bounded
domain. Moreover, ν(c) > 0 is the viscosity of the mixture, ε>0 is a (small)
parameter, which will be related to the “thickness” of the interfacial region, and
φ =Φ
, where Φ is the homogeneous free energy density specified below.
It is assumed that the densities of both components as well as the density of
the mixture are constant and for simplicity equal to one. We note that capillary
forces due to surface tension are modeled by an extra contribution ε∇c ⊗∇c in
the stress tensor leading to the term on the right-hand side of (1.1). Moreover, we
note that in the modeling diffusion of the fluid components is taken into account.
Therefore mΔμ is appearing in (1.3), where m>0 is the mobility coefficient,
which is assumed to be constant.
We close the system by adding the boundary and initial conditions
v|
∂Ω
=0 on∂Ω × (0, ∞), (1.5)
∂
n
c|
∂Ω
= ∂
n
μ|
∂Ω
=0 on∂Ω × (0, ∞), (1.6)
(v, c)|
t=0
=(v
0
,c
0
)inΩ. (1.7)
Here (1.5) is the usual no-slip boundary condition for viscous fluids, n is the
exterior normal on ∂Ω, ∂
n
μ|
∂Ω
= 0 means that there is no flux of the components
through the boundary, and ∂
n
c|
∂Ω
= 0 describes a “contact angle” of π/2ofthe
diffused interface and the boundary of the domain.
We note that (1.1) can be replaced by
∂
t
v + v ·∇v − div(ν(c)Dv)+∇g = μ∇c (1.8)
with g = p +
ε
2
|∇c|
2
+ ε
−1
Φ(c)since
μ∇c = ∇
ε
2
|∇c|
2
+ ε
−1
Φ(c)
− ε div(∇c ⊗∇c). (1.9)
The total energy of the system above is given by E(c, v)=E
free
(c)+E
kin
(v),
where
E
free
(c)=
1
2
Ω
ε|∇c(x)|
2
dx +
Ω
ε
−1
Φ(c(x)) dx, (1.10)
E
kin
(v)=
1
2
Ω
|v(x)|
2
dx.
Double Obstacle Limit 3
Here the free energy E
free
(c) describes an interfacial energy associated with the
region where c is not close to the minima of Φ(c)andE
kin
(v) is the kinetic energy of
the fluid. The system is dissipative. More precisely, for sufficiently smooth solutions
d
dt
E(c(t),v(t)) = −
Ω
ν(c(t))|Dv(t)|
2
dx − m
Ω
|∇μ(t)|
2
dx.
Since we will consider (1.1)–(1.7) only for fixed ε>0, we will assume for simplicity
that ε = 1 in the following. But all statements remain true for arbitrary ε>0
(with constants depending on ε).
The assumptions on the homogeneous free energy density Φ are motivated by
the so-called regular solution model free energy suggested by Cahn and Hilliard [7]:
Φ(c)=
θ
2
((1 + c)ln(1+c)+(1− c)ln(1− c)) −
θ
c
2
c
2
(1.11)
with θ, θ
c
> 0. We note that Φ(c) is not convex if and only if 0 <θ<θ
c
.Butwe
have the decomposition
Φ(s)=θΦ
0
(s) −
θ
c
2
s
2
,φ(s)=θφ
0
(s) − θ
c
s
where Φ
0
∈ C([−1, 1]) ∩C
∞
((−1, 1)) is convex and θ, θ
c
> 0. Finally, we note that
φ
0
(s) →
s→±1
±∞.
−1
−0.8
−0.6
−0.4
−0.2
0
0.2
0.4
0.6
0.8
1
−0.5
−0.4
−0.3
−0.2
−0.1
0
0.1
0.2
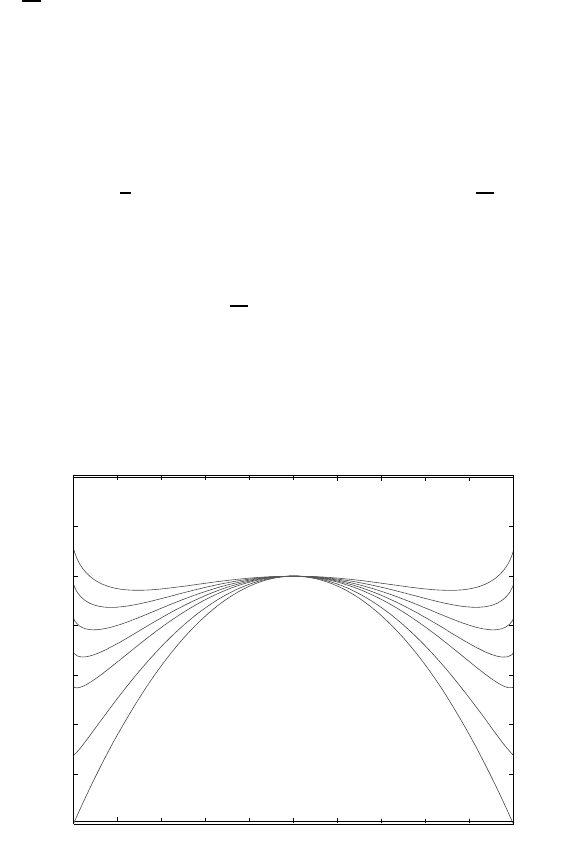
Figure 1. Logarithmic free energy density for θ =0.8, 0.7, 0.6,
0.5, 0.4, 0.2, 0.0 (from top to bottom) and θ
c
=1

4H.Abels
In Figure 1 the free energy density is plotted for some choices of θ, θ
c
.Note
that, if θ>0, then the minima are never ±1. (Although Figure 1 for θ =0.2
suggests that the minima are ±1.) But the minima are close to ±1ifθ is small in
comparison with θ
c
. Since for two macroscopically immiscible fluids mixing costs
a lot of energy, we think that a small θ in comparison with θ
c
is physically the
most meaningful choice. Since qualitatively the free energy density for θ =0.2in
Figure 1 looks already the same as for θ = 0, it is very reasonable to choose θ =0
directly, i.e., to choose the free energy density
Φ(c)=
−
θ
c
2
c
2
if c ∈ [−1, 1]
+∞ else.
The free energy density is called to be of double obstacle type because of the con-
straint c ∈ [−1, 1] for all c with Φ(c) < ∞. The Cahn-Hilliard equation with the
latter free energy was first studied by Blowey and Elliott [6]. Elliott and Luck-
haus [8] have shown that as θ → 0 the solutions of the Cahn-Hilliard equation
with the logarithmic free energy density converge to solutions of the latter free
energy of double obstacle type. Physically this limit describes the dynamics of
phase separating binary mixture, where the absolute temperature θ is far from the
critical temperature θ
c
below which phase separation occurs.
The main result of this contribution is that weak solutions of the Model H
(1.1)–(1.7) converge as θ → 0 (for a suitable subsequence) to weak solutions of the
corresponding Navier-Stokes/Cahn-Hilliard system, where (1.4) is replaced by a
differential inclusion related to the subgradient of the double obstacle free energy,
cf. Section 4 for details. In the following we will assume a slightly more general
form of the free energy than (1.11). More precisely, we assume that
Φ(s)=θΦ
0
(s) −
θ
c
2
s
2
,φ(s)=θφ
0
(s) − θ
c
s (1.12)
where θ, θ
c
> 0, Φ
0
∈ C([a, b]) ∩ C
2
((a, b)) is convex, φ(s)=Φ
(s), a<b,and
φ
0
(s) →
s→a
−∞ φ
0
(s) →
s→b
∞. (1.13)
We note that this assumption implies the (θ-independent) assumption made in [3]
for the free energy density.
The structure of the article is as follows: First we fix some notation and recall
some basic lemmas in Section 2. Then we study the double obstacle limit for the
convex part of the free energy E
free
and the convective Cahn-Hilliard equation
(1.3)–(1.4) in Section 3. In Section 4 we state and prove our main result on con-
vergence of weak solutions of (1.1)–(1.7) as θ → 0. We conclude with two results
on uniqueness and regularity of weak solutions for the limit system, which are the
same in [3] for the case θ>0. These results are part of the author’s Habilitation
thesis [1].

Double Obstacle Limit 5
2. Notation and preliminaries
Throughout the article Ω ⊂ R
d
, d =2, 3, will denote a bounded domain with
C
3
-boundary and Q
T
:= Ω × (0,T),Q:= Q
∞
.
We use the same notation as in [3] and refer to the latter article for precise
definitions and references. Let us just recall some notation. The inner product of
a Hilbert space H is denoted by (., .)
H
and we use the abbreviation (., .)
M
for
(., .)
L
2
(M)
. The duality product of a Banach space X and its dual X
is denoted
by ., .
X
,X
or just ., ..
Moreover,
L
2
σ
(Ω) =
f ∈ L
2
(Ω)
d
:divf =0,n· f|
∂Ω
=0
,
V
s
2
(Ω) =
H
s
(Ω)
d
∩ H
1
0
(Ω)
d
∩L
2
σ
(Ω) if s ≥ 1,
H
s
(Ω)
d
∩ L
2
σ
(Ω) if 0 ≤ s<
1
2
and V
2
(Ω) := V
1
2
(Ω).
For m ∈ R we set
L
q
(m)
(Ω) :=
f ∈ L
q
(Ω) : m(f):=
1
|Ω|
Ω
f(x) dx = m
, 1 ≤ q ≤∞,
and P
0
f := f − m(f) is the orthogonal projection onto L
2
(0)
(Ω). Furthermore, we
define
H
1
(0)
≡ H
1
(0)
(Ω) = H
1
(Ω) ∩L
2
(0)
(Ω),H
−1
(0)
≡ H
−1
(0)
(Ω) = H
1
(0)
(Ω)
.
We equip H
1
(0)
(Ω) with the inner product (c, d)
H
1
(0)
(Ω)
:= (∇c, ∇d)
L
2
(Ω)
. Then the
Riesz isomorphism R: H
1
(0)
(Ω) → H
−1
(0)
(Ω) is given by
Rc, d
H
−1
(0)
,H
1
(0)
=(c, d)
H
1
(0)
=(∇c, ∇d)
L
2
,c,d∈ H
1
(0)
(Ω),
i.e., R = −Δ
N
is the negative (weak) Laplace operator with Neumann boundary
conditions. We note that, if u ∈ H
1
(0)
(Ω) solves Δ
N
u = f for some f ∈ L
q
(0)
(Ω),
1 <q<∞,and∂ΩisofclassC
2
, then it follows from standard elliptic theory
that u ∈ W
2
q
(Ω) and Δu = f a.e. in Ω and ∂
n
u|
∂Ω
= 0 in the sense of traces. If
additionally f ∈ W
1
q
(Ω) and ∂Ω ∈ C
3
,thenu ∈ W
3
q
(Ω). Moreover,
u
W
k+2
q
(Ω)
≤ C
q
f
W
k
q
(Ω)
for all f ∈ W
k
q
(Ω) ∩ L
q
(0)
(Ω),k =0, 1, (2.1)
with a constant C
q
depending only on 1 <q<∞, d, k, and Ω. Finally we denote
W
2
p,N
(Ω) =
u ∈ W
2
p
(Ω) : ∂
n
u|
∂Ω
=0
,
where 1 <p<∞.
Concerning vector-valued spaces, we recall that BC(0,T; X) is the Banach
space of all bounded and continuous f :[0,T) → X equipped with the supremum
norm and BUC(0,T; X) is the subspace of all bounded and uniformly contin-
uous functions, where X is a Banach space. Moreover, we define BC
w
(0,T; X)
as the topological vector space of all bounded and weakly continuous functions

6H.Abels
f :[0,T) → X.Furthermore,f ∈ L
q
loc
([0, ∞); X) if and only if f ∈ L
q
(0,T; X)
for every T>0. Moreover, L
q
uloc
([0, ∞); X) denotes the uniformly local variant of
L
q
(0, ∞; X) consisting of all strongly measurable f :[0, ∞) → X such that
f
L
q
uloc
([0,∞);X)
=sup
t≥0
f
L
q
(t,t+1;X)
< ∞.
In order to derive some regularity estimates we will use vector-valued Besov spaces
B
s
q∞
(I; X), where s ∈ (0, 1), 1 ≤ q ≤∞, I is an interval, and X is a Banach space.
They are defined as
B
s
q∞
(I; X)=
f ∈ L
q
(I; X):f
B
s
q∞
(I;X)
< ∞
,
f
B
s
q∞
(I;X)
= f
L
q
(I;X)
+sup
0<h≤1
Δ
h
f(t)
L
q
(I
h
;X)
,
where Δ
h
f(t)=f (t + h) − f(t)andI
h
= {t ∈ I : t + h ∈ I}.Moreover,weset
C
s
(I; X)=B
s
∞∞
(I; X), s ∈ (0, 1). Finally, B
s
q∞,uloc
([0, ∞); X) is defined in the
obvious way replacing L
q
(0, ∞; X)-norms by L
q
uloc
([0, ∞); X)-norms.
Let us conclude with two useful lemmas for the following.
Lemma 2.1. Let X, Y be two Banach spaces such that Y→ X and X
→ Y
densely and let 0 <T≤∞.ThenL
∞
(0,T; Y )∩BUC([0,T]; X) → BC
w
([0,T]; Y ).
We refer to [2, Lemma 4.1] for a proof.
Lemma 2.2. Let E :[0,T) → [0, ∞), 0 <T ≤∞, be a lower semi-continuous
function and let D :(0,T) → [0, ∞) be an integrable function. Then
E(0)ϕ(0) +
T
0
E(t)ϕ
(t) dt ≥
T
0
D(t)ϕ(t) dt (2.2)
holds for all ϕ ∈ W
1
1
(0,T) with ϕ(T )=0if and only if
E(t)+
t
s
D(τ) dτ ≤ E(s) (2.3)
holds for all s ≤ t<T and almost all 0 ≤ s<T including s =0.
See [2, Lemma 4.3] for a proof.
3. Double obstacle limit for the Cahn-Hilliard equation
3.1. Limit of the energy
In this section we study the “convex part” of E
free
as in (1.10), namely
E
θ
(c)=
Ω
|∇c|
2
2
dx +
Ω
θΦ
0
(c(x)) dx, θ > 0, (3.1)
as θ → 0, where Φ
0
is the same as in (1.12), (1.13).
Firstly, E
θ
is defined on L
2
(m)
(Ω), m ∈ (a, b), with
dom E
θ
=
c ∈ H
1
(Ω) ∩ L
2
(m)
(Ω) : c(x) ∈ [a, b]a.e.
.
Double Obstacle Limit 7
But we will assume in the following m = 0 without loss of generality. By a simple
shift of c and Φ by m we can always reduce to this case.
We denote by ∂E
θ
(c): L
2
(0)
(Ω) →P(L
2
(0)
(Ω)) the subgradient of E
θ
at c ∈
dom E
θ
, i.e., w ∈ ∂E
θ
(c) if and only if
(w, c
− c)
L
2
≤ E
θ
(c
) − E
θ
(c) for all c
∈ L
2
(0)
(Ω).
From [3, Corollary 1], see also [4, Corollary 4.4], we recall:
Lemma 3.1. Let E
θ
be as above and extend E
θ
toafunctional
E
θ
: H
−1
(0)
(Ω) →
R ∪{+∞} by setting
E
θ
(c)=E
θ
(c) if c ∈ dom E
θ
and
E
θ
(c)=+∞ else. Then
E
θ
is a proper, convex, and lower semi-continuous functional, ∂
E
θ
is a maximal
monotone operator with ∂
E
θ
(c)=−Δ
N
∂E
θ
(c),and
D(∂
E
θ
)=
c ∈D(∂E
θ
):∂E
θ
(c)=−Δc + θP
0
φ
0
(c) ∈ H
1
(0)
(Ω)
, (3.2)
where
D(∂E
θ
)=
c ∈ H
2
(Ω) ∩ L
2
(0)
(Ω) : φ
0
(c) ∈ L
2
,φ
0
(c)|∇c|
2
∈ L
1
,∂
n
c|
∂Ω
=0
and ∂E
θ
(c)=−Δc + θP
0
φ
0
(c). Moreover, for every c ∈D(∂
E
θ
)
c
W
2
r
+ φ
0
(c)
r
≤ C
r,θ
∂E
θ
(c)
H
1
(0)
+ c
2
+1
, (3.3)
where r =6if d =3and 2 ≤ r<∞ is arbitrary if d =2.
Remark 3.2. We note that in [3, Corollary 1] the case θ = 1 is considered. This
implies the lemma for every θ>0whereC
r,θ
in (3.3) depends on θ>0. But
one crucial observation for the following is that the estimate (3.3) is valid with a
constant C
r
independent of 0 <θ≤ 1.
Proposition 3.3. Let E
θ
, 0 <θ≤ 1, be as above, let
E
θ
be the extension to H
−1
(0)
(Ω),
let R>0 and let r =6if d =3and 2 ≤ r<∞ arbitrary if d =2. Then there are
constants C(R),C
(r, R) > 0 independent of 0 <θ≤ 1 such that
c
H
2
(Ω)
+ θφ
0
(c)
L
2
(Ω)
≤ C(R)
∂E
θ
(c)
L
2
(Ω)
+1
(3.4)
for all c ∈D(∂E
θ
) with c
L
2
(Ω)
≤ R and
c
W
2
r
(Ω)
+ θφ
0
(c)
L
r
(Ω)
≤ C
(r, R)
∂
E
θ
(c)
H
−1
(0)
(Ω)
+1
(3.5)
for all c ∈D(∂
E
θ
) with c
L
2
(Ω)
≤ R.
Proof. Let c ∈D(∂E
θ
). First we show a suitable estimate for Δc and θφ
0
(c)in
L
2
(Ω) which is independent of θ ∈ (0, 1]. Taking the L
2
-inner product of ∂E
θ
(c)=
−Δc + P
0
θφ
0
(c)and−Δc, we conclude that
Ω
|Δc|
2
dx + θ
Ω
φ
0
(c)|∇c|
2
dx = −(∂E
θ
(c), Δc)
Ω
.
