Escher J., Guidotti P., Hieber M. et al. (editors) Parabolic Problems: The Herbert Amann Festschrift
Подождите немного. Документ загружается.

28 M. Pires and A. Sequeira
4. Numerical approximation and results
We use finite element methods to obtain approximate solutions to problem (3.4).
Here and in the remaining sections, only steady solutions will be considered.
4.1. Setting of the approximated problem
Let {T
h
}
h>0
be a family of regular triangulations of the rectangle Σ defined by
(3.3), and denote by
X
h
=(X
h
)
3
=
v
h
∈ C(Σ) ∩ H
1
0
(Σ) | v
h
|K
∈ P
2
(K), ∀K ∈T
h
3
,
Q
h
=
q
h
∈ C(Σ) ∩ L
2
0
(Σ) | q
h
|K
∈ P
1
(K), ∀K ∈T
h
,
and
T
h
=(T
h
)
3×3
= {τ
h
∈ L
2
(Σ) | τ
h
|K
∈ P
1
, ∀K ∈T
h
}
3×3
the finite element spaces. System (3.4) is approximated by the following problem
Find (u
h
,p
h
,
τ
h
) ≡ (u,p,
τ ) ∈ X
h
×Q
h
×T
h
solution of
⎧
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎩
−A
r,γ
ψ
γ
(2(1 − ε)Du −Re u ⊗u)
+ ψ
γ+1
∂p
∂r
, φ
1
=(A
r,γ
(
τ ) , φ
1
) ,
−A
θ,γ
ψ
γ
(2(1 − ε)Du −Re u ⊗ u)
+ βψ
γ
∂p
∂θ
, φ
2
=(A
θ,γ
(
τ ) , φ
2
) ,
−A
s,γ
ψ
γ
(2(1 − ε)Du −Re u ⊗ u)
− p
∗
rψ
γ
, φ
3
=(A
s,γ
(
τ ) , φ
3
) ,
∂
∂r
(rβu)+
∂
∂θ
(βv),ϕ
=0,
rβ
τ
ij
, σ
+ We B
h
u, v,
τ
ij
, σ
=
G
ij
(u,
τ ) , σ
,
u
|
∂Σ
=0
(4.1)
for every (φ
1
, φ
2
, φ
3
,ϕ) ∈ V
δ,h
× Q
h
,where
V
δ,h
= {v
h
∈ X
h
|∇
·(β v
h
)=0},δ∈ [0, 1[
and every σ
∈ T
h
( =1,...,6), with B
h
defined by
B
h
u, v, τ, σ
=
rβu
∂τ
∂r
+ βv
∂τ
∂θ
+
1
2
∂
∂r
(rβu)+
∂
∂θ
(βv)
τ,σ
h
−
τ
+
− τ
−
,σ
+
h,u,v
where
(·, ·)
h
=
!
K∈T
h
(·, ·)
K
,
σ, τ
h,u,v
=
!
K∈T
h
∂K
−
(ru,v)
τσβ(run
r
+ vn
θ
) ds,
∂K
−
(ψ, ζ)={s ∈ ∂K | (ψ, ζ) · (n
r
,n
θ
) < 0},
and where (n
r
,n
θ
) is the outward unit normal vector to element K ∈T
h
.

Flows of Generalized Oldroyd-B Fluids in Curved Pipes 29
Using standard integration by parts we show that problem (4.1) can be rewrit-
tenintheform
(P
h
)Find(u
h
,p
h
,
τ
h
) ≡ (u,p,
τ ) ∈ X
h
× Q
h
× T
h
solution of
2K
γ
ψ
γ
∂u
∂r
, φ
1
+ L
γ
βψ
γ−1
∂u
∂θ
, φ
1
+2
ψ
γ−1
β
2
+ β
2
2
u, φ
1
+ L
γ
βψ
γ−1
r
∂v
∂r
−v
, φ
1
+2
ψ
γ−1
β
2
∂v
∂θ
− β
1
β
2
v
, φ
1
−
1
1−ε
K
γ+1
ψ
γ
p, φ
1
+
Re
1−ε
K
γ
ψ
γ
u
2
, φ
1
+ L
γ
ψ
γ
uv, φ
1
+
Re
1−ε
ψ
γ
β
2
w
2
+ βv
2
, φ
1
= −
1
1−ε
K
γ
(
τ
rr
, φ
1
)+L
γ
(
τ
rθ
, φ
1
)+
β
2
τ
ss
+ β
τ
θθ
, φ
1
,
K
γ
βψ
γ−1
r
∂v
∂r
−v
, φ
2
+2L
γ
βψ
γ−1
∂v
∂θ
, φ
2
+
ψ
γ−1
β
2
+2β
2
1
v − rβ
2
∂v
∂r
, φ
2
+ K
γ
βψ
γ−1
∂u
∂θ
, φ
2
+2L
γ
βψ
γ−1
u, φ
2
−
ψ
γ−1
β
2
∂u
∂θ
+2β
1
β
2
u
, φ
2
−
1
1−ε
L
γ+1
ψ
γ
p, φ
2
+
Re
1−ε
K
γ
ψ
γ
uv, φ
2
+ L
γ
ψ
γ
v
2
, φ
2
−
Re
1−ε
ψ
γ
β
1
w
2
+ βuv
, φ
2
= −
1
1−ε
K
γ
(
τ
θr
, φ
2
)+L
γ
(
τ
θθ
, φ
2
) −
β
1
τ
ss
+ β
τ
rθ
, φ
2
,
K
γ
ψ
γ−1
rβ
∂w
∂r
−β
2
w
, φ
3
+ L
γ
ψ
γ−1
β
∂w
∂θ
+ β
1
w
, φ
3
+
ψ
γ−1
(rδ)
2
w + ββ
1
∂w
∂θ
− rββ
2
∂w
∂r
, φ
3
−
1
1−ε
rψ
γ
p
∗
, φ
3
+
Re
1−ε
K
γ
ψ
γ
uw, φ
3
+ L
γ
ψ
γ
vw, φ
3
−
Re
1−ε
ψ
γ
(β
2
u − β
1
v) w, φ
3
= −
1
1−ε
K
γ
(
τ
sr
, φ
3
)+L
γ
(
τ
sθ
, φ
3
)+
β
1
τ
θs
− β
2
τ
rs
, φ
3
,
∂
∂r
(rβu)+
∂
∂θ
(βv),ϕ
=0, for every (φ
1
, φ
2
, φ
3
,ϕ) ∈ V
δ,h
× Q
h
,and
(
τ
ij
,rβσ
)
h
+ We B
h
(u, v,
τ
ij
, σ
)=(G
ij
(u,
τ ) , σ
)
h
for all σ ∈ (T
h
)
6
with
B
h
= −
rβu
∂σ
∂r
+ βv
∂σ
∂θ
−
1
2
∂
∂r
(rβu)+
∂
∂θ
(βv)
σ, τ
h
+ τ
−
,σ
+
−σ
−
h,u,v
,
with K
γ
(σ, ϕ)=
σ, rβ
∂ϕ
∂r
+ γ (β + β
2
) ϕ
, L
γ
(σ, ϕ)=
σ, β
∂ϕ
∂θ
− γβ
1
ϕ
and G
given by (3.5).
30 M. Pires and A. Sequeira
4.2. Algorithm
Next we define the algorithm to solve the approximated problem (P
h
) (as usual,
the index h is dropped to simplify the presentation).
• Givenaniterate
τ
k
, find u
k
≡ (u
k
,v
k
,w
k
), and p
k
solutions of the following
Navier-Stokes system (NS)
k
2K
γ
ψ
γ
∂u
k
∂r
,φ
1
+ L
γ
βψ
γ−1
∂u
k
∂θ
, φ
1
+2
ψ
γ−1
β
2
+ β
2
2
u
k
, φ
1
+ L
γ
βψ
γ−1
r
∂v
k
∂r
−v
k
, φ
1
+2
ψ
γ−1
β
2
∂v
k
∂θ
− β
1
β
2
v
k
, φ
1
−
1
1−ε
K
γ+1
ψ
γ
p
k
, φ
1
+
Re
1−ε
K
γ
ψ
γ
(u
k
)
2
, φ
1
+
Re
1−ε
L
γ
ψ
γ
u
k
v
k
, φ
1
+
ψ
γ
β
2
(w
k
)
2
+ β(v
k
)
2
, φ
1
= −
1
1−ε
K
γ
(
τ
k
rr
, φ
1
)+L
γ
(
τ
k
rθ
, φ
1
)+
β
2
τ
k
ss
+ β
τ
k
θθ
, φ
1
,
K
γ
βψ
γ−1
r
∂v
k
∂r
− v
k
, φ
2
+2L
γ
βψ
γ−1
∂v
k
∂θ
, φ
2
+
ψ
γ−1
β
2
+2β
2
1
v
k
− rβ
2
∂v
k
∂r
, φ
2
+ K
γ
βψ
γ−1
∂u
k
∂θ
, φ
2
+2L
γ
βψ
γ−1
u
k
, φ
2
−
ψ
γ−1
β
2
∂u
k
∂θ
+2β
1
β
2
u
k
, φ
2
−
1
1−ε
L
γ+1
ψ
γ
p
k
, φ
2
+
Re
1−ε
K
γ
ψ
γ
u
k
v
k
, φ
2
+
Re
1−ε
L
γ
ψ
γ
(v
k
)
2
, φ
2
−
ψ
γ
β
1
(w
k
)
2
+ βu
k
v
k
, φ
2
= −
1
1−ε
K
γ
(
τ
k
θr
, φ
2
)+L
γ
(
τ
k
θθ
, φ
2
) −
β
1
τ
k
ss
+ β
τ
k
rθ
, φ
2
,
K
γ
ψ
γ−1
rβ
∂w
k
∂r
−β
2
w
k
, φ
3
+ L
γ
ψ
γ−1
β
∂w
k
∂θ
+ β
1
w
k
, φ
3
+
ψ
γ−1
(rδ)
2
w
k
+ ββ
1
∂w
k
∂θ
−rββ
2
∂w
k
∂r
, φ
3
−
1
1−ε
rψ
γ
p
∗
, φ
3
+
Re
1−ε
K
γ
ψ
γ
u
k
w
k
, φ
3
+
Re
1−ε
L
γ
ψ
γ
v
k
w
k
, φ
3
−
ψ
γ
β
2
u
k
− β
1
v
k
w
k
, φ
3
= −
1
1−ε
K
γ
(
τ
k
sr
, φ
3
)+L
γ
(
τ
k
sθ
, φ
3
)+
β
1
τ
k
θs
− β
2
τ
k
rs
, φ
3
,
∂
∂r
rβu
k
+
∂
∂θ
(βv
k
),ϕ
=0, for every (φ
1
, φ
2
, φ
3
,ϕ) ∈ V
δ,h
× Q
h
.
• Calculate the new iterate
τ
k+1
as the solution of the transport problem
τ
k+1
ij
,rβσ
+WeB
h
u
k
,v
k
,
τ
k+1
ij
, σ
=
G
ij
u
k
,
τ
k
, σ
∀σ ∈ (T
h
)
6
.
• Find u
k+1
≡ (u
k+1
,v
k+1
,w
k+1
,p
k+1
) solution of the Navier-Stokes system
(NS)
k+1
.
Flows of Generalized Oldroyd-B Fluids in Curved Pipes 31
Taking into account this algorithm, our aim is to write the linear systems cor-
responding to problem (P
h
) at a given iteration k. To simplify the presentation,
we will consider the case of creeping non-Newtonian flows, which corresponds to
Re =0.
Given
τ
k
, expressing the corresponding approximate solutions u
k
, v
k
, w
k
and
p
k
in the basis of V
δ,h
and Q
h
u
k
=
n
h
!
i=1
u
k
i
φ
i
1
,v
k
=
n
h
!
i=1
v
k
i
φ
i
2
,w
k
=
n
h
!
i=1
w
k
i
φ
i
3
,p
k
=
m
h
!
i=1
p
k
i
ϕ
i
,
we obtain the following linear system
⎛
⎜
⎜
⎝
A
1
A
2
0
1
1−ε
A
3
A
4
A
5
0
1
1−ε
A
6
00A
7
0
A
8
A
9
00
⎞
⎟
⎟
⎠
⎛
⎜
⎜
⎝
u
k
v
k
w
k
p
k
⎞
⎟
⎟
⎠
=
⎛
⎜
⎜
⎝
b
k
1
b
k
2
b
k
3
0
⎞
⎟
⎟
⎠
where
(A
1
)
ij
=2K
γ
ψ
γ
∂φ
j
1
∂r
,φ
i
1
+ L
γ
βψ
γ−1
∂φ
j
1
∂θ
,φ
i
1
+2
ψ
γ−1
β
2
+ β
2
2
φ
j
1
,φ
i
1
,
(A
2
)
ij
= L
γ
ψ
γ−1
rβ
∂φ
j
2
∂r
− βφ
j
2
,φ
i
1
+2
ψ
γ−1
β
2
∂φ
j
2
∂θ
−β
1
β
2
φ
j
2
,φ
i
1
,
(A
3
)
ij
= −K
γ+1
ψ
γ
ϕ
j
,φ
i
1
,
(A
4
)
ij
= K
γ
βψ
γ−1
∂φ
j
1
∂θ
,φ
j
2
+2L
γ
βψ
γ−1
φ
j
1
,φ
j
2
−
ψ
γ−1
β
2
∂φ
j
1
∂θ
+2β
1
β
2
φ
j
1
,φ
i
2
,
(A
5
)
ij
= K
γ
ψ
γ−1
rβ
∂φ
j
2
∂r
− βφ
j
2
,φ
i
2
+2L
γ
βψ
γ−1
∂φ
j
2
∂θ
,φ
i
2
+
ψ
γ−1
β
2
+2β
2
1
φ
j
2
−rβ
2
∂φ
j
2
∂r
,φ
i
2
,
(A
6
)
ij
= −L
γ+1
ψ
γ
ϕ
j
,φ
j
2
,
(A
7
)
ij
= K
γ
ψ
γ−1
rβ
∂φ
j
3
∂r
− β
2
φ
j
3
,φ
i
3
+ L
γ
ψ
γ−1
β
∂φ
j
3
∂θ
+ β
1
φ
j
3
,φ
i
3
+
ψ
γ−1
(rδ)
2
φ
j
3
+ ββ
1
∂φ
j
3
∂θ
− rββ
2
∂φ
j
3
∂r
,φ
i
3
,
(A
8
)
ij
=
rβ
∂φ
j
1
∂r
+(β + β
2
)φ
j
1
,ϕ
j
,
(A
9
)
ij
=
β
∂φ
j
2
∂θ
− β
1
φ
j
2
,ϕ
j
,
and where the vectors b
j
(j =1, 3) are given by
b
k
1
i
= −
1
1−ε
K
γ
(
τ
k
rr
,φ
i
1
)+L
γ
(
τ
k
rθ
,φ
i
1
)+
β
2
τ
k
ss
+ β
τ
k
θθ
,φ
i
1
,
b
k
2
i
= −
1
1−ε
K
γ
(
τ
k
θr
,φ
i
2
)+L
γ
(
τ
k
θθ
,φ
i
2
) −
β
1
τ
k
ss
+ β
τ
k
rθ
,φ
i
2
,

32 M. Pires and A. Sequeira
b
k
3
i
= −
1
1−ε
K
γ
(
τ
k
sr
,φ
i
3
)+L
γ
(
τ
k
sθ
,φ
i
3
)+
β
1
τ
k
θs
−β
2
τ
k
rs
,φ
i
3
+
1
1−ε
rψ
γ
p
∗
,φ
i
3
.
After obtaining (u
k
, v
k
, w
k
, p
k
), we consider the transport equation to get
τ
k+1
≡
τ
k+1
ij
. Using the local basis functions {ζ
}
=1,2,3
⊂ T
h
,thelocalsys-
tem for the approximate transport problem can be written as
A
k
τ
k+1
ij
+
A
k
−
τ
k+1
ij
−
= G
k
ij
,i,j=1, 2, 3
with
A
k
m
=
ζ
m
,rβζ
l
K
−We
ζ
m
,rβu
k
∂ζ
l
∂r
+ βv
k
∂ζ
l
∂θ
K
−
We
2
rβ
∂u
k
∂r
+ β
∂v
k
∂θ
+(β + β
2
)u
k
− β
1
v
k
ζ
m
,ζ
l
K
,
A
k
−
m
= We
∂K
−
(ru
h
,v
h
)
βζ
−
m
ζ
l
− ζ
−
l
ru
k
nr + v
k
n
θ
ds,
G
k
ij
=
G
ij
u
k
,
τ
k
,ζ
K
,
where ζ
−
denotes the th basis function over the correspondent adjacent element
to K by an inflow edge, G is the function given by (3.5). The local systems lead
to a linear system of the form
M
k
τ
k+1
i
= C
k
i
,
where M
k
is a non-symmetric matrix whose dimension is twice the number of
nodes in the triangulation.
4.3. Numerical results
The domain Σ defined by (3.3) is discretized using triangles. Referring to the
algorithm, we see that a Navier-Stokes system has to be solved for (u, v, p), a
Poisson equation for w and a transport equation for
τ . The velocity is set to zero
on the lateral surface of the pipe. The non-dimensional stream function ψ can be
written with respect to the components u and v,as
u = −
1
rβ
∂ψ
∂θ
,v=
1
β
∂ψ
∂r
.
and the wall-shear stress is τ
w
= −(T · n) · λ |
r=1
. In this particular case, τ
w
is
given by
τ
w
= − 2(1 − ε)
∂u
∂r
−
∂v
∂θ
+ u
|
r=1
sin θ cos θ
− (1 − ε)
∂v
∂r
+
∂u
∂θ
− v
|
r=1
sin
2
θ − cos
2
θ
− (τ
rr
−τ
θθ
)|
r=1
sin θ cos θ − τ
rθ
|
r=1
(sin
2
θ − cos
2
θ).
In what follows, we consider the numerical simulation of fully developed
steady Oldroyd-B flows with constant and non constant viscosity, in a curved
pipe with constant cross section. The behavior of creeping (i.e., Reynolds number

Flows of Generalized Oldroyd-B Fluids in Curved Pipes 33
set to zero) and inertial flows (non-zero Reynolds number) is analyzed for different
values of the parameter involved in the governing equations (the Reynolds number
Re, the Weissenberg number We, the curvature ration δ, the non-dimensional vis-
cosity parameter η and the exponent q appearing in the power-law type viscosity).
A continuation method is carried out to implement these different tests.
4.3.1. Creeping generalized Oldroyd-B flows. In this section, we are interested
in the qualitative study of creeping flows (Re = 0) for generalized Oldroyd-B
fluids, and especially on the behavior of the secondary motions and of the wall
shear stress. In order to analyse the combined effect of the viscoelasticity, the
non-constant viscosity and the curvature ratio, several calculations were achieved.
Figure 2. Streamlines (top) and wall shear stress (bottom) for
creeping Oldroyd-B flows, for the curvature ratio δ =0.001.
It is well known that in the case of creeping Oldroyd-B fluids, the viscoelastic-
ity promotes secondary flows characterized by two counter-rotating vortices, that
the global behavior is stable, and is of Newtonian type. We did not observe any
notable changes in the nature of the flow when varying the characteristic para-
meters (Weissenberg number and curvature ratio). The only difference lies in the
values of the stream function and of the wall shear stress, which increase with
these parameters, and also in a slight shift to the left of the vortices with increas-
ing curvature ratio. Figure 2 displays the flow behavior for the curvature ratio
δ =0.001.
In a second step, we consider the more general case of Oldroyd-B fluids with
non constant viscosity. Fixing the curvature ratio δ and the viscosity parameter η,
we implement a continuation method with respect to the exponent q,fordifferent
−1
−1 10
−1 10
0
1
−1
0
1
−2.13e−06
−1.94e−06
−1.94e−06
−1.76e−06
−1.76e−06
−1.57e−06
6
0−e75.1−
−1.39e−06
−1.39e−06
−1.39e−06
−1.2e−06
−1.2e−06
−1.2e−06
−1.02e−06
−1.02e−06
−1.02e−06
−1.02e−06
−8.32e−07
−8.32e−07
−8.32e−07
−8.32e−07
−6.47e−07
−6.47e−07
−6.47e−07
−6.47e−07
−4.62e−07
−4.62e−07
−4.62e−07
−4.62e−07
−4.62e−07
−2.77e−07
−2.77e−07
−2.77e−07
−2.77e−07
−2.77e−07
−9.25e−08
−9.25e−08
−9.25e−08
−9.25e−08
−9.25e−08
−9.25e−0
8
9.25e−08
9.25e−08
9.25e−08
9.25e−08
9.25e−08
9.25e−08
2.77
e−07
2.77e−07
2.77e−07
2.77e−07
2.77e−07
4.62e−07
4.62e−07
4.62e−
07
4.62e−07
6.47e−07
6.47e−07
6.47e−07
6.47e−07
8.32e−07
8.32e−07
8.32e−07
8.32e−07
1.02e−06
1.02e−06
1.02e−06
1.2e−06
1.2e−06
1.2e−06
1.39e−06
1.39e−06
1.39e−06
1.57e−06
60−e75.1
1.76e−0
6
1.76e−06
1.94e−06
1.94e−06
2.13e−06
(a)
−1.06e−05
−9.71e−06
−9.71e−06
−8.78e−06
−8.78e−06
−7.86e−06
60−e68.7−
−6.93e−06
−6.93e−06
−6.93e−06
−6
.0
1e−06
−6.01e−06
−
6.01e−06
−5.08e−06
−5.08e−06
−5.08e−06
−5.08e−06
−4.16e−06
−4.16e−06
−4.16e−06
−4.16e−06
−
3.24e−06
−3.24e−06
−3.24e−06
−3.24e−06
−2.31e−06
−2.31e−06
−2.31e−06
−2.31e−06
−2.31e−06
60−e9
3
.1−
−1.39e−06
−1.39e−0
6
−1.39e−06
−1.39e−06
−4.62e−07
−4.62e−07
−4.62e−07
−4.62e−07
−4.62e−07
−4.62e−07
4.63e−07
4.63e−07
4.63e−07
4.63e−07
4.63e−07
4.63e−07
1.39e−06
1.39e−06
1.39e−06
1.39e−06
1.39e−06
2.31e−06
2.31e−06
2.31e−06
2.31e−06
3.24e−06
3.24e−06
3.24e−06
3.24e−06
4.16e−06
4.16e−06
4.16e−06
4.16e−06
5.08e−06
5.08e−06
5.08e−06
6.01e−06
6.01e−06
6.01e−06
6.93e−06
6.93e−06
6.93e−06
7.8
6e−06
7.86e−06
7.86e−06
8.78e−06
8.78e−06
9.71e−06
9.71e−06
1.06e−05
(b)
1 2 3 4 5 6
q
−0.0002
−0.0001
0.0001
0.0002
t
w
We 5
We 4
We 3
We 2
We 1
We =1
We =5
5

34 M. Pires and A. Sequeira
values of the Weissenberg number. The values of the maximum exponent for which
convergence is ensured are shown in Table 1. As one can see, and as expected, q
max
depends on the different parameters. In particular, the values decrease when these
parameters increase. We also observe that there is no convergence, for the curvature
ratio δ =0.2, with We = 5 and the same values of the viscosity parameter η.
We 1 2 3 4 5
δ =0.001
η =0.4 21.6 6.80 6.75 7.32 6.93
0.5 4.70 4.57 4.45 4.15 3.95
0.6 3.05 2.85 2.60 2.30 2.00
δ =0.1
η =0.4 8.92 1.02 0.58 0.45 0.36
0.5 1.53 0.60 0.42 0.32 0.26
0.6 0.80 0.45 0.32 0.26 0.21
δ =0.2
η =0.4 3.31 0.62 0.42 0.32 −
0.5 0.91 0.45 0.32 0.24 −
0.6 0.60 0.34 0.24 0.19 −
Table 1. Maximum values of |q|.
Numerical results (using finite element methods) show some changes in flow
characteristics and that the viscosity influences its behavior. In summary, we have
two phases:
• A phase of variation in the behavior passing from the standard Oldroyd-B
type to a new type.
• A phase of stabilisation in the new type.
More precisely, for small values of |q|, we observe a surprising phenomenon. Ini-
tially, the secondary flows involve non-zero values and are characterized by two
counter-rotating vortices. As q increases in absolute value, the streamlines in the
core region become less dense, the size of the couple of vortices reduces, and the
flow is driven near the wall pipe. We observe the formation of boundary layers
flows with a pair of new vortices, initially weak and elongated, strengthening and
dominating as the viscosity exponent increases. In contrast, the original secondary
flows become more and more weak before vanishing when the level of the exponent
viscosity reaches a critical value. The orientation of the new contours is opposite,
as well as the sign of the stream function, suggesting a transition to a different
regime.
It is interesting to observe that this behavior is global, in the sense that it is
seems to be independent of the Weissenberg number and of the curvature ratio,
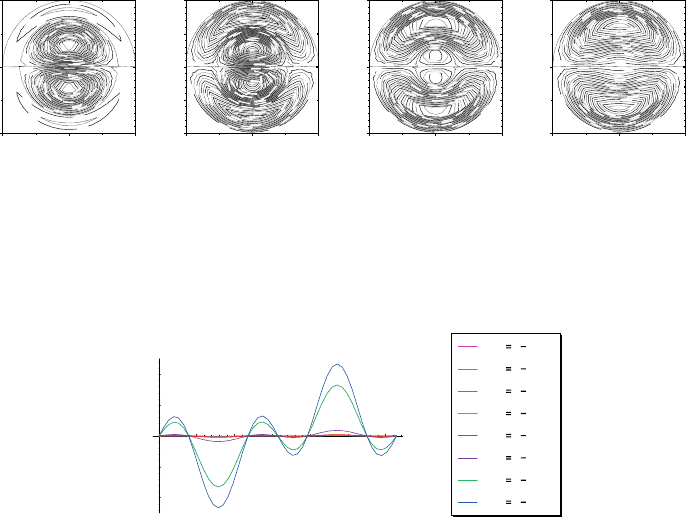
and occurs for the same values of the viscosity exponent q. Figure 3 illustrates the
behavior of the streamlines in the particular case of a curvature ratio δ =0.001 and
Flows of Generalized Oldroyd-B Fluids in Curved Pipes 35
viscosity parameter η =0.4. The influence of the viscosity parameter is evident,
and as η increases the transition occurs earlier. Moreover, because of the effect
of the curvature, the new two vortices are not localized in the center of the cross
section but are slightly translated.
Figure 3. Qualitative behavior of the streamlines for creeping
generalized Oldroyd-B flows, with η=0.4 and for different values
of |q| (δ=0.001).
Figure 4. Wall shear stress for creeping generalized Oldroyd-B
flows, with η=0.4(δ=0.001).
We also noticed variations in the wall shear stress (see Figure 4). It can be
observed that during the transition, the amplitude of the wall shear stress decreases
and the corresponding curves are inverted in comparison with the Oldroyd-B case.
After the transition phase, and before reaching some “critical” value of the
viscosity exponent, the flow is qualitatively more stable. The streamlines are sym-
metric and the global behavior of the wall shear stress remains unchanged. This
critical value of q depends on the viscoelastic parameter, on the viscosity parame-
ter, and particularly on the curvature ratio. Globally, the changes which occur from
now on, are similar in some aspects to those already noticed for the generalized
Newtonian flows [1, 3].
In particular, for η =0.4, for relatively small Weissenberg numbers (We =
2, 3, 4), and especially in the case of small curvature ratio, we observe a variation
10−1 10−1 10−1 10−1
−1
0
1
−1
0
1
−1
0
1
−1
0
1
−4.94e−07
−4.51e−07
−4.08e−07
−3.65e−07
−3.65e−07
−3.22e−07
−3.22e−07
−2.79e−07
−2.79e−07
−2.36e−07
−2.36e−07
−2.36e−07
−1.93e−07
−1.93e−07
−1.93e−
07
−1.5e−07
−1.5e−07
−1.5e−07
−1.07e−07
−1.07e−07
−1.07e−07
−1.07e−07
−6.45e−08
−6.45e−08
−6.45e−08
−6.45e−08
−2.15e−08
−2.15e−
08
−2.15e−08
−2.15e−08
−2.15e−08
−2.15e−08
−2.15e−08
−2.15e−08
−2.15e−08
2.15e−08
2.15e−08
2.15e−08
2.15e−
08
2.15e−08
2.15e−08
2.15e−08
2.15e−08
2.15e−08
6.45e−08
6.45e−08
6.45e−08
6.45e−08
1.07e−07
1.07e−07
1.07e−07
1.5e−07
1.5e−07
1.5e−07
1.93e−07
1.93e−07
1.93e−07
2.36e−07
2.36e−07
2.36e−07
2.79e−07
2.79e−07
3.22e−07
3.22e−07
3.65e−07
3.65e−07
4.08e−07
4.08e−07
4.51e−07
4.94e−07
(a)
−2.41e−07
−2.18e−07
−1.95e−07
−1.95e−07
−1.72e−07
−1.72e−07
−1.72e−07
−1.72e−07
−1.49e−07
−1.49e−07
−1.49e−07
−1.49e−07
−1.49e−07
−1.26e−07
−1.26e−07
−1.26e−07
−1.26e−07
−1.26e−07
−1.03e−07
−1.03e−07
−1.03e−07
−1.03e−07
−1.03e−07
−1.03e−07
−8.04e−08
−8.04
e−08
−8.0
4e−
08
−8.04e−08
−
8.0
4e−
08
−8.04e−08
−8.04e−08
−5.74e−08
−5.74e−08
−5.74e−08
−5.74e−08
−5.74e−08
−5.74e−08
−5.74e−08
−5.74e−08
−3.44e−08
−3.44e−08
−3.44e−08
−3.44e−08
−3.44e−08
−3.44e−08
−3.44e−08
−3.44e−08
−3.44e−08
−1.15e−08
−1.15e−08
−1.15e−08
−1.15e−08
−1.15e−08
−1.15e−08
−1.15e−08
−1.15e−08
−1.15e−08
1.15e−08
1.15e−08
1
.
15
e−08
1.15e−08
1.15e−08
1.15e−08
1.15e−08
1.15e−08
1.15e−08
1.15
e−08
3.45e−08
3.45e−08
3.45e−08
80
−
e54
.
3
3.45e−08
3.45e−
08
3.45e−08
3.45e−08
3.45e−08
5.74e−08
5.74e−08
5.74e−08
5.74e−08
5.74e−08
5.74e−08
5.74e−08
5.74e−08
8.04e−08
8.04e−08
8.04e−08
8.04e−08
8.04e−08
8.04e−08
1.03e−07
1.03e−07
1.03e−07
1.03e−07
1.03e−07
1.03e−07
1.26e−07
1.26e−07
1.26e−07
1.26e−07
1.26e−07
1.26e−07
1.49e−07
1.49e−07
1.49e−07
1.49e−
07
1.49e−07
1.72e−07
1.72e−07
1.72e−07
1.72e−07
1.95e−07
1.95e−07
2.18e−07
4.2
70−
e1
2.64e−07
(b)
−3.81e−07
−3.48e−07
−3.48e−07
−3.15e−07
−3.15e−07
−2.82e−
07
−2
.8
2e−07
−2.82e−07
−2.49e−07
−2.49e−07
−2.49e−07
−2.49e−07
−2.15e−07
−2.15e−07
−2.15e−07
−2.15e−07
−1.82e−07
−1.82e−07
−1.82e−07
−1.82e−07
−1.49e−07
−1.49e−07
70−e94.1−
−1.49e−07
−
1.16e−07
−1.16e−07
−1.16e−07
−1.16e−07
−1.16e−07
−8.29e−08
−8.29e−08
−8.29e−08
−8.29e−
08
−8.29e−08
−4.97e−08
−4.97e−08
−4.97e−08
−4.97e−08
−4.97e−08
−
4.9
7
e−08
−4.97e−08
−1.66e−08
−1.66e−08
−1.66e−08
−
1.6
6e−08
−1.66e−08
−1.66e−08
−1.66e−08
1.66e−08
1.66e−08
1.66e−
08
1.66e−08
1.66e−08
1.66e−08
1.66e−08
4.97e−08
4.97e−08
4.97e−08
4.97e−08
4.97e−08
4.97e−0
8
4.97e−08
80−e
9
2.
8
8.29e−08
8.29e−08
8.29e−08
8.29e−08
1.16e−07
1.16e−07
1.16e−07
1.16e−07
1.16e−07
1.49e−07
1.49e−07
1.49e−07
1.49e−07
1.82e−07
1.82e−07
1.82e−07
1.82e−07
2.15e−07
2.15e−
07
2.15e−07
2.15e−07
2.49e−07
2.49e−07
2.49e−07
2.82e−07
2.82e−07
2.82e−07
3.15e−07
3.15e−07
3.15e−07
3.48e−07
3.48e−07
3.81e−07
(c)
−6.54e−07
−5.97e−07
−5.97e−07
−5.41e−07
−5.41e−07
−4.84e−07
−
4.84e−07
−4.84e−07
−4.27e−07
−4.27e−07
−4.27e−07
−3.7e−07
−3.7e−07
−
3.7e−07
−3.13e−07
−3.13e−07
−3.13e−07
−3.13e−07
−2.56e−07
−2.56e−07
−2.56e−0
7
−2.56e−07
−
1.99e−07
−1.99e−07
−1.99e−07
−1.99e−07
−1.42e−0
7
−1.42e−07
−1.42e−07
−1.42e−07
−1.42e−07
−8.53e−08
−8.53e−08
−8.53e−08
−8.53e−08
−8.53e−08
−2.84e−08
−2.84e−08
−2.84e−08
−2.84e−08
−2.84e−08
−2.84e−08
2.85e−08
2.85e−08
2
.
85
e−0
8
2.85e−08
2.85e−08
2.85e−08
8.54e−
08
8.54e−08
8.54e−08
8.54e−08
8.54e−08
8.54e−08
1.42e−07
1.42e−
07
1.42e−07
1.42e−07
1.42e−07
1.99e−07
1.99e−07
1.99e−07
1.99e−07
1.99e−07
2.56e−07
2.56e−07
2.56e−07
2.56e−0
7
3.13e−07
3.13e−07
3.13
e−07
3.13e−07
3.7e−07
3.7e−07
3.7e−07
3.7e−07
4.27e−07
4.27e−07
4.27e−07
4.84e−07
4.84e−
0
7
4.84e−07
5.41e−07
5.41e−07
5.97e−07
5.97e−07
6.54e−07
6.54e−07
(d)
q = −0.17 q = −0.18 q = −0.19 q = −0.2
1
2 3 4 5
6
q
−0.002
−0.001
0.001
0.002
q 5.
q 1.
q 0.30
q 0.20
q 0.19
q 0.18
q 0.17
q 0.16
t
w

36 M. Pires and A. Sequeira
Figure 5. Streamlines for creeping generalized Oldroyd-B flows
with η=0.4and|q| =6, 6.4, 6.5 (from left to right), for different
Weissenberg numbers We (δ=0.001).
in the shape of the vortices, their displacement to the core region, the concentration
of the contours in this region and the beginning of a counter-clockwise rotation.
In Figure 5, we plot the streamlines corresponding to this case. The rotation
is more pronounced when the Weissenberg number is small suggesting that the
viscoelasticity, as well as the inertial forces in the case of generalized Newtonian
flows, has an opposite effect [1, 3].
However, contrarily to the generalized Newtonian flows, the viscosity expo-
nent corresponding to the initiation of the rotation is not constant. As can be
seen in Table 2, it depends on We and as this parameter increases, the rotation
initiates earlier. Moreover, the viscoelastic parameter affects the maximum angle
and the development of the rotation: for We = 2, the contours are left-rotating
(L), for We = 3 they are initially left-rotating and then right-rotating (R) before
stabilizing symmetrically (S). Finally, when the We increases, there is no more
rotation and the contours remain symmetric.
10−1 10−1 10−1
10−110−110−1
10
−1
10−110−1
−1
0
1
−1
0
1
−1
0
1
−1
0
1
−1
0
1
−1
0
1
−1
0
1
−1
0
1
−1
0
1
−8
.63e−05
−7.88e−05
−7.88e−05
−7.1
3e−05
−7.13e−05
−6.38e−05
−6.38e−05
−5.62e−05
−5.62e−05
−5.62e
−05
−4.87e−05
−4.87e−05
−4. 8
7e−
05
−4.12e−05
−
4.1
2e−05
−
4.12e−
05
−3.37e−05
−3.37e−
05
−3.37e−05
−2.62e−05
−2.62e−05
−2.62e−05
−2.62e−05
−1.87e−05
−1.87e−05
−1.87e−05
−1.87e−05
−1.87e−05
−1.12e−05
−1.12e−05
−1.12e−05
−1.12e−05
−1.12e
−05
−3.72e−06
−3.72e−06
−3.72e−06
−3.72e−06
−3.72e−06
60−e27.3−
3.78e−06
3.78e−06
3.78e−06
3.78e−06
3.78e−06
1.13e−05
1.13e
−05
1.13e−05
1.13e−05
1.13e−05
1.88e−
05
1.88e−05
1.88e−05
1.88e−05
2.63e−05
2.63e−05
2.63e−05
2.63e
−05
3.38e−0
5
3.38e−05
3.38e−05
3.38e−05
4.13e−05
4.13e−05
4.13e−0
5
4.88e−05
4.88e−05
4.8
8e−05
5.63e−05
5.63e
−05
6.38e−05
6.38e−05
7.13e−05
7.13e−05
7.88e−05
8.63e−05
−0.000141
−0.000128
−0.000116
−
0.00011
6
−0.000104
−0.000
104
−9.17e−05
−9.17e−05
−9.17e−
05
−7.94e−05
−7.94e−05
−7.94e−05
−6.71e−05
−6.71e
−05
−6.71e−05
−5.48e−05
−
5.48e−05
−5.48e−05
−4.25e−05
−4.25e−05
−4.25e−05
−4.25e−05
−3.02e−05
−3.02e−0
5
−3.02e−05
−3.02e−05
−3.02e−05
−1.8e−05
−1.8e−05
−1.8e−05
−1.8e−05
−1.8e−05
−5. 69
e−06
−5.69e−06
−5.69e−06
−5.69e−06
−5.69e−06
6.59e−06
6.59e−0
6
6.59e−06
6.59e−06
6.59e−0
6
6.59e−06
1.89e−05
1.89e−05
1.89e−05
1.89e−05
3.12e−05
3.12e−05
3.12e−05
3.12e−05
4.34e−05
4.34
e−05
4.34e−05
4.34
e
−05
5.57e−05
5.57e−05
5.57e−05
6.8e−05
6.8e−05
6.8e−05
8.03e−05
8.03e−05
8.03e−05
9.26e−05
9.26e−05
9.26e−05
0.000105
0.000105
0.000117
0.000117
0.000129
0
.000129
0.000142
−0.000622
−0.000567
−0.000513
−0.000459
−0.000404
−0.00035
−0.00035
−0.000296
−0.000296
−0.000296
−0.000241
−0.000241
−0.000241
−0.000187
−0.000187
−0.000187
−0.000132
−0.0
00132
−0.000132
−0.000132
−7.8e−05
−7.8e−05
−7.8e−05
−7.8e−05
−2.36e−05
−2.36e−05
−2.36e−0
5
−2.36e−05
−2.36e−05
3.08e−05
3.08e−05
3.08e−05
3.08e−05
3.08e−05
8.52e−05
8.52e−05
8.52e−05
8.52e−05
0.00014
0.00014
0.00014
0.00014
0.000194
0.000194
0.000194
0.000248
0.000248
0.000248
0.000303
0.000303
0.000303
0.000357
0.000357
0.000412
0.000412
0.000466
0.000466
0.00
052
0.000575
−0.000
136
−0.000
12
4
−0.000124
−0.000112
−0.000112
−0.0001
−0.0001
−8.84e−05
−8.84e−05
−8.84e−05
−7.66e−05
−7.66e−05
−7.66e−05
−6.48e−05
−6.48e−05
−6.48e−05
−5.3e−05
−5.3e−05
−5. 3e− 05
−4.12e−05
−4.12e−05
−4.12e−05
−4.12e−05
−2.94e−05
−2.94e−05
−2.94e−05
−2.94e−05
−1.76e−05
−1.76e−05
−1.76e−05
−1.76e−05
−1.76e−05
−5.76e−06
−5.76e−06
−5.76e−06
−5.76e−06
−5.76e−06
60−e67.5−
6.04e−06
6.04e−06
6.04e−06
6.04e−06
6.04e−06
1.79e−05
1.79e−0
5
1.79e−05
1.79e−05
1.79e−05
2.97e−05
2.97e−05
2.97e−05
2.97e−05
4.15e−05
4.15e−05
4.15e−05
4.15e−05
5.33e−05
5.33e−05
5.33e−05
5.33e−05
6.51e−05
6.51e−05
6.51e−05
7.69e−05
7.69e−05
7.69e−05
8.87e−05
8.87e−05
0.000101
0.000101
0.000112
0.0001
12
0.000124
0.000136
−0.00052
−0.000474
−0.000429
−0.000383
−0.000383
−0.000338
−0.000338
−0.000293
−0.000293
−0.000247
−0.000247
−0.000247
−0.000202
−0.0002
02
−0.000202
−0.000157
−0.000157
−0.000157
−0.000111
−0.000111
−0
.000111
−0.000111
−6.59e−05
−6.59e−05
−6.59e−05
−6
.59
e−05
50−
e
9
5
.6
−
−2.06e−05
−2.06e−05
−2.06e−05
−2.06e−05
−2.06e−05
2.48e−05
2.48e−05
2.48e−05
2.48e−05
2.48e−05
7.02e−05
7.02e−05
7.02e−05
7.02e−05
0.000116
0.000116
0.000116
0.000116
0.000161
0.000161
0.000161
0
.000161
0.000206
0.000206
0.000206
25
2
0
0
0.
0
0.000252
0.000252
0.00
0297
0.000297
0.000342
0.000342
0.000388
0.000388
0.000433
0.000478
0.000524
−0.0005
−0.000457
−0.000413
−0.000369
−0.000369
62
30
0
0.
0−
−0.000326
−0.000282
2
8
2
00
0
.
0−
9320
0
0.
0−
−0.000239
−0.000239
−0.000195
−0.000195
−0.000195
−0.000151
−0.000151
−0.000151
−0.000108
−0.000108
−0.000108
−0.000108
−6.42e−05
−6.4
2
e−05
−6.42e−05
−6.42e−05
−2.06e−05
−2.06e−05
−2.06e−05
−2
.06e−05
−2.06e−05
2.3e−05
2.3e−05
2.3e−05
2.3e−
05
2.3e−05
6.66e−05
6.66e−05
6.6
6e−05
6.66e−05
0.00011
0.00011
1
10
0
0.0
0.00011
0.000154
0.000154
0.000154
0.000154
0.000197
0.000197
0.000197
0.000241
0.000241
0.000241
0.0
00
28
5
0.000285
0.00032
8
0.00032
8
0.000372
0.000372
0.000415
0.000459
0.000503
−0.000136
−0.00012
4
−0.000124
−0.000112
−0.000112
−0.0001
−0.0001
−8.84e−05
−8.84e−05
−8.84e−05
−7.66e−05
−7.66e−
05
−7.66e−05
−6.48e−05
−6.48e−05
−6.48e−05
−5.3e−05
−5.3e−05
−5.3e−05
−4.12e−05
−4.12e−05
−4.12e−05
−4.12e−05
−2.94e−05
−2.94e−05
−2.94e−05
−2.94e−05
−1.76e−05
−1.76e−05
−1.76e−05
−1.76e−05
−1.76e−05
−5.76e−06
−5.76e−06
−5.76e−06
−5.76e−06
−
5.76e−06
−5.76e−06
6.04e−06
6.04e−06
6.04e−06
6.04e−06
6.04e−06
1.79e−05
1.79e−05
1.79e−05
1.79e−05
1.79e−05
2.97e−05
2.97e−05
2.97e−05
2.97e−05
4.15e−05
4.15e−05
4.15e−05
4.15e−05
5.33e−05
5.33e−05
5.33e−05
5.33e−05
6.51e−05
6.51e−05
6.51e−05
7.69e−05
7.69e−05
7.69e−05
8.87e−05
50−e
78
.8
0.000101
0.000101
0.000112
0.000112
0.000124
0.000136
−0.000446
−0.000407
−0.000368
−0.000329
−
0.0
00329
−0.000291
−0.000291
−0.000252
−0.000252
−0.000213
−0.000213
−0.000213
−0.000174
−0.000174
−0.000174
−0.000135
−0.000135
−0.000135
−0.000135
−9.67e−05
−9.67e−05
−9.67e−05
−9.67e−05
−5.8e−05
−5.8e−05
−5.8e−05
−5.8e−05
−1.92e−05
−1.92e−05
−1.92e−05
−
1.92e−05
−
1.92e−0
5
1.95e−05
1.95e−05
1.95e−05
1.95e−05
1.95e−05
5.83e−05
5.83e−05
5.83e−05
5.83e−05
9.7e−05
9.7e−05
9.7e−05
9.7e−05
0.000136
0.000136
0.000136
0.000136
0.000175
0.000175
0.000175
0.0
00213
0.000213
0.000213
0.000252
0.000252
0.000252
0.000291
0.000291
0.00033
0.00033
0.000368
0.000368
0.000407
0.000446
−0.000433
−0.000395
−0.000358
−0.00032
−0.00032
−0.000282
−0.000282
−0.000245
−0.000245
−0.000207
−0.000207
−0.000207
−0.000169
−0.000169
−0.000169
−0.000132
−0.000132
−0.000132
−9.41e−05
−9.41e−05
−9.41e−05
−9.41e−05
−5.64e−05
−5.64e−05
−5.64e−05
−5.64e−05
−1.88e−05
−1.88e−05
−1.88e−05
−
1.8
8e−05
−1.88e−05
1.89e−05
1.89e−05
1.89e−05
1.89e−05
1.89e−05
5.66e−05
5.66e−05
5.66e−05
5.66e−05
5.66e−05
9.43e−05
9.43e−05
9.43e−05
9.43e−05
0.000132
0.000132
0.000132
0.000132
0.00017
0.00017
0.00017
0.000207
0.000207
0.000207
0.000245
0.000245
0.000245
0.000283
0.000283
0.00032
0.00032
0.000358
0.000358
0.000396
0.000433
We =2
We =3
We =4
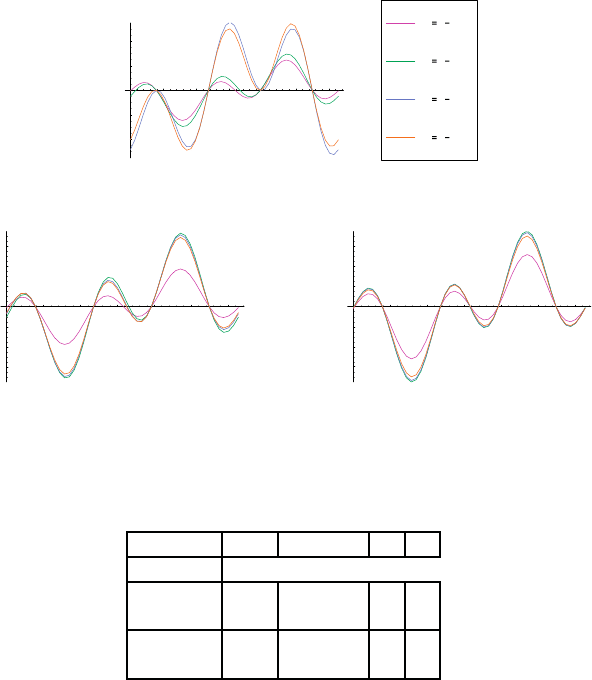
Flows of Generalized Oldroyd-B Fluids in Curved Pipes 37
Figure 6. Wall shear stress for creeping generalized Oldroyd-B
creeping flows with η=0.4and|q| =6, 6.4, 6.5, 6.8(δ=0.001).
We 2 3 4 5
δ =0.001
η =0.4 6.30 6.25 − −
L L-S S S
0.5 4.50 4.30 − −
R R(slight) S −
Table 2. Values of |q| initiating the rotation.
Parallel modifications can be observed concerning the wall shear stress. Fig-
ure 6 shows the corresponding curves for η =0.4 and for different values of the
Weissenberg number. For We = 5, the curves corresponding to different viscosity
exponents q are identical, suggesting that the wall shear stress is stable in this case.
For We = 4, the global behavior of the curves is similar but with variations in the
amplitudes. When the viscoelastic parameter is set to 3, small modifications could
be observed in comparison to the previous case. In particular, for q greater than
the critical value q
var
initiating the rotation, we lose the symmetry with respect
to the horizontal axis, and the wall shear stress takes negative values at θ =0and
2π. This fact is more pronounced for We = 2, with lost of symmetry with respect
to the axis θ = π. The same differences are obtained when η =0.5. The sign of the
wall shear stress for values of q greater than q
var
is positive. This strongly suggests
1 2 3 4 5 6
q
q
q
−0.004
−0.002
0.002
0.004
−0.002
−0.004
−0.006
0.002
0.004
0.006
q 6.8
q 6.5
q 6.4
q 6.
We =2
We
=3
We
=4
1 2 3 4 5 6 1 2 3 4 5 6
−0.006
−0.004
−0.002
0.002
0.004
0.006
t
w
t
w
t
w
