Escher J., Guidotti P., Hieber M. et al. (editors) Parabolic Problems: The Herbert Amann Festschrift

Подождите немного. Документ загружается.

18 H. Abels

holds too. Therefore c is a solution of (3.24)–(3.27) due to Theorem 3.10. Using

(4.6) and the bounds on (v

,μ

), one obtains that ∂

∈ L

uloc

([0, ∞); V

(Ω)



)

is uniformly bounded. Hence v

→

j→∞

v in L

(0,T; H

(Ω)) for all s<1.

Moreover, since ∂

∈ L

(0, ∞; H

−1

(0)

(Ω)) is uniformly bounded due to (3.21),

→

k→∞

c in L

(0,T; W

(Ω)) for all 0 <T<∞ because of the Lemma of

Aubin-Lions. Hence we can pass to the limit in (4.1) for (v

,μ

)andthe

initial values (v

0,k

) and conclude that (v, c,μ) solve (4.1) too. Moreover,

since v



j→∞

v ∈ W

(0,T; V

(Ω)



)andc



j→∞

c ∈ H

(0,T; H

−1

(0)

(Ω)) for

all 0 <T <∞,weobtain(v

0,k

)=(v

t=0

→

j→∞

)=(v, c)|

t=0

weakly in V

(Ω)



×H

−1

(0)

(Ω). Because of Lemma 2.1. (v, c) ∈ BC

(0, ∞; L

×H

Furthermore, because of Lemma 2.2, the energy inequality (4.4) for (v

,μ

)

is equivalent to



∞

(t),v

(t),μ

(t))ϕ(t) dt

≤ E

0,k

)ϕ(0) +



∞

(t),v

(t))ϕ



(t) dt

for all ϕ ∈ W

(0, ∞), ϕ ≥ 0, where E

(c, v) denotes the total energy E(c, v)with

respect to Φ

(c)=θ

and

(t),v

(t),μ

(t)) =



2ν(c

(t))|Dv

(t)|

dx + ∇μ

(t)

Since

D(c(t),v(t),μ(t))



2ν(c(t))|Dv(t)|

dx + ∇μ(t)

≤ lim inf

k→∞

(t),v

(t),μ

(t))

by the weak lower semi-continuity of the L

-norm and

(t),v

(t)) →

j→∞

E(c(t),v(t)) for almost all 0 <t<∞,

we obtain

E(c

)ϕ(0) +



∞

E(c(t),v(t))ϕ



(t) dt ≥



∞

D(c(t),v(t),μ(t))ϕ(t) dt

for all ϕ ∈ W

(0, ∞), ϕ ≥ 0, where E(c, v)=E

free

(c)+E

kin

(v). Using Lemma 2.2

again, we have proved (4.4).

Finally, the regularity statements for c, μ follow from Theorem 3.10 since for

given v (4.8)–(4.9) together with (1.6)–(1.7) has a unique solution (c, μ). 

Since the Cahn-Hilliard equation (4.8)–(4.9) has the same structure as in

the case θ>0 and the same regularity results, cf. Lemma 3.11 are available, it

is easy to obtain the same uniqueness and regularity results as for θ>0, cf. [3,

Proposition 1, Theorem 2]. These are as follows:

Double Obstacle Limit 19

Proposition 4.4. (Uniqueness)

Let 0 <T ≤∞, q =3if d =3and let q>2 if d =2. Moreover, assume

that v

∈ W

q,0

(Ω) ∩ L

(Ω) and let c

∈ C

0,1

(Ω) with c

(x) ∈ [a, b] for all x ∈

Ω.Ifthereisaweaksolution(v, c,μ) of (4.6)–(4.9), (1.5)–(1.7) on (0,T) with

v ∈ L

∞

(0,T; W

(Ω)) and ∇c ∈ L

∞

), then any weak solution (v



,μ



) of

(4.6)–(4.9), (1.5)–(1.7) on (0,T) with the same initial values and ∇c



∈ L

∞

)

coincides with (v, c, μ).

Proof. The proof is literally the same as the proof of [3, Lemma 7]. One just has

to replace the ﬁrst equality in the proof by

∂

˜c + a

−a

= −θ

Δ˜c −w ·∇c

−v

·∇˜c,

where a

(t) ∈A

(t)),j =1, 2, for almost all t ∈ (0,T)andw = v

−v

and has

to use (3.31). 

Theorem 4.5. (Regularity of Weak Solutions)

Assume that c

∈D(∂



) ∩ H

(Ω),where



is as in Lemma 3.5.

1. Let d =2and let v

∈ V

1+s

(Ω) with s ∈ (0, 1], s =

. Then every weak

solution (v, c) of (4.6)–(4.9), (1.5)–(1.7) on (0, ∞) satisﬁes

v ∈ L

(0, ∞; V

2+s



(Ω)) ∩ H

(0, ∞; V



(Ω)) ∩ BUC([0, ∞); H

1+s−ε

(Ω))

for all s



∈ [0,

)∩[0,s] and all ε>0 as well as ∇

c, φ(c) ∈ L

∞

(0, ∞; L

(Ω))

for every 1 <r<∞. In particular, the weak solution is unique.

2. Let d =2, 3. Then for every weak solution (v, c,μ) of (4.6)–(4.9), (1.5)–(1.7)

on (0, ∞) there is some T>0 such that

v ∈ L

(T,∞; V

2+s

(Ω)) ∩ H

(T,∞; V

(Ω)) ∩ BUC([T,∞); H

2−ε

(Ω))

for all s ∈ [0,

) and all ε>0 as well as ∇

c, φ(c) ∈ L

∞

(T,∞; L

(Ω)) with

r =6if d =3and 1 <r<∞ arbitrary if d =2.

3. If d =3and v

∈ V

s+1

(Ω), s ∈ (

, 1], then there is some T

> 0 such that

every weak solution (v, c) of (4.6)–(4.9), (1.5)–(1.7) on (0,T

) satisﬁes

v ∈ L

(0,T

; V

2+s



(Ω)) ∩ H

(0,T

; V



(Ω)) ∩ BUC([0,T

]; H

1+s−ε

(Ω))

for all s



∈ [0,

) and all ε>0 as well as ∇

c, φ(c) ∈ L

∞

(0,T

; L

(Ω)).In

particular, the weak solution is unique on (0,T

Proof. The proof is the same as the one of [3, Theorem 2]. Its proof only relies

on the available regularity results for c solving (1.3)–(1.4), which are the same

for (4.8)–(4.9), as well as the uniqueness statement of [3, Proposition 1], which is

replaced by Proposition 4.4. Therefore the proof directly carries over. 

20 H. Abels

References

[1] H. Abels. Diﬀuse interface models for two-phase ﬂows of viscous incompressible

ﬂuids. Lecture Notes, Max Planck Institute for Mathematics in the Sciences, No.

36/2007, 2007.

[2] H. Abels. Existence of weak solutions for a diﬀuse interface model for viscous, in-

compressible ﬂuids with general densities. Comm. Math. Phys., 289(1):45–73, 2009.

[3] H. Abels. On a diﬀuse interface model for two-phase ﬂows of viscous, incompressible

ﬂuids with matched densities. Arch. Rat. Mech. Anal., 194(2):463–506, 2009.

[4] H. Abels and M. Wilke. Convergence to equilibrium for the Cahn-Hilliard equation

with a logarithmic free energy. Nonlinear Anal., 67(11):3176–3193, 2007.

[5] D.M. Anderson, G.B. McFadden, and A.A. Wheeler. Diﬀuse-interface methods in

ﬂuid mechanics. In Annual review of ﬂuid mechanics, Vol. 30, volume 30 of Annu.

Rev. Fluid Mech., pages 139–165. Annual Reviews, Palo Alto, CA, 1998.

[6] J.F. Blowey and C.M. Elliott. The Cahn-Hilliard gradient theory for phase separation

with nonsmooth free energy. I. Mathematical analysis. European J. Appl. Math.,

2(3):233–280, 1991.

[7] J.W. Cahn and J.E. Hilliard. Free energy of a nonuniform system. I. Interfacial

energy. J. Chem. Phys., 28, No. 2:258–267, 1958.

[8] C.M. Elliott and S. Luckhaus. A generalized equation for phase separation of a multi-

component mixture with interfacial free energy. Preprint SFB 256 Bonn No. 195,

1991.

[9] M.E. Gurtin, D. Polignone, and J. Vi˜nals. Two-phase binary ﬂuids and immiscible

ﬂuids described by an order parameter. Math. Models Methods Appl. Sci., 6(6):815–

831, 1996.

[10] P.C. Hohenberg and B.I. Halperin. Theory of dynamic critical phenomena. Rev. Mod.

Phys., 49:435–479, 1977.

[11] N. Kenmochi, M. Niezg´odka, and I. Pawlow. Subdiﬀerential operator approach to

the Cahn-Hilliard equation with constraint. J. Diﬀerential Equations, 117(2):320–

356, 1995.

Helmut Abels

NWF I – Mathematik

Universit¨at Regensburg

D-93040 Regensburg, Germany

e-mail: Helmut.Abels@mathematik.uni-regensburg.de

Progress in Nonlinear Diﬀerential Equations

and Their Applications, Vol. 80, 21–43

 2011 Springer Basel AG

Flows of Generalized Oldroyd-B Fluids

in Curved Pipes

Mar´ılia Pires and Ad´elia Sequeira

Dedicated to Prof. Herbert Amann on the occasion of his 70th birthday

Abstract. The aim of this work is to present a numerical study of generalized

Oldroyd-B ﬂows with shear-thinning viscosity in a curved pipe of circular cross

section and arbitrary curvature ratio. Flows are driven by a given pressure

gradient and behavior of the solutions is discussed with respect to diﬀerent

rheologic and geometric ﬂow parameters.

Mathematics Subject Classiﬁcation (2000). Primary 76A05; Secondary 74S05.

Keywords. Curved pipe, ﬁnite elements, ﬂuids non-Newtonian.

1. Introduction

Complex rheological phenomena such as shear dependent viscosity, stress relaxa-

tion, nonlinear creeping and normal stress diﬀerences can be found in many ﬂuids

like inks, polymer melts, suspensions, liquids crystals or biological ﬂuids. These

properties, which cannot be captured by the classical Navier-Stokes equations,

lead to non-constant viscosity or to viscoelastic behavior described by nonlinear

relations between the Cauchy stress and the strain tensor. Fluids of this type are

called non-Newtonian [20].

There are many ways to generalize the Newtonian law of viscosity. The sim-

plest case is the generalized Newtonian model where the extra-stress incorporates

a shear-rate dependent viscosity. However, the generalized Newtonian ﬂuids can-

not account for the eﬀects described above, namely the viscoelasticity, but they

are often used to model simple ﬂows and to study the ﬂow rate in a pipe, as a

function of the pressure drop. Suitable viscoelastic constitutive equations are then

This work has been partially supported by CIMA/Univ.

Evora, by CEMAT/IST through FCT’s

Funding Program and by the Project PTDC/MAT/68166/2006.

22 M. Pires and A. Sequeira

required. In general terms, non-Newtonian viscoelastic ﬂuids exhibit both viscous

and elastic properties and can be classiﬁed as ﬂuids of diﬀerential type, rate type

and integral type. We refer to the monographs [5], [15], [26], [29] for relevant issues

related to non-Newtonian ﬂuids behavior and modeling. Models of rate type such

as Oldroyd-B ﬂuids can predict stress relaxation and are used to describe ﬂows in

polymer processing. However they cannot capture the complex rheological behavi-

or of many real ﬂuids, such as blood in which the non-Newtonian viscosity eﬀects

are of major importance.

Over the past twenty years, a signiﬁcant progress has been made in the math-

ematical analysis of the equations of motion of non-Newtonian viscoelastic ﬂuids.

Usually, the constitutive equations lead to highly nonlinear systems of partial dif-

ferential equations of a combined parabolic-hyperbolic type (or elliptic-hyperbolic,

for steady ﬂows) closed with appropriate initial and/or boundary conditions. The

study of the behavior of their solutions in diﬀerent geometries requires the use of

speciﬁc techniques of nonlinear analysis, such as ﬁxed-point arguments associated

to auxiliary linear sub-problems. We refer to [21] and [22] for an introduction to

existence results for viscoelastic ﬂows.

The hyperbolic nature of the constitutive equations is responsible for many of

the diﬃculties associated with the numerical simulation of viscoelastic ﬂows. Some

factors including singularities in the geometry, boundary layers in the ﬂow and the

dominance of the nonlinear terms in the equations, result in numerical instabilities

for high values of Weissenberg number (non-dimensional viscoelastic parameter).

A variety of alternative numerical methods have been developed to overcome this

diﬃculty, but many challenges still remain, in particular for viscoelastic ﬂows in

complex geometries (see, e.g., [16], [17] and the references cited therein).

It is known since the pioneering experimental works of Williams et al. [30],

Grindley and Gibson [14], and Eustice ([11], [12]) that ﬂows in curved pipes are

very challenging and considerably more complex than ﬂows in straight pipes. Due

to ﬂuid inertia, a secondary motion appears in addition to the primary axial ﬂow.

It is induced by an imbalance between the cross-stream pressure gradient and the

centrifugal force and consists of a pair of counter-rotating vortices, which appear

even for the most mildly curved pipe. This results in asymmetrical wall stresses

with higher shear and low pressure regions ([4], [18], [27]).

Steady fully developed viscous ﬂows in curved pipes of circular, elliptical

and annular cross-section of both Newtonian and non-Newtonian ﬂuids, have been

studied by several authors ([1]–[4],[13], [19], [23], [24], [27]) following the funda-

mental work of Dean ([9], [10]) for circular cross-section pipes. Using regular per-

turbation methods around the curvature ratio, Dean obtained analytical solutions

in the case of Newtonian ﬂuids. These results have been extended for a larger range

of curvature ratio and Reynolds number, showing the existence of additional pairs

of vortices and multiple solutions ([8], [31]).

The great interest in the study of curved pipe ﬂows is due to its wide range

of applications in engineering (e.g., hydraulic pipe systems related to corrosion fai-

lure) and in bioﬂuid dynamics, such as blood ﬂow in vascular regions of low shear

Flows of Generalized Oldroyd-B Fluids in Curved Pipes 23

(in healthy or disease states), where the shear-thinning viscosity and viscoelastic

behavior should not be neglected ([6], [7], [25], [28]).

This paper is concerned with the numerical study of the behavior of fully

developed ﬂows of shear-thinning generalized Oldroyd-B ﬂuids in curved pipes

with circular cross-section and arbitrary curvature ratio, for a prescribed pressure

gradient. Numerical results show interesting viscosity and viscoelastic eﬀects: for

suﬃciently small curvature ratio and certain range of viscosity parameters, the

ﬂow ﬁeld is quite complex, showing counter-clockwise rotation of the secondary

streamlines and loss of symmetry of the ﬂow ﬁeld. Stronger inertial eﬀects result

in a deformation of the pair of vortices and rotation of the ﬂow in an opposite

direction. These eﬀects become weaker for higher values of the Weissenberg num-

ber. We remark that for generalized Oldroyd-B ﬂuids the second normal stress

diﬀerence is zero, as in the particular case of Oldroyd-B, and consequently the

second normal stress diﬀerence has no impact on the secondary ﬂows ([13]).

The paper is organized as follows. After introducing the governing equations

and formulating the problem in polar toroidal coordinates (Section 2 and 3), we

consider in Section 4 the numerical approximation of the steady Oldroyd-B model

with non constant shear-dependent viscosity, in the above-described geometry.

The original problem is decomposed into a Navier-Stokes system and a tensorial

transport equation. Using the ﬁnite element method and a ﬁxed point algorithm to

couple the auxiliary problems, numerical results are obtained for a certain range of

non-dimensional ﬂow parameters (viscosity exponent, Reynolds and Weissenberg

numbers) associated to the model. A continuation method is used to ﬁnd the

initial guess of the iterations and to increase the absolute value of the viscosity

parameter.

Existence and uniqueness of approximated solutions, as well as a priori error

estimates to the coupled full problem have already been proved, under a natural

restriction on the curvature ratio (see [2]). In a future work, the systematic nume-

rical study presented in this paper will be complemented by a theoretical analysis

to justify the complex qualitative behavior of the combined eﬀects of viscosity,

inertial and viscoelastic parameters.

2. Governing equations

This paper is concerned with ﬂows of incompressible viscoelastic Oldroyd-B ﬂuids

with shear dependent viscosity in a curved pipe Ω ⊂ R

with boundary ∂Ω. For

these ﬂuids, the extra-stress tensor is related to the kinematic variables through

S + λ

∇



ν + ν

(1 + |Du|

)



Du +2λ

∇

Du, (2.1)

where u is the velocity ﬁeld, Du =

(∇u + ∇u



∂u

∂x

∂u

∂x



i,j=1,2

denotes

the symmetric part of the velocity gradient, |Du| is the shear rate, q is a real

number, ν and ν

are nonnegative real numbers satisfying ν + ν

> 0, λ

> 0and

24 M. Pires and A. Sequeira

> 0 are viscoelastic constants. The symbol

∇

denotes the objective derivative

of Oldroyd type deﬁned by

∇



∂

∂t

+ u ·∇



S − S ∇u − (∇u)

The Cauchy stress tensor is given by T = −pI+S,wherep represents the pressure.

The equations of conservation of momentum and mass hold in the domain Ω,



∂u

∂t

+ u ·∇u



+ ∇p = ∇·S + f, ∇·u =0, (2.2)

where ρ>0 is the (constant) density of the ﬂuid and f is an external force.

We ﬁrst decompose the extra-stress tensor S into the sum of its Newtonian part

Du and its viscoelastic part τ. Introducing the quantities

x =

x

,t=



,u=

u

,p=

pL

(ν + ν

τ =



τ L

(ν + ν

, f =



f L

(ν + ν

where the symbol is attached to dimensional parameters (L represents a reference

length and U a characteristic velocity of the ﬂow). We also set

ε =1−

(ν + ν

)

,η=

ν + ν

and deﬁning the Reynolds number and the Weissenberg number as

Re =

ρUL

ν + ν

, We =

we can write (2.1)–(2.2) in dimensionless form

⎧

⎪

⎨

⎪

⎩

−(1 − ε)Δu + Re



∂u

∂t

+ u ·∇u



+ ∇p = f + ∇·τ ,

∇·u =0,

τ + We



∂τ

∂t

+ u ·∇τ −g(∇u, τ )





ε + ησ



|Du|



Du,

(2.3)

with

g(∇u, τ )=τ ∇u +(∇u)

τ , σ(x)=(1+x)

− 1.

This system is supplemented with a Dirichlet homogeneous boundary condition

u = 0 on ∂Ω.

In a simple shear this model predicts shear dependent viscosity (shear-thinning

for q<0 and shear-thickening for q>0) and normal stress coeﬃcients Ψ

and Ψ

given by (see, e.g., [5], [17], [29])

(|Du|)=2



ε + ησ



|Du|



|Du|

(|Du|)=0.

Note that the model reduces to Oldroyd-B when q =0.

Flows of Generalized Oldroyd-B Fluids in Curved Pipes 25

3. Equivalent formulation in polar toroidal coordinates

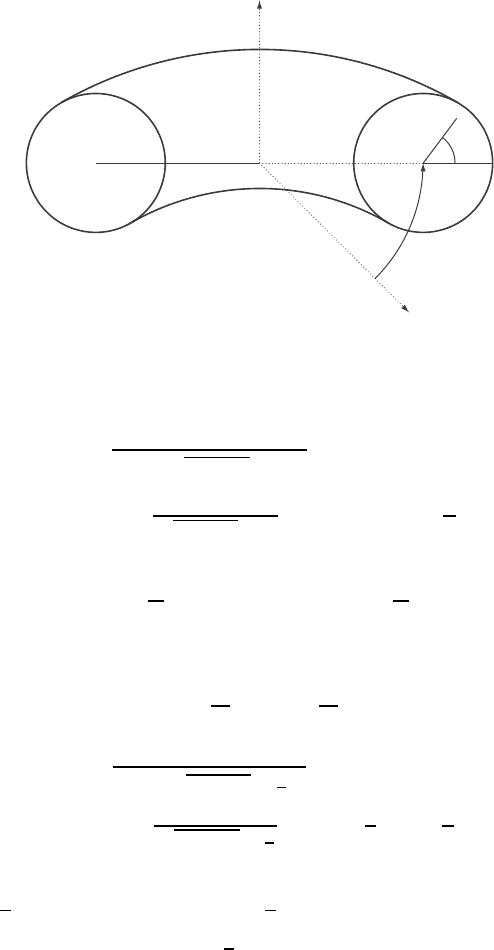
We consider fully developed ﬂows in a curved pipe with circular cross-section (see

Figure 1).



Figure 1. Polar toroidal coordinates.

For this pipe geometry, it is more convenient to use the polar toroidal coordinate

system, in the variables (r, θ, s), deﬁned with respect to the rectangular cartesian

coordinates (x, y, z) through the relations

r =



z





x

+ y

− R



θ =arctan

z



x

+ y

− R

, s = R arctan

y

x

and the inverse relations

x =(R + r cos θ)cos

s

, y =(R + r cos θ)sin

s

, z = r sin θ,

with 0 <r

<R,0 θ<2π and 0  s<πR,whereR>r  0 is the constant

centerline radius. Introducing

s =

s

,δ=

we see that the corresponding non-dimensional coordinate systems are given by

r =







+ y

−



θ =arctan



+ y

−

,s=

arctan

and the inverse relations

x =



+ r cos θ



cos(sδ),y=



+ r cos θ



sin(sδ),z= r sin θ,

with δ<1, 0  θ<2π and 0  s<

26 M. Pires and A. Sequeira

Let us now formulate system (2.3) in this new coordinate system. For conve-

nience, we keep the notation as for the cartesian system (e.g., u ≡ u ·e

, v ≡ v ·e

and w ≡ w · e

). To simplify the notation we set

≡ β

(r, θ)=rδ sin θ, β

≡ β

(r, θ)=rδ cos θ,

β ≡ β(r, θ)=1+rδ cos θ.

By using standard arguments, we rewrite the problem (2.3) in the toroidal coor-

dinates (r, θ, s), and we see that the problem reads as

Find (u ≡ (u, v, w),p,τ )solutionof

⎧

⎪

⎨

⎪

⎩

−(∇·(2(1 − ε)Du + τ −Re u ⊗ u))

+ Re

∂u

∂t

∂p

∂r

=0,

−(∇·(2(1 − ε)Du + τ −Re u ⊗u))

+ Re

∂v

∂t

∂p

∂θ

=0,

−(∇·(2(1 − ε)Du + τ −Re u ⊗u))

+ Re

∂w

∂t

∂p

∂s

=0,

∂

∂r

(rβu)+

∂

∂θ

(βv)+

∂

∂s

(rw)=0,

τ + We



∂

∂r

∂

∂θ

∂

∂s



τ + We

∂τ

∂t

rβ

F(u, τ )+2



ε − η +

(rβ)



(rβ)

+ |rβDu|



Du,

∂Ω

(3.1)

where for third-order tensor σ, ∇·σ is given by

(∇·σ)

rβ



∂

∂r

(rβσ

∂

∂θ

(βσ

rθ

∂

∂s

(rσ

) −β

−βσ

θθ



(∇·σ)

rβ



∂

∂r

(rβσ

θr

∂

∂θ

(βσ

θθ

∂

∂s

(rσ

θs

)+β

+ βσ

rθ



(∇·σ)

rβ



∂

∂r

(rβσ

∂

∂θ

(βσ

sθ

∂

∂s

(rσ

) − β

θs

+ β



and the velocity gradient and the symmetric tensor F are given by

∇u =

⎛

⎜

⎝

∂u

∂r

∂v

∂r

∂w

∂r

∂u

∂θ

−

∂v

∂θ

∂w

∂θ

∂u

∂s

−

rβ

∂v

∂s

rβ

∂w

∂s

rβ

u −

rβ

⎞

⎟

⎠

(u, τ )=2



rβ

∂u

∂r

+ β

∂u

∂θ

rθ

+ r

∂u

∂s



rθ

(u, τ )=β



∂v

∂r

−v



+ β



∂v

∂θ

+ u + r

∂u

∂r



rθ

+ r

∂v

∂s

+ β

∂u

∂θ

θθ

+ r

∂u

∂s

θs

(u, τ )=



rβ

∂w

∂r

− β





∂w

∂θ

+ β



rθ

+ β

∂u

∂θ

θs



∂w

∂s

+ β

u − β

v + rβ

∂u

∂r



+ r

∂u

∂s

θθ

(u, τ )=2



∂v

∂r

− v



rθ

+ β



∂v

∂θ

+ u



θθ

+ r

∂v

∂s

θs



Flows of Generalized Oldroyd-B Fluids in Curved Pipes 27

θs

(u, τ )=



rβ

∂w

∂r

− β



rθ



∂w

∂θ

+ β



θθ

+ β



∂v

∂r

−v





∂w

∂s

+ β

u − β

v + β

∂v

∂θ

+ βu



θs

+ r

∂v

∂s

(u, τ )=2



rβ

∂w

∂r

− β





∂w

∂θ

+ β



θs





∂w

∂s

+ β

u − β



Considering fully developed ﬂows, the velocity, the pressure and the stress tensor

τ are independent of the variable s. Consequently, they satisfy respectively,

∂u

∂s

∂v

∂s

∂w

∂s

≡ 0,

∂p

∂s

= −p

∗

and

∂



∂s

≡ 0. (3.2)

Using (3.2), problem (3.1) deﬁned in the set

Σ=



(r, θ) ∈ R

| 0 <r<1, 0 <θ≤ 2π



(3.3)

reads as follows

Find (u ≡ (u, v, w),p,



τ )solutionof

P =

⎧

⎪

⎨

⎪

⎩

−A

r,γ



(2(1 − ε)Du −Re u ⊗ u)+





+ Re

∂u

∂t

+ ψ

γ+1

∂p

∂r

=0,

−A

θ,γ



(2 (1 − ε) Du −Re u ⊗ u)+





+ Re

∂v

∂t

+ βψ

∂p

∂θ

=0,

−A

s,γ



(2 (1 − ε) Du −Re u ⊗ u)+





+ Re

∂w

∂t

= p

∗

rψ

∂

∂r

(rβu)+

∂

∂θ

(βv)=0,

rβ



τ + We



∂

∂t

+ rβu

∂

∂r

+ βv

∂

∂θ





τ = G(u,



τ )

∂Σ

(3.4)

where for a tensor σ,

ξ,γ

(σ)=rβ(∇·σ)

−γ



(β + β

)σ

ξr

− β

ξθ



, for any ξ = r, θ, s

and

G(u,



τ )=We



F(u,



τ )+γ ((β + β

) u − β





+2(ε − η) ψ

+2ηψ

γ−2q+1



(rβ)

+ |rβDu|



Du,

(3.5)

where γ =2max(q, 0) + 1, ψ

=(rβ)

and



τ ≡ ψ

τ .