Escher J., Guidotti P., Hieber M. et al. (editors) Parabolic Problems: The Herbert Amann Festschrift
Подождите немного. Документ загружается.


638 G. Seregin
4. Spatial decay for ancient solutions
We know that
u
(k)
(·, −1)
3
≤ M
and thus by (3.3)
u(·, −1)
3
≤ M. (4.1)
Now, let us consider the following Cauchy problem
∂
t
w + w ·∇w − Δ w = −∇r
div w =0
in
Q = R
3
×] −1, 1[, (4.2)
w(·, −1) = u(·, −1). (4.3)
We would like to construct a solution to problem (4.2), (4.3) satisfying the local
energy inequality. To this end, let us recall notation and some facts from [7].
L
m,unif
= {u ∈ L
m,loc
: u
L
m,unif
=sup
x
0
∈R
3
B(x
0
,1)
|u(x)|
m
dx
1/m
< +∞},
E
m
= {u ∈ L
m,unif
:
B(x
0
,1)
|u(x)|
m
dx → 0as|x
0
|→+∞},
◦
E
m
= {u ∈ E
m
:divu =0 in R
3
}.
Apparently,
u(·, −1) ∈
◦
E
2
. (4.4)
Definition 4.1. A pair of functions w and r defined in the space-time cylinder
Q
is called a local energy weak Leray-Hopf solution or simply local energy solution
to the Cauchy problem (4.2), (4.3) if the following conditions are satisfied:
w ∈ L
∞
(−1, 1; L
2,unif
), sup
x
0
∈R
3
1
−1
B(x
0
,1)
|∇w|
2
dz < +∞,
r ∈ L
3
2
(−1, 1; L
3
2
,loc
(R
3
)); (4.5)
w and r meet (4.2) in the sense of distributions; (4.6)
the function t →
R
3
w(x, t) · w(x) dxis continuous on [−1, 1] (4.7)
for any compactly supported function w ∈ L
2
(R
3
); for any compact K,
w(·,t) − u(·, −1)
L
2
(K)
→ 0 as t →−1+0; (4.8)
R
3
ϕ|w(x, t)|
2
dx +2
t
−1
R
3
ϕ|∇w|
2
dxdt
≤
t
−1
R
3
|w|
2
(∂
t
ϕ +Δϕ)+w ·∇ϕ(|w|
2
+2r)
dxdt (4.9)
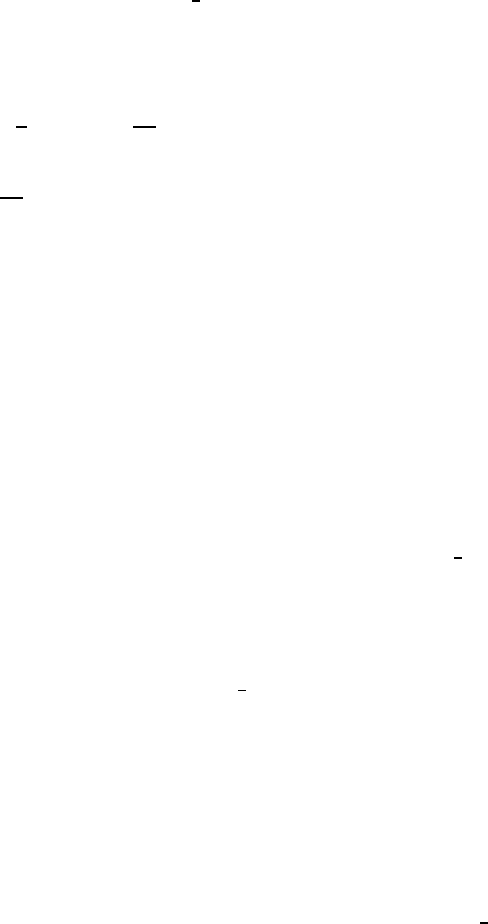
Blowups for Navier-Stokes Equations 639
for a.a. t ∈] −1, 1[ and for all nonnegative functions ϕ ∈ C
∞
0
(R
3
×] −1, 2[); for any
x
0
∈ R
3
, there exists a function c
x
0
∈ L
3
2
(−1, 1) such that
r
x
0
(x, t) ≡ r(x, t) − c
x
0
(t)=r
1
x
0
(x, t)+r
2
x
0
(x, t), (4.10)
for (x, t) ∈ B(x
0
, 3/2)×] − 1, 1[, where
r
1
x
0
(x, t)=−
1
3
|w(x, t)|
2
+
1
4π
B(x
0
,2)
K(x − y):w(y, t) ⊗ w(y, t) dy,
r
2
x
0
(x, t)=
1
4π
R
3
\B(x
0
,2)
(K(x − y) − K(x
0
− y)) : w(y, t) ⊗ w(y, t) dy
and K(x)=∇
2
(1/|x|).
We have, see [4] and also [7].
Proposition 4.1. Under assumption (4.4), there exists at least one local energy
solution to problem (4.2), (4.3).
To describe spatial decay of local energy solution, we need additional notation
α
w
(t)=w(·,t)
2
L
2,unif
,β
w
(t)= sup
x
0
∈R
3
t
−1
B(x
0
,1)
|∇w|
2
dxdt
,
γ
w
(t)= sup
x
0
∈R
3
t
−1
B(x
0
,1)
|w|
3
dxdt
,δ
r
(t)= sup
x
0
∈R
3
t
−1
B(x
0
,3/2)
|r
x
0
|
3
2
dxdt
.
One of the most important properties of local energy solutions is a kind of uniform
local boundedness of the energy, i.e.,
sup
−1≤t≤1
α
w
(t)+β
w
(1) + γ
2
3
w
(1) ≤ A<+∞. (4.11)
Next, fix a smooth cut-off function χ so that χ(x)=0ifx ∈ B, χ(x)=1if
x/∈ B(2), and then let χ
R
(x)=χ(x/R). Hence, one can define
α
R
w
(t)=χ
R
w(·,t)
2
L
2,unif
,β
R
w
(t)= sup
x
0
∈R
3
t
−1
B(x
0
,1)
|χ
R
∇w|
2
dxdt
,
γ
R
w
(t)= sup
x
0
∈R
3
t
−1
B(x
0
,1)
|χ
R
w|
3
dxdt
,δ
R
r
(t)= sup
x
0
∈R
3
t
−1
B(x
0
,3/2)
|χ
R
r
x
0
|
3
2
dxdt
.
As it was shown in [7], the following decay estimate is true.
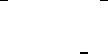
640 G. Seregin
Lemma 4.2. Assume that the pair w and r is a local energy solution to (4.2), (4.3).
Then
sup
−1≤t≤
α
R
w
(t)+β
R
w
(1) + (γ
R
w
)
2
3
(1) + (δ
R
r
)
4
3
(1)
≤ C(A)
1
χ
R
u(·, −1)
2
L
2,unif
+1/R
2
3
2
.
(4.12)
Since any local energy solution to the Cauchy problem (4.2), (4.3) is also
a suitable weak solution to the Navier-Stokes equations, one can apply the local
regularity theory to them and deduce from Lemma 4.2 that there exists a positive
number R
∗
such that
|w(z)| + |∇w(z)|≤A
1
(4.13)
for all z =(x, t) ∈
R
3
\ B(R
∗
)
× [−(5/6)
2
, 1].
If we would show that
u ≡ w (4.14)
on R
3
× [0, 1[, this would make it possible to apply backward uniqueness results
(actually, to vorticity equations) and conclude that u =0onR
3
× [−(3/4)
2
, 0]
which contradicts (3.12). So, the rest of the paper is devoted to a proof of (4.14).
Our first observation in this direction is that u is C
∞
-function in Q
−
.This
follows from (3.5). Detail discussion on differentiability properties of bounded an-
cient solutions can be found in [8] and [10]. In addition, the pressure p(·,t)isa
BMO-solution to the pressure equations
−Δp(·,t)=divdivu(·,t) ⊗ u(·,t)
in R
3
.
Using a suitable cut-off function in time and differentiability properties of w
and u, we can get the following three relations:
R
3
ϕ(x)w(x, τ) · u(·,t)dx
"
"
"
τ=t
τ=−1
=
t
−1
R
3
(w ⊗ w −∇w):(ϕ∇u + u ⊗∇ϕ)dxdτ
+
t
−1
R
3
ru ·∇ϕdxdτ +
t
−1
R
3
φw · ∂
t
udxdτ;
R
3
ϕ(x)|w(x, τ )|
2
dx
"
"
"
τ =t
τ =−1
+2
t
−1
R
3
ϕ|∇w|
2
dxdτ
≤
t
−1
R
3
|w|
2
Δ ϕ + w ·∇ϕ(|w|
2
+2r)
dxdτ;
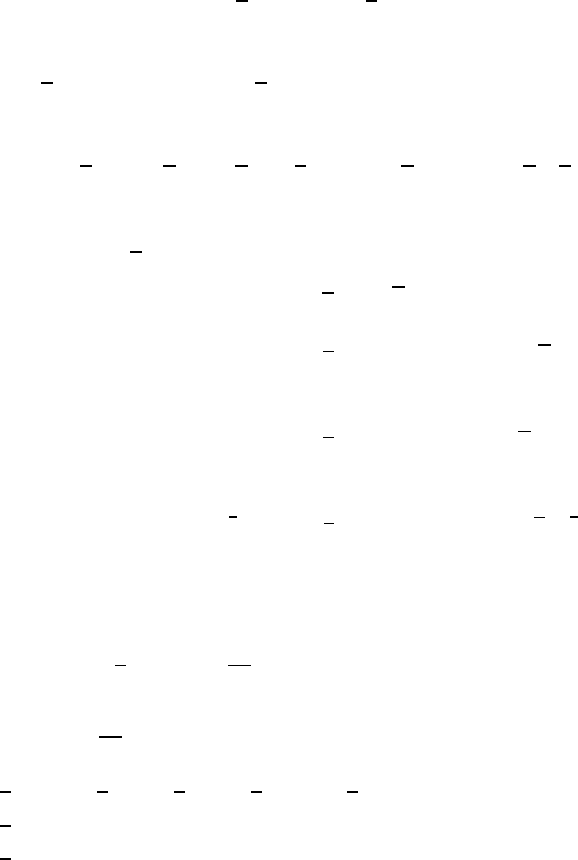
Blowups for Navier-Stokes Equations 641
R
3
ϕ(x)|u(x, τ)|
2
dx
"
"
"
τ =t
τ =−1
+2
t
−1
R
3
ϕ|∇u|
2
dxdτ
=
t
−1
R
3
|u|
2
Δ ϕ + u ·∇ϕ(|u|
2
+2p)
dxdτ
for any 0 ≤ ϕ ∈ C
∞
0
(R
3
). Letting u = w −u and p = r −p, we can find from them
the main inequality
R
3
ϕ(x)|u(x, t)|
2
dx +2
t
−1
R
3
ϕ|∇u|
2
dxdτ (4.15)
≤
t
−1
R
3
|u|
2
Δ ϕ + u ·∇ϕ(|u|
2
+2p)+u ·∇ϕ|u|
2
− 2ϕ∇u : u ⊗ u
dxdτ
for a.a. t in ] −1, 0[.
Next, for u and u, we may introduce the analogous quantities
α
u
(t)=u(·,t)
2
L
2,unif
,α
u
(t)=u(·,t)
2
L
2,unif
β
u
(t)= sup
x
0
∈R
3
t
−1
B(x
0
,1)
|∇u|
2
dxdt
,β
u
(t)= sup
x
0
∈R
3
t
−1
B(x
0
,1)
|∇u|
2
dxdt
,
γ
u
(t)= sup
x
0
∈R
3
t
−1
B(x
0
,1)
|u|
3
dxdt
,γ
u
(t)= sup
x
0
∈R
3
t
−1
B(x
0
,1)
|u|
3
dxdt
,
δ
p
(t)= sup
x
0
∈R
3
t
−1
B(x
0
,3/2)
|p
x
0
|
3
2
dxdt
,δ
p
(t)= sup
x
0
∈R
3
t
−1
B(x
0
,3/2)
|p
x
0
|
3
2
dxdt
where
p
x
0
(x, t) ≡ p(x, t) − p
0
x
0
(t)=p
1
x
0
(x, t)+p
2
x
0
(x, t),
p
1
x
0
(x, t)=−
1
3
|u(x, t)|
2
+
1
4π
B(x
0
,2)
K(x −y):u(y, t) ⊗ u(y, t) dy,
p
2
x
0
(x, t)=
1
4π
R
3
\B(x
0
,2)
(K(x − y) − K(x
0
− y)) : u(y, t) ⊗ u(y,t) dy,
p
x
0
(x, t) ≡ p(x, t) − p
0
x
0
(t)=p
1
x
0
(x, t)+p
2
x
0
(x, t),
p
1
x
0
(x, t)=r
1
x
0
(x, t) −p
1
x
0
(x, t),
p
2
x
0
(x, t)=r
2
x
0
(x, t) −p
2
x
0
(x, t).
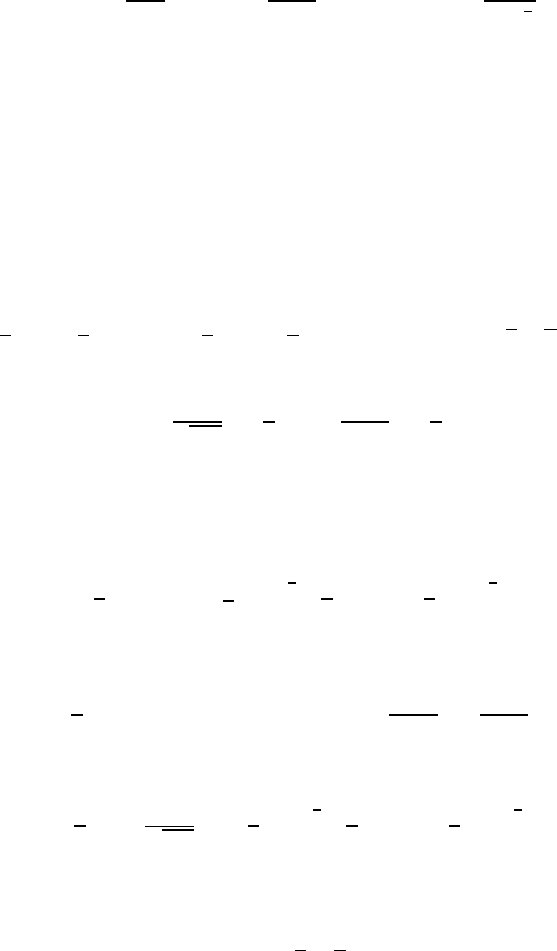
642 G. Seregin
By (3.5) and by our definitions,
α
u
(t) ≤
c
(−t)
,β
u
(t) ≤
c
(−t)
2
,γ
u
(t)+δ
p
(t) ≤
c
(−t)
3
2
(4.16)
for all −1 ≤ t<0. Indeed, the first bound follows directly from (3.5). To get the
second one, we need to use (3.5), BMO-estimate of the pressure via velocity field,
and then local regularity theory in the same way as in the proof of Lemma 2.1. It
is useful to note that the above arguments imply the estimate |∇u(x, t)|≤c/(−t)
for all (x, t) ∈ Q
−
. As to the third bound, the second term is estimated with the
help of the singular integral theory, (3.5), and definitions of p
1
x
0
and p
2
x
0
.
We fix x
0
∈ R
3
and a smooth non-negative function ϕ such that ϕ ≡ 1
in B and spt ϕ ⊂ B(3/2) and let ϕ
x
0
(x)=ϕ(x − x
0
). Considering (4.15) with
such a cut-off function ϕ
x
0
, taking into account (4.11) and (4.16), and arguing for
example as in [7], we can find the inequality
α
u
(t
0
)+β
u
(t
0
) ≤ c
.
t
0
−1
α
u
(t)dt + γ
u
(t
0
)+ sup
x
0
∈R
3
t
0
−1
B(x
0
,3/2)
|p
x
0
||u|dxdt
+
c
√
−t
0
t
0
−1
α
u
(t)dt +
c
(−t
0
)
t
0
−1
α
u
(t)dt
/
(4.17)
for all −1 ≤ t
0
< 0.
Next, we can re-write the well-known (in the theory of the Navier-Stokes
equations) multiplicative inequality in terms of quantities introduced above
γ
u
(t
0
) ≤ c
t
0
−1
α
3
u
(t)dt
1
4
β
u
(t
0
)+
t
0
−1
α
u
(t)dt
3
4
.
To simplify the latter, we first make use of (4.11) and (4.16) in the following way
α
u
(t
0
) ≤ c(α
w
(t
0
)+α
u
(t
0
)) ≤ c
A +
c
(−t
0
)
≤
C(A)
(−t
0
)
for all −1 ≤ t
0
< 0. And thus
γ
u
(t
0
) ≤
C(A)
√
−t
0
t
0
−1
α
u
(t)dt
1
4
β
u
(t
0
)+
t
0
−1
α
u
(t)dt
3
4
(4.18)
It remains to estimate the third term on the right-hand side of (4.17)
I =sup
x
0
∈R
3
t
0
−1
B(x
0
,3/2)
|p
x
0
||u|dxdt ≤ I
1
+ I
2
, (4.19)
Blowups for Navier-Stokes Equations 643
where
I
1
=sup
x
0
∈R
3
t
0
−1
B(x
0
,3/2)
|p
1
x
0
||u|dxdt ≤ I
1
+ I
1
,
I
2
=sup
x
0
∈R
3
t
0
−1
B(x
0
,3/2)
|p
2
x
0
||u|dxdt,
and
I
1
= c sup
x
0
∈R
3
t
0
−1
B(x
0
,3/2)
"
"
"
|w|
2
−|u|
2
"
"
"
|u|dxdt,
I
1
= c sup
x
0
∈R
3
t
0
−1
B(x
0
,3/2)
"
"
"
B(x
0
,2)
K(x − y):
w(y, t) ⊗w(y, t)
− u(y, t) ⊗u(y,t)
dy
"
"
"
|u(x, t)|dxdt.
I
1
is evaluated easily, namely,
I
1
≤ c sup
x
0
∈R
3
t
0
−1
B(x
0
,3/2)
|u|
2
(|u| +2|u|)dxdt ≤ cγ
u
(t
0
)+
c
√
−t
0
t
0
−1
α
u
(t)dt. (4.20)
To estimate I
1
, we exploit the same idea and L
3
2
-andL
2
-estimates for singular
integrals
I
1
≤ c sup
x
0
∈R
3
t
0
−1
B(x
0
,3/2)
|u(x, t)|
"
"
"
B(x
0
,2)
K(x − y):u(y, t) ⊗ u(y,t)dy
"
"
"
+
"
"
"
B(x
0
,2)
K(x − y):
u(y,t) ⊗u(y,t)+u(y,t) ⊗ u(y,t)
dy
"
"
"
dxdt
≤ cγ
u
(t
0
)+
c
√
−t
0
t
0
−1
α
u
(t)dt.
So, by (4.20), we have
I
1
≤ cγ
u
(t
0
)+
c
√
−t
0
t
0
−1
α
u
(t)dt. (4.21)
644 G. Seregin
In order to find upper bound for I
2
, we simply repeat arguments of Lemma
2.1 in [7] with R = 1 there. This gives us the following estimate
|p
2
x
0
(x, t)|≤c
R
3
\B(x
0
,2)
"
"
"
K(x −y) − K(x
0
− y)
"
"
"
"
"
"
w(y, t) ⊗w(y, t)
−u(y,t) ⊗u(y,t)
"
"
"
dx
≤ cw(·,t) ⊗ w(·,t) − u(·,t) ⊗u(·,t)
L
1,unif
being valid for any x ∈ B(x
0
, 32/) and thus
I
2
≤ c sup
x
0
∈R
3
t
0
−1
w(·,t) ⊗ w(·,t) − u(·,t) ⊗u(·,t)
L
1,unif
B(x
0
,3/2)
|u(x, t)|dx.
Furthermore, by (4.11),
w(·,t) ⊗ w(·,t) − u(·,t) ⊗ u(·,t)
L
1,unif
=sup
x
0
∈R
3
B(x
0
,1)
|u(y,t) ⊗ w(y, t)+u(y,t) ⊗u(y,t)|dx
≤ α
1
2
u
(t)α
1
2
w
(t)+α
1
2
u
(t)α
1
2
u
(t) ≤
C(A)
√
−t
α
1
2
u
(t).
So,
I
2
≤
C(A)
√
−t
0
t
0
−1
α
u
(t)dt
and, by (4.18) and (4.21), we have
I ≤ cγ
u
(t
0
)+
C(A)
√
−t
0
t
0
−1
α
u
(t)dt
≤
C(A)
√
−t
0
1
t
0
−1
α
u
(t)dt
1
4
β
u
(t
0
)+
t
0
−1
α
u
(t)dt
3
4
+
t
0
−1
α
u
(t)dt
2
. (4.22)
Combining (4.17) and (4.22) and applying Young inequality, we arrive at the final
estimate
α
u
(t
0
) ≤ C(A, δ)
t
0
−1
α
u
(t)dt
which is valid for all −1 ≤ t
0
≤ δ<0. The latter says that α
u
(t)=0in[−1, 0[
and, hence, u(·,t)=w(·,t) for the same t.
This completes the proof of Theorem 1.1.
Blowups for Navier-Stokes Equations 645
Acknowledgment
This work was partially supported by the RFFI grant 08-01-00372-a.
References
[1] Caffarelli, L., Kohn, R.-V., Nirenberg, L., Partial regularity of suitable weak solutions
of the Navier-Stokes equations. Comm. Pure Appl. Math., XXXV (1982), 771–831.
[2] Escauriaza, L., Seregin, G.,
ˇ
Sver´ak, V., L
3,∞
-Solutions to the Navier-Stokes Equa-
tions and Backward Uniqueness. Russian Mathematical Surveys, 58 (2003), 211–250.
[3] Ladyzhenskaya, O.A., Seregin, G.A., On partial regularity of suitable weak solutions
to the three-dimensional Navier-Stokes equations. J. Math. Fluid Mech., 1 (1999),
356–387.
[4] Lemarie-Riesset, P.G., Recent developments in the Navier-Stokes problem. Chap-
man&Hall/CRC Research Notes in Mathematics Series, 431.
[5] Leray, J., Sur le mouvement d’un liquide visqueux emplissant l’espace. Acta Math.
63 (1934), 193–248.
[6] Lin, F.-H., A new proof of the Caffarelly-Kohn-Nirenberg theorem. Comm. Pure Appl.
Math., 51 (1998), 241–257.
[7] Kikuchi, N., Seregin, G., Weak solutions to the Cauchy problem for the Navier-Stokes
equations satisfying the local energy inequality. AMS translations, Series 2, 220, 141–
164.
[8] Koch, G., Nadirashvili, N., Seregin, G.,
ˇ
Sver´ak, V., Liouville theorems for Navier-
Stokes equations and applications. Acta Mathematica, 203 (2009), 83–105.
[9] Seregin, G.A., Navier-Stokes equations: almost L
3,∞
-cases. Journal of Mathematical
Fluid Mechanics, 9 (2007), 34–43.
[10] Seregin, G.,
ˇ
Sver´ak, V., On Type I singularities of the local axi-symmetric solutions
of the Navier-Stokes equations. Communications in PDE’s, 34 (2009), 171–201.
[11] Seregin, G., Zajaczkowski, W., A sufficient condition of regularity for axially sym-
metric solutions to the Navier-Stokes equations. SIMA J. Math. Anal., 39 (2007),
669–685.
Gregory Seregin
Mathematical Institute
University of Oxford
24–29 St. Giles
Oxford, OX1 3LB, UK
e-mail: seregin@maths.ox.ac.uk


Progress in Nonlinear Differential Equations
and Their Applications, Vol. 80, 647–686
c
2011 Springer Basel AG
Local Solvability of Free Boundary Problems
for the Two-phase Navier-Stokes Equations
with Surface Tension in the Whole Space
Senjo Shimizu
Dedicated to Professor Herb ert Amann on the occasion of his 70th birthday.
Abstract. We consider the free boundary problem of the two-phase Navier-
Stokes equation with surface tension and gravity in the whole space. We prove
a local-in-time unique existence theorem in the space W
2,1
q,p
with 2 <p<∞
and n<q<∞ for any initial data satisfying certain compatibility conditions.
Our theorem is proved by the standard fixed point argument based on the
maximal L
p
-L
q
regularity theorem for the corresponding linearized equations.
Mathematics Subject Classification (2000). Primary 35R35; Secondary 35Q30,
76D05, 76D03, 76T10.
Keywords. Navier-Stokes equations, free boundary problems, surface tension,
gravity force, local solvability.
1. Introduction and results
In this paper, we show the results for a local-in-time existence theorem of the free
boundary problems related to the motion of a viscous, incompressible fluid for the
two-phase Navier-Stokes equations in the whole space R
n
(n ≥ 2). The effect of
surface tension on a free boundary and the effect of gravity force are included.
The free interface Γ(t) is given only at initial time t =0as
Γ(0) = {x =(x
,x
n
) ∈ R
n
| x
n
= α(x
),x
∈ R
n−1
}
for α(x
) ∈ W
3−1/q
q
(R
n−1
), while that at t>0 remains to be determined. We set
Ω(t)=Ω
+
(t) ∪ Ω
−
(t)=R
n
\ Γ(t).
This work was partially supported by JSPS Grant-in-aid for Scientific Research (C) #20540164.
