Emmrich E., Wittbold P. (editors) Analytical and Numerical Aspects of Partial Differential Equations: Notes of a Lecture Series

Подождите немного. Документ загружается.

Atomistic to continuum coupling methods 2

Lemma 4.14. Le

t g ∈ W

1,1

(0, L) with L = N h. Then



g(x) dx −h

i=1

g(ih)



≤ hkg

′

(0,L)

Let ψ ∈ X

. Recall that Ω

= (P h, L) with L = Nh. Then

(ψ) − B

(Eψ) =

P h

f(x) ψ(x) dx − h

i=P +1

f(ih) ψ(ih).

We want to use Lemma 4.14 with g = fψ. In view of assumption (H4), we have

f ∈ C



Ω



Since ψ ∈ X

, we have ψ ∈ C



Ω



nd ψ

′

∈ L

(Ω

Let us now make the additional assumption that the body force f satisﬁes f

′

∈

(Ω

). Then

(ψ) − B

(Eψ)| ≤ hk(f ψ)

′

(Ω

)

≤ h



′

ψk

(Ω

)

+ kfψ

′

(Ω

)



≤ h



′

(Ω

)

kψk

∞

(Ω

)

+ kfk

∞

(Ω

)

kψ

′

(Ω

)



We work with ψ ∈ X

, so that ψ(L) = 0. Therefore, we have kψk

∞

(Ω

)

≤

kψ

′

(Ω

)

≤

√

L kψ

′

(Ω

)

≤

√

L |ψ|

)

and ﬁnd

(ψ) − B

(Eψ)| ≤ h

√



′

(Ω

)

+ kfk

∞

(Ω

)



|ψ|

)

n view of the deﬁnition (4.37) of τ, this yields

τ ≤ h

√



′

(Ω

)

+ kfk

∞

(Ω

)



. (

4.38)

We thus obtain the following result.

Theorem 4.15. Assume that (H3) and (H4) hold, and that the partition Ω = Ω

∪Ω

is such that f

′

∈ L

(Ω

). We also assume that

Ω

= (0, P h], Ω

= (P h, L),

for some P that depends on h such that P h is constant. Then

|φ

− Iφ

)

≤ C h



′

(Ω

)

+ kfk

∞

(Ω

)



where C only depends on L, α and β.

Proof. In view of Theorem 4.13 and equation (4.38), we have

|φ

− Iφ

)

≤

√



′

(Ω

)

+ kfk

∞

(Ω

)



2β

C hkφ

′′

(Ω

)

216 F

rédéric Legoll

where C o

nly depends on Ω = (0, L). In view of Lemma 4.9, we also have

kφ

′′

(Ω

)

= kψ

′′

(Ω

)

≤ kψ

(Ω

)

≤

kfk

(Ω

)

≤

√

kfk

∞

(Ω

)

here ψ

(x) = φ

(x) − ax/L, and where C only depends on Ω. We hence obtain the

claimed bound.

Theorem 4.15 provides a bound on the ﬁrst derivatives of the deformations. This

hence a bound on strains, in a L

-kind of norm. Using a Poincaré inequality, we

deduce from it a bound on the deformations, e.g., a bound on kφ

−Iφ

)

, where

the norm k ·k

)

is deﬁned on X

∀ψ ∈ X

, kψk

)

P h

(x) dx + h

i=0





Remark 4.16. We observe that, if we choose the partition according to the assump-

tions of Theorem 4.15 with f and f

′

small on Ω

(in the L

∞

- and the L

-norm,

respectively), then the coupled problem is a good (and converging, when h → 0) ap-

proximation of the microscopic problem. Hence, we can deﬁne an appropriate partition

based on the knowledge of the body forces only. This is related to the convexity as-

sumption. Indeed, due to the convexity of the problems, the Euler–Lagrange equations

of the problems are uniformly elliptic, hence their solutions are "singular" only where

the datum f is singular. In the nonconvex case, the situation is different, as is shown in

Section 4.3.

Remark 4.17. The above estimates involve L

-bounds on the deformation and its ﬁrst

derivative. It is also possible to obtain L

∞

-bounds, as is shown in [23, 24], where a

different strategy is followed. See also [42].

4.3 A nonconvex case: the Lennard–Jones case

We now consider a particular example of nonconvex potential, namely the Len

nard–

Jones potential

(x) =

−

. (

4.39)

We observe that lim

x→0

(x) = +∞ and lim

x→+∞

(x) = 0, which are physically

relevant properties (see Remark 2.2). Actually, the property that we use in the sequel

is lim

x→+∞

(x)/x = 0, rather than lim

x→+∞

(x) = 0 (see Remark 4.19 for the

mechanical implication of this property). Note also that V

attains its unique minimum

at x = 1.

Remark 4.18. The particular choice of exponents in V

(6 and 12) has no inﬂuence

on the following analysis. Similar results hold for the potential V (x) =

−

with

p > q > 0.

Atomistic to continuum coupling methods 2

Remark 4.19. F

or a one-dimensional solid described by the continuum energy

(φ) =

W (φ

′

(x)) dx,

the behaviour of W (x)/x when x → +∞ is related to the cost of making a fracture in

the material. Consider indeed a nonnegative energy density W that attains its unique

minimum at x = 1, and for which c = lim

x→+∞

W (x)/x exists, c ∈ [0, +∞]. Let

a > L and 0 < ℓ < L, and consider the deformations φ

deﬁned by φ

(0) = 0 and

′

(x) =

(

1 on



0, ℓ −



∪

(

ℓ

, L

)

n(a −L) + 1 on



ℓ −

ℓ



which all satisfy the same boundary conditions φ

(0) = 0 and φ

(L) = a. This

sequence represents conﬁgurations with a strain larger and more localized when n in-

creases. In the limit n → +∞, it represents a fractured material. The energy of the

conﬁguration φ

(φ

) =



L −



W (1)

W (n(a − L)

+ 1),

hence

lim

n→+∞

(φ

) = LW (1) + c(a − L).

If c = +∞, then making a fracture costs an inﬁnite energy. If c = 0, then making

a fracture costs no energy: lim

n→+∞

(φ

) is equal to the energy of the reference

conﬁguration φ(x) = x. If c ∈ (0, +∞), then making a fracture costs a ﬁnite amount

of energy.

In this nonconvex case, we show that expression (4.13) for the coupled energy might

be inappropriate, and we describe several ways to circumvent this difﬁculty. The com-

plete analysis of this case can be read in [23]. Here, we brieﬂy summarize it (see also

[155]).

We consider a material that occupies the domain Ω = (0, L) in the reference conﬁg-

uration and that is put in tension. We focus on the case when there are no body forces:

f ≡ 0. Taking into account body forces does not change the qualitative conclusions

of the analysis. If the material is compressed rather than extended, then the analysis is

very similar to the convex case analysis (see, for instance, [23, Theorem 2.1]).

We ﬁrst look at the macroscopic problem (4.10) with the macroscopic energy

(φ) =

(φ

′

(x)) dx

and the variational space



φ ∈ W

1,1

(0, L);

′

(x)

∈ L

(0, L), φ(0) = 0, φ(L) = a



. (4.40)

We consider here the tension case: a > L.

218 F

rédéric Legoll

Lemma 4.20. Th

e minimum I

in (4.10) is equal to inf V

. In addition, the inﬁmum

in the problem (4.10) is not attained: there exists no φ ∈ X

such that E

(φ) = I

Proof. For any φ ∈ X

, we have that E

(φ) ≥ infV

. Hence, E

is lower-bounded

and I

≥ infV

> −∞. Consider now the following sequence of continuous func-

tions:

(x) =

(

x on



0, L −



a + n



a − L +



(x − L) o



L −



The function φ

is piecewise afﬁne, satisﬁes the boundary conditions φ

(0) = 0,

(L) = a, and

′

(x) = 1 on



0, L −



′

(x) = n



a −L +



lsewhere.

We ﬁnd

(φ

) =



1 −



(

n(a −L) + 1

)

Since lim

x→+∞

(x)/x = 0, we obtain lim

n→+∞

(φ

) = inf V

. As E

(φ

) ≥

, this yields infV

≥ I

. Therefore, we get I

= infV

Let us now assume that there exists φ ∈ X

such that E

(φ) = I

. This implies

(φ

′

(x)) dx = L infV

and thus V

(φ

′

(x)) = infV

almost everywhere on

(0, L). We conclude φ

′

(x) = 1 almost everywhere, which is in contradiction with the

boundary conditions φ(0) = 0, φ(L) = a > L. Hence, the inﬁmum in the problem

(4.10) is not attained.

If the variational space is enlarged (in (4.40), replace W

1,1

(0,

L) by SBV (0, L),

whose deﬁnition is recalled below), then the problem (4.10) has an inﬁnite number of

solutions with jumps. They are of the form

φ(x) = x +

j∈J

H(x − y

), (4.41)

where J ⊂ N, y

are any points in Ω = (0, L),

= a − L, and H is the Heaviside

function: H(t) = 1 if t ≥ 0, H(t) = 0 otherwise. This statement can be shown by

arguments similar to the ones used to prove Theorem 2.1 of [23]. We recall (see [3, 5])

that the set SBV (0, L) of special functions of bounded variation is

SBV (0, L) =







u ∈ D

′

(0, L); u

′

= D

u +

j∈N

, D

u ∈ L

(0, L),

∈ (0, L),

j∈N

| < +∞







where δ

is the Dirac distribution centered at y

(note that H

′

(· − y

) = δ

in the

distributional sense).

Atomistic to continuum coupling methods 2

Note that, with the above continuum model, neither the number nor the locations

f the fractures are determined. All the conﬁgurations (4.41) have the same energy,

whatever J, v

and y

are.

The fully atomistic model can be analyzed with methods similar to the ones used in

[23, Section 2.2]. It turns out that the minimizers of this model have a unique fracture,

whose location is not determined (the energy is the same whatever the fracture location

is).

Hence, working with the Lennard–Jones potential and tension boundary conditions

is interesting, since it leads to a deformation with a singularity (here, a jump, which

represents a fracture in the one-dimensional bar). Our aim is thus to design a multi-

scale method able to describe this singularity by an atomistic model, while keeping a

continuum description where it is accurate enough. Since the location of the fracture is

not prescribed by the atomistic model, we can afford to ﬁx a priori the partition of Ω,

with the aim to ﬁnd the singularity in Ω

Let us now follow the strategy explained in Section 4.2. We consider a given parti-

tion of Ω, and, to simplify notations, we again assume that this partition is (4.12). In

the spirit of the coupled energy (4.13) and the coupled space (4.14), we consider the

energy

(φ) =

(φ

′

(x)) dx +

P −1



i+1

− φ



, (

4.42)

deﬁned on the variational space

(

φ; φ

|Ω

∈ SBV (Ω

), 1/φ

′

∈ L

(Ω

|Ω

= {φ

}

0≤i≤P

∈ R

P +1

, φ

= 0, φ(L) = a, φ

= φ(P h)

)

. (4.43)

We consider the tension case: a > L. Following the arguments of [23, Lemma 2.3],

one can show that the minimizers of

inf{E

(φ); φ ∈ X

}

are of the form

= ih, 0 ≤ i ≤ P,

φ(x) = x +

j∈J

H(x −y

), ∀x ≥ P h,

where J ⊂ N, y

are any points in Ω

and

= a − L. Therefore, as in the com-

pletely macroscopic description, the material breaks. However, the fracture is always

in the domain Ω

, in which the deformation φ is assumed to be regular (since we use a

macroscopic model in that domain). Hence, we do not reach our aim with the coupled

method (4.42)–(4.43).

Proving the above statement is quite technical. The following calculations help

to understand why the fracture systematically occurs in the continuum domain. We

consider two conﬁgurations, the ﬁrst one with a fracture in Ω

and the second one

with a fracture in Ω

, and compare their energies.

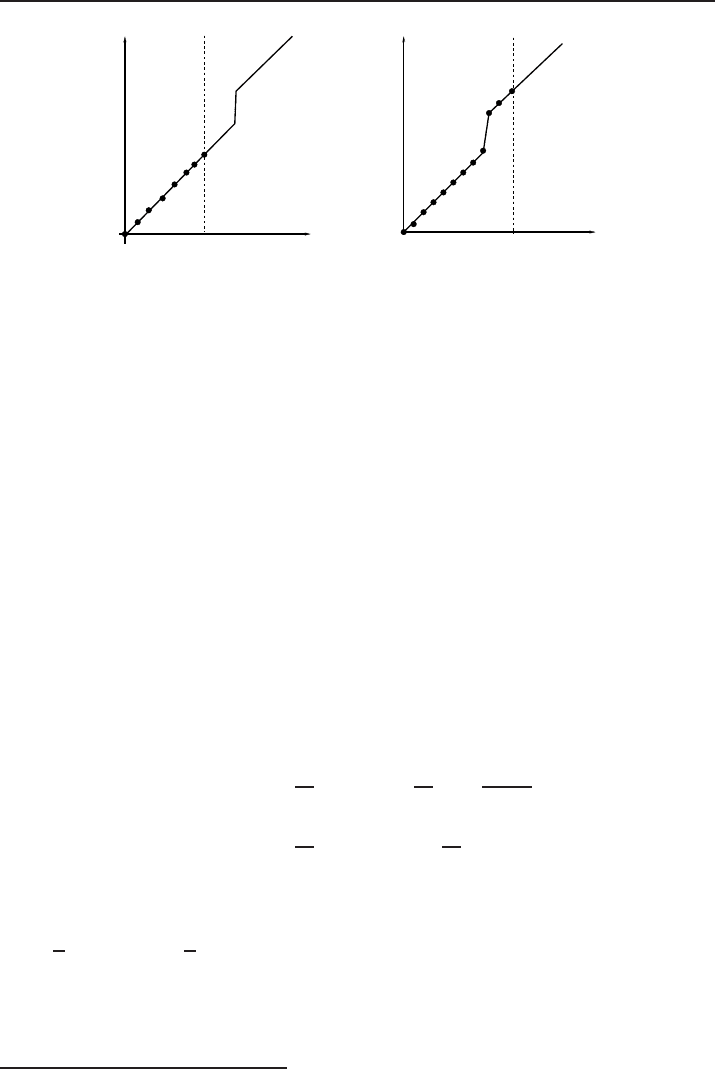
220 F

rédéric Legoll

Ω

Figure 3. Conﬁgurations φ

(with a crack in Ω

) and φ

(with a crack in Ω

Let us deﬁne φ

∈ X

= ih, 0 ≤ i ≤ P,

(x) = x + (a −L)H(x − y

), ∀x ≥ P h,

(4.44)

where y

is any real number, P h < y

< L (see Figure 3). The map φ

represents a

deformation with a fracture in Ω

, located at y

. We also consider φ

∈ X

deﬁned by

= ih, 0 ≤ i ≤ Q

= ih + (a − L), 1 + Q

≤ i ≤ P,

(x) = x + (a −L), ∀x ≥ P h,

(4.45)

which represents a deformation with a fracture in Ω

on the atomic bond (Q

, 1+ Q

with arbitrary integer Q

∈ [0, P − 1].

Their energies are

(φ

) = V

(1),

(φ

) =



1 −



(1) +



a − L

+ 1





1 −



(1) + o





ence, E

(φ

) > E

(φ

): a conﬁguration with a fracture in Ω

has a lower energy

than a conﬁguration with a fracture in Ω

. Actually, the energy cost for a fracture in

Ω

(1)| + o





whereas the cost for a fracture in Ω

is zero

. Hence, even

if the difference E

(φ

) −E

(φ

) is small, the minimization of E

leads to locating the

fracture in Ω

There are several ways out of this difﬁculty: First, it is possible to modify the

deﬁnition of the coupled energy. More precisely, the idea is to modifythe elastic energy

We deﬁne the cost of a fracture by the difference between the energy of a conﬁguration with a fracture and

the energy of the reference conﬁguration.

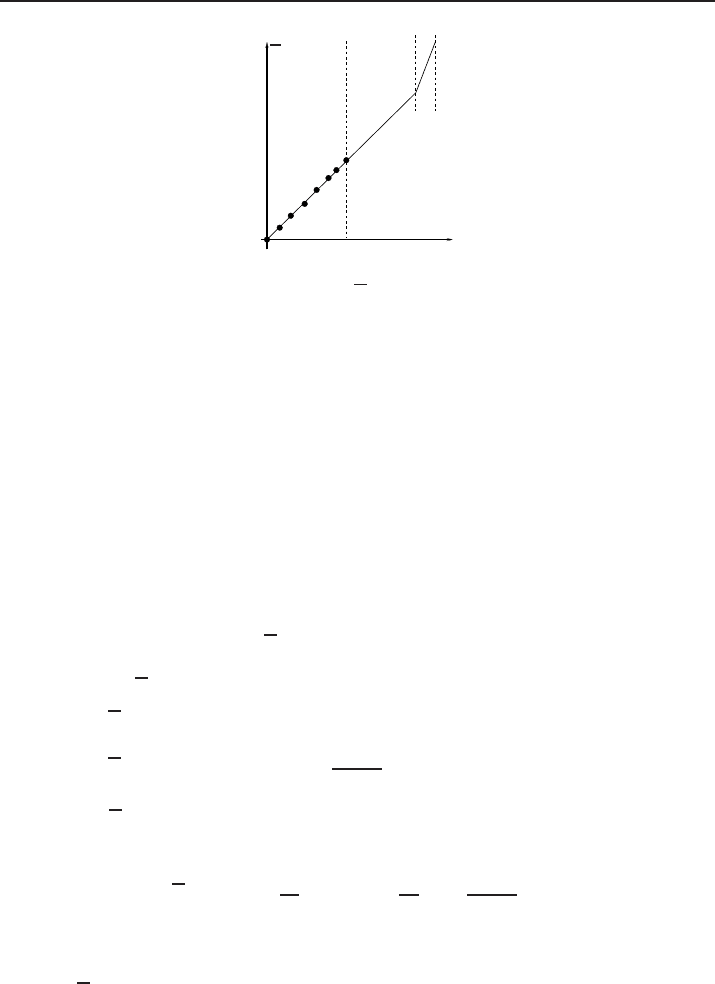
Atomistic to continuum coupling methods 2

Ω

igure 4. Conﬁguration

(

with a crack in Ω

density that is used in Ω

in such a way as it remains consistent with the atomistic

model, and such that making a fracture in Ω

costs more than making a fracture in

Ω

. See [23] (in particular, Section 2.4) for details. Introducing this modiﬁed coupled

energy is possible because we have a very detailed understanding of the difﬁculties

associated with the coupled energy (4.42).

Second, we notice that, in practice, one does not work with functions in the space

(4.43), but within a ﬁnite dimensional subset of it. Consider for instance the Galerkin

approximation

= {φ ∈ X

; φ is piecewise afﬁne on Ω

on a mesh of size H}. (4.46)

Let us again compare the energies of cracked conﬁgurations. We see that φ

deﬁned

by (4.45) belongs to X

. However, φ

deﬁned by (4.44) does not belong to X

. Let

us deﬁne its discretized version

∈ X

= i

h, 0 ≤ i ≤ P,

(x)

= x, P h ≤ x ≤ L −H,

(x)

= a + (x − L)



a − L

+ 1



L −H ≤ x ≤ L.

The map

elongs to X

and represents a deformation with a fracture in Ω

located in the last ﬁnite element (see Figure 4). We ﬁnd







1 −



(1) +



a −L

+ 1



f H is chosen such that H ≫ h (which makes the problem deﬁned on X

cheaper

to solve than the fully atomistic problem, since it involves fewer degrees of freedom),

then E





(φ

). Actually, one can prove that the minimizers of the coupled

energy E

on X

have a fracture which occurs in the atomistic domain Ω

Let us summarize our observations:

•

Minimizing the coupled energy (4.42) on the space (4.43) leads to issues, since a

fracture appears in the continuum domain.

222 F

rédéric Legoll

•

ntroducing a (coarse enough) mesh in the continuum domain regularizes the

problem: when minimizing the coupled energy (4.42) on the space (4.46), a frac-

ture appears, which is contained in the atomistic domain.

The situation is hence saved by the fact that we look at a discretized version of the

problem, for a sufﬁciently large discretization parameter H.

This discussion shows that the nonconvex case is much more challenging than the

convex case, and that unexpected difﬁculties appear, although the general setting is

extremely simple (a one-dimensional system with nearest-neighbour interactions). We

expect to meet similar difﬁculties in more general settings (problems in higher dimen-

sion or long-range interactions).

5 Discussion

In this section, we review some general questions about the modelling and setting of

the problem. We also review some methods recently proposed and discuss some open

questions at the front of research.

5.1 The nearest-neighbour assumption

We gather here some remarks concerning the atomistic model (2.4) that we

used:

(φ

, . . . , φ

) =

j6=i

V (φ

− φ

In general, the potential energy V (φ

− φ

) tends to zero when the distance between

atoms i and j goes to +∞ (see Remark 2.2). Hence, one often simpliﬁes the expres-

sion (2.4) (which is a sum of N

/2 terms) by introducing a cutoff r

cut

> 0 in V : we

approximate E

(φ

, . . . , φ

) by

cut

(φ

, . . . , φ

) =

j6=i,kφ

−φ

k≤r

cut

V (φ

− φ

), (5.1)

which is cheaper to evaluate than (2.4), in general (indeed, only a ﬁnite number of

atoms j are within the cutoff radius of any atom i for reasonable deformations). Ana-

lyzing a model such as (2.4) is difﬁcult due to the long-range interactions (whose range

increases when N increases!). Analyzing a model based on (5.1) is also challenging,

because we do not know a priori which atoms interact with each other. Hence, for

analysis purposes, a further simpliﬁcation is often made: instead of considering the

energy (5.1), with a ﬁnite range of interaction in terms of the distance between atoms,

we consider an energy with a ﬁnite range of interaction in terms of atoms indices:

(φ

, . . . , φ

) =

i=1

j6=i,kj−ik≤I

V (φ

− φ

), (5.2)

Atomistic to continuum coupling methods 2

for some cutoff I

In a one-dimensional setting, the extreme case is I

= 1, corre-

sponding to nearest-neighbour interactions.

When making the above assumption of working with (5.2), we implicitly assume

that the ordering of the atoms in the deformed conﬁguration is the same as the or-

dering in the reference conﬁguration. Consider indeed the case of nearest-neighbour

interactions for a one-dimensional model:

(φ

, . . . , φ

) =

N−1

i=1

V (φ

i+1

− φ

). (5.3)

If the ordering in the current (deformed) conﬁguration is not the original one, then we

have one of the following situations:

•

There exist indices i and j, 1 ≤ i, j ≤ N , with j > i+1, such that φ

≤ φ

i+1

The interaction between atoms i and j is not taken into account in (5.3), although

they are closer to each other than atoms i and i + 1, whose interaction is taken

into account in (5.3). This does not make sense.

•

There exist indices i and j, 1 ≤ i, j ≤ N , with j ≤ i−1, such that φ

≤ φ

i+1

Again, it does not make sense not to consider the couple (j, i + 1) whereas the

couple (i, i + 1) is considered.

So, when working with (5.2), a natural assumption is that the ordering of the atoms is

preserved by the deformation. A simple way to enforce this is to impose the constraint

i+1

≥ φ

for all i in the variational space.

For pedagogical purposes, we have not included this constraint in the atomistic

variational space (4.8). See [23, 24] for an analysis of the same models as in Section

4, where the variational spaces include this ordering constraint. We show there that, if

the boundary value a is large enough (recall that, in (4.8), we impose φ

= a), then

the constraint is not attained, and the analysis is exactly the same as the one without

constraint that we perform here. On the other hand, if a is not large enough, then the

variational problems do not have any solution.

5.2 Beyond global minimization

In these notes, we have adopted a variational viewpoint: we have deﬁned the

solution

of the various models as the global minimizer of the respective energies (as we did

in [23, 24]). This approach was also followed in [102], where problems similar to

the one studied here were studied. More precisely, a ﬁnite one-dimensional atomistic

chain is considered, with the energy (2.4), and the Lennard–Jones interaction potential

(4.39) for V . There are no body forces and no boundary conditions (except a Dirichlet

condition to remove translational invariance). The reference problem is hence written

inf







i=1

j6=i

(φ

− φ

); φ ∈ R

, φ

= 0, φ

i+1

> φ







224 F

rédéric Legoll

The inﬂuence, on the solution of the above variational problem, of introducing a cutoff

adius in V

, as well as the inﬂuence of making a QuasiContinuum like approximation

(see Section 5.3) are analyzed.

An alternative approach to global minimization is to look for local minimizers (see,

for instance, [63, 64, 66]). A difﬁculty linked to this approach is that there are in

general many local minimizers. In that setting, one often proves that, close to a given

atomistic solution, there exists a solution of the hybrid model.

Another possibility is to try and select one local minimizer by some criterion. For

instance, one can consider a gradient ﬂow dynamics [128, 138], which writes, in its

simplest formulation,

dφ

= −

∇E

(φ).

In the long-time limit, the solution of the above dynamical system converges to a con-

ﬁguration which is a local minimizer of the energy, and which is considered as the

reference solution of the atomistic model.

Yet another option is to study critical points of the energy rather than local mini-

mizers. See [129, 130] for such a choice in an atomistic to continuum setting (and also

[103] for a study in a two-dimensional setting, under some simplifying assumptions,

reminiscent of convexity assumptions). Note that critical points are also considered in

[12, 153], where the authors go beyond standard continuum mechanics models by con-

sidering elastic densities that depend on second derivatives of the deformation, hence

obtaining a continuum model with a small parameter (see Section 5.5, and energy

(5.11) in particular).

5.3 The QuasiContinuum method and the ghost forces

The method that we have analyzed in Section 4 is a toy example for more advan

ced

methods such as the QuasiContinuum method (QCM). In its initial version [150, 151],

this method starts from the continuum scale, with a standard continuum mechanics

model, discretized by a ﬁnite element method. The multiscale feature of the method

appears when the elastic energy of an element is computed. Depending on some crite-

ria, some elements are declared to be too heterogeneously strained for a macroscopic

description to hold, and they are considered as a set of discrete particles. The energy

of each element is computed according to the scale at which the element is described:

either the element is too heterogeneously strained, and its energy is computed on the

basis of an underlying atomistic model, or a standard continuum mechanics formula is

used.

In the second version of the method [146], that we describe below, the opposite

viewpoint is adopted. The starting point is a multibody atomistic energy, which is such

that it is possible to deﬁne the energy E

(φ) of the atom i when the current conﬁgura-

tion of the atomistic system is φ. We start from the energy

(φ) =

i=1

(φ). (5.4)