Emmrich E., Wittbold P. (editors) Analytical and Numerical Aspects of Partial Differential Equations: Notes of a Lecture Series
Подождите немного. Документ загружается.


Atomistic to continuum coupling methods 2
05
Since we minimize the energy, this term plays no role, so we omit it. The atomistic
e
nergy hence becomes
e
µ
(φ
0
, . . . , φ
N
) =
1
2N
N
X
i=
0
X
j6=i
V
0
φ
j
− φ
i
h
−
1
N
N
X
i=
0
f(x
i
)φ
i
.
We make the further approximation of nearest neighbour interaction. Note that this is
a strong assumption (see Section 5.1 for some discussion). On the other hand, it allows
us to pursue the analysis quite far. The atomistic energy hence becomes
e
µ
(φ
0
, . . . , φ
N
) =
1
N
N−1
X
i=
0
V
0
φ
i+1
− φ
i
h
−
1
N
N
X
i=
0
f(ih) φ
i
. (4.6)
Remark 4.2. Assume that V
0
= V
0
(r) attains its minimum at a unique value, that is
r = 1. When the material is submitted to no body forces (f ≡ 0) and no boundary con-
ditions, e
µ
attains its minimum for configurations φ such that φ
i+1
− φ
i
= h. Hence,
the reference configuration corresponds to atoms located on a periodic lattice of pa-
rameter h. This shows, at least in this simple case, that introducing the scaling (3.1) is
consistent with the assumption (H1).
We consider here that the microscopic equilibrium configuration is a solution of the
variational problem
I
µ
= inf
e
µ
(φ
0
, . . . , φ
N
); φ ∈ X
µ
, (4.7)
where the variational space is
X
µ
=
φ ∈ R
N+1
; φ
0
= 0, φ
N
= a
. (4.8)
Note that we have imposed fixed displacement boundary conditions. We look for a
global minimizer of the energy (see Section 5.2 for some alternative approaches).
In the continuum mechanics model, the solid deformation is described by the map
φ : Ω = (0, L) → R. Following the same arguments as in the proof of Theorem
3.1, one can show that, for sufficiently regular deformations φ and potentials V
0
, the
atomistic energy e
µ
(φ(0), φ(h), . . . , φ(N h)) converges to the continuum mechanics
expression
E
M
(φ) =
1
L
Z
L
0
V
0
(φ
′
(x)
) dx −
1
L
Z
L
0
f(x) φ(x) d
x. (4.9)
We define the macroscopic configuration as a solution of the minimization problem
I
M
= inf{E
M
(φ); φ ∈ X
M
} (4.10)
with
X
M
=
φ ∈ H
1
(0, L); φ(0) = 0, φ(L) = a
. (4.11)
We assume here that the energy E
M
(φ) is well-defined as soon as φ ∈ H
1
(0, L).
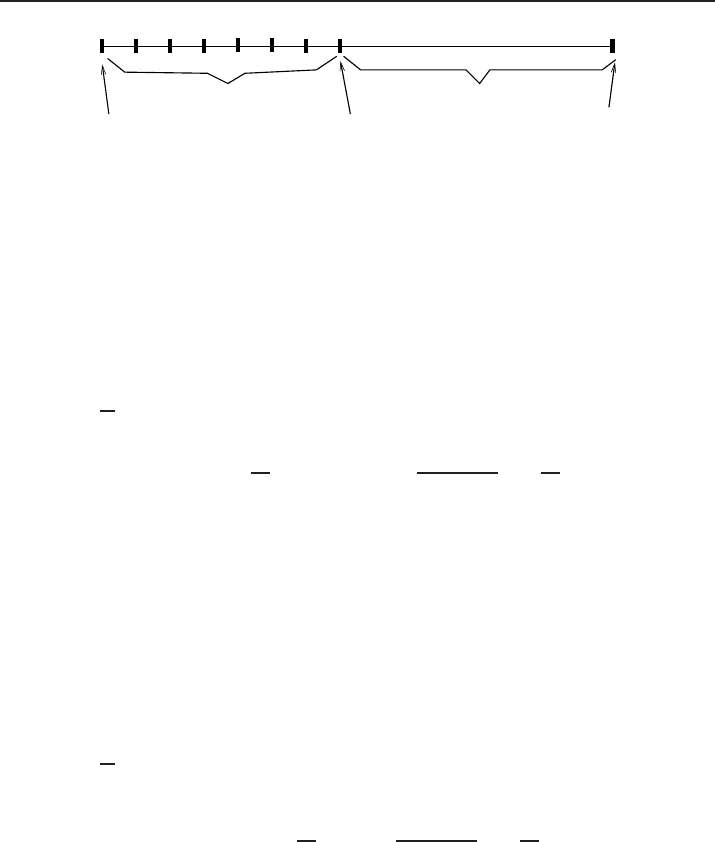
206 F
rédéric Legoll
L = N
h0
P h
Atomistic model Continuum model
Figure 2. Partition of Ω = (0, L) according to (4.12).
We expect that solving (4.9)–(4.10) gives a good approximation of the solution of
the atomistic problem when the equilibrium deformation is smooth. When non-regular
deformations are expected to appear, we approximate the solution of the atomistic
problem with the solution of a coupled model. In the spirit of (4.4), we introduce a
partition Ω = (0, L) = Ω
M
∪ Ω
µ
of the domain, and we consider the coupled energy
E
c
(φ) =
1
L
Z
Ω
M
[
V
0
(φ
′
(x)
) − f(x)φ(x)
]
dx
+
1
N
X
i; i
h,ih+h∈Ω
µ
V
0
φ
i+1
− φ
i
h
−
1
N
X
i;i
h∈Ω
µ
f(ih)φ
i
.
To simplify notations, we assume that Ω
M
and Ω
µ
are connected subdomains of Ω. To
fix ideas, we make the choice
Ω
µ
= (0, P h], Ω
M
= (P h, L), (4.12)
for some P that depends on h such that P h is constant. Similar results are obtained
without making assumption (4.12) with more technical proofs (see [23, 24]).
The coupled energy hence becomes
E
c
(φ) =
1
L
Z
L
P
h
[
V
0
(φ
′
(x)) − f(x)φ(x)
]
dx
+
1
N
P −1
X
i=
0
V
0
φ
i+1
− φ
i
h
−
1
N
P
X
i=
0
f(ih) φ
i
(4.13)
and is defined on the variational space
X
c
=
(
φ; φ
|Ω
M
∈ H
1
(Ω
M
), φ
|Ω
µ
= {φ
i
}
0≤i≤P
∈ R
P +1
,
φ
0
= 0, φ(L) = a, φ
P
= φ(P h)
)
. (4.14)
The expression of the boundary conditions φ
0
= 0 and φ(L) = a reflects the fact
that 0 ∈ ∂Ω
µ
and L ∈ ∂Ω
M
. The interface condition between the macroscopic and the
microscopic domains reads φ
P
= φ(P h). We hence enforce a continuity-like condition
on the deformation at the boundary.

Atomistic to continuum coupling methods 2
07
Remark 4.3. I
n a two-dimensional situation, writing down the interface condition is
less straightforward. Actually, there are several possibilities. One can first decrease
the mesh size in Ω
M
down to the atomistic lattice size for mesh elements close to the
interface and enforce equality of displacements of atoms and mesh nodes. Since the
mesh size can only evolve smoothly (to keep good mesh qualities, hence accuracy, on
the domain Ω
M
), this strategy is expensive. Another possibility is to request that the
positions of the atoms along (or close to) the interface are obtained from interpolation
from the positions of the mesh nodes on the interface. This constraint can also be
implemented in the spirit of mortar finite element methods [21].
Hence, the coupled problem we consider is
I
c
= inf{E
c
(φ); φ ∈ X
c
}. (4.15)
The questions we address here are:
•
Is the definition (4.13) of the coupled energy always the most appropriate? We
require that the coupled energy is consistent with the atomistic energy, and that it
leads to an efficient and accurate variational problem. The definition (4.13) is a
natural choice, but it is certainly not the only possible one.
•
How to (adaptively) define the partition Ω = Ω
M
∪ Ω
µ
such that the solution of
the coupled problem (4.13)–(4.15) is a good approximation of the solution of the
atomistic problem (4.6)–(4.7)?
•
Can error bounds be obtained?
We study both the general case of a convex energy density and a specific example
of nonconvex energy, the Lennard–Jones case. See [23] and [24] for an analysis of a
very similar problem. In [23] and [24], we followed a proof strategy to obtain W
1,∞
-
estimates. In this contribution, we present a different proof strategy
9
and obtain H
1
-
estimates (see Theorem 4.15 below).
4.2 The convex case
We assume here that V
0
is a
convex potential. In this case, we show that we can
propose an a priori definition for the partition which is only based on properties of the
body forces f . Vaguely stated, the subdomain Ω
M
(in which the continuum mechanics
model is used) is the part of the domain Ω where the body force f and its derivative f
′
are small.
With thisdefinition, we show that thesolution of the coupled problem (4.13)–(4.15)
is a good approximation of the solution of the atomistic problem (4.6)–(4.7): when
the atomic lattice parameter h goes to zero, the deformation and the strain given by
the coupled model converge to the deformation and the strain given by the atomistic
model. The main result of this section is Theorem 4.15 below.
9
This strategy is actually the one mentioned in Remark 1.3 of [23].
208 F
rédéric Legoll
We now proceed in details. We make the convexity assumption
(
H3) V
0
∈ C
2
(R), V
′
0
(1) = 0, ∃α, β ∈ R ∀x ∈ R : 0 < α ≤ V
′′
0
(x) ≤ β,
and the regularity assumption
(H4) f ∈ C(R).
Note that (H4) is required in order to give a sense to the atomistic energy (4.6). From
(H3), we deduce that, for all x and y,
α
2
(x −1)
2
≤ V
0
(x) −V
0
(1), (
4.16)
α(x −y)
2
≤
(
V
′
0
(x) −V
′
0
(y)
)
(x − y), (4.17)
|V
′
0
(x) −V
′
0
(y)| ≤ β|x − y|, (4.18)
|V
0
(x)| ≤ |V
0
(1)| +
β
2
|x −1|
2
, (
4.19)
|V
0
(x) −V
0
(y)| ≤ β|x − y|
(
|x| + |y| + 2
)
. (4.20)
We first consider the macroscopic problem (4.10), where the macroscopic energy is
(4.9), and the variational space is (4.11). In view of (4.19), E
M
(φ) is well-defined for
φ ∈ X
M
.
Theorem 4.4. Under the assumptions (H3) and (H4), the macroscopic variational
problem (4.10) has a unique solution φ
M
.
Proof. We first prove existence of a minimizer. On X
M
, the energy E
M
is lower-
bounded. Indeed, making use of (4.16), we obtain
E
M
(φ) ≥ V
0
(1) +
α
2L
Z
L
0
(φ
′
(x) −1)
2
d
x −
1
L
kfk
L
2
(0,
L)
kφk
L
2
(0,L)
. (4.21)
Using a Poincaré inequality for the function ψ : x 7→ φ(x) − ax/L, which belongs to
H
1
0
(0, L), with the Poincaré constant C
Ω
, which only depends on Ω = (0, L), we find
kφk
2
H
1
(0,L)
≤
kψk
H
1
(0,L)
+ C
2
≤ 2kψk
2
H
1
(0,L)
+ 2C
2
≤ 2C
2
Ω
kψ
′
k
2
L
2
(0,L)
+ 2C
2
≤ 4C
2
Ω
kφ
′
− 1k
2
L
2
(0,L)
+
e
C,
where C is the H
1
(0, L)-norm of the function x 7→ a x/L. In the above bound, the
constant
e
C only depends on a and L. We now insert this estimate into (4.21) and
obtain
E
M
(φ) ≥ C +
α
8LC
2
Ω
kφk
2
H
1
(0,L)
−
1
L
kfk
L
2
(0,L)
kφk
H
1
(0,L)
(4.22)

Atomistic to continuum coupling methods 2
09
for some constant C.
Since the function t ∈ R
+
7→ C +
α
8L
C
2
Ω
t
2
−
t
L
kfk
L
2
(0,
L)
is
lower-bounded, we obtain that E
M
is lower-bounded on X
M
.
Let us consider a minimizing sequence of functions φ
n
. By definition, E
M
(φ
n
) is
bounded, hence, in view of (4.22), we obtain that kφ
n
k
H
1
(0,L)
is bounded. Since Ω =
(0, L) is bounded, we infer from Rellich’s theorem (compact embedding of H
1
(0, L)
into L
2
(0, L)) that there exists
φ ∈ X
M
s
uch that, possibly for a subsequence only, φ
n
converges to
φ w
eakly in H
1
(0, L) and strongly in L
2
(0, L).
The energy E
M
is continuous for the strong topology of H
1
(0, L). Indeed, for θ
1
and θ
2
in H
1
(0, L), we have, using (4.20),
|E
M
(θ
1
) −E
M
(θ
2
)| ≤
Z
L
0
|V
0
(θ
′
1
(x)) −V
0
(θ
′
2
(x))| dx
+
Z
L
0
|f(x)| |θ
1
(x) −θ
2
(x)| dx
≤ β
Z
L
0
|θ
′
1
(x) −θ
′
2
(x)|
(
|θ
′
1
(x)| + |θ
′
2
(x)| + 2
)
dx
+ kfk
L
2
(0,L)
kθ
1
− θ
2
k
L
2
(0,L)
≤ βkθ
1
− θ
2
k
H
1
(0,L)
k|θ
′
1
|+ |θ
′
2
| + 2k
L
2
(0,L)
+ kfk
L
2
(0,L)
kθ
1
− θ
2
k
H
1
(0,L)
.
This inequality yields the continuity of E
M
. Since E
M
is also convex, it is weakly
lower semi-continuous in H
1
(0, L) (see, e.g., [34, Corollaire III.8]). We hence infer
from φ
n
⇀
φ in H
1
(0,
L) that
E
M
φ
≤ lim
infE
M
(φ
n
) = limE
M
(φ
n
) = I
M
.
Since
φ ∈ X
M
,
we also have I
M
≤ E
M
φ
.
As a consequence, I
M
= E
M
φ
,
and
φ
is
a minimizer of (4.10).
Since V
0
is strictly convex, the energy E
M
is a strictly convex function on the con-
vex set X
M
, hence the minimizer of (4.10) is unique.
In order to write the weak formulation of (4.10), we introduce the forms
A
M
(φ
, ψ) =
Z
L
0
V
′
0
(φ
′
(x)) ψ
′
(x) dx,
B
M
(ψ) =
Z
L
0
f(x) ψ(x) dx,
defined on H
1
(0, L) ×H
1
(0, L) and H
1
(0, L), respectively. Note that A
M
is nonlinear
with respect to φ.
Lemma 4.5. The macroscopic solution φ
M
defined by Theorem 4.4 satisfies
∀ψ ∈ H
1
0
(0, L), A
M
(φ
M
, ψ) = B
M
(ψ). (4.23)
210 F
rédéric Legoll
In addition, the function ψ
M
: x 7→ φ
M
(x) − a
x/L is in H
2
(0, L) and satisfies the
estimate
kψ
M
k
H
2
(0,L)
≤
C
α
kfk
L
2
(0,
L)
(4.24)
for some C that only depends on the domain Ω = (0, L).
Proof. Equation (4.23) is the weak formulation of the variational problem (4.10). It
implies that, in D
′
(0, L),
−V
′′
0
(φ
′
M
) φ
′′
M
= −
(
V
′
0
(φ
′
M
)
)
′
= f.
Since V
′′
0
(x) ≥ α > 0 and since f ∈ C
0
(0, L) ⊂ L
2
(0, L), we obtain that φ
′′
M
∈
L
2
(0, L), and
kψ
′′
M
k
L
2
(0,L)
= kφ
′′
M
k
L
2
(0,L)
≤
1
α
kfk
L
2
(0,
L)
. (4.25)
Hence ψ
M
is in H
2
(0, L). Let us now upper-bound this function in the H
1
-norm. We
first note that ψ
M
∈ H
1
0
(0, L). In view of (4.17) and (4.23), we have
α
φ
′
M
−
a
L
2
L
2
(0,
L)
≤
Z
L
0
V
′
0
(φ
′
M
(x)) − V
′
0
a
L
φ
′
M
(x) −
a
L
d
x
=
Z
L
0
V
′
0
(φ
′
M
(x))
φ
′
M
(x) −
a
L
d
x
= A
M
(φ
M
, ψ
M
)
= B
M
(ψ
M
)
≤ kfk
L
2
(0,L)
kψ
M
k
H
1
(0,L)
,
where we have used, in the second line, that
R
L
0
φ
′
M
(x) −
a
L
d
x = 0 since ψ
M
(x) :=
φ
M
(x) − ax/L vanishes for x = 0 and x = L. Using a Poincaré inequality for the
function ψ
M
, we obtain
kψ
M
k
H
1
(0,L)
≤
C
α
kfk
L
2
(0,
L)
for a constant C that only depends on Ω = (0, L). This bound, combined with (4.25),
yields (4.24).
We now consider the microscopic problem (4.7), where the microscopic energy
is
(4.6) and the variational space is (4.8). The following theorem is the microscopic
counterpart of Theorem 4.4.
Theorem 4.6. Under the assumptions (H3) and (H4), the microscopic variational prob-
lem (4.7) has a unique solution φ
µ
.

Atomistic to continuum coupling methods 2
11
We skip the proof of this theorem which follows the same lines as the proof of
T
heorem 4.4. In order to write the weak formulation of (4.7), we introduce the forms
A
µ
(φ, ψ) = h
N−1
X
i=0
V
′
0
φ
i+1
− φ
i
h
ψ
i+
1
− ψ
i
h
,
B
µ
(ψ)
= h
N
X
i=0
f(ih) ψ
i
,
defined on R
N+1
× R
N+1
and R
N+1
, respectively, and the homogeneous microscopic
space
X
0
µ
=
ψ ∈ R
N+1
; ψ
0
= 0, ψ
N
= 0
.
Lemma 4.7. The microscopic solution φ
µ
defined by Theorem 4.6 satisfies
∀ψ ∈ X
0
µ
, A
µ
(φ
µ
, ψ) = B
µ
(ψ). (4.26)
We now introduce a coupled problem based on a given partition of Ω = (0, L) =
Ω
M
∪Ω
µ
. We recall that, in order to simplify the notations, we work with the choice
Ω
µ
= (0, P h], Ω
M
= (P h, L),
for some P that depends on h such that P h is constant (see (4.12) and Figure 2).
The following theorem is the coupled counterpart of Theorem 4.4.
Theorem 4.8. Under the assumptions (H3) and (H4), the coupled variational problem
(4.15) has a unique solution φ
c
.
We skip the proof of this theorem, which again follows the same lines as the proof
of Theorem 4.4. In order to write the weak formulation of (4.15), we introduce the
forms
A
c
(φ, ψ) = h
P −1
X
i=0
V
′
0
φ
i+1
− φ
i
h
ψ
i+
1
− ψ
i
h
+
Z
L
P
h
V
′
0
(φ
′
(x)) ψ
′
(x) dx,
B
c
(ψ) = h
P
X
i=0
f(ih) ψ
i
+
Z
L
P h
f(x) ψ(x) dx,
defined on X
c
× X
c
and X
c
, respectively, and the homogeneous coupled space
X
0
c
=
ψ ∈ X
c
; ψ
0
= 0, ψ(L) = 0
. (4.27)
Lemma 4.9. The coupled solution φ
c
defined by Theorem 4.8 satisfies
∀ψ ∈ X
0
c
, A
c
(φ
c
, ψ) = B
c
(ψ). (4.28)
In addition, the function ψ
c
: x ∈ Ω
M
7→ φ
c
(x) −ax/L is in H
2
(Ω
M
) and satisfies the
estimate
kψ
c
k
H
2
(Ω
M
)
≤
C
α
kfk
L
2
(Ω
M
)
(4.29)
for some C that only depends on the domain Ω.

212 F
rédéric Legoll
Proof. T
he proof of (4.28) follows the same lines as the proof of (4.23) of Lemma 4.5.
The proof of (4.29) follows the same lines as the proof of (4.24): we make use of a
Poincaré inequality on Ω
M
, with a constant C
Ω
M
, which is next upper-bounded by the
Poincaré constant of Ω = (0, L).
We now aim at estimating the distance between φ
c
a
nd φ
µ
. We introduce an aux-
iliary problem, which is the discretization of the coupled problem by a finite element
method, using a mesh on Ω
M
of mesh size h. Of course, the resulting problem is as
expensive to solve as the full microscopic problem (both problems involve as many
variables), but it helps us in the numerical analysis.
We hence introduce the space
X
h
c
= {θ ∈ X
c
; θ is piecewise affine on Ω
M
on a mesh of size h},
and its homogeneous version
X
0h
c
= X
h
c
∩ X
0
c
.
We introduce the discretized coupled problem
inf
E
c
(φ); φ ∈ X
h
c
. (4.30)
As for the coupled problem (4.15), the above problem has a unique solution φ
h
c
, which
satisfies the weak formulation (see Lemma 4.9)
∀ψ ∈ X
0h
c
, A
c
(φ
h
c
, ψ) = B
c
(ψ). (4.31)
To estimate the difference between the solution φ
c
of the coupled problem and the
solution φ
µ
of the atomistic problem, we first estimate the distance between φ
c
and φ
h
c
,
solutions of the non-discretized and discretized coupled problem, respectively. Next,
we estimate the distance between φ
h
c
and φ
µ
.
To measure distances in X
c
, we introduce the mixed semi-norm (recall Ω
M
=
(P h, L))
|ψ|
2
H
1
(X
c
)
:=
Z
L
P h
ψ
′2
(x) dx + h
P −1
X
i=0
ψ
i+1
− ψ
i
h
2
.
W
e have the following estimates for the form A
c
:
Lemma 4.10. Assume that (H3) holds. For all u and g in X
c
, we have the strong
monotonicity
A
c
(u, u −g) −A
c
(g, u − g) ≥ α|u − g|
2
H
1
(X
c
)
. (4.32)
For all u, g and θ in X
c
, we have the Lipschitz-continuity
|A
c
(u, θ) −A
c
(g, θ)| ≤ 2β |u −g|
H
1
(X
c
)
|θ|
H
1
(X
c
)
. (4.33)
Proof. The bound (4.32) is a direct consequence of (4.17). The bound (4.33) follows
from (4.18).
Atomistic to continuum coupling methods 2
13
The above lemma shows that A
c
f
ulfills the assumptions (of strong monotonicity
and Lipschitz continuity) of the theorem of Zarantonello [160, Theorem 25.B], which
is a generalization of the Lax-Milgram theorem to the nonlinear setting. The following
lemma provides an estimate of the distance between φ
c
and φ
h
c
, and is a generalization
of the Céa lemma.
Lemma 4.11. The coupled solution φ
c
, which is defined by Theorem 4.8, and its dis-
cretized counterpart φ
h
c
, solution of (4.30), satisfy
φ
c
− φ
h
c
H
1
(X
c
)
≤
2β
α
C
h kφ
′′
c
k
L
2
(Ω
M
)
for some C that only depends on Ω.
Proof. Using (4.32), (4.28) and (4.31), we have
α
φ
c
− φ
h
c
2
H
1
(X
c
)
≤ A
c
(φ
c
, φ
c
− φ
h
c
) −A
c
(φ
h
c
, φ
c
− φ
h
c
)
= A
c
(φ
c
, φ
c
− φ
h
c
+ ψ) −A
c
(φ
h
c
, φ
c
− φ
h
c
+ ψ)
for any ψ ∈ X
0h
c
. With (4.33), we therefore obtain for any ψ ∈ X
h
c
α
φ
c
− φ
h
c
2
H
1
(X
c
)
≤ A
c
(φ
c
, φ
c
− ψ) − A
c
(φ
h
c
, φ
c
− ψ)
≤ 2β
φ
c
− φ
h
c
H
1
(X
c
)
|φ
c
− ψ|
H
1
(X
c
)
.
Hence,
φ
c
− φ
h
c
H
1
(X
c
)
≤
2β
α
in
f
ψ∈X
h
c
|φ
c
− ψ|
H
1
(X
c
)
. (4.34)
We have shown in Lemma 4.9 that φ
c
∈ H
2
(Ω
M
). By a standard approximation result,
we thus have
inf
ψ∈X
h
c
|φ
c
− ψ|
H
1
(X
c
)
≤ C h kφ
′′
c
k
L
2
(Ω
M
)
, (4.35)
where C only depends on Ω
M
and can be bounded by a constant that only depends on
Ω. Collecting (4.34) and (4.35), we obtain the claimed estimate.
We now estimate the distance between φ
µ
a
nd φ
h
c
. We make use of the weak formu-
lations of thecorresponding variational problems (see Lemma 4.7 and equation (4.31)).
To compare the configurations φ
µ
and φ
h
c
, that belong to different spaces, we introduce
the evaluation operator
E : X
c
→ X
µ
ψ 7→ Eψ
defined by (Eψ)
i
= ψ
i
for 0 ≤ i ≤ P , and (Eψ)
i
= ψ(ih) for ih ≥ P h. We also
introduce the interpolation operator
I : X
µ
→ X
c
ψ 7→ Iψ

214 F
rédéric Legoll
defined by (I
ψ)
i
= ψ
i
for 0 ≤ i ≤ P , and Iψ
|Ω
M
is the piecewise affine interpolation
of ψ
|Ω
M
. We note that I(X
µ
) ⊂ X
h
c
and
∀φ, ψ ∈ X
µ
, A
µ
(φ, ψ) = A
c
(Iφ, Iψ). (4.36)
Lemma 4.12. Assume that (H3) and (H4) hold. Then
φ
h
c
− Iφ
µ
H
1
(X
c
)
≤
τ
α
,
w
here
τ = sup
ψ∈X
0h
c
, ψ6=0
|B
c
(ψ) − B
µ
(Eψ)|
|ψ|
H
1
(X
c
)
. (
4.37)
Proof. Let ψ ∈ X
0h
c
. Using (4.31) and (4.26), we obtain
A
c
(φ
h
c
, ψ) = B
c
(ψ)
= B
µ
(Eψ) + B
c
(ψ) − B
µ
(Eψ)
= A
µ
(φ
µ
, Eψ) + B
c
(ψ) −B
µ
(Eψ)
= A
c
(Iφ
µ
, ψ) + B
c
(ψ) −B
µ
(Eψ),
where, in the last line, we have used (4.36) and the fact that IEψ = ψ for any ψ ∈ X
h
c
.
We hence obtain, for any ψ ∈ X
0h
c
,
A
c
(φ
h
c
, ψ) − A
c
(Iφ
µ
, ψ) ≤ τ|ψ|
H
1
(X
c
)
,
where τ is defined by (4.37). We now choose ψ = φ
h
c
− Iφ
µ
and use (4.32):
α
φ
h
c
− Iφ
µ
2
H
1
(X
c
)
≤ A
c
(φ
h
c
, φ
h
c
− Iφ
µ
) −A
c
(Iφ
µ
, φ
h
c
− Iφ
µ
)
≤ τ
φ
h
c
− Iφ
µ
H
1
(X
c
)
,
which yields the claimed bound.
Combining Lemma 4.11 and 4.12, we obtain the following result:
T
heorem 4.13. Assume that (H3) and (H4) hold. Then
|φ
c
− Iφ
µ
|
H
1
(X
c
)
≤
τ
α
+
2β
α
C
h k φ
′′
c
k
L
2
(Ω
M
)
,
where τ is defined by (4.37) and C only depends on Ω.
We now address the question of how to define the partition Ω = (0, L) = Ω
M
∪Ω
µ
.
Our aim is to upper-bound τ that appears in the estimate of Theorem 4.13. We use the
following result, which can be proved by Taylor expansion:
