Ellis A.M., Feher M., Wright T. Electronic and Photoelectron Spectroscopy: Fundamentals and Case Studies
Подождите немного. Документ загружается.

21 ZEKE spectroscopy of Al(H
2
O) and Al(D
2
O)
175
r
Al-O
/Å
Al + H
2
O
Al
+
+ H
2
O
IE(Al)
n
00
D
0
+
D
0
Al(H
2
O)
+
Al(H
2
O)
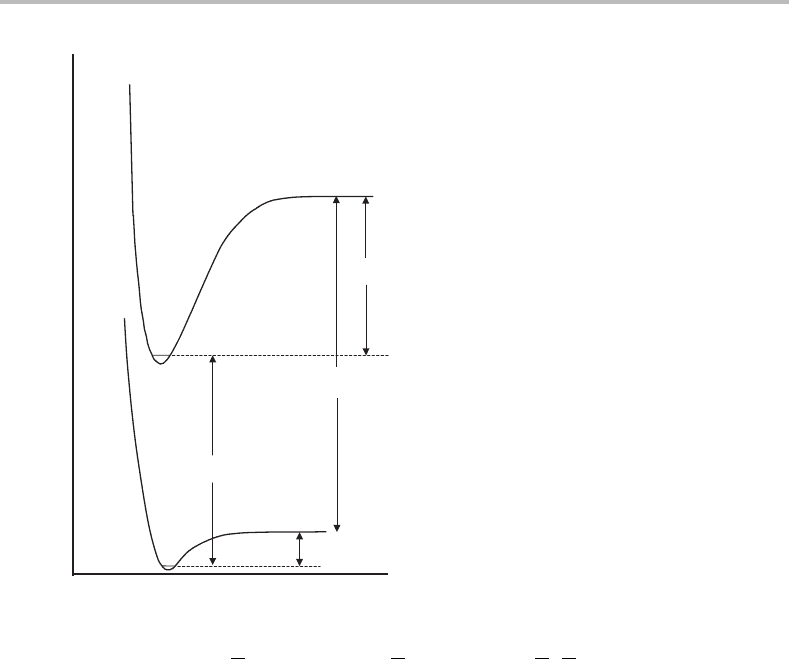
Figure 21.3 Schematic potential energy curves for Al(H
2
O). The potential energy is assumed to be a
function of only the Al
O distance, i.e. the O H bonds and the H O H angle are fixed. The quantit-
ies shown are as follows: D
0
= dissociation energy of neutral complex; D
+
0
= dissociation energy of
the cation; ν
00
is the energy of the 0
0
0
transition; IE(Al) = ionization energy of the aluminium atom.
21.3 Dissociation energies
An energy cycle, summarized in Figure 21.3, can be used to link the dissociation energies
of the neutral and cationic complexes. The dissociation energy of the neutral complex, D
0
,
to give an Al atom and a free H
2
O molecule, is related to that of the cation (D
+
0
)bythe
expression
D
0
= v
00
+ D
+
0
− IE(Al) (21.1)
where ν
00
is the energy of the 0
0
0
(electronic origin) transition and IE(Al) is the ionization
energy of the aluminium atom. Notice that the 0
0
0
transition energy in this case is identical
to the adiabatic ionization energy of the Al-H
2
O complex.
The electronic origin transition is readily identified from the ZEKE spectrum. The
main vibrational progression is short, with the first member being relatively intense. There
are no further members to lower energy and so the 0
0
0
transition is undoubtedly the first
observed member of the progressions for Al(H
2
O) and Al(D
2
O) shown in Figure 21.1.
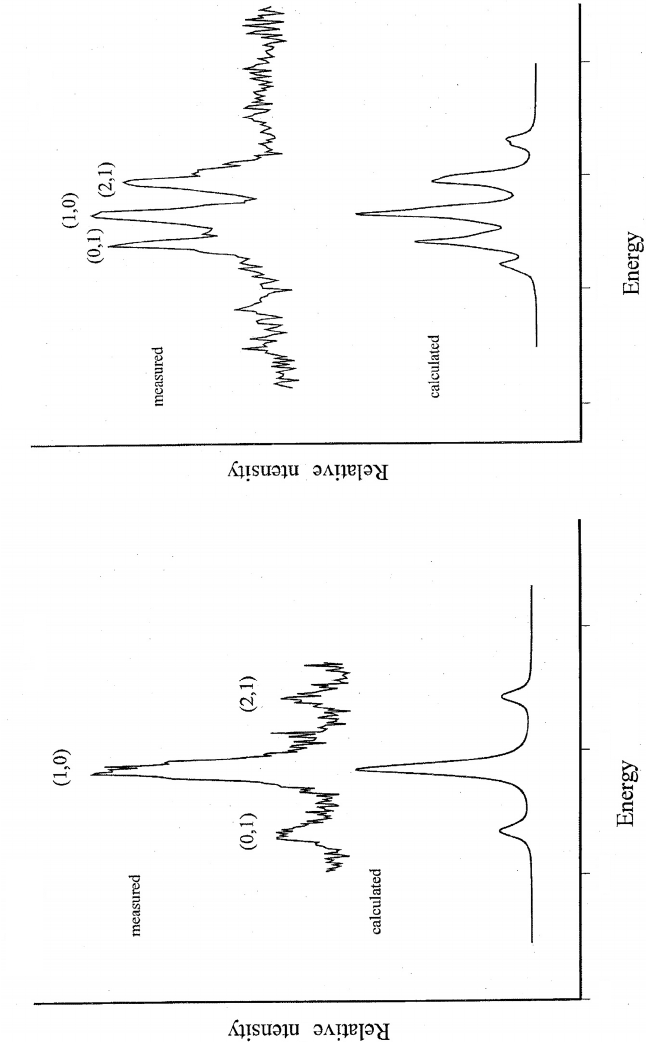
A1
+
-- H
2
O
A1
+
-- D
2
O
+
+
(cm
−1
)
i
i
40940
40990 41040 41090
41225
41275
(cm
−1
)
41325 41375
(K
a
, K
a
)
(K
a
, K
a
)
Figure 21.4 Rotational contours for Al(H
2
O) and Al(D
2
O). The bands shown are the electronic origin band (0
0
0
) for Al(H
2
O) and the 3
1
0
band for Al(D
2
O).
Beneath the ZEKE–PFI spectra are simulated band envelopes. The simulations assumed a rotational temperature of 10 K and the rotational constants in the
neutral and ionic complexes were adjusted to achieve the best agreement with experiment. (Reproduced from J. K. Agreiter, A. M. Knight, and M. A. Duncan,
Chem. Phys. Lett. 313 (1999) 162, with permission from Elsevier.)

21 ZEKE spectroscopy of Al(H
2
O) and Al(D
2
O)
177
Agreiter et al. identified the positions of these transitions as 41 018 ± 5cm
−1
for Al(H
2
O)
and 40 994 ± 5cm
−1
for Al(D
2
O). The ionization energy of Al is known rather precisely,
48 278 cm
−1
. This leaves the two dissociation energies as unknowns.
In principle, a Birge–Sponer extrapolation (see Case Study 23 for details) of the vibra-
tional progression in the ZEKE spectrum could be attempted to estimate the dissociation
energy of the cation. However, because the progression is relatively short this is likely to
give a poor approximation to the true D
+
0
.Fortunately, D
+
0
has been determined elsewhere
in a mass spectrometry experiment in which the Al(H
2
O)
+
ions were subjected to collisions
with noble gas atoms [3]. The value obtained was 8700 ± 1260 cm
−1
.
Substituting the above values into equation (21.1), we find that the dissociation energy
of the neutral complex is 1440 ± 1260 cm
−1
. The precision on this value is poor and so it
is difficult to draw firm conclusions. However, as pointed out by Agreiter et al.,ifthe mean
value of 1440 cm
−1
is taken as representative, this indicates that the neutral complex might
be rather strongly bound for this type of complex. A possible explanation for this is given
in the next section.
21.4 Rotational structure
At higher resolution some coarse rotational structure is resolved in the ZEKE spectra of
Al(H
2
O) and Al(D
2
O) (see Figure 21.4). At the relatively low resolution of the ZEKE data,
the fine detail of the rotational structure is not revealed. Nevertheless, it is still possible to
extract some useful information on the molecular structures.
If C
2v
symmetry applies to both states, then although the neutral and ionic complexes
will be asymmetric rotors, they will approximate prolate symmetric tops. In this limit the a
inertial axis lies along the Al
O bond and therefore the A rotational constant is determined
solely by the distance of the two H atoms from this axis. In a free water molecule the
corresponding rotational constant is approximately equal to 14.5 cm
−1
.
In a prolate symmetric top, the observed rotational structure depends on whether the
transition moment is parallel or perpendicular to the a axis. In the parallel case, the selection
rules are
K = 0 and J = 0, ±1
whereas for a perpendicular transition
K =±1 and J = 0, ±1
At the relatively low resolution in the ZEKE experiments, the only structure that could
possibly be resolved is the coarse structure due to K =±1 transitions. It can therefore
be concluded that the transition moment is perpendicular to the a axis.
2
Combining the
K =±1 selection rule with the formula for the energies of prolate symmetric rotors
2
In near-prolate asymmetric rotors there are two ‘perpendicular’ inertial axes, b and c. The rotational structure for
transition moments directed along these axes will differ, noticeably so if the corresponding rotational constants B
and C differ substantially. It turns out that for Al(H
2
O) a b-type transition gives the best agreement with experiment.

178 Case Studies
(equation (6.15)), a set of K sub-bands is expected in the perpendicular case with adjacent
pairs separated by ∼2A (since A B in Al(H
2
O)). The structure resolved in Figure 21.4
is consistent with this prediction. A strong central band is observed corresponding to the
K
+
= 1 ← K = 0 sub-band. The P, Q, and R branch structure expected for this sub-band is
unresolved in the ZEKE experiments. Either side of the central band are two weaker transi-
tions originating out of the first excited K level, i.e. K
+
=0 ←K =1 and K
+
=2 ←K =1.
These weaker bands are separated from the strongest band by ∼28 cm
−1
for Al(H
2
O), i.e.
∼2A.InAl(D
2
O) the A constant will be a factor of two smaller and the actual band sep-
arations reflect this. In both isotopomers the populations of K > 1levels are too small to
register observable structure.
The comments above are consistent with the assumed C
2v
symmetries for both neutral
and cationic complexes. However, there is a further test that can be applied to the rotational
structure to establish whether this symmetry really is applicable. In a C
2v
geometry the
two H atoms are equivalent and can be interchanged by a C
2
rotation about the a axis. It
is therefore necessary to consider the effect of nuclear spin statistics (see Appendix F)in
analysing the rotational structure. We will not attempt to derive the nuclear spin statistics for
this particular case, but merely note the result. If the complex has C
2v
symmetry then nuclear
spin statistics introduces a 3:1 degeneracy ratio for odd:even levels of K.
3
The population
of odd K levels is therefore boosted by a factor of three compared with even K levels. The
effect of this is to increase the intensities of the K
+
= 0 ← K = 1 and K
+
= 2 ← K = 1
sub-bands relative to K
+
= 1 ← K = 0.
Simulations of the rotational structure by Agreiter et al. show that these nuclear spin
statistics do not hold. In particular, the K
+
= 0 ← K = 1 and K
+
= 2 ← K = 1 sub-bands
are far weaker than expected for a C
2v
geometry. The simulated spectra shown beneath the
actual ZEKE spectra in Figure 21.4 were generated assuming a non-planar (C
s
) structure for
the neutral complex. Ab initio calculations on Al(H
2
O) and Al(H
2
O)
+
had been attempted
by several groups prior to the ZEKE studies [3–5]. All agree that the cation is planar, but
there is disagreement on whether the neutral complex is planar or not. The evidence from
the ZEKE work suggests that the neutral complex is non-planar.
21.5 Bonding in Al(H
2
O)
The simulated rotational structure in Figure 21.4 was obtained with a value of 11.75 cm
−1
for the A rotational constant in the neutral complex. This is significantly smaller than the
value in Al
+
(H
2
O), which is similar to that expected for a free water molecule. A smaller
value in the neutral complex could be obtained by a substantial lengthening of the O
H
bonds and/or an opening out of the H
O H bond angle; however, the changes required in
these structural parameters are unreasonably large for such a weakly bound complex. The
more likely explanation, already hinted at in the previous section,isthat the complex is
non-planar. Agreiter et al. were unable to suggest a unique equilibrium structure based on
3
The deuterium nuclei are bosons and therefore a different nuclear spin degeneracy ratio of K = odd:even = 2:1
applies for Al(D
2
O) in C
2v
symmetry.

21 ZEKE spectroscopy of Al(H
2
O) and Al(D
2
O)
179
the limited rotational structure in their ZEKE spectra, but they estimate a distortion from
planarity of 30–40
◦
.
This non-planarity is taken as evidence for some covalent bonding. The best estimates for
the Al
O binding energy from ab initio calculations fall in the range 30–40 kJ mol
−1
[6],
which corresponds to 2500–3300 cm
−1
. This is still a weak bond compared to typical cova-
lent bond energies, but it is larger than expected on the basis of van der Waals forces alone.
The ab initio estimates suggest that the mean value for the binding energy derived earlier,
from a combination of the cation dissociation energy and the ZEKE data, underestimates
the true bond energy in Al(H
2
O).
References
1. J. K. Agreiter, A. M. Knight, and M. A. Duncan, Chem. Phys. Lett. 313 (1999) 162.
2. F. Misaizu, K. Tsukamoto, M. Sanekata, and K. Fuke, Z. Phys. D. 26 (1993) 177.
3. N. F. Dalleska, B. L. Tjelta, and P. B. Armentrout, J. Phys. Chem. 98 (1994) 4191.
4. S. Sakai, J. Phys. Chem. 97 (1993) 8917.
5. B. S. Jursic, Chem. Phys. Lett. 237 (1998) 51.
6. T. F ¨angstr¨om, S. Lunell, P. Kasai, and L. Eriksson, J. Phys. Chem. A 102 (1998) 1005.

22
Rotationally resolved electronic
spectroscopy of the NO free
radical
Concepts illustrated: REMPI spectroscopy; cooling in molecular beams; rotationally
resolved spectroscopy of an open-shell molecule; Hund’s coupling cases.
A rotationally resolved electronic spectrum of NO is shown in Figure 22.1. This was obtained
for NO seeded into a very cold argon molecular beam. The electronic transition excited is
the lowest energy allowed transition of the molecule and the spectrum was obtained using
one-colour REMPI spectroscopy.
A molecular orbital diagram can easily be constructed for NO and it is readily seen
that one unpaired electron resides in a 2pπ* orbital, making the ground electronic state a
2
state. The lowest energy transition that is observed turns out to be due to excitation of
the 2pπ * electron up into a previously vacant σ orbital, leading to an excited electronic
state of symmetry which is ‘Rydberg’ in character. A Rydberg state is essentially one
where the electron resides in an orbital that is large compared to the remaining core (NO
+
in this case), and the Rydberg energy levels take on a pattern rather similar to orbitals of
atomic hydrogen. In the case of NO, the lowest state has the electron in a 3s-like orbital,
and is denoted the A
2
+
state. The A refers to the fact that this is the lowest optically
accessible excited electronic state. The electronic transition therefore labelled as A
2
+
←
X
2
electronic transition.
The first thing to note is that the spectrum consists of more than one line; attempts to cool
the molecular beam further lead to a slightly simpler spectrum consisting of three lines, but
further cooling does not significantly change the spectrum. We generally expect a single
rotational line for a closed-shell molecule in the limit of zero absolute temperature, with
this line corresponding to a transition from the lowest rotational level (J
=0) in the ground
electronic state to the J
= 1level in the upper electronic state.
1
The additional lines for NO
1
A closed-shell diatomic molecule will always have a
1
+
electronic ground state. If the excited state is also a
1
+
state then the rotational selection rule is J =±1, i.e. the Q branch is absent. If the transition is to a
1
excited
state then the selection rule is modified to J = 0, ±1. However, the lowest possible value of J in a
1
state is J = 1
and so the first member of the Q branch is Q(1). In the limit of T = 0Kthe J = 1levelin a
1
+
state will not be
populated and therefore, despite the possibility of Q branch transitions, only the R(0) transition can be observed.
180
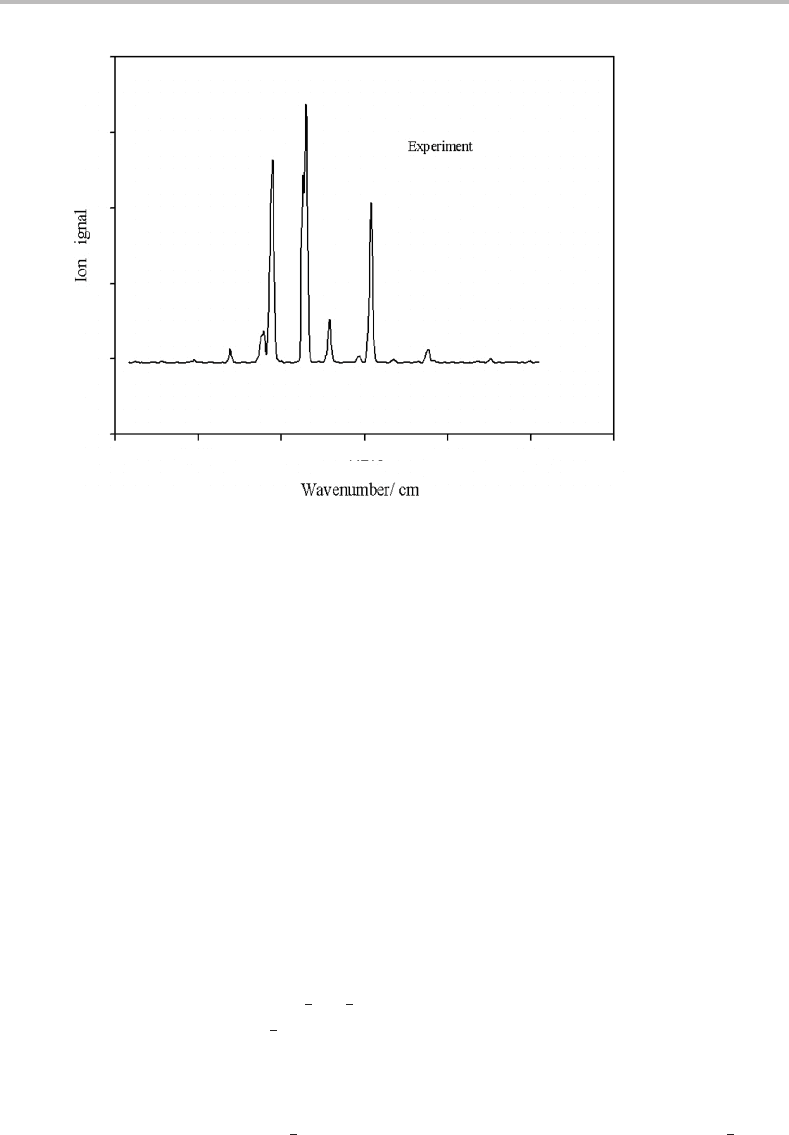
22 Rotationally resolved spectroscopy of NO free radical
181
s
44180
44190 44200
44210
44220 44230 44240
−1
Figure 22.1 One-colour (1 + 1) REMPI spectrum of the NO A
2
+
← X
2
electronic transition
recorded under molecular beam conditions.
must be the result of its open outer electronic shell, and in order to explain these lines it is
necessary to consider how the rotational energy levels of open-shell molecules differ from
closed-shell molecules.
The key thing to note is that open-shell molecules have spin and orbital angular momenta
associated with the unpaired electron(s), and these angular momenta can couple with the
rotational angular momentum of the molecule. This coupling can occur in several ways, but
the two most common are outlined in Appendix G and are known as Hund’s cases (a) and
(b) – a fuller account of Hund’s coupling cases may be found in References [1] and [2]. It
is known that the X
2
state of NO closely matches Hund’s case (a) behaviour, the reason
being the large magnitude of the spin–orbit coupling (the splitting between the
2
1/2
and
2
3/2
spin–orbit sub-states is >120 cm
−1
) relative to the rotational constant (<2cm
−1
).
The A
2
+
state has no orbital angular momentum and therefore exhibits Hund’s case
(b) behaviour.
In the X
2
state the spin and orbital angular momenta couple together to give a total
electronic angular momentum along the internuclear axis, which is represented by the quan-
tum number ,where =
1
2
or
3
2
.Aformal definition of is given in Appendix G.It
turns out that the =
1
2
spin–orbit component is the lower in energy. Both spin–orbit
components will have associated with them a series of rotational energy levels formed
by coupling with R,where R is the rotational angular momentum of the molecule.
The coupling together of and R gives a total angular momentum denoted by quantum
number J. Since the =
3
2
manifold lies more than 120 cm
−1
above the =
1
2
mani-
fold, then under efficient jet-cooling conditions only transitions from the lower spin–orbit

182 Case Studies
J
J
1
3
5
2
4
0
1/2
5/2
7/2
9/2
11/2
13/2
15/2
17/2
J
3/2
5/2
7/2
9/2
11/2
13/2
15/2
17/2
2
Π
3/2
2
Π
1/2
3/2
5/2
7/2
9/2
11/2
1/2
1/2
3/2
5/2
7/2
9/2
Q
11
(1/2)
Q
12
(
1/2
)
R
11
(1/2)
R
12
(1/2)
P
21
(3/2)
N
1
3
5
2
4
0
6
7
8
N
1
3
5
2
4
0
6
7
8
N
2
Σ
+
Figure 22.2 Rotational energy level scheme in the A
2
+
and X
2
states of NO. The diagram is not
to scale. The transitions responsible for the main lines seen in Figure 22.1 are also shown.

22 Rotationally resolved spectroscopy of NO free radical
183
component should be observed. The energy level pattern is described by equation (G.2)in
Appendix G.
As already mentioned, the A
2
+
state follows Hund’s case (b) coupling, and in this case
the spin angular momentum of the unpaired electron cannot couple to the orbital angular
momentum, since the latter is absent. However, to be consistent with other Hund’s case
(b) molecules, cases where the orbital angular momentum might not be zero, the quantum
number N is used to represent the total angular momentum (orbital + rotational) minus
spin. Here, the spin angular momentum couples to N to give the total angular momentum
J. This has the effect of splitting each N level into two sub-levels, the splitting being known
as spin–rotation splitting. One level in the spin–rotation pair has J = N +
1
2
and the other
J = N −
1
2
. The former levels are referred to as the F
1
manifold, and the latter as the F
2
manifold, with the energies being given by
F
1
(N ) = BN(N + 1) +
1
2
γ N
F
2
(N ) = BN(N + 1) −
1
2
γ (N + 1)
where the quantity γ is known as the spin–rotation constant (which can be positive or
negative, but is usually >0).
The arrangements of the rotational levels in the upper and lower electronic states of NO
are illustrated in Figure 22.2. Note that for the lowest level in the
2
+
state there is no
spin–rotation splitting since the molecule is not rotating (N = 0) in this level, and so there
is no rotational angular momentum to which S can couple.
At the very lowest temperatures, we expect that only the lowest level in the X
2
state, the
J =
1
2
level of the =
1
2
manifold, will be populated. Since the transition involves = 0,
the selection rule for J is J = 0, ± 1. Consequently, the J =
1
2
and
3
2
levels in the
2
+
state
can be accessed from the J =
1
2
level in the X
2
state. Because of spin–rotation splitting
there are actually four accessible levels, which we denote as (N, J), as follows:
0,
1
2
,
1,
1
2
,
1,
3
2
, and
2,
3
2
The possible transitions can be labelled P, Q, and R in the usual manner where these denote
J =−1, 0 and +1, respectively. The full labels used are Q
11
(
1
2
), Q
12
(
1
2
), R
11
(
1
2
), and R
12
(
1
2
),
where the first subscript labels the initial F manifold and the second labels the terminating
manifold. The number in parentheses is the value of J in the lower state, J
.
Figure 22.3 shows simulations of the A
2
+
← X
2
spectrum of NO at temperatures
of 1, 3, and 10 K. The procedure employed to generate simulations like these is outlined
in Appendix H.Atthe lowest temperature only three lines appear, which is consistent with
the conclusion earlier based on experimental studies but which apparently contradicts the
prediction above of a minimum of four rotational lines even at a temperature of abso-
lute zero. However, the astute reader might attach significance to the fact that the middle
line in the1Ksimulation is considerably more intense than the other two. Referring to the
energy level diagram, and considering the transitions described above, we see that two of the
transitions terminate at N = 1intheA
2
+
state, but with different J values. The splitting
between these two levels is determined by the spin–rotation constant, ,which is normally
very small compared to the rotational constant. The resolution used in the simulation is too
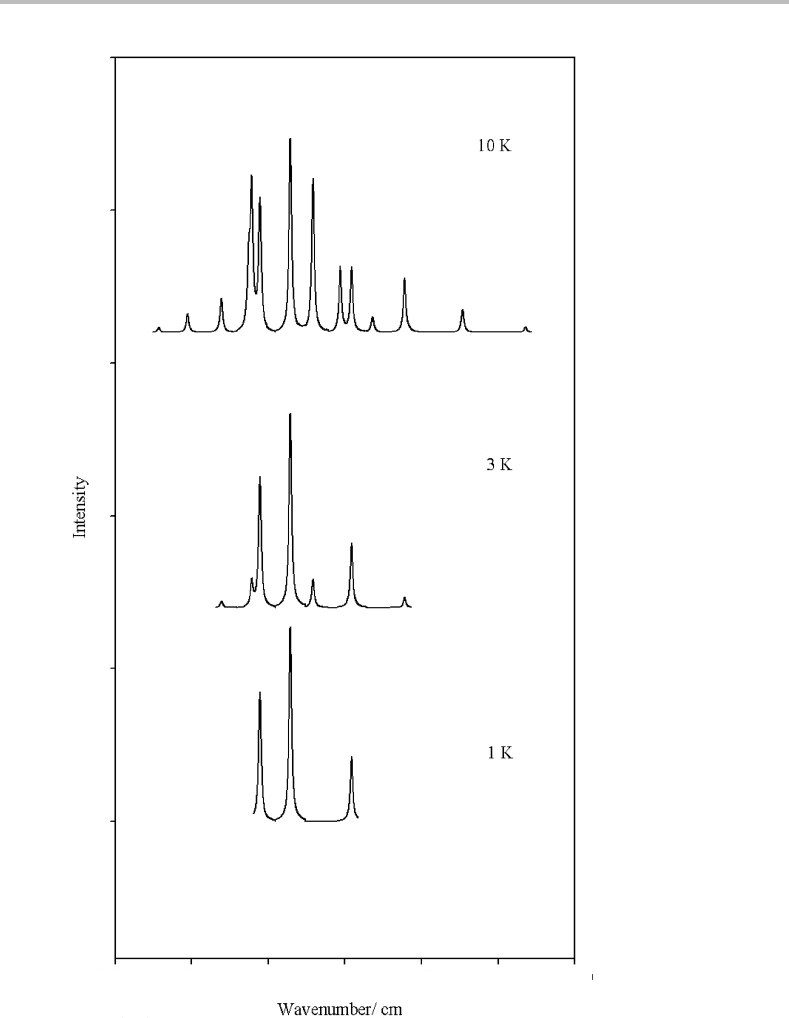
184 Case Studies
44180
44190
44200
44210 44220 44230 44240
−1
Figure 22.3 Simulations of the A
2
+
← X
2
spectrum of NO at 1, 3, and 10 K.
