Елисеев В.В. Механика деформируемого твердого тела

Подождите немного. Документ загружается.

4.8 Кручение стержней

-l

Рис. 7

При x

= 0 имеем

u = Re g =



0, |x

| > l

− x

, |x

| < l

, (4.7.7)

где знак (+) относится к верхнему берегу раз-

реза, а (−) — к нижнему. Разрыв u означает, что

разрез существует реально.

Напряжения таковы:

− iτ

= −iτ

√

− l

−−−→

z→∞

−iτ. (

4.7.8)

На бесконечности τ

= 0, τ

= τ . Итак, имеем сдвиг (в плоскости x

)

пространства с разрезом (трещиной). На фронте трещины

(z = ±l) напряжения неограниченно возрастают — это нельзя объяснить

так элементарно, как в случае сосредоточенной силы.

Рассмотрим другой пример:

g(z) =



z +



⇒ τ

− iτ

= τ



1 −



. (4.7.9)

Здесь тоже сдвиг пространства с напряжением τ — но в плоско сти x

На окружности |z| = a

z = ae

iθ

, τ

− iτ

= τ



1 − e

−2iθ



, n ·τ = τ

cos θ + τ

sin θ = 0 —

вместо трещины на рис. 7 имеем окружность радиусом a. Максимум мо-

дуля напряжения

+ τ

равен 2τ и достигается при θ = ±π/2.

В заключение отметим, что перемещение u удовлетворяет тому же

уравнению, что и двумерное стационарное температурное поле:

∇·(µ∇u) + f = 0. (4.7.10)

4.8 Кручение стержней

Сен-Венан рассмотрел задачу о равновесии цилиндра с нагрузкой на тор-

цах (рис. 8). Поверхностные силы в граничных условиях

Классическая линейная упругость

Рис. 8

z = z

: k ·T = p (x

) ,

z = 0 : −k ·T = p

) (4.8.1)

имеют следующие главные вектор и момент

Q =

p dF, M =

x × p dF — (4.8.2)

интегралы по сечению стержня.

Закон суперпозиции позволяет выделить четыре задачи: 1) Q = Qk,

M = 0 — о растяжении; 2) Q = 0, M ⊥k — о «чистом» изгибе; 3) Q = 0,

M = Mk — о кручении; 4) Q ⊥k, M = 0 — об изгибе силой. Задачи

расположены в порядке возрастания сложности. Во всех книгах по теории

упругости представлена задача кручения — достаточно простая, но уже

нетривиальная.

Ясно, что при кручении в сечениях z = const возникают касательные

напряжения. Попробуем в тензоре напряжений оставить только их:

T = τ k + kτ , τ = τ

. (4.8.3)

Из условий равновесия части стержня в промежутке (z, z

) следует

τ dF = 0,

x × τ ·k dF = M. (4.8.4)

Оператор Гамильтона представим далее в виде ∇

= ∇ + k∂

, где

∇ = e

∂

— «двумерный». Используем уравнение баланса сил

∇

· T = 0 ⇒ ∇·τ = 0, τ = τ (x) . (4.8.5)

Далее по уравнению Бельтрами

∆

T +

1 + ν

∇

σ = 0 ⇒ ∆τ = 0. (4.8.6)

Из (4.8.5) и (4.8.6) следует

τ = ∇ϕ × k, ∆ϕ = const ≡ −2µα. (4.8.7)

Введена функция напряжений ϕ, осталось поставить граничное условие на

контуре сечения ∂F и определить константу α.

4.8 Кручение стержней

Орт n на ∂F является нормалью и на контуре, и на боковой цилиндри-

ческой поверхности. Имеем

n · T

= 0 ⇒ n ·τ = 0 = ∇ϕ · l = ∂

ϕ, l = k × n, (4.8.8)

где l — дуговая координата на ∂F , l — орт касательной.

Для односвязного сечения границей ∂F является только наружный кон-

тур. Без ущерба для общности можно считать ϕ



∂F

= 0 (ϕ определена с

точностью до аддитивной константы).

Осталось рассмотреть крутящий момент. Из (4.8.4) и (4.8.7) имеем

M = −

x · ∇ϕ dF = 2

ϕ dF −

n ·x ϕ dl. (4.8.9)

Контурный интеграл пропадает благодаря граничному условию. Можем

найти α, поскольку ϕ ей пропорциональна.

Полученные результаты перепишем в виде

ϕ = µαΦ, ∆Φ = −2, Φ



∂F

= 0,

M = µαC, C = 2

Φ dF, τ = µα∇Φ × k. (4.8.10)

Здесь вся информация о напряжениях при кручении. C называется геомет-

рической жёсткостью.

Обратимся к перемещениям. Они определяются интегрированием со-

отношений Гука

∇

= (∇ + ∂

k) (u

⊥

+ u

2µ



T −

1 + ν

σE



2µ

(τ k + kτ ) ⇒ ∇u

⊥

= 0 (a), ∂

= 0 (b),

∇u

+ ∂

⊥

2µ

τ = α∇Φ × k (c). (4.8.11)

Из (a,b) имеем

⊥

= U (z) + ω(z)k × x, u

= αW (x), (4.8.12)

что позволяет переписать (4.8.11):

α (∇W − ∇Φ × k) + U

+ ω

k × x = 0. (4.8.13)

Классическая линейная упругость

Применим операцию (∇ × ):

α∇ × (∇Φ × k) = ω

∇ × (k × x) ⇒ −α∆Φ = 2ω

⇒ α = ω

. (4.8.14)

Найден геометрический смысл α — это угол закручивания на единицу дли-

ны. Можем представить (4.8.13) в виде



∇W − ∇



Φ +



× k



= −U

— (4.8.15)

это равно некоторой константе a, поскольку слева функция от x, а справа —

от z. При a = 0

U = const, ∇W = ∇



Φ +



× k — (4.8.16)

условия Коши — Римана. Если же a 6= 0, получим дополнительные слагае-

мые перемещения твёрдого тела — они всегда появляются при определении

перемещений по деформациям.

Гармоническая «функция депланации» W определяется по «функции

Прандтля» Φ посредством (4.8.16). Прандтль обнаружил аналогию задач для

Φ и для прогиба мембраны.

Рассмотрим примеры. Для эллиптического сечения имеем

∂F :

= 1, Φ = A



1 −

−



, A =

+ b

= −2µα

+ b

, τ

= 2µα

+ b

C = 2

Φ dF = π

+ b

. (4.8.17)

При вычислении C ввели новые координаты: x

= aρ cos θ, x

= bρ sin θ

с якобианом J = abρ. Отметим, что максимум напряжения — на концах

короткого диаметра.

Депланация находится из (4.8.16):

∂

W = ∂

Φ + x

, ∂

W = −∂

Φ − x

⇒ W =

− a

+ b

. (4.8.18)

В круге (a = b) депланации нет, подтверждается элементарная теория

из сопротивления материалов.

4.8 Кручение стержней

Рис. 9

Более сложный пример — круговое сечение

с выточкой (рис. 9). На большой окружности

r = 2R cos θ, на малой r = a. Функция

Φ =



r −



(2R cos θ − r) (4.8.19)

является решением. Она содержит гармони-

ческие слагаемые — реальные части функ-

ций комплексного переменного: r cos θ = Re z,

cos θ/r = Re 1/z.

Определив касательное напряжение

τ = µα



∂



Φ × k,

обнаружим максимум при θ = 0, r = a; при малой выточке он примерно

вдвое больше, чем без неё.

Вернёмся к теории и отметим теорему о циркуляции напряжений:

µα

τ · dr =

∂

Φ dl = −2F — (4.8.20)

для любого замкнутого контура с площадью F внутри. Доказательство ос-

новано на (4.8.15):

∇Φ × k =

µα

τ = ∇W − x × k,

∇W · dr = 0,

k × dr = −n dl,

n ·x dl = 2F.

Для односвязного сечения теорема является тожде ством и не даёт новой

информации:

Рис. 10

∂

Φ dl =

∆Φ dF = −2F. (4.8.21)

Иное — в случае многосвязного сечения

(рис. 10). На каждом из граничных контуров Γ

Φ = const = C

, но эти постоянные различны.

Можно принять Φ



= 0 и представить реше-

ние в виде

Φ = Φ

∆Φ

= −2, Φ



∂F

= 0, ∆Φ

= 0, Φ



= δ

. (4.8.22)

Классическая линейная упругость

Теорема о циркуляции позволяет найти C

. Записав (4.8.20) для каждого из

контуров Γ

, получим линейную алгебраическую систему

∂

dl +

∂

dl = −2F

. (4.8.23)

Почему случай многосвязного сечения потребовал особого рассмотре-

ния? Потому, что здесь возможны дислокационные воздействия. Теорема о

циркуляции выражает их отсутствие. В противном случае

du = b — «вектор Бюргерса винтовой дислокации».

В задаче о кручении применяются и вариационные методы. Краевой

задаче (

4.8.10) для Φ соответствует вариационное уравнение

(∆Φ + 2) δΦ dF = 0, Φ



∂F

= 0. (4.8.24)

Можно использовать процедуру Ритца

Φ =

(x), ϕ



∂F

= 0,

(∆Φ + 2) ϕ

dF = 0.

Но для вытянутых сечений более эффективен метод сведения к обыкно-

венным дифференциальным уравнениям (Л. В. Канторовича). Для прямо-

угольного сечения |x

| 6 a, |x

| 6 b  a будем искать приближённое

решение

Φ = ϕ(x

)



− x



, (4.8.25)

где ϕ — неизвестная варьируемая функция; ϕ(±a) = 0. Из (4.8.24) получаем

одномерную вариационную постановку

−a



− ϕ + 1



δϕ dx

= 0 (4.8.26)

с решением

ϕ = 1 −

⇒

⇒ C = 2

Φ dF =

1 −

. (4.8.27)

Найденные значения C практически совпадают с точными, полученными

методом собственных функций.

4.9 Плоская задача

Плоской деформацией называются решения со следующим полем переме-

щений

u(x

, z) = u

) e

≡ u

⊥

(x) , (4.9.1)

перпендикулярным оси z и независящим от z. Так будет в длинном цилин-

дре с нагрузками f

⊥

(x), p

⊥

(x).

Оператор Гамильтона и тензор деформации «двумерны», но у напряже-

ния есть компонента σ

τ = τ

⊥

+ σ

kk, σ

= νσ

⊥

(Eε

= 0 = σ

− νσ

⊥

) . (4.9.2)

Ограничимся решениями без объёмных сил. В этом случае вводится

функция напряжений Эри:

∇·τ

⊥

= 0 ⇒ τ

⊥

= −k × ∇∇Φ × k. (4.9.3)

Для обоснования рассмотрим уравнения в компонентах

∂

+ ∂

= 0 ⇒ τ

= ∂

, τ

= −∂

;

∂

+ ∂

= 0 ⇒ τ

= ∂

, τ

= −∂

;

= τ

⇒ Φ

= ∂

Φ, Φ

= ∂

Φ ⇒

⇒ τ

= ∂

Φ, τ

= ∂

Φ, τ

= −∂

∂

Φ. (4.9.4)

Знаменитое бигармоническое уравнение

∆∆Φ = 0 (4.9.5)

следует из уравнения Бельтрами:

∆τ + ∇∇ σ

⊥

= 0 ⇒ ∆∂

Φ + ∂

∆Φ = 0, . . .

Рис. 11

Отметим некоторые общие правила постро-

ения бигармонических функций. Если g(x) —

гармоническая, то будут бигармоническими

Φ : x

g, x

g. (4.9.6)

Однако необходимо поставить граничные

условия к (4.9.5). В каждой точке граничного кон-

тура (рис. 11) их два. Сначала имеем

n ·τ = −n × k · ∇∇Φ × k = ∂

∇Φ × k = p. (4.9.7)

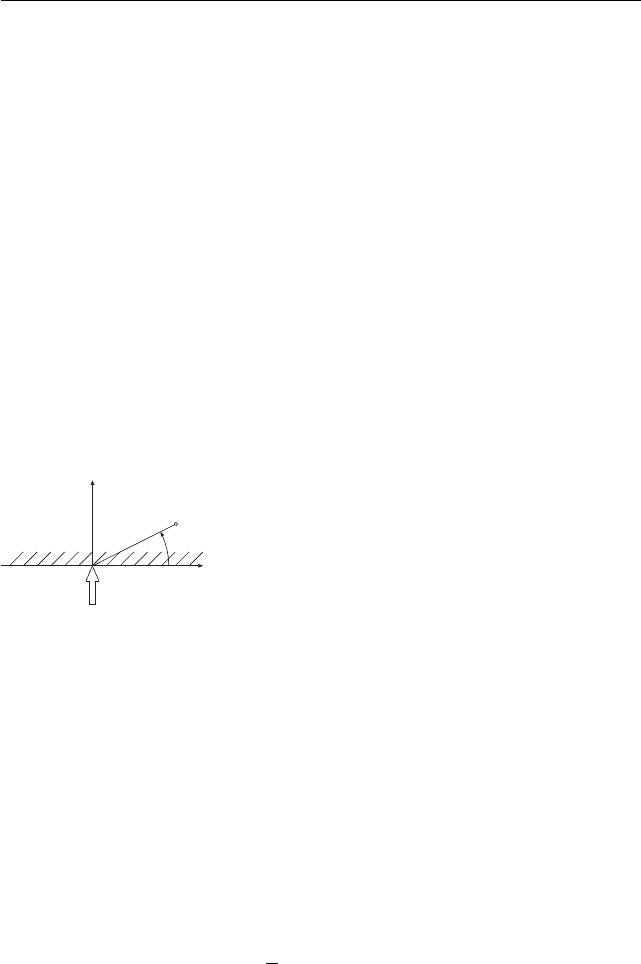
Классическая линейная упругость

Далее выбираем какую-либо точку O на контуре за начальную (l = 0) и

находим главный вектор нагрузок на участке OM:

P =

p dl = ∇Φ



×k. (4.9.8)

Но Φ определена с точностью до произвольного линейного слагаемого

(a ·x + const, a = const), поэтому можно ∇Φ



= 0. Тогда

∂

Φ = −P

. (4.9.9)

Второе условие связано с моментом (относительно «крайней» точки):

Φ = M ≡

(x − x

) × p dl · k (4.9.10)

(интегрируется по частям).

Рис. 12

Для примера рассмотрим задачу Фламана о

полуплоскости x

> 0 с сосредоточенной нор-

мальной силой на границе (рис. 12). В каче-

стве начальной точки примем x

→ −∞. Тогда

P = 0 при x

< 0 и P = Qe

для x

> 0, на

всей оси x

: ∂

Φ = −∂

Φ = 0. Второе условие

Φ =



0, x

< 0

−Qx

, x

> 0

. (4.9.11)

Учитывая соображения размерности, решение ищем в виде

Φ = Qrf(θ) (4.9.12)

(безразмерная f не может зависеть от размерного r). Для f(θ) можно вы-

вести обыкновенное дифференциальное уравнение. Но с помощью (4.9.6)

легко строится общее решение

f = C

cos θ + C

sin θ + C

θ cos θ + C

θ sin θ. (4.9.13)

Четыре постоянные находятся из граничных условий f(0) = −1, f(π) =

(0) = f

(π) = 0. В итоге получим

Φ =

Qrθ cos θ + . . . , (4.9.14)

4.9 Плоская задача

где отброшены линейные по x слагаемые. Напряжения таковы

⊥

= −k ×



∂



Φ × k ⇒

⇒ σ



∂



Φ = −

πr

sin θ,

= ∂

Φ = 0, τ

rθ

= −∂



∂



= 0. (4.9.15)

При r → 0 τ = O(r

−1

), что связано с балансом сил. Линии уровня

= const — окружности, касающиеся оси x

в точке x = 0.

Обратимся к перемещениям. Чтобы получить их общее представление,

заметим, что гармоническая функция ∆Φ является реальной частью неко-

торой регулярной функции S

(z) (z = x

+ ix

S = S

+ iS

, S

= ∂

+ i∂

= ∂

− i∂

∆Φ = ∂

= ∂

. (4.9.16)

Тогда легко интегрируются соотношения закона Гука

2µ∂

= τ

− νσ

⊥

= −∂

Φ + (1 − ν) ∂

⇒

⇒ 2µu

= −∂

Φ + (1 − ν)S

+ f

2µu

= −∂

Φ + (1 − ν)S

+ f

);

µ (∂

+ ∂

) = τ

⇒ f

) = −f

) = −ω = const . (4.9.17)

Последнее означает: f

и f

определяют перемещение твёрдого тела и мо-

гут быть отброшены. Итоговая формула имеет вид

2µu = −∇Φ + (1 − ν)S — (4.9.18)

с вектором, соответствующим комплексному числу S.

В задаче Фламана

∆Φ = −

πr

sin θ = Re



−

2iQ

πz



⇒ S = −

2iQ

ln z =

(θ −i ln r) ,

∇Φ =

θ cos θ + e

(cos θ − θ sin θ)] ,

2µu



sin 2θ + (1 − 2ν) θ



2µu

= −



cos

θ + 2 (1 − ν) ln r



. (4.9.19)

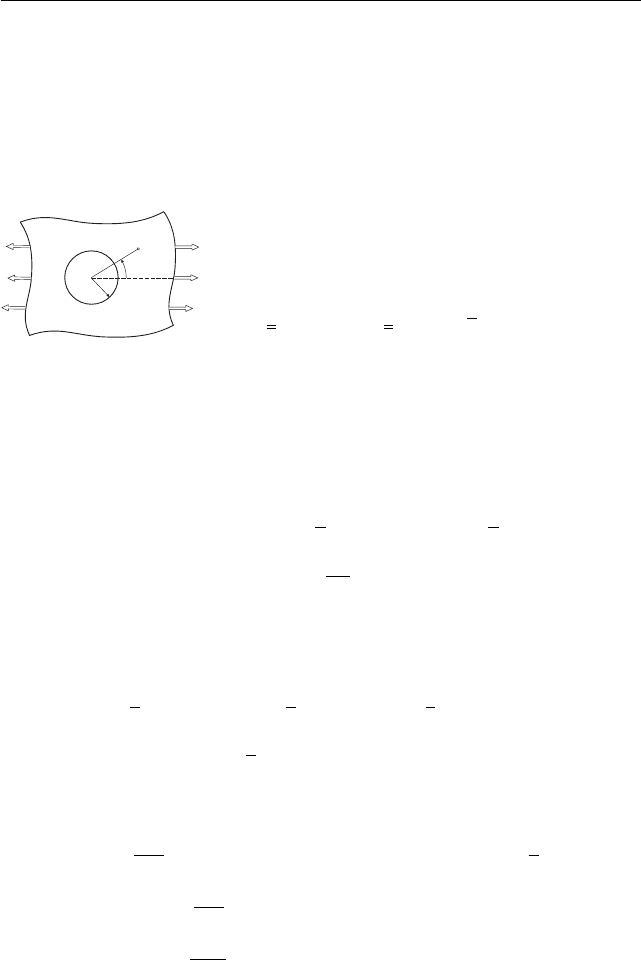
Классическая линейная упругость

Эти выражения удивляют: u

постоянно на лучах θ = const и имеет разрыв

при r = 0, u

неограниченно растёт при r → ∞. . . Естественно лишь то,

что u = O (ln r) при r → 0. Но заметим, что подобные странные явления

встречаются и в двумерных задачах вне теории упругости: электростатиче-

ский потенциал бесконечной прямой равномерно заряженной линии тоже

содержит ln r.

Рис. 13

Рассмотрим далее известную задачу Кир-

ша о растяжении плоскости с круговым отвер-

стием (рис. 13). Выделим возмущения, вноси-

мые отверстием:

τ = p e

+ τ

, Φ =

p x

+ Φ

. (4.9.20)

Поскольку x

= r

(1 − cos 2θ)



2, решение

ищем в виде

= f

(r) + f

(r) cos 2θ. (4.9.21)

С помощью правила (4.9.6) находим

= A

+ B

+ C

+ D

= A

+ C

+ D

. (4.9.22)

Напряжения от Φ

затухают на бесконечности, поэтому отбрасываем C

, A

и C

. При r = a равны нулю Φ и ∂

Φ:

+ f

(a) = −

+ f

(a) =

pa + f

(a) =

= −

pa + f

(a) = 0. (4.9.23)

Определив отсюда A

, B

и D

, найдём напряжения:

2σ

= 1 − η



1 − 4η

+ 3η



cos 2θ, η ≡

2σ

= 1 + η

−



1 + 3η



cos 2θ,

2τ

rθ



−1 − 2η

+ 3η



sin 2θ. (4.9.24)