Елисеев В.В. Механика деформируемого твердого тела
Подождите немного. Документ загружается.

7.6 Вращение гибкого вала в трубке-оболочке
Отметим, что кривизна k и кручение τ полностью определяются формой
трубки согласно (1.2.2, гл. 1), а k
0
и τ
0
— начальным состоянием. Основным
результатом является зависимость ϕ(l) = φ
l
(φ
0
) — для проверки (7.6.1).
Пример: форма трубки — дуга окружности, начальная форма вала —
дуга окружности другого радиуса, жёсткости на изгиб равны. В этом слу-
чае τ = τ
0
= 0 (всегда для плоской кривой), ϕ
0
= 0, k и k
0
— const,
a
1
= a
2
= a, и задача принимает вид
ϕ
00
= p
2
sin ϕ, ϕ(0) = φ
0
, ϕ
0
(l) = 0
p
2
≡ k
0
ka/a
3
. (7.6.6)
Решим по схеме (5.2.18, гл. 5):
1
2
ϕ
02
+ p
2
cos ϕ = p
2
cos φ
l
⇒ ϕ
02
= 4p
2
cos
2
φ
l
2
− cos
2
ϕ
2
;
cos
ϕ
2
= q sin ψ, q ≡ cos
φ
l
2
⇒ ϕ
0
= −2pq cos ψ,
qψ
0
cos ψ = −
ϕ
0
2
sin
ϕ
2
= pq cos ψ
q
1 − q
2
sin
2
ψ ⇒
ψ
0
p
1 − q
2
sin
2
ψ
= p;
ps =
ψ
Z
ψ
0
dψ
p
1 − q
2
sin
2
ψ
= F (ψ, q) − F (ψ
0
, q). (7.6.7)
Введение переменной ψ — известный прием интегрирования «уравне-
ния обращённого маятника». При возрастании s от 0 до l угол ϕ убы-
вает от φ
0
до φ
l
, cos ϕ/2 соответственно возрастает, а ψ возрастает от
ψ
0
= arcs in(q
−1
cos φ
0
/2) до π/2. Появляются эллиптические интегралы
первого рода — неполный и полный [45]:
F (ψ, q) =
ψ
Z
0
dψ
p
1 − q
2
sin
2
ψ
, K(q) = F
π
2
, q
. (7.6.8)
Параметр q пока неизвестен. Но он определяется из (7.6.7) при s = l:
pl = K(q) − F (ψ
0
, q) ⇒ q(φ
0
). (7.6.9)
Чтобы найти ϕ(s), необходимы эллиптические функции (Якоби) ампли-
туды и синуса:
F = F (ψ, q) ⇒ ψ = am(F, q); sin ψ = sn(F, q). (7.6.10)
171
Устойчивость равновесия
Из (7.6.7) и (7.6.9) получим
ψ = am [K(q) − p(l −s), q] , ϕ = 2 arcc os(q sin ψ). (7.6.11)
Искомая связь поворотов:
φ
0
= 2 arccos (q sn [K(q) − pl, q]) , q = cos φ
l
/2 — (7.6.12)
параметрическое задание функции φ
l
(φ
0
).
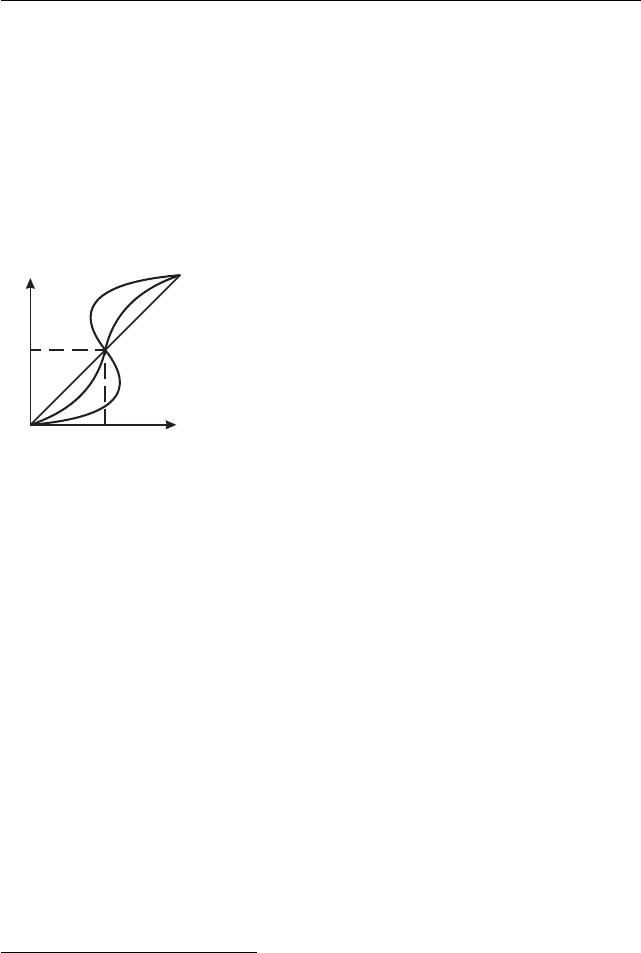
f
l
f
0
p
p
Рис. 25
Эти зависимости
1
представлены на рис. 25 —
для различных значений pl. При pl < π/2 име-
ем однозначную нелинейную зависимость, вра-
щение ведомого конца более или менее плавное.
Но в случае pl > π/2 зависимость неоднозначна,
плавное возрастание φ
l
вместе с φ
0
заканчивается
перескоком, вращение становится резко неравно-
мерным.
Если в начальном состоянии вал прямой, то
k
0
= 0, p = 0 и φ
l
= φ
0
— идеальная равномер-
ность. Но реально это недостижимо, всегда есть
искривлённость.
Библиография
Необходимые сведения из общей теории устойчивости содержатся в книге
Д. Р. Меркина [61].
Очень интересные детали и парадоксы описаны В. И. Феодосьевым
[106], Я. Г. Пановко и И. И. Губановой [75]. Нельзя не отметить книги Г. Циг-
лера [111], С. П. Тимошенко [95], а также А. С. Вольмира [17] и Н. А. Алфу-
това [4].
Сложные вопросы устойчивости оболочек рассмотрены П. Е. Товсти-
ком [100], Э. И. Григолюком и В. В. Кабановым [25].
Особенности неконсервативных задач раскрыты у В. В. Болотина [12].
1
Построены Т. В. Зиновьевой
172
Глава 8
Малые пластические
деформации
8.1 Экспериментальные данные
Прекрасная модель упругого тела построена умозрительно, без ссылки на
опыт. При описании же пластических деформаций ссылки на эксперимент
обязательны — и прежде всего на диаграмму деформирования малоуглеро-
дистой стали.
e
s
O
A
B
C
D
E
F
Рис. 26
Имеется в виду цилиндрический образец
с деформацией растяжения ε и соответству-
ющим напряжением σ. В некоей испытатель-
ной машине задаётся ε(t) (т. е. функция вре-
мени) и измеряется σ(t). На рис. 26 сплошной
линией OABCD показан процесс при задан-
ном монотонном возрастании ε от нуля (это
не график σ(ε)!). Прямой (почти «вертикаль-
ный») участок OA соответствует линейной
упругости. Далее — «площадка текучести»
AB: деформация растёт при неизменном σ.
Затем начинается «участок упрочнения» BD.
Пунктирная линия CEF получается при разгрузке: в точке C становит-
ся ˙ε < 0. Участок разгрузки CE параллелен OA, за ним следует площадка
текучести при сжатии EF , и далее упрочнение.
На рис. 26 не показаны результаты повторной нагрузки: если разгрузку
закончить где-то между C и E, то нагрузка «пойдет» по линии ECD. В
роли «предела текучести» выступит напряжение в точке C — а не в A, как
сначала.
173

Малые пластические деформации
Очень важно, что диаграмма 26 не зависит от скорости деформирова-
ния — линия OABCD одинакова для всех монотонно возрастающих функ-
ций ε(t). Разумеется, это идеализация. Но без подобных упрощений моде-
лирование невозможно.
Следует отметить эффект Баушингера: |σ
E
| < σ
A
— предел текучести
при разгрузке меньше, чем первоначальный при нагрузке.
С параллельностью участков OA и EC связано правило сложения де-
формаций: ε = ε
e
+ ε
p
, где упругая деформация ε
e
связана с напряжением
законом Гука, а пластическая деформация ε
p
начинается лишь за пределом
упругости.
Для пластичности металлов найдено объяснение на микроуровне. В
идеальных монокристаллах с периодической структурой решетки пластич-
ности нет — для сдвига по кристаллической плоскости на период потре-
бовалось бы напряжение на два порядка выше предела текучести. Пла-
стичность возникает от движения дислокаций — дефектов решетки в виде
краев не законченных плоскостей и других особых линий [49, 93]. В состо-
янии текучести дислокации легко перемещаются до остановки на границах
зерен. Заметим, что в теории упругости дислокации были описаны на чет-
верть века раньше, чем их нашли физики-экспериментаторы.
При описании пластичности изотропных материалов полезно выде-
лить в напряжениях и деформациях шаровые части и девиаторы:
ε =
1
3
θE + e, e ≡ Dev ε, τ =
1
3
σE + S, S ≡ Dev τ . (8.1.1)
Первый инвариант (след) девиатора равен нулю. В опытах обнаружено,
что эффекты пластичности проявляются лишь в девиаторах. Шаровые же
части связаны как в упругом теле: σ = θE/(1 − 2ν).
Начало пластического течения при нагрузке определяется условием те-
кучести
F (τ ) = k, (8.1.2)
где k — константа материала. В случае изотропии опытным путём найдены
два варианта:
F
1
(τ ) =
1
2
(σ
1
− σ
3
) = max t
n
, F
2
(τ ) =
q
S··S/2, (8.1.3)
нормы Треска и Мизеса. Сопоставим их для напряжённых состояний одно-
174

8.2 Определяющие уравнения
осного растяжения и чистого сдвига:
1
◦
. τ = σii, σ = σ
1
> 0, σ
2
= σ
3
= 0, F
1
= σ/2,
S = τ −
1
3
σE =
1
3
σ(2ii − jj − kk), F
2
= σ/
√
3;
2
◦
. τ = τ (ij + ji) = S, F
1
= F
2
= τ. (8.1.4)
Расхождение лишь в первом случае, но незначительное. Оба варианта при-
емлемы.
8.2 Определяющие уравнения
В теории пластичности связь напряжений и деформаций много сложнее,
чем в теории упругости. Для идеально-пластического тела общепризнано
следующее
ε = ε
e
+ ε
p
, ε
e
=
4
S··τ ,
˙
ε
p
=
0, F (τ ) < k
λ ∂F/∂τ , F = k
. (8.2.1)
Упругая деформация ε
e
связана с напряжением законом Гука (с тензором
податливости
4
S; τ
=
4
C ··ε
e
). Пластиче ская деформация ε
p
развивает-
ся лишь при достижении F предела текучести k. Формула для
˙
ε
p
выра-
жает ассоциированный закон течения, в нём содержится та же функция
F (τ ), что и в условии текучести. Скаляр λ является самостоятельной неиз-
вестной (это некий множитель Лагранжа). Появление новой неизвестной
λ компенсируется условием F = k.
К (8.2.1) необходимо добавить принцип максимума Мизеса: при задан-
ной
˙
ε
p
D(τ ) ≡ τ ··
˙
ε
p
→ max . (8.2.2)
Отсюда следует ассоциированный закон течения. Ведь имеем задачу на
условный экстремум с решением по методу Лагранжа:
D
ˆ
(τ ) = D − λF,
∂D
ˆ
∂τ
= 0 ⇒ (8.2.1).
Другим следствием (8.2.2) является выпуклость поверхности текучести:
(τ − τ
0
)··
˙
ε
p
> 0. (8.2.3)
175

Малые пластические деформации
«Концы векторов τ и τ
0
лежат на поверхности текучести, вектор ˙ε
p
направ-
лен по нормали, поверхность расположена по одну сторону от касательной
плоскости» — но эта геометрическая интерпретация необязательна.
Выясним смысл величины D, рассматривая баланс энергии. Мощность
внешних сил
Z
O
n ·τ ·
˙
u dO +
Z
V
f ·
˙
u dV =
Z
V
(∇·τ + f ) ·
˙
u + τ ··
˙
ε
dV
превышает скорость изменения механической энергии
Z
V
(Π +
1
2
ρ ˙u
2
)˙dV =
Z
V
(τ ··
˙
ε
e
+ ρ
˙
u ·
¨
u) dV
на величину
R
D dV — D есть скорость диссипации энергии в единице объ-
ёма. К заключению о максимуме D можно прийти, рассматривая обычные
силы сухого трения — их направление обеспечивает максимум диссипации.
Принцип (8.2.2) раскрывает связь τ с
˙
ε
p
и является одним из важнейших
положений теории пластичности.
При условии текучести Мизеса с F
2
(τ ) (8.1.3) ассоциированный закон
сводится к следующему
˙
ε
p
=
˙
e
p
= λS, (8.2.4)
поскольку
δF
2
=
1
2F
2
S··δS =
∂F
2
∂τ
··
δS +
1
3
δσE
=
= Dev
∂F
2
∂τ
··δS +
1
3
tr
∂F
2
∂τ
δσ ⇒
∂F
2
∂τ
=
1
2F
2
S.
Если же принять условие Треска, закон течения усложнится.
Модель идеально-пластического тела соответствует на диаграмме де-
формирования (рис. 26) участку OAB. Для описания упрочнения (BCD)
необходимо заменить условие текучести условием упрочнения. В простей-
шем случае можно считать k функцией некоторого параметра упрочнения:
k = k(A
p
), A
p
≡
Z
τ ·· dε
p
— (8.2.5)
энергетическое условие. Пластическая деформация начинается при F (τ ) =
k(0). Далее имеем подвижную поверхность нагружения, на которой
F = k,
˙
ε
p
=
0,
˙
F 6 0
λ ∂F/∂τ ,
˙
F > 0
. (8.2.6)
176

8.2 Определяющие уравнения
Эта поверхность служит для разграничения нагрузки и разгрузки — по
знаку
˙
F .
При идеальной пластичности k = const, и в состоянии течения
˙
F = 0.
В случае упрочнения это равенство означает остановку течения («ней-
тральное нагружение»).
В модели с упрочнением можно получить универсальное выражение
λ, продифференцировав условие текучести:
˙
F =
∂F
∂
˙
τ
··
˙
τ = k
0
(A
p
)τ ··
˙
ε
p
⇒ λ = Λ··
˙
τ , Λ ≡
∂F/∂τ
k
0
(A
p
)
∂F
∂τ
··τ
. (8.2.7)
Ничего подобного нет при идеальной пластичности — там получается не-
определённость 0/0. Учитывая правило сложения деформаций, получим
˙
ε =
4
S +
∂F
∂τ
Λ
··
˙
τ — (8.2.8)
как в линейно упругой среде с переменной податливостью.
Энергетическое условие упрочнения (8.2.5) означает изотропное расши-
рение поверхности текучести в пространстве напряжений и потому не опи-
сывает эффект Баушингера. Для учёта последнего необходимы более слож-
ные условия.
При идеальной пластичности изотропного материала
˙
e =
1
2µ
˙
S +
0, τ (S) ≡ F
2
< k
λS, τ = k
— (8.2.9)
это соотношение Прандтля будем часто использовать.
В каче стве примера рассмотрим растяжение и кручение тонкостен-
ной трубки. При осевой силе P и крутящем моменте M тензор напряже-
ний
τ ≈ σ
z
e
z
e
z
+ τ
zϕ
(e
z
e
ϕ
+ e
ϕ
e
z
), σ
z
=
P
2πRh
, τ
zϕ
=
M
2πR
2
h
, (8.2.10)
где z и ϕ — цилиндрические координаты, R — радиус трубки, h — толщина
стенки. По удлинению W и углу поворота торца Φ находят ся деформации
ε
z
= W/l, ε
zϕ
= ΦR/2l (l — длина трубки). Задаём программу мыслен-
ного эксперимента: сначала только кручение с растущим Φ до появления
пластических деформаций, затем растяжение с постоянным Φ. Из (8.2.10) и
177
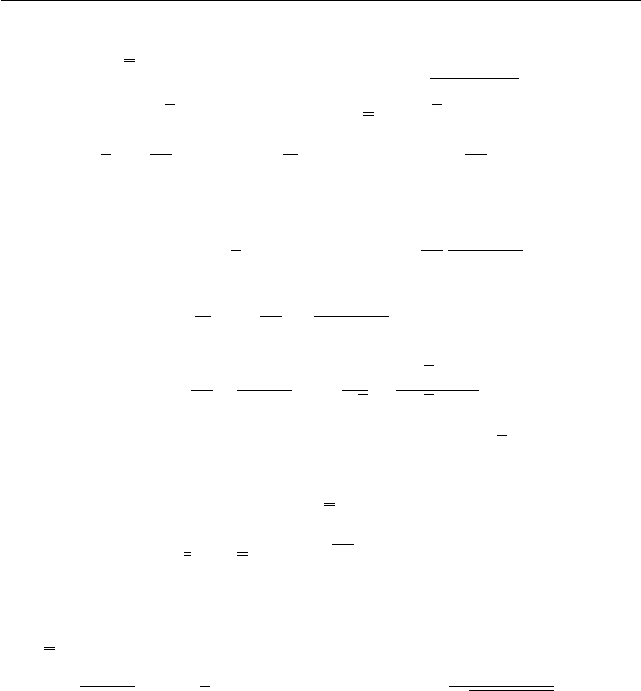
Малые пластические деформации
(8.2.9) находим S,
S
z
=
2
3
σ
z
, S
zϕ
= τ
zϕ
, τ(S) =
r
1
3
σ
2
z
+ τ
2
zϕ
,
˙ε
z
=
1
3
˙
θ +
1
2µ
˙
S
z
+ λS
z
=
1
E
˙σ
z
+ λS
z
, ˙ε
zϕ
=
1
2µ
˙τ
zϕ
+ λτ
zϕ
. (8.2.11)
На этапе растяжения имеем ˙ε
zϕ
= 0, τ
2
zϕ
+ σ
2
z
/3 = k
2
,
τ
zϕ
˙τ
zϕ
+
1
3
σ
z
˙σ
z
= 0 ⇒ λ =
1
2µ
σ
z
˙σ
z
3k
2
− σ
2
z
,
ε
z
=
1
E
σ
z
+
1
3µ
σ
z
Z
0
σ
2
z
3k
2
− σ
2
z
dσ
z
=
=
1
6µ
1 − 2ν
1 + ν
σ
z
+
k
√
3
ln
k
√
3 + σ
z
k
√
3 − σ
z
!
— (8.2.12)
плавная зависимость с асимптотой на уровне σ
z
= k
√
3. При этом τ
zϕ
убывает до нуля.
Вернёмся к (8.2.9) и допустим, что
˙
S ≡ 0. Тогда
e = ΨS
Ψ =
1
2µ
+
Z
λ dt
. (
8.2.13)
Такое соотношение (без скоростей) характерно для деформационной тео-
рии пластичности. Некоторые авторы считают её верной и при непостоян-
стве S. В примере с (8.2.10)
ε
z
=
1 − 2ν
3E
σ
z
+ Ψ
2
3
σ
z
, ε
zϕ
= Ψτ
zϕ
⇒ Ψ =
ε
zϕ
p
k
2
− σ
2
z
/3
, (8.2.14)
и кривая растяжения σ
z
(ε
z
) отличается от (8.2.13).
8.3 Полый шар под действием внутреннего дав-
ления
Задача линейной термоупругости со сферической симметрией была рас-
смотрена в п. 4.11. Вид тензора напряжений, уравнения баланса сил и сов-
местности (4.11.5, 4.11.6, гл. 4) сохраняются. Граничные условия:
σ
r
(a) = −p, σ
r
(b) = 0; (8.3.1)
178

8.3 Полый шар под действием внутреннего давления
давление p монотонно возрастает от нуля. Имеем
σ = tr τ = σ
r
+ 2σ
ϕ
, S = S
r
e
r
e
r
+ S
ϕ
(E − e
r
e
r
),
S
r
=
2
3
(σ
r
− σ
ϕ
) = −2S
ϕ
, τ(S) =
|σ
ϕ
− σ
r
|
√
3
. (8.3.2)
Очевидно σ
r
< 0, σ
ϕ
> 0 — знак модуля в τ не нужен (ссылки на очевид-
ность характерны для задач теории пластичности).
Упругое поведение будет при p < p
0
, где p
0
пока неизвестно; везде τ <
k. Можем воспользоваться уравнением (4.11.8, гл. 4) — без температурного
слагаемого. Решаем уравнение Эйлера:
σ
r
= r
n
, n(n − 1) + 4n = 0 ⇒ n
1
= 0, n
2
= −3;
σ
r
= A −
B
r
3
= −p
1 − b
3
/r
3
1 − b
3
/a
3
; σ
ϕ
=
r
2
σ
0
r
+ σ
r
= A +
B
2r
3
. (8.3.3)
Пластическая деформация начнется на внутреннем радиусе, поскольку τ =
B
√
3/2r
3
. Найдём p
0
:
B
√
3
2a
3
= k ⇒ p
0
=
2k
√
3
1 −
a
3
b
3
. (8.3.4)
В упруго-пластической стадии (p > p
0
) естественно предположить на-
личие двух зон: пластичности (r < ρ) и упругости (r > ρ). Радиус ρ неиз-
вестен, на нём непрерывны σ
r
и τ. В зоне упругости
σ
r
= B
1
b
3
−
1
r
3
;
B
√
3
2ρ
3
= k. (8.3.5)
В пластической зоне решение оказывается на удивление простым:
σ
0
r
= 2
σ
ϕ
− σ
r
r
=
2k
√
3
r
⇒ σ
r
= −p + 2k
√
3 ln
r
a
. (8.3.6)
Осталось найти ρ из условия непрерывности σ
r
:
− p + 2k
√
3 ln
ρ
a
=
2k
√
3
ρ
3
b
3
− 1
⇒ ρ(p). (
8.3.7)
Функция ρ(p) возрастает до значения b при давлении
p
∗
= 2k
√
3 ln
b
a
. (8.3.8)
179
Малые пластические деформации
Такова несущая способность модели, равновесие с p > p
∗
невозможно
(только течение с ускорением).
Заметим, что p
∗
можно найти очень просто, если в (8.3.6) потребовать
и σ
r
(b) = 0 — т. е. по условию разрешимости уравнения первого поряд-
ка с двумя граничными условиями. Это математическое явление позднее
рассмотрим в общей постановке.
Перемещение u = u(r)e
r
можно определить двумя способами. Первый
связан с определяющими уравнениями (8.2.13) — условие
˙
S = 0 выполняет-
ся. Неизвестную функцию Ψ(r) можно найти из уравнения совместности.
Но проще другой способ, основанный на законе Гука для первых инвари-
антов:
u
0
+ 2
u
r
=
1 − 2ν
E
(σ
r
+ 2σ
ϕ
). (8.3.9)
Правая часть известна, u(r) находится интегрированием (после умножения
на r
2
).
Разгрузка описывается уравнениями линейной упругости. Они связы-
вают разности p −p
1
, τ −τ
1
, . . . , где (. . .)
1
— значения в начале разгрузки.
В частности,
σ
r
− σ
1
r
= −(p − p
1
)
1 −
b
3
r
3
.
1 −
b
3
a
3
,
σ
1
r
= −p
1
+ 2k
√
3 ln
r
a
(r < ρ(p
1
)). (8.3.10)
Полагая p = 0, получим выражение остаточного напряжения.
8.4 Балки и диски
Рассмотрим элементарную теорию упруго-пластического изгиба балки Бер-
нулли — Эйлера. Ось x направлена вдоль балки через центры тяжести се-
чений; в плоскости y, z сечение занимает область |y| 6 h/2, |z| 6 b(y)/2.
При изгибе в плоскости xy имеем силовые факторы
Q =
Z
τ
xy
dF =
b/2
Z
−b/2
dy
b/2
Z
−b/2
τ
xy
dz, M = −
Z
yσ
x
dF
с уравнениями баланса (5.1.2, гл. 5): Q
0
= −q, M
0
= −Q.
Гипотезы (5.1.3, гл. 5) сохраняются при пластических деформациях. По-
прежнему ε
x
= −v
00
y. В упругой зоне σ
x
= Eε
x
, а в пластической
180
