Елесин В.Ф., Кашурников В.А. Физика фазовых переходов
Подождите немного. Документ загружается.


>@
CNVT V
2
2
ch { }
E
.
2.5.4. Ɉɩɪɟɞɟɥɢɬɶ ɷɧɟɪɝɢɸ ɩɪɢ ɩɨɥɟ H=0. Ɋɚɫɫɦɨɬɪɟɬɶ
ɫɥɭɱɚɣ V>0 ɢ V<0 .
Ɉɬɜɟɬ
: ɨɛɚ ɫɥɭɱɚɹ ɫɨɜɩɚɞɚɸɬ:.ENV th
E
V
2.5.5. ɇɚɣɬɢ ɦɚɝɧɢɬɧɭɸ ɜɨɫɩɪɢɢɦɱɢɜɨɫɬɶ V =
rP
0
J.
Ɉɬɜɟɬ:
>@
FP EP
r
0
2
0
2
2TTexp( / )
.
2.5.
6
. Ɂɚɩɢɫɚɬɶ ɫɬɚɬɢɫɬɢɱɟɫɤɭɸ ɫɭɦɦɭ ɧɚ ɫɥɭɱɚɣ ɤɨɧɟɱ-
ɧɨɣ ɰɟɩɨɱɤɢ N >>1. Ɋɚɫɫɱɢɬɚɬɶ ɩɨɩɪɚɜɤɭ ɤ ɜɨɫɩɪɢɢɦɱɢɜɨɫɬɢ
ɨɞɧɨɦɟɪɧɨɣ ɰɟɩɨɱɤɢ ɡɚ ɫɱɟɬ ɤɨɧɟɱɧɨɫɬɢ ɫɢɫɬɟɦɵ.
Ⱦɜɭɦɟɪɧɚɹ ɦɨɞɟɥɶ ɂɡɢɧɝɚ; ɪɟɲɟɧɢɟ Ɉɧɡɚɝɟɪɚ.
ȼ 1944
ɝ. Ɉɧɡɚɝɟɪɨɦ ɛɵɥɨ ɩɪɟɞɥɨɠɟɧɨ ɬɨɱɧɨɟ ɪɟɲɟɧɢɟ ɡɚɞɚɱɢ ɨ ɮɚɡɨ-
ɜɨɦ ɩɟɪɟɯɨɞɟ ɜ ɦɨɞɟɥɢ ɂɡɢɧɝɚ ɧɚ ɞɜɭɦɟɪɧɨɣ ɤɜɚɞɪɚɬɧɨɣ ɪɟ-
ɲɟɬɤɟ. Ɉɫɧɨɜɧɨɣ ɜɵɜɨɞ - ɫɭɳɟɫɬɜɭɟɬ ɩɟɪɟɯɨɞ ɜ ɮɟɪɪɨɦɚɝɧɢɬ-
ɧɨɟ ɫɨɫɬɨɹɧɢɟ, ɩɪɢɱɟɦ Ɉɧɡɚɝɟɪɭ ɭɞɚɥɨɫɶ ɬɨɱɧɨ ɪɚɫɫɱɢɬɚɬɶ ɫɬɚ-
ɬɢɫɬɢɱɟɫɤɭɸ ɫɭɦɦɭ. Ⱦɥɹ ɩɨɞɪɨɛɧɨɝɨ ɨɡɧɚɤɨɦɥɟɧɢɹ ɫ ɷɬɢɦ ɢɡ-
ɜɟɫɬɧɵɦ ɪɟɡɭɥɶɬɚɬɨɦ ɦɵ ɨɬɫɵɥɚɟɦ ɱɢɬɚɬɟɥɟɣ ɤ ɤɧɢɝɚɦ [16,17].
Ɇɵ ɤɨɫɧɟɦɫɹ ɡɞɟɫɶ ɤɨɧɫɩɟɤɬɢɜɧɨ ɥɢɲɶ ɨɫɧɨɜɧɵɯ ɷɬɚɩɨɜ ɪɚɫ-
ɱɟɬɚ ɢ ɨɛɫɭɞɢɦ ɩɨɥɭɱɟɧɧɵɟ Ɉɧɡɚɝɟɪɨɦ ɬɨɱɧɵɟ pɟɡɭɥɶɬɚɬɵ.
Ɋɚɫɫɦɨɬɪɢɦ ɞɜɭɦɟɪɧɭɸ ɤɜɚɞɪɚɬɧɭɸ ɪɟɲɟɬɤɭ ɫ ɩɟɪɢɨ-
ɞɢɱɟɫɤɢɦɢ ɝɪɚɧɢɱɧɵɦɢ ɭɫɥɨɜɢɹɦɢ ɢ N ɭɡɥɚɦɢ, ɤɚɠɞɵɣ ɢɡ ɤɨ-
ɬɨɪɵɯ ɢɦɟɟɬ ɟɞɢɧɢɱɧɵɣ ɫɩɢɧ
P
=
r
. Ɍɨɝɞɚ ɭɞɨɛɧɨ ɜɜɟɫɬɢ ɧɭ-
ɦɟɪɚɰɢɸ ɭɡɥɨɜ ɩɨ ɢɯ ɤɨɨɪɞɢɧɚɬɚɦ x = ka, y = la, ɝɞɟ a - ɩɟɪɢɨɞ
ɪɟɲɟɬɤɢ; k,l - ɰɟɥɵɟ ɱɢɫɥɚ 1< k,l < L, L
2
=N. ȼ ɷɬɨɦ ɫɥɭɱɚɟ ɝɚ-
ɦɢɥɶɬɨɧɢɚɧ ɂɡɢɧɝɚ ɜ ɩɪɢɛɥɢɠɟɧɢɢ ɛɥɢɠɚɣɲɢɯ ɫɨɫɟɞɟɣ ɢ ɜ
ɨɬɫɭɬɫɬɜɢɢ ɜɧɟɲɧɟɝɨ ɩɨɥɹ ɧɚ ɬɚɤɨɣ ɪɟɲɟɬɤɟ ɢɦɟɟɬ ɜɢɞ:
HV
kl kl kl k l
kl
L
¦
()
,
PP PP
1
1
1
1
. (2.33)
ɋɬɚɬɢɫɬɢɱɟɫɤɚɹ ɫɭɦɦɚ ɬɚɤɨɣ ɫɢɫɬɟɦɵ:
Q
kl kl kl k l
kl
L
n
¦
®
¯
½
¾
¿
¦
exp ( )
,
{}
TPP PP
1
1
, (2.34)
40
ɝɞɟ
4
=
E
V, ɚ {n} ɨɡɧɚɱɚɟɬ ɫɭɦɦɢɪɨɜɚɧɢɟ ɩɨ ɜɫɟɦ ɜɨɡɦɨɠɧɵɦ
ɫɨɫɬɨɹɧɢɹɦ ɫɢɫɬɟɦɵ. ȼɨɫɩɨɥɶɡɭɟɦɫɹ ɬɟɦ ɮɚɤɬɨɦ, ɱɬɨ
P
2
kl
=1.
Ɍɨɝɞɚ ɧɟɫɥɨɠɧɨ ɩɨɥɭɱɢɬɶ ɫɥɟɞɭɸɳɟɟ ɬɨɠɞɟɫɬɜɨ:
exp{
4P
kl
P
k’l’
} = ch
4
+
P
kl
P
k’l’
sh
4
= ch
4
(1+
P
kl
P
k’l’
th
4
). (2.35)
ɂɫɩɨɥɶɡɭɹ (2.35), ɩɪɟɞɫɬɚɜɢɦ ɫɬɚɬɢɫɬɢɱɟɫɤɭɸ ɫɭɦɦɭ ɫɥɟɞɭɸ-
ɳɢɦ ɨɛɪɚɡɨɦ:
41
,
th .
QxS
N
()1
2
(2.36)
Sxxx
kl kl kl k l
kl
L
n
¦
()(),
,
{}
11
11
1
PP PP T
(2.37)
Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɢɫɤɨɦɚɹ ɫɬɚɬɢɫɬɢɱɟɫɤɚɹ ɫɭɦɦɚ ɹɜɥɹɟɬɫɹ ɫɭɦ-
ɦɨɣ ɛɨɥɶɲɨɝɨ ɱɢɫɥɚ ɩɨɥɢɧɨɦɨɜ ɩɨ ɫɬɟɩɟɧɹɦ x ɢ
P
kl
. ɉɨɫɤɨɥɶ-
ɤɭ ɤɚɠɞɵɣ ɭɡɟɥ (k,l) ɫɜɹɡɚɧ ɫ ɱɟɬɵɪɶɦɹ ɫɨɫɟɞɹɦɢ, ɬɨ ɤɚɠɞɨɟ
P
kl
ɦɨɠɟɬ ɜɫɬɪɟɬɢɬɶɫɹ ɜ ɩɨɥɢɧɨɦɟ ɜ ɫɬɟɩɟɧɹɯ ɨɬ ɧɭɥɟɜɨɣ ɞɨ ɱɟɬ-
ɜɟɪɬɨɣ. ɉɨɫɥɟ ɫɭɦɦɢɪɨɜɚɧɢɹ ɩɨ ɜɫɟɦ
P
kl
=rɱɥɟɧɵ, ɫɨɞɟɪɠɚ-
ɳɢɟ ɧɟɱɟɬɧɵɟ ɫɬɟɩɟɧɢ
P
k
, ɨɛɪɚɬɹɬɶɫɹ ɜ ɧɭɥɶ, ɬɚɤ ɱɬɨ ɧɟɧɭɥɟ-
ɜɨɣ ɜɤɥɚɞ ɞɚɞɭɬ ɬɨɥɶɤɨ ɱɥɟɧɵ, ɫɨɞɟɪɠɚɳɢɟ
P
k
ɜ ɫɬɟɩɟɧɹɯ 0, 2 ɢ
4. Ȼɨɥɟɟ ɬɨɝɨ, ɩɨɫɤɨɥɶɤɭ
P
0
kl
=
P
2
kl
=
P
4
kl
=1, ɬɨ ɤɚɠɞɵɣ ɱɥɟɧ
ɩɨɥɢɧɨɦɚ, ɫɨɞɟɪɠɚɳɢɣ ɜɫɟ ɩɟɪɟɦɟɧɧɵɟ
P
kl
ɜ ɱɟɬɧɵɯ ɫɬɟɩɟɧɹɯ,
ɞɚɫɬ ɜɤɥɚɞ ɜ ɫɭɦɦɭ, ɩɪɨɩɨɪɰɢɨɧɚɥɶɧɵɣ ɩɨɥɧɨɦɭ ɱɢɫɥɭ ɤɨɧɮɢ-
ɝɭɪɚɰɢɣ 2
N
.
ɉɨɫɥɟ ɷɬɨɝɨ Ɉɧɡɚɝɟɪ ɩɪɟɞɥɨɠɢɥ, ɩɨɠɚɥɭɣ, ɨɞɢɧ ɢɡ ɩɟɪ-
ɜɵɯ ɜɚɪɢɚɧɬɨɜ ɞɢɚɝɪɚɦɦɧɨɣ ɬɟɯɧɢɤɢ ɞɥɹ ɫɭɦɦɢɪɨɜɚɧɢɹ (2.36)-
(2.37), ɤɨɬɨɪɚɹ ɜ ɧɚɫɬɨɹɳɟɟ ɜɪɟɦɹ ɲɢɪɨɤɨ ɢɫɩɨɥɶɡɭɟɬɫɹ ɜ ɬɟɨ-
ɪɢɢ ɤɨɧɞɟɧɫɢɪɨɜɚɧɧɨɝɨ ɫɨɫɬɨɹɧɢɹ. Ɉɧ ɡɚɦɟɬɢɥ, ɱɬɨ ɤɚɠɞɨɦɭ
ɱɥɟɧɭ ɩɨɥɢɧɨɦɚ ɦɨɠɧɨ ɨɞɧɨɡɧɚɱɧɨ ɩɨɫɬɚ
ɜɢɬɶ ɜ ɫɨɨɬɜɟɬɫɬɜɢɟ ɫɨɜɨɤɭɩɧɨɫɬɶ ɥɢɧɢɣ (ɝɪɚɮɢɤɨɜ), ɫɨɟɞɢ-
ɧɹɸɳɢɯ ɧɟɤɨɬɨɪɵɟ ɩɚɪɵ ɫɨɫɟɞɧɢɯ ɭɡɥɨɜ ɪɟɲɟɬɤɢ. Ɍɚɤ, ɢɡɨ-
ɛɪɚɠɟɧɧɵɦ ɧɚ ɪɢɫ.8 ɝɪɚɮɢɤɚɦ ɫɨɨɬɜɟɬɫɬɜɭɸɬ ɱɥɟɧɵ ɩɨɥɢɧɨ-
ɦɚ:
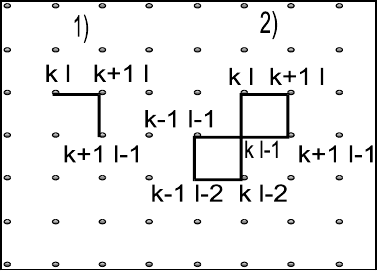
Ɋɢɫ.8. Ⱦɢɚɝɪɚɦɦɧɚɹ ɬɟɯɧɢ-
ɤɚ Ɉɧɡɚɝɟɪɚ ɧɚ ɩɥɨɫɤɨɣ
ɤɜɚɞɪɚɬɧɨɣ ɪɟɲɟɬɤɟ ɞɥɹ
ɦɨɞɟɥɢ ɂɡɢɧɝɚ
42
g
1) x
2
P
kl
P
2
k+1l
P
k+1l-1
,
(2.38)
2) x
8
P
2
kl
P
2
k+1l
P
2
k+1l-1
P
4
kl-1
P
2
kl-2
P
2
k-1l-1
P
2
k-1l-2
.
Ʉɚɠɞɨɣ ɥɢɧɢɢ ɝɪɚɮɢɤɚ ɫɨɩɨɫɬɚɜɥɹɟɬɫɹ ɦɧɨɠɢɬɟɥɶ x, ɚ ɤɚɠɞɨ-
ɦɭ ɟɟ ɤɨɧɰɭ - ɦɧɨɠɢɬɟɥɶ
P
kl
. Ɍɚɤ ɤɚɤ ɨɬɥɢɱɧɵɣ ɨɬ ɧɭɥɹ ɜɤɥɚɞ ɜ
ɫɬɚɬɢɫɬɢɱɟɫɤɭɸ ɫɭɦɦɭ ɞɚɸɬ ɥɢɲɶ ɱɥɟɧɵ ɩɨɥɢɧɨɦɚ, ɫɨɞɟɪɠɚ-
ɳɢɟ ɱɟɬɧɵɟ ɫɬɟɩɟɧɢ
P
kl
, ɬɨ ɜ ɤɚɠɞɨɦ ɭɡɥɟ ɝɪɚɮɢɤɚ ɞɨɥɠɧɵ
ɨɤɚɧɱɢɜɚɬɶɫɹ ɥɢɛɨ ɞɜɟ, ɥɢɛɨ ɱɟɬɵɪɟ ɫɜɹɡɢ. Ⱦɪɭɝɢɦɢ ɫɥɨɜɚɦɢ,
ɫɭɦɦɢɪɨɜɚɧɢɟ ɜɟɞɟɬɫɹ ɬɨɥɶɤɨ ɩɨ ɡɚɦɤɧɭɬɵɦ ɝɪɚɮɢɤɚɦ, ɩɪɢɱɟɦ
ɞɨɩɭɫɤɚɟɬɫɹ ɫɚɦɨɩɟɪɟɫɟɱɟɧɢɟ.
Ɉɤɨɧɱɚɬɟɥɶɧɨ, ɫɭɦɦɚ Q ɦɨɠɟɬ ɛɵɬɶ ɩɪɟɞɫɬɚɜɥɟɧɚ ɜ
ɫɥɟɞɭɸɳɟɦ ɜɢɞɟ:
. (2.39)
Qx
Nr
r
r
¦
2
{}
ɝɞɟ g
r
- ɱɢɫɥɨ ɡɚɦɤɧɭɬɵɯ ɝɪɚɮɢɤɨɜ, ɫɨɫɬɚɜɥɟɧɧɵɯ ɢɡ ɱɟɬɧɨɝɨ
ɱɢɫɥɚ r ɫɜɹɡɟɣ.
Ⱦɚɥɟɟ Ɉɧɡɚɝɟɪ ɪɚɡɪɚɛɨɬɚɥ ɫɩɨɫɨɛ ɩɟɪɟɛɨɪɚ ɝɪɚɮɢɤɨɜ ɢɡ
ɫɭɦɦɵ (2.39) ɫ ɩɨɦɨɳɶɸ ɫɩɟɰɢɚɥɶɧɨɣ ɢɯ ɤɥɚɫɫɢɮɢɤɚɰɢɢ ɩɨ
ɞɥɢɧɟ ɫɜɹɡɟɣ r ɢ ɢɫɩɨɥɶɡɨɜɚɥ ɩɨɞɯɨɞ “ɛɥɭɠɞɚɸɳɟɣ” ɲɚɝ ɡɚ
ɲɚɝɨɦ ɩɨ ɪɟɲɟɬɤɟ ɬɨɱɤɢ ɫ ɜɟɪɨɹɬɧɨɫɬɶɸ ɩɟɪɟɯɨɞɚ, ɨɩɪɟɞɟɥɹɟ-
ɦɨɣ ɫɩɟɰɢɚɥɶɧɨɣ ɦɚɬɪɢɰɟɣ ɩɟɪɟɯɨɞɚ. ɂɡ-ɡɚ ɷɤɨɧɨɦɢɢ ɦɟɫɬɚ
ɦɵ ɩɪɢɜɟɞɟɦ
ɭɠɟ ɨɤɨɧɱɚɬɟɥɶɧɵɣ ɪɟɡɭɥɶɬɚɬ, ɚ ɜɫɟ ɩɨɞɪɨɛɧɨɫɬɢ
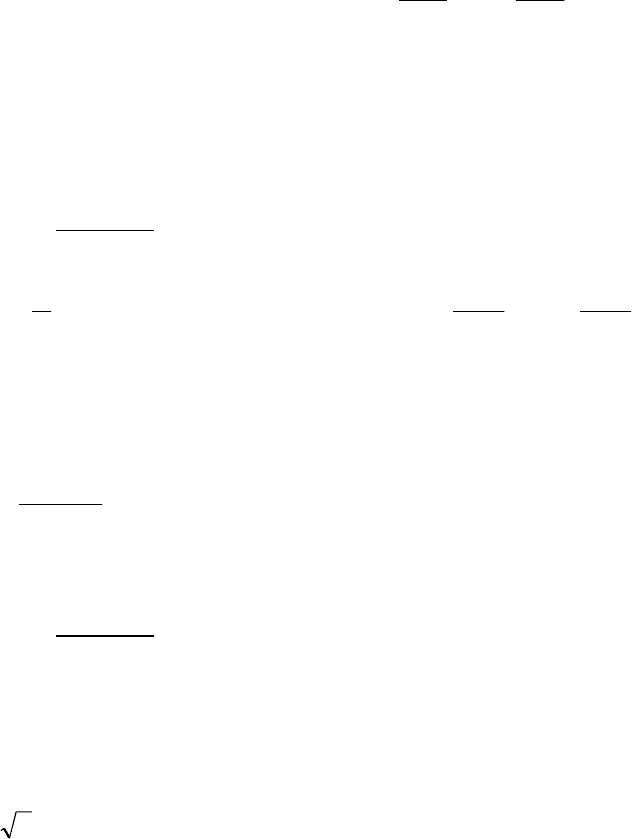
ɪɚɫɱɟɬɚ ɢɡɥɨɠɟɧɵ ɜ ɤɧɢɝɟ [16]. Ɉɤɨɧɱɚɬɟɥɶɧɨɟ ɬɨɱɧɨɟ ɜɵɪɚ-
ɠɟɧɢɟ ɞɥɹ ɫɬɚɬɢɫɬɢɱɟɫɤɨɣ ɫɭɦɦɵ ɢɦɟɟɬ ɜɢɞ:
Qx
xxx
p
L
q
L
NN
pq
L
u
u
ª
¬
«
º
¼
»
21
121
22
2
2
2
2
12
1
()
()(cos cos)
/
,
SS
.
(2.40)
Ɂɚɞɚɱɢ
2.5.7. Ɋɚɫɫɱɢɬɚɬɶ ɫɜɨɛɨɞɧɭɸ ɷɧɟɪɝɢɸ ɞɜɭɦɟɪɧɨɣ ɦɨɞɟ-
ɥɢ ɂɡɢɧɝɚ F= - 1
E
lnQ.
Ɋɟɲɟɧɢɟ
. ɂɫɩɨɥɶɡɭɹ ɜɵɪɚɠɟɧɢɟ (2.40), ɧɚɯɨɞɢɦ:
FNT NT x
Txxx
p
L
q
L
pq
L
ª
¬
«
º
¼
»
¦
ln ln( )
( )(cos cos ) .
,
21
1
2
121
22
2
2
2
2
0
SS
ɉɟɪɟɣɞɟɦ ɨɬ ɫɭɦɦɢɪɨɜɚɧɢɹ ɤ ɢɧɬɟɝɪɢɪɨɜɚɧɢɸ ɜ ɩɪɟɞɟ-
ɥɟ
L, N
of
:
>@
FNT NT x
NT
xxx dd
³³
ln ln( )
()
ln ( ) (cos cos ) .
21
22
121
2
2
2
2
2
12
0
2
0
2
12
S
ZZZ
SS
Z
2.5.
8. ɂɫɫɥɟɞɨɜɚɬɶ ɫɜɨɛɨɞɧɭɸ ɷɧɟɪɝɢɸ ɜɛɥɢɡɢ ɤɪɢɬɢɱɟ-
ɫɤɨɣ ɬɟɦɩɟɪɚɬɭɪɵ ɢ ɪɚɫɫɱɢɬɚɬɶ ɤɪɢɬɢɱɟɫɤɭɸ ɬɟɦɩɟɪɚɬɭɪɭ.
Ɋɟɲɟɧɢɟ
. Ɏɭɧɤɰɢɹ F(T) ɢɦɟɟɬ ɨɫɨɛɭɸ ɬɨɱɤɭ ɩɪɢ ɬɨɦ
ɡɧɚɱɟɧɢɢ x (x = th (V/T) ), ɩɪɢ ɤɨɬɨɪɨɦ ɚɪɝɭɦɟɧɬ ɥɨɝɚɪɢɮɦɚ
ɩɨɞ ɡɧɚɤɨɦ ɢɧɬɟɝɪɚɥɚ ɦɨɠɟɬ ɨɛɪɚɬɢɬɶɫɹ ɜ ɧɭɥɶ. Ʉɚɤ ɮɭɧɤɰɢɹ
Z
1
ɢ
Z
2
ɷɬɨɬ ɚɪɝɭɦɟɧɬ ɦɢɧɢɦɚɥɟɧ ɩɪɢ cos
Z
1
= =cos
Z
2
=1, ɜ
ɷɬɨɦ ɫɥɭɱɚɟ ɨɧ ɪɚɜɟɧ (1+x
2
)
2
- 4x(1-x
2
). ɗɬɨ ɜɵɪɚɠɟɧɢɟ ɢɦɟɟɬ
ɦɢɧɢɦɭɦ, ɜ ɤɨɬɨɪɨɦ ɨɧɨ ɨɛɪɚɳɚɟɬɫɹ ɜ ɧɭɥɶ ɩɪɢ x = x
c
= 2
ɩɪɢ ɷɬɨɦ ɫɨɨɬɜɟɬɫɬɜɭɸɳɚɹ ɬɟɦɩɟɪɚɬɭɪɚ T
c
(th V/T
c
=
x
c
) ɢ ɹɜɥɹɟɬɫɹ ɬɨɱɤɨɣ ɮɚɡɨɜɨɝɨ ɩɟɪɟɯɨɞɚ. Ɇɨɠɧɨ ɩɨɤɚɡɚɬɶ, ɱɬɨ
43
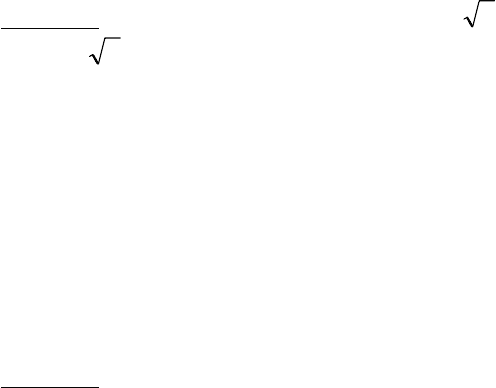
ɫɜɨɛɨɞɧɚɹ ɷɧɟɪɝɢɹ ɩɨɧɢɠɚɟɬɫɹ ɩɪɢ T<T
c
, ɧɟɩɪɟɪɵɜɧɚ ɩɪɢ
T=T
c
, ɚ ɬɟɩɥɨɟɦɤɨɫɬɶ ɢɫɩɵɬɵɜɚɟɬ ɥɨɝɚɪɢɮɦɢɱɟɫɤɭɸ ɨɫɨɛɟɧ-
ɧɨɫɬɶ ɜ ɬɨɱɤɟ ɩɟɪɟɯɨɞɚ, ɬ.ɟ. ɷɬɨ - ɬɢɩɢɱɧɵɣ ɬɟɪɦɨɞɢɧɚɦɢɱɟ-
ɫɤɢɣ ɩɟɪɟɯɨɞ ɜɬɨɪɨɝɨ ɪɨɞɚ. Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɜ ɞɜɭɦɟɪɧɨɣ ɦɨɞɟ-
ɥɢ ɂɡɢɧɝɚ ɧɚɛɥɸɞɚɟɬɫɹ ɮɚɡɨɜɵɣ ɩɟɪɟɯɨɞ ɩɚɪɚɦɚɝɧɟɬɢɤ-
ɮɟɪɪɨɦɚɝɧɟɬɢɤ ɩɪɢ ɤɨɧɟɱɧɨɣ ɬɟɦɩɟɪɚɬɭɪɟ.
2.5.
9. ɋɪɚɜɧɢɬɶ ɤɪɢɬɢɱɟɫɤɭɸ ɬɟɦɩɟɪɚɬɭɪɭ, ɩɨɥɭɱɟɧɧɭɸ
Ɉɧɡɚɝɟɪɨɦ, ɫ ɪɟɡɭɥɶɬɚɬɨɦ ɬɟɨɪɢɢ ɫɪɟɞɧɟɝɨ ɩɨɥɹ.
Ɋɟɲɟɧɢɟ
. ɂɫɯɨɞɹ ɢɡ ɭɪɚɜɧɟɧɢɹ thV/T
c
= 2
ɧɚɯɨɞɢɦ
T
c
=2V/ ln(1+ 2 ) |2J. Ɋɟɡɭɥɶɬɚɬ ɬɟɨɪɢɢ ɫɪɟɞɧɟɝɨ ɩɨɥɹ:
T
c
=ZV=4V. Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɬɨɱɧɨɟ ɪɟɲɟɧɢɟ ɦɟɧɶɲɟ ɩɪɢɛɥɢ-
ɠɟɧɧɨɝɨ “ɫɪɟɞɧɟɩɨɥɟɜɨɝɨ” ɩɪɢɦɟɪɧɨ ɧɚ ɜɟɥɢɱɢɧɭ ~1/Z. ɂɧɬɟ-
ɪɟɫɧɨ ɨɬɦɟɬɢɬɶ, ɱɬɨ ɫ ɷɬɨɣ ɬɨɱɤɢ ɡɪɟɧɢɹ ɜ ɨɞɧɨɦɟɪɧɨɦ ɫɥɭɱɚɟ
ɪɟɡɭɥɶɬɚɬ ɬɟɨɪɢɢ ɫɪɟɞɧɟɝɨ ɩɨɥɹ ɞɚɟɬ ɬɚɤɠɟ “ɡɚɜɵɲɟɧɧɵɣ ɪɟ-
ɡɭɥɶɬɚɬ” (T
c
=2V) ɩɨ ɫɪɚɜɧɟɧɢɸ ɫ ɬɨɱɧɵɦ (T
ɫ
=0).
2.5.
10. ɂɫɩɨɥɶɡɭɹ ɜɵɪɚɠɟɧɢɟ ɞɥɹ ɫɜɨɛɨɞɧɨɣ ɷɧɟɪɝɢɢ,
ɩɨɤɚɡɚɬɶ, ɱɬɨ ɜɛɥɢɡɢ ɤɪɢɬɢɱɟɫɤɨɣ ɬɟɦɩɟɪɚɬɭɪɵ ɡɚɜɢɫɢɦɨɫɬɶ
ɫɜɨɛɨɞɧɨɣ ɷɧɟɪɝɢɢ ɧɟɩɪɟɪɵɜɧɚ, ɚ ɬɟɩɥɨɟɦɤɨɫɬɶ ɪɚɫɯɨɞɢɬɫɹ
ɥɨɝɚɪɢɮɦɢɱɟɫɤɢ.
Ɋɟɲɟɧɢɟ
. ɇɟɨɛɯɨɞɢɦɨ ɪɚɡɥɨɠɢɬɶɫɹ ɩɨ ɫɬɟɩɟɧɹɦ T-T
c
ɢ
ɪɚɫɫɦɚɬɪɢɜɚɬɶ ɬɨɥɶɤɨ ɩɨɫɥɟɞɧɢɣ ɢɧɬɟɝɪɚɥɶɧɵɣ ɱɥɟɧ ɜ ɫɜɨɛɨɞ-
ɧɨɣ ɷɧɟɪɝɢɢ, ɢɦɟɸɳɢɣ ɨɫɨɛɟɧɧɨɫɬɢ. ɉɨɫɥɟ ɪɚɡɥɨɠɟɧɢɹ ɚɪɝɭ-
ɦɟɧɬɚ ɥɨɝɚɪɢɮɦɚ ɜɛɥɢɡɢ ɟɝɨ ɦɢɧɢɦɭɦɚ ɩɨ ɫɬɟɩɟɧɹɦ
Z
1,2
ɢ T-
T
c
ɢɦɟɟɦ:
>@
FAtB t
c
~ln ( ) ,
2
1
2
2
2
0
2
0
2
12
³³
ZZ ZZ
SS
dd TT
c
,
ɝɞɟ A,B - ɩɨɫɬɨɹɧɧɵɟ. Ɋɚɫɱɢɬɵɜɚɹ ɷɬɨ ɜɵɪɚɠɟɧɢɟ ɩɪɢ t
o
0,
ɧɚɯɨɞɢɦ:.FTT TTC TT
cc
~ | | ln| |, ~ ln| |
2
44
45
3.
ɎɅɍɄɌɍȺɐɂɂ ȼ ɎȿɊɊɈɆȺȽɇȿɌɂɄȺɏ
Ɍɟɨɪɢɹ ɫɪɟɞɧɟɝɨ ɩɨɥɹ ɧɟɚɞɟɤɜɚɬɧɨ ɨɩɢɫɵɜɚɟɬ ɨɛɥɚɫɬɶ
ɩɨ ɬɟɦɩɟɪɚɬɭɪɟ ɜ ɧɟɩɨɫɪɟɞɫɬɜɟɧɧɨɣ ɛɥɢɡɨɫɬɢ ɬɨɱɤɢ ɮɚɡɨɜɨɝɨ
ɩɟɪɟɯɨɞɚ ɢɡ-ɡɚ ɬɨɝɨ, ɱɬɨ ɧɟ ɭɱɢɬɵɜɚɟɬ ɮɥɭɤɬɭɚɰɢɢ, ɪɟɡɤɨ ɜɨɡ-
ɪɚɫɬɚɸɳɢɟ ɢɦɟɧɧɨ ɜ ɨɤɪɟɫɬɧɨɫɬɢ ɷɬɨɣ ɬɨɱɤɢ ɩɪɢ ɮɚɡɨɜɨɦ ɩɟ-
ɪɟɯɨɞɟ ɜɬɨɪɨɝɨ ɪɨɞɚ. ȼ ɷɬɨɣ ɝɥɚɜɟ ɦɵ ɭɱɬɟɦ ɮɥɭɤɬɭɚɰɢɢ ɢ ɩɨ-
ɤɚɠɟɦ, ɤɚɤ ɷɬɨ ɩɨɡɜɨɥɹɟɬ ɥɭɱɲɟ ɨɩɢɫɚɬɶ ɷɤɫɩɟɪɢɦɟɧɬɚɥɶɧɵɟ
ɞɚɧɧɵɟ ɩɨ ɬɟɩɥɨɟɦɤɨɫɬɢ ɢ ɜɨɫɩɪɢɢɦɱɢɜɨɫɬɢ ɜ ɮɟɪɪɨɦɚɝɧɟɬɢ-
ɤɚɯ.
3.1.
Ȼɥɢɠɧɢɣ ɢ ɞɚɥɶɧɢɣ ɩɨɪɹɞɨɤ
.
Ɏɭɧɤɰɢɹ ɤɨɪɪɟɥɹɰɢɢ
ȼɜɟɞɟɦ ɩɨɧɹɬɢɟ ɞɚɥɶɧɟɝɨ ɢ ɛɥɢɠɧɟɝɨ ɩɨɪɹɞɤɚ ɜ ɫɩɢɧɨ-
ɜɵɯ ɦɨɞɟɥɹɯ.
Ɍɢɩɢɱɧɵɣ ɞɚɥɶɧɢɣ ɩɨɪɹɞɨɤ ɢɦɟɟɬ ɦɟɫɬɨ ɜ ɫɥɭɱɚɟ ɭɩɨ-
ɪɹɞɨɱɟɧɧɨɣ ɮɟɪɪɨɦɚɝɧɢɬɧɨɣ ɮɚɡɵ, ɤɨɝɞɚ <
P
j
>
z
0, ɧɟ ɡɚɜɢɫɢɬ
ɨɬ ɧɨɦɟɪɚ ɭɡɥɚ ɢ ɧɟ ɫɩɚɞɚɟɬ ɞɚɠɟ ɧɚ ɛɨɥɶɲɨɦ ɪɚɫɫɬɨɹɧɢɢ ɨɬ
ɭɡɥɚ j. Ⱦɚɥɶɧɢɣ ɩɨɪɹɞɨɤ ɫɩɨɧɬɚɧɧɨ ɢɫɱɟɡɚɟɬ ɜ ɬɨɱɤɟ ɩɟɪɟɯɨɞɚ.
Ȼɥɢɠɧɢɣ ɩɨɪɹɞɨɤ ɫɜɹɡɚɧ ɫ ɥɨɤɚɥɶɧɵɦɢ ɮɥɭɤɬɭɚɰɢɹɦɢ
ɫɩɢɧɨɜ ɧɚ ɛɥɢɡɤɢɯ ɪɚɫɫɬɨɹɧɢɹɯ. ȼ ɬɟɨɪɢɢ ɫɪɟɞɧɟɝɨ ɩɨɥɹ ɬɚɤɢɟ
ɮɥɭɤɬɭɚɰɢɢ ɧɟ ɭɱɢɬɵɜɚɸɬɫɹ, ɩɨɷɬɨɦɭ ɜ ɩɪɢɛɥɢɠɟɧɢɢ ȼɟɣɫɫɚ ɫ
ɢɫɱɟɡɧɨɜɟɧɢɟɦ ɫɩɨɧɬɚɧɧɨɣ ɧɚɦɚɝɧɢɱɟɧɧɨɫɬɢ ɢɫɱɟɡɚɟɬ ɢ ɷɧɟɪ-
ɝɢɹ ɜɡɚɢɦɨɞɟɣɫɬɜɢɹ ɫɩɢɧɨɜ, ɬ.ɟ. ɛɥɢɠɧɢɣ ɩɨɪɹɞɨɤ:
<
P
i
P
j
>=<
P
i
><
P
j
>=0, ɟɫɥɢ <
P
i
>=<
P
>=0.
Ɉɞɧɚɤɨ ɟɫɥɢ ɬɚɤɨɟ ɭɩɨɪɹɞɨɱɟɧɢɟ ɢɦɟɟɬ ɦɟɫɬɨ, ɬɨ
<
P
i
P
j
>
z
ɞɚɠɟ ɟɫɥɢ <
P
>=0, ɬ.ɟ. ɤɨɪɪɟɥɹɰɢɢ ɜɨɡɦɨɠɧɵ ɢ ɡɚ
ɬɨɱɤɨɣ ɮɚɡɨɜɨɝɨ ɩɟɪɟɯɨɞɚ. ɂɫɫɥɟɞɭɟɦ ɜɨɡɦɨɠɧɨɫɬɶ ɪɟɚɥɢɡɚ-
ɰɢɢ ɛɥɢɠɧɟɝɨ ɩɨɪɹɞɤɚ ɜ ɫɩɢɧɨɜɨɣ ɫɢɫɬɟɦɟ ɢ ɨɰɟɧɢɦ ɮɭɧɤɰɢɸ
ɤɨɪɪɟɥɹɰɢɢ <
P
i
P
j
>. Ɋɚɫɫɦɨɬɪɢɦ ɫɢɬɭɚɰɢɸ ɜɵɲɟ ɬɨɱɤɢ ɮɚɡɨɜɨ-
ɝɨ ɩɟɪɟɯɨɞɚ T >
4
. ȼ ɷɬɨɦ ɫɥɭɱɚɟ ɫɩɨɧɬɚɧɧɚɹ ɧɚɦɚɝɧɢɱɟɧɧɨɫɬɶ
<
P
>=0. ȼɵɞɟɥɢɦ ɞɜɚ ɫɩɢɧɚ ɢ ɨɰɟɧɢɦ ɫɧɚɱɚɥɚ ɤɨɪɪɟɥɹɰɢɸ

<
P
1
P
2
> ɜ ɩɪɟɧɟɛɪɟɠɟɧɢɢ ɮɥɭɤɬɭɚɰɢɹɦɢ ɨɫɬɚɥɶɧɵɯ ɫɩɢɧɨɜ.
ɉɭɫɬɶ ɜɧɟɲɧɟɟ ɩɨɥɟ ɪɚɜɧɨ ɧɭɥɸ. Ɍɨɝɞɚ
PP
P
P
E
P
P
EPP
E
E
EEE E E
12
12 1212
12 1 2
12
12
12 12 12 12 12
22
Sp V
Sp V
V
V
VVV V V
exp( )
exp( )
.eee e e e th
ɍɱɬɟɦ, ɱɬɨ V
12
#
V - ɜɡɚɢɦɨɞɟɣɫɬɜɢɟ ɫ ɛɥɢɠɚɣɲɢɦɢ ɫɨɫɟɞɹɦɢ,
ɚ ɬɚɤɠɟ th[
E
V](T >
4
)
t
th [
V/
4
@ . Ʉɪɨɦɟ ɬɨɝɨ,
VVVr
ij
j
ij
j
() (| |)0
¦¦
r =
VZ,
ɝɞɟ
Z
- ɱɢɫɥɨ ɛɥɢɠɚɣ-
ɲɢɯ ɫɨɫɟɞɟɣ, ɚ ɬɚɤɠɟ
4
V(0)
#
VZ
. Ɉɬɫɸɞɚ ɧɟɫɥɨɠɧɨ ɨɰɟɧɢɬɶ
ɦɚɫɲɬɚɛ ɛɥɢɠɧɢɯ ɤɨɪɪɟɥɹɰɢɣ: <
P
1
P
2
>~th1/Z~ 1/Z ɩɪɢ Z>>1.
Ɂɧɚɱɢɬ, ɱɟɦ ɛɨɥɶɲɟ ɱɢɫɥɨ ɛɥɢɠɚɣɲɢɯ ɫɨɫɟɞɟɣ, ɬɟɦ ɫɥɚɛɟɟ
ɤɨɪɪɟɥɹɰɢɢ, ɬɟɦ ɥɭɱɲɟ ɪɚɛɨɬɚɟɬ ɩɪɢɛɥɢɠɟɧɢɟ ɫɪɟɞɧɟɝɨ ɩɨɥɹ.
Ɉɬɦɟɬɢɦ, ɱɬɨ ɝɪɚɧɢɱɧɨɟ ɡɧɚɱɟɧɢɟ Z
c
, ɤɨɝɞɚ ɤɨɪɪɟɥɹɰɢɢ
ɧɚɱɢɧɚɸɬ ɫɭɳɟɫɬɜɟɧɧɨ ɪɚɡɪɭɲɚɬɶ ɞɚɥɶɧɢɣ ɩɨɪɹɞɨɤ, ɡɚɜɢɫɢɬ ɨɬ
ɦɨɞɟɥɢ. Ʉɚɤ ɦɵ ɜɢɞɟɥɢ ɜ ɩɪɟɞɵɞɭɳɟɣ ɝɥɚɜɟ, ɜ ɨɞɧɨɦɟɪɧɨɣ
ɦɨɞɟɥɢ ɂɡɢɧɝɚ ɩɪɢ Z=2 ɩɟɪɟɯɨɞ ɨɬɫɭɬɫɬɜɭɟɬ, ɚ ɜ ɞɜɭɦɟɪɧɨɣ
ɪɟɲɟɬɤɟ ɫ Z=4 ɮɥɭɤɬɭɚɰɢɢ ɭɠɟ ɧɟ ɪɚɡɪɭɲɚɸɬ ɞɚɥɶɧɢɣ ɩɨɪɹ-
ɞɨɤ. Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɦɨɠɧɨ ɨɰɟɧɢɬɶ, ɱɬɨ ɞɥɹ ɦɨɞɟɥɢ ɂɡɢɧɝɚ ɫ
ɜɡɚɢɦɨɞɟɣɫɬɜɢɟɦ ɬɨɥɶɤɨ ɛɥɢɠɚɣɲɢɯ ɫɨɫɟɞɟɣ ɤɪɢɬɢɱɟɫɤɨɟ
ɡɧɚɱɟɧɢɟ Z
c
~ 3.
3.2. Ɏɭɧɤɰɢɹ ɤɨɪɪɟɥɹɰɢɢ ɦɚɝɧɢɬɧɵɯ ɦɨɦɟɧɬɨɜ
ɜ ɦɨɞɟɥɢ ɂɡɢɧɝɚ
Ɉɩɪɟɞɟɥɢɦ ɛɨɥɟɟ ɬɨɱɧɨ ɮɭɧɤɰɢɸ ɩɚɪɧɨɣ ɤɨɪɪɟɥɹɰɢɢ
<
P
1
P
2
>, ɤɨɬɨɪɚɹ, ɜɨɨɛɳɟ ɝɨɜɨɪɹ, ɧɟ ɨɛɪɚɳɚɟɬɫɹ ɜ ɧɭɥɶ ɩɪɢ
ɢɫɱɟɡɧɨɜɟɧɢɢ ɞɚɥɶɧɟɝɨ ɩɨɪɹɞɤɚ. Ɇɵ ɭɠɟ ɨɰɟɧɢɥɢ ɟɟ ɩɨɪɹɞɨɤ
ɜɟɥɢɱɢɧɵ <
P
1
P
2
> ~ 1/Z. ɑɬɨɛɵ ɩɨɥɭɱɢɬɶ ɤɨɥɢɱɟɫɬɜɟɧɧɵɣ ɪɟ-
ɡɭɥɶɬɚɬ, ɢɫɩɨɥɶɡɭɟɦ ɬɭ ɠɟ ɢɞɟɸ ɫɚɦɨɫɨɝɥɚɫɨɜɚɧɧɨɝɨ ɩɨɥɹ.
Ɋɚɫɫɦɨɬɪɢɦ ɦɨɞɟɥɶ ɂɡɢɧɝɚ ɩɪɢ T>
4
, T
o4
. ɉɭɫɬɶ ɢɦɟɟɬɫɹ
46

ɜɵɞɟɥɟɧɧɵɣ ɦɨɦɟɧɬ ɫɨ ɡɧɚɱɟɧɢɟɦ
P
1
=+1. Ɍɨɝɞɚ ɮɭɧɤɰɢɹ ɤɨɪ-
ɪɟɥɹɰɢɢ ɟɫɬɶ ɩɪɨɫɬɨ ɫɪɟɞɧɟɟ <
P
2
> ɜ ɭɞɨɜɥɟɬɜɨɪɹɸɳɟɦ ɷɬɨɦɭ
ɭɫɥɨɜɢɸ ɚɧɫɚɦɛɥɟ:
!
!
PP
P
P
PE
E
12
2
1
2
1
Sp H
Sp H
eff
eff
exp( )
exp( )
. (3.1)
Ɂɞɟɫɶ H
eff
- ɷɮɮɟɤɬɢɜɧɵɣ ɝɚɦɢɥɶɬɨɧɢɚɧ, ɫɨɨɬɜɟɬɫɬɜɭɸɳɢɣ
ɷɬɨɦɭ ɚɧɫɚɦɛɥɸ.
ɉɨɥɚɝɚɹ ɜɧɟɲɧɟɟ ɩɨɥɟ ɧɭɥɟɜɵɦ, ɭɱɬɟɦ, ɱɬɨ ɞɟɣɫɬɜɭɸ-
ɳɟɟ ɧɚ ɫɩɢɧ 2 ɜɧɭɬɪɟɧɧɟɟ ɩɨɥɟ, ɫɨɡɞɚɜɚɟɦɨɟ ɫɩɢɧɨɦ 1, ɚ ɬɚɤɠɟ
ɢ ɨɫɬɚɥɶɧɵɦɢ ɫɩɢɧɚɦɢ, ɪɚɜɧɨ
HV V
jj
j
221 2
1
z
¦
P
. (3.2)
ɋɪɟɞɧɟɟ ɩɨɥɟ ɫɨɨɬɜɟɬɫɬɜɟɧɧɨ, ɢɦɟɟɬ ɜɢɞ
! !
zz
¦
!
¦
HV V V V
jj
j
j
j
221 2
1
21 2 1
1
PP
j
P
!
)
j
)
)
)
. (3.3)
ɍɱɢɬɵɜɚɹ ɭɪɚɜɧɟɧɢɟ ȼɟɣɫɫɚ (1.11), ɧɟɦɟɞɥɟɧɧɨ ɩɨɥɭɱɚɟɦ
! !
®
¯
½
¾
¿
z
¦
PP E E PP
12 2 21 2 1
1
th thHVV
jj
j
. (3.4)
Ɉɛɨɡɧɚɱɢɦ ɮɭɧɤɰɢɸ ɤɨɪɪɟɥɹɰɢɢ . ɉɟɪɟ-
ɩɢɲɟɦ ɭɪɚɜɧɟɧɢɟ (3.4):
!
oo
PP
1
1
j
j
gR R(
gRR VRR VRRgRR
j
j
() ()()(
oo oo o o oo
z
®
¯
½
¾
¿
¦
12 12 2 1
1
th
E
. (3.5)
ȼ ɩɪɢɛɥɢɠɟɧɢɢ ȼɟɣɫɫɚ ɮɭɧɤɰɢɹ = 0. ɂɳɟɦ ɧɟɬɪɢ-
ɜɢɚɥɶɧɨɟ ɪɟɲɟɧɢɟ ɢ ɩɨɥɨɠɢɦ
gR R
j
(
oo
1
gR R
j
(
oo
1
<<1, VR <<
4
.R
j
()
oo
2
ɉɨɫɥɟɞɧɟɟ ɧɟɪɚɜɟɧɫɬɜɨ ɫɩɪɚɜɟɞɥɢɜɨ ɜ ɩɪɟɞɟɥɟ ɛɨɥɶɲɨɝɨ ɱɢɫ-
ɥɚ ɛɥɢɠɚɣɲɢɯ ɫɨɫɟɞɟɣ 1/Z <<1 (
4
=ZV). Ɉɬɫɸɞɚ:
47

48
j
)gRR VRR VRRgRR
j
j
()()()(
oo oo o o oo
z
®
¯
½
¾
¿
¦
12 12 2 1
1
E
. (3.6)
ɍɪɚɜɧɟɧɢɟ (3.6) ɪɟɲɚɟɦ ɩɪɟɨɛɪɚɡɨɜɚɧɢɟɦ Ɏɭɪɶɟ:
gR
N
gq iqR
q
() ()exp( )
oo
¦
1
oo
o
,
gq gR R iqR R
ij
ij
ij
() ( )exp( [ ])
ooo
z
oo o
¦
, (3.7)
Vq VR R iqR R
ij
ij
ij
() ( )exp( [ ])
ooo
z
oo o
¦
.
ɉɪɨɢɧɬɟɝɪɢɪɨɜɚɜ ɭɪɚɜɧɟɧɢɟ (3.6) ɫ ɦɧɨɠɢɬɟɥɟɦ
exp(-iqR) ɩɨ ɤɨɨɪɞɢɧɚɬɟ, ɩɨɥɭɱɚɟɦ ɞɥɹ ɮɭɪɶɟ-ɤɨɦɩɨɧɟɧɬɵ
ɤɨɪɪɟɥɹɰɢɨɧɧɨɣ ɮɭɧɤɰɢɢ:
gq Vq g qVq() () ( )()
ooo
®
¯
½
¾
¿
E
. (3.8)
ȼɜɢɞɭ ɨɞɧɨɪɨɞɧɨɫɬɢ ɢ ɢɡɨɬɪɨɩɧɨɫɬɢ ɩɪɨɫɬɪɚɧɫɬɜɚ
gR g R() (||)
oo
,
VR
,
VR() (||)
oo
ɨɬɤɭɞɚ ɫɥɟɞɭɟɬ, ɱɬɨ (ɷɬɨ ɧɟɫɥɨɠɧɨ ɩɨɤɚɡɚɬɶ ɩɪɹ-
ɦɨ ɢɡ (3.7)). Ɉɤɨɧɱɚɬɟɥɶɧɨ ɩɨɥɭɱɚɟɦ:
gq g q() ( )
oo
gq
Vq
Vq
T()
()
()
,
o
o
o
!
E
E
T
1
. (3.9)
ȼ ɞɥɢɧɧɨɜɨɥɧɨɜɨɦ ɩɪɟɞɟɥɟ ɮɭɧɤɰɢɹ V(q)= V(0) =
4
. ȼ
ɫɜɨɸ ɨɱɟɪɟɞɶ
gq
T
T()
/
,
o
of o
ET
T
T
1
.
Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɜɢɞɧɨ, ɱɬɨ ɮɭɪɶɟ-ɤɨɦɩɨɧɟɧɬɚ ɪɚɫɯɨɞɢɬɫɹ ɩɪɢ
ɩɪɢɛɥɢɠɟɧɢɢ ɤ ɬɨɱɤɟ ɮɚɡɨɜɨɝɨ ɩɟɪɟɯɨɞɚ. ɂɫɫɥɟɞɭɟɦ ɩɪɨ-
ɫɬɪɚɧɫɬɜɟɧɧɭɸ ɡɚɜɢɫɢɦɨɫɬɶ ɮɭɧɤɰɢɢ ɤɨɪɪɟɥɹɰɢɢ:
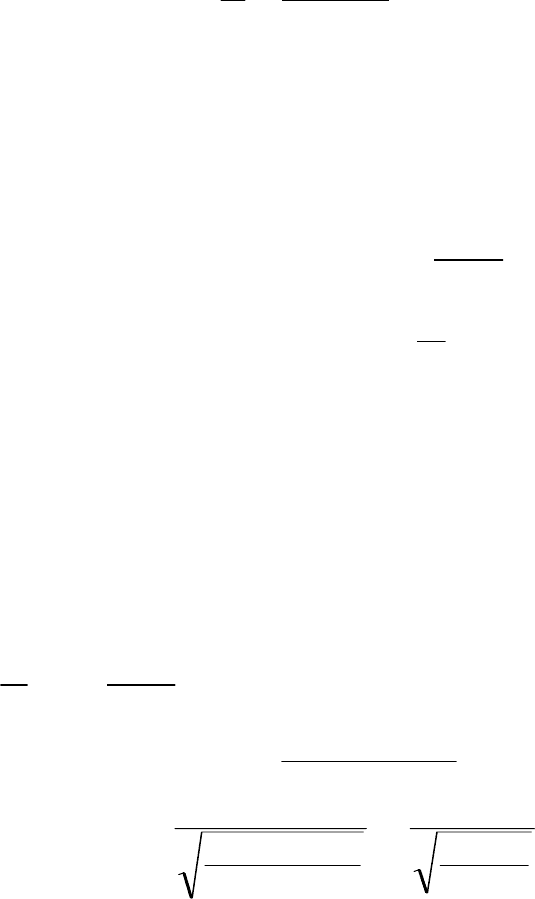
gR
N
Vq
Vq
iqR
q
()
()
()
exp( )
o
o
o
oo
¦
1
1
E
E
. (3.10)
Ɋɚɫɫɦɨɬɪɢɦ ɞɥɢɧɧɨɜɨɥɧɨɜɵɣ ɩɪɟɞɟɥ q o0 (ɬ.ɟ. ɢɫɫɥɟ-
ɞɭɟɦ ɫɢɬɭɚɰɢɸ ɜ ɩɪɟɞɟɥɟ ɛɨɥɶɲɢɯ ɤɨɪɪɟɥɹɰɢɨɧɧɵɯ ɞɥɢɧ
R
of
ɨɤɨɥɨ ɬɨɱɤɢ ɮɚɡɨɜɨɝɨ ɩɟɪɟɯɨɞɚ. Ɍɨɝɞɚ ɮɭɪɶɟ-
ɤɨɦɩɨɧɟɧɬɚ ɜɡɚɢɦɨɞɟɣɫɬɜɢɹ ɩɪɢɛɥɢɠɟɧɧɨ ɦɨɠɟɬ ɛɵɬɶ ɩɪɟɞ-
ɫɬɚɜɥɟɧɚ ɫɥɟɞɭɸɳɢɦ ɨɛɪɚɡɨɦ:
Vq V r iqr
qr
Vq Vr
r
q
r
r
() (||)(
()
)
() , (||) .
o
o
ooo
oo
o
¦
¦
0
2
2
2
1
2
0
3
DD
(3.11)
ɉɚɪɚɦɟɬɪ
D
ɩɨ ɩɨɪɹɞɤɭ ɜɟɥɢɱɢɧɵ ɪɚɜɟɧ
D
~V(0)/r
2
ɯɚɪ
~
4
/r
2
ɯɚɪ
,
ɝɞɟ r
ɯɚɪ
- ɯɚɪɚɤɬɟɪɧɚɹ ɞɥɢɧɚ, ɧɚ ɤɨɬɨɪɨɣ ɞɟɣɫɬɜɭɟɬ ɜɡɚɢɦɨɞɟɣ-
ɫɬɜɢɟ (ɦɨɠɧɨ ɩɨɤɚɡɚɬɶ, ɱɬɨ ɩɪɟɞɫɬɚɜɥɟɧɢɟ (3.11) ɩɪɢɜɨɞɢɬ ɤ
ɷɤɫɩɨɧɟɧɰɢɚɥɶɧɨɦɭ ɫɩɚɞɭ
V(r) ~ (1/r)exp (- r/r
ɯɚɪ
) - ɫɦ.ɡɚɞɚɱɭ 3.2.1).
ɉɨɞɫɬɚɜɥɹɹ (3.11) ɜ (3.10), ɧɚɯɨɞɢɦ ɩɪɨɫɬɪɚɧɫɬɜɟɧɧɭɸ
ɡɚɜɢɫɢɦɨɫɬɶ ɤɨɪɪɟɥɹɰɢɨɧɧɨɣ ɮɭɧɤɰɢɢ ɜ ɩɪɟɞɟɥɟ
Do
0 (ɢɧɬɟ-
ɝɪɚɥ (3.10) ɛɟɪɟɬɫɹ ɜ ɫɮɟɪɢɱɟɫɤɢɯ ɤɨɨɪɞɢɧɚɬɚɯ ɩɨ q, ɬɚɤ ɱɬɨ
1
2
0
3
2
1
1
00
2
N
qq
q
¦
³³³
f
:
()
cos
S
T
S
dd d
M
) :
gr
rd
r
d
VT
()
/
,
()
,
o
#
|
exp[ ]
1
10
1
E
ED
T
D
(3.12)
ɝɞɟ d - ɯɚɪɚɤɬɟɪɧɚɹ ɤɨɪɪɟɥɹɰɢɨɧɧɚɹ ɞɥɢɧɚ;
:
0
- ɨɛɴɟɦ ɷɥɟɦɟɧ-
ɬɚɪɧɨɣ ɹɱɟɣɤɢ.
49
