Елесин В.Ф., Кашурников В.А. Физика фазовых переходов
Подождите немного. Документ загружается.

(ɦɢɧɢɦɭɦ) ɩɪɢ R
z
0
(ɪɢɫ.5), ɩɪɢ ɷɬɨɦ ɡɧɚɱɟɧɢɟ
ɩɚɪɚɦɟɬɪɚ ɩɨɪɹɞɤɚ R ɹɜ-
ɥɹɟɬɫɹ ɧɟɬɪɢɜɢɚɥɶɧɵɦ
ɪɟɲɟɧɢɟɦ ɭɪɚɜɧɟɧɢɹ
ȼɟɣɫɫɚ (2.6), (2.12). ȼɛɥɢ-
ɡɢ ɬɨɱɤɢ ɩɟɪɟɯɨɞɚ T
o
4
ɜɨɫɩɨɥɶɡɭɟɦɫɹ ɪɚɡ-
ɥɨɠɟɧɢɟɦ ɭɪɚɜɧɟɧɢɹ
ȼɟɣɫɫɚ (ɩɪɢ R
o
0):
R#
4
R/T - 1/3(
4
3
/T
3
)R
3
,
ɨɬɤɭɞɚ R
2
= 3(
4
/T-1), ɢ
1
20
2
2
N
FR T
ww T
/() !,
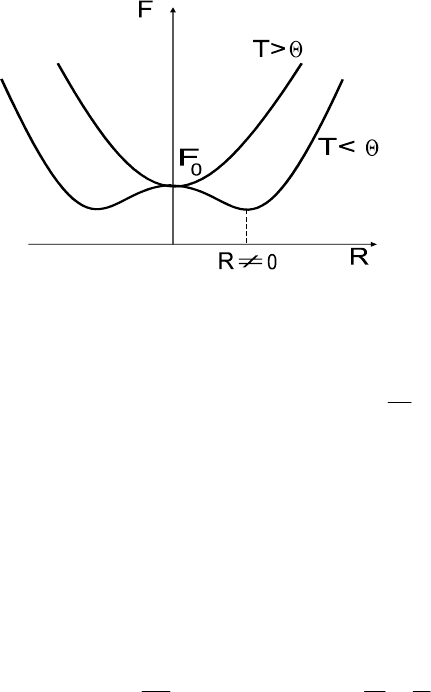
ɬ.ɟ. ɞɟɣɫɬɜɢɬɟɥɶɧɨ ɫɜɨɛɨɞɧɚɹ ɷɧɟɪɝɢɹ ɢɦɟɟɬ ɦɢɧɢɦɭɦ. Ʉɚɤ
ɜɢɞɧɨ ɢɡ ɪɢɫ.5, ɬɨɱɤɚ ɷɬɨɝɨ ɦɢɧɢɦɭɦɚ ɥɟɠɢɬ ɧɢɠɟ ɬɨɱɤɢ ɷɤɫ-
ɬɪɟɦɭɦɚ ɩɪɢ R=0, ɱɬɨ ɝɨɜɨɪɢɬ ɨ ɜɵɝɨɞɧɨɫɬɢ ɮɟɪɪɨɦɚɝɧɢɬɧɨɝɨ
ɫɨɫɬɨɹɧɢɹ R
z
0 ɩɪɢ T<
4
.
Ɋɢɫ
.5.
ɋɜɨɛɨɞɧɚɹ ɷɧɟɪɝɢɹ ɮɟɪɪɨ
-
ɦɚɝɧɟɬɢɤɚ ɜ ɦɨɞɟɥɢ ɂɡɢɧɝɚ ɤɚɤ
ɮɭɧɤɰɢɹ ɩɚɪɚɦɟɬɪɚ ɩɨɪɹɞɤɚ R
ɍɛɟɞɢɦɫɹ ɚɧɚɥɢɬɢɱɟɫɤɢ, ɱɬɨ ɮɟɪɪɨɦɚɝɧɟɬɢɡɦ ɜɵɝɨɞɟɧ ɢ
ɩɪɢ ɧɢɡɤɢɯ ɬɟɦɩɟɪɚɬɭɪɚɯ. ȼ ɩɪɟɞɟɥɟ T
o
0 ɩɚɪɚɦɟɬɪ ɩɨɪɹɞɤɚ
R = 1- 2exp(-2
4
/T). ɉɨɞɫɬɚɜɥɹɹ ɷɬɨ ɜɵɪɚɠɟɧɢɟ ɜ (2.13), ɩɨɥɭ-
ɱɚɟɦ
11
4
20
22
N
FR T
T
T
ww
T
T
/( /) !exp[ ]
,
ɬ.ɟ. ɦɢɧɢɦɭɦ ɫɨɯɪɚɧɹɟɬɫɹ.
Ɂɚɦɟɬɢɦ, ɱɬɨ ɱɢɫɥɟɧɧɨ ɦɨɠɧɨ ɩɨɤɚɡɚɬɶ, ɱɬɨ ɜɨ ɜɫɟɦ
ɞɢɚɩɚɡɨɧɟ
T <
4
ɜɵɝɨɞɧɨ R
z
0.
Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɬɨɱɤɚ ɮɚɡɨɜɨɝɨ ɩɟɪɟɯɨɞɚ ɯɚɪɚɤɬɟɪɢɡɭ-
ɟɬɫɹ ɩɨɹɜɥɟɧɢɟɦ ɝɥɨɛɚɥɶɧɨɝɨ ɦɢɧɢɦɭɦɚ ɫɜɨɛɨɞɧɨɣ ɷɧɟɪɝɢɢ ɫ
ɧɟɬɪɢɜɢɚɥɶɧɵɦ ɡɧɚɱɟɧɢɟɦ ɩɚɪɚɦɟɬɪɚ ɩɨɪɹɞɤɚ, ɫɢɦɜɨɥɢɡɢ-
ɪɭɸɳɟɝɨ ɮɟɪɪɨɦɚɝɧɢɬɧɨɟ ɭɩɨɪɹɞɨɱɟɧɢɟ.
Ɂɚɞɚɱɢ
2.2.1. ɇɚɣɬɢ ɫɜɨɛɨɞɧɭɸ ɷɧɟɪɝɢɸ ɜ ɦɨɞɟɥɢ ɂɡɢɧɝɚ ɜ
ɩɪɢɛɥɢɠɟɧɢɢ ɫɪɟɞɧɟɝɨ ɩɨɥɹ ɢɫɯɨɞɹ ɢɡ ɩɨɥɭɱɟɧɨɝɨ ɜ ɡɚɞɚɱɟ
30

(2.1.2) ɜɵɪɚɠɟɧɢɹ ɞɥɹ ɫɬɚɬɢɫɬɢɱɟɫɤɨɣ ɫɭɦɦɵ Q. Ⱦɨɤɚɡɚɬɶ, ɱɬɨ
ɩɨɥɭɱɟɧɧɵɣ ɪɟɡɭɥɶɬɚɬ ɫɨɜɩɚɞɚɟɬ ɫ ɪɟɡɭɥɶɬɚɬɨɦ ɩɨɞɯɨɞɚ Ȼɪɷɝ-
ɝɚ-ȼɢɥɶɹɦɫɚ (2.11).
Ɉɬɜɟɬ
:
>@
FTQNHR TN HH ln / ln { ( )}
EP EP
00 0 0
22ch
.
ȿɫɥɢ ɭɱɟɫɬɶ ɭɪɚɜɧɟɧɢɟ ȼɟɣɫɫɚ (2.12), ɬɨ ɥɟɝɤɨ ɞɨɤɚɡɚɬɶ ɷɤɜɢ-
ɜɚɥɟɧɬɧɨɫɬɶ ɩɨɥɭɱɟɧɧɨɝɨ ɜɵɪɚɠɟɧɢɹ ɢ (2.11).
2.2.
2. ɂɡ ɭɫɥɨɜɢɹ ɦɢɧɢɦɭɦɚ ɫɜɨɛɨɞɧɨɣ ɷɧɟɪɝɢɢ
w
F/
w
R=0, ɩɨɥɭɱɟɧɧɨɣ ɜ ɩɪɟɞɵɞɭɳɟɣ ɡɚɞɚɱɟ, ɩɨɥɭɱɢɬɶ ɭɪɚɜɧɟ-
ɧɢɟ ȼɟɣɫɫɚ ɧɚ ɩɚɪɚɦɟɬɪ ɩɨɪɹɞɤɚ R.
2.2.
3. ɇɚɣɬɢ ɬɟɦɩɟɪɚɬɭɪɭ Ʉɸɪɢ-ȼɟɣɫɫɚ
4
ɢ ɢɫɫɥɟɞɨ-
ɜɚɬɶ ɩɨɜɟɞɟɧɢɟ ɩɚɪɚɦɟɬɪɚ ɩɨɪɹɞɤɚ R ɩɪɢ T
o
0 ɢ T
o4
ɜɦɨɞɟ-
ɥɢ ɂɡɢɧɝɚ ɜ ɩɪɢɛɥɢɠɟɧɢɢ ɫɪɟɞɧɟɝɨ ɩɨɥɹ.
Ɋɟɲɟɧɢɟ
. ɂɫɩɨɥɶɡɭɟɦ ɭɪɚɜɧɟɧɢɟ ȼɟɣɫɫɚ
R = th{ R
4
/T}. ɍɱɢɬɵɜɚɟɦ, ɱɬɨ:
th thxxx x x x x x o of
35
32 45 0 12//,, exp(), .
Ɉɬɫɸɞɚ ɧɚɯɨɞɢɦ:
RTT
Ryy y T T Z
o
o
12 2 0
312 5 1
22
0
2
exp( / ), ,
/, ( )/ , , .
T
TT TTP
J
2.2.4. ɂɫɫɥɟɞɨɜɚɬɶ ɩɨɜɟɞɟɧɢɟ ɫɜɨɛɨɞɧɨɣ ɷɧɟɪɝɢɢ F ɩɪɢ
H=0, T
o
0 ɢ T
o4
. ȼɨɫɩɨɥɶɡɨɜɚɬɶɫɹ ɪɟɡɭɥɶɬɚɬɨɦ ɡɚɞɚɱɢ 2.2.1 ɢ
ɞɨɤɚɡɚɬɶ ɭɫɬɨɣɱɢɜɨɫɬɶ ɮɟɪɪɨɦɚɝɧɢɬɧɨɝɨ ɫɨɫɬɨɹɧɢɹ ɜ ɷɬɢɯ ɫɥɭ-
ɱɚɹɯ. ɉɨɥɭɱɢɬɶ ɪɚɡɥɨɠɟɧɢɟ F ɩɨ ɩɚɪɚɦɟɬɪɭ ɩɨɪɹɞɤɚ ɜ ɩɪɟɞɟɥɟ
R
o
0 .
Ɉɬɜɟɬ
:
FN O T T
FN T Ry R y T T
//(exp{/}),,
/ln / /,()/,.
o
o
TT
TT TTT
22 0
2212
24
Ʉɪɨɦɟ ɬɨɝɨ,
FR FR N y y T() ( ) ( /)[ /] , o034 50
23
T
T
.
31

2.3.
Ɍɟɩɥɨɟɦɤɨɫɬɶ ɜ ɩɪɢɛɥɢɠɟɧɢɢ ɫɪɟɞɧɟɝɨ ɩɨɥɹ
ɜ ɦɨɞɟɥɢ ɂɡɢɧɝɚ
Ɋɚɫɫɦɨɬɪɢɦ ɜɚɠɧɭɸ ɷɤɫɩɟɪɢɦɟɧɬɚɥɶɧɨ ɢɡɦɟɪɹɟɦɭɸ
ɮɢɡɢɱɟɫɤɭɸ ɜɟɥɢɱɢɧɭ - ɬɟɩɥɨɟɦɤɨɫɬɶ C - ɤɨɥɢɱɟɫɬɜɨ ɷɧɟɪɝɢɢ,
ɤɨɬɨɪɭɸ ɡɚɩɚɫɚɟɬ ɫɢɫɬɟɦɚ ɩɪɢ ɩɨɜɵɲɟɧɢɢ ɬɟɦɩɟɪɚɬɭɪɵ ɧɚ 1Ʉ
(ɧɚɩɪɢɦɟɪ, ɡɚ ɫɱɟɬ ɩɟɪɟɨɪɢɟɧɬɚɰɢɢ ɫɩɢɧɨɜ ɢ ɜɨɡɛɭɠɞɟɧɢɹ
ɤɨɥɟɛɚɬɟɥɶɧɵɯ ɫɬɟɩɟɧɟɣ ɫɜɨɛɨɞɵ). Ɋɚɫɫɱɢɬɚɟɦ ɟɟ ɜ
ɩɪɢɛɥɢɠɟɧɢɢ ɫɪɟɞɧɟɝɨ ɩɨɥɹ ɜ ɦɨɞɟɥɢ ɂɡɢɧɝɚ. ɂɡ ɜɵɪɚɠɟɧɢɹ
ɞɥɹ ɷɧɟɪɝɢɢ (2.8) ɩɨɥɭɱɚɟɦ:
CET
N
R
ww
T
T
ww
/
2
2
/
. (2.14)
Ɉɬɫɸɞɚ, ɜɨɫɩɨɥɶɡɨɜɚɜɲɢɫɶ ɢɡɜɟɫɬɧɵɦɢ ɩɪɟɞɟɥɶɧɵɦɢ ɫɨɨɬɧɨ-
ɲɟɧɢɹɦɢ ɞɥɹ ɩɚɪɚɦɟɬɪɚ ɩɨɪɹɞɤɚ, ɢɦɟɟɦ:
C
NT
TN T T
o
o
®
°
¯
°
3
2
42
2
,;
(/) exp / , .
T
TT
0
(2.15)
Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɩɪɢ ɧɢɡɤɢɯ ɬɟɦɩɟɪɚɬɭɪɚɯ ɬɟɩɥɨɟɦɤɨɫɬɶ
ɷɤɫɩɨɧɟɧɰɢɚɥɶɧɨ ɫɬɪɟɦɢɬɫɹ ɤ ɧɭɥɸ, ɬɚɤ ɤɚɤ ɜ ɫɢɫɬɟɦɟ ɢɦɟɟɬɫɹ
ɤɨɧɟɱɧɚɹ ɳɟɥɶ (2
4
) ɦɟɠɞɭ ɨɫɧɨɜɧɵɦ ɢ ɜɨɡɛɭɠɞɟɧɧɵɦɢ ɫɨ-
ɫɬɨɹɧɢɹɦɢ. ȼ ɬɨɱɤɟ ɩɟɪɟɯɨɞɚ ɨɧɚ ɤɨɧɟɱɧɚ (ɪɢɫ.6). ɑɢɫɥɟɧɧɵɣ
ɦɧɨɠɢɬɟɥɶ 3/2 ɧɟ ɫɥɭɱɚɟɧ - ɨɧ ɫɜɹɡɚɧ ɫ ɱɢɫɥɨɦ ɫɬɟɩɟɧɟɣ ɫɜɨ-
ɛɨɞɵ ɜ ɬɪɟɯɦɟɪɧɨɣ ɫɢɬɭɚɰɢɢ (~1/2 kT ɧɚ ɤɚɠɞɭɸ). (Ɉɬɦɟɬɢɦ,
ɱɬɨ ɜ ɩɪɢɛɥɢɠɟɧɢɢ ɫɪɟɞɧɟɝɨ ɩɨɥɹ ɦɟɪɧɨɫɬɶ ɩɪɨɫɬɪɚɧɫɬɜɚ ɜɯɨ-
ɞɢɬ ɜ ɨɬɜɟɬ ɬɨɥɶɤɨ ɱɟɪɟɡ ɱɢɫɥɨ ɛɥɢɠɚɣɲɢɯ ɫɨɫɟɞɟɣ Z, ɫ ɷɬɨɣ
ɬɨɱɤɢ ɡɪɟɧɢɹ ɩɪɢ Z >>1 ɡɚɞɚɱɚ ɜɫɟɝɞɚ ɤɚɤ ɦɢɧɢɦɭɦ ɬɪɟɯɦɟɪ-
ɧɚ.) ɋɥɟɞɭɟɬ ɡɚɦɟɬɢɬɶ, ɱɬɨ ɧɚ ɷɤɫɩɟɪɢɦɟɧɬɟ ɧɚɛɥɸɞɚɟɬɫɹ ɨɫɨ-
ɛɟɧɧɨɫɬɶ ɜɛɥɢɡɢ ɬɨɱɤɢ ɩɟɪɟɯɨɞɚ (ɪɢɫ.7), ɱɬɨ ɝɨɜɨɪɢɬ ɨ ɧɟɩɪɢ-
ɦɟɧɢɦɨɫɬɢ ɩɪɢɛɥɢɠɟɧɢɹ ɫɪɟɞɧɟɝɨ ɩɨɥɹ ɜ ɷɬɨɣ ɨɛɥɚɫɬɢ. Ⱦɚɥɟɟ
ɜ ɝɥɚɜɟ 3 ɦɵ ɩɨɤɚɠɟɦ, ɤɚɤ ɦɨɠɧɨ ɨɛɴɹɫɧɢɬɶ ɷɬɨɬ ɷɤɫɩɟɪɢɦɟɧ-
ɬɚɥɶɧɵɣ ɮɚɤɬ, ɪɚɫɲɢɪɢɜ ɜɨɡɦɨɠɧɨɫɬɢ ɩɨɞɯɨɞɚ ɫ ɭɱɟɬɨɦ ɮɥɭɤ-
ɬɭɚɰɢɣ.
32
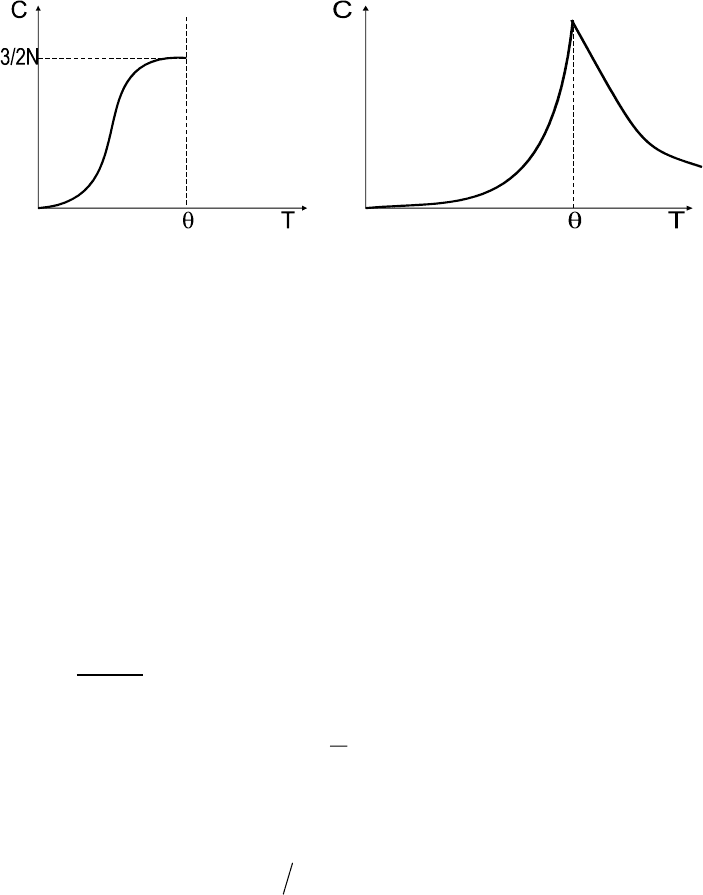
Ɋɢɫ.6. Ɍɟɩɥɨɟɦɤɨɫɬɶ ɜ ɦɨɞɟ-
ɥɢ ɂɡɢɧɝɚ ɜ ɩɪɢɛɥɢɠɟɧɢɢ
ɫɪɟɞɧɟɝɨ ɩɨɥɹ
Ɋɢɫ.7. ɗɤɫɩɟɪɢɦɟɧɬɚɥɶɧɨ ɧɚ-
ɛɥɸɞɚɟɦɵɟ ɨɫɨɛɟɧɧɨɫɬɢ ɬɟɩɥɨ-
ɟɦɤɨɫɬɢ ɜɛɥɢɡɢ ɬɨɱɤɢ ɮɟɪɪɨ-
ɦɚɝɧɢɬɧɨɝɨ ɩɟɪɟɯɨɞɚ
(
O
- ɬɨɱɤɚ)
Ɂɚɞɚɱɢ
2.3.
1. ȼɵɪɚɡɢɬɶ ɬɟɩɥɨɟɦɤɨɫɬɶ ɦɨɞɟɥɢ ɂɡɢɧɝɚ C ɱɟɪɟɡ
ɩɚɪɚɦɟɬɪ ɩɨɪɹɞɤɚ R, ɢɫɩɨɥɶɡɭɹ C= - T
w
2
F/
w
T
2
ɢ ɫɜɨɛɨɞɧɭɸ
ɷɧɟɪɝɢɸ ɢɡ ɡɚɞɚɱɢ 2.2.1. Ɋɚɫɫɦɨɬɪɟɬɶ ɩɪɟɞɟɥɶɧɵɟ ɫɥɭɱɚɢ
T
o
0 ɢ T
o4
.
Ɉɬɜɟɬ
:
CN R T
CN T T
CN T T T
//,
//[()/],
/()exp(/),
o
,
.o
T
ww
TT
TT
2
321 8 5
42
2
2
T
0
33

2.4.
Ɇɚɝɧɢɬɧɚɹ ɜɨɫɩɪɢɢɦɱɢɜɨɫɬɶ ɜ ɩɪɢɛɥɢɠɟɧɢɢ
ɫɪɟɞɧɟɝɨ ɩɨɥɹ ɜ ɦɨɞɟɥɢ ɂɡɢɧɝɚ
ɉɨɥɭɱɢɦ ɡɚɤɨɧ Ʉɸɪɢ-ȼɟɣɫɫɚ ɞɥɹ ɜɨɫɩɪɢɢɦɱɢɜɨɫɬɢ ɬɢ-
ɩɚ (1.14) ɢɫɯɨɞɹ ɢɡ ɭɪɚɜɧɟɧɢɹ ȼɟɣɫɫɚ (2.6). ɉɨ ɨɩɪɟɞɟɥɟɧɢɸ:
F
w
w
P
o
d
d
M
H
M
N
F
H
R
H 0
0
1
,
@
R
, (2.16)
ɩɪɢ ɷɬɨɦ
F
- ɩɨɥɧɚɹ ɩɪɨɢɡɜɨɞɧɚɹ ɨɬ ɦɚɝɧɢɬɧɨɝɨ ɦɨɦɟɧɬɚ (ɤɨ-
ɷɮɮɢɰɢɟɧɬ ɩɪɢ ɩɟɪɜɨɣ ɩɨɩɪɚɜɤɟ ɪɚɡɥɨɠɟɧɢɹ ɩɨ ɩɨɥɸ), ɜɬɨ
ɜɪɟɦɹ ɤɚɤ ɦɚɝɧɢɬɧɵɣ ɦɨɦɟɧɬ - ɷɬɨ ɬɟɪɦɨɞɢɧɚɦɢɱɟɫɤɚɹ ɩɪɨɢɡ-
ɜɨɞɧɚɹ ɩɨ ɩɨɥɸ ɨɬ ɫɜɨɛɨɞɧɨɣ ɷɧɟɪɝɢɢ. ȼ (2.16) ɭɱɬɟɧɚ ɬɚɤɠɟ
ɪɚɡɦɟɪɧɨɫɬɶ ɦɚɝɧɢɬɧɨɝɨ ɦɨɦɟɧɬɚ (~
P
0
) . ɂɫɩɨɥɶɡɭɹ ɭɪɚɜɧɟɧɢɟ
ȼɟɣɫɫɚ:
>
RH th
EP T
0
(2.17)
ɢ (2.16), ɩɪɨɞɢɮɮɟɪɟɧɰɢɪɭɟɦ (2.17) ɩɨ ɩɨɥɸ (ɩɨɥɧɭɸ ɩɪɨɢɡ-
ɜɨɞɧɭɸ), ɢɦɟɹ ɜɜɢɞɭ ɡɚɜɢɫɢɦɨɫɬɶ R(H). Ɍɨɝɞɚ ɩɨɥɭɱɢɦ ɡɚɦɤ-
ɧɭɬɨɟ ɭɪɚɜɧɟɧɢɟ ɧɚ
F
, ɨɬɤɭɞɚ ɨɤɨɧɱɚɬɟɥɶɧɨ
F
P
T
0
22
2
1
1
(
()
R
TR
)
. (2.18)
Ɋɚɫɫɦɨɬɪɢɦ ɩɪɟɞɟɥɶɧɵɟ ɫɥɭɱɚɢ. ȼɵɪɚɠɟɧɢɟ (2.18) ɫɭɱɟɬɨɦ
ɢɡɜɟɫɬɧɨɝɨ ɪɚɡɥɨɠɟɧɢɹ ɩɚɪɚɦɟɬɪɚ ɩɨɪɹɞɤɚ R ɩɪɢɜɨɞɢɬ ɤ ɫɥɟ-
ɞɭɸɳɟɦɭ (ɭɱɢɬɵɜɚɹ ɬɚɤɠɟ, ɱɬɨ R=0 ɩɪɢ T>
4
):
F
PT
P
T
P
T
T
T
®
°
°
°
¯
°
°
°
o
o
o
4
2
2
0
0
0
0
2
0
2
0
2
TT
T
T
T
T
T
exp( ),
()
,
,
;
;
.
(2.19)
34
Ƚɪɚɮɢɤ
F
(T) ɩɨɤɚɡɚɧ ɧɚ ɪɢɫ.4. Ʉɚɤ ɜɢɞɧɨ ɢɡ ɪɢɫɭɧɤɚ ɢ
ɪɚɡɥɨɠɟɧɢɣ (2.19), ɜɛɥɢɡɢ ɨɛɥɚɫɬɢ ɮɚɡɨɜɨɝɨ ɩɟɪɟɯɨɞɚ ɧɚɛɥɸ-
ɞɚɟɬɫɹ ɬɢɩɢɱɧɵɣ ɡɚɤɨɧ Ʉɸɪɢ-ȼɟɣɫɫɚ
F
~ 1 / | T -
4
|. Ɉɛɪɚɳɚɟɦ

ɜɧɢɦɚɧɢɟ ɧɚ ɪɚɡɥɢɱɢɟ ɤɨɷɮɮɢɰɢɟɧɬɨɜ ɩɪɢ ɩɨɞɯɨɞɟ ɫɥɟɜɚ ɢ
ɫɩɪɚɜɚ ɤ ɬɨɱɤɟ ɩɟɪɟɯɨɞɚ (ɫɦ.(2.19)), ɫɜɹɡɚɧɧɨɟ ɫ ɪɚɡɥɢɱɢɟɦ
ɮɚɡɨɜɵɯ ɫɨɫɬɨɹɧɢɣ - ɤɨɧɞɟɧɫɢɪɨɜɚɧɧɨɝɨ ɢ ɧɟɭɩɨɪɹɞɨɱɟɧɧɨɝɨ -
ɢ ɧɚɥɢɱɢɟɦ ɧɟɧɭɥɟɜɨɝɨ ɦɚɝɧɢɬɧɨɝɨ ɦɨɦɟɧɬɚ ɩɪɢ T<
4
, ɧɚɪɭ-
ɲɚɸɳɟɝɨ ɫɢɦɦɟɬɪɢɸ ɫɢɫɬɟɦɵ.
ɉɪɢ ɧɢɡɤɢɯ ɬɟɦɩɟɪɚɬɭɪɚɯ ɦɵ ɬɚɤ ɠɟ, ɤɚɤ ɢ ɜ ɬɟɦɩɟɪɚ-
ɬɭɪɧɨɣ ɡɚɜɢɫɢɦɨɫɬɢ ɬɟɩɥɨɟɦɤɨɫɬɢ, ɧɚɛɥɸɞɚɟɦ ɷɤɫɩɨɧɟɧɰɢ-
ɚɥɶɧɭɸ ɡɚɜɢɫɢɦɨɫɬɶ ɜɨɫɩɪɢɢɦɱɢɜɨɫɬɢ, ɫɜɹɡɚɧɧɭɸ ɫ ɤɨɧɟɱɧɨɣ
ɳɟɥɶɸ ɜ ɫɩɟɤɬɪɟ ɜɨɡɛɭɠɞɟɧɢɣ ɦɨɞɟɥɢ ɂɡɢɧɝɚ.
Ɂɚɞɚɱɢ
2.4.1. Ɋɚɫɫɱɢɬɚɬɶ ɦɚɝɧɢɬɧɭɸ ɜɨɫɩɪɢɢɦɱɢɜɨɫɬɶ ɞɥɹ ɦɨ-
ɞɟɥɢ ɂɡɢɧɝɚ ɜ ɩɪɢɛɥɢɠɟɧɢɢ ɫɪɟɞɧɟɝɨ ɩɨɥɹ. Ɋɚɫɫɦɨɬɪɟɬɶ ɩɪɟ-
ɞɟɥɶɧɵɟ ɫɥɭɱɚɢ T
o
0 ɢ T
o4
, T
o4
2.4.2. ȼɵɪɚɡɢɬɶ ɦɚɝɧɢɬɧɭɸ ɜɨɫɩɪɢɢɦɱɢɜɨɫɬɶ ɱɟɪɟɡ
ɫɪɟɞɧɟɤɜɚɞɪɚɬɢɱɧɭɸ ɮɥɭɤɬɭɚɰɢɸ ɦɚɝɧɢɬɧɨɝɨ ɦɨɦɟɧɬɚ.
Ɉɬɜɟɬ
:
FE
E
!!
!!
o
(/ ) / | / [ ]
/[ ].
1
0
22
2
NM H N M M
NM M
H
dd
2.4.
3. ɇɚɣɬɢ ɮɥɭɤɬɭɚɰɢɸ ɦɚɝɧɢɬɧɨɝɨ ɦɨɦɟɧɬɚ <M
2
> ɜ
ɩɪɢɛɥɢɠɟɧɢɢ ɫɪɟɞɧɟɝɨ ɩɨɥɹ ɜ ɦɨɞɟɥɢ ɂɡɢɧɝɚ ɩɪɢ H
o
0.
Ɉɬɜɟɬ
ɜɵɪɚɡɢɬɶ ɱɟɪɟɡ ɩɚɪɚɦɟɬɪ ɩɨɪɹɞɤɚ R.
Ɉɬɜɟɬ
:
>@
!
MQQH
FH FH
RTRH RT
RT RT R
222
2222
00
2
0
22
0
22 2 2 1
1
11
[/ ] ( )
([]) ()
{}
(){()}
wwE
Ew wE Ew wE
PP P F
PT
dd
(ɫɪɚɜɧɢ ɫ ɨɬɜɟɬɨɦ ɩɪɟɞɵɞɭɳɟɣ ɡɚɞɚɱɢ).
35
2.5.
Ɉɞɧɨɦɟɪɧɚɹ ɦɨɞɟɥɶ ɂɡɢɧɝɚ
.
Ɉɬɫɭɬɫɬɜɢɟ ɮɚɡɨɜɨɝɨ ɩɟɪɟɯɨɞɚ
ȼ ɧɢɡɤɨɪɚɡɦɟɪɧɨɣ ɫɢɬɭɚɰɢɢ ɜ ɩɪɢɛɥɢɠɟɧɢɢ ɛɥɢɠɚɣɲɢɯ
ɫɨɫɟɞɟɣ ɭɞɚɟɬɫɹ ɬɨɱɧɨ (ɛɟɡ ɩɪɢɛɥɢɠɟɧɢɹ ɫɪɟɞɧɟɝɨ ɩɨɥɹ) ɪɚɫ-
ɫɱɢɬɚɬɶ ɫɬɚɬɢɫɬɢɱɟɫɤɢɟ ɫɜɨɣɫɬɜɚ ɦɨɞɟɥɢ ɂɡɢɧɝɚ ɢ ɢɫɫɥɟɞɨɜɚɬɶ
ɩɪɨɛɥɟɦɭ ɮɚɡɨɜɨɝɨ ɩɟɪɟɯɨɞɚ ɜ ɧɟɣ.
ȼ ɷɬɨɦ ɩɚɪɚɝɪɚɮɟ ɦɵ ɩɨɤɚɠɟɦ, ɱɬɨ ɜ ɫɥɭɱɚɟ ɨɞɧɨɦɟɪ-
ɧɨɣ ɫɩɢɧɨɜɨɣ ɰɟɩɨɱɤɢ, ɨɩɢɫɵɜɚɟɦɨɣ ɝɚɦɢɥɶɬɨɧɢɚɧɨɦ ɂɡɢɧɝɚ
ɜ ɩɪɢɛɥɢɠɟɧɢɢ ɛɥɢɠɚɣɲɢɯ ɫɨɫɟɞɟɣ, ɧɟ ɧɚɛɥɸɞɚɟɬɫɹ ɮɚɡɨɜɨɝɨ
ɩɟɪɟɯɨɞɚ.
Ɋɚɫɫɦɨɬɪɢɦ ɰɟɩɨɱɤɭ ɢɡ N ɫɩɢɧɨɜ, ɡɚɦɤɧɭɬɭɸ ɜ ɤɨɥɶɰɨ:
pnppnnnppn.................................... n
1
ɬɚɤ ɱɬɨ
P
N+1
=
P
1
, ɬ.ɟ. ɩɟɪɢɨɞɢɱɟɫɤɢɟ ɭɫɥɨɜɢɹ. ȿɫɥɢ ɭɱɢɬɵɜɚɬɶ
ɜɡɚɢɦɨɞɟɣɫɬɜɢɟ ɬɨɥɶɤɨ ɛɥɢɠɚɣɲɢɯ ɫɨɫɟɞɟɣ, ɬɨ ɝɚɦɢɥɶɬɨɧɢɚɧ
ɫɢɫɬɟɦɵ ɦɨɠɧɨ ɩɪɟɞɫɬɚɜɢɬɶ ɨɞɧɨɤɪɚɬɧɨɣ ɫɭɦɦɨɣ:
HV H
ii
i
i
¦
()
PP P
1
, (2.20)
ɝɞɟ V - ɜɡɚɢɦɨɞɟɣɫɬɜɢɟ ɦɟɠɞɭ i-ɦɢi+1-ɦ ɫɩɢɧɚɦɢ (ɜɡɚɢɦɨ-
ɞɟɣɫɬɜɢɟ ɦɟɠɞɭ ɫɩɢɧɚɦɢ ɩɪɟɞɩɨɥɚɝɚɟɬɫɹ ɨɞɢɧɚɤɨɜɵɦ ɢ ɧɟ
ɡɚɜɢɫɹɳɢɦ ɨɬ ɧɨɦɟɪɚ ɭɡɥɚ, ɬ.ɟ. ɩɨɥɧɚɹ ɬɪɚɧɫɥɹɰɢɨɧɧɚɹ ɢɧɜɚ-
ɪɢɚɧɬɧɨɫɬɶ). ɋɥɚɝɚɟɦɵɯ ɜ ɫɭɦɦɟ ɪɨɜɧɨ N.
Ʌɸɛɭɸ ɢɧɬɟɪɟɫɭɸɳɭɸ ɧɚɫ ɬɟɪɦɨɞɢɧɚɦɢɱɟɫɤɭɸ ɜɟɥɢ-
ɱɢɧɭ ɦɨɠɧɨ ɜɵɪɚɡɢɬɶ ɱɟɪɟɡ ɫɬɚɬɢɫɬɢɱɟɫɤɭɸ ɫɭɦɦɭ
QSp HkT exp[ ] ɢɥɢ ɟɟ ɬɟɪɦɨɞɢɧɚɦɢɱɟɫɤɢɟ ɩɪɨɢɡ-
ɜɨɞɧɵɟ. ɇɚɩɪɢɦɟɪ, ɫɪɟɞɧɢɣ ɦɚɝɧɢɬɧɵɣ ɦɨɦɟɧɬ ɦɨɠɧɨ ɩɪɟɞ-
ɫɬɚɜɢɬɶ ɤɚɤ ɩɪɨɢɡɜɨɞɧɭɸ ɥɨɝɚɪɢɮɦɚ ɫɬɚɬɫɭɦɦɵ ɩɨ ɦɚɝɧɢɬɧɨ-
ɦɭ ɩɨɥɸ:
!
P
PE
E
w
w
11
N
Sp H
QNH
Q
i
exp[ ]
ln
. (2.21)
36
Ɍɚɤɢɦ ɨɛɪɚɡɨɦ ɡɚɞɚɱɚ ɫɜɨɞɢɬɫɹ ɤ ɜɵɱɢɫɥɟɧɢɸ ɫɬɚɬɢɫɬɢɱɟɫɤɨɣ
ɫɭɦɦɵ Q. ɉɪɟɞɫɬɚɜɢɦ ɟɟ ɫɥɟɞɭɸɳɢɦ ɨɛɪɚɡɨɦ, ɢɦɟɹ ɜɜɢɞɭ
ɩɨɥɧɵɣ ɩɟɪɟɛɨɪ ɜɨɡɦɨɠɧɵɯ ɦɝɧɨɜɟɧɧɵɯ ɪɟɚɥɢɡɚɰɢɣ ɪɚɫɩɨɥɨ-
ɠɟɧɢɣ ɫɩɢɧɨɜ ɜ ɰɟɩɨɱɤɟ:
37
H QV
VHV H
N
NN
r r r
¦¦ ¦
PP P
EPP EP
EPP EP EPP EP
12
11 1
12 1
23 2 1
........... exp (
........ ).
(2.22)
ɉɨ ɜɢɞɭ ɝɚɦɢɥɶɬɨɧɢɚɧɚ (2.20) ɹɫɧɨ, ɱɬɨ ɭɞɨɛɧɨ ɩɟɪɟɛɢɪɚɬɶ
ɫɨɫɬɨɹɧɢɹ ɫɢɫɬɟɦɵ ɧɟ ɩɨ ɨɬɞɟɥɶɧɵɦ ɭɡɥɚɦ, ɚ ɩɨ ɩɚɪɚɦ i ɢ i+1.
Ⱦɥɹ ɭɞɨɛɫɬɜɚ ɜɜɟɞɟɦ ɦɚɬɪɢɰɭ 22:
u
^`
PH
jj jj j
()exp
PP EPP E P
11
,
ɢɥɢ ɩɨɤɨɦɩɨɧɟɧɬɧɨ:
P
VH VH
VH VH
jj
()
PP
EE EE
EE EE
§
©
¨
·
¹
¸
1
exp[ ] exp[ ]
exp[ ] exp[ ]
. (2.23)
Ɇɚɬɪɢɰɚ (2.23) ɨɩɢɫɵɜɚɟɬ ɜɫɟ ɜɨɡɦɨɠɧɵɟ ɫɨɫɬɨɹɧɢɹ ɩɚɪɵ ɭɡ-
ɥɨɜ j , j+1. ɍɫɥɨɜɧɨ ɦɨɠɧɨ ɬɚɤɠɟ ɡɚɩɢɫɚɬɶ:
, (2.24)
P
jj
()
PP
nn pn
np pp
§
©
¨
·
¹
¸
1
ɝɞɟ ɹɜɧɨ ɩɨɤɚɡɚɧɵ ɪɚɫɩɨɥɨɠɟɧɢɹ ɫɩɢɧɨɜ ɜ j-ɦɢj+1-ɦ ɫɨɫɬɨɹ-
ɧɢɹɯ.
Ɍɨɝɞɚ ɫɬɚɬɢɫɬɢɱɟɫɤɚɹ ɫɭɦɦɚ ɛɭɞɟɬ ɢɦɟɬɶ ɜɢɞ ɫɭɦɦɵ ɛɨɥɶɲɨɝɨ
ɱɢɫɥɚ ɩɪɨɢɡɜɟɞɟɧɢɣ ɦɚɬɪɢɰ (2.23):
QPP
N
N
r r r
¦¦ ¦
PP P
PP PP P P
12
11
12
1
23 1
........ ( ) ( )...... ( )P
)
)
. (2.25)
ɉɪɢ ɷɬɨɦ ɟɫɥɢ ɭɱɟɫɬɶ, ɱɬɨ
, (2.26)
PP P()()(
PP PP PP
P
12 23
2
13
2
¦
ɢ ɩɪɢɦɟɧɢɬɶ ɷɬɨ ɫɜɨɣɫɬɜɨ ɤɨ ɜɫɟɦ ɦɚɬɪɢɰɚɦ ɜ (2.25), ɬɨ
QP
N
¦
(
PP
P
11
1
, (2.27)
ɬ.ɟ. ɫɬɚɬɢɫɬɢɱɟɫɤɚɹ ɫɭɦɦɚ ɪɚɜɧɚ ɫɭɦɦɟ ɞɢɚɝɨɧɚɥɶɧɵɯ ɷɥɟɦɟɧ-
ɬɨɜ (ɲɩɭɪɭ) N -ɝɨ ɩɪɨɢɡɜɟɞɟɧɢɹ ɦɚɬɪɢɰ P.
Ɍɨ, ɱɬɨ ɧɚ ɝɥɚɜɧɵɯ ɞɢɚɝɨɧɚɥɹɯ ɩɪɢ ɩɟɪɟɦɧɨɠɟɧɢɢ ɦɚɬ-
ɪɢɰ P ɫɨɛɢɪɚɸɫɹ ɜɫɟ ɜɨɡɦɨɠɧɵɟ ɪɟɚɥɢɡɚɰɢɢ ɪɚɫɩɨɥɨɠɟɧɢɣ
ɫɩɢɧɨɜ, ɬ.ɟ. ɫɬɚɬɢɫɬɢɱɟɫɤɚɹ ɫɭɦɦɚ, ɜɢɞɧɨ ɭɠɟ ɩɪɢ ɨɞɧɨɤɪɚɬɧɨɦ
ɭɦɧɨɠɟɧɢɢ. Ɍɚɤ, ɟɫɥɢ ɜɨɫɩɨɥɶɡɨɜɚɬɶɫɹ (2.24), ɢɦɟɟɦ
nn pn
np pp
§
©
¨
·
¹
¸
u
nn pn
np pp
§
©
¨
·
¹
¸
nnnnpnnp nnpnpnpp
npnnppnp nppnpppp
§
©
¨
·
¹
¸
ȼɢɞɧɨ, ɱɬɨ ɧɚ ɝɥɚɜɧɵɯ ɞɢɚɝɨɧɚɥɹɯ ɭɠɟ ɩɟɪɟɛɪɚɧɵ ɜɫɟ ɜɨɡ-
ɦɨɠɧɵɟ ɪɟɚɥɢɡɚɰɢɢ ɞɜɭɯ ɭɡɥɨɜ (ɟɫɥɢ N=2, ɬɨ
P
3
=
P
1
ɢɡ-ɡɚ ɩɟ-
ɪɢɨɞɢɱɟɫɤɢɯ ɝɪɚɧɢɱɧɵɯ ɭɫɥɨɜɢɣ).
ɂɡɜɟɫɬɧɨ, ɱɬɨ ɲɩɭɪ ɦɚɬɪɢɰɵ ɧɟ ɦɟɧɹɟɬɫɹ ɩɪɢ ɟɟ ɩɪɟɨɛ-
ɪɚɡɨɜɚɧɢɢ ɤ ɞɪɭɝɨɦɭ ɩɪɟɞɫɬɚɜɥɟɧɢɸ ɜ ɩɪɨɫɬɪɚɧɫɬɜɟ 2 u 2. ȿɫɥɢ
ɦɚɬɪɢɰɭ P ɩɪɟɞɫɬɚɜɢɬɶ ɜ ɞɢɚɝɨɧɚɥɶɧɨɦ ɜɢɞɟ, ɬɨ
QP
N
k
k
N
¦
()
PP O
P
11
1
2
1
¦
, (2.28)
ɝɞɟ O
k
- ɫɨɛɫɬɜɟɧɧɵɟ ɡɧɚɱɟɧɢɹ ɦɚɬɪɢɰɵ P. Ⱦɢɚɝɨɧɚɥɢɡɭɟɦ ɦɚɬ-
ɪɢɰɭ P. Ⱦɥɹ ɷɬɨɝɨ ɪɟɲɢɦ ɫɟɤɭɥɹɪɧɨɟ ɭɪɚɜɧɟɧɢɟ
ee
ee
EE EE
EE EE
O
O
VH VH
VH VH
0
. (2.29)
Ɉɬɫɸɞɚ
OE E
EE
12
22 2
,
r
ech e sh e
VV
HH
E
V
. (2.30)
Ɂɚɦɟɬɢɦ, ɱɬɨ
O
1
>
O
2
. ɉɨɷɬɨɦɭ ɫɬɚɬɢɫɬɢɱɟɫɤɚɹ ɫɭɦɦɚ ɜ ɩɪɟɞɟɥɟ
ɛɨɥɶɲɢɯ N ɜɵɪɚɠɚɟɬɫɹ ɬɨɥɶɤɨ ɱɟɪɟɡ ɨɞɧɨ ɫɨɛɫɬɜɟɧɧɨɟ ɱɢɫɥɨ
O
1
:
^`
QQ
N
N
N
N
of
OOO O
121 1
1 , ln lnN
O
1
. (2.31)
ɂɡ (2.31), ɢɫɩɨɥɶɡɭɹ ɫɨɨɬɧɨɲɟɧɢɟ (2.21), ɦɨɠɧɨ ɩɨɥɭɱɢɬɶ ɜɵ-
ɪɚɠɟɧɢɟ ɞɥɹ ɫɪɟɞɧɟɣ ɧɚɦɚɝɧɢɱɟɧɧɨɫɬɢ:
38

!
P
E
EE
sh
sh
H
HV
2
4exp[ ]
. (2.32)
ɉɪɨɚɧɚɥɢɡɢɪɭɟɦ ɩɨɥɭɱɟɧɧɨɟ ɬɨɱɧɨɟ ɜɵɪɚɠɟɧɢɟ. ȼɨɬ-
ɫɭɬɫɬɜɢɢ ɜɡɚɢɦɨɞɟɣɫɬɜɢɹ (V=0) ɢɡ (2.32) ɩɨɥɭɱɚɟɦ ɨɛɵɱɧɨɟ
ɜɵɪɚɠɟɧɢɟ ɞɥɹ ɧɚɦɚɝɧɢɱɟɧɧɨɫɬɢ ɫɢɫɬɟɦɵ ɧɟɜɡɚɢɦɨɞɟɣɫɬɜɭɸ-
ɳɢɯ ɫɩɢɧɨɜ (ɫɦ.(1.3)): <
P
> = th
E
H. ɋ ɞɪɭɝɨɣ ɫɬɨɪɨɧɵ, ɜ ɩɪɟ-
ɞɟɥɟ ɫɥɚɛɨɝɨ ɩɨɥɹ H
o
0 ɢɦɟɟɦ:
sh
E
H ~
E
H
o
0, <
P
> =0.
ɇɚɦɚɝɧɢɱɟɧɧɨɫɬɶ ɧɟ ɢɦɟɟɬ ɨɫɨɛɟɧɧɨɫɬɟɣ ɧɢ ɩɨ ɜɡɚɢɦɨɞɟɣɫɬ-
ɜɢɸ, ɧɢ ɩɨ ɩɨɥɸ, ɢɫɱɟɡɚɟɬ ɩɪɢ ɜɵɤɥɸɱɟɧɢɢ ɩɨɥɹ, ɬ.ɟ. ɩɪɨɹɜɥɹ-
ɟɬ ɹɜɧɵɟ ɩɚɪɚɦɚɝɧɢɬɧɵɟ ɫɜɨɣɫɬɜɚ. Ɏɚɡɨɜɨɝɨ ɩɟɪɟɯɨɞɚ ɧɟɬ.
Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɜ ɨɞɧɨɦɟɪɧɨɣ ɰɟɩɨɱɤɟ ɜ ɩɪɢɛɥɢɠɟɧɢɢ
ɛɥɢɠɚɣɲɢɯ ɫɨɫɟɞɟɣ ɮɥɭɤɬɭɚɰɢɢ ɧɚɫɬɨɥɶɤɨ ɫɢɥɶɧɵ, ɱɬɨ ɩɪɟ-
ɩɹɬɫɬɜɭɸɬ ɭɫɬɚɧɨɜɥɟɧɢɸ ɫɩɨɧɬɚɧɧɨɣ ɧɚɦɚɝɧɢɱɟɧɧɨɫɬɢ, ɢɮɚ-
ɡɨɜɵɣ ɩɟɪɟɯɨɞ ɩɚɪɚɦɚɝɧɟɬɢɤ - ɮɟɪɪɨɦɚɝɧɟɬɢɤ ɨɬɫɭɬɫɬɜɭɟɬ.
Ɂɚɞɚɱɢ
2.5.1. ɇɚɣɬɢ ɫɜɨɛɨɞɧɭɸ ɷɧɟɪɝɢɸ ɮɟɪɪɨɦɚɝɧɢɬɧɨɣ ɨɞ-
ɧɨɦɟɪɧɨɣ ɦɨɞɟɥɢ ɂɡɢɧɝɚ ɢɫɯɨɞɹ ɢɡ ɜɵɪɚɠɟɧɢɹ ɞɥɹ ɫɬɚɬɢɫɬɢ-
ɱɟɫɤɨɣ ɫɭɦɦɵ (2.31). Ɋɚɫɫɱɢɬɚɬɶ ɩɪɟɞɟɥɶɧɵɣ ɫɥɭɱɚɣ H
o
0.
Ɉɬɜɟɬ:
FT
TN V H V H V
TN V
H
o
ln
ln[exp( ) exp( )]
ln[ ] .
O
EE E E E
E
1
2
0
22
2
ch exp( )sh
ch
2.5.2. ɇɚɣɬɢ ɫɬɚɬɢɫɬɢɱɟɫɤɭɸ ɫɭɦɦɭ ɢ ɫɜɨɛɨɞɧɭɸ ɷɧɟɪ-
ɝɢɸ ɚɧɬɢɮɟɪɪɨɦɚɝɧɢɬɧɨɣ ɨɞɧɨɦɟɪɧɨɣ ɦɨɞɟɥɢ ɂɡɢɧɝɚ.
Ɋɟɲɟɧɢɟ
. Cɥɟɞɭɟɬ ɩɪɨɫɬɨ ɡɚɦɟɧɢɬɶ V ɧɚ - V ɜ ɪɟɲɟɧɢɢ
ɩɪɟɞɵɞɭɳɟɣ ɡɚɞɚɱɢ.
2.5.3. ɇɚɣɬɢ ɬɟɩɥɨɟɦɤɨɫɬɶ ɩɪɢ ɩɨɥɟ H=0. Ɋɚɫɫɦɨɬɪɟɬɶ
ɫɥɭɱɚɣ V>0 ɢ V<0 (ɮɟɪɪɨɦɚɝɧɟɬɢɤ ɢ ɚɧɬɢɮɟɪɪɨɦɚɝɧɟɬɢɤ).
39
Ɉɬɜɟɬ: ɨɛɚ ɫɥɭɱɚɹ ɫɨɜɩɚɞɚɸɬ:
